第6章 滤波器原理与结构1
现代信号处理--清华胡广书讲义-第6章滤波器组基础
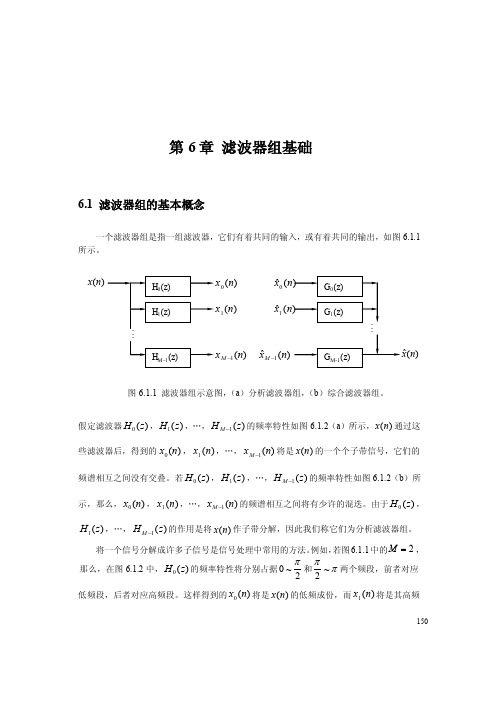
150第6章 滤波器组基础6.1 滤波器组的基本概念一个滤波器组是指一组滤波器,它们有着共同的输入,或有着共同的输出,如图6.1.1所示。
图6.1.1 滤波器组示意图,(a )分析滤波器组,(b )综合滤波器组。
假定滤波器)(0z H ,)(1z H ,…,)(1z H M -的频率特性如图6.1.2(a )所示,)(n x 通过这些滤波器后,得到的)(0n x ,)(1n x ,…,)(1n x M -将是)(n x 的一个个子带信号,它们的频谱相互之间没有交叠。
若)(0z H ,)(1z H ,…,)(1z H M -的频率特性如图6.1.2(b )所示,那么,)(0n x ,)(1n x ,…,)(1n x M -的频谱相互之间将有少许的混迭。
由于)(0z H ,)(1z H ,…,)(1z H M -的作用是将)(n x 作子带分解,因此我们称它们为分析滤波器组。
将一个信号分解成许多子信号是信号处理中常用的方法。
例如,若图6.1.1中的2=M ,那么,在图6.1.2中,)(0z H 的频率特性将分别占据2~0π和ππ~2两个频段,前者对应低频段,后者对应高频段。
这样得到的)(0n x 将是)(n x 的低频成份,而)(1n x 将是其高频)(0n x )(1n x )(1n x M -)(n x(ˆ0x (ˆ1x)(ˆ1n xM -)(ˆn x151成份。
我们可依据实际工作的需要对)(0n x 和)(1n x 作出不同的处理。
例如,若我们希望对)(n x 编码,设)(n x 的抽样频率为20KHz ,若每个数据点用16bit ,那么每秒钟需要的码图6.1.2 分析滤波器组的频率响应,(a )无混迭,(b )稍有混迭流为320Kbit 。
若)(n x 是一低频信号,也即)(n x 的有效成份(或有用成份)大都集中在)(0n x 内,)(1n x 内含有很少的信号能量。
这样,我们可对)(0n x 仍用16bit ,对)(1n x 则用8bit ,甚至是4bit ,由于)(0n x 和)(1n x 的带宽分别比)(n x 减少了一倍,所以,)(0n x 和)(1n x 的抽样频率可降低一倍。
数字滤波器的基本结构

H (z)
A
m1 N1
m1 N2
(1 ck z1) (11k z1 2k z2 )
k 1
k 1
将单实根因子看作二阶因子的特例:
46
M 1 2
(1 1m z1 2m z2 )
H (z) A m1 N 1 2 (1 1k z1 2k z2 ) k 1
:表示取整。
其中
Hi
(z)
1 1i z1 11i z1
2i 2i
z 2 z 2
,
级联结构:
i 0,1,..., m
X(n) H1(Z)
H2(Z)
。。。
Y(n) Hm(Z)
48
H(Z)的实现结构即可表示为基本二阶节 的级联形式。每个二阶节用典范型实现:
Z-1
Z 1 a1
y(n 1)
Z 1
a2
y(n 2)
Z 1 bM
x(n M )
Z 1
aN 1
y(n N 1)
Z 1
aN
y(n N)
实现N阶差分方程的直接I型结构
36
M=N
37
1)可直接差分方程或系统函数的标准形式画 出。两个网络级联:第一个横向结构M节延 时网络实现零点(分子,输入),第二个有 反馈的N节延时网络实现极点(分母,输 出) 。需要N+M级延时单元。
32
◦ 系统函数 ◦ 差分方程
M
bk z k
H(z)
k 0 N
1 ak zk
Y (z) X (z)
k 1
N
M
y(n) ak y(n k) bk x(n k)
通信原理讲义-第六章 数字信号的载波传输1二进制调制

数字信号的调制可以看成特殊调制信号 的模拟调制,类似模拟调制的情况,数 字调制也是用调制信号调制载波的三个 参数:振幅、频率、相位。 相应地称为:幅度键控、频率键控、相 位键控。
6.1 二进制数字调制
二进制数字调制是指调制信号为二进制 基带信号,这种调制信号仅有两种电平, 表示为“1”和“0”: 二进制数字调制又分为: 二进制幅度键控 二进制频率键控 二进制相位键控
数字基 带信号 二进制幅度键控s2ASK(t)
载波Acoswct
二进制幅度键控解调(非相干)
带通 滤波器
1 0.5 0 -0.5 -1 0 1 0.5 0 -0.5 -1 0 1 0.5 0 -0.5 -1 0 100 200 300 400 500 600 100 200 300 400 500 600 100 200 300 400 500 600
1 A1 0 0 0 1 ……
由调频理论,调制后信号的瞬时频率 w(t)=w0+KFMf(t) 而对单极性二元基带信号只有两种电平: f(t)=0或1, 故:w1= w0+KFM w2= w0。
二进制频率键控调制后的时域波形
1
1 0.8 0.6 0.4 0.2 0 -0.2 -0.4 -0.6 -0.8 -1
二进制差分相位键控的调制方法
二元单 极性码 输入 相对码 差分编码 二进制差分相位 键控DPSK输出
Acos(wct)
载波发生器
差分编码原理:
后一位与新生成的前一位码做模2和得到新生成的码
绝对码:1 0 0 1 0 1 1 0 相对码:1 1 1 0 0 1 0 0
二进制差分相位键控的解调(相干)
数字信号处理 第六章

各种数字滤波器的理想幅度频率响应 数字滤波器的设计步骤 理想滤波器的逼近 数字滤波器的系统函数H(z) IIR滤波器设计方法
6.1 引言
数字滤波器的设计步骤:
按任务要求,确定滤波器性能要求。 用一个因果稳定的离散线性移不变的系统函数去逼 近这一性能要求。逼近所用系统函数有无限冲激响 应(IIR)系统函数与有限长单位冲激响应(FIR) 系统函数两种。 利用有限精度算法来实现这个系统函数。 实际的技术实现。
零极点分布对系统相角的影响
相位“延时”(或相位“滞后”)系统
最小相位延时系统 最大相位延时系统 最大相位超前系统 最小相位超前系统
相位“超前”(或相位“领先”)系统
当全部零点在单位圆外时,相位变化最大,又是负数, 当全部零点在单位圆外时,相位变化最小, 当全部零点在单位圆内时,相位变化最大, 当全部零点在单位圆内时,相位变化最小, 故称为最小相位超前系统。 故称为最大相位超前系统。 故称为最大相位延时系统。 故称为最小相位延时系统。
2、可实现Ha(s)Ha(-s)零极点分布
j
σ
1、零极点中一半属Ha(s),另一 半属Ha(-s)。如要求系统稳定, 则左半平面极点属于Ha(s)。 2、挑选零点时,不加任何限制, 则Ha(s)的解不唯一。 3、如限定Ha(s)是最小相位的, 则只能取所有左半平面的零极 点作为Ha(s)的零极点,Ha(s) 的解唯一。 4、虚轴上的零点阶数减半分配给 Ha(s)。 5、稳定系统虚轴上无极点,临界 稳定时虚轴上才会有极点。
第6章 无限冲激响应IIR 数字滤波器的设计方法
刘笑楠
第6章 无限冲激响应IIR 数字滤波器的设计方法
微型计算机控制 第6章 数字滤波技术

6 .1 .7
复合数字滤波
这种滤波方法的原理可由下式表示。 若 X(1)≤X(2)≤…≤X(N), 3≤ N≤14
则
X (2) X (3) X ( N 1) Y (k )
N 2
1 N 1 X (i ) (6-10) N 2 i 2
式(6-10)也称作防脉冲干扰的平均值滤波,它的程序设计方 法读者可根据以前的知识自行设计。 此外,也可采用双重滤波的方法,即把采样值经过低通滤波后, 再经过一次高通滤波,这样,结果更接近理想值,这实际上相 当于多级RC滤波器。
微机控制技术
6.1.8
各种数字滤波性能的比较
以上介绍了七种数字滤波方法,读者可根据需要 设计出更多的数字滤波程序。每种滤波程序都有其各 自的特点,可根据具体的测量参数进行合理的选用。
微机控制技术
6.1.8
各种数字滤波性能的比较
1. 滤波效果 (1)变化比较慢的参数,如温度,用程序判断滤波及 一阶滞后滤波方法。 (2)变化比较快的脉冲参数,如压力、流量等,则可 选择算术平均和加权平均滤波法,特别是加权平均 滤波法更好。 (3)要求比较高的系统,需要用复合滤波法。 (4)在算术平均滤波和加权平均滤波中,其滤波效果 与所选择的采样次数N有关。N越大,则滤波效果越 好,但花费的时间也愈长。 (5)高通及低通滤波程序是比较特殊的滤波程序,使 用时一定要根据其特点选用。
C
i0
n 1
i
1
微机控制技术
6.1.4
加权平均值滤波
式中C0、Cl、…、Cn-1为各次采样值的系数,它体现 了各次采样值在平均值中所占的比例,可根据具体情况 决定。一般采样次数愈靠后,取的比例愈大,这样可增 加新的采样值在平均值中的比例。这种滤波方法可以根 据需要突出信号的某一部分,抑制信号的另一部分。
现代信号处理基础及应用6章-白化滤波器

内积空间:
设有 M 个两两正交的随机矢量 ε1, ε2, , εM ,满足
εi , εj 0, i j
令 Y=ε1, ε2,
εM , 是由这 M 个随机矢量张成的线
性子空间,那么随机矢量就是该内积空间的正交基底。
根据正交分解定理,对于任何随机矢量 x , 相对于线性子空间 Y ,可唯一分解为两个互 相正交的部分,即
D(
z)
可能不是因果的,
D(z) G(z)
就不是因果的;
D(z) (3) G(z) 对应的是一个因果稳定的 IIR 滤波器,而所
设计的 H(z) 是一个 n 阶的 FIR 滤波器。
上述因素都会使滤波器的实际输出 y = g* h 不一定等
于期望输出 d 。
设 d l2 g l2 ,且 g 是因果的。则滤波器实际输出 y 与期望
lim n
δ-
gh
2
1
1 2
例 6.2 假设信道的传递函数为G(z) 1 z2 ,它是非最小相 4
设 x = x1 + x2 ,其中 x1 与 y 相关, x2 与 y 不相关,由 于 Rxy R[ xyT ] E[( x1 x2 ) yT ] Rx1y Rx2 y Rx1y
所以, xˆ Rxy Ry1 y Rx1y Ry1 y xˆ1,因此, xˆ 实际上就 是对 xˆ1的估计,即对 x 中与 y 相关部分的估计。所 以相关抵消器的输出中与 y 相关的部分 x1 得到了 尽可能大的抵消。
Yn ε1, ε2 , , εn y1, y2,
, yn
用符号 yˆn n1 来表示 yn 在子空间Yn1 上的正交投影即
n 1
1
yˆn n1 E yni E ii i
信号处理课件第6章无限冲激响应(IIR)滤波器设计
3. 滤波器的技术要求
低通:
:通带允许的最大衰减; :阻带内应达到的最小衰减
单位 (dB)
若幅度下降到 0.707, 则幅平方下降 0.5 (半 功率点):
若幅度下降到 0.01:
高通:
:通带允许的最大衰减; :阻带内应达到的最小衰减
带通:
:通带允许的最大衰减; : 阻带内应达到的最小衰减
带阻:
最直接到方法,将:
p ,s , p ,s
利用:
利用上一节的方法,可设计出模拟滤波器
G( p), G(s)
H(z)
H (z) G(s) s 1 ln z Ts
但这样做,H (z) 将不再是 z 的有理多项式,给
极-零分析带来困难。
数字滤波器的 单位抽样响应
模拟滤波器 的冲激响应
令:
冲激响应 不变法
(2)
b, a 是AF LP 的分子、分母的系数向量,B, A是转换后 的的分子、分母的系数向量;在(1)中,Wo是低通或 高通滤波器的截止频率;在(2)中,Wo是带通或带阻 滤波器的中心频率,Bw是其带宽。
4.bilinear.m :双线性变换,由模拟滤波器 得到数字滤波器。
[Bz, Az]=bilinear(B, A, Fs) 式中B, A分别是G(s)的分子、分母多项式 的系数向量,Bz, Az分别是H(z)的分子、分 母多项式的系数向量,Fs是抽样频率。
2. 切比雪夫I型(Chebyshev-I)滤波器
3. 切比雪夫II型滤波器
4. 椭圆滤波器
Un2() :Jacobian 函数 本课程只讨论 Butterworth 和 Chebyshev-I
滤波器的设计
二、Butterworth滤波器的设计
数字信号处理第六章
1)幅度函数特点:
H a ( j)
2
1 1 c
2
2N
0
c
H a ( j) 1 H a ( j) 1/ 2 1 3dB 3dB不变性
2
c 通带内有最大平坦的幅度特性,单调减小
c 过渡带及阻带内快速单调减小
3、逼近情况
1)
s平面虚轴
2)
z平面单位圆
s平面
左半平面
z平面 单位圆内 单位圆外 单位圆上
右半平面
虚轴
例7.4
已知模拟滤波器的传输函数为
1 H a ( s) 2 2s 3s 1
采用双线性变换法将其转换为数字滤波 器的系统函数,设T=2s 解 将s代入Ha(s)可得
H ( z ) H a ( s ) s 2 1 z 1 ,T 2
i 1,2,..., m
例6.4.1试分别用脉冲响应不变法和双 线性不变法将图6.4.4所示的RC低通滤波器 转换成数字滤波器。 解 首先按照图6.4.4写出该滤波器的传 输函数Ha(s)为 1
H a ( s)
s
,
RC
利用脉冲响应不变法转换,数字滤波器的系统函 数H1(z)为
低通
0 高通
0 带通 0
带阻
0
全通 0
通带
阻带 过渡带 平滑过渡
三、DF频响的三个参量 1、幅度平方响应
2、相位响应
3、群延迟
它是表示每个频率分量的延迟情况;当其为常 数时, 就是表示每个频率分量的延迟相同。 四、DF设计内容 1、按任务要求确定Filter的性能指标; 2、用因果稳定LSI的系统函数去逼近这一性 能要求; 3、选择适当的运算结构实现这个系统函数; 4、用软件还是用硬件实现。
数字信号处理 第6章
H ( z ) h( n) z n
n 0
N 1
(6.1.2)
(6.1.1)式中的H(z)称为N阶IIR数字滤波器系统函数; (6.1.2) 式中的H(z)称为N-1阶FIR数字滤波器系统函数。这两种 数字滤波器的设计方法有很大区别,因此下面分成两章分 别进行学习。
第6章 无限脉冲响应数字滤波器的设计
s 20 lg
| H (e j0 ) |
j s
dB
(6.1.4b)
p 20 lg | H (e
j p
) | dB
(6.1.5)
s 20 lg | H (e js ) | dB
(6.1.6)
第6章 无限脉冲响应数字滤波器的设计
当幅度下降到 2 / 2 时,标记ω=ωc,此时 p 3dB,称 ωc为3 dB通带截止频率。ωp、ωc和ωs统称为边界频率, 它们是滤波器设计中所涉及到的很重要的参数。对其他 类型的滤波器,(6.1.3b)式和(6.1.4b)式中的H(ej0)应改 成
拟滤波器得到系统函数Ha (s),然后将Ha(s)按某种方法转
换成数字滤波器的系统函数H(z)。这是因为模拟滤波器的 设计方法已经很成熟,不仅有完整的设计公式,还有完善
的图表和曲线供查阅; 另外,还有一些典型的优良滤波
器类型可供我们使用。直接法直接在频域或者时域中设计 数字滤波器,由于要解联立方程,设计时需要计算机辅助 设计。FIR滤波器不能采用间接法,常用的设计方法有窗 函数法、频率采样法和切比雪夫等波纹逼近法。
第6章 无限脉冲响应数字滤波器的设计
图6.1.3所示的单调下降幅频特性,p和s别可以表
示为
p 20 lg
| H (e j0 ) | | H (e
布通滤波器工作原理
布通滤波器工作原理
布通滤波器的工作原理主要是通过电感和电容组成的低通滤波电路来实现的。
这种滤波器允许有用信号的电流通过,同时对频率较高的干扰信号有较大的衰减作用。
布通滤波器的基本原理有三种:
1. 利用电容通高频隔低频的特性,将火线、零线高频干扰电流导入地线(共模),或将火线高频干扰电流导入零线(差模)。
2. 利用电感线圈的阻抗特性,将高频干扰电流反射回干扰源。
3. 利用干扰抑制铁氧体可将一定频段的干扰信号吸收转化为热量的特性,针对某干扰信号的频段选择合适的干扰抑制铁氧体磁环、磁珠直接套在需要滤波的电缆上即可。
布通滤波器的作用是消除某些特定频率的信号,因此其幅频特性(也就是信号通过滤波器后的频率分布)至关重要。
此外,还有高通滤波器和带通滤波器,分别使信号中高于某个特定频率或某个特定频带的信号成分通过,而极大地衰减其他频率或频带的成分。
以上内容仅供参考,如需更多信息,建议查阅电子技术相关专业书籍或咨询电子技术专业人士。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一、巴特沃斯低通滤波器设计方法
巴特沃斯低通滤波器 的幅度平方函数 2
H ( j )
1
2N
1 c
(6-8)
N称为滤波器的阶数,零频率的时候,幅频特性等 于1,截止频率的时候,幅频特性等于0.707,大 于截止频率,幅度迅速下降,下降的速度与阶数N 有关,N愈大,幅度下降的速度愈快,过渡带愈窄。 幅频特性和N的关系如图所示。 H ( j )
2
p , | H a ( j ) | 1 / 1 2
22 1/ 1 1 / 1 通带内:在 1 和 间等波纹起 p p 伏 p p 通带外:迅速单调下降趋向0
3)Chebyshev低通滤波器的三个参量:
p :通带截止频率,给定 :表征通带内波纹波动大小,通带波纹表示 A2 ( ) max 10lg 2 A ( ) min
Butterworth Filter N=2 N=4 N = 10
1
(3)幅频特性的陡峭程度 由阶数N决定。 (4)幅频特性单调下降。
Magnitude
0.8 0.6 0.4 0.2 0 0 1 2
幅频响应
3
N阶巴特沃斯低通滤波器没有零点,是 一个全极点滤波器。可以证明,H(s)H(-s)的 2N个极点为
H( z )
N 1 n 0
h( n )z n
(6-2)
三、数字滤波器技术要求
常用的数字滤波器一般属于选频滤波器。数字滤波 器的传递函数 H (e j )用下式表示
H (e ) | H (e ) | e
幅频特性, 反映各频率 的衰减情况
j
j
jQ( )
相频特性,反映各频 率成分通过滤波器之 后在时间轴上的延时 情况
sk 1 c e
1 2N
jc
1 2 k 1 j 2 2N
k 1,2,...,2 N
N阶巴特沃斯低通滤波器的H(s)H(-s)的 2N个极点的分布特点: (1)2N个极点在s平面呈象限对称分布,均 匀分布在Buttterworth圆上。 (2)极点间的角度间隔为 (rad ) 。 N (3)极点不在虚轴上。 (4)当N为奇数时,实轴上有极点。 (5)当N为偶数时,实轴上无极点。
滤波器可以用描述线性时不变系统的输入输出关 系的数学函数来表示,如图6-1所示。
x(n) h(n) 线性时不变 y(n)
图6-1
滤波器的时域输入输出关系
一、滤波器基本概念
在时域中输入输出关系用公式表示为
y( n ) x( n )* h( n )
若x(n),y(n)的傅里叶变换存在,则输入输出的 频域关系为:
相同的幅频特性,相频特性不同,相同的输入其输出波形也不同。
选频滤波器的技术要求一般由幅频特性给出,相频特性一般不作 要求,但如果对输出波形有要求,则需要考虑相频特性的技术 指标,例如在语音合成、波形传输、图像信号处理等应用场合。 如果对输出波形有严格要求,则需要设计线性相位数字滤波器。
三、数字滤波器技术要求
一、巴特沃斯低通滤波器设计方法
3)将 H a p 去归一化。将 p s c 代入H a p ,得 到实际的滤波器传递函数 H s 。其中3dB截止频 率 c,如果技术指标没有给出,可以按照式(619)或式(6-20)求出。
一、巴特沃斯低通滤波器设计方法
图6-7 例6-1幅频特性曲线
A ( ) max 1. A ( ) min
2 2
1 1 2
10lg(1 )
2
10
2
0.1
1
由通带衰减决定
滤波器阶数N的确定
设阻带的起始点频率(阻带截止频率)用 s 表示,在 s 处的 A2 (s ) 为 :
二、滤波器分类
从实现的网络结构或者从单位冲激响应分类:数字 滤波器可以分成无限脉冲响应(IIR)滤波器和有 限脉冲响应(FIR)滤波器。这两种都是典型线性 时不变离散系统,其系统函数分别为
H( z ) r 0 1
br z
N k 1
M
r
N阶滤波器
akz
k
(6-1)
N-1阶滤波器
设计滤波器:一般有设计指标,求出模平方函数,再求出系统 函数。模平方函数在模拟滤波器的设计中起着重要的作用。不 同的模拟滤波器,其幅度模平方函数有不同的表达式。 但系统函数必须是稳定的,极点落在S平面的左半平面。
主要内容
一
巴特沃斯低通滤波器设计方法
二
切比雪夫滤波器的设计方法
三
模拟滤波器的频率变换-模拟高通、带通 、带阻滤波器的设计
1
x
C5 ( x)
1
图 6-9
N=0,4,5切比雪夫多项式曲线
二、切比雪夫滤波器的设计方法
A2 ( )
N=4 巴特沃斯
1.0 1 1 2 0.50
N=4 切比雪夫
O
p
c
图 6-10
2 切比雪夫Ⅰ型与巴特沃斯低通的 A ( ) 曲线
2) Chebyshev低通滤波器幅度平方函数特点:
2 O
p c
s
图6-4
低通滤波器的技术要求
第二节 常用模拟滤波器的设计
模拟滤波器的理论和设计方法相当成熟,典型的 模拟器滤波器有巴特沃斯、切比雪夫、椭圆、贝 塞尔滤波器等。各种滤波器各有特点,如单调下 降、通带或者阻带内波动、线性相位特性等。 模拟滤波器按幅频特性可分为低通、高通、带通 和带阻滤波器。设计滤波器时,总是先设计低通 滤波器,再通过频带变换将低通滤波器转换成希 望类型的滤波器。下面先介绍模拟低通滤波器的 设计方法,然后再介绍模拟高通、带通、带阻滤 波器的设计方法。
H (e j)
1-1 0.707 1
理想滤波器是不可实现的,实际使用时,用一个 因果可实现的滤波器去逼近,但实用中的通带和 阻带中允许有一定的误差容限,通带不是完全水 平,阻带不一定衰减到零,通带和阻带之间还有 过渡带。
通带和阻带截止频率,通带内的最大衰减、阻带 内的最小衰减,3分贝通带截止频率。
H a ( j )
H a ( j )
1 C 2 2 p 1 CN ( )
2 2 N
1
1
H a ( j )
N为奇数
1
1 1 2
0
N为奇数 N为偶数
p
| H a ( j 0) | 1
O
p
s
| H a ( j 0) | 1 / 1
二、切比雪夫滤波器的设计方法
1)Chebyshev低通滤波器的幅度平方函数
A2 ( ) H a ( j )
2
1 1 C p
2 2 N
为小于1的正数,表示通带内波动的幅度,值越大,波动幅度也越大,
H a ( j )
N为奇数
H a ( j )
从功能上分类:滤波器可以分为低通、高通、带通和带阻滤 波器。它们的理想幅频特性如图6-3所示。
H a ( j )
H a ( j )
H a ( j ) 带通
H a ( j )
低通
0
高通
带阻
0
0
0
图6-3
各种理想滤波器的幅频特性
上述滤波器是理想的,实际是不可实现的,原因是其单位冲激响 应是非因果且无限长,实际滤波器只能按照某些设计准则,使特 性尽可能地去逼近。还有数字滤波器是以2PI为周期的,因此低 频位于2PI的整数倍处,高频位于PI的奇数倍处。
低通巴特沃斯滤波器的设计步骤如下 s 和 s ,用式(6-18) p 、 1)据技术指标 p 、 求出滤波器的阶数N。 2)按照式(6-14),求出归一化极点 pk,pk 将代 入式(6-13),得到归一化传递函数 H a p 。也 可以根据阶数N,直接查表6-1,得到极点 pk 和归 一化传递函数 H a p 。
能迭代下一个
二、切比雪夫滤波器的设计方法
高阶切比雪夫多项式的递推公式为
CN 1 x 2xCN x CN 1 x
C N ( x)
C5 ( x)
(6-23)
C4 ( x)
C4 ( x) C0 ( x)
1
1
O
N的影响: N越大阻带衰减越快;阶数 N影响过渡带的带宽,同 时也影响通带内波动的疏 密,因为N等于通带内最 大值与最小值的总个数.
Y( e j ) X( e j )H( e j )
不同的
H (e jw ) 就可以得到不同的滤波效果。
二、滤波器分类
根据滤波器所处理的信号不同:分为模拟滤波器和 数字滤波器两种形式。模拟滤波器输入输出信号 为模拟信号,数字滤波器输入输出信号为数字信 号。 数字滤波器具有精度高、稳定、体积小、重量轻、 灵活、不要求阻抗匹配以及可以实现模拟滤波器 无法实现的特殊滤波功能。如果是处理的模拟信 号,可以利用A/D、D/A转换,使用数字滤波器对 模拟信号进行滤波。
模拟滤波器的设计指标有: p , p , s , s 分别称为通带最大 衰减系数,通带截止频率,阻带最小衰减系数和阻带截止频率, 衰减系数一般用dB表示。
一般滤波器的单位冲激响应为实数,
* | Ha ( j) |2 Ha (s)Ha (s) |s j Ha ( j)Ha ( j)
第六章 滤波器原理与结构
6.1 滤波器的原理及分类 6.2 常用模拟滤波器的设计 6.3 数字滤波器的基本网络结构及其信号流图
内容提要
离散傅立叶变换和数字滤波器是数字信号处理的 两大基本内容。 数字滤波器属于线性时不变离散时间系统的范畴。 它具有稳定性好、精度高、灵活性大等突出优点。 本章主要介绍滤波器的原理及分类、常用模拟滤 波器的设计方法及数字滤波器的基本结构
