2019贵州省普通高中会考数学试题

合集下载

2019贵州省普通高中会考数学试题

10520佃年贵州省普通高中会考数学试题填空题：本大题共35个小题，每小题共60分，把答案填在题中的横线上。

.3A. {1，2, 4, 5, 7}B. {3，4, 5} C ∙{5}D. {2，5}3.函数f 0∂ =石二 1的定义域是()A. ⅛∣-≥i}B.C.嗚CXD.阖以壬4直线y = 3x 6在y 轴上的截距为() A. -6 B. -3 C. 3 D. 62 2X_ 一匕=15双曲线42 32 的离心率为B. 2C.D. 22.设集合A={1，2,5，7}，B={2，4，5},则 AUB =1. Sin 150；的值为9. 若a0D. ∣a ∣>∣b ∣ 11已知数列 2n}满足a 1 =1,a n 卑=3a n +1,贝U a 3 = A. 4 B. 7 C. 10 D. 13f （X ） = kx 1为R 上的增函数，则实数 k 的值为（） A. （-： , 2） B.（- 2, ：） C. （-： , 0） D. （0,二） 14.已知y =f （χ）是定义在R 上的奇函数，［「釘-kiflF =（ A. 2 B. 1 C. 0 D. -115.已知 ABC 中，且 A = 60° , B = 30° ,b =1,则 a = ()16.不等式（x-3）（x P 0的解集是（）12.抛物线 2y =4X 的准线方程为A. x=4B. x=1C. x=-1D. x=213.若函数 A. 1B. -2C. 3D. 6A. {x -5 X 3}B.{xx -5,或 X 3}C.{x-3c X v5}D.{xx -3,或 X 5}19•甲、乙两名同学五场篮球比赛得分情况的茎叶图如图所示，记甲、乙两名同学得分的众数分别为 m,n,则m 与n 的关系是（）121.〉=30 ° 是 Sin （：•） = i 的什么条件（）A. e-3,1)B.(1,∖3)C.(¥「3) D .存,甞)33 223. 某地区有高中生 1000名，初中生 6000人，小学生13000人, 为了解该地区学生的近视情况，从中抽取一个容量为 200的样本,用下列哪种方法最合适（）A.系统抽样B.抽签法C.分层抽样D.随机数法24. 图是某校100名学生数学竞赛成绩的频率分布直方图，则a 值为A. 0.025B. 0.03C. 0.035D. 0.32 225、圆X y =1的圆心到直线x-y+2=0的距离为（）甲乙2 072 7 7 6 2 2 30 4A. m=nB. m<nC. m>nD.不确定20.在等比数列｛a n ｝中，a 1 =1,a 4 =27,则公比 q =( A. -- B. -3 C. 3 3 D.A.充分必要B.充分不必要C.必要不充分D.既不充分也不必要22. 直线l 的倾斜角,则其斜率的取值范围为）01)4α (In 2 0.01°50 60 70 SO 如A .1 B. 2C. 3D. 226. 根据如图所示的程序框图，若输入m的值是8,则输出的T值是（）A.3B. 1C.0D.227. 经过点（3,0）且与直线y - -2x • 5平行的的直线方程为（）28. 若A,B 互为对立事件，则（）33. 从0, 1, 2, 3, 4中任取3个数字组成没有重复数字的三位数，共有个数是（）A. 10B. 20C. 30D. 602 234. 已知圆C:X y ^2x 4y ^0关于直线l:3ax Jby+0对称，则由点M^b ）向圆C 所作的切线中，切线长的最小值是（）A. 2B. 5C. 3D. 13A. y 2x - 6 二 0B. X - 2y - 3 = 0C. X - 2y 3 二 0D. 2x y - 7 二 0A.P(A)+P(B)<1B. P(A)+P(B)>1C. P(A)+P(B)=1D. P(A)+P(B)=029.—个几何体的三视图如图所示，贝S 该几何体的体积为（A. 27B. 9C. 21D. 292 2 2 230.已知 X 0, y 0,若Xy 二3,则X y 的最小值为（） A. 3B.2C. 2 3D.131.已知 x, y 满足B. 2 32.棱长为 A. 3Λ>0 j>0 .V +j<2C. 3 约束条件则Z = X 2y 的最大值为D. 42的正方体.汀匸亠上E ；：的内切球的表面积为（） B. 4 C. 37D. 4 二值范围是（）A. J ： , - 2B. — - , -1C. I.- 2, -11 D .〔- 2,亠」二、填空题：本大题共5个小题，每小题共15分，把答案填在题中的横线上。

2019-2020学年贵州省高二12月普通高中学业水平考试数学试题(解析版)

2019-2020学年贵州省高二12月普通高中学业水平考试数学试题一、单选题1．已知{1,1},{0,1}A B =-=，则A ∩B=（） A ．{1} B ．{0}C ．{}1-D ．{}0,1【答案】A【解析】根据集合的交集的概念及运算，可得A B ，得到答案.【详解】由题意，集合{1,1},{0,1}A B =-=，根据集合的交集的概念及运算，可得{1}A B ⋂=. 故选：A. 【点睛】本题主要考查了集合表示，以及集合的交集的概念及运算，其中熟记集合交集的概念及运算是解答的关键，属于容易题.2．在等差数列{}n a 中，12a =，公差1d =，则3a =（） A ．6 B ．5C ．4D ．3【答案】C【解析】根据等差数列的通项公式可得答案. 【详解】3122214a a d =+=+⨯=.故选：C. 【点睛】本题考查了等差数列的通项公式的应用，属于基础题. 3．已知向量(1,1),(2,2)a b ==，则a b +=（） A ．(0,0) B ．(3,3)C ．(4,4)D ．(5,5)【答案】B【解析】利用向量加法坐标运算公式直接计算即可.解：根据向量加法坐标运算公式得:()()()1,12,23,3a b +=+=. 故选：B. 【点睛】本题考查了向量加法的坐标运算，属于基础题.4．某班有男生20人，女生25人，用分层抽样的方法从该班抽取9人参加志愿者活动，则应抽取的女生人数为（） A ．2 B ．3C ．4D ．5【答案】D【解析】先求出女生所占的比例，再求出应抽取的女生人数得解. 【详解】由题得女生所占的比例为25255==20+25459，所以用分层抽样的方法从该班抽取9人参加志愿者活动，则应抽取的女生人数为59=59⨯.故选：D. 【点睛】本题主要考查分层抽样的应用，意在考查学生对该知识的理解掌握水平. 5．如图所示茎叶图的数据中，众数是（）A ．18B ．23C ．25D ．31【答案】C【解析】根据茎叶图得到10个数据，再根据众数的概念可得答案. 【详解】根据茎叶图可得10个数据为：15，18，23，23，25，25，25，31，34，36. 因为数据25的个数最多，所以根据众数的概念可知，众数为25.本题考查了由茎叶图求众数，考查了众数的概念，属于基础题. 6．函数1()2f x x =-的定义域是（） A ．{|2}x x C ．RD ．{|2}x x ≠【答案】D【解析】由20x -≠，即可得出定义域. 【详解】20x -≠ 2x ∴≠即函数1()2f x x =-的定义域为{|2}x x ≠ 故选：D 【点睛】本题主要考查了求具体函数的定义域，属于基础题. 7．已知等比数列{}n a 的前n 项和为n S ，11a =，公比2q ，则2S =（）A ．3B ．4C ．5D ．6【答案】A【解析】由题意12112S a a a a q =+=+，即求2S . 【详解】{}n a 是等比数列，11a =，公比2q，122111123S a a a a q =+=+=+⨯=∴.故选：A . 【点睛】本题考查等比数列求和，属于基础题.8．如图，将一个圆八等分，在圆内任取一点P ，则点P 取自阴影部分的概率为（）5311【解析】根据几何概型概率公式求解，测度为面积. 【详解】设圆面积为1，则阴影部分的面积为38所以在圆内任取一点P ，点P 取自阴影部分的概率为33818=故选：B 【点睛】本题考查几何概型概率，考查基本分析求解能力，属基础题. 9．若向量(1,2),(2,)a b x ==，若//a b ，则x =（） A ．4 B ．2C ．1D ．-1【答案】A【解析】根据平面向量的共线条件，列出方程，即可求解. 【详解】由题意，向量(1,2),(2,)a b x ==，因为//a b ，可得1220x ⨯-⨯=，解得4x =. 故选：A. 【点睛】本题主要考查了向量的坐标表示，以及平面向量的共线条件的坐标表示，着重考查运算与求解能力，属于基础题. 10．tan 45的值是（）A ．2B CD ．1【答案】D【解析】由tan 451=，即可得出答案. 【详解】tan 451=故选：D 【点睛】本题主要考查了求特殊角的三角函数值，属于基础题.11．执行如图所示的程序框图，若输入的12r πθ==，，则输出l 的值为（）A ．2πB ．πC ．32π D ．2π【答案】A【解析】直接按照流程图计算可得答案. 【详解】因为1r =，2πθ=，则122l r ππθ==⨯=.故选：A. 【点睛】本题考查了程序框图，属于基础题.12．下列函数中，在(0,)+∞上为减函数的是（） A ．()ln f x x = B ．1()f x x=C ．()2x f x =D ．()1f x x =+【答案】B【解析】根据基本初等函数的性质，逐项判定，即可求解. 【详解】由对数函数的性质，可得函数()ln f x x =在(0,)+∞为单调递增函数，不符合题意；由幂函数的性质，可得函数1()f x x=在(0,)+∞为单调递减函数，符合题意；由指数函数的性质，可得函数()2x f x =在(0,)+∞为单调递增函数，不符合题意；由一次函数的性质，可得函数()1f x x =+在(0,)+∞为单调递增函数，不符合题意。

2019贵州省普通高中会考数学试题

2019贵州省普通高中会考数学试题2019年贵州省普通高中会考数学试题二、填空题：本大题共35个小题，每小题1分，共35分，把答案填在题中的横线上。

1.sin150的值为（）A。

-1/2 B。

1/2 C。

-√3/2 D。

√3/22.设集合A={1，2，5，7}，B={2，4，5}，则AB=（）A。

{1，2,4，5，7} B。

{3，4，5} C。

{5} D。

{2，5}3.函数的定义域是（）A。

R B。

R-{0} C。

R+ D。

R-4.直线y=3x+6在y轴上的截距为（）A。

-6 B。

-3 C。

3 D。

65.双曲线42-32=1的离心率为（）A。

2 B。

4 C。

3 D。

56.已知平面向量a=(1,3),b=(x,6),且a//b，则x=（）A。

-3 B。

-2 C。

3 D。

27.函数y=sin(2x+1)的最小正周期是（）A。

π B。

2π C。

3π D。

4π8.函数f(x)=x-1的零点是（）A。

-2 B。

1 C。

2 D。

39.若a<b<0，则下列不等式成立的是（）A。

a0 D。

|a|>|b|11.已知数列{an}满足an+1=3an+1，a1=1，则a3=（）A。

4 B。

7 C。

10 D。

1312.抛物线y2=4x的准线方程为（）A。

x=4 B。

x=1 C。

x=-1 D。

x=213.若函数f(x)=kx+1为R上的增函数，则实数k的值为（）A。

(-∞,2) B。

(-2,+∞) C。

(-∞,) D。

(。

+∞)14.已知y=f(x)是定义在R上的奇函数，f(0)=2，则f(-2)=（）A。

2 B。

1 C。

0 D。

-115.已知△ABC中，∠A=60°。

∠B=30°。

b=1，则a=（）A。

1 B。

2 C。

3 D。

616.不等式(x-3)(x+5)>0的解集是（）A。

{x|x-53} C。

{x|35}17.已知在幂函数y=f(x)的图像过点(2,8)，则这个函数的表达式为（）A。

贵州省普通高中会考数学试题(优质教学)

2019年贵州省普通高中会考数学试题二、填空题：本大题共35个小题，每小题105分，共60分，把答案填在题中的横线上。

1.sin150的值为（）A .3-B.3C.12-D.122. 设集合A={1，2，5，7}，B={2，4，5}，则A B=（）A. {1，2, 4，5，7}B. {3，4，5}C .{5} D. {2，5}3. 函数的定义域是（）A. B. C. D.4.直线y = 3x + 6 在y 轴上的截距为（）A. -6B. -3C. 3D. 65.双曲线2222143x y-=的离心率为（）A. 2B. 54 C.53 D.346.已知平面向量xbaxba则,//且),6,(),3,1(=== （）A. -3B. -2C. 3D. 27.函数y=sin(2x+1)的最小正周期是（）A. πB. 2πC. 3πD. 4π8. 函数f (x) = x -1的零点是（）得分评卷人A. -2B. 1C. 2D. 39. 若a0D. |a|>|b|11.已知数列=+==+311,13,1}{a a a a a n n n 则满足（）A. 4B. 7C. 10D. 1312.抛物线24y x =的准线方程为（）A. x=4B. x=1C. x=-1D. x=213.若函数 f (x) = kx +1为R 上的增函数，则实数 k 的值为（）A.（-∞，2）B.（- 2，+ ∞）C.（-∞，0）D. （0，+ ∞）14.已知)(x f y =是定义在R 上的奇函数，=（） A. 2 B. 1 C. 0 D. -115.已知 ∆ABC 中，且 A = 60° , B = 30°,b =1,则a = （）A. 1B. 2C. 3D. 616.不等式0)5)(3(>+-x x 的解集是（）A. }35{<<-x xB.}3,5{>-<x x x 或C. }53{<<-x xD.}5,3{>-<x x x 或17.已知在幂函数)(x f y =的图像过点(2,8)，则这个函数的表达（）A. 3x y =B. 2-=x yC. 2x y =D.3x y -=18.为了得到函数的图像可由函数R x x y ∈=,sin 图像（）A. 向左平移4π个单位长度B. 向右平移4π个单位长度C. 向左平移41个单位长度D. 向右平移41个单位长度19.甲、乙两名同学五场篮球比赛得分情况的茎叶图如图所示，记甲、乙两名同学得分的众数分别为 m,n,则 m 与 n 的关系是（）A. m=nB. m<nC. m>nD. 不确定20.在等比数列===q a a a n 则公比中，,27,1}{41（）A. 31-B. -3C. 3D. 3121.30=α°是sin(α) =21的什么条件（） A. 充分必要 B. 充分不必要 C. 必要不充分 D. 既不充分也不必要 22. 直线l 的倾斜角)3,4(ππα∈,则其斜率的取值范围为（） A. )1,33( B.)3,1( C.)3,22( D.)22,33( 23.某地区有高中生 1000 名，初中生 6000 人，小学生13000 人，为了解该地区学生的近视情况，从中抽取一个容量为 200 的样本，用下列哪种方法最合适（）A. 系统抽样B. 抽签法C. 分层抽样D. 随机数法24.图是某校 100 名学生数学竞赛成绩的频率分布直方图，则 a 值为A. 0.025B. 0.03C. 0.035D. 0.325、圆221x y +=的圆心到直线x-y+2=0的距离为（）A .1 B. 2 C. 3 D. 226.根据如图所示的程序框图，若输入 m 的值是 8，则输出的 T 值是（）A.3B. 1C.0D.227.经过点（3,0）且与直线 y = -2x + 5 平行的的直线方程为（）A. y + 2x - 6 = 0B. x - 2y - 3 = 0C. x - 2y + 3 = 0D. 2x + y - 7 = 028.若A,B 互为对立事件，则（）A.P(A)+P(B)<1B. P(A)+P(B)>1C. P(A)+P(B)=1D. P(A)+P(B)=029.一个几何体的三视图如图所示，则该几何体的体积为（）A. 227B. 29C. 221D. 229 30.已知 x > 0, y > 0,若 xy = 3,则x + y 的最小值为（）A. 3B.2C. 23D.131.已知 x, y 满足约束条件则 z = x + 2y 的最大值为（）.A. 0 B. 2 C. 3 D. 432.棱长为2 的正方体的内切球的表面积为（）A. 3B. 4C. 3πD. 4π33.从0，1，2，3，4中任取3个数字组成没有重复数字的三位数，共有个数是（）A. 10B. 20C. 30D. 6034.已知圆0142:22=++-+y x y x C 关于直线0423:=++by ax l 对称，则由点),(b a M 向圆C 所作的切线中，切线长的最小值是（）A. 2B. 5C. 3D.1335.若函数在 R 上是减函数，则实数 a 取值范围是（）A. (-∞，- 2]B. (-∞，-1]C. [- 2，-1] D .[- 2，+ ∞)二、填空题：本大题共5个小题，每小题3分，共15分，把答案填在题中的横线上。

贵州高中会考试题后附答案(数学)

贵州省普通高中会考数学试题1、sin150 的值为（）（A ）32-（B ）32（C ）12-（D ）122、设集合A={1，2，3，5，7}，B={3，4，5}，则A B =（）（A ）{1，2，3，4，5，7}（B ）{3，4，5}（C ）{5}（D ）{1，2}3、不等式|x|<1的解集是（）（A ）{x|x>1}（B ）{x|x<-1}（C ）{x|-1<x<1}（D ）{x|x<-1或x>1}4、双曲线2222143x y -=的离心率为（）（A ）2（B ）54（C ）53（D ）345、已知向量a=(2,3),b=(3,-2)则a·b=（）（A ）2（B ）-2（C ）1（D ）06、函数y=sin2x 的最小正周期是（）（A ）π（B ）2π（C ）3π（D ）4π7、若a<b<0，则下列不等式成立的是（）（A ）22a b <（B ）22a b ≤（C ）a-b>0（D ）|a|>|b|8、已知点A （2，3），B （3，5），则直线AB 的斜率为（）（A ）2（B ）-2（C ）1（D ）-19、抛物线24y x =的准线方程为（）（A ）x=4（B ）x=1（C ）x=-1（D ）x=210、体积为43π的球的半径为（）（A ）1（B ）2（C ）3（D ）411、从1，2，3，4，5中任取3个数字组成没有重复数字的三位数，共有个数是（）（A ）10（B ）20（C ）30（D ）6012、圆221x y +=的圆心到直线x-y+2=0的距离为（）（A ）1（B）（C）（D ）2二、填空题：本大题共4个小题，每小题3分，共12分，把答案填在题中的横线上。

13、已知函数3()log f x a x =+的图象过点A （1，1），则a=_________14、在ABC 中，BC=2，CA=1，30B ∠= ，则A ∠=___________15、棱长为2的正方体的对角线长为__________16、()72x +的展开式中含5x 项的系数为_________三、解答题：本大题共6个小题，共52分，解答题应写出文字说明、说明过程或推演步骤。

2019年七月贵州省普通高中毕业会考

2019年七月贵州省普通高中毕业会考数学试卷注意事项：1、全卷共三大题，计100分，考试时间120分钟；2、用签字笔或钢笔直接答在试卷中；一、选择题：本大题共12个小题，每小题3分，共36分，每小题给出的四个选项中，只有一项符合题目的要求，把所选项前的字母填在题后括号内。

1、sin150的值为（）（A ） 2-（B ） 2 （C ） 12- （D ） 122、设集合A={1，2，3，5，7}，B={3，4，5}，则A B =（）（A ） {1，2，3，4，5，7} （B ） {3，4，5} （C ）{5} （D ） {1，2}3、不等式|x|<1的解集是（）（A ） {x|x>1} （B ） {x|x<-1} （C ） {x|-1<x<1} （D ） {x|x<-1或x>1}4、双曲线2222143x y -=的离心率为（）（A ） 2 （B ）54 （C ） 53 （D ） 345、已知向量a=(2,3),b=(3,-2)则a ·b= （）（A ） 2 （B ） -2 （C ） 1 （D ） 06、函数y=sin2x 的最小正周期是（）（A ） π （B ） 2π （C ） 3π （D ） 4π7、若a<b<0，则下列不等式成立的是（）（A ） 22a b < （B ） 22a b ≤ （C ） a-b>0 （D ） |a|>|b|8、已知点A （2，3），B （3，5），则直线AB 的斜率为（）（A ） 2 （ B ） -2 （C ） 1 （ D ） -19、抛物线24y x =的准线方程为（）（A ） x=4 （ B ） x=1 （C ） x=-1 （D ） x=210、体积为43π的球的半径为（）（A ） 1 （ B ） 2 （ C ） 3 （ D ） 411、从1，2，3，4，5中任取3个数字组成没有重复数字的三位数，共有个数是（）（A ） 10 （ B ） 20 （ C ） 30 （D ） 6012、圆221x y +=的圆心到直线x-y+2=0的距离为（）（A ）1 （B ）（C ）（ D ） 2 二、填空题：本大题共4个小题，每小题3分，共12分，把答案填在题中的横线上。

2019年贵州省贵阳市中考(学业)数学真题

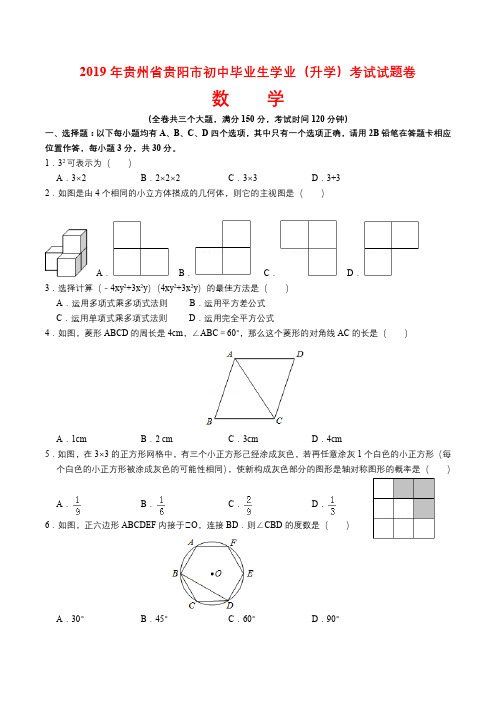
2019年贵州省贵阳市初中毕业生学业（升学）考试试题卷数学（全卷共三个大题，满分150分，考试时间120分钟）一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B铅笔在答题卡相应位置作答，每小题3分，共30分。

1．32可表示为（）A．3×2B．2×2×2C．3×3D．3+32．如图是由4个相同的小立方体搭成的几何体，则它的主视图是（）A．B．C．D．3．选择计算（﹣4xy2+3x2y）（4xy2+3x2y）的最佳方法是（）A．运用多项式乘多项式法则B．运用平方差公式C．运用单项式乘多项式法则D．运用完全平方公式4．如图，菱形ABCD的周长是4cm，∠ABC＝60°，那么这个菱形的对角线AC的长是（）A．1cm B．2 cm C．3cm D．4cm5．如图，在3×3的正方形网格中，有三个小正方形己经涂成灰色，若再任意涂灰1个白色的小正方形（每个白色的小正方形被涂成灰色的可能性相同），使新构成灰色部分的图形是轴对称图形的概率是（）A．B．C．D．6．如图，正六边形ABCDEF内接于⊙O，连接BD．则∠CBD的度数是（）A．30°B．45°C．60°D．90°7．如图，下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图，根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中，正确的是（）A．甲比乙大B．甲比乙小C．甲和乙一样大D．甲和乙无法比较8．数轴上点A，B，M表示的数分别是a，2a，9，点M为线段AB的中点，则a的值是（）A．3B．4.5C．6D．189．如图，在△ABC中，AB＝AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D，再分别以点B，D为圆心，大于BD长为半径画弧，两弧相交于点M，作射线CM交AB于点E．若AE＝2，BE ＝1，则EC的长度是（）A．2B．3C．D．10．在平面直角坐标系内，已知点A（﹣1，0），点B（1，1）都在直线y＝x+上，若抛物线y＝ax2﹣x+1（a≠0）与线段AB有两个不同的交点，则a的取值范围是（）A．a≤﹣2 B．a＜C．1≤a＜或a≤﹣2 D．﹣2≤a＜二、填空题：每小题4分，共20分。

贵州省2019年7月普通高中学业水平考试数学试卷高清答案版

贵州省2019年7月普通高中学业水平考试数学试卷参考公式：柱体体积公式：V=Sh ；锥体体积公式：V=31Sh(S 为底面面积，h 为高)。

第I 卷(第Ⅰ卷包括35小题，每题3分，共计105分)一、选择题：每小题给出的四个选项中，只有一项是符合题意的。

1．已知A={x|x<2}，B={1，2，3}，则A ∩B=A ．{ 1}B ．{2}C ．{2，3}D ．{0，1，3} 2．函数f (x)=2-x 的定义域为A ．{x|x ≥1}B ．{x ≥2}C ．{x|x ≤1}D ．{x|x ≤2} 3．以矩形的一边所在直线为旋转轴，其余三边旋转形成的面所围成的旋转体是A ．圆柱B ．圆锥C ．圆台D ．球体 4．已知向量a =(1，-2)，b =(2，3)，则a -b =A ．(4，-1)B ．(2，5))C ．(-3，2)D ．(-1，-5) 5．设等差数列{a n }的前n 项和是S n ，若首项a 1=1，公差d =2，则S 3=A ．7B ．9C ．11D ．13 6．函数f (x)=(k+3)x+1在R 上是增函数，则实数k 的取值范围是A ．k>-3B ．k<-3C ．k>-2D ． k<-27．如图，九宫格由九个小正方形组成在该九宫格内随机取一点P ，则点P 在阴影部分的概率为A ．91 B ．61 C ．31 D ．21 8．已知向量a =(2，7)，则｜a ｜＝A ．2B ．3C ．4D ．59．各项均为正数的等比数列{a n }满足a 3=1．a 5=36，则a 4=A ．3B ．4C ．5D ．6 10．函数y=|x-1|的图象是A B C D11已知直线/：y=4x-5，其斜率为A ．1B ．2C ．3D ．412．右图是某城市2017年各月的平均气温(°C)数据的茎叶图，则这组数据的众数为A ．17B ．19C ．21D ．2313．角a 的顶点与原点O 重合，始边与x 轴的非负半轴重合，若a 的终边经过点P(2，2)，则tan a 的值为A ．1B ．2C ．3D ．4 14．幂函数f (x)=x a 的图象经过点(2，4)，则f (x)的解析式为A ．f (x)=x -1B ． f(x)=xC ． f(x)=x 2D ． f(x)=x 3 15．已知sin a =31，则sin(a +2 )的值为 A ．-31 B ．31 C ．-61 D ．6116．在△ABC 中，角A ，B ，C 的对边分别是a ，b ，c ．若A=60°，a =3，b=1，则BA ．30°B ．45°C ．60°D ．135°17．某班有男生30名，女生24名．现用分层抽样的方法从全班同学中抽取若干名同学参加一项活动，若男生抽取5名，则女生抽取的人数为A ．2B ．3C ．4D ．518．如图，在直二面角A-BC-D 中，M ，N 分别是线段AB ，AC 的中点，则直线MN 与平面BCD 的位置关系是A ．直线M 在平面BCD 内B ．直线MN 与平面BCD 平行C ．直线MN 与平面BCD 相交1 1xy 01 1xy1 1xy1 1xyAB CDMND ．以上位置关系均有可能 19．已知函数f (x)=e x +e -x ，则f (x)为A ．奇函数B ．偶函数C ．既是奇函数又是偶函数D ．既不是奇函数又不是偶函数20．掷一枚质地均匀的骰子一次，出现点数不大于5的的概率为A ．31 B ．21 C ．32D ．65 21．已知a ，b ，c 均为实数，且a >b ，则以下选项正确的是A ．a 2>b 2B ． ac> bcC ．a-c>b-cD ．ba 11> 22．计算sin17°cos28°+cos17°sin28°的结果等于A ．-23 B ．-22 C ．22 D ．2323．已知log a 4=1，则a 的值为A ．3B ．4C ．5D ．624已知e 1与e 2为两个不共线的向量，则与e 1+2e 2平行的向量是A ．e 1+ e 2B ．2 e 1+ e 2C ．2 e 1+3 e 2D ．2 e 1+4 e 2 25．△ABC 的内角A ，B ，C 对边分是a ，b ，c ，a =3，b =5，c =7，则C 的大小为A ．120°B ．90°C ． 45°D ．30° 26．函数f (x)=x 3-10的零点所在的区间是A ．（0，1）B ．（1，2）C ．(2，3)D ．(3，4) 27．甲与乙进行象棋比赛，甲获胜的概率为31，甲与乙和棋(平局)的概率为61，则乙获胜的概率为A ．21 B ．41 C ．61D ．8128．若变量x ，y 满足约束条件⎪⎩⎪⎨⎧≥+≥+≤-0,2y -x 0,y x ,02x ，则z=3x+y 的最大值是A ．-2B ．4C ．8D ．10 29．已知a =30.2，b =30.5，c =30.9，则a ，b ，c 的大小关系为A ．a<b<cB ． c<a<bC ． a<c<bD ．b<c<a30．为了落实“振兴乡村战略”，某市拟定从2018年至2023年，年投入“振兴乡村战略”的项目资金从200亿元增加到300亿元，则这几年间该市投入该项目资金的年平均增长率x 应满足的关系式为A．200(1+x)=300B ．200x=300C ．200(1+x)5=300D ．200x 5=300 31．将函数y=cos 2x-sin 2x 的图象上所有点向左平移6π个单位长度，所得图象的函数解析式为A ．y=cos(2x+6π) B ． y =cos(2x-6π) C ．y=cos(2x+3π) D ． y=cos(2x-3π)32．已知正实数a ，b 满足a +b =2，则b a 11+，的最小值是A ．2B ．49C ．38D ．82533．△ABC 的内角A ，B ，C 的对边分别是a ，b ，c ．若△ABC 的面积是)(123222a cb -+则A=A ．90°B ．60°C ．45°D ．30° 34．定义bc ad dc b a -=，则函数f (x)=132cos 2sin x x 的图象的一个对称中心为A ．（4π，0） B ．（3π，0） C ．（125π，0） D ．（32π，0）35．若函数f (x)=x 2-2x+m 在区间[1，n]上的值域仍为[1，n] ( n>1)，则m+n 的值为A ．3B ．4C ．3或4D ．0第Ⅱ卷(第Ⅱ卷包括8小题，共45分)二、填空题：本大题共5小题，每小题3分，共15分。

贵州省普通高中会考数学试题及答案

普通高中会考数学试题1、sin150的值为（）（A ） 2-（B ） 2 （C ） 12- （D ） 122、设集合A={1，2，3，5，7}，B={3，4，5}，则A B =（）（A ） {1，2，3，4，5，7} （B ） {3，4，5} （C ）{5} （D ） {1，2}3、不等式|x|<1的解集是（）（A ） {x|x>1} （B ） {x|x<-1} （C ） {x|-1<x<1} （D ） {x|x<-1或x>1}4、双曲线2222143x y -=的离心率为（）（A ） 2 （B ）54 （C ） 53 （D ） 345、已知向量a=(2,3),b=(3,-2)则a ·b= （）（A ） 2 （B ） -2 （C ） 1 （D ） 06、函数y=sin2x 的最小正周期是（）（A ） π （B ） 2π （C ） 3π （D ） 4π7、若a<b<0，则下列不等式成立的是（）（A ） 22a b < （B ） 22a b ≤ （C ） a-b>0 （D ） |a|>|b|8、已知点A （2，3），B （3，5），则直线AB 的斜率为（）（A ） 2 （ B ） -2 （C ） 1 （ D ） -19、抛物线24y x =的准线方程为（）（A ） x=4 （ B ） x=1 （C ） x=-1 （D ） x=210、体积为43π的球的半径为（）（A ） 1 （ B ） 2 （ C ） 3 （ D ） 411、从1，2，3，4，5中任取3个数字组成没有重复数字的三位数，共有个数是（）（A ） 10 （ B ） 20 （ C ） 30 （D ） 6012、圆221x y +=的圆心到直线x-y+2=0的距离为（）（A ）1 （B ）（C ）（ D ） 2 二、填空题：本大题共4个小题，每小题3分，共12分，把答案填在题中的横线上。

贵州省2019年7月普通高中学业水平考试数学试卷WORD

18. 三个内角所对边分别是 .若
19.设数列满足
20.已知则有的终边在
21.如图，正方体中，
直线所成的角是
22.已知向量
月份
1
2
3
4
用水量
4.5
4
3
2.5
23.右表是某厂月份用水量的统计数据，其月份与用水量（单位：百吨）之间具有线性相关关系，则根据该统计数据求是的回归过点
24.《九章算术》是中国古代的数学专著，其中的“更相减损术”可以用来求两个数的最大公约数.那以与的最大公约数是
25.为了得到函数的图象，只需把图象上所有点
26. 且与直线平行的直线方程是
27.如图，在矩形将矩形绕边所在直线旋转一周形成一个圆柱，则该圆柱的体积为
28.不等式的解集是
29.已知实数满足约束条件，则实数对可以是
30.已知直线的方程分别是，若，则的值为
31.函数的图象大致为
32.若
33.已知圆，则直线截圆所得的弦长为
34. 三个内角所对边分别是 .若，则角的最大值是
35.已知为定义在上的奇函数，当时，设方程有四个互不相等的实根，则实数的取值范围是
第Ⅱ卷
（第Ⅱ卷包括8小题，共计45分）
二、填空题：本大题共5小题，每小题3分，共15分.把答案填在答题卡上.
共30分.解答应写出文字说明、证明过程或推演步骤.
41.已知函数，
（1）求的值；
（2）若，试求的取值范围.
42.如图，在四棱锥中,四边形是矩形, 是正三角形，且
（1）求三棱锥的体积；
（2）若分别是的中点，求证： .
43.已知数列的前项和

贵州省2019年高一年级学业水平测试卷数学试题(带答案解析)

贵州省2019年高一年级学业水平测试卷数学试题第I 卷（选择题)一、单选题1．下列四个数中，最大的是( )A B ．4π C ．23D ．22．王明同学随机抽查某市10个小区所得到的绿化率情况如下表所示：则关于这10个小区绿化率情况，下列说法错误的是( ) A ．方差是13%B ．众数是25%C ．中位数是25%D ．平均数是26.2%3．下列计算正确的是( ) A ．339a a a ⋅=B ．877222-=C ．()328=a a D ．0(1)1b aa b⋅-= 4．把五个边长为1的正方形按如图所示的方式摆放在平面直角坐标系中，经过坐标原点的一条直线l 将这五个正方形分成面积相等的两部分，则该直线的表达式为( )A ．35y x =B ．34y x =C ．54y x =D ．y x =5．如图，在ABC V 中，90A ∠=︒，2AB AC ==，点O 是边BC 的中点，半圆O 与ABC V 相切于点D ，E ，则阴影部分的面积等于( )A ．14π-B ．4π C ．18π-D ．8π 6．如图，⊙O 的半径等于2，弦BC 平行于x 轴，将劣弧BC 沿弦BC 对称，恰好经过原点O .如果直线–y x m =+与这两段弧只有两个交点，则m 的取值不可能是( )A ．94-B ．0C ．34D ．27．如图，抛物线2–43y x x =+-与x 轴交于A ，B 两点，把该抛物线在x 轴及其上方的部分记作1C ，将1C 向右平移得到2C ，2C 与x 轴交于B ，D 两点，如果直线–y kx k=与1C ，2C 共有3个不同交点，则k 的最大值是( )A ．13B ．6C ．6+D ．6-8．若20a b -=，36ab =-，且||||a b <，则ba等于( ) A ．19-B ．54-C ．4-D ．–99．如图，正方形ABCD 的边长为2，且BE EC =，将正方形的边CD 沿DE 折叠到DF ，延长EF 交AB 于点G ，则点B 到GE 的距离是( )A ．45B ．2C D ．5910．如图，90ABC ∠=︒，BA BC =，45DBE ∠=︒，4=AD ，2EC =，则DE 等于( )A ．2B ．C ．D ．4第II 卷（非选择题)二、填空题11．因式分解：33a b += _________________. 12．若关于x ，y 的二元一次方程组23142x y ax y +=⎧⎨+=⎩无解，则a =________________.13．在平面直角坐标系中，直线–y x a =+与反比例函数1y x=图象有两个公共点，则实数a 的取值范围是________________.14．某地移动分公司为打破“流量月清零”的做法，推出流量“季度包”“半年包”“一年以上”三种业务.甲乙丙分别随机选择其中一种流量业务，则至少有一人选择“半年包”业务的概率是__________.15．如图，在平行四边形ABCD 中，AE BC ⊥，垂足为点E ，如果5AB =，8BC =，4sin 5B =，则tan CDE ∠=____________.三、解答题16．计算： 112cos602-⎛⎫+︒ ⎪⎝⎭. 17．求值：22314411a a a a a a a +++⎛⎫-÷ ⎪---⎝⎭，其中3a =. 18．解不等式组10360x x +≥⎧⎨-<⎩①②.第一步：解不等式①，得____________；第二步：解不等式②，得__________；第三步：在数轴上分别把不等式①②的解的范围表示出来，第四步：从两个范围中找出公共部分，得不等式组的解为_____________.19．某学校开展主题为“垃圾分类，绿色生活新时尚”的宣传活动，为了解学生对垃圾分类知识的掌握情况，该校环保社团成员在校园内随机抽取了部分学生进行问卷调查，将他们的得分按优秀、良好、合格、待合格四个等级进行统计，并绘制了如下不完整的统计表和条形统计图.请根据以下信息，解答下列问题：（1）本次调查随机抽取了__________名学生，表中m =__________，n =__________；（2）补全条形统计图；（3）若全校有2000名学生，请你估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有多少人.20．A 、B 两地相距49千米，小明步行从A 第出发，分三段以不同的速度走完全程，共用10小时.已知第一段，第二段，第三段的速度分别是6千米/小时，4千米/小时，5千米/小时，若他走完各段路所用时间都是整数，求他在每段路上所用的时间. 21．一个楼梯有7级台阶，若已知小狗每步可以迈1级，2级或者3级台阶，那么这只小狗迈3步就爬上去的概率是多少？22．在ABC V 中，a ，b ，c 分别为角A ∠、B Ð，C ∠的对边，若60B ∠=︒，求c aa b b c+++的取值.23．如图1，点O 是正方形ABCD 的中心，分别延长OD 到点G ，OC 到点E ，使得2OG OD =，2OE OC =，然后以OG 、OE 为领边做正方形OEFG ，连接AC .DE 使得正方形ABCD 固定，正方形OEFG 绕点О旋转α角（0360α︒<<︒），得到正方形OE F G '''，如图2：（1）求线段DE '与AG '的关系（2）若正方形ABCD 的边长为1，在旋转过程中，求AF '的最大值及相应的α的度数. 24．如图1，ABC V 是等边三角形，D .E 分别是BC .AC 上两点，且AE DC =，BE 与AD 交于点H ，链接CH .（1）当90BHC ∠=︒时，求BHHC的值；（2）如图2，当150BHC ∠=︒时，BH HC =__________；BDDC= __________. 25．对于给定的抛物线23y x ax =+-，使得实数p 、q 满足32apq =-. （1）若22()12p a a -≥+，求证：抛物线2y x px q +=+与x 轴有交点.（2）证明：抛物线2––y x px q =-的最大值大于等于抛物线2–3y x ax =+的最小值.参考答案1．B 【解析】【分析】求出各选项的数的范围，即可求出结论. 【详解】52.2 2.3,0.60.6<<<<，20.75,0.67,0.71432π><<，四个数中4π最大. 故选:B. 【点睛】本题考查比较数的大小，属于基础题题. 2．A 【解析】【分析】分别求出众数、中位数、平均数、方差，逐项验证. 【详解】根据表格数据，众数为25%，选项B 正确；中位数为25% ，选项C 正确；平均数为2022543033226.210⨯+⨯+⨯+=，选项D 正确；方差为22221[2(2026.2)4(2526.2)3(3026.2)(3226.2)]15.9610-+-+-+-=；选项A 错误. 故选:A. 【点睛】本题考查方差、众数、中位数、平均数的计算，意在考查数学计算能力，属于基础题. 3．B 【解析】【分析】根据指数幂的运算法则，逐项判断，即可求解. 【详解】336a a a ⋅=，选项A 错误；87777222222-=⨯-=，选项B 正确；()326a a =，选项C 错误；10b aa b⋅-=，选项D 错误. 故选:B. 【点睛】本题考查指数幂的运算，属于基础题. 4．C 【解析】【分析】根据已知在直线下方是面积为52的直角三角形，求出直线与2x =的交点，即可求出方程【详解】直线l 将这五个正方形分成面积相等的两部分，在直线下方是面积为52的直角三角形，所以直线过5(2,)2，所以直线l 方程为54y x =. 故选:C. 【点睛】本题考查直线方程，属于基础题.5．B 【解析】【分析】如图所示连,,,,OA OD OE DE OD BE F =I ，根据图形关系可证BDF EOF ≅V V ，即可求解. 【详解】连接,,,,OA OD OE DE OD BE F =I ,,,OA OD OE DE ，半圆O 与ABC V 相切于点D ，E ，所以,,OD AD OE AE OD OE ⊥⊥=，四边形ODAE 为正方形，2,1AB AC BC OA AD AE ======Q ，,D E ∴为,AB AC 中点，所以四边形BOED 为平行四边形，,BDF EOF BDF EOF S S ≅=V V V V ，所以阴影部分面积等于扇形DOE 的面积为4π.故选;B.【点睛】本题考查不规则图形的面积，注意隐含条件的挖掘，应用割补法求面积，意在考查直观想象能力，属于中档题. 6．C 【解析】【分析】根据已知，分别求出直线过,B C 以及与两段弧相切时m 的值，再结合图形，即可求出结论.【详解】将劣弧BC 沿弦BC 对称，恰好经过原点O ，(1),1)B C ∴--如下图所示，当直线过(1)B -时，1m =-当直线过1)C -时，1m =-+当直线l 与圆弧BOC 相切时，2m =，当直线l 与⊙O 弧相切时，m =，当11m -<<-+2m << 直线–y x m =+与两段弧有两个交点.所以m 的取值不可能是34. 故选:C.【点睛】本题考查直线与圆的位置关系，考查数形结合思想，属于中档题. 7．D 【解析】【分析】由已知可得直线–y kx k =过(1,0)A ，直线–y kx k =与1C ，2C 共有3个不同交点，可得0k =或直线与2C 相切，即可求解.【详解】抛物线2–43y x x =+-与x 轴交于A ，B 两点，令20,430,1y x x x =-+==或3x =，所以(1,0),(3,0)A B ，将1C 向右平移得到2C ， 2C 与x 轴交于B ，D 两点，(5,0)D ，2C 方程为2(3)(5)815y x x x x =---=-+-，如果直线–y kx k =过(1,0)A 点，与1C ，2C 共有3个不同交点，则0k =，或0k >时，与2C 相切，所以22815,(8)150x x kx k x k x k -+-=-+-+-= ①只有一个实数解，22(8)4(15)1240,6k k k k k ∆=---=-+==+6-当6k =+1x =-，当6k =-1x =+，所以线–y kx k =与1C ，2C 共有3个不同交点，则0k =或6-故选:D.【点睛】本题考查抛物线与x 轴交点、二次函数图像、直线与抛物线的位置关系，数形结合是解题的关键，属于中档题.8．D【解析】【分析】根据,a b 关系解方程组，结合||||a b <，即可求解.【详解】20,20a b a b -=∴=+代入36ab =-，得220360b b ++=，解得2b =-或18b =-，当2b =-时，18,||||a a b =>（舍去），当18b =-时，2,9b a a=∴=-. 故选:D.【点睛】本题考查解方程组，意在考查数学计算能力，属于基础题.9．A【解析】【分析】连接GD ，根据折叠关系，可证Rt DAG Rt DFG ≅V V ，从而有AG GF =，设AG x =，在Rt BGE V 中，建立关于x 的方程，进而求出BG ，即可求解.【详解】连接GD ，正方形的边CD 沿DE 折叠到DF ， 0,90DF DC DA DFE DAG ∴==∠=∠=，,Rt DAG Rt DFG AG GF ∴≅∴=V V ，设,2,1AG x BG x GE x ==-=+，在Rt BGE ∆中，22222,(1)1(2)GE BE BG x x =++=+-，解得245,,333x GB GE ===，点B 到GE 的距离是45GB BE GE ⋅=. 故选:A.【点睛】本题考查了翻折变换性质和正方形性质，全等三角形判定定理和勾股定理，属于中档题.10．C【解析】【分析】将BCE ∆绕着点B 旋转至BC 与BA 重合，得到ABE '∆，连DE '，证明BDE BDE '∆≅∆，得DE DE ='，解三角形ADE '∆，即可求解.【详解】将BCE ∆绕着点B 旋转至BC 与BA 重合，,,2BE BE ABE CBE AE CE '''∴=∠=∠==，4DBE DBA ABE DBA CBE DBE π''∴∠=∠+∠=∠+∠==∠，,BDE BDE DE DE ''∴∆≅∆=， C BAE '∠=∠Q ，090DAE DAB BAE DAB C ''∠=∠+∠=∠+∠=，DE DE '∴==∴=故选:C.【点睛】本题考查三角形旋转变换、三角形全等、勾股定理，解题的关键将问题转化为解直角三角形，属于较难题.11．22()()a b a ab b +-+【解析】【分析】根据立方和公式，即可求解.【详解】3322()()a b a b a ab b +=+-+.故答案为:22()()a b a ab b +-+.【点睛】本题考查立方和公式，熟记公式是解题的关键，属于基础题.12．83 【解析】【分析】根据方程组无解，两方程所对应两直线没有交点，故平行，即可求解.【详解】方程组23142x y ax y +=⎧⎨+=⎩无解，两方程所对应的直线没有交点，即平行，即方程为211,3342a y x y =-+=-+的两直线平行， 28,343a a ==. 故答案为:83. 【点睛】本题考查二元一次方程组的几何意义，意在考查直观想象能力，属于基础题.13．2a <-或2a >【解析】【分析】联立两方程，确定方程组有两解的不等量关系，即可求解.【详解】联立1y x a y x =-+⎧⎪⎨=⎪⎩，整理得210x ax -+=，① 直线–y x a =+与反比例函数1y x=图象有两个公共点，方程组有两个解，即方程①有两个不同的解，240,2a a ∆=-><-或2a >.故答案为:2a <-或2a >.【点睛】本题考查方程解的个数、根的判别式，属于基础题.14．1927【解析】【分析】记“季度包”“半年包”“一年以上”为1,2,3，列出甲、乙所选业务的所有选法（前面数字代表甲所选的业务流量），确定出满足条件的基本事件，即可求解.【详解】记“季度包”“半年包”“一年以上”分别为1,2,3，甲、乙、丙分别随机选择其中一种流量业务，用实数对表示如下（数字顺序对应甲、乙、丙所选的业务流量）：{1,1,1},{1,1,2},{1,1,3},{1,2,1},{1,2,2},{1,2,3},{1,3,1},{1,3,2},{1,3,3}，{2,1,1},{2,1,2},{2,1,3},{2,2,1},{2,2,2},{2,2,3},{2,3,1},{2,3,2},{2,3,3}，{3,1,1},{3,1,2},{3,1,3},{3,2,1},{3,2,2},{3,2,3},{3,3,1},{3,3,2},{3,3,3}共有27种选择方法，至少有一人选择“半年包”业务有19种选择方法，所以概率为1927. 故答案为:1927. 【点睛】本题考查古典概型概率，用列举法求解，属于基础题.15．12【解析】【分析】根据已知和勾股定理可得5CE =，所以CE CD =，进而有CDE CED ADE ∠=∠=∠，在直角三角形ADE 中，即可求解.【详解】在Rt ABE △中，AE BC ⊥，4sin ,55B AB ==， 4,3,5AE BE EC BC BE ∴==∴=-=，Q 平行四边形ABCD ，5CD AB ∴==，CDE ∴∆是等腰三角形，CDE CED ∴∠=∠，//,E A D D BC CE AD ∴∠=∠，CDE ADE ∠=∠，,AE BC AE AD ⊥∴⊥Q ，在Rt ADE V 中，4,8AE AD BC ===，11tan ,tan 22AE ADE CDE AD ∠==∴∠=. 故答案为:12. 【点睛】本题考查解直角三角形、勾股定理、平行四边形的性质、三角函数，解题的关键是找到图形中相等的角，属于中档题.16．1【解析】【分析】根据绝对值，指数幂运算法则，特殊角三角函数值，即可求解.【详解】112cos602-⎛⎫+-÷-︒ ⎪⎝⎭211==.【点睛】本题考查代数式运算，熟记运算公式是解题的关键，属于基础题.17．35【解析】【分析】先将代数式按分式加法和除法运算化简，3a =代入，即可求解.【详解】22231442(1)111(2)2a a a a a a a a a a a a a a ++++-⎛⎫-÷=⋅= ⎪----++⎝⎭，当3a =，原式35=. 【点睛】本题考查了分式的化简求值，意在考查数学计算能力，属于基础题.18．1x >-； 2x <； 12x -<<.【解析】【分析】分别求出不等式组中两个不等式的解，利用数轴确定公共部分，即可求出方程组的解.【详解】解不等式组10360x x +≥⎧⎨-<⎩①②.第一步：解不等式①，得__1x >-_；第二步：解不等式②，得___2x <___；第三步：在数轴上分别把不等式①②的解的范围表示出来，第四步：从两个范围中找出公共部分，得不等式组的解为___12x -<<___.【点睛】本题考查解一元一次不等式组的方法，属于基础题.19．（1）50，20m =，12n =；（2）详见解析；（3）1640人.【解析】【分析】（1）根据优秀组频率和频数，求出随机抽取的人数，以及,m n 的值；（2）根据（1）中的m 值，补全条形统计图；（3）根据样本中达到“优秀”和“良好”等级的频率，即可求解.【详解】（1）优秀有21人，频率为42%，所以抽取样本人数为21500.42=， 500.420m ∴=⨯=，6%100%12%,1250n n =⨯=∴=；（2）条形图如下：（3）抽取的样本中达到“优秀”和“良好”等级的频率为82%，200082%1640⨯=人，所以估计该校掌握垃圾分类知识达到“优秀”和“良好”等级的学生共有1640人.【点睛】本题考查补全条形统计图和条形图的应用，属于基础题.20．1,2,7a b c ===或2,3,5a b c ===或3,4,3a b c ===或4,5,1a b c ===.【解析】【分析】可设小明第一段、第二段、第三段所用的时间分别为a 小时，b 小时和c 小时，根据等量关系：A 、B 两地相距49千米，共用10小时；列出方程组，再根据正整数的意义，即可求解.【详解】设小明第一段、第二段、第三段所用的时间分别为a 小时，b 小时和c 小时，依题意有6454910a b c a b c ++=⎧⎨++=⎩消去b ，可得92c a =-，因为各路段所用的时间都是整数，所以1,2,7a b c ===或2,3,5a b c ===或3,4,3a b c ===或4,5,1a b c ===.【点睛】本题考查了三元一次不定方程，意在考查数学建模、逻辑推理、数学计算能力，属于中档题. 21．322【解析】【分析】求出小狗走完7级台阶的所有情况，再确定满足条件基本量的个数，即可求解.【详解】小狗走完：7级台阶分为：7步走完有1种；6步走完：5步走1阶，一步走2阶，共有6种；5步走完分为：4步1阶，1步3阶有5种，和3步1阶，2步2阶有10种，共有15种；4步走完分为：2步1阶，1步2阶和1步3阶有12种，和1步1阶和3步2阶有4种，共有16种；3步走完分为：1步1阶，2步3阶有3种，和2步2阶，1步3阶有3种，共有6种所以7步走完共有44种走法，其中3步走完共有6种走法，这只小狗迈3步就爬上去的概率是634422=. 【点睛】本题考查古典概型概率，解题关键是合理分类列出所有基本事件，属于中档题. 22．1【解析】【分析】运用余弦定理可得222a c b ac +=+，然后将所求的代数式先通分求和，再把22a c +用2b ac +代替，即可求解.【详解】2222260,2cos B b a c ac B a c ac ∠=︒∴=+-=+-Q ，222a c b ac +=+，22221()()c a bc c a ab bc b ac ab a b b c a b b c ab ac b bc+++++++===+++++++. 【点睛】本题考查了分式的运算、余弦定理等知识，意在考查逻辑推理和数学计算，属于中档题.23．（1）DE AG ''=，证明详见解析；（2）AF '的最大值为2+315α=︒. 【解析】【分析】（1）通过证明DOE AOG ''∠=∠，可证E OD G OA ''∆≅∆，即可证明结论；（2）根据题意和图形分析可知，当点F '在线段AC 的延长线上时，AF '的长最大，即可求出结论.【详解】（1）DE AG ''=证明如下：图2中，90DOE DOG AOG DOG ''''∠+∠=∠+∠=︒Q ，,,DOE AOG OE OG OD OA ''''∴∠=∠==，,E OD G OA DE AG ''''∴∆≅∆∴=；（2）当正方形ABCD 的边长为1时，OA =2OF OF '====，当,,A O F '三点不共线时，AF OA OF ''<+，当,,A O F '三点共线，且F '在AC 的延长线时，22AF OA OF ''=+=+，AF '∴最大值为22+， 45,315COE α'∠=︒∴=︒Q .【点睛】本题考查了正方形的性质、全等三角形的判定和性质、旋转变换的性质、三角形边长关系的综合应用，属于中档题.24．（1）3；（2）3；12. 【解析】【分析】（1）根据题意可得ABE CAD ≅V V ，得出ABE CAD ∠=∠，证明,,,C D H E 四点共圆，连接DE ，由圆周角定理得出0030,90,DEC DHC EDC EHC ∠=∠=∠=∠=得出 11,22DC CE DC BD ==，作DM BE ⊥于M 则090,//DMH DM CH ∠=，得出:2:3MD HC =，利用平行线的比例关系，结合Rt MDE V 边角关系，即可得出结果；（2）同（1）得：,,,C D H E 四点共圆，连接DE ，由圆周角定理得出090DEC DHC ∠=∠=，030EDC EHC ∠=∠=，得出11,22CE DC BD DC ==，得出12BD DC =，作DM AD ⊥交BE 于M ，则//DM CH ，得出:1:3MD HC =，与（1）同理，可得出结论.【详解】（1）ABC QV 是等边三角形，AB BC CA ∴==060,,,BAE ACD AE DC ABE CAD ABE CAD ∠=∠==≅∠=∠V V ，060BHD ABE BAH CAD BAH BAC ∴∠=∠+∠=∠+∠=∠=，0000120,12060180DHE DHE BCA ∴∠=∴∠+∠=+=，,,,C D H E 四点共圆，连接DE ，如图（1）所示，则000906030DEC DHC BHC BHD ∠=∠=∠-∠=-=，00118090,2EDC EHC BHC DC CE ∠=∠=-∠=∴=， 1,,2AE DC BD CE DC BD ===，作DM BE ⊥于M ，则090,//DMH DM CH ∠=， :::2:3MD HC BM BH BD BC ∴===，设2MD x =，则3HC x =，在Rt DMH V 中，030,,MDH MH MD x BH ∠===∴=，33BH HC x ==；（2）同（1）得：,,,C D H E 四点共圆，连接DE ，000150,60,90BHC BHD DHC DEC ∠=∠=∴∠==Q ，00018015030EDC EHC ∠=∠=-=11,,,22CE DC AE DC BD CE BD DC ∴====Q ，12BD DC ∴=，作DM AD ⊥交BE 于M ，则090MDH ∠=，//DM CH ，:::1:3MD HC BM BH BD BC ∴===，设MD x =，则3HC x =，在Rt DMH V 中，030DMH ∠=，0,cos30MD MH x BH ∴==∴=，33BH HC x ∴==.【点睛】本题考查等边三角形性质、全等三角形的判定和性质、四点共圆、圆周角定理、平行线性质、三角函数等知识，意在考查直观想象、逻辑推理能力，属于较难题.25．（1）详见解析；（2）详见解析.【解析】【分析】（1）要证抛物线2y x px q +=+与x 轴有交点，只需证240p q ∆=-≥，将已知条件化简消去a ，即可证明结论；（2）分别求出抛物线2––y x px q =-的最大值和抛物线2–3y x ax =+的最小值，作差，结合已知,,a p q 关系，即可证明结论.【详解】（1）由32ap q =-，得2226,()12ap q p a a =--≥+， 222241212,40p ap p q p q -=-+≥∴-≥，抛物线22,40y x px q p q =+∆+=-≥，所以抛物线2y x px q +=+与x 轴有交点.（2）抛物线2––y x px q =-的最大值为224444q p p q --=-，抛物线2–3y x ax =+的最小值为2124a --，32ap q =-Q 2222224124124(3)4444p q a p q a p q a ----++--+-== 222222()4120,4444p pa a p a p q a -+----==≥∴≥，即抛物线2––y x px q =-的最大值大于等于抛物线2–3y x ax =+的最小值.【点睛】本题考查根的判别式、二次函数的最值以及不等式的证明，意在考查逻辑推理和数学计算能力，属于中档题.。

贵州省2019年12月普通高中学业水平考试(word版)

机密★开考前贵州省2019年12月普通高中学业水平考试数学试卷注意事项:1．本试卷分为选择题和非选择题两部分，本试卷共6页，共43题，满分150分。

考试用．时120分钟。

2．答题前，考生务必用黑色字迹的钢笔或签字笔将自己的姓名、准考证号码填写在答题卡上。

将条形码准确粘贴在答题卡“考生条形码区”区域内。

3．选择题选出答案后，用2B 铅笔把答题卡上对应题目选项的答案信息点涂黑，如需改动，用橡皮擦干净后，再选涂其它答案，所有题目答案不能答在试卷上。

4．考生必须保持答题卡的整洁。

考试结束后，将试卷和答题卡一并交回。

参考公式:柱体体积公式:Sh V =体体积公式: Sh V 31=( S 为底面积，h 为高); 球的表面积公式: 24R V π=，球的体积公式: 334R V π= ( R 为球的半径)。

第I 卷(第I 卷包括35小题，每小题3分，共计105分)一、选择题:每小题给出的四个选项中，只有．．一项．．是符合题意的。

1．已知A={-1，1}，B={0，1}，则A∩B=A ．{1}B ． {0}C ． {-1}D ． {0，1} 2．在等差数列{a n }中，a 1=2，公差d=1，则a 3=A ． 6B ．5C ．4D ．3 3．已知向量a =(1，1)，b =(2，2)，则a +b =A ． (0，0)B ． (3，3)C ． (4，4)D ． (5，5)4．某班有男生20人，女生25人，用分层抽样的方法从该班抽取9人参加志愿者活动，则应抽取的女生人数为A ．2B ． 3C ．4D ．55．如图所示茎叶图表示的数据中，众数是 A ．18 B ．23 C ．25 D ．316．函数21)(-=x x f 的定义域是A ． {x|x<2}B ． {x|x>2}C ． RD ． e {x|x≠2} 7．已知等比数列{a n }的前n 项和为S n ，a 1=1，公比q=2，则S 2=A ．3B ．4C ．5D ．6 8．如图，将一个圆八等分，在圆内任取一点P ，则点P 取自阴影部分的概率为A ． 85B ． 83C ． 41D ．81 9．已知向量a =(1，2)，b =(2，x)，若a //b ，则实数x=A ．4B ．2C ．1D ． -1 10． tan45° 的值是 A ． 2 B ．3 C ． 2 D ．111．执行右图所示的程序框图，若输入的r=l ，θ=号，则输出1的值为A ．2πB ． πC ． 23π D ． π212．下列函数中，在(0，+∞)上为减函数的是 A ． x x f ln )(= B ． xx f 1)(=C ． 2)(=x fD ． 1)(+=x x f13．已知函数⎪⎩⎪⎨⎧>-≤=2,21,2,2)(x x x x f x ，则=+)3()0(f fA ． -2B ． -1C ．1D ．21 582 335553 14614．△ABC 三内角A ，B ，C 所对边分别是a ，b ，c ．若a=3，b=4，c=5，则C= A ．120° B ．90° C ．．60° D ．30° 15．不等式3x+2y- 6≤0表示的平面区域是16．下列不等关系正确的是A ．若a>b ，c∈R ，则a+c>b+cB ．若a>b ，c∈R ，则ac>bcC ．若a>b ，c<d ，则a+c<b+d)D ．若a>b ，c<d ，则ac<bd17．为了得到函数)4cos(π-=x y ，x∈R 的图象，只需把函数x y cos =的图象上所有的点A ．向左平移4π个单位长度 B ．向右平移4π个单位长度 C ．向左平移2π个单位长度 D ．向右平移2π个单位长度18．一个球的俯视图是以2为半径的圆，则这个球的表面积是A ．34π B ．316π C ．8π D ．16π 19．过点(2，0)且与直线y=2x+5垂直的直线l 的方程是A ． y=2x-4B ． y=-2x+4C ．121-=x y D ． 121+-=x y 20．某同学从家到学校需经过一处红绿灯，某天这位同学骑车上学，一路匀速行驶到红绿灯处正好遇上红灯，停留了90秒，然后加速行驶至学校．在这一过程中，该同学行驶的路程s 与时间t 的函数图象可能是21.从1，2，3，4四个数中任取两个数，则这两个数之和大于5的概率为 A.31 B.21 C.32 D. 43 22.已知平面上两点A(1，2)，B(3，0)，则线段AB 的中点坐标是A. (-2，2)B. (2，-2)C. (2，1)D. (3，0) 23.已知向量a =(3，4)，则a 的模|a |=A.5B.4C.3D.224. △ABC 三内角A ，B ，C 所对边分别是a ，b ，c.若4=30°，B=60°，a=1，则b= A.1 B. 2 C. 3 D.225.已知53)sin(=-απ，则=αsin = A. 54 B. 53 C. 53- D. 54-26.函数R x x f ∈=sin,2)(的最小正周期是 A.2πB. πC. π2D. π4 27.根据如图所示样本数据的频率分布直方图，估计样本中位数的值为A.95B.85C.75D.65 28.不等式12<x 的解集是A. (-∞，-1)B. (1，+∞)C. [-1，1]D. (-1，1) 29.已知幂函数αx x f =)(的图象过点P(2，4)，则=α A ．21B.1 C ．2 D.3 30.偶函数f(x)，x∈R 在[0，+∞)上是增函数。

贵州省2019年12月普通高中学业水平考试数学试题(含答案)

贵州省2019年12月普通高中学业水平考试数学试题第I 卷(选择题)一、单选题1.已知A ={-1,1},B ={0,1}，则A ∩B =()A.{1}B.{0}C.{-1}D.0,12.在等差数列{a n }中，a 1=2，公差d =1，则a 3=()A.6B.5C.4D.33.已知向量a =(1,1),b =(2,2)，则a +b =()A.(0,0)B.(3,3)C.(4,4)D.(5,5)4.某班有男生20人，女生25人，用分层抽样的方法从该班抽取9人参加志愿者活动，则应抽取的女生人数为()A.2B.3C.4D.515823355531465.如图所示茎叶图的数据中，众数是()A.18B.23C.25D.316.函数f (x )=1x -2的定义域是()A.{x |x <2}B.{x |x >2}C.RD.{x |x ≠2}7.已知等比数列{a n }的前n 项和为S n ，a 1=1，公比q =2，则S 2=()A.3B.4C.5D.68.如图，将一个圆八等分，在圆内任取一点P ，则点P 取自阴影部分的概率为()A.58B.38C.14D.189.若向量a =(1,2),b =(2,x )，若a //b，则x =()A.4B.2C.1 D.-110.tan45∘的值是()A.2B.3C.2D.111.执行如图所示的程序框图，若输入的r =1，θ=π2，则输出l 的值为()A.π2B.πC.3π2D.2π12.下列函数中，在(0,+∞)上为减函数的是()A.f (x )=ln xB.f (x )=1xC.f (x )=2xD.f (x )=x +113.已知函数f (x )=2x ,x ≤21x -2,x >2，则f (0)+f (3)=()A.-2B.-1C.1D.214.△ABC 三内角A ，B ，C 所对边分别是a ，b ，c ，若a =3,b =4,c =5，则C =()A.120°B.90°C.60°D.30°15.不等式3x +2y -6≤0表示的区域是()A.B.C.D.16.下列不等关系正确的是()A.若a >b ,c ∈R ，则a +c >b +cB.若a >b ,c ∈R ，则ac >bcC.若a >b ,c <d ，则a +c b ,c <d ，则ac <bd17.为了得到函数y =cos x -π4,x ∈R 的图象，只需把函数y =cos x 的图象上所有的点()A.向左平移π4 个单位长度B.向右平移π4 个单位长度C.向左平移π2 个单位长度D.向右平移π2个单位长度18.一个球的俯视图是以2为半径的圆，则这个球的表面积是()A.4π3B.16π3C.8πD.16π19.过点2,0 且与直线y =2x +5垂直的直线l 的方程是()A.y =2x -4B.y =-2x +4C.y =12x -1D.y =-12x +120.某同学从家到学校需经过一处红绿灯，某天这位同学骑车上学，一路匀速行驶到红绿灯处正好遇上红灯，停留了90秒，然后加速行驶至学校.在这一过程中，该同学行驶的路程S 与时间t 的函数图象可能是()A. B.C. D.21.从1，2，3，4四个数中任取两个数，则这两个数之和大于5的概率为()A.13B.12C.23D.3422.已知平面上两点A (1,2)，B (3,0)，则线段AB 的中点坐标是()A.(-2,2)B.(2,-2)C.(2,1)D.(3,0)23.已知a =(3,4)，则a 的模a=()A.5B.4C.3D.224.△ABC 三内角A ，B ，C 所对边分别是a ，b ，c .若A =30°，B =60°，a =1，则b =()A.1 B.2 C.3 D.625.已知sin (π-α)=35，则sin α=()A.45B.35C.-35D.-4526.函数f (x )=2sin x ,x ∈R 的最小正周期是()A.π2B.πC.2πD.4π27.根据如图所示样本数据的频率分布直方图，估计样本中位数的值为()A.95B.85C.75D.6528.不等式x 2<1的解集是()A.(-∞,-1)B.(1,+∞)C.[-1,1]D.(-1,1)29.已知幂函数f (x )=x α的图象过点P (2,4)，则α=()A.12B.1C.2D.330.偶函数f (x ),x ∈R 在[0,+∞)上是增函数，若f (1)=0，则不等式f (x )≤0的解集为()A.(-∞,-1)B.(1,+∞)C.RD.[-1,1]31.已知角α的顶点与平面直角坐标系的原点重合，始边与x 轴非负半轴重合，终边经过点P (1,-3 )，则cos α=()A.-3 2B.-12C.12D.3 2 32.在正方体ABCD -A 1B 1C 1D 1中，异面直线AC 与BC 1所成的角为()A.30°B.45°C.60°D.90°33.计算sin105∘cos75∘-cos105∘sin75∘的值为()A.-12B.12C.-22D.334.已知函数f (x )=x 2-2x -3 -m 有四个不同的零点，则实数m 的取值范围是()A.[0,4]B.(0,4]C.[0,4)D.(0,4)35.已知数列{a n }前n 项和S n =n 2+n ,9m S m +n S n=λ(m ,n ∈N *，λ为常数).当a m +a n 的最小值为12时，λ的值是()A.2B.32C.1D.12第II 卷(非选择题)二、填空题36.已知等比数列{a n }中，a 1=2，公比q =2，则a 2=.37.已知向量m =(2,3)，n =(4,1)，则m ⋅n=.38.已知直线l 1:x +y -2=0,l 2:3x +ay +5=0，若l 1//l 2，则实数a =.39.已知m ≤2x +1在x ∈[0,+∞)上恒成立，则实数m 的最大值是.40.在△ABC 中，D 为边AB 的中点，AC =2，CD =22 ，cos A =34，则△ABC 的面积为.三、解答题41.已知函数f (x )=x 2-mx +2.(1)求f (0)和f (m )的值；(2)若f (x )的最小值为1，求实数m 的值.42.如图，在三棱锥P -ABC 中，M 是PB 的中点，AP =AB ，AM =3，CM =4，AC =5.(1)求证：AM ⊥平面PBC ；(2)若CP =CB =5，求三棱锥P -ABC 的体积.43.已知直线l 过点A (-2,0)且斜率为3 ，直线l 被以原点O 为圆心的圆截得的弦长为2.(1)求圆O 的方程；(2)设点B (4,0)，点P (x ,y )(x ≥0)为圆O 上一点，求2PA 2 +1PB2的最小值.贵州省2019年12月普通高中学业水平考试数学试题第I 卷(选择题)一、单选题1.已知A ={-1,1},B ={0,1}，则A ∩B =(A )A.{1}B.{0}C.{-1}D.0,12.在等差数列{a n }中，a 1=2，公差d =1，则a 3=(C )A.6B.5C.4D.33.已知向量a =(1,1),b =(2,2)，则a +b =(B )A.(0,0)B.(3,3)C.(4,4)D.(5,5)4.某班有男生20人，女生25人，用分层抽样的方法从该班抽取9人参加志愿者活动，则应抽取的女生人数为(D )A.2B.3C.4D.515823355531465.如图所示茎叶图的数据中，众数是(C )A.18B.23C.25D.316.函数f (x )=1x -2的定义域是(D )A.{x |x <2}B.{x |x >2}C.RD.{x |x ≠2}7.已知等比数列{a n }的前n 项和为S n ，a 1=1，公比q =2，则S 2=(A )A.3B.4C.5D.68.如图，将一个圆八等分，在圆内任取一点P ，则点P 取自阴影部分的概率为(B )A.58B.38C.14D.189.若向量a =(1,2),b =(2,x )，若a //b，则x =(A )A.4B.2C.1D.-110.tan45∘的值是(D )A.2B.3C.2D.111.执行如图所示的程序框图，若输入的r =1，θ=π2，则输出l 的值为(A )A.π2B.πC.3π2D.2π12.下列函数中，在(0,+∞)上为减函数的是(B )A.f (x )=ln xB.f (x )=1xC.f (x )=2xD.f (x )=x +113.已知函数f (x )=2x ,x ≤21x -2,x >2，则f (0)+f (3)=(D )A.-2B.-1C.1D.214.△ABC 三内角A ，B ，C 所对边分别是a ，b ，c ，若a =3,b =4,c =5，则C =(B )A.120°B.90°C.60°D.30°15.不等式3x +2y -6≤0表示的区域是(C )A.B.C.D.16.下列不等关系正确的是(A )A.若a >b ,c ∈R ，则a +c >b +cB.若a >b ,c ∈R ，则ac >bcC.若a >b ,c <d ，则a +c b ,c <d ，则ac <bd17.为了得到函数y =cos x -π4,x ∈R 的图象，只需把函数y =cos x 的图象上所有的点(B )A.向左平移π4 个单位长度B.向右平移π4 个单位长度C.向左平移π2 个单位长度D.向右平移π2个单位长度18.一个球的俯视图是以2为半径的圆，则这个球的表面积是(D )A.4π3B.16π3C.8πD.16π19.过点2,0 且与直线y =2x +5垂直的直线l 的方程是(D )A.y =2x -4B.y =-2x +4C.y =12x -1D.y =-12x +120.某同学从家到学校需经过一处红绿灯，某天这位同学骑车上学，一路匀速行驶到红绿灯处正好遇上红灯，停留了90秒，然后加速行驶至学校.在这一过程中，该同学行驶的路程S 与时间t 的函数图象可能是(B )A. B.C. D.21.从1，2，3，4四个数中任取两个数，则这两个数之和大于5的概率为(A )A.13B.12C.23D.3422.已知平面上两点A (1,2)，B (3,0)，则线段AB 的中点坐标是(C )A.(-2,2)B.(2,-2)C.(2,1)D.(3,0)23.已知a =(3,4)，则a 的模a=(A )A.5B.4C.3D.224.△ABC 三内角A ，B ，C 所对边分别是a ，b ，c .若A =30°，B =60°，a =1，则b =(C )A.1B.2C.3D.625.已知sin (π-α)=35，则sin α=(B )A.45B.35C.-35D.-4526.函数f (x )=2sin x ,x ∈R 的最小正周期是(C )A.π2B.πC.2πD.4π27.根据如图所示样本数据的频率分布直方图，估计样本中位数的值为(B )A.95B.85C.75D.6528.不等式x 2<1的解集是(D )A.(-∞,-1)B.(1,+∞)C.[-1,1]D.(-1,1)29.已知幂函数f (x )=x α的图象过点P (2,4)，则α=(C )A.12B.1C.2D.330.偶函数f (x ),x ∈R 在[0,+∞)上是增函数，若f (1)=0，则不等式f (x )≤0的解集为(D )A.(-∞,-1)B.(1,+∞)C.RD.[-1,1]【答案】D【解析】因为f (x )是偶函数，且f (1)=0，所以f (-1)=f (1)=0，又因为f (x )在[0,+∞)上是增函数，所以f (x )在(-∞,0]上是减函数，当x ≥0时，f (x )是增函数，由f (x )≤0=f (1)可得x ≤1，即0≤x ≤1；当x <0时，f (x )是减函数，由f (x )≤0=f (-1)可得x ≥-1，即-1≤x <0；综上可得，不等式f (x )≤0的解集为[-1,1].故选：D .31.已知角α的顶点与平面直角坐标系的原点重合，始边与x 轴非负半轴重合，终边经过点P (1,-3 )，则cos α=(C )A.-3 2B.-12C.12D.3 2【答案】C【解析】终边经过点P (1,-3 )，得：∵cos α=x r =x x 2+y 2=11+3 =12 32.在正方体ABCD -A 1B 1C 1D 1中，异面直线AC 与BC 1所成的角为(C )A.30°B.45°C.60°D.90°【答案】C【解析】连接AD 1,CD 1．因为ABCD -A 1B 1C 1D 1为正方体，所以AD 1//BC 1,，则∠D 1AC 是异面直线AC 和BC 1所成角．又AD 1=CD 1=AC ,可得ΔACD 1为等边三角形，则∠D 1AC =60o ，所以异面直线AC 与BC 1所成角为60∘，故选：C33.计算sin105∘cos75∘-cos105∘sin75∘的值为(B )A.-12B.12C.-2 2D.334.已知函数f (x )=x 2-2x -3 -m 有四个不同的零点，则实数m 的取值范围是(D )A.[0,4]B.(0,4]C.[0,4)D.(0,4)【答案】D【解析】由题意，函数f (x )=x 2-2x -3-m 有四个不同的零点，等价于函数y =x 2-2x -3 和y =m 的图象有四个不同的交点，作出函数y =x 2-2x -3 =x 2-2x -3,x ∈(-∞,-1)∪(3,+∞)-x 2+2x +3,x ∈[-1,3]的图象，如图所示，要使得函数y =x 2-2x -3 和y =m 的图象有四个不同的交点，则0<m <4，即实数m 的取值范围是(0,4).故选：D .35.已知数列{a n }前n 项和S n =n 2+n ,9m S m +n S n=λ(m ,n ∈N *，λ为常数).当a m +a n 的最小值为12时，λ的值是(A )A.2B.32C.1D.12【答案】A【解析】∵S n =n 2+n ,∴n =1,a 1=S 1=12+1=2,当n ≥2时a n =S n -S n -1=n 2+n -(n -1)2-(n -1)=2n∵n =1,2n =2,∴a n =2n (n ∈N *)∵S n =n 2+n ,9m S m +n S n =λ∴9m m 2+m +n n 2+n=λ∴9m +1 +1n +1 =λ∵m +1>0,n +1>0，∴λ>0∴a m +a n =2m +2n =2(m +1+n +1-2)⋅1λ(9m +1 +1n +1 )=2λ [10+9(n +1)m +1 +m +1n +1 -2(9m +1 +1n +1 )]=2λ [10+9(n +1)m +1 +m +1n +1 ]-4≥2λ [10+29(n +1)m +1 ⋅m +1n +1 ]-4=32λ-4，当且仅当m +1=3(n +1)时取等号因为a m +a n 的最小值为12，所以32λ-4=12∴λ=2，此时m =5,n =1,故选：A第II 卷(非选择题)二、填空题36.已知等比数列{a n }中，a 1=2，公比q =2，则a 2=4.37.已知向量m =(2,3)，n =(4,1)，则m ⋅n =11.38.已知直线l 1:x +y -2=0,l 2:3x +ay +5=0，若l 1//l 2，则实数a =3.【答案】3【解析】由题意直线l 1的斜率k 1=-1.∵l 1//l 2，直线l 2的方程为3x +ay +5=0，∴直线l 2的斜率k 2=-3aa ≠0 .∴k 2=k 1，即-3a =-1,∴a =3.故答案为：3.39.已知m ≤2x +1在x ∈[0,+∞)上恒成立，则实数m 的最大值是2.【答案】2【解析】由指数函数的性质，可得y =2x 在[0,+∞)为单调递增函数，所以2x ≥1，可得2x +1≥2，即2x +1最小值为2，又由m ≤2x +1在x ∈[0,+∞)上恒成立，所以m ≤2，即实数m 的最大值2.故答案为：2.40.在△ABC 中，D 为边AB 的中点，AC =2，CD =22 ，cos A =34 ，则△ABC 的面积为27 .【答案】27【解析】在△ACD 中，由余弦定理可得cos A =AC 2+AD 2-CD 22AC ⋅AD =4+AD 2-84AD=34 ，解得AD =4或AD =-1(舍)，所以AB =8，因为cos A =34 ，所以sin A =1-cos 2A =1-916 =7 4 ；所以△ABC 的面积为12 AB ⋅AC sin A =12 ×8×2×7 4=27 .故答案为：27 .三、解答题41.已知函数f (x )=x 2-mx +2.(1)求f (0)和f (m )的值；(2)若f (x )的最小值为1，求实数m 的值.【答案】(1)f (0)=2，f (m )=2；(2)m =±2.【解析】(1)因为f (x )=x 2-mx +2，所以f (0)=2，f (m )=m 2-m 2+2=2；(2)因为f (x )=x 2-mx +2是开口向上，以x =m 2为对称轴的二次函数，又f (x )的最小值为1，所以f m 2 =m 24 -m 22 +2=2-m 24=1，解得：m =±2.42.如图，在三棱锥P -ABC 中，M 是PB 的中点，AP =AB ，AM =3，CM =4，AC =5.(1)求证：AM ⊥平面PBC ；(2)若CP =CB =5，求三棱锥P -ABC 的体积.【答案】(1)证明见详解；(2)20.【解析】(1)因为M 是PB 的中点，AP =AB ，所以AM ⊥PB ；又AM =3，CM =4，AC =5，所以AM 2+CM 2=AC 2，因此AM ⊥CM ；又PB ∩CM =M ，PB ⊂平面PBC ，CM ⊂平面PBC ；所以AM ⊥平面PBC ；(2)因为M 是PB 的中点，所以CM =12 CP +12 CB ，因此CM =12 CP +12 CB 2 =14 CP 2+14 CB 2+12CP ⋅CB ，又CP =CB =5，CM =4，所以4=254 +254 +252 cos ∠PCB =252 +252 cos ∠PCB ，即cos ∠PCB =725 ，因此sin ∠PCB =1-cos 2∠PCB =2425，所以S △PBC =12CP ⋅CB ⋅sin ∠PCB =12，因此三棱锥P -ABC 的体积为V P -ABC =13 S △PBC ⋅AM =13×12×5=20.43.已知直线l 过点A (-2,0)且斜率为3 ，直线l 被以原点O 为圆心的圆截得的弦长为2.(1)求圆O 的方程；(2)设点B (4,0)，点P (x ,y )(x ≥0)为圆O 上一点，求2PA 2 +1PB2 的最小值.【答案】(1)x 2+y 2=4(2)14【解析】(1)设圆O 的方程为x 2+y 2=r 2由题意可知，直线l 的方程为y =3 (x +2)，即3 x -y +23 =0圆心0,0 到直线l 的距离d =|23 |4 =3 则r =d 2+222 =3+1 =2∴x 2+y 2=4(2)∵点P (x ,y )(x ≥0)为圆O 上一点，∴x 2+y 2=4,x ∈[0,2]|PA |2=(x +2)2+y 2=x 2+4x +4+4-x 2=4x +8PB 2=(x -4)2+y 2=x 2-8x +16+4-x 2=-8x +20∴2PA 2 +1PB 2 =12x +4 +1-8x +20 =34 x -4(x +2)(2x -5)令t =x -4，t ∈[-4,-2]，则x =t +4∴x -4(x +2)(2x -5) =t (t +6)(2t +3) =t 2t 2+15t +18 =12t +18t+15 设y =2t +18t,t ∈[-4,-2]对于任意的-4≤t 1<t 2≤-2，y 1-y 2=2t 1-t 2 +18t 1 -18t 2 =2t 1-t 2 t 1t 2-9 t 1t 2当-4≤t 1<t 2≤-3时，t 1-t 2<0,t 1t 2-9>0∴y 1-y 2<0，即y 1<y 2当-3<t 1<t 2≤-2时，t 1-t 2<0,t 1t 2-9<0∴y 1-y 2>0，即y 1>y 2∴y=2t+18t 在[-4,-3]上单调递增，在[-3,-2]上单调递减则y max=2×-3+18-3=-12即2PA2+1PB2的最小值为341-12+15=14 .。

2019年贵州省贵阳市中考数学试卷以及逐题解析版

2019年贵州省贵阳市中考数学试卷以及逐题解析一、选择题：以下每小题均有A、B、C、D四个选项，其中只有一个选项正确，请用2B 铅笔在答题卡相应位置作答，每小题3分，共30分1．（3分）23可表示为()A．32B．222C．33D．332．（3分）如图是由4个相同的小立方体搭成的几何体，则它的主视图是() A．B．C．D．xy x y xy x y的最佳方法是()(43)(43)3．（3分）选择计算2222A．运用多项式乘多项式法则B．运用平方差公式C．运用单项式乘多项式法则D．运用完全平方公式ABC，那么这个菱形的对角线AC的长4．（3分）如图，菱形ABCD的周长是4cm，60是()A．1cm B．2 cm C．3cm D．4cm5．（3分）如图，在33的正方形网格中，有三个小正方形己经涂成灰色，若再任意涂灰1个白色的小正方形（每个白色的小正方形被涂成灰色的可能性相同），使新构成灰色部分的图形是轴对称图形的概率是()A．19B．16C．29D．136．（3分）如图，正六边形ABCDEF内接于O，连接BD．则CBD的度数是()A．30B．45C．60D．907．（3分）如图，下面是甲乙两位党员使用“学习强国APP”在一天中各项目学习时间的统计图，根据统计图对两人各自学习“文章”的时间占一天总学习时间的百分比作出的判断中，正确的是()A．甲比乙大B．甲比乙小C．甲和乙一样大D．甲和乙无法比较8．（3分）数轴上点A，B，M表示的数分别是a，2a，9，点M为线段AB的中点，则a 的值是()A．3B．4.5C．6D．189．（3分）如图，在ABC中，AB AC，以点C为圆心，CB长为半径画弧，交AB于点B和点D ，再分别以点B ，D 为圆心，大于12BD 长为半径画弧，两弧相交于点M ，作射线CM交AB 于点E ．若2AE，1BE ，则EC 的长度是()A ．2B ．3C ．3D ．510．（3分）在平面直角坐标系内，已知点(1,0)A ，点(1,1)B 都在直线1122yx上，若抛物线21(0)yaxx a 与线段AB 有两个不同的交点，则a 的取值范围是()A ．2a,B ．98aC ．918a,或2a,D ．928a,二、填空题：每小题4分，共20分。