高考数学必考之圆的方程
(江苏专用)高考数学总复习 第八章第3课时 圆的方程课件

【解】 设点M的坐标是(x,y),点A 的坐标是(x0,y0),由于点B的坐标是 (4,3)且M是线段AB的中点,
所以 x=x0+2 4,y=y0+2 3, 于是有 x0=2x-4,y0=2y-3. ① 因为点 A 在圆(x+1)2+y2=4 上运动,
所以点 A 的坐标满足方程(x+1)2+y2= 4, 即(x0+1)2+y20=4. ② 把 ①代入 ②, 得(2x- 4+ 1)2+ (2y- 3)2 =4,
(2)求圆的方程有两类方法 ①几何法,即通过研究圆的性质、直 线和圆、圆和圆的位置关系,进而求 得圆的基本量(圆心、半径)和方程;
②代数法,即用“待定系数法”求圆 的方程,其一般步骤是:a.根据题意 选择方程的形式——标准形式或一般 形式(本例题中涉及圆心及切线,故设 标准形式较简单);b.利用条件列出关 于a,b,r或D,E,F的方程组;c.解 出a,b,r或D,E,F,代入所设的标 准方程或一般方程.
第八章 平面解析几何
第3课时 圆的方程
回归教材•夯实双基
基础梳理 1.圆的方程 (1)标准方程:(x-a)2+(y-b)2=r2,其中 (a_,__b_)____为圆心,r为半径.
(2)一般方程:x2+y2+Dx+Ey+F=
0(D2+E2-4F>0)其中圆心为
__-__D2_,__-__E2___,半径为_12__D__2_+__E_2- __4_F_.
d=|2--1-1|= 2.
1+1
又直线y=x-1被圆截得的弦长为2, ∴2=2,即2=2,解得r=2. ∴所求圆的方程为(x-2)2+(y+1)2= 4.
(2)法一:设圆的标准方程为(x-a)2+(y
-b)2=r2,则有
b=-4a,
3-a2+-2-b2=r2, |a+b-1|=r, 2
高考数学专题突破教师版-圆的方程(考点讲析)
22
2
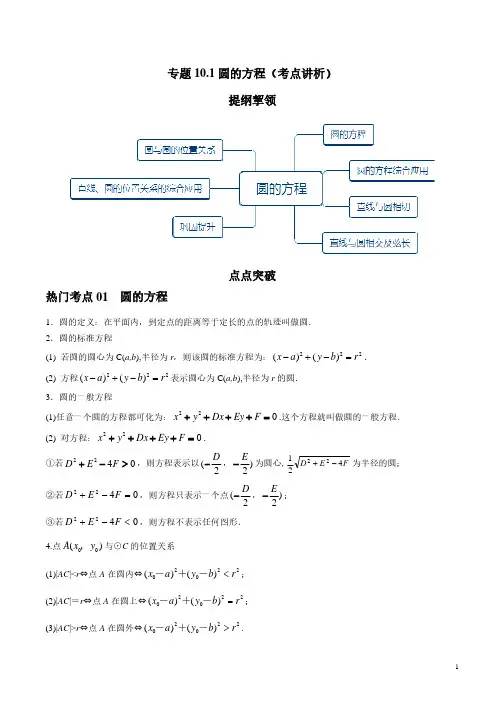
②若 D 2 E 2 4F 0 ,则方程只表示一个点 ( D , E ) ; 22
③若 D 2 E 2 4F 0 ,则方程不表示任何图形.
4.点 A(x0,y0 ) 与⊙C 的位置关系
(1)|AC|<r⇔点 A 在圆内⇔ (x0-a)2+( y0-b)2 r 2 ;
(2)|AC|=r⇔点 A 在圆上⇔ (x0-a)2+( y0-b)2 r 2 ;
.
【解析】
AOB 120 , OA OB 2
PO
AO cos 60
4 ,即 x02
y02
16
6
又 PC x0 82 y02 且 PO PC
解得:
x0
5 2 1 2
5
1 2
2
x0
82
y02
16
且
0
x02 y02 16
4 x0 4
4
5
1 2
4 ,解得:
1 3
【典例 12】(江苏高考真题)在平面直角坐标系 xOy 中,圆 C 的方程为 x2 y2 8x 15 0 ,若直线 y kx 2
上至少存在一点,使得以该点为圆心,1 为半径的圆与圆 C 有公共点,则 k 的最大值为__________. 【答案】 4
3
【解析】 ∵圆 C 的方程为 x2+y2-8x+15=0,整理得:(x-4)2+y2=1,即圆 C 是以(4,0)为圆心,1 为半径的圆;又直 线 y=kx-2 上至少存在一点,使得以该点为圆心,1 为半径的圆与圆 C 有公共点,∴只需圆 C′:(x-4)2+y2=4
中,
.
故答案为 4
【典例 11】(2019·江苏高三)已知圆 O:x2+y2=4 和圆 O 外一点 P( x0 , y0 ),过点 P 作圆 O 的两条切线, 切点分别为 A,B,且∠AOB=120°.若点 C(8,0)和点 P 满足 PO= PC,则 的范围是_______.
高考数学一轮单元复习:第44讲 圆的方程
2 2
。
│要点探究
要点探究
► 探究点1 探究点 求圆的方程
重庆卷] 轴上, 例 1 [2009·重庆卷 圆心在 y 轴上,半径为 1, 重庆卷 ,且过点 (1,2)的圆的方程为 的圆的方程为( ) , 的圆的方程为 A. x2+(y-2)2=1 - B. x2+(y+2)2=1 + C. (x-1)2+(y-3)2=1 - - D. x2+(y-3)2=1 -
│要点探究
思路】 二次函数图象与x轴有两个交点 【思路】 (1)二次函数图象与 轴有两个交点,与y轴 二次函数图象与 轴有两个交点, 轴 的交点中b≠0,(2)设圆的一般方程用待定系数法,(3)含 设圆的一般方程用待定系数法, 含 的交点中 , 设圆的一般方程用待定系数法 b的两项为一组,并提取 , 不含 的为另一组, 用恒等 的两项为一组, 的为另一组, 的两项为一组 并提取b,不含b的为另一组 式求. 式求
│要点探究
江苏卷]在平面 变式题 [2008·江苏卷 在平面直角坐标系 xOy 中, 江苏卷 在平面直角坐标系 记二次函数 f(x)=x2+2x+b(x∈R)与两坐标轴有三个交 = + ∈ 与两坐标轴有三个交 点,经过三个交点的圆记为 C。 。 (1)求实数 b 的取值范围; 求实数 的取值范围; (2)求圆 C 的方程; 求圆 的方程; (3)问圆 C 是否经过定点 其坐标与 b 无关 ?请证明你 问圆 是否经过定点(其坐标与 无关)? 的结论。 的结论。
│要点探究
【解答】 (1)设所求圆的方程为 解答】 设所求圆的方程为 x2+y2+Dx+Ey+F=0,则由题意有 + + = ,
2020-2021学年高考数学(理)考点:圆的方程

2020-2021学年高考数学(理)考点:圆的方程圆的定义与方程概念方法微思考1.二元二次方程Ax 2+Bxy +Cy 2+Dx +Ey +F =0表示圆的条件是什么? 提示 ⎩⎪⎨⎪⎧A =C ≠0,B =0,D 2+E 2-4AF >0.2.点与圆的位置关系有几种?如何判断? 提示 点和圆的位置关系有三种.已知圆的标准方程(x -a )2+(y -b )2=r 2,点M (x 0,y 0), (1)点在圆上:(x 0-a )2+(y 0-b )2=r 2; (2)点在圆外:(x 0-a )2+(y 0-b )2>r 2; (3)点在圆内:(x 0-a )2+(y 0-b )2<r 2.1.(2020•北京)已知半径为1的圆经过点(3,4),则其圆心到原点的距离的最小值为( ) A .4 B .5C .6D .7【答案】A 【解析】如图示:,半径为1的圆经过点(3,4),可得该圆的圆心轨迹为(3,4)为圆心,1为半径的圆, 故当圆心到原点的距离的最小时,连结OB ,A 在OB 上且1AB =,此时距离最小, 由5OB =,得4OA =,即圆心到原点的距离的最小值是4, 故选A .2.(2018•天津)在平面直角坐标系中,经过三点(0,0),(1,1),(2,0)的圆的方程为__________. 【答案】22(1)1x y -+=(或2220)x y x +-= 【解析】【方法一】根据题意画出图形如图所示, 结合图形知经过三点(0,0),(1,1),(2,0)的圆, 其圆心为(1,0),半径为1, 则该圆的方程为22(1)1x y -+=.【方法二】设该圆的方程为220x y Dx Ey F ++++=, 则042020F D F D E F =⎧⎪++=⎨⎪+++=⎩, 解得2D =-,0E F ==;∴所求圆的方程为2220x y x +-=.故答案为:22(1)1x y -+=(或2220)x y x +-=.3.(2017•上海)若P 、Q 是圆222440x y x y +-++=上的动点,则||PQ 的最大值为__________. 【答案】2【解析】圆222440x y x y +-++=,可化为22(1)(2)1x y -++=,P 、Q 是圆222440x y x y +-++=上的动点,||PQ ∴的最大值为2,故答案为2.1.(2020•江西模拟)圆C 的半径为5,圆心在x 轴的负半轴上,且被直线3440x y ++=截得的弦长为6,则圆C 的方程为( ) A .22230x y x +--= B .2216390x x y +++= C .2216390x x y -+-= D .2240x y x +-=【答案】B【解析】设圆心为(a ,0)(0)a <,由题意知圆心到直线3440x y ++=的距离为|34|45a d +==,解得8a =-, 则圆C 的方程为22(8)25x y ++=,即为2216390x x y +++=, 故选B .2.(2020•西城区模拟)若圆22420x y x y a +-++=与x 轴,y 轴均有公共点,则实数a 的取值范围是( ) A .(-∞,1] B .(-∞,0] C .[0,)+∞ D .[5,)+∞【答案】A【解析】圆2222420(2)(1)5x y x y a x y a +-++=⇒-++=-;圆心(2,1)-,r =圆与x ,y 轴都有公共点; ∴2515150a a a a ⎧-⎪⎪-⇒⎨⎪->⎪⎩; 故选A .3.(2020•全国Ⅱ卷模拟)已知圆C 过点(4,6),(2,2)--,(5,5),点M ,N 在圆C 上,则CMN ∆面积的最大值为( ) A .100 B .25 C .50 D .252【答案】D【解析】设圆C 的方程为220x y Dx Ey F ++++=, 将(4,6),(2,2)--,(5,5)代入可得,52460822050550D E F D E F D E F +++=⎧⎪--+=⎨⎪+++=⎩,解得2D =-,4E =-,20F =-,故圆C 的一般方程为2224200x y x y +---=, 即22(1)(2)25x y -+-=, 故CMN ∆的面积1125||||sin 55222S CM CN MCN =∠⨯⨯=, 故选D .4.(2020•长春三模)已知圆E 的圆心在y 轴上,且与圆22:20C x y x +-=的公共弦所在直线的方程为0x =,则圆E 的方程为( )A .22(2x y +-=B .22(2x y +=C .22(3x y +=D .22(3x y ++=【答案】C【解析】圆E 的圆心在y 轴上,∴设圆心E 的坐标为(0,)b ,设半径为r , 则圆E 的方程为:222()x y b r +-=,即222220x y by b r +-+-=, 又圆C 的方程为:2220x y x +-=,两圆方程相加得公共弦所在直线的方程为:2202b r x by --+=,又公共弦所在直线的方程为0x =,∴2202b b r ⎧=⎪⎨-=⎪⎩,解得b r ⎧=⎪⎨=⎪⎩∴圆E的方程为:22(3x y +=,故选C .5.(2020•怀柔区一模)已知圆C 与圆22(1)1x y -+=关于原点对称,则圆C 的方程为( ) A .221x y += B .22(1)1x y ++= C .22(1)1x y +-= D .22(1)1x y ++=【答案】D【解析】圆22(1)1x y -+=的圆心坐标为(1,0),半径为1. 点(1,0)关于原点的对称点为(1,0)-, 则所求圆的方程为22(1)1x y ++=. 故选D .6.(2020•郑州二模)圆22(2)(12)4x y ++-=关于直线80x y -+=对称的圆的方程为( ) A .22(3)(2)4x y +++= B .22(4)(6)4x y ++-= C .22(4)(6)4x y -+-= D .22(6)(4)4x y +++=【答案】C【解析】由圆22(2)(12)4x y ++-=可得圆心坐标(2,12)-,半径为2,由题意可得关于直线80x y -+=对称的圆的圆心与(2,12)-关于直线对称,半径为2, 设所求的圆心为(,)a b 则21280221212a b b a -+⎧-+=⎪⎪⎨-⎪=-⎪+⎩解得:4a =,6b =,故圆的方程为:22(4)(6)4x y -+-=, 故选C .7.(2020•西城区一模)设(2,1)A -,(4,1)B ,则以线段AB 为直径的圆的方程是( )A .22(3)2x y -+=B .22(3)8x y -+=C .22(3)2x y ++=D .22(3)8x y ++=【答案】A【解析】弦长AB =(3,0), 所以圆的方程22(3)2x y -+=, 故选A .8.(2020•拉萨二模)圆心为(2,1)且和x 轴相切的圆的方程是( ) A .22(2)(1)1x y -+-= B .22(2)(1)1x y +++= C .22(2)(1)5x y -+-= D .22(2)(1)5x y +++=【答案】A【解析】圆心为(2,1)且和x 轴相切的圆,它的半径为1, 故它的的方程是22(2)(1)1x y -+-=, 故选A .9.(2020•绵阳模拟)已知圆22:6890C x y x y +--+=,点M ,N 在圆C 上,平面上一动点P 满足||||PM PN =且PM PN ⊥,则||PC 的最大值为( )A .8B .C .4D .【答案】D【解析】根据题意,若平面上一动点P 满足||||PM PN =,又由||||CM CN =,则PC 为线段MN 的垂直平分线,设MN 的中点为G ,||NG n =,||CG m =,又由||||PM PN =且PM PN ⊥,则PMN ∆为等腰直角三角形,故||||PG NG n ==, 圆22:6890C x y x y +--+=,即22(3)(4)16x y -+-=, 则2216m n +=,则||()16(PC m n m =++当且仅当m n =时等号成立,故||PC 的最大值为 故选D .10.(2020•绵阳模拟)已知圆22:280C x y x +--=,直线l 经过点(2,2)M ,且将圆C 及其内部区域分为两部分,则当这两部分的面积之差的绝对值最大时,直线l 的方程为( ) A .220x y -+= B .260x y +-= C .220x y --= D .260x y +-=【答案】D【解析】如图所示:圆22:280C x y x +--=,化为标准方程为:22(1)9x y -+=,∴圆心(1,0)C ,当直线l 与CM 垂直时,直线l 分圆C 的两部分的面积之差的绝对值最大, 20221CM k -==-, ∴直线l 的斜率12k =-, ∴直线l 的方程为:12(2)2y x -=--,即260x y +-=,故选D .11.(2020•和平区校级二模)已知圆C 的圆心在直线230x y --=上,且过点(2,3)A -,(2,5)B --,则圆C 的标准方程为__________. 【答案】22(1)(2)10x y +++=【解析】根据题意,圆C 的圆心在直线230x y --=上,设圆心的坐标为(23,)t t +, 圆C 经过点(2,3)A -,(2,5)B --,则有2222(232)(3)(232)(5)t t t t +-++=++++, 解可得2t =-,则231t +=-,即圆心C 的坐标为(1,2)--, 圆的半径为r ,则2222||(12)(23)10r CA ==--+-+=, 故圆C 的标准方程为22(1)(2)10x y +++=; 故答案为:22(1)(2)10x y +++=.12.(2020•江苏模拟)在平面直角坐标系xOy 中,已知圆M 经过直线:0l x -+=与圆22:4C x y +=的两个交点.当圆M 的面积最小时,圆M 的标准方程为__________.【答案】223(()12x y ++-=【解析】根据题意,直线:0l x -+=与圆22:4C x y +=相交,设其交点为A 、B ,则有2204x x y ⎧-+⎪⎨+=⎪⎩,联立解可得:1x y ⎧=⎪⎨=⎪⎩02x y =⎧⎨=⎩,即A 、B 的坐标为(1)和(0,2);当AB 为圆M 的直径时,圆M 的面积最小,此时圆M的圆心(M ,3)2,半径1||12r AB ==; 则此时圆M的标准方程为:223(()12x y +-=;故答案为:223(()12x y ++-=. 13.(2020•河东区一模)已知圆O 过点(0,0)A 、(0,4)B 、(1,1)C ,点(3,4)D 到圆O 上的点最小距离为__________.【解析】设圆O 的方程为220x y dx ey f ++++=,圆O 过点(0,0)A 、(0,4)B 、(1,1)C , ∴0016040110f e f d e f =⎧⎪++++=⎨⎪++++=⎩,求得240d e f =⎧⎪=-⎨⎪=⎩,故圆的方程为22240x y x y ++-=,即22(1)(2)5x y ++-=,表示圆心为(1,2)-的圆.||DO =故点(3,4)D 到圆O上的点最小距离为.14.(2020•南通模拟)在平面直角坐标系xOy 中,已知过点(10,0)-的圆M 与圆22660x y x y +--=相切于原点,则圆M 的半径是__________. 【答案】【解析】圆22660x y x y +--=化为22(3)(3)18x y -+-=, 圆心坐标为(3,3),半径为 如图,所求的圆与圆22660x y x y +--=相切于原点,∴两圆圆心的连线在直线y x =上,可设所求圆的圆心为(,)a a 解得5a=-,∴所求圆M 的半径为故答案为:15.(2020•滨海新区模拟)以点(1,0)C 为圆心,且被y 轴截得的弦长为2的圆的方程为__________. 【答案】22(1)2x y -+= 【解析】如图,圆的半径为r . 又圆心为(1,0),∴所求圆的方程为22(1)2x y -+=.故答案为:22(1)2x y -+=.16.(2020•东城区一模)圆心在x 轴上,且与直线1:l y x =和2:2l y x =-都相切的圆的方程为__________. 【答案】221(1)2x y -+=【解析】设所求圆的方程为222()x a y r -+=, 因为圆与直线1:l y x =和2:2l y x =-r ==,解得1a =,r ,所以圆的方程为221(1)2x y -+=. 故答案为:221(1)2x y -+=. 17.(2020•河西区一模)已知圆C 的圆心在第一象限,且在直线2y x =上,圆C 与抛物线24y x =的准线和x 轴都相切,则圆C 的方程为__________. 【答案】22(1)(2)4x y -+-=【解析】圆C 的圆心在第一象限,且在直线2y x =上, 故可设圆心为(,2)C a a ,0a >,圆C 与抛物线24y x =的准线1x =-和x 轴都相切,故圆的半径|1||2|a a +=,解得1a =,或13a =-(舍去),故半径为2,则圆C 的方程为22(1)(2)4x y -+-=, 故答案为:22(1)(2)4x y -+-=.18.(2020•宿迁模拟)在平面直角坐标系中,A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2100x y +-=相切,当圆C 面积最小时,圆C 的标准方程为__________. 【答案】22(2)(1)5x y -+-=【解析】A ,B 分别是x 轴和y 轴上的动点,若以AB 为直径的圆C 与直线2100x y +-=相切,所以原点(0,0)在圆上,原点(0,0)到直线2100x y +-=的距离d ==(0,0)到直线的距离为直径时,该圆最小.即2dr =直线2100x y +-=与圆的切点坐标满足210012x y y x +-=⎧⎪⎨=⎪⎩,解得42x y =⎧⎨=⎩,所以圆心坐标为40222012a b +⎧==⎪⎪⎨+⎪==⎪⎩,故圆的方程为22(2)(1)5x y -+-=. 故答案为:22(2)(1)5x y -+-=.19.(2020•滨海新区模拟)已知圆心为C 的圆经过点(1,1)A --和(2,2)B -,且圆心C 在直线:10l x y --=上,则圆心为C 的圆的标准方程是__________.【答案】22(3)(2)25x y -+-=【解析】由(1,1)A --,(2,2)B -,得AB 的中点为3(2-,1)2,又12312AB k --==--+,AB ∴的垂直平分线方程为113()232y x -=+,即330x y -+=. 联立33010x y x y -+=⎧⎨--=⎩,解得32x y =⎧⎨=⎩.∴圆心坐标为(3,2)C ,半径为||5CA =.∴圆心为C 的圆的标准方程是22(3)(2)25x y -+-=.故答案为:22(3)(2)25x y -+-=.20.(2020•如皋市校级模拟)在平面直角坐标系xOy 中,若(0,1)A ,点B 是圆22:230C x y x ++-=上的动点,则2AB BO +的最小值为__________.【解析】由(0,1)A ,圆22:230C x y x ++-=上可化为22(1)4x y ++=, 设点(,)B x y ,则2AB BO +=====这表示圆C 上的点B 到点A 的距离与到点(3,0)D 的距离的和, 所以点B 在线段AD 上时,2AB BO +取得最小值,如图所示,所以2AB BO +的最小值是AD21.(2020•江苏一模)在平面直角坐标系xOy 中,已知圆22:48120M x y x y +--+=,圆N 与圆M 外切于点(0,)m ,且过点(0,2)-,则圆N 的标准方程为__________. 【答案】22(2)8x y ++=【解析】已知圆22:48120M x y x y +--+=,整理得:22(2)(4)8x y -+-=, 令0y =,圆的方程转换为:28120y y -+=,解得2y =或6. 由于圆N 与圆M 相切于(0,)m 且过点(0,2)-. 所以2m =.即圆N 经过点(0,2)A ,(0,2)B -. 所以圆心在这两点连线的中垂线x 轴上,x 轴与MA 的交点为圆心N .所以:2MA y x =+. 令0y =,则2x =-. 即(2,0)N -,|R NA ==.所以圆N 的标准方程为:22(2)8x y ++=. 故答案为:22(2)8x y ++=.22.(2020•南通模拟)在平面直角坐标系xOy 中,已知圆C 圆心在直线:21l y x =-上,若圆C 上存在一点P ,使得直线1:20l ax y --=与直线2:20l x ay +-=交于点P ,则当实数a 变化时,圆心C 的横坐标x 的取值范围是__________. 【答案】[1-,7]5【解析】因为直线1:20l ax y --=与直线2:20l x ay +-=互相垂直,且分别过定点(0,2)A -,(2,0)B ,故点P 在以AB 为直径的圆上运动,直径AB ,圆心坐标为(1,1)-, 又因为点P 在圆C 上,故两圆有公共点,所以两圆的圆心距d 满足022d , 即220(1)(211)22x x -+-+,解得715x-, 故答案为[1-,7]5.23.(2020•南通模拟)已知半径为1的圆C 的圆心在射线2(1)y x x =-+上,若圆C 上有且仅有一点Q ,满足226QA QB +=,其中(1,1)A ,(3,3)B ,则圆C 的方程为__________. 【答案】22(2)1x y -+=【解析】设(,)Q x y ,则由22||||6QA QB +=得:2222[(1)(1)][(3)(3)]6x y x y -+-+-+-=, 整理得22(2)(2)1x y -+-=,所以点Q 在以(2,2)为圆心,半径为1的圆上;又点Q 在圆22()[(2)]1(1)x a y a a -+--+=上, 且两圆有唯一公共点,则两圆相切,如图所示; 当两圆外切时,22(2)[2(2)]4a a -+--+=,解得2a =或0a =,应取2a =;当两圆内切时,22(2)[2(2)]0a a -+--+=, 此时方程无实数解,a 的值不存在; 综上知,圆C 的圆心为(2,0), 圆C 的方程为22(2)1x y -+=. 故答案为:22(2)1x y -+=.24.(2020•许昌一模)若圆22420x y x y F +--+=的半径为3,则F =__________. 【答案】4-【解析】根据题意,圆22420x y x y F +--+=的半径为33=, 解可得:4F =-; 故答案为:4-.25.(2020•南开区校级模拟)过点(3,2)A -,(5,2)B --,且圆心在直线3240x y -+=上的圆的半径为__________.【解析】(3,2)A -,(5,2)B --,∴2225(3)AB k --==---,AB 的中点坐标为(4,0)-,AB ∴的垂直平分线方程为1(4)2y x =-+,即240x y ++=.联立2403240x y x y ++=⎧⎨-+=⎩,解得21x y =-⎧⎨=-⎩.∴所求圆的圆心坐标为(2,1)--,半径r26.(2020•洛阳二模)已知点A ,B 分别在x 轴,y 轴上,||3AB =,2BM MA =. (1)求点M 的轨迹C 的方程;(2)过点(0,1)N 作两条互相垂直的直线1l ,2l ,与曲线C 分别交于P ,Q (不同于点)N 两点,求证:直线PQ 过定点.【解析】(1)设点M 的坐标为(,)M x y ,(,0)A a ,(0,)B b .由2BM MA =得21(,)33M a b所以3,32a xb y == 因为229a b += 所以223()(3)92x y +=则2214xy += (2)由题可知,直线NP 的斜率存在,设直线1()NP l 的方程:1y kx =+ 联立22114y kx x y =+⎧⎪⎨+=⎪⎩得:22(14)80k x kx ++=,解得12280,14k x x k -==+ 则222814(,)1414k k P k k --++,由于1l ,2l 为过N 互相垂直的直线,同理得22284(,)44k k Q k k -++直线PQ 的斜率为22222224141414885414k k k k k k k k k k k----++==--++ 直线PQ 的方程为2222418()454k k ky x k k k ---=-++化简得:21355k y x k -=-因此直线PQ 恒过点3(0,)5-.27.(2019•西湖区校级模拟)如图,已知圆M 过点(10,4)P ,且与直线43200x y +-=相切于点(2,4)A (1)求圆M 的标准方程;(2)设平行于OA 的直线l 与圆M 相交于B 、C 两点,且||||BC OA =,求直线l 的方程;【解析】(1)过点(2,4)A 且与直线43200x y +-=垂直的直线方程为34100x y -+=①;AP 的垂直平分线方程为6x =;由①②联立得圆心(6,7)M ,半径||5r AM =; 圆M 的方程为22(6)(7)25x y -+-=. (2)因为直线//l OA ,所以直线l 的斜率为40220-=-. 设直线l 的方程为2y x m =+,即20x y m -+= 则圆心M 到直线l 的距离d =因为BC OA ==,而222()2BC MC d =+,所以2(5)2555m +=+,解得5m =或15m =-. 故直线l 的方程为250x y -+=或2150x y --=.28.(2019•西湖区校级模拟)已知圆22:(3)(4)4C x y -+-=, (Ⅰ)若直线1l 过定点(1,0)A ,且与圆C 相切,求1l 的方程;(Ⅱ)若圆D 的半径为3,圆心在直线2:20l x y +-=上,且与圆C 外切,求圆D 的方程.【解析】(Ⅰ)①若直线1l 的斜率不存在,即直线是1x =,符合题意. ②若直线1l 斜率存在,设直线1l 为(1)y k x =-,即0kx y k --=. 由题意知,圆心(3,4)到已知直线1l 的距离等于半径2,2=解之得34k =. 所求直线方程是1x =,3430x y --=.(Ⅱ)依题意设(,2)D a a -,又已知圆的圆心(3,4)C ,2r =,由两圆外切,可知5CD =∴5=,解得3a =,或2a =-, (3,1)D ∴-或(2,4)D -,∴所求圆的方程为22(3)(1)9x y -++=或22(2)(4)9x y ++-=.。
高考数学圆的方程与性质选择题

高考数学圆的方程与性质选择题1. 请根据圆的标准方程 (x-a)^2 + (y-b)^2 = r^2,判断圆心坐标和半径。
2. 圆的方程 (x-2)^2 + (y+1)^2 = 9 是一个什么圆?3. 已知一个圆的方程是 (x-1)^2 + (y-2)^2 = 16,请问这个圆的半径是多少?4. 如果一个圆的方程是 x^2 + y^2 = 1,那么这个圆的圆心坐标和半径分别是什么?5. 已知一个圆的方程是 (x-2)^2 + (y-3)^2 = 4,请判断这个圆是否是圆心在原点的圆。
6. 请根据圆的方程 x^2 + y^2 - 2x - 4y + 5 = 0,判断这个圆的圆心坐标和半径。
7. 已知一个圆的方程是 (x-3)^2 + (y+2)^2 = 1,请问这个圆的半径是多少?8. 请判断圆的方程 x^2 + y^2 - 4x + 2y - 15 = 0 是否是一个标准圆的方程。
9. 如果一个圆的方程是 (x-1)^2 + (y-2)^2 = 5,请问这个圆的圆心坐标和半径分别是什么?10. 已知一个圆的方程是 (x+2)^2 + (y-3)^2 = 1,请判断这个圆的圆心坐标和半径。
11. 请根据圆的方程 (x-2)^2 + (y+1)^2 = 4,判断这个圆的半径。
12. 已知一个圆的方程是 x^2 + y^2 = 4,请问这个圆的圆心坐标和半径分别是什么?13. 请判断圆的方程 x^2 + y^2 - 2x - 4y + 5 = 0 是否是一个标准圆的方程。
14. 如果一个圆的方程是 (x-3)^2 + (y+2)^2 = 1,请问这个圆的半径是多少?15. 请根据圆的方程 (x-2)^2 + (y+1)^2 = 4,判断这个圆的圆心坐标和半径。
16. 已知一个圆的方程是 (x+2)^2 + (y-3)^2 = 1,请判断这个圆的圆心坐标和半径。
17. 请根据圆的方程 (x-2)^2 + (y+1)^2 = 4,判断这个圆的半径。
高考数学一轮复习圆的方程

F=0,
16+4D+F=0, 2-D+E+F=0,
D=-4,
解得E=-6, F=0,
易得 D2+E2-4F>0,所以过这
三点的圆的方程为 x2+y2-4x-6y=0,即(x-2)2+(y-3)2=13.
若圆过(0,0),(4,0),(4,2)三点, 设过这三点的圆的一般方程为 x2+y2+Dx+Ey+F=0,分别将三点
第二节
圆与方程
第二节 圆与方程
1.回顾确定圆的几何要素,掌握圆的标准方程与一般方程. 2.初步了解用代数方法处理几何问题的思想. 3.能根据给定直线、圆的方程,判断直线与圆、圆与圆的位置关系. 4.能用直线和圆的方程解决一些简单的问题.
必备知识·系统归纳 先整体系统知识,再分课时研究题点考法
Ⅰ.主干知识的再认再现
圆心到直线 l 的距离为 2 = 2<2,所以直线 l 与圆相交.又圆 心不在直线 l 上,所以直线不过圆心.故选 D. 答案:D
4.(人教 A 版选择性必修①P98·T3 改编)直线 y= 3x 被圆 C:x2+y2-2x
=0 截得的线段长为
()
A.2
B. 3
C.1
D. 2
解析:圆 C:x2+y2-2x=0 的圆心为(1,0),半径为 1,圆心到直线 y = 3x 的距离为 d= |3+3| 1= 23,弦长为 2· 1- 232=1,故选 C.
16+4D+F=0,
可 得 2-D+E+F=0, 20+4D+2E+F=0,
D=-156, 解 得 E=-2,
F=-156,
易得 D2+E2-
4F>0,所以过这三点的圆的方程为 x2+y2-156x-2y-156=0,即x-852 +(y-1)2=12659.
高中数学必考内容,圆的方程,(高考热点)
2 2
(2)当D2+E2-4F=0时,方程只有一组解X=-D/2
D E y=-E/2,表示一个点( 2 , 2 )
(3)当D2+E2-4F<0时,方程(1)无实数解,所以 不表示任何图形。
所以形如x2 +y 2+Dx+Ey+F=0 (D2+E2-4F>0) 可表示圆的方程
思考5:方程 x y Dx Ey F 0 2 2 ( D E 4F 0)叫做圆的一般方程,其 圆心坐标和半径分别是什么?
用待定系数法求圆方程的基本步骤: (1)设圆方程 ;(2)列方程组; (3)求系数; (4)小结.
例2 方程 x y ax 2ay 2a a 1 0 表示的图形是一个圆,求a的取值范围.
2 2 2
求动点轨迹的步骤:
1.建立坐标系,设动点坐标M(x, y);
2.列出动点M满足的等式并化简; 3.说明轨迹的形状.
圆的方程
问题提出 1.在平面直角坐标系中,两点确定一条 直线,一点和倾斜角也确定一条直线, 那么在什么条件下可以确定一个圆呢?
圆心和半径
2.直线可以用一个方程表示,圆也可 以用一个方程来表示,怎样建立圆的 方程是我们需要探究的问题.
知识探究一:圆的标准方程
思考1:圆可以看成是平面上的一条曲线,在 平面几何中,圆是怎样定义的?
x y 8x 6 y 0
2 2
用待定系数法求圆的方程的步骤: 1)根据题意设所求圆的方程为标准式或一般式; 2)根据条件列出关于a、b、r或D、E、F的方程; 3)解方程组,求出a、b、r或D、E、F的值,代入 所设方程,就得要求的方程.
根据题目条件,恰当选择圆方程形式: ①若知道或涉及圆心和半径,我们一般采用圆的标准方程较简单. ②若已知三点求圆的方程,我们常常采用圆的一般方程用待定系数 法求解.
2025高考数学一轮复习-圆的方程-专项训练【含解析】
课时过关检测(四十八)圆的方程【原卷版】1.圆心为(2,1)且和x轴相切的圆的方程是()A.(x-2)2+(y-1)2=1B.(x+2)2+(y+1)2=1C.(x-2)2+(y-1)2=5D.(x+2)2+(y+1)2=52.设a∈R,则“a>2”是“方程x2+y2+ax-2y+2=0的曲线是圆”的()A.充分不必要条件B.必要不充分条件C.充要条件D.既不充分也不必要条件3.若x2+y2=8,则2x+y的最大值为()A.8B.4C.210D.54.已知圆C:(x-3)2+(y-1)2=1和两点A(-t,0),B(t,0)(t>0),若圆C上存在点P,使得∠APB=90°,则t的取值范围是()A.(0,2]B.[1,2]C.[2,3]D.[1,3]5.点M为圆C:(x+2)2+(y+1)2=1上任意一点,直线(1+3λ)x+(1+2λ)y=2+5λ过定点P,则|MP|的最大值为()A.23B.13C.23+1D.13+16.(多选)已知圆x2+y2-4x-1=0,则下列关于该圆说法正确的有()A .关于点(2,0)对称B .关于直线y =0对称C .关于直线x +3y -2=0对称D .关于直线x -y +2=0对称7.(多选)已知圆C 关于y 轴对称,经过点(1,0)且被x 轴分成两段,弧长比为1∶2,则圆C 可能的方程为()A .x 2=43B .x 2=43C .(x -3)2+y 2=43D .(x +3)2+y 2=438.已知三个点A (0,0),B (2,0),C (4,2),则△ABC 的外接圆的圆心坐标是________.9.已知点P 为圆C :x 2+y 2-4x -2y +1=0上任意一点,A ,B 为直线3x +4y +5=0上的两动点,且|AB |=2,则△ABP 的面积的取值范围是________.10.已知以点P 为圆心的圆经过点A (-1,0)和B (3,4),线段AB 的垂直平分线交圆P 于点C 和D ,且|CD |=410.(1)求直线CD 的方程;(2)求圆P 的方程.11.瑞士数学家欧拉在其所著的《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.若已知△ABC 的顶点A (-4,0),B (0,4),其欧拉线方程为x -y +2=0,则顶点C 的坐标可以是()A .(1,3)B .(3,1)C .(-2,0)D .(0,-2)12.写出一个关于直线x +y -1=0对称的圆的方程____________.13.已知A (-2,0),B (2,0),动点M 满足|MA |=2|MB |,则点M 的轨迹方程是____________________;又若MA ―→·MB ―→=0,此时△MAB 的面积为________.14.已知点P (2,2),圆C :x 2+y 2-8y =0,过点P 的动直线l 与圆C 交于A ,B 两点,线段AB 的中点为M ,O 为坐标原点.(1)求点M 的轨迹方程;(2)当|OP |=|OM |时,求l 的方程及△POM 的面积.15.(多选)设有一组圆C k :(x -k )2+(y -k )2=4(k ∈R ),下列命题正确的是()A .不论k 如何变化,圆心C 始终在一条直线上B .所有圆C k 均不经过点(3,0)C .经过点(2,2)的圆C k 有且只有一个D .所有圆的面积均为4π16.已知曲线T :F (x ,y )=0,对坐标平面上任意一点P (x ,y ),定义F [P ]=F (x ,y ),若两点P ,Q 满足F [P ]·F [Q ]>0,称点P ,Q 在曲线T 同侧;F [P ]·F [Q ]<0,称点P ,Q 在曲线T 两侧.(1)直线过l 原点,线段AB 上所有点都在直线l 同侧,其中A (-1,1),B (2,3),求直线l 的斜率的取值范围;(2)已知曲线F (x ,y )=(3x +4y -5)4-x 2-y 2=0,O 为坐标原点,求点集S ={P |F [P ]·F [O ]>0}的面积.课时过关检测(四十八)圆的方程【解析版】1.圆心为(2,1)且和x 轴相切的圆的方程是()A .(x -2)2+(y -1)2=1B .(x +2)2+(y +1)2=1C .(x -2)2+(y -1)2=5D .(x +2)2+(y +1)2=5解析:A 圆心为(2,1)且和x 轴相切的圆,它的半径为1,故它的方程是(x -2)2+(y -1)2=1,故选A .2.设a ∈R ,则“a >2”是“方程x 2+y 2+ax -2y +2=0的曲线是圆”的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件解析:A方程x 2+y 2+ax -2y +2=0的曲线是圆,则有D 2+E 2-4F =a 2+4-8>0,解得a >2或a <-2,则“a >2”是“a >2或a <-2”的充分不必要条件,所以“a >2”是“方程x 2+y 2+ax -2y +2=0的曲线是圆”的充分不必要条件.故选A .3.若x 2+y 2=8,则2x +y 的最大值为()A .8B .4C .210D .5解析:C 设2x +y =t ,则y =t -2x ,当直线y =t -2x 与x 2+y 2=8相切时,t 取到最值,所以|t |5≤22,解得-210≤t ≤210,所以2x +y 的最大值为210,故选C .4.已知圆C :(x -3)2+(y -1)2=1和两点A (-t,0),B (t,0)(t >0),若圆C 上存在点P ,使得∠APB =90°,则t 的取值范围是()A .(0,2]B .[1,2]C .[2,3]D .[1,3]解析:D圆C :(x -3)2+(y -1)2=1的圆心C (3,1),半径为1,因为圆心C 到O (0,0)的距离为2,所以圆C 上的点到O (0,0)的距离最大值为3,最小值为1,又因为∠APB =90°,则以AB 为直径的圆和圆C 有交点,可得|PO |=12|AB |=t ,所以有1≤t ≤3,故选D .5.点M 为圆C :(x +2)2+(y +1)2=1上任意一点,直线(1+3λ)x +(1+2λ)y =2+5λ过定点P ,则|MP |的最大值为()A .23B .13C .23+1D .13+1解析:D 整理直线方程得:(x +y -2)+(3x +2y -5)λ=0+y -2=0,x +2y -5=0得=1,=1,∴P (1,1),由圆的方程知圆心C (-2,-1),半径r =1,∴|MP |max =|CP |+r =(-2-1)2+(-1-1)2+1=13+1.故选D .6.(多选)已知圆x 2+y 2-4x -1=0,则下列关于该圆说法正确的有()A .关于点(2,0)对称B .关于直线y =0对称C .关于直线x +3y -2=0对称D .关于直线x -y +2=0对称解析:ABCx 2+y 2-4x -1=0⇒(x -2)2+y 2=5,所以圆心的坐标为(2,0),半径为5.A项,圆是关于圆心对称的中心对称图形,而点(2,0)是圆心,所以本选项正确;B 项,圆是关于直径所在直线对称的轴对称图形,直线y =0过圆心,所以本选项正确;C 项,圆是关于直径所在直线对称的轴对称图形,直线x +3y -2=0过圆心,所以本选项正确;D 项,圆是关于直径所在直线对称的轴对称图形,直线x -y +2=0不过圆心,所以本选项不正确.故选A 、B 、C .7.(多选)已知圆C 关于y 轴对称,经过点(1,0)且被x 轴分成两段,弧长比为1∶2,则圆C 可能的方程为()A .x 2=43B .x 2=43C .(x -3)2+y 2=43D .(x +3)2+y 2=43解析:AB由题意知圆心在y 轴上,且被x 轴所分劣弧所对圆心角为2π3,设圆心C (0,a ),半径为r ,则r sin π3=1,r cos π3=|a |,解得r =23,即r 2=43,|a |=33,即a =±33,故圆C的方程为x 2=43.8.已知三个点A (0,0),B (2,0),C (4,2),则△ABC 的外接圆的圆心坐标是________.解析:设圆的方程为x 2+y 2+Dx +Ey +F =0,则=0,+2D +F =0,+4D +2E +F =0,解得=-2,=-6,=0,所以圆的方程为x 2-2x +y 2-6y =0,即(x -1)2+(y -3)2=10,所以圆心坐标为(1,3).答案:(1,3)9.已知点P 为圆C :x 2+y 2-4x -2y +1=0上任意一点,A ,B 为直线3x +4y +5=0上的两动点,且|AB |=2,则△ABP 的面积的取值范围是________.解析:圆C 的标准方程为(x -2)2+(y -1)2=4,圆心C (2,1),半径r =2,圆心C 到直线3x +4y +5=0的距离d =|6+4+5|32+42=3,设P 到直线AB 的距离为h ,则S △ABP =12·|AB |·h=h ,∵d -r ≤h ≤d +r ,∴1≤h ≤5,∴S △ABP ∈[1,5],即△ABP 的面积的取值范围为[1,5].答案:[1,5]10.已知以点P 为圆心的圆经过点A (-1,0)和B (3,4),线段AB 的垂直平分线交圆P 于点C 和D ,且|CD |=410.(1)求直线CD 的方程;(2)求圆P 的方程.解:(1)直线AB 的斜率k =1,AB 的中点坐标为(1,2).所以直线CD 的方程为y -2=-(x -1),即x +y -3=0.(2)设圆心P (a ,b ),则由点P 在CD 上得a +b -3=0.①又直径|CD |=410,所以|PA |=210.所以(a +1)2+b 2=40.②=-3,=6=5,=-2,所以圆心P (-3,6)或P (5,-2),所以圆P 的方程为(x +3)2+(y -6)2=40或(x -5)2+(y +2)2=40.11.瑞士数学家欧拉在其所著的《三角形的几何学》一书中提出:任意三角形的外心、重心、垂心在同一条直线上,后人称这条直线为欧拉线.若已知△ABC 的顶点A (-4,0),B (0,4),其欧拉线方程为x -y +2=0,则顶点C 的坐标可以是()A .(1,3)B .(3,1)C .(-2,0)D .(0,-2)解析:D ∵A (-4,0),B (0,4),∴AB 的垂直平分线方程为x +y =0,又外心在欧拉线x-y +2=0+y =0,-y +2=0,解得三角形ABC 的外心为G (-1,1),又r =|GA |=(-1+4)2+(1-0)2=10,∴△ABC 外接圆的方程为(x +1)2+(y -1)2=10.设C (x ,y ),则三角形ABC 即x -43-y +43+2=0.整理得x -y -2=0.联x +1)2+(y -1)2=10,-y -2=0,=0,=-2=2,=0.∴顶点C 的坐标可以是(0,-2).故选D .12.写出一个关于直线x +y -1=0对称的圆的方程____________.解析:设圆心坐标为C (a ,b ),因为圆C 关于x +y -1=0对称,所以C (a ,b )在直线x +y -1=0上,则a +b -1=0,取a =1⇒b =0,设圆的半径为1,则圆的方程(x -1)2+y 2=1.答案:(x -1)2+y 2=1(答案不唯一)13.已知A (-2,0),B (2,0),动点M 满足|MA |=2|MB |,则点M 的轨迹方程是____________________;又若MA ―→·MB ―→=0,此时△MAB 的面积为________.解析:设M (x ,y ),由|MA |=2|MB |,得(x +2)2+y 2=2(x -2)2+y 2,整理得3x 2+3y 2-20x +12=0.以AB 为直径的圆的方程为x 2+y 2=4,x 2+3y 2-20x +12=0,2+y 2=4,解得|y |=85.即M 点的纵坐标的绝对值为85.此时△MAB 的面积为S =12×4×85=165.答案:3x 2+3y 2-20x +12=016514.已知点P (2,2),圆C :x 2+y 2-8y =0,过点P 的动直线l 与圆C 交于A ,B 两点,线段AB 的中点为M ,O 为坐标原点.(1)求点M 的轨迹方程;(2)当|OP |=|OM |时,求l 的方程及△POM 的面积.解:圆C :x 2+(y -4)2=42,故圆心为C (0,4),半径为4.(1)当C ,M ,P 三点均不重合时,∠CMP =90°,所以点M 的轨迹是以线段PC 为直径的圆(除去点P ,C ),线段PC 中点为(1,3),12|PC |=12(2-0)2+(2-4)2=2,故M 的轨迹方程为(x -1)2+(y -3)2=2(x ≠2,且y ≠2或x ≠0,且y ≠4).当C ,M ,P 三点中有重合的情形时,易求得点M 的坐标为(2,2)或(0,4).综上可知,点M 的轨迹是一个圆,轨迹方程为(x -1)2+(y -3)2=2.(2)由(1)可知点M 的轨迹是以点N (1,3)为圆心,2为半径的圆.法一(几何法):由于|OP |=|OM |,故O 在线段PM 的垂直平分线上.又P 在圆N 上,从而ON⊥PM.因为ON的斜率为3,所以直线l的斜率为-13,故直线l的方程为y=-13x+83,即x+3y-8=0.又易得|OM|=|OP|=22,点O到直线l的距离为812+32=4105,|PM|==4105,所以△POM的面积为12×4105×4105=165.法二(代数法):设M(x,y),由|OM|=|OP|=22得x2+y2=8,2+y2=8,①-1)2+(y-3)2=2,②①-②得直线l方程为x+3y-8=0,将x=8-3y代入①得5y2-24y+28=0,解得y1=145,y2=2.从而x1=-25,x2=2.所以M-25,|PM|==4105.又点O到l距离d=812+32=4105,所以△POM的面积S=12|PM|·d=12×4105×4105=165.15.(多选)设有一组圆C k:(x-k)2+(y-k)2=4(k∈R),下列命题正确的是()A.不论k如何变化,圆心C始终在一条直线上B.所有圆C k均不经过点(3,0)C.经过点(2,2)的圆C k有且只有一个D.所有圆的面积均为4π解析:ABD圆心坐标为(k,k),在直线y=x上,A正确;令(3-k)2+(0-k)2=4,化简得2k2-6k+5=0,∵Δ=36-40=-4<0,∴2k2-6k+5=0无实数根,B正确;由(2-k)2+(2-k)2=4,化简得k2-4k+2=0,∵Δ=16-8=8>0,有两不等实根,∴经过点(2,2)的圆C k有两个,C错误;由圆的半径为2,得圆的面积为4π,D正确.故选A、B、D.16.已知曲线T:F(x,y)=0,对坐标平面上任意一点P(x,y),定义F[P]=F(x,y),若两点P,Q满足F[P]·F[Q]>0,称点P,Q在曲线T同侧;F[P]·F[Q]<0,称点P,Q在曲线T 两侧.(1)直线过l原点,线段AB上所有点都在直线l同侧,其中A(-1,1),B(2,3),求直线l 的斜率的取值范围;(2)已知曲线F(x,y)=(3x+4y-5)4-x2-y2=0,O为坐标原点,求点集S={P|F[P]·F[O]>0}的面积.解:(1)由题意,显然直线l斜率存在,设方程为y=kx,则F(x,y)=kx-y=0,因为A(-1,1),B(2,3),线段AB上所有点都在直线l同侧,则F[A]·F[B]=(-k-1)(2k-3)>0,解得-1<k<3 2.(2)因为F[O]<0,所以F[P]=(3x+4y-5)·4-x2-y2<0,x+4y-5<0,2+y2<4,点集S为圆x2+y2=4在直线3x+4y-5=0下方内部,如图所示,设直线与圆的交点为A,B,则O到AB的距离为1,故∠AOB=2π3,因此,所求面积为S=12·4π3·22+12·32·22=8π3+3.。
2024高考数学常考题型 第18讲 直线与圆常考6种题型总结(解析板)
第18讲直线与圆常考6种题型总结【考点分析】考点一:圆的定义:在平面上到定点的距离等于定长的点的轨迹是圆考点二:圆的标准方程设圆心的坐标()C a b ,,半径为r ,则圆的标准方程为:()()222x a y b r -+-=考点三:圆的一般方程圆的一般方程为220x y Dx Ey F ++++=,圆心坐标:()22D E --,,半径:r =注意:①对于F E D 、、的取值要求:2240D E F +->当2240D E F +-=时,方程只有实数解22D E x y =-=-,.它表示一个点()22D E--,当2240D E F +-<时,方程没有实数解,因而它不表示任何图形.②二元二次方程220Ax Bxy Cy Dx Ey F +++++=,表示圆的充要条件是22040A C B D E AF =≠⎧⎪=⎨⎪+->⎩考点四:以1122()()A x y B x y ,,,为直径端点的圆的方程为1212()()()()0x x x x y y y y -⋅-+--=考点五:阿波罗尼斯圆设A B ,为平面上相异两定点,且||2(0)AB a a =>,P 为平面上异于A B ,一动点且||||PA PB λ=(0λ>且1λ≠)则P 点轨迹为圆.考点六:直线与圆的位置关系设圆心到直线的距离d ,圆的半径为r ,则直线与圆的位置关系几何意义代数意义公共点的个数①直线与圆相交r d <0>∆两个②直线与圆相切r d =0=∆一个③直线与圆相离r d >0<∆0个注:代数法:联立直线方程与圆方程,得到关于x 的一元二次方程2Ax Bx C ++=考点七:直线与圆相交的弦长问题法一:设圆心到直线的距离d ,圆的半径为r ,则弦长222d r AB -=法二:联立直线方程与圆方程,得到关于x 的一元二次方程20Ax Bx C ++=,利用韦达定理,弦长公式即可【题型目录】题型一:圆的方程题型二:直线与圆的位置关系题型三:直线与圆的弦长问题题型四:圆中的切线切线长和切点弦问题题型五:圆中最值问题题型六:圆与圆的位置关系问题【典型例题】题型一:圆的方程【例1】AOB 顶点坐标分别为()2,0A ,()0,4B ,()0,0O .则AOB 外接圆的标准方程为______.【答案】()()22125x y -+-=【解析】设圆的标准方程为()()222x a y b r -+-=,因为过点()2,0A ,()0,4B ,()0,0O 所以()()()()()()222222222200400a b r a b r a b r ⎧-+-=⎪⎪-+-=⎨⎪-+-=⎪⎩解得2125a b r =⎧⎪=⎨⎪=⎩则圆的标准方程为()()22125x y -+-=故答案为:()()22125x y -+-=【例2】已知圆22(1)(2)4x y +++=关于直线()200,0ax by a b ++=>>对称,则12a b+的最小值为()A .52B .92C .4D .8故选:B【例3】过点(1,1),(3,5)A B -,且圆心在直线220x y ++=上的圆的方程为_______.【例4】设甲:实数3a <;乙:方程2230x y x y a +-++=是圆,则甲是乙的()A .充分不必要条件B .必要不充分条件C .充要条件D .既不充分也不必要条件【例5】苏州有很多圆拱的悬索拱桥(如寒山桥),经测得某圆拱索桥(如图)的跨度100AB =米,拱高10OP =米,在建造圆拱桥时每隔5米需用一根支柱支撑,则与OP 相距30米的支柱MN 的高度是()米.(注意:≈3.162)A .6.48B .5.48C .4.48D .3.48【答案】A【解析】以O 为原点,以AB 所在直线为x 轴,以OP 所在直线为y 轴建立平面直角坐标系.设圆心坐标为(0,a ),则P (0,10),A (-50,0).可设圆拱所在圆的方程为()222x y a r +-=,由题意可得:()()222221050a r a r ⎧-=⎪⎨-+=⎪⎩解得:2120,16900a r =-=.所以所求圆的方程为()2212016900x y ++=.将x =-30代入圆方程,得:()290012016900y ++=,因为y >0,所以12040 3.162120 6.48y =≈⨯-=.故选:A.【例6】阿波罗尼斯(约公元前262-190年)证明过这样一个命题:在平面内到两定点距离之比为常数(0,1)k k k >≠的点的轨迹是圆,后人将这个圆称为阿氏圆.若平面内两定点A ,B 间的距离为2,动点P 满足||||PA PB =,则PAB △面积的最大值是()AB .2C.D .4【答案】C【解析】设经过点A ,B 的直线为x 轴,AB的方向为x 轴正方向,线段AB 的垂直平分线为y 轴,线段AB 的中点O 为原点,建立平面直角坐标系.则()1,0A -,()10B ,.设(),P x y,∵PA PB==两边平方并整理得22610x y x +-+=,即()2238x y -+=.要使PAB △的面积最大,只需点P到AB (x 轴)的距离最大时,此时面积为122⨯⨯故选:C.【题型专练】1.设点M 在直线210x y +-=上,点(3,0)和(0,1)均在M 上,则M 的方程为______________.2.经过三个点00()(02)()0A B C -,,,,的圆的方程为()A .(()2212x y ++=B .(()2212x y +-=C .(()2214x y ++=D .(()2214x y +-=中的三点的一个圆的方程为____________.【答案】22420x y x y +--=或22460x y x y +--=或22814033x y x y +--=或2216162055x y x y +---=(答案不唯一,填其中一个即可)【解析】设圆的方程为220x y Dx Ey F ++++=若圆过(0,0),(4,0),(4,2)三点,则0164020420F D F D E F =⎧⎪++=⎨⎪+++=⎩,解得420D E F =-⎧⎪=-⎨⎪=⎩,故圆的方程为22420x y x y +--=;若圆过(0,0),(4,0),(1,1)-三点,则0164020F D F D E F =⎧⎪++=⎨⎪-++=⎩,解得460D E F =-⎧⎪=-⎨⎪=⎩,故圆的方程为22460x y x y +--=;若圆过(0,0),(1,1)-,(4,2)三点,则02020420F D E F D E F =⎧⎪-++=⎨⎪+++=⎩,解得831430D E F ⎧=-⎪⎪⎪=-⎨⎪=⎪⎪⎩,故圆的方程为22814033x y x y +--=;若圆过(4,0),(1,1)-,(4,2)三点,则16402020420D F D E F D E F ++=⎧⎪-++=⎨⎪+++=⎩,解得1652165D E F ⎧=-⎪⎪=-⎨⎪⎪=-⎩,故圆的方程为2216162055x y x y +---=.4.已知“m t ≤”是“220x y m ++=”表示圆的必要不充分条件,则实数t 的取值范围是()A .()1,-+∞B .[)1,+∞C .(),1-∞D .(),1-∞-5.若两定点()1,0A ,()4,0B ,动点M 满足2MA MB =,则动点M 的轨迹围成区域的面积为().A .2πB .5πC .3πD .4π6.古希腊著名数学家阿波罗尼斯发现:平面内到两定点A ,B 的距离之比为定值λ(λ≠1)的点的轨迹是圆,此圆被称为“阿波罗尼斯圆”.在平面直角坐标系xOy 中,A (-2,0),B (4,0),点P 满足PA PB=12.设点P 的轨迹为C ,则下列结论正确的是()A .轨迹C 的方程为(x +4)2+y 2=9B .在x 轴上存在异于A ,B 的两点D ,E 使得PD PE=12C .当A ,B ,P 三点不共线时,射线PO 是∠APB 的平分线D .在C 上存在点M ,使得2MO MA =【答案】BC【分析】根据阿波罗尼斯圆的定义,结合两点间距离公式逐一判断即可.MA MO,则在O,A,M三点所能构成7.已知动点M与两个定点O(0,0),A(3,0)的距离满足2=的三角形中面积的最大值是()A.1B.2C.3D.4易知90MBO ∠=︒时,MOA S △取得最大值3.故选:C .题型二:直线与圆的位置关系【例1】直线:10l kx y k -+-=与圆223x y +=的位置关系是()A .相交B .相离C .相切D .无法确定【例2】(黑龙江哈尔滨市)若过点()4,3A 的直线l 与曲线()()22231x y -+-=有公共点,则直线l 的斜率的取值范围为()A .⎡⎣B .(C .,33⎡-⎢⎣⎦D .,33⎛⎫- ⎪ ⎪⎝⎭【答案】C【解析】由题意知,直线的斜率存在,设直线的斜率为k ,则直线方程为()43-=-x k y ,即043=-+-k y kx ,圆心为()3,2,半径为1,所以圆心到直线得距离1211433222+≤-⇒≤+-+-=k k k kk d ,解得3333≤≤-k【例3】直线:20l kx y --=与曲线1C x -只有一个公共点,则实数k 范围是()A .(3,)(,3)+∞-∞- B .3,2⎡⎫+∞⎪⎢⎣⎭C .4(2,4]3⎧⎫⎨⎬D .(-由图知,当24k <≤或故选:C【例4】已知直线2:0l ax by r +-=与圆222:C x y r +=,点(),A a b ,则下列说法正确的是()A .若点A 在圆C 上,则直线l 与圆C 相切B .若点A 在圆C 内,则直线l 与圆C 相交C .若点A 在圆C 外,则直线l 与圆C 相离D .若点A 在直线l 上,则直线l 与圆C 相切【答案】AD【分析】根据直线与圆的位置关系相应条件判断即可.【题型专练】1.直线():120l kx y k k R -++=∈与圆22:5C x y+=的公共点个数为()A .0个B .1个C .2个D .1个或2个【答案】D【解析】将直线l 变形为()012=+-+y x k ,令⎩⎨⎧=+-=+0102y x ,解得⎩⎨⎧=-=12y x ,所以直线过定点()1,2-P ,因为()51222=+-,所以点P 在圆上,所以直线与圆相切或者相交2.已知关于x 的方程2(3)1k x ++有两个不同的实数根,则实数k 的范围______.当直线与半圆相切时,圆心O 到直线1l 的距离d 解得:13265k -=(舍),或13265k +=当直线过点(2,0)-时,可求得直线2l 的斜率2k =则利用图像得:实数k 的范围为3261,5⎡⎫+⎪⎢⎪⎣⎭故答案为:3261,5⎡⎫+⎪⎢⎪⎣⎭3.(2022全国新高考2卷)设点A (-2,3),B (0(x +3)2+(y +2)2=1有公共点,则a 的取值范围为_______.【答案】13,32⎡⎤⎢⎥⎣⎦【解析】()2,3A -关于y a =对称的点的坐标为()2,23A a '--,()0,B a 在直线y a =上,所以A B '所在直线即为直线l ,所以直线l 为32a y x a -=+-,即()3220a x y a -+-=;圆()()22:321C x y +++=,圆心()3,2C --,半径1r =,依题意圆心到直线l 的距离1d =≤,即()()2225532a a -≤-+,解得1332a ≤≤,即13,32a ⎡⎤∈⎢⎥⎣⎦;故答案为:13,32⎡⎤⎢⎥⎣⎦题型三:直线与圆的弦长问题【例1】已知圆C :()()22210x y a a +-=>与直线l :x -y -1=0相交于A ,B 两点,若△ABC 的面积为2,则圆C 的面积为()A .πB .2πC .4πD .6π【答案】C 【解析】如图,由圆C 方程可知圆心()0,1C ,半径为a ,由点到直线的距离公式可知圆心C到直线l 的距离d =又△ABC 的面积为11222S AB d =⋅==,解得AB =2222a ⎛+= ⎝⎭,则a =2,即圆C 的半径为2.则圆C 的面积为24S a ππ==.故选:C.【例2】已知圆22:60M x y x +-=,过点()1,2的直线1l ,2l ,…,()*n l n ∈N 被该圆M 截得的弦长依次为1a ,2a ,…,n a ,若1a ,2a ,…,n a 是公差为13的等差数列,则n 的最大值是()A .10B .11C .12D .13【答案】D【分析】求出弦长的最小和最大值,根据等差数列的关系即可求出n 的最大值此时,直线DE 的解析式为:3y x =-+直线BC 的解析式为:=+1y x 圆心到弦BC 所在直线的距离:AM 连接BM ,由勾股定理得,()22=322=1AB -x y+=交于,A B两点,过,A B分别作l的垂线与x轴交于【例3】已知直线:10l mx y+--=与圆2216,C D两点,则当AB最小时,CD=()A.4B.C.8D.故选:D【例4】(多选题)若直线l 经过点0(3,1)P -,且被圆2282120x y x y +--+=截得的弦长为4,则l 的方程可能是()A .3x =B .3y =C .34130x y --=D .43150x y --=【题型专练】1.直线:l y x m =+与圆224x y +=相交于A ,B 两点,若AB ≥m 的取值范围为()A .[]22-,B .⎡⎣C .[]1,1-D .,22⎡⎤⎢⎥⎣⎦【答案】B【解析】令圆224x y +=的圆心(0,0)O 到直线l 的距离为d ,而圆半径为2r =,弦AB 长满足AB ≥,则有1d =,又d =1≤,解得m ≤≤所以实数m 的取值范围为⎡⎣.故选:B2.在圆22420x y x y +-+=内,过点()1,0E 的最长弦和最短弦分别是AC 和BD ,则四边形ABCD 的面积为()A .B .C .D .【答案】D【解析】圆22420x y x y +-+=化简为22(2)(1)5x y -++=可得圆心为(2,1),r -=易知过点()1,0E 的最长弦为直径,即||AC =而最短弦为过()1,0E 与AC 垂直的弦,圆心(2,1)-到()1,0E 的距离:d ==所以弦||BD ==所以四边形ABCD 的面积:12S AC BD =⋅=故选:D.3.若直线1y kx =+与圆221x y +=相交于B A ,两点,且60AOB ∠= (其中O 为原点),则k 的值为()A .3-或3B .3C .D 4.直线l :()()2110m x m y -+-+=与圆C :2260x x y -+=相交于A ,B 两点,则AB 的最小值是()A .B .2C .D .4【答案】D【解析】分别取1,2m m ==,则1010x y -+=⎧⎨-+=⎩,得11x y =⎧⎨=⎩,即直线l 过定点(1,1)P ,将圆C 化为标准方程:22(3)9x y -+=,圆心为(3,0),半径3r =.如图,因为AB =,所以当圆心到直线距离最大时AB 最小.当CP 不垂直直线l 时,总有d CP <,故当CP l ⊥时AB 最小,因为CP =所以AB的最小值为4=.故选:D题型四:圆中的切线切线长和切点弦问题【例1】直线l 过点(2,1)且与圆22:(1)9C x y ++=相切,则直线l 的方程为______________.【例2】已知圆C :228240x y y +--+=,且圆外有一点()0,2P ,过点P 作圆C 的两条切线,且切点分别为A ,B ,则AB =______.【例3】点P 在圆C :()()22334x y -+-=上,()2,0A ,()0,1B ,则PBA ∠最大时,PB =___________.【答案】3【分析】根据题意PBA ∠最大时,直线【详解】点P 在圆C :()23x -+如图将BA 绕点B 沿逆时针方向旋转,当刚好与圆当旋转到与圆相切于点2P 时,∠【例4】过点()2,1P 作圆O :221x y +=的切线,切点分别为,A B ,则下列说法正确的是()A.PA B .四边形PAOB 的外接圆方程为222x y x y +=+C .直线AB 方程为21y x =-+D .三角形PAB 的面积为85【题型专练】1.过点(0,2)作与圆2220x y x +-=相切的直线l ,则直线l 的方程为()A .3480x y -+=B .3480x y +-=C .0x =D .1x =2.直线40x y +-=平分圆222:2250C x y bx by b +---+=的周长,过点()1,P b --作圆C 的一条切线,切点为Q ,则PQ =()A .5B .4C .3D .2【答案】B【详解】圆222:2250C x y bx by b +---+=的圆心为(,)C b b ,半径为r =因为直线40x y +-=平分圆222:2250C x y bx by b +---+=的周长,所以直线40x y +-=经过(,)C b b ,所以40b b +-=,故2b =,由已知()1,2P --,(2,2)C ,||PC ,圆的半径为3,所以4PQ =,故选:B.3.过点(2,2)P 作圆224x y +=的两条切线,切点分别为A 、B ,则直线AB 的方程为_______.【答案】2+-x y 0=【分析】由题知()0,2A 、()2,0B ,进而求解方程即可.【详解】解:方法1:由题知,圆224x y +=的圆心为()0,0,半径为2r =,所以过点(2,2)P 作圆224x y +=的两条切线,切点分别为()0,2A 、()2,0B ,所以1AB k =-,所以直线AB 的方程为2y x =-+,即2+-x y ;方法2:设()11,A x y ,()22,B x y ,则由2211111142.12x y y y x x ⎧+=⎪-⎨=-⎪-⎩,可得112x y +=,同理可得222x y +=,所以直线AB 的方程为2+-x y 0=.故答案为:2+-x y 题型五:圆中最值问题【例1】已知l :4y x =+,分别交x ,y 轴于A ,B 两点,P 在圆C :224x y +=上运动,则PAB △面积的最大值为()A .82-B .1682-C .842+D .162+【答案】C 【解析】如图所示,以AB 为底边,则PAB △面积最大等价于点P 到l 距离最大,而点P 到l 距离最大值等于O 到l 的距离加半径看,O 到l 的距离422d =O 的半径2r =,()4,0A -,()0,4B ,则42AB =PAB △面积的最大值为()14222822⨯=+故选:C【例2】已知点P 是圆()()2241625x y -+-=上的点,点Q 是直线0x y -=上的点,点R 是直线125240x y -+=上的点,则PQ QR +的最小值为()A .7B .335C .6D .295【答案】B【分析】设圆心()1,6C ,记点()6,1E ,作圆()()224:1625C x y -+-=关于直线0x y -=的对称圆()()224:6125E x y -+-=,计算出圆心E 到直线125240x y -+=的距离d ,结合对称性可得出PQ QR +的最小值为25d -,即可得解.【详解】设圆心()1,6C ,记点()6,1E ,作圆()()224:1625C x y -+-=关于直线0x y -=的对称圆()()224:6125E x y -+-=,由对称性可知CQ EQ =,点E 到直线125240x y -+=的距离为()221265247125d ⨯-+==+-,【例3】已知直线:320l x y ++=与x 、轴的交点分别为A 、B ,且直线1:310l mx y m --+=与直线2:310l x my m +--=相交于点P ,则PAB 面积的最大值是()A .103+B .103+C D【例4】已知圆()()22:254C x y -+-=的圆心为C ,T 为直线220x y --=上的动点,过点T 作圆C 的切线,切点为M ,则TM TC ⋅的最小值为()A .10B .16C .18D .20()2TM TC TC CM TC TC CM ⋅=+⋅=+ CM TM ⊥ ,CM CT CM CT ∴⋅=⋅ 24TM TC TC ∴⋅=- ,【例5】已知复数z 满足1i 1z +-=(i 为虚数单位),则z 的最大值为()A .2B 1C 1D .1【答案】B【解析】令i z x y =+,x ,y ∈R ,则()1i 11i 1z x y +-=++-=,即()()22111x y ++-=,表示点(),x y 与点()1,1-距离为1的点集,此时,i z x y =-()()22111x y ++-=上点到原点距离,所以z 的最大值,即为圆上点到原点的距离的最大值,,且半径为1,1.故选:B .【例6】若0x =,则2yx -的取值范围为【答案】11[,]22-【解析】因为0x +=x =-所以()2210x y x +=≤如图,此方程表示的是圆心在原点,半径为1的半圆,2yx -的几何意义是点(),x y 与点()2,0连线的斜率如图,()()0,1,0,1A B -,()2,0P101022PA k -==--,101022PB k --==-所以2y x -的取值范围为11[,]22-故选:D【例】AB 为⊙C :(x -2)2+(y -4)2=25的一条弦,6AB =,若点P 为⊙C 上一动点,则PA PB ⋅的取值范围是()A .[0,100]B .[-12,48]C .[-9,64]D .[-8,72]【答案】D 【解析】【分析】取AB 中点为Q ,利用数量积的运算性质可得2||9PA PB PQ ⋅=- ,再利用圆的性质可得||PQ 取值范围,即求.【详解】取AB 中点为Q ,连接PQ2PA PB PQ ∴+= ,PA PB BA -= 221()()4PA PB PA PB PA PB ⎡⎤∴⋅=+--⎣⎦ 2214||||4PQ BA ⎡⎤=-⎣⎦ ,又||6BA = ,4CQ =2||9PA PB PQ ∴⋅=-,∵点P 为⊙C 上一动点,∴max min ||9,|5|15PQ Q P C Q Q C =+=-==PA PB ∴⋅的取值范围[-8,72].故选:D.【题型专练】1.直线20x y +-=分别与x 轴,y 轴交于,A B 两点,点P 在圆22(2)2x y ++=上,则ABP 面积的取值范围是()A .[]2,6B .[]4,8C .D .⎡⎣2.(多选题)已知点P 在圆O :224x y +=上,直线l :43120x y +-=分别与x 轴,轴交于,A B 两点,则()A .过点B 作圆O 的切线,则切线长为B .满足0PA PB ⋅=的点P 有3个C .点P 到直线l 距离的最大值为225D .PA PB +的最小值是1【答案】ACD【分析】对于A,根据勾股定理求解即可;对于B,0PA PB ⋅=即PA PB ⊥,所以点P 在以AB 为直径的圆上,设AB 的中点为M ,写出圆M 的方程,根据两个圆的交点个数即可判断正误;对于C,根据圆上一点到直线的最大3.已知动点A ,B 分别在圆1C :()2221x y ++=和圆2C :()2244x y -+=上,动点P 在直线10x y -+=上,则PA PB +的最小值是_______【答案】3-##3-+如图,设点()10,2C -关于直线10x y -+=对称的点为()030,C x y ,所以,00002121022y x x y +⎧=-⎪⎪⎨-⎛⎫⎪-+= ⎪⎪⎝⎭⎩,解得003,1x y =-=,即()33,1C -,所以,3252C C =所以,32523PA B C P C r R --+=-≥,即PA PB +的最小值是523-.故答案为:523-4.过直线3450x y +-=上的一点P 向圆()()22344x y -+-=作两条切线12l l ,.设1l 与2l 的夹角为θ,则θ的最大值为______.【答案】π3##60︒【分析】由题可得圆心为()3,4C ,半径为2,设12l l ,与圆C 切于,A B ,根据圆的性质结合条件可得1sin sin22APC θ∠=≤,进而即得.【详解】由()()22344x y -+-=,可得圆心为()3,4C ,半径为2,设12l l ,与圆C 切于,A B ,则2APB APC θ=∠=∠,在Rt APC △中,2AC =,2sin sin 2CA APC CP CPθ∠===又()3,4C 到直线3450x y +-=的距离为223344534⨯+⨯-+所以4CP ≥,1sin sin22APC θ∠=≤,所以APC ∠的最大值为π6,即θ的最大值为π3.故答案为:π3.5.已知圆22:410,+--=M x y x (),P x y 是圆M 上的动点,则3t x =+的最大值为_________;22x y +的最小值为____________.6.18世纪末,挪威测量学家维塞尔首次利用坐标平面上的点来表示复数,使复数及其运算具有了几何意义,例如z OZ =,也即复数z 的模的几何意义为z 对应的点Z 到原点的距离.已知复数z 满足2z =,则34i z --的最大值为()A .3B .5C .7D .9【答案】C【解析】2z = ,z ∴对应的点(),Z x y 的轨迹为圆224x y +=;34i z -- 的几何意义为点(),Z x y 到点()3,4的距离,max 34i 27z ∴--==.故选:C.题型六:圆与圆的位置关系问题【例1】已知圆221:1C x y +=与圆222:(3)(4)4C x y -+-=,则圆1C 与2C 的位置关系是()A .内含B .相交C .外切D .相离【例2】已知点P 在圆O :224x y +=上,点()30A -,,()0,4B ,满足AP BP ⊥的点P 的个数为()A .3B .2C .1D .0【答案】B【解析】【分析】设(,)P x y ,轨迹AP BP ⊥ 可得点P 的轨迹方程,即可判断该轨迹与圆的交点个数.设点(,)P x y ,则224x y +=,且(3,)(,4)AP x y BP x y =+=- ,,由AP BP ⊥,得22(3)(4)340AP BP x x y y x y x y ⋅=++-=++-= ,即22325()(2)24x y ++-=,故点P 的轨迹为一个圆心为3(,2)2-、半径为52的圆,则两圆的圆心距为52,半径和为59222+=,半径差为51222-=,有159222<<,所以两圆相交,满足这样的点P 有2个.故选:B.【例3】圆221:22260O x y x y +---=与圆222:820O x y y +--=的公共弦长为()A .B .C .D .【例4】已知圆C :()()22681x y -+-=和两点(),0A m -,()(),00B m m >,若圆C 上存在点P ,使得90APB ∠=︒,则m 的最大值为()A .12B .11C .10D .9【答案】B【分析】由题意得P 点轨迹,转化为有交点问题【详解】90APB ∠=︒,记AB 中点为O ,则||OP m =,故P 点的轨迹是以原点为圆心,m 为半径的圆,又P 在圆C 上,所以两圆有交点,则|1|||1m OC m -≤≤+,而||10OC =,得911m ≤≤.故选:B【题型专练】1.写出与圆221x y +=和圆()2264x y -+=都相切的一条直线的方程______.2.(2022全国新高考1卷)写出与圆x 2+y 2=1和(x -3)2+(y -4)2=16都相切的一条直线的方程_______.【答案】3544y x =-+或7252424y x =-或1x =-【解析】【分析】先判断两圆位置关系,分情况讨论即可.【详解】圆221x y +=的圆心为()0,0O ,半径为1,圆22(3)(4)16x y -+-=的圆心1O 为(3,4),半径为4,5=,等于两圆半径之和,故两圆外切,如图,当切线为l 时,因为143OO k =,所以34l k =-,设方程为3(0)4y x t t =-+>O 到l 的距离1d ==,解得54t =,所以l 的方程为3544y x =-+,当切线为m 时,设直线方程为0kx y p ++=,其中0p >,0k <,由题意14⎧=⎪⎪=,解得7242524k p ⎧=-⎪⎪⎨⎪=⎪⎩,7252424y x =-当切线为n 时,易知切线方程为1x =-,故答案为:3544y x =-+或7252424y x =-或1x =-.3.(多选题)圆221:20x y x O +-=和圆222:240O x y x y ++-=的交点为A ,B ,则有()A .公共弦AB 所在直线的方程为0x y -=B .公共弦AB 所在直线的方程为10x y +-=C .公共弦ABD .P 为圆1O 上一动点,则P 到直线AB 14.已知点()()2,3,5,1A B -,则满足点A 到直线l 的距离为1,点B 到直线l 距离为3的直线l 的条数有()A .1B .2C .3D .4【答案】D【解析】【分析】以A 为圆心,1为半径,B 为圆心,3为半径分别画圆,将所求转化为求圆A 与圆B 的公切线条数,判断两圆的位置关系,从而得公切线条数.【详解】以A 为圆心,1为半径,B 为圆心,3为半径分别画圆,如图所示,由题意,满足点A 到直线l 的距离为1,点B 到直线l 距离为3的直线l 的条数即为圆A 与圆B 的公切线条数,因为513AB ==>+,所以两圆外离,所以两圆的公切线有4条,即满足条件的直线l 有4条.故选:D5.已知圆()()221:111C x y -++=,圆()()222:459C x y -+-=,点M 、N 分别是圆1C 、圆2C 上的动点,点P 为x 轴上的动点,则PN PM -的最大值是()A .4B .9C .7D .2【答案】B【解析】【分析】分析可知()21max 4PN PM PC PC -=-+,设点()24,5C 关于x 轴的对称点为()24,5C '-,可得出22PC PC '=,求出21PC PC '-的最大值,即可得解.【详解】圆()()221:111C x y -++=的圆心为()11,1C -,半径为1,圆()()222:459C x y -+-=的圆心为()24,5C ,半径为3.()max min max PN PM PN PM -=- ,又2max 3PN PC =+,1min 1PMPC =-,()()()2121max 314PN PM PC PC PC PC ∴-=+--=-+.点()24,5C 关于x 轴的对称点为()24,5C '-,2121125PC PC PC PC C C ''-=-≤==,所以,()max 549PN PM -=+=,故选:B .。
高考数学复习:圆的方程
命题角度4 利用函数或基本不等式求最值问题
例6 设圆x2+y2=2的切线l与x轴正半轴、y轴正半轴分别交于点A,B,当
x+y-2=0
|AB|取最小值时,切线l的方程为
设点 A,B 的坐标分别为 A(a,0),B(0,b)(a>0,b>0),则直线 AB
又所求圆在直线 x-y-3=0 上截得的弦长为√6,
圆心(a,-a)到直线 x-y-3=0 的距离
∴d +
2
√6
2
2
2
(2-3)
=r2,即
2
|2-3|
d=
,
√2
3
+ =2a2,
2
解得 a=1.故所求圆的方程为(x-1)2+(y+1)2=2.
(方法二)设所求圆的方程为(x-a)2+(y-b)2=r2(r>0),
故 y-x 的最大值为-2+√6,最小值为-2-√6.
命题角度3 距离型最值问题
例5 在例3的条件下求x2+y2的最大值和最小值.
解 如图,x2+y2表示圆上的一点与原点距离的平方,由平面几何知识知,在
原点和圆心连线与圆的两个交点处取得最大值和最小值.
因为圆心到原点的距离为 (2-0)2 + (0-0)2 =2,
例2 如图,已知点A(-1,0),B(1,0),C是圆x2+y2=1上的动点,连接BC并延长
至点D,使得|CD|=|BC|,求AC与OD的交点P的轨迹方程.
解 设动点P(x,y),由题意可知P是△ABD的重心.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高考数学必考之圆的方程考点一 圆的方程1.圆心为()3,1,半径为5的圆的标准方程是【答案】()()223125x y -+-=【解析】∵所求圆的圆心为()3,1,半径为5,∴所求圆的标准方程为:()()223125x y -+-=,2.已知点()3,6A ,()1,4B ,()1,0C ,则ABC ∆外接圆的圆心坐标为 【答案】()5,2【解析】线段AB 中点坐标为()2,5,线段AB 斜率为64131-=-,所以线段AB 垂直平分线的斜率为1-,故线段AB 的垂直平分线方程为()52y x -=--,即7y x =-+.线段AC 中点坐标为()2,3,线段AC 斜率为60331-=-,所以线段AC 垂直平分线的斜率为13-,故线段AC 的垂直平分线方程为()1323y x -=--,即11133y x =-+.由75111233y x x y y x =-+⎧=⎧⎪⇒⎨⎨==-+⎩⎪⎩.所以ABC ∆外接圆的圆心坐标为()5,2. 3.方程x 2+y 2+ax +2ay +2a 2+a -1=0表示圆,则a 的范围是【答案】-2<a <23【解析】由题意可得圆的标准方程2223()()124a x y a a a +++=--,由23104a a -->解得223a -<<.考点二 点与圆的位置关系1.点()1,1在圆()2211x y +-=的( )A .圆上B .圆内C .圆外D .无法判定【答案】A【解析】将点()1,1的坐标代入圆()2211x y +-=的方程即()221111+-=,∴点()1,1在圆()2211x y +-=上,2.经过点(1,2)A 可做圆22240x y mx y ++-+=的两条切线,则m 的范围是( )A .(,(23,)-∞-+∞B .(5,(23,)--+∞C .(,)-∞-⋃+∞D .(5,(22,)--+∞【答案】B【解析】圆22240x y mx y ++-+=,即为222()(1)324m m x y -+-=-, 2304m ∴->⇒m <-m > 由题意知点A 在圆外,14440m ∴++-+>,解得5m >-.所以5m -<<-m >故选B3.若坐标原点在圆22222240x y mx my m +-++-=的内部,则实数m 的取值范围是( )A .()1,1-B .,22⎛-⎝⎭C .(D .(【答案】D【解析】把原点坐标代入圆的方程得:222002020240m m m +-⨯+⨯+-<解得:m <本题正确选项:D考点三 直线与圆1.已知直线0x y +=与圆22(1)()2x y b -+-=相切,则b = 。
【答案】3-或1=∴|1|2b +=∴13b b ==-或2.已知定点()00,P x y 在单位圆221x y +=内部,则直线001x x y y +=与圆221x y +=的位置关系是 。
【答案】相离【解析】()00,p x y 在圆221x y +=的内部22001x y ∴+<因为圆心为(0,0),半径为r,所以圆心到直线的距离1d r =>=∴直线与圆相离,3.圆2228130+--+=x y x y 的圆心到直线10ax y ++=的距离为1,则a = 。
【答案】125-【解析】因为2228130+--+=x y x y 可转化为()()22144x y -+-=, 所以圆的圆心为()1,4,半径为2,因为圆心到直线10ax y ++=的距离为1,所以24111a a ,解得125a =-, 4.圆2228130+--+=x y x y 截直线10axy +-=所得的弦长为a = 。
【答案】43-【解析】圆2228130+--+=x y x y ,即()()22144x y -+-=1=根据点到直线距离公式可知1d ==,化简可得()2231a a +=+ 解得43a =-5.已知不全为0的实数a ,b ,c 满足2b a c =+,则直线0ax by c -+=被曲线22220x y x y +--=截得的弦长的最小值为().A B .1C .D .2【答案】D【解析】2b a c =+∴直线0ax by c -+=过定点(1,2)A ,因为22220x y x y +--=,所以22(1)(1)2x y -+-=因此当圆心(1,1)C 与(1,2)A 连线垂直直线0ax by c -+=时,直线0ax by c -+=被曲线22220x y x y +--=截得的弦长最小,此时最小值为212==⨯=故选:D6.已知O 为坐标原点,点P 在单位圆上,过点P 作圆C :22(4)(3)4x y -+-=的切线,切点为Q ,则PQ的最小值为()AB .C .2D .4【答案】B【解析】根据题意,圆22:(4)(3)4C x y -+-=,其圆心(4,3)C ,半径2r ,过点P 作圆22:(4)(3)4C x y -+-=的切线,切点为Q ,则||PQ =,当||PC 最小时,||PQ 最小,又由点P 在单位圆上,则||PC 的最小值为||114OC -==,则||PQ =; 故选:B .考点四 圆与圆1.若圆()()221:221C x y ++-=,()()222:2516C x y -+-=,则1C 和2C 的位置关系是( ) A .外离 B .相交C .内切D .外切【答案】D【解析】可知,圆1C 的圆心为()12,2C -,半径为11r =,圆2C 的圆心()22,5C ,半径为24r =,12125C C r r ===+,因此,圆1C 与圆2C 外切.故选:D.2.若圆221:4C x y +=与圆222:680C x y x y m +--+=外切,则实数m =( )A .24-B .16-C .24D .16【答案】D【解析】圆1C 的圆心为()0,0,半径为2,圆2C 的圆心为()3,45=.由于两个圆外切,所以25=,解得16m =. 故选:D3.若圆222x y a +=与圆2260x y ay ++-=的公共弦长为a 的值为( ) A .2 B .2±C .1D .±1【答案】B【解析】圆222x y a +=的圆心为原点O ,半径r a =将圆222x y a +=与圆2260x y ay ++-=的左右两边分别相减,可得260ay a +-=,即得两圆的公共弦所在直线方程为260ay a +-=.原点O 到260ay a +-=的距离6d a a=-,根据垂径定理可得2226a a a ⎛⎫=+- ⎪⎝⎭, 24a ∴=2a ∴=±故选:B.4.已知圆221:(2)(3)1C x y -+-=,圆222:(3)(4)9C x y -+-=,,M N 分别为圆12,C C 上的点,P 为x 轴上的动点,则||||PM PN +的最小值为( )A B 1C .6-D .4【答案】D【解析】如图所示,圆1C 关于x 轴的对称圆的圆心坐标3(2,)A -,半径为1,圆2C 的圆心坐标为(3,4),,半径为3,由图象可知,当,,P M N 三点共线时,||||PM PN +取得最小值,且||||PM PN +的最小值为圆3C 与圆2C 的圆心距减去两个圆的半径之和,即23144AC --==, 故选D .5.圆221:2410C x y x y ++++=与圆222:4410C x y x y +---=的公切线有几条() A .1条 B .2条 C .3条 D .4条【答案】C【解析】圆()()221:124C x y +++=,圆心1C ()1,2-- ,12r =,圆()()222:229C x y -+-= ,圆心2C ()2,2,23r =,圆心距125C C ==1212C C r r =+ ∴两圆外切,有3条公切线.故选C.6.若圆1C :2246120x y x y ++--=与圆2C :()()2245x y m -++=有且仅有3条公切线,则实数m的值为( ) A .4 B .25C .5D .16【答案】B【解析】依题意,圆1C :()()222325x y ++-=,由题得1C 与2C 外切,则1212C C r r =+,5=25m =,故选:B.。
