3-6气体在喷管中的流动
拉伐尔喷管的设计——小论文

拉伐尔喷管的设计摘 要:本文针对拉伐尔喷管的几何条件和力学条件进行了推导。
建立了喷管截面积变化与流速、压强、密度、温度等流动性能参数间的关系,分析了喷管出口截面下游的外界反压对拉伐尔喷管工作过程的影响.推导建立了拉伐尔喷管主要性能参数的计算方法。
针对实际流动损失的存在,为得到喷管的实际流动性能,对理论性能参数提出了修正方法。
提出了拉伐尔喷管的设计方法.本文研究内容为拉伐尔喷管的设计提供依据.关键词:变截面;力学条件;性能参数;流动损失1.引言拉伐尔喷管是火箭发动机和航空发动机最常用的构件,由两个锥形管构成,如图1所示,其中一个为收缩管,另一个为扩张管.拉瓦尔喷管是推力室的重要组成部分。
喷管的前半部是由大变小向中间收缩至喷管喉部。
喉部之后又由小变大向外扩张。
燃烧室中的气体受高压流入喷嘴的前半部,穿过喉部后由后半部逸出。
这一架构可使气流的速度因喷截面积的变化而变化,使气流从亚音速到音速,直至加速至超音速。
所以,人们把这种喷管叫跨音速喷管.瑞典工程师De Laval 在1883年首先将它用于高速汽轮机,现在这种喷管广泛应用于喷气发动机和火箭发动机.图1。
1 拉伐尔喷管结构图2.拉伐尔喷管的几何条件2.1变截面一维定常等熵流动在变截面一维定常流动中只考虑截面积变化这一种驱动势,忽略摩擦、传热、重力等其他驱动势,因此流动是绝热无摩擦的,即等熵流动,变截面定常等熵流动模型如图2所示。
变截面一维定常等熵流动的控制方程组为:Const m VA ρ==(2.1。
1) 0dp VdV ρ+= (2。
1.2)控制体p +dpdxρ+d ρV +dV T +dT A +dAp ρ T A图2.1 变截面一维定常等熵流动模型2102d h V ⎛⎫+= ⎪⎝⎭ (2.1。
3)2.2截面积变化对流动特性的影响管道的形状变化可以用截面积变化dA 来表示。
(a ) 截面积变化对流速的影响对连续方程(1)取对数微分,得0d dV dAV Aρρ++= (2.2.1) 将(2.1.2)两边同除以ρ,得20dV dp d V V d ρρρ+⋅= (2.2。
第二章习题第二部分
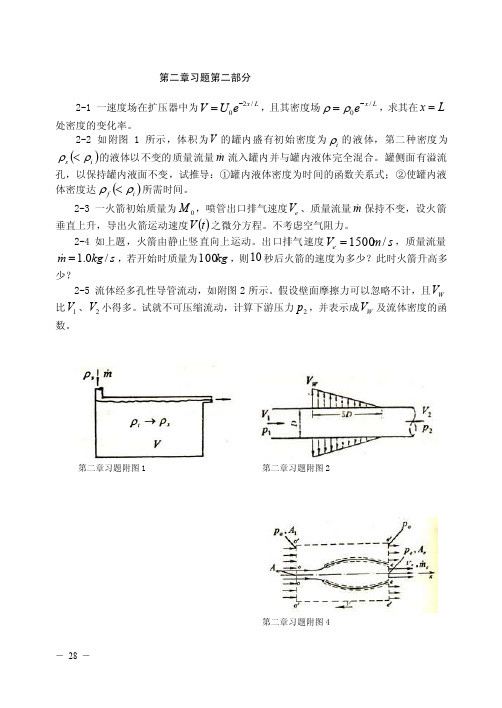
第二章习题第二部分2-1 一速度场在扩压器中为L x e U V /20-=,且其密度场L x e /0-=ρρ,求其在L x =处密度的变化率。
2-2 如附图1所示,体积为V 的罐内盛有初始密度为i ρ的液体,第二种密度为()i s ρρ<的液体以不变的质量流量m流入罐内并与罐内液体完全混合。
罐侧面有溢流孔,以保持罐内液面不变,试推导:①罐内液体密度为时间的函数关系式;②使罐内液体密度达()i f ρρ<所需时间。
2-3 一火箭初始质量为0M ,喷管出口排气速度e V 、质量流量m 保持不变,设火箭垂直上升,导出火箭运动速度()t V 之微分方程。
不考虑空气阻力。
2-4 如上题,火箭由静止竖直向上运动。
出口排气速度s m V e /1500=,质量流量s kg m/0.1= ,若开始时质量为kg 100,则10秒后火箭的速度为多少?此时火箭升高多少?2-5 流体经多孔性导管流动,如附图2所示。
假设壁面摩擦力可以忽略不计,且W V 比1V 、2V 小得多。
试就不可压缩流动,计算下游压力2p ,并表示成W V 及流体密度的函数。
第二章习题附图1 第二章习题附图2第二章习题附图42-7 空气通过压气机,进口C t 201=,s m V /101=;出口C t 1002=,s m V /802=,质量流量为s kg m /561.0= 。
设为定常流动,忽略热量交换,计算作用于流体上的机械功率。
()K kg J c p ⋅=/1005。
2-8 最早计算声速的科学家是牛顿,他假设声波的传播过程是等温过程,推导出的声速公式为ρ/p c =,因而在标准状况下,s m c /287≈。
试推导牛顿声速公式。
2-9 一架飞机以s m V /75=的速度在高度为m H 10000=的高空飞行。
计算飞机相对于空气的马赫数。
2-10 空气流的速度为s m /250,静温为K 300,静压为Pa 5100133.1⨯。
喷管中气体流动特性分析_郑玉

第22卷 第7期2006年7月甘肃科技Gansu S cience and Technolo gyVol.22 N o.7J uly. 2006喷管中气体流动特性分析郑 玉1,张永恒2(1兰州交通大学数理与软件工程学院,甘肃兰州730030;2.兰州交通大学机电工程学院,甘肃兰州730070)摘 要:分析各种工况下气流流经渐缩喷管和缩放喷管各个截面压力和流量的变化规律,比较两种喷管的基本特性,确定工作条件对喷管中气体流动的影响。
并介绍了实际气流曲线偏离理想气流曲线的因素。
关键词:喷管;压力;流量中图分类号:TQ 0281 引言喷管是利用气体的压力降低使气流加速的特殊管道。
它广泛应用于汽轮机等动力设备中,也应用于通风、空调等热力设备中。
例如在燃气轮机和汽轮机里都需要装设喷管,利用气体流经喷管获得高速气流推动叶轮叶片而作功。
喷管是使流体增速的变截面流道,气流在管道中流动时的状态变化情况和管道截面积的变化情况有密切关系。
由于喷管的长度较短,流速较高,气流从进入喷管到流出喷管的时间很短,因此可以认为喷管中气体流动是可逆的绝热流动过程。
喷管一般分为渐缩喷管和缩放喷管。
渐缩喷管如图1所示,缩放喷管如图2所示。
渐缩喷管沿流动方向截面积是逐渐减小的,气流作亚音速流动。
缩放喷管中气流在渐缩部分作亚音速流动,在渐放部分作超音速流动,在最小截面,即喉部是亚音速流动向超音速流动的转折点,这时流速等于当地音速。
本文通过分析空气流经渐缩喷管和缩放喷管各个截面压力变化和流量变化的规律,气流在喷管内完全膨胀,膨胀过度和膨胀不足等现象,分析研究两种喷管的特性以及工作条件的改变对喷管中气体流动的影响。
2 实验方法实验中必须测量四个变量,测压孔在喷管内不同截面位置X ,气流在该截面上的压力P ,背压P b ,(喷管出口外介质的压力),流量m 。
这些量分别用位移指针位置,可移动真空表,背压真空表以及U 型管压差计来显示。
实验是在一喷管实验台上进行,采用真空泵为动力,大气为气源。
喷管中气体流动特性的测定

喷管中气体流动特性的测定喷管是一些热工设备的重要部件,这些设备工作过程和喷管中气体的流动过程有密切的关系。
一、实验目的1、观察气流完全膨胀时沿喷管的压力变化,测定流量曲线和临界压力比。
2、了解喷管中气体流动现象的基本特性。
3、观察渐缩渐扩喷管中膨胀不足和膨胀过度的影响。
4、了解工作条件对喷管中流动过程的影响。
二、实验原理气体流经喷管的流动过程中,气流状态参数υ、流速c 和喷管截面积f 之间的基本关系如下: 0=−+vdv f df c dc (1) 喷管可以用f=F (x )表示截面积轴向距离x (自进口截面积算起)的变化。
在设计的进气压力和排气压力(常称为背压)条件下,气体在喷管内绝热流动时的压力变化可用下式表示为:()dx df M f kM Pdx dp 1122−= (2) 式中M 为马赫数:是表示气体流动特性的一个重要值。
M 〈1时,表示气体流速小于当地音速,为亚音速流动;M=1时,气体流速等于当地音速值;M 〉1时,气流做超音速流动。
当喷管的使用条件改变时,喷管内气流的压力分布发生变化,气流的流速和质量流量也将发生不同的变化。
1、渐缩喷管气体流经喷管的膨胀程度可以用喷管的背压P 2和进口压力P 1之比β表示,12P P =β称为压力比。
气体在渐缩喷管内绝热流动的最大膨胀程度决定于临界压力比βc : 1/112−⎟⎠⎞⎜⎝⎛+==k k c c k P P β (3)临界压力比只和气体的绝热指数有关。
对于空气等双原子气体k=1.4,b c =0.528。
上式中P c 为气体在减缩喷管中膨胀所能达到的最低压力,称为临界压力P c =b c 。
P 1决定于进口压力。
气体在减缩喷管中由P 1膨胀到P 2=P c ,如图3.1曲线1所示,是最充分的完全膨胀情况。
这时,喷管出口的气体流速达到当地音速的数值,称为临界流速。
当备压P 2低于临界压力P c 时,气体在减缩喷管中不能继续膨胀到备压P 2,只能膨胀到临界压力P c 。
热力学喷管实验指导书

空气在喷管中流动性能测定实验一、实验目的:1、验证和加深理解喷管中气体流动的基本理论。
2、观察气流在喷管中各截面的流速,流量,压力变化规律及掌握有关测试方法。
3、熟悉不同形式喷管的机理,加深对流动的临界状态基本概念的理解。
二、实验原理:1、喷管中气体流动的基本规律气体在喷管中作一元稳定等熵流动中,压力降低,流速增加。
气流速度C ,密度ρ及压力P 的变化与截面A 的变化及马赫数Ma (速度与音速之比)的大小有关。
它们的变化规律如下表: dx d ρ dx d ρ (1)在亚音速(Ma<1)等熵流动中,气体在0<dx dA 的管道(渐缩管)里,速度C 增加,而密度ρ,压力P 降低,在0>dx dA 的管道(渐扩管)里,速度C 减小,而密度ρ,压力P 增大。
(2)在超音速(Ma>1)等熵流动中,气体在渐缩管中,速度C 减小,而压力P ,密度ρ增大,在渐扩管中,速度C 增加,压力P ,密度ρ降低。
(3)在Ma=1,即达到临界流动状态,此时,压力为临界压力,气流速度为音速。
2、喷管中流量的计算(1)理论流量:根据气体一元稳定等熵流动中,任何截面上质量流量都相等,且不随时间变化。
流量大小由连续方程、动量方程、能量方程及绝热气体方程,等熵过程方程,得到气体在喷管中流量的计算式:⎥⎥⎦⎤⎢⎢⎣⎡-⋅-==+00011221211002222)()(12γγγγγP P P P V P A V C A q m (kg/s ) 式中:0γ—绝热指数C2—出口速度m/s A2—出口截面积m2V2—出口比体积(m3/kg ) P2—出口压力(MPa )P1—进口压力(MPa ) V1—进口比体积(m3/kg )若:P1=P2时 0=m q P2=0时 0=m q ,即在0<P2≤Pc 渐缩喷管的出口压力P2或缩放喷管的喉部压力Pth 降至临界压力时,喷管中的流量达最大值,计算式如下:1112000min max ,)12(12V P A q k m ⋅++=-γγγ 临界压力Pc 为:11000)12(P P c ⋅+=+γγγ将0γ=1.4代入Pc=0.528P1(2)、实测流量由于气流与管内壁间的摩擦产生的边界层,减少了流动截面,因为实际流量是小于理论流量,本实验台采用孔板流量计来测量喷管的流量。
工程热力学与传热学第7章气体的流动.

第七章 气体的流动(Gas Flow)第一节 气体在喷管和扩压管中的流动主题1:喷管和扩压管的断面变化规律一、稳定流动基本方程气体在喷管和扩压管中的流动过程作可逆绝热过程,气体流动过程所依据的基本方程式有:连续性方程式、能量方程式、及状态方程式。
1、连续性方程连续性方程反映了气体流动时质量守恒的规律。
定值=⋅=vf mg ω写成微分形式ggd v dv f df ωω-=7-1它给出了流速、截面面积和比容之间的关系。
连续性方程从质量守恒原理推得,所以普遍适用于稳定流动过程,即不论流体的性质如何(液体和气体),或过程是否可逆。
2、能量方程能量方程反映了气体流动时能量转换的规律。
由式(3-8),对于喷管和扩压管中的稳定绝热流动过程,212122)(21h h g g -=-ωω 写成微分形式dh d g -=221ω7-23、过程方程过程方程反映了气体流动时的状态变化规律。
对于绝热过程,在每一截面上,气体基本热力学状态参数之间的关系:定值=k pv写成微分式0=+vdv k p dp 7-3二、音速和马赫数音速是决定于介质的性质及介质状态的一个参数,在理想气体中音速可表示为kRT kpv a ==7-4因为音速的大小与气体的状态有关,所以音速是指某一状态的音速,称为当地音速。
流速与声速的比值称为马赫数:M ag=ω 7-5利用马赫数可将气体流动分类为:m 2g v 222图7-1管道稳定流动示意图亚声速流动:1<M a g <ω超声速流动:1>M a g >ω 临界流动: 1=Ma g =ω三、促使气体流速变化的条件 1、力学条件由式(3-5),对于开口系统可逆稳定流动过程,能量方程⎰-∆=21vdp h q 或 vdp dh q -=δ,式中0=q δ所以 vdp dh = 7-6 联合(7-2)和(7-6)vdp d g g -=ωω7-7由式7-7可见,气体在流动中流速变化与压力变化的符号始终相反,表明气流在流动中因膨胀而压力下降时,流速增加;如气流被压缩而压力升高时,则流速必降低。
喷管实验指导书(2010.11.24)

连接。 在实验中必须测量四个变量,即测压孔在喷管内的不同截面位置x、
气流在该截面上的压力p、背压pb、流量m,这些量可分别用位移指针的 位置、可移动真空表、背压真空表以及U形管压差计(或差压传感器) 的读数来显示。
三、实验原理
1、喷管中气流的基本规律
(1)、由能量方程:
及热力学第二定律的第二解析式:
进气管(1)为ф57×3.5无缝钢管,内径φ50。.空气吸气口(2) 进入进气管,流过孔板流量计(3)。孔板孔径φ7,采用角接环室取 压。流量的大小可从U形管压差计(4)或微压传感器读出。喷管(5) 用有机玻璃制成。配给渐缩喷管和缩放喷管各一只,见图二和图四。根 据实验的要求,可松开夹持法兰上的固紧螺丝,向左推开进气管的三轮 支架(6),更换所需的喷管。喷管各截面上的压力是由插入喷管内的 测压探压针(7)(外径φ1.0)连至“可移动真空表”(8)测得,它 们的移动通过螺杆机构移动,标尺或位移传感器(9)实现。由于喷管 是透明的,测压探针上的测压孔(φ0.5)在喷管内的位置可从喷管外 部看出,也可从装在“可移动真空表”下方的指针在“喷管轴向坐标 板”(在图中未画出)上所指的位置来确定。喷管的排气管上还装 有“背压真空表”,背压用调节阀(11)调节。真空罐(12)直径 φ400,体积0.118m3。起稳定压的作用。罐的底部有排污口,供必要时 排除积水和污物之用。为减小震动,真空罐与真空泵之间用软管(13)
图五 渐缩渐扩喷管压力分布曲线及流量曲线 B—被压低于设计被压()时,气流在喷管内仍按曲线A那样膨胀 到设计压力。当气流一离开出口截面便与周围介质汇合,其压力立即降 至实际被压值,如图五曲线B所示,流量仍为最大流量。 C—被压高于设计被压()时,气流在喷管内膨胀过渡,其压力低 于被压,以至于气流在未达到出口截面处便被压缩,导致压力突然升跃 (即产生激波),在出口截面处,其压力达到被压。如图五中的曲线C 所示。激波产生的位置随着背压的升高而向喷管入口方向移动,激波在 未达到喉部之前,其喉部的压力仍保持临界压力,流量仍为最大流量。 当背压升高到某一值时,将脱离临界状态,其流量低于最大流量。
工程热力学实验指导书:实验三 空气在喷管内流动性能测定实验

实验三 空气在喷管内流动性能测定实验一、实验目的(1)巩固和验证有关气体在喷管内流动的基本理论,掌握气流在喷管中流速、流量、压力的变化规律,加深临界状态参数、背压、出口压力等基本概念的理解。
(2)测定不同工况(b p >cr p ,cr b p p =,cr b p p <)下,气流在喷管内流量m的变化,绘制s b p p m- 曲线;分析比较max m 的计算值和实测值;确定临界压力cr p 。
(3)测定不同工况时,气流沿喷管各截面(轴相位置X )的压力变化情况,绘制1p p X x-关系曲线,分析比较临界压力的计算值和实测值。
二、实验类型综合性实验 三、实验仪器本实验装置由实验本体、真空泵及测试仪表等组成。
其中实验本体由进气管段,喷管实验段(渐缩喷管与渐缩渐扩喷管各一),真空罐及支架等组成,实验装置系统图见图3.1,采用真空泵作为气源设备,装在喷管的排气侧。
喷管入口的气体状态用测压计6和温度计7测量。
气体流量用风道上的孔板流量计2测量。
喷管排气管道中的压力p 2用真空表11测量。
转动探针移动机构4的手轮,可以移动探针测压孔的位置,测量的压力值由真空表12读取。
实验中要求喷管的入口压力保持不变。
风道上安装的调节阀门3,可根据流量增大或减小时孔板压差的变化适当开大或关小调节阀。
应仔细调节,使实验段1前的管道中的压力维持在实验选定的数值。
喷管排气管道中的压力p 2由调节阀门3控制,真空罐13起稳定排气管压力的作用。
当真空泵运转时,空气由实验本体的吸气口进入并依次通过进气管段,孔板流量计,喷管实验段然后排到室外。
喷管各截面上的压力采用探针测量,如图3.2所示,探针可以沿喷管的轴线移动,具体的压力测量是这样的:用一根直径为1.2mm 的不锈钢制的探针贯通喷管,起右端与真空表相通,左端为自由端(其端部开口用密封胶封死),在接近左端端部处有一个0.5mm 的引压孔。
显然真空表上显示的数值应该是引压孔所在截面的压力,若移动探针(实际上是移动引压孔)则可确定喷管内各截面的压力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上式表明,定熵流动中,如果气体流速增大 ( dc f 0 ),则气体的压力必降低( dp 0);
如果气体流速减小(dc f 0),则气体的压力 必增高( dp 0)。这就是喷管和扩压管的流 动特征。也就是说,喷管的目的是使气体和蒸 汽降压增速;而扩压管的目的是增压减速。为 了更好地实现这一目的,还需要有管道截面变 化来配合。
p p
2 1
将临界压力比公式3-120带入3-119可得临界流 速为:
cf ,cr
k k 2 p11 2 RgT1 k 1 k 1
二、喷管中气体的流量
将式 3-111可得:
qm
v p2 1 p1 v2
及3-119带入连续性方程式
k 1 k k p2 2 p11 1 p1 k 1
q (h2 h1 ) wt
q dh dwt
当q=0,且可逆时:
q dh wt dh vdp 0
vdp dh
cdc vdp
将稳定流动能量方程式3-114带入得: 说明在流动过程中,工质的流速增加,必须 有压力降低。所以压差是提高工质流动速度 的必要条件,也是流速提高的动力。
由过程方程式3-115和连续性方程式3-112可得:
dc f dA 2 ( Ma 1) A cf
上式称为管内流动特征方程,给出了马赫数、 截面面积变化率与流速变化率之间的关系。
根据特征方程:
dA dc 2 M a 1 A c
对于拉伐尔喷管,其减缩部分在亚声速范围内 工作,而渐扩部分在超声速范围内工作,其最小截 面处(称为喉部),流速恰好达到当地声速,此处 是气流从亚声速变化到超声速的转折点,通常称为 临界截面。临界截面处的气体参数称为临界参数, 用下角标cr表示。
m
v
qm1 qm 2
A1c1 A2 c2 Ac const v1 v2 v
微分方程:
dA dv dc A v c
上式称为连续性方程式,它表达了气体 流经喷管时流速变化与体积变化及喷管截面 变化之间的制约关系,适用于任何工质的可 逆与不可逆稳定流动过程。
(二)稳定流动能量方程式
s
s
对于理想气体的定熵过程, c 将过程方程式带入上式有:
kp kR g T
显然,声速不是一个常数,它取决于气体的性质
及所处的状态。由上式可知,理想气体中的声速 只取决于其热力学温度,所以声速通常是指某一 状态下的声速,称为当地声速。例如,在 0℃的 空气中的声速为331m/s;20℃的空气中的声速 为343m/s。 在讨论气体和蒸汽流动特性时,流体的流动速度 和当地声速的比值称为马赫数,用符号 Ma 表示, 即: c
说明工质的速度升高来源于流动过程中的焓降。
微分形式
cdc dh(适用于可逆及不可逆过程 )
(三)过程方程
气体在喷管中的流动可以视为绝热过程,此 外喷管内表面光滑,摩擦阻力很小,加之形状设 计合理,可以避免漩涡发生,因此可以近似认为 流动过程是可逆的。当气体为理想气体且比热容 为常量时: k 根据可逆绝热过程方程有: pv 常数 对此式进行微分可得:
三、喷管中气体的流速和流量
由上式可见,喷管出口截面的流速取决 于工质的性质、进口截面处工质的状态与进 出口截面处工质的压力比p2/p1。当工质与进 口截面处的状态确定时,喷管出口截面的流 速只取决于压力比p2/p1 ,并且随p2/p1的减小 而增大。 定熵流动过程中,临界截面上气体的流 速等于当地声速,临界截面上气体的压力与p1 之比称为临界压力比。
p2
1
qmax
0
1 4
1 2
3 4
1 p 2
p
1
但若继续降低喷管出口所在的空间压力 (背压),流量并未继续增大,而是维持最 大值不变。原因是减缩喷管中的压力不可能 降至临界压力以下。代入临界压力比的计算 公式3-120后可得气体最大流量值为: 2 k 2 k 1 p1 qm,max Amin 2 k 1 k 2 v1 由于缩放喷管一般都工作在背压小于临 界压力的情况下,其喉部截面上的压力总保 持为临界压力,其流量总保持最大值,不随 背压的降低而增大,所以上式同样适用于缩 放喷管。
vcr pcr
p
1
根据临界截面处流体流速等于当地声速有:
ccr
k 1 k pcr k 2 Rg 1 p k 1 T 1 1
cf ,cr
pcr
1
kRg Tcr
p kRg T 1 cr p 1
A2c f 2
2
2
A2
A2
2 k 1 k k k p1 p2 p2 2 p k 1 1 p1 1
当喷管出口截面积 A 和进口参数一定时,气体 流量随压比 p 变化,流量与压比的变化关系如下 图所示。当压比值为1时,气体的流量为零,当 压比逐渐减小时,流量逐渐增加,至临界压比时, 气体的流量达到最大值。
喷管中的实际流动过程是稳定的或接近稳定的。 对于一维稳定流动,气体的热力参数和力学参数只 沿喷管的轴向发生变化。实际上,在垂直于流动方 向的同一截面上各点的参数并不完全相同,可近似 取截面平均值进行计算。 (一)连续性方程 一维稳定流动中,根据质量守恒原理,任一截 面的流动参数不变,流经任一截面的质量流量应为 常数。 q Ac const
dp dv k 0 p v
dp dv 整理后得: k p v
声速和马赫数 在气体高速流动的分析中,声速和马赫数是十分 重要的两个参数。 声速是声音在介质中的传播速度,即微弱扰动产 生的压力波在连续介质中传播的速度,用符号c 表示。压力波在气体和蒸汽中的传播过程可视为 是定熵过程,由物理学可知,气体或蒸汽的声速 计算公式为: c ( p ) 2 ( p )
1 2 2 q (h2 h1 ) (c2 c1 ) g ( z2 z1 ) ws 2
q 0, ws 0, g ( z2 z1 ) 0
2 (c2 c12 ) 2(h2 h1 )
c 2 2h
上式表明喷管任一截面上的焓与动能之和保持定值。
Ma
f
c
根据马赫数的大小可将气体和蒸汽的流动分为:
二、喷管截面的变化规律: 喷管的设计应该使喷管在给定的进口状态和出口 压力下,尽可能获得更多的动能,这就要求喷管 的流道形状符合流动过程的规律,不产生任何能 量损失,使气体在喷管中进行可逆绝热流动,即 定熵流动。这时喷管截面积的变化和气体流速变 化、状态变化之间的关系,就可由上述喷管流动 基本方程式求得。 对于喷管定熵稳定流动过程:
k k 1
k 1 k
整理后有:
p
2 vcr k 1
临界压力比与绝热指数有关,取决于气体的热力 性质,当比热容为定值时:
临界压力比是喷管设计计算的一个重要 参数,是选择喷管形状的重要依据,由式3119可得:
p
p2
1
vcr
vcr
选用渐缩形喷管 选用缩放形喷管
3-6 气体在喷管中的流动 喷管:使流体压力降低,增加气体或蒸汽 流速的变截面短管。 例如:工业上常用的各种喷射泵、引射器、 抽气器等都要用到喷管。 扩压管:使气流压力升高而流速降低的变 截面短管。 气体在扩压管中所经历的过程是喷管中过 程的逆过程,这里重点介绍气体在喷管中 的流动过程。
一、喷管中的稳定流动基本方程式
