2021年高考数学大数据分析预测高考中常见的不等式(选做题)解法
2021年高考数学真题和模拟题分类汇编专题19不等式选讲含解析
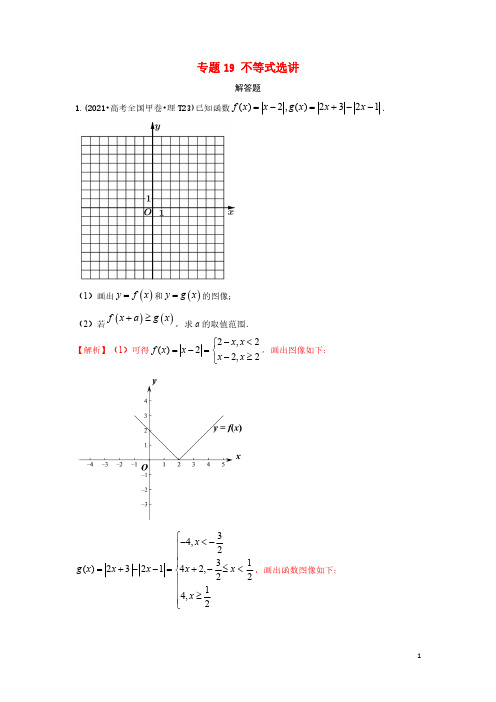
专题19不等式选讲解答题1.(2021•高考全国甲卷•理T23)已知函数()2,()2321f x x g x x x =-=+--.(1)画出()y f x =和()y g x =的图像;(2)若()()f x ag x +≥,求a 的取值范围.【解析】(1)可得2,2()22,2x x f x x x x -<⎧=-=⎨-≥⎩,画出图像如下:34,231()232142,2214,2x g x x x x x x ⎧-<-⎪⎪⎪=+--=+-≤<⎨⎪⎪≥⎪⎩,画出函数图像如下:(2)()|2|f x a x a +=+-,如图,在同一个坐标系里画出()(),f x g x 图像,()y f x a =+是()y f x =平移了a 个单位得到,则要使()()f x a g x +≥,需将()y f x =向左平移,即0a >,当()y f x a =+过1,42A ⎛⎫⎪⎝⎭时,1|2|42a +-=,解得112a =或52-(舍去),则数形结合可得需至少将()y f x =向左平移112个单位,112a ∴≥.2.(2021•高考全国乙卷•文T23)已知函数()3f x x a x =-++.(1)当1a =时,求不等式()6f x ≥的解集;(2)若()f x a>-,求a 的取值范围.【解析】(1)当1a =时,()13f x x x =-++,13x x -++表示数轴上的点到1和3-的距离之和,则()6f x ≥表示数轴上的点到1和3-的距离之和不小于6,故4x ≤-或2x ≥,所以()6f x ≥的解集为(][),42,-∞-+∞ .(2)依题意()f x a >-,即3a x a x -+>-+恒成立,333x a x x a a x -++-+=≥++,故3a a +>-,所以3a a +>-或3a a +<,解得32a >-.所以a 的取值范围是3,2⎛⎫-+∞ ⎪⎝⎭.3.(2021•河南郑州三模•理T23)已知函数f (x )=|x +1|﹣|2x ﹣4|.(Ⅰ)在平面直角坐标系中画出函数f (x )的图象;(Ⅱ)若对∀x ∈R ,f (x )≤t 恒成立,t 的最小值为m ,且正实数a ,b ,c 满足a +2b +3c =m ,求的最小值.【解析】(Ⅰ),图象如图所示,(Ⅱ)由(Ⅰ)知,f (x )max =3,则t ≥3,故m =3,即a +2b +3c =3,由柯西不等式有,,∴的最小值为3,当且仅当a +c =b +c =1时等号成立.4.(2021•河南开封三模•文理T23)已知函数,g (x )=|x ﹣1|.(1)求函数y =f (x )+g (x )的最小值;(2)已知θ∈[0,2π),求关于θ的不等式的解集.【解析】(1)由已知可得,当且仅当即时等号成立,所以函数y =f (x )+g (x )的最小值为.(2)由已知,原不等式可化为,①当时,,原不等式化为sin θ﹣cos θ>2,此时无解,②当时,,原不等式化为sin θ+cos θ<﹣1,即,所以,,综上所述,不等式的解集为(π,).5.(2021•河南焦作三模•理T23)已知函数f(x)=|x+1|+|2x﹣5|﹣7.(Ⅰ)在如图所示的网格中画出y=f(x)的图象;(Ⅱ)若当x<1时,f(x)>f(x+a)恒成立,求a的取值范围.【解析】(Ⅰ)当x<﹣1时,f(x)=﹣x﹣1﹣2x+5﹣7=﹣3x﹣3,当﹣1≤x≤时,f(x)=x+1﹣2x+5﹣7=﹣x﹣1,当x>时,f(x)=x+1+2x﹣5﹣7=3x﹣11,综上f(x)=,则对应的图象如图:(Ⅱ)当a=0时,不等式不成立,当a<0时,y=f(x)的图象向右平移﹣a个单位得到y=f(x+a)的图象,此时对任意x<1时,y=f(x+a)总在y=f(x)的上方,不满足条件.当a>0时,y=f(x+a)的图象最多平移到与y=f(x)的图象交于点(1,﹣2)的位置,此时a=2,此时a的取值范围是(0,2].6.(2021•四川内江三模•理T23)已知a>0,b>0,4a+b=2ab.(1)求a+b的最小值;(2)若a+b≥|2x﹣1|+|3x+2|对满足题中条件的a,b恒成立,求实数x的取值范围.【解析】(1)因为a>0,b>0,所以,所以a+b=(a+b)((4+)=,当且仅当且,即a=,a+b的最小值;(2)若a+b≥|2x﹣2|+|3x+2|对满足题中条件的a,b恒成立,则,当x时,原不等式可化为2x﹣1+4x+2,所以;当时,原不等式可化为﹣2x+4+3x+2,所以,当x时,原不等式可化为﹣2x+8﹣3x﹣2,所以﹣,综上,x的取值范围[﹣].7.(2021•安徽蚌埠三模•文T23)已知函数f(x)=m﹣|x|﹣|x﹣1|,m∈R,且f(x)的最大值为1,(1)求实数m的值;(2)若a>0,b>0,a+b=m,求证:.【解析】(1)解:∵|x|+|x﹣1|≥|x﹣(x﹣1)|=1,当x(x﹣1)≤0时取到等号,∴f(x)max=m﹣1=1,∴m=2.(2)证明:由a>0,b>0,a+b=2≥2,∴ab≤1,∴++=+=≥4,当且仅当a=b=1时取等号.8.(2021•贵州毕节三模•文T23)已知函数f(x)=|x+1|+|x﹣2|.(Ⅰ)解不等式f(x)<x+4;(Ⅱ)若k是f(x)的最小值,已知m>0,n>0,且(k+1)m+n=1,求证:k2mn≤m+n.【解析】(Ⅰ)f(x)=|x+1|+|x﹣2|=,故当x>2时,f(x)<x+4⇔2x﹣1<x+4,解得:x<5,∴2<x<5.当﹣1≤x≤2时,f(x)<x+4⇔3<x+4,解得x>﹣1,∴﹣1<x≤2.当x<﹣1时,f(x)<x+4⇔﹣2x+1<x+4,解得x>﹣1,∴此时x无解.综上,f(x)<x+4的解集为{x|﹣1<x<5};证明:(Ⅱ)由(Ⅰ)知,f(x)≥3,∴k=3.由(k+1)m+n=1,得4m+n=1,要证k2mn≤m+n,即9mn≤m+n,即证,就是证,又∵m>0,n>0,∵,当且仅当,即时取“=”,∴k2mn≤m+n成立.9.(2021•河南济源平顶山许昌三模•文T23.)已知函数f(x)=|x+2|﹣m|x+1|.(1)若m=﹣2,求不等式f(x)≥8的解集;(2)若关于x的不等式f(x)≤m|x+3|对于任意实数x恒成立,求实数m的取值范围.【解析】(1)当m=﹣2时,f(x)=|x+2|+2|x+1|=,当x≤﹣2时,﹣3x﹣4≥8,解得x≤﹣4;当﹣2<x<﹣1时,不等式无解;当x≥﹣1时,3x+4≥8,解得x≥.综上,不等式的解集为(﹣∞﹣4]∪[,+∞).(2)关于x的不等式f(x)≤m|x+3|对于任意实数x恒成立,即为|x+2|≤m(|x+1|+|x+3|),由于|x+1|+|x+3|≥|x+1﹣x﹣3|=2,当且仅当﹣3≤x≤﹣1时,等号成立,所以m≥,记g(x)=,当x≥﹣1时,g(x)==;当x≤﹣3时,g(x)==.则g(x)=,所以g(x)∈[0,],所以m≥,所以实数m的取值范围为[,+∞).10.(2021•四川泸州三模•理T23.)已知函数f(x)=|x+6|﹣|x2﹣2x+2|.(Ⅰ)求不等式f(x)≥6的解集;(Ⅱ)设函数f(x)的最大值为m,正数a,b,c满足a+b+c=+,求证:.【解析】(Ⅰ)∵x2﹣2x+2=(x﹣1)2+1>0,∴f(x)=|x+6|﹣x2+2x﹣2,不等式f(x)≥6等价于|x+6|﹣x2+2x﹣2≥6,即或,解得1≤x≤2或∅,∴不等式f(x)≥6的解集为[1,2];(Ⅱ)证明:由(Ⅰ)可知,当时,,∴,又∵a,b,c为正实数,a+b+c=4,∴,∴,当且仅当时等号成立,原命题得证.11.(2021•宁夏中卫三模•理T23.)设函数f(x)=|1﹣2x|﹣3|x+1|,f(x)的最大值为M,正数a,b满足+=Mab.(Ⅰ)求M;(Ⅱ)是否存在a,b,使得a6+b6=?并说明理由.【解析】(1)分三类讨论如下:①当x<﹣1时,f(x)=x+4,单调递增,f(x)<3;②当﹣1≤x≤时,f(x)=﹣5x﹣2,单调递减,f(x)max=f(﹣1)=3,③当x>时,f(x)=﹣x﹣4,单调递减,f(x)<f()=﹣,综合以上讨论得,f(x)的最大值M=3;(2)假设存在正数a,b,使得a6+b6=≥2=2a3b3,所以,≤,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣①又因为+=Mab=3ab≥2•,所以,≥,﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣﹣②显然①②相互矛盾,所以,假设不成立,即不存在a,b使得a6+b6=.12.(2021•江西南昌三模•理T23.)已知函数f(x)=|x﹣3|+2|x﹣1|.(Ⅰ)求f(x)的最小值m;(Ⅱ)已知a>0,b≥0,若a+2b=m时,正常数t使得ta+ab的最大值为2,求t的值.【解析】(Ⅰ)因为,所以当x=1时,f(x)min=m=2,(Ⅱ)因为m=2,所以a+2b=2,则a+2(b+t)=2t+2,又因为,所以,则,所以,则t=1或t=﹣3(舍),当且仅当a=2(b+1),即a=2,b=0时,等号成立.13.(2021•江西上饶三模•理T23.)已知函数f(x)=|x+2|﹣|x﹣2|.(1)解不等式f(x)≥2;(2)若_____,求a的最小值.①不等式f(x)≥a2+3a有解;②不等式f(x)≥a2+5a恒成立.请从上述两种情形中任选一种作答.【解析】(1)f(x)=,因为f(x)≥2,当x≤﹣2时,﹣4≥2不成立,解得x∈∅;当﹣2<x<2时,由2x≥2,得1≤x<2;当x≥2时,由4≥2恒成立,解得当x≥2;综上,f(x)≥2解集为[1,+∞);(2)若选①不等式f(x)≥a2+3a有解,则f(x)max≥a2+3a,由(1)知,f(x)max=4,所以a2+3a﹣4≤0,解得﹣4≤a≤1;所以a min=﹣4;若选②不等式f(x)≥a2+5a恒成立,则f(x)min≥a2+3a,由(1)知,f(x)min=﹣4,所以a2+5a+4≤0,解得﹣4≤a≤﹣1;所以a min=﹣4.14.(2021•安徽宿州三模•文理T23.)已知函数f(x)=|x﹣2|﹣|x+1|.(Ⅰ)求不等式f(x)≤1的解集;(Ⅱ)若函数f(x)的最大值为m,且正实数a,b满足2a+b=m,求证:a2+4b2≥.【解析】(Ⅰ)|x﹣2|与|x+1|的零点分别是x=2,x=﹣1,整个定义域被划分成3个区间,分别讨论如下:1)当x≤﹣1时,f(x)=﹣x+2+x+1=3,f(x)≤1的解集为空集∅,2)当﹣1<x≤2时,f(x)=﹣x+2﹣x﹣1=﹣2x+1,﹣2x﹣2x+1≤1,x≤0,取交集得f (x)≤1的解集为[0,2],3)当2<x时,f(x)=x﹣2﹣x﹣1=﹣3,f(x)≤1的解集为[2,+∞),对以上三种情况的结果取并集,不等式f(x)≤1的解集为[0,+∞),(II)证明:分段函数的最值在分段点处取得,由此可以比较函数在三个分段区间上的最大值,取最大者得m=3.由2a+b=3,,原不等式等价于,即17(a2+4b2)≥4(2a+b)2,做差比较证明(a﹣8b)2≥0,这是显然的.15.(2021•安徽马鞍山三模•文理T23.)已知函数f(x)=|2x+3|.(1)解不等式f(x)+f(x﹣3)≤8;(2)已知关于x的不等式f(x)+|x+a|≤x+5,在x∈[﹣1,1]上有解,求实数a的取值范围.【解析】(1)函数f(x)=|2x+3|.不等式f(x)≤5﹣f(x﹣3),即|3x+3|+|3x﹣3|≤5,等价于或或,解得:﹣2≤x≤2,所以原不等式的解集为{x|﹣2≤x≤2};(2)当x∈[﹣1,1]时,不等式f(x)+|x+a|≤x+5,即|x+a|≤2﹣x,所以|x+a|≤2﹣x在[﹣1,1]上有解,即﹣2≤a≤2﹣2x在[﹣1,1]上有解,所以﹣2≤a≤4.实数a的取值范围:[﹣2,4].16.(2021•江西九江二模•理T23.)已知函数f(x)=|x+2|﹣|ax﹣2|(a∈R).(Ⅰ)当a=2时,解不等式f(x)≥1;(Ⅱ)当x∈[﹣2,2]时,求证:f(x)+f(﹣x)≤0.【解析】(Ⅰ)当a=2时,f(x)≥1即|x+2|﹣|2x﹣2|≥1等价为或或,解得x∈∅或≤x<1或1≤x≤3,所以原不等式的解集为[,3];(Ⅱ)证明:当x∈[﹣2,2]时,f(x)=|x+2|﹣|ax﹣2|=x+2﹣|ax﹣2|,f(﹣x)=2﹣x﹣|ax+2|,f(x)+f(﹣x)=4﹣(|ax﹣2|+|ax+2|),因为|ax﹣2|+|ax+2|≥|ax﹣2﹣(ax+2)|=4,当(ax﹣2)(ax+2)≤0时,取得等号,所以4﹣(|ax﹣2|+|ax+2|)≤0,即f(x)+f(﹣x)≤0.17.(2021•江西上饶二模•理T23.)设函数f(x)=|2x﹣1|﹣|x+1|+2ax,a∈R.(1)若,求不等式f(x)>0的解集;(2)若函数f(x)恰有三个零点,求实数a的取值范围.【解析】(1)当a=时,不等式f(x)>0,即|2x﹣1|﹣|x+1|+x>0,则或或,解得x≤﹣1或﹣1<x<0或x>1,∴不等式f(x)>0的解集为(﹣∞,0)∪(1,+∞);(2)由f (x )=|2x ﹣1|﹣|x +1|+2ax =0,得|2x ﹣1|﹣|x +1|=﹣2ax ,设g (x )=|2x ﹣1|﹣|x +1|=,h (x )=﹣2ax ,如图,要使y =g (x )与y =﹣2ax 有3个不同交点,则﹣3<﹣2a <﹣1,即<a <.∴实数a 的取值范围是(,).18.(2021•江西鹰潭二模•理T23.)设x ,y ,z ∈R ,z (x +2y )=m .(1)若x 2+2y 2+3z 2的最小值为4,求m 的值;(2)若,证明:m ≤﹣1或m ≥1.【解析】(1)x 2+2y 2+3z 2=(x 2+z 2)+2(y 2+z 2)≥2xz +4yz =2(xy +2yz ),当且仅当x =y =z ,上式取得等号,由题意可得2(xy +2yz )=2m =4,∴m =2.(2)证明:∵a 2+b 2≥2|ab |,∴2(a 2+b 2)≥(a +b )2,∴,∴|m |≥1,可得m ≤﹣1或m ≥1.19.(2021•吉林长春一模•文T23.)已知0,0, 4.a b a b >>+=(I)求证:;(Ⅱ)求证:1212223a b+++.【解析】(1)证明:因为0,0a b >>,2222224a b a b ab+++()22a b +=,(当且仅当2a b ==时取等号)(5分)(2)因为4a b +=,所以26,a b ++=所以()221111*********a a b ba b a b a b ⎛⎫+++⎛⎫⎛⎫+=+=+++ ⎪ ⎪⎪+++⎝⎭⎝⎭⎝⎭(1123623+=+,)2a b +=时取等号(10分)20.(2021•新疆乌鲁木齐二模•文T23.)已知a ,b ∈R +,(a ﹣b )2=(ab )3,a +b ≤2ab .(Ⅰ)求证:a +b ≥2ab ;(Ⅱ)求a 与b 的值.【解析】(Ⅰ)证明:∵a ,b ∈R +,(a ﹣b )2=(ab )3,∴(a +b )2=(a ﹣b )2+4ab =(ab )3+4ab ,则a +b ≥2ab ;(Ⅱ)由(Ⅰ)知,a +b ≥2ab ,又a +b ≤2ab ,∴a +b =2ab ,又取等号时,(ab )3=4ab ,即ab =2,联立,解得或.21.(2021•安徽淮北二模•文T23.)设函数f (x )=|2x ﹣a |+|x +|(a >0).(Ⅰ)证明:f (x )≥2;(Ⅱ)若f (1)<4,求实数a 的取值范围.【解析】(Ⅰ)证明:∵f (x )=|2x ﹣a |+|x +|=,∴f (x )在(﹣∞,﹣)单调递减,在[﹣,]单调递减,在(,+∞)上单调递减,∴f (x )min =f ()=+≥2,当且仅当x =且a =2时取最小值,∴f (x )≥2;(Ⅱ)∵f(1)=|2﹣a|+|1+|<4(a>0),∴|2﹣a|<3﹣,∴3﹣>0,解得:a>①,当a≤2时,有2﹣a<3﹣,∴a<﹣2或a>1,结合①得:1<a≤2,当a>2时,有a﹣2<3﹣,∴2<a<,综上:实数a的取值范围是(1,).22.(2021•宁夏银川二模•文T23.)已知函数f(x)=|x+a|﹣2|x﹣b|(a>0,b>0).(1)当a=b=1时,解不等式f(x)>0;(2)若函数g(x)=f(x)+|x﹣b|的最大值为2,求的最小值.【解析】(1)当a=b=1时,f(x)=|x+1|﹣2|x﹣1|,①当x≤﹣1时,f(x)=﹣(x+1)+2(x﹣1)=x﹣3>0,∴x>3,∴无解,②当﹣1<x<1时,f(x)=(x+1)+2(x﹣1)=3x﹣1>0,∴<x<1,③当x≥1时,f(x)=(x+1)﹣2(x﹣1)=﹣x+3>0,∴1≤x<3,综上所述:不等式f(x)>0的解集为(,3).(2)g(x)=)=|x+a|﹣2|x﹣b|+|x﹣b|=|x+a|﹣|x﹣b|,∵|x+a|﹣|x﹣b|≤|(x+a)﹣(x﹣b)|=|a+b|,∴g(x)max|=|a+b|=2,∵a>0,b>0,∴a+b=2,∴+=(+)(a+b)×=(++5)×≥(2+5)×=,当且仅当=,即b=2a时取等号,∴+的最小值为.23.(2021•山西调研二模•文T23)(1)证明:2+1≥(2)若>0,>0,求B+2+2+1的最大值.【解析】(1)证明:∵≥r2,当且仅当=时,等号成立,∴令=1,则有2≥r1,当且仅当=1时,等号成立,即2+1≥2+1≥(r1)22,当且仅当=1时,等号成立,(2)解:由(1)得2+1≥∴B+2+2+1=(r1)(22(r1)(r1)22+,又∵(r1)22+2≥=2(+1)⋅,=时,等号成立,即+1= 2,即=12时,等号成立,∴(r1)(r1)22+2≤=,即B+2+2+1≤∴当=1=2时,B+22取得最大值,且最大值为【解析】(1)≥r2,令=1即可得证;(2)利用(1)的结论可得B+2+2+1≤本题考查不等式的证明,考查最值的求解,考查逻辑推理能力,属于中档题.24.(2021•河南郑州二模•文T23.)已知函数f(x)=|2x﹣4|+|x+a|(a>0).(Ⅰ)若a=1,求不等式f(x)≥5的解集;(Ⅱ)若f(x)≥a2﹣2a+4恒成立,求实数a的取值范围.【解析】(Ⅰ)若a=1,不等式f(x)≥5即为|2x﹣4|+|x+1≥5,等价为或或,解得x≤﹣1或﹣1<x≤0或x≥4,所以原不等式的解集为(﹣∞,0]∪[4,+∞):(Ⅱ)若f(x)≥a2﹣2a+4恒成立,即为(|2x﹣4|+|x+a|)min≥a2﹣2a+4,a>0,而|2x﹣4|+|x+a|=|x﹣2|+(|x﹣2|+|x+a|)≥|2﹣2|+|x﹣2﹣x﹣a|=|a+2|=a+2,当x=2时,上式取得等号,所以a2﹣2a+4≤a+2,即a2﹣3a+2≤0,解得1≤a≤2,即a的取值范围是[1,2].。
2021年高考数学题型:不等式解题方法总结题型归纳

2021年高考数学题型:不等式解题方法总结题型归纳任两个正数的算术平均数不小于它们的几何平均数。
整理了不等式解题方法总结,帮助广大高中学生学习数学知识!不等式不等式这部分知识,渗透在中学数学各个分支中,有着十分广泛的应用。
因此不等式应用问题体现了一定的综合性、灵活多样性,对数学各部分知识融会贯通,起到了很好的促进作用。
在解决问题时,要依据题设与结论的结构特点、内在联系、选择适当的解决方案,最终归结为不等式的求解或证明。
不等式的应用范围十分广泛,它始终贯串在整个中学数学之中。
诸如集合问题,方程(组)的解的讨论,函数单调性的研究,函数定义域的确定,三角、数列、复数、立体几何、解析几何中的最大值、最小值问题,无一不与不等式有着密切的联系,许多问题,最终都可归结为不等式的求解或证明。
知识整合1。
解不等式的核心问题是不等式的同解变形,不等式的性质则是不等式变形的理论依据,方程的根、函数的性质和图象都与不等式的解法密切相关,要善于把它们有机地联系起来,互相转化。
在解不等式中,换元法和图解法是常用的技巧之一。
通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数、数形结合,则可将不等式的解化归为直观、形象的图形关系,对含有参数的不等式,运用图解法可以使得分类标准明晰。
2。
整式不等式(主要是一次、二次不等式)的解法是解不等式的基础,利用不等式的性质及函数的单调性,将分式不等式、绝对值不等式等化归为整式不等式(组)是解不等式的基本思想,分类、换元、数形结合是解不等式的常用方法。
方程的根、函数的性质和图象都与不等式的解密切相关,要善于把它们有机地联系起来,相互转化和相互变用。
3。
在不等式的求解中,换元法和图解法是常用的技巧之一,通过换元,可将较复杂的不等式化归为较简单的或基本不等式,通过构造函数,将不等式的解化归为直观、形象的图象关系,对含有参数的不等式,运用图解法,可以使分类标准更加明晰。
4。
证明不等式的方法灵活多样,但比较法、综合法、分析法仍是证明不等式的最基本方法。
高考数学中的不等式求解方法总结

高考数学中的不等式求解方法总结高考数学中不等式求解是一个重要的知识点,也是备战高考时需要重点掌握的内容之一。
不等式本身在数学领域具有广泛的应用,掌握不等式的求解方法也有助于学生更好地理解和应用数学知识。
在本文中,我们将总结高考数学中的不等式求解方法。
一、最值法当不等式的二次项系数为正数(即$ax^2+bx+c$,其中$a>0$)时,可使用最值法。
该方法的基本思路是,先确定 $x$ 的取值范围,然后通过求函数的最值来确定函数的正负性和取值范围。
如下例子:$$ x^2 - 6x + 5 > 0 $$该不等式中 $a=1$,所以最值法适用。
首先,我们需要求出二次函数 $y=x^2 - 6x + 5$ 的对称轴,即 $\frac{-b}{2a}=\frac{6}{2}=3$,也就是说,当 $x=3$ 时,函数取到最小值 $y=-1$。
因此我们可以将不等式转化为 $(x-3)^2-1>0$,进一步化简为 $|x-3| >1$。
根据绝对值的定义可知,$|x-3| >1$ 相当于$x<2$ 或 $x>4$。
因此该不等式的解集为 $(-\infty,2)\cup(4,+\infty)$。
二、配方法配方法是不等式求解的一种比较通用的方法,它的基本思路是,将不等式中的项按一定的方式加减或乘除,使得原不等式变为一个可以比较的简单的不等式。
常见的配方法有以下几种:1. 同除法通过同除法,将不等式中的一次项的系数变为 $1$,例如:$$ \frac{1}{x} + \frac{2}{x+2} < 1 $$可同除以 $x(x+2)$,得到:$$ 1< x(x+2)+2x $$化简得:$$ -x^2 -4x +1 <0 $$代数式的符号是问题的重点,由于 $a<0$,所以合法解集为 $-2+\sqrt{3} < x < -2-\sqrt{3}$。
2. 变量代换通过将不等式中的变量做适当的代换,将原不等式转化为一个更容易求解的不等式。
怎样解决高中数学的不等式问题

怎样解决高中数学的不等式问题在高中数学学习中,不等式问题是一个重要的内容,也是学生们常常遇到的挑战之一。
解决不等式问题需要一定的方法和技巧,本文将介绍几种常用的解不等式问题的方法,并提供相应的例子进行说明。
一、图像法图像法是解决一元一次不等式问题的常用方法之一。
这种方法将不等式以函数图像的形式表示出来,通过观察图像来确定不等式的解集。
例如,解不等式2x - 3 < 5,我们可以绘制出函数y = 2x - 3的图像,然后观察函数图像与y = 5的关系。
通过观察可以发现,函数图像在y= 5的下方,因此解集为x < 4。
二、代数法代数法是解决一元一次不等式问题的另一种常用方法。
这种方法通过对不等式进行代数变换,将不等式转化为等价的形式,从而求得解集。
例如,解不等式3x + 2 > 7,我们可以通过代数变换来求解。
首先,将不等式两边减去2,得到3x > 5,然后将不等式两边除以3,得到x > 5/3。
因此,解集为x大于5/3。
三、区间法区间法是解决一元一次不等式问题的另一种有效的方法。
这种方法将不等式中的未知数x的取值范围分成若干个区间,然后通过讨论每个区间的符号关系来确定解集。
例如,解不等式2x - 3 ≥ 1,我们可以通过区间法来求解。
首先,将不等式转化为等价的形式2x - 3 - 1 ≥ 0,化简得到2x - 4 ≥ 0,然后求解等式2x - 4 = 0,得到x = 2。
接下来,我们将x的取值范围分成三个区间:x < 2, x = 2, x > 2。
通过在每个区间内代入x的值来判断符号关系,进而确定解集。
根据符号关系的判断,可以得到解集为x ≥ 2。
四、分段讨论法分段讨论法适用于解决一元二次不等式问题,通过将一元二次不等式分成若干个区间,分别讨论每个区间内的不等式关系,进而确定解集。
例如,解不等式x² - 3x + 2 ≤ 0,首先,我们将不等式化简得到(x - 1)(x - 2) ≤ 0。
2021年高考数学分项汇编 专题7 不等式(含解析)理

2021年高考数学分项汇编专题7 不等式(含解析)理一.基础题组1. 【xx全国卷Ⅰ,理3】不等式||<1的解集为…()A.{x|0<x<1}∪{x|x>1}B.{x|0<x<1}C.{x|-1<x<0}D.{x|x<0}【答案】:D2. 【xx全国,理14】设x,y满足约束条件130,x yx yxy≥⎧⎪≤⎪⎨≥⎪⎪≥⎩--,+,,,则z=x-2y的取值范围为__________.【答案】:[-3,3]3. 【xx全国1,理13】若满足约束条件则的最大值为.【答案】:9.4. 【xx全国,理14】设,式中变量x、y满足下列条件则z的最大值为。
【答案】115. 【xx 全国1,理13】若正整数m 满足)3010.02.(lg ________,102105121≈=<<-m mm 则【答案】155二.能力题组1. 【xx 课标Ⅰ,理9】不等式组的解集为D,有下面四个命题:, ,,其中的真命题是( )A .B . C. D .【答案】B x y–1–2–3–41234–1–2–3–41234O A2. 【xx 全国1,理9】在坐标平面上,不等式组所表示的平面区域的面积为( )A.B.C.D.【答案】B3. 【xx高考新课标1,理15】若满足约束条件,则的最大值为 .【答案】3【考点定位】线性规划解法三.拔高题组1. 【2011全国新课标,理13】若变量x,y满足约束条件则z=x+2y的最小值为__________.【答案】-634017 84E1 蓡36611 8F03 較22408 5788 垈25533 63BD 掽32762 7FFA 翺21068 524C 剌L]L26426 673A 机 36249 8D99 趙:31784 7C28 簨31869 7C7D 籽。
高考数学中的解不等式题技巧

高考数学中的解不等式题技巧高中数学中的解不等式是一个常见、重要而又复杂的话题,这也是每年高考必考的内容之一。
为了在高考中拿到更高的数学成绩,解不等式题的优秀技巧和方法就是必不可少的。
本文将为大家详细介绍高考数学中的解不等式题技巧。
一、确定不等式类型解不等式首先要确定不等式的类型,例如一次不等式、二次不等式以及一次不等式与二次不等式混合形式。
不同类型的不等式可能需要不同的解题方法和工具,所以正确地区分不同类型的不等式是解题的第一要素。
二、移项变号不等式中的每项都可以加上或减去相同的数,也可以乘以或除以相同的数,但是要注意判断是不是乘以负数。
在移项变号的过程中,必须保证不等式的方向不变,因为在不等式两侧同时加上一个正数,不等式转化成一个更大的不等式,而在不等式两侧同时加上一个负数,不等式转化成一个更小的不等式。
三、化简如果一个不等式的系数较复杂或有分数,可以通过合并同类项、约分、通分等等化简的方式,使其变得更简单明了,从而更方便地应用解不等式的技巧。
四、双边平方在处理二次不等式时,我们可以使用“双边平方”的方式将其化简成一次不等式,并继续应用一次不等式的解题方法。
不过,需要注意的是,双边平方的过程会使原不等式一些根号项的变化,并且有时会引入不合法解。
因此,在解二次不等式时,需要先判断根号里面的内容的正负,再进行双边平方,确定解的范围,并得出正确的解。
五、裂项在解不等式时,有时我们发现一个不等式的系数和项数都很复杂,难以应用一般的解题方法,这时候可以尝试使用“裂项”的方法,将不等式分解成几个部分,然后分别处理每个部分,最后得到整个不等式的解。
裂项方法的使用需要观察不等式的因式分解式,找到化简的方法,并找出合理的间隔点以及分段条件。
六、代入对于较复杂的不等式,我们可以先猜测一个解,然后代入验证是否成立,从而快速或全面地解出不等式的解。
这种方法的优点是简单易行,而且针对某些形式的不等式,代入还可以直接得到答案,缩短解题时间。
高中数学不等式求解方法及应用

高中数学不等式求解方法及应用引言:在高中数学中,不等式是一个重要的概念和工具。
它不仅在数学理论中有着广泛的应用,而且在实际问题中也有着重要的意义。
本文将介绍高中数学中常见的不等式求解方法,并通过具体的例题来分析和说明这些方法的应用。
一、一元一次不等式的求解方法一元一次不等式是高中数学中最简单的不等式之一。
常见的一元一次不等式形式为ax + b > 0或ax + b < 0。
对于这种类型的不等式,我们可以使用图像法或代数法进行求解。
1. 图像法图像法是一种直观的方法,通过绘制一元一次不等式的图像,可以直观地看出不等式的解集。
例如,对于不等式2x + 3 > 0,我们可以绘制出一元一次函数y = 2x + 3的图像,并找出图像上y > 0的部分,即为不等式的解集。
2. 代数法代数法是一种更为常用和通用的方法,通过对不等式进行代数运算,可以得到不等式的解集。
例如,对于不等式2x + 3 > 0,我们可以通过移项和分析系数的正负来得到解集。
首先,移项得到2x > -3,然后除以2得到x > -3/2,即x的取值范围为(-3/2, +∞)。
二、一元二次不等式的求解方法一元二次不等式是高中数学中常见的不等式之一。
常见的一元二次不等式形式为ax^2 + bx + c > 0或ax^2 + bx + c < 0。
对于这种类型的不等式,我们可以使用图像法或代数法进行求解。
图像法同样是一种直观的方法,通过绘制一元二次不等式的图像,可以直观地看出不等式的解集。
例如,对于不等式x^2 - 4x + 3 > 0,我们可以绘制出一元二次函数y = x^2 - 4x + 3的图像,并找出图像上y > 0的部分,即为不等式的解集。
2. 代数法代数法同样是一种常用和通用的方法,通过对不等式进行代数运算,可以得到不等式的解集。
例如,对于不等式x^2 - 4x + 3 > 0,我们可以通过求解二次方程x^2 - 4x + 3 = 0,并分析二次函数的凹凸性质来得到解集。
高考数学如何解决复杂的不等式题目

高考数学如何解决复杂的不等式题目不等式是高考数学中一个重要的考点,也是考生们容易遇到困惑的难题。
通过掌握一定的解题思路和技巧,我们可以有效地解决复杂的不等式题目。
本文将介绍一些解决不等式题目的方法和策略,帮助考生们应对高考中的挑战。
一、一元一次不等式的解法一元一次不等式是最简单的不等式形式,其解法与一元一次方程相似。
我们可以通过移项和化简的方式来求解。
首先,将所有的项都移到同一边,得到一个等式。
然后我们可以根据系数的正负以及零的位置来判断解集的情况,最后得到不等式的解。
二、二次不等式的解法二次不等式的解法相对复杂一些,需要通过因式分解或配方法等方式来求解。
在解二次不等式时,我们首先要将其转化为一个二次方程,然后再找到方程的解集。
我们可以通过以下两种方法来解二次不等式:1. 因式分解法:将二次不等式化为一个二次方程,通过因式分解将其展开为二个一次因式相乘的形式,然后根据因式的正负来确定解的范围。
2. 配方法:对于一般的二次不等式,我们可以通过配方法将其转化为完全平方的形式。
通过将方程配成完全平方后,我们可以通过解方程的方式来求解不等式。
三、绝对值不等式的解法绝对值不等式是一种特殊的不等式形式,在解法上需要注意绝对值的性质。
对于一元绝对值不等式,我们可以根据绝对值的定义将其分为两种情况来解决:1. 绝对值的定义:|a| = a (a≥0); |a| = -a (a<0)。
2. 情况一:如果不等式中的绝对值对应的是一个非负数,我们可以直接去掉绝对值符号,根据非负数的性质来解不等式。
3. 情况二:如果不等式中的绝对值对应的是一个负数,我们需要将绝对值转化为相反数的形式,然后在解不等式。
四、多元不等式的解法多元不等式是由多个变量构成的不等式,其解法要考虑多个变量之间的关系。
在解多元不等式时,我们可以通过以下步骤来进行:1. 将所有的项移到同一边,化简成一个等式。
2. 利用一元不等式的解法,将多元不等式转化为一元不等式。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021年高考数学大数据分析预测高考中常见的不等式(选做题)的解法目录一、基础知识点: (2)二、七种含有绝对值的不等式 (2))()(,)(R a a x f a x f ∈><型不等式 (2)题型二:形如)0()(>><<a b b x f a 型不等式 (3)()(x g x f <)()(x g x f >型不等式 (3)()(x g x f < (3))()(),()(x f x f x f x f ><型不等式 (3)c n x m x c n x m ≥-+-≥---,恒成立型不等式. (4)a x g x <±)()(型不等式 (4)三、2011—2020年十年高考题(不等式选做) (5)题型一:绝对值不等式的求解 (5)题型二:含绝对值不等式的恒成立问题 (8)题型三:不等式的证明 (14)四、大数据分析预测高考 (18)一、基础知识点:绝对值三角不等式1.定理1:如果a ,b 是实数,则|a +b|≤|a|+|b|,当且仅当ab ≥0时,等号成立.2.定理2:如果a ,b ,c 是实数,则|a -c |≤|a -b |+|b -c |,当且仅当(a -b )(b -c )≥0时,等号成立. 绝对值不等式的解法(1)|a x +b|≤c ⇔-c ≤a x +b ≤c ;(2)|a x +b|≥c ⇔a x +b ≥c 或a x +b ≤-c .3.|x -a |+|x -b|≥c(c>0)和|x -a |+|x -b |≤c(c>0)型不等式的解法方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.方法二:利用“零点分段法”求解,体现了分类讨论的思想;方法三:通过构造函数,利用函数的图像求解,体现了函数与方程的思想.绝对值不等式的解法(1)|a x +b|≤c ⇔-c ≤ax +b ≤c ;(2)|a x +b|≥c ⇔ax +b ≥c 或ax +b ≤-c .3.|x -a|+|x -b|≥c(c>0)和|x -a|+|x -b|≤c(c>0)型不等式的解法方法一:利用绝对值不等式的几何意义求解,体现了数形结合的思想.方法二:利用“零点分段法”求解,体现了分类讨论的思想;方法三:通过构造函数,利用函数的图像求解,体现了函数与方程的思想.二、七种含有绝对值的不等式题型一:形如)()(,)(R a a x f a x f ∈><型不等式解法:根据a 的符号,准确的去掉绝对值符号,再进一步求解.这也是其他类型的解题基础.1、当0>a 时,a x f a a x f <<-⇔<)()( a x f a x f >⇔>)()(或a x f -<)(2、当0=a a x f <)(,无解⇔>a x f )(使0)(≠x f 的解集3、当0<a 时,a x f <)(,无解 ⇔>a x f )(使)(x f y =成立的x 的解集.例1 (2008年四川高考文科卷)不等式22<-x x 的解集为( )A.)2,1(-B.)1,1(-C.)1,2(-D.)2,2(-解:因为 22<-x x ,所以222<-<-x x .即⎪⎩⎪⎨⎧<-->+-020222x xx x ,解得:⎩⎨⎧<<-∈21x R x ,所以 )2,1(-∈x ,故选A. 题型二:形如)0()(>><<a b b x f a 型不等式解法:将原不等式转化为以下不等式进行求解:b x f a a b b x f a <<⇔>><<)()0()(或a x f b -<<-)(需要提醒一点的是,该类型的不等式容易错解为:b x f a a b b x f a <<⇔>><<)()0()(例2:不等式311<+<x 的解集为( )A .)2,0( B.)4,2()0,2( - C .)0,4(- D.)2,0()2,4( -- 解:311311<+<⇔<+<x x 或11,3-<+<-x20<<⇔x 或24-<<-x ,故选D 题型三:形如)()(x g x f <,)()(x g x f >型不等式这类不等式如果用分类讨论的方法求解,显得比较繁琐,其简洁解法如下解法:把)(x g 看成一个大于零的常数a 进行求解,即:)()()()()(x g x f x g x g x f <<-⇔<,)()()()(x g x f x g x f >⇔>或)()(x g x f -<例3设函数312)(++-=x x x f ,若5)(≤x f ,则x 的取值范围是 解:53125)(≤++-⇔≤x x x f 2122212+-≤-≤-⇔+-≤-⇔x x x x x⎩⎨⎧+-≤--≥-⇔212212x x x x 1111≤≤-⇔⎩⎨⎧≤-≥⇔x x x ,故填:[]1,1-. 题型四:形如)()(x g x f <型不等式解法:可以利用两边平方,通过移项,使其转化为:“两式和”与“两式差”的积的方法进行,即:22)()()()(x g x f x g x f <⇔<0)]()()][()([0)]([)]([22<-+⇔<-⇔x g x f x g x f x g x f例4:不等式0212<---x x 的解集为解:2120212-<-⇔<---x x x x 0)2()12(2122222<---⇔-<-⇔x x x x0)]2()12)][(2()12[(<----+-⇔x x x x 11<<-⇔x 所以原不等式的解集为{}11<<-x x 题型五:形如)()(),()(x f x f x f x f ><型不等式解法:先利用绝对值的定义进行判断,再进一步求解,即:)()(x f x f <,无解0)()()(<⇔>x f x f x f 例5:解关于x 的不等式a x xa x x+-->+--1111 解:0111111<+--⇔+-->+--a x x a x x a x x a x a x -<-⇔<+-⇔11011(1) 当0=a 时,原不等式等价于:1011<⇔<-x x(2) 当0>a 时,原不等式等价于:111011<<-⇔<-<-x a x a(3) 当0<a 时,原不等式等价于:01<-x 或a x 11->-1<⇔x 或a x 11->综上所述(1) 当0=a 时,原不等式的解集为:{}1<x x(2) 当0>a 时,原不等式的解集为:⎭⎬⎫⎩⎨⎧<<-111x a x(3) 当0<a 时,原不等式的解集为:⎭⎬⎫⎩⎨⎧-><a x x x 111或 题型六:形如使c n x m x c n x m x ≥-+-≥---,恒成立型不等式. 解法:利用和差关系式:b a b a b a +≤±≤-,结合极端性原理即可解得,即:()()()m n n x m x n x m x c n x m x c -=---=---≥⇔---≥max ;()()()m n n x m x n x m x c n x m x c -=---=---≤⇔-+-≤min ;例6不等式a a x x 3132-≤--+对任意的实数恒成立,则实数a 的取值范围是()A .(][)+∞-∞-,41, B.(][)+∞-∞-,52,C.[]2,1D.(][)+∞-∞-,21,解: 设函数()()41313)(=--+≤--+=x x x x x f所以4)(max =x f 而不等式a a x x 3132-≤--+对任意的实数x 恒成立故41432≥-≤⇒≥-a a a a 或,故选择A 类型七:形如a x g x f <±)()(型不等式 还有如下:()为常数a a x g x f >-)()( )()()(x h x g x f <-,)()()(x h x g x f >-,)()(a x g x f <+()为常数a a x g x f >+)()( )()()(x h x g x f <+,)()()(x h x g x f >+解法:对于解含有多个绝对值项的不等式,常采用零点分段法,根据绝对值的定义分段去掉绝对值号,最后把各种情况综合得出答案,其步骤是:找出零点,确定分段区间;分段求解,确定各段解集;综合取并,去掉所求解集,亦可集合图像进行求解.例7 (2009年高考福建理科卷)解不等式112+<-x x 分析:找出零点:21,0==x x 确定分段区间:21,210,0≥<≤<x x x 解:(1)当0<x 时,原不等式可化为:112+-<+-x x 解得:0>x 因为 0<x ,所以 x 不存在(2)当210<≤x 时,原不等式可化为:112+<+-x x 解得:0>x ,又因为 21<≤x x ,所以 21<<x x (3)当21≥x 时,原不等式可化为:112+<-x x ,解得2<x 又 21≥x ,所以221<≤x 综上所述,原不等式的解集为:{}20<<x x特别地,对于形如,)()(a x g x f <+()为常数a a x g x f >+)()( )()()(x h x g x f <+,)()()(x h x g x f >+型不等式的解法,除了可用零点分段法外,更可转化为以下不等式,即:⇔<+)()()(x h x g x f ⎪⎩⎪⎨⎧<-<+)()()()()()(x h x g x f x h x g x f )()()(x h x g x f >+⇔)()()(x h x g x f >+或)()()(x h x g x f >-例8设函数a x x x f -+-=1)((1)若1-=a ,解不等式3)(≥x f (2)如果,2)(,≥∈∀x f R x 求a 的范围解:当时,1-=a 11)(++-=x x x f 由3)(≥x f 得:311)(≥++-=x x x f即:()()311≥++-x x 或 ()()311≥+--x x 解得:32≥x ,即:23-≤x 或 23≥x。
