2020-2021学年八年级上学期12月月考抽测数学试题
河南省新乡市红旗区新乡学院附属中学2020-2021学年八年级上学期第二次月考数学试题及参考答案
C． D．
6．如图，在△ABC中，AB=5，AC=3，AD是BC边上的中线，AD的取值范围是（）
A．1＜AD＜6B．1＜AD＜4C．2＜AD＜8D．2＜AD＜4
7．若把分式 的x和y都扩大3倍，那么分式 的值（）
A．扩大3倍B．扩大9倍C．扩大4倍D．不变
8．已知 － =3，则 的值是（ ）
∴∠ACB=180°-∠A-∠CBA=180°-40°-60°=80°，
∵P点在AB边上且不与A、B重合，
∴0°＜∠ACP＜80°，
∴0°＜2∠BOC-220°＜80°，
∴110°＜∠BOC＜150°，
∴m=110，n=150．
∴n-m=40．
故选：B．
【点睛】
本题考查了角平分线的性质，三角形内角和定理，一元一次不等式组的解法，熟练掌握三角形内角和定理是解题的关键．
22．甲、乙两商场自行定价销售某一商品．
（1）甲商场将该商品提价15%后的售价为1.15元，则该商品在甲商场的原价为元；
（2）乙商场将该商品提价20%后，用6元钱购买该商品的件数比没提价前少买1件，求该商品在乙商场的原价是多少？
（3）在（1）、（2）的结论下，甲、乙两商场把该商品均按原价进行了两次价格调整．
14．一个长方形的两邻边分别是 ， ，若 ，则这个长方形的面积是_________
15．观察下列各式：1×3=3，而22-1=3；3×5=15，而42-1=15；5×7=35，而62-1=35；…；11×13=143，而122-1=143．将你发现的规律用含有一个字母的式子表示为_____
三、解答题
（1）若点Q的运动速度与点P的运动速度相等，当t＝1时，△ACP与△BPQ是否全等，并判断此时线段PC和线段PQ的位置关系，请分别说明理由；
2020-2021学年南通市崇川区启秀中学八年级(上)月考数学试卷(12月份) word版含解析
2020-2021学年江苏省南通市崇川区启秀中学八年级（上）月考数学试卷（12月份）一、选择题（本大题共10小题，每小题3分，共30分） 1．（3分）下列运算结果为a ﹣1的是（ ） A ．a 2−1a ⋅a a+1B ．1−1aC ．a+1a÷a a−1D ．a 2+2a+1a+12．（3分）下列运算正确的是（ ） A ．3a +2a ＝5a 2 B ．x 2﹣4＝（x +2）（x ﹣2） C ．（x +1）2＝x 2+1 D ．（2a ）3＝6a 23．（3分）如果将分式x+y 6xy中的x 和y 都扩大为原来的3倍，那么分式的值（ ）A ．缩小到原来的13B ．扩大到原来的3倍C ．不变D ．扩大到原来的9倍4．（3分）估计√32×√12+√20的运算结果应在（ ） A ．6到7之间B ．7到8之间C ．8到9之间D ．9到10之间5．（3分）一个等腰三角形两边的长分别为√75和√18，则这个三角形的周长为（ ） A ．10√3+3√2B ．5√3+6√2C ．10√3+3√2或5√3+6√2D ．无法确定6．（3分）已知√5=a ，√14=b ，用含a 、b 的式子表示√0.063，则下列结果正确的是（ ） A ．ab 10B ．3ab 10C ．ab100D ．3ab 1007．（3分）小颖用4张长为a ，宽为b （a ＞b ）的长方形纸片，按如图的方式拼成一个边长为（a +b ）的正方形，图中空白部分的面积为S 1，阴影部分的面积为S 2．若a ＝2b ，则S 1，S 2之间的数量关系为（ ）A ．S 1=32S 2B ．S 1＝2S 2C ．S 1=52S 2D ．S 1＝3S 28．（3分）把(x −1)√−1x−1根号外的因式移入根号内，化简的结果是（ ） A ．√1−xB ．√x −1C ．−√x −1D ．−√1−x9．（3分）已知x 2﹣3x ﹣4＝0，则代数式xx 2−x−4的值是（ ）A ．3B ．2C ．13D ．1210．（3分）如图，大正方形的边长为m ，小正方形的边长为n ，x ，y 表示四个相同长方形的两边长（x ＞y ）．则①x ﹣y ＝n ；②xy =m 2−n 24；③x 2﹣y 2＝mn ；④x 2+y 2=m 2−n 22中，正确的是（ ）A ．①②③B ．①②④C ．①③④D ．①②③④二、填空题（本大题共8小题，11′12题，每小题3分，13～18题，每题4分，共30分） 11．（3分）若分式2x−6x+1的值为0，则x 的值为 ．12．（3分）分解因式：a ﹣6ab +9ab 2＝ ． 13．（4分）当x 时，√x+1|x|−2有意义． 14．（4分）若a 2＝3b ＝81，则代数式a ﹣2b ＝ ．15．（4分）若△ABC 三边a 、b 、c 满足a 2﹣ab ﹣ac +bc ＝0，则△ABC 是 三角形． 16．（4分）若整数x 满足|x |≤3，则使√7−x 为整数的x 的值是 （只需填一个）． 17．（4分）关于x 的分式方程x x−1+k x−1−x x+1=0无解，则k 的值为 ．18．（4分）已知方程3−a a−4−a =14−a ，且关于x 的不等式组{x ＞a x ≤b只有4个整数解，那么b 的取值范围是 ．三、解答题（本大题共8小题，共92分） 19．（20分）计算：（1）（a +b ）2+a （a ﹣2b ）；（2）（2.5×1012）﹣2÷（2×10﹣2）6；（结果用科学记数法表示）（3）√20+√5√5−√13×√12；（4）√15÷(1√31√5)． 20．（15分）化简： （1）√2−2√2⋅√5+5；（2）√(x −1x )2+4−√(x +1x )2−4（0＜x ＜1）；（3）当a =1−3时，求a 2−1a−1−√a 2+2a+1a 2+a −1a的值．21．（10分）解方程： （1）2x−1=4x 2−1；（2）(x 2−x+7x+1−x −1)÷x 2−4x+1=1．22．（7分）已知x =2−3，x 的整数部分为a ，小数部分为b ，求a−b−2a+b的值． 23．（8分）已知实数a 满足|2020﹣a |+√a −2021=a ，求a ﹣20202的值． 24．（8分）当x 取什么整数时，3x+6x+1−x−1x÷x 2−1x 2+2x的值是整数．25．（12分）新冠肺炎疫情爆发后，国内口罩需求激增，某地甲、乙两个工厂同时接到200万个一次性医用外科口罩的订单，已知甲厂每天比乙厂多生产2万个口罩，且甲厂生产50万个口罩所用的时间与乙厂生产40万个口罩所用的时间相同． （1）求甲、两厂每天各生产多少万个一次性医用外科口罩．（2）已知甲、乙两个工厂每天生产这种口罩的原料成本分别是4万元和3万元，若两个工厂一起生产这400万个口罩，生产一段时间后，乙停产休整，剩下订单由甲单独完成若本次生产过程中，原料总成本不超过156万元，那么两厂至少一起生产了多少天？ 26．（12分）先阅读下列的解答过程，然后作答：形如√m ±2√n 的化简，只要我们找到两个数a 、b 使a +b ＝m ，ab ＝n ，这样（√a ）2+（√b ）2＝m ，√a •√b =√n ，那么便有√m ±2√n =√(√a ±√b)2=√a ±√b （a ＞b ）例如：化简√7+4√3解：首先把√7+4√3化为√7+2√12，这里m ＝7，n ＝12； 由于4+3＝7，4×3＝12，即（√4）2+（√3）2＝7，√4•√3=√12，∴√7+4√3=√7+2√12=√(√4+√3)2=2+√3由上述例题的方法化简：（1）√13−2√42；（2）√7−√40；（3）√2−√3．2020-2021学年江苏省南通市崇川区启秀中学八年级（上）月考数学试卷（12月份）参考答案与试题解析一、选择题（本大题共10小题，每小题3分，共30分） 1．（3分）下列运算结果为a ﹣1的是（ ） A ．a 2−1a ⋅a a+1B ．1−1a C ．a+1a÷a a−1D ．a 2+2a+1a+1【解答】解：A 、原式=(a−1)(a+1)a •aa+1=a ﹣1，符合题意； B 、1−1a =a−1a ，故此选项不合题意；C 、原式=a+1a •a−1a =a 2−1a 2，故此选项不合题意；D 、原式=(a+1)2a+1=a +1，故此选项不合题意；故选：A ．2．（3分）下列运算正确的是（ ） A ．3a +2a ＝5a 2 B ．x 2﹣4＝（x +2）（x ﹣2） C ．（x +1）2＝x 2+1D ．（2a ）3＝6a 2【解答】解：A 、3a +2a ＝5a ，故此选项不符合题意； B 、x 2﹣4＝（x +2）（x ﹣2），正确，故此选项符合题意； C 、（x +1）2＝x 2+2x +1，故此选项不符合题意； D 、（2a ）3＝8a 3，故此选项不符合题意； 故选：B ． 3．（3分）如果将分式x+y 6xy中的x 和y 都扩大为原来的3倍，那么分式的值（ ）A ．缩小到原来的13B ．扩大到原来的3倍C ．不变D ．扩大到原来的9倍【解答】解：因为3(x+y)9×6xy=13×x+y 6xy，所以分式的值变为原来的13．故选：A ．4．（3分）估计√32×√12+√20的运算结果应在（ ）A ．6到7之间B ．7到8之间C ．8到9之间D ．9到10之间【解答】解：∵√32×√12+√20=4+√20，而4＜√20＜5， ∴原式运算的结果在8到9之间； 故选：C ．5．（3分）一个等腰三角形两边的长分别为√75和√18，则这个三角形的周长为（ ） A ．10√3+3√2B ．5√3+6√2C ．10√3+3√2或5√3+6√2D ．无法确定【解答】解：（1）若√18=3√2为腰长，√75=5√3为底边长， ∵6√2＜5√3， ∴三角形不存在；（2）若5√3为腰长，所以这个三角形的周长为10√3+3√2． 故选：A ．6．（3分）已知√5=a ，√14=b ，用含a 、b 的式子表示√0.063，则下列结果正确的是（ ） A ．ab 10B ．3ab 10C ．ab100D ．3ab 100【解答】解：∵√5=a ，√14=b ， ∴√0.063=√9×7010000=√9×√7010000=3×√5×√14100=3ab100． 故选：D ．7．（3分）小颖用4张长为a ，宽为b （a ＞b ）的长方形纸片，按如图的方式拼成一个边长为（a +b ）的正方形，图中空白部分的面积为S 1，阴影部分的面积为S 2．若a ＝2b ，则S 1，S 2之间的数量关系为（ ）A ．S 1=32S 2B ．S 1＝2S 2C ．S 1=52S 2D ．S 1＝3S 2【解答】解：S 1=12b （a +b ）×2+12ab ×2+（a ﹣b ）2＝a 2+2b 2， S 2＝（a +b ）2﹣S 1＝（a +b ）2﹣（a 2+2b 2）＝2ab ﹣b 2，∵a ＝2b ，∴S 1＝a 2+2b 2＝6b 2，S 2＝2ab ﹣b 2＝3b 2 ∴S 1＝2S 2， 故选：B ．8．（3分）把(x −1)√−1x−1根号外的因式移入根号内，化简的结果是（ ） A ．√1−xB ．√x −1C ．−√x −1D ．−√1−x【解答】解：由已知可得，x ﹣1＜0，即1﹣x ＞0，所以，(x −1)√−1x−1=−√−(1−x)2x−1=−√1−x ．故选：D ．9．（3分）已知x 2﹣3x ﹣4＝0，则代数式xx 2−x−4的值是（ ）A ．3B ．2C ．13D ．12【解答】解：已知等式整理得：x −4x=3， 则原式=1x−4x−1=13−1=12， 故选：D ．10．（3分）如图，大正方形的边长为m ，小正方形的边长为n ，x ，y 表示四个相同长方形的两边长（x ＞y ）．则①x ﹣y ＝n ；②xy =m 2−n 24；③x 2﹣y 2＝mn ；④x 2+y 2=m 2−n 22中，正确的是（ ）A ．①②③B ．①②④C ．①③④D ．①②③④【解答】解：①x ﹣y 等于小正方形的边长，即x ﹣y ＝n ，正确； ②∵xy 为小长方形的面积， ∴xy =m 2−n 24， 故本项正确；③x 2﹣y 2＝（x +y ）（x ﹣y ）＝mn ，故本项正确； ④x 2+y 2＝（x +y ）2﹣2xy ＝m 2﹣2×m 2−n 24=m 2+n 22， 故本项错误． 所以正确的有①②③． 故选：A ．二、填空题（本大题共8小题，11′12题，每小题3分，13～18题，每题4分，共30分） 11．（3分）若分式2x−6x+1的值为0，则x 的值为 3 ．【解答】解：由题意可得：2x ﹣6＝0且x +1≠0， 解得x ＝3． 故答案为：3．12．（3分）分解因式：a ﹣6ab +9ab 2＝ a （1﹣3b ）2 ． 【解答】解：a ﹣6ab +9ab 2， ＝a （1﹣6b +9b 2）， ＝a （1﹣3b ）2． 故答案为：a （1﹣3b ）2．13．（4分）当x ≥﹣1且x ≠2． 时，√x+1|x|−2有意义． 【解答】解：由题意得，x +1≥0且|x |﹣2≠0， 解得x ≥﹣1且x ≠±2． 故x 取值范围是x ≥﹣1且x ≠2． 故答案为：≥﹣1且x ≠2．14．（4分）若a 2＝3b ＝81，则代数式a ﹣2b ＝ ﹣17或1 ． 【解答】解：∵a 2＝3b ＝81，（±9）2＝34＝81， ∴a ＝±9，b ＝4， 则a ﹣2b ＝﹣17或1． 故答案为：﹣17或1．15．（4分）若△ABC 三边a 、b 、c 满足a 2﹣ab ﹣ac +bc ＝0，则△ABC 是 等腰 三角形． 【解答】解：∵a 2﹣ab ﹣ac +bc ＝0， ∴（a ﹣b ）（a ﹣c ）＝0，∴a ﹣b ＝0或a ﹣c ＝0，即a ＝b 或a ＝c ，∴△ABC 是等腰三角形， 故答案为：等腰．16．（4分）若整数x 满足|x |≤3，则使√7−x 为整数的x 的值是 ﹣2或3 （只需填一个）． 【解答】解：∵|x |≤3， ∴﹣3≤x ≤3，∴当x ＝﹣2时，√7−x =√7−(−2)=3， x ＝3时，√7−x =√7−3=2．故，使√7−x 为整数的x 的值是﹣2或3（填写一个即可）． 故答案为：﹣2或3． 17．（4分）关于x 的分式方程x x−1+k x−1−x x+1=0无解，则k 的值为 ﹣2或﹣1 ．【解答】解：方程两边同乘（x +1）（x ﹣1）得：x （x +1）+k （x +1）﹣x （x ﹣1）＝0， 整理得：（2+k ）x ＝﹣k ，当2+k ＝0时，整式方程无解，即k ＝﹣2，当x ＝1或x ＝﹣1时，代入（2+k ）x ＝﹣k 得k ＝﹣1． ∴k ＝﹣2或﹣1时，分式方程x x−1+k x−1−x x+1=0无解，故答案为：﹣2或﹣1． 18．（4分）已知方程3−aa−4−a =14−a ，且关于x 的不等式组{x ＞a x ≤b只有4个整数解，那么b 的取值范围是 3≤b ＜4 ．【解答】解：分式方程去分母得：3﹣a ﹣a 2+4a ＝﹣1，即a 2﹣3a ﹣4＝0， 分解因式得：（a ﹣4）（a +1）＝0， 解得：a ＝﹣1或a ＝4，经检验a ＝4是增根，分式方程的解为a ＝﹣1，当a ＝﹣1时，由{x ＞−1x ≤b 只有4个整数解，得到3≤b ＜4． 故答案为：3≤b ＜4．三、解答题（本大题共8小题，共92分） 19．（20分）计算：（1）（a +b ）2+a （a ﹣2b ）；（2）（2.5×1012）﹣2÷（2×10﹣2）6；（结果用科学记数法表示）（3）√20+√5√5−√13×√12；（4）√15÷(1√31√5)． 【解答】解：（1）原式＝a 2+2ab +b 2+a 2﹣2ab ＝2a 2+b 2；（2）原式＝2.5﹣2×10﹣24÷（26×10﹣12）＝2.5﹣2×10﹣24×2﹣6×1012＝5×10﹣15；（3）原式=√205+1−√13×12 ＝2+1﹣2 ＝1；（4）原式=√15÷√5+√3√5×√3=√15√155+3=√5−√3)(5+3)(5−3)=15√5−15√32． 20．（15分）化简： （1）√2−2√2⋅√5+5；（2）√(x −1x )2+4−√(x +1x )2−4（0＜x ＜1）；（3）当a =1−3时，求a 2−1a−1−√a 2+2a+1a 2+a −1a的值．【解答】解：（1）原式=√(√2)2−2×√2×√5+(√5)2 =√(√2−√5)2 =√5−√2；（2）原式=√(x +1x )2−√(x −1x )2 ＝|x +1x |﹣|x −1x | ∵0＜x ＜1，∴原式＝x +1x +x −1x＝2x ；（3）a =3−1=−（√3+1）=−√3−1， 原式=(a+1)(a−1)a−1−√(a+1)2a(a+1)−1a＝a +1−−(a+1)a(a+1)−1a＝a +1 =−√3−1+1=−√3．21．（10分）解方程： （1）2x−1=4x 2−1；（2）(x 2−x+7x+1−x −1)÷x 2−4x+1=1． 【解答】解：（1）方程变形为：2x−1=4(x+1)(x−1)，两边同乘以（x +1）（x ﹣1），去分母得：2（x +1）＝4，解得x ＝1，把x ＝1代入（x +1）（x ﹣1）＝（1+1）（1﹣1）＝0，∴x ＝1是原方程的增根，∴原方程无解．（2）方程变形为：[x 2−x+7x+1−(x+1)2x+1]÷(x+2)(x−2)x+1=1， −3(x−2)x+1•x+1(x+2)(x−2)=1， −3x+2=1，两边同乘以x +2得：x +2＝﹣3，解得x ＝﹣5，把x ＝﹣5代入原方程，左边＝[(−5)2−(−5)+7−5+1−（﹣5）﹣1]÷(−5)2−4−5+1=1，右边＝1， ∴左边＝右边，∴原方程的解为x ＝﹣5．22．（7分）已知x =2−3，x 的整数部分为a ，小数部分为b ，求a−b−2a+b 的值． 【解答】解：∵2−√3=√3)(2−√3)(2+√3)=2+√3，∴x 的值为2+√3，∵1＜3＜4，∴1＜√3＜2，∴1+2＜2+√3＜2+2，即3＜2+√3＜4，∴x 的整数部分a ＝3，小数部分b ＝2+√3−3=√3−1，∴a−b−2a+b =√3−1)−23+3−1 =2−√32+√3 =(2−√3)(2−√3)(2+3)(2−3)＝（2−√3）2＝4﹣4√3+3＝7﹣4√3．23．（8分）已知实数a 满足|2020﹣a |+√a −2021=a ，求a ﹣20202的值．【解答】解：∵要使√a −2021有意义，∴a ﹣2021≥0，解得a ≥2021，∴a ﹣2020+√a −2021=a ，即√a −2021=2020，∴a ﹣2021＝20202，∴a ＝20202+2021，∴原式＝20202+2021﹣20202＝2021．24．（8分）当x 取什么整数时，3x+6x+1−x−1x ÷x 2−1x +2x 的值是整数．【解答】解：原式=3x+6x+1−x−1x •x(x+2)(x+1)(x−1)=3x+6x+1−x+2x+1=4x+8x+1＝4+4x+1，当x ＝﹣5、﹣3、﹣2、0、1、3时，4x+1为整数， 由题意得：x ≠±1，0，﹣2，∴x ＝﹣5，﹣3，3时，原式为整数．25．（12分）新冠肺炎疫情爆发后，国内口罩需求激增，某地甲、乙两个工厂同时接到200万个一次性医用外科口罩的订单，已知甲厂每天比乙厂多生产2万个口罩，且甲厂生产50万个口罩所用的时间与乙厂生产40万个口罩所用的时间相同．（1）求甲、两厂每天各生产多少万个一次性医用外科口罩．（2）已知甲、乙两个工厂每天生产这种口罩的原料成本分别是4万元和3万元，若两个工厂一起生产这400万个口罩，生产一段时间后，乙停产休整，剩下订单由甲单独完成若本次生产过程中，原料总成本不超过156万元，那么两厂至少一起生产了多少天？【解答】解：（1）设乙厂每天生产x 万个口罩，则甲厂每天生产（x +2）万个， 由题意可得：50x+2=40x ，解得：x ＝8，经检验得：x ＝8是原方程的根，故x +2＝10（万个），答：乙厂每天生产8万个口罩，甲厂每天生产10万个；（2）设两厂一起生产了a 天，甲一共生产b 天，由题意可得：{8a +10b =400①3a +4b ≤156②， 由①得：b ＝40﹣0.8a ，代入②得：a ≥20，答：两厂至少一起生产了20天．26．（12分）先阅读下列的解答过程，然后作答：形如√m ±2√n 的化简，只要我们找到两个数a 、b 使a +b ＝m ，ab ＝n ，这样（√a ）2+（√b ）2＝m，√a•√b=√n，那么便有√m±2√n=√(√a±√b)2=√a±√b（a＞b）例如：化简√7+4√3解：首先把√7+4√3化为√7+2√12，这里m＝7，n＝12；由于4+3＝7，4×3＝12，即（√4）2+（√3）2＝7，√4•√3=√12，∴√7+4√3=√7+2√12=√(√4+√3)2=2+√3由上述例题的方法化简：（1）√13−2√42；（2）√7−√40；（3）√2−√3．【解答】解：（1）√13−2√42=√(√7−√6)2=√7−√6；（2）√7−√40=√7−2√10=√(√5−√2)2=√5−√2；（3）√2−√3=√8−434=√6−√22．。
2020-2021学年陕西省渭南市韩城市八年级(上)第一次月考数学试卷
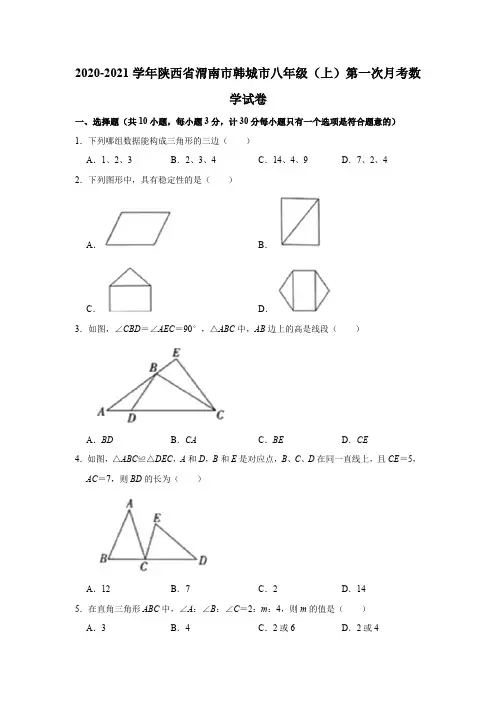
2020-2021学年陕西省渭南市韩城市八年级（上）第一次月考数学试卷一、选择题（共10小题，每小题3分，计30分每小题只有一个选项是符合题意的）1．下列哪组数据能构成三角形的三边（）A．1、2、3B．2、3、4C．14、4、9D．7、2、42．下列图形中，具有稳定性的是（）A．B．C．D．3．如图，∠CBD＝∠AEC＝90°，△ABC中，AB边上的高是线段（）A．BD B．CA C．BE D．CE4．如图，△ABC≌△DEC，A和D，B和E是对应点，B、C、D在同一直线上，且CE＝5，AC＝7，则BD的长为（）A．12B．7C．2D．145．在直角三角形ABC中，∠A：∠B：∠C＝2：m：4，则m的值是（）A．3B．4C．2或6D．2或46．如图，将一副直角三角板按如图所示叠放，其中∠C＝90°，∠B＝45°，∠E＝30°，则∠BFD的大小是（）A．30°B．25°C．15°D．10°7．如图是由相同的小正方形组成的网格，点A、B、C均在格点上，连接AB，AC．则∠1+∠2的度数为（）A．80°B．90°C．100°D．120°8．如图所示，三角形纸片被正方形纸板遮住了一部分，小明根据所学知识画出了一个与该三角形完全重合的三角形，那么这两个三角形完全重合的依据是（）A．SSS B．SAS C．AAS D．ASA9．如图，AE是△ABC的角平分线，AD⊥BC于点D若∠BAC＝76°，∠C＝64°，则∠DAE 的度数是（）A．18°B．15°C．12°D．10°10．如图，BD＝BC，BE＝CA，∠DBE＝∠C＝62°，∠BDE＝75°，则∠AFE的度数等于（）A．148°B．140°C．135°D．128°二、填空题（共4小题，每小题3分，计12分）11．一个n边形从一个顶点出发引出的对角线可将其分割成5个三角形，则n的值为．12．如图，已知在△ABD和△ABC中，∠DAB＝∠CAB，点A、B、E在同一条直线上，若使△ABD≌△ABC，则还需添加的一个条件是（只填一个即可）．13．如图，已知△ABC，∠ABC的角平分线与△ACB的外角角平分线交于点D，∠ABC的外角角平分线与∠ACB的外角角平分线交于点E，则∠E+∠D的度数为．14．如图，在△ABC中，AB＝AC，AB＞BC，点D在边BC上，CD＝3BD，点E、F在线段AD上，∠1＝∠2＝∠BAC．若△ABC的面积为12，则△ACF与△BDE的面积之和为．三、解答题（共11小题，计78分.解答应写出过程）15．一个多边形的内角和与外角和的差为1260°，求它的边数．16．如图已知△ABC．，请用尺规在BC的同侧作△BCD，使△BCD≌△CBA（点A与点D 不重合）．（不写作法，保留作图痕迹）17．如图，点C，F，B，E在同一条直线上，AC⊥CE，DF⊥CE，垂足分别为C，F，且AB＝DE，，CF＝BE．求证：CA＝CD．18．若三角形三边长分别为2x，3x，10，其中x为正整数，且周长不超过30，求这个三角形的三边长．19．如图，在五边形ABCDE中满足AB//CD．（1）求图形中的x的值；（2）∠D．∠E的外角和比∠B、∠C的外角和小多少？20．如图，在线段BC，上有两点E，F，在线段CB的异侧有两点A，D，满足AB＝DC，AE＝DF，CE＝BF，连接AF．（1）求证：∠B＝∠C；（2）若∠B＝40°，∠DFC＝30°，当AF平分∠BAE时，求∠BAF．21．如图，四边形ABCD中，∠A＝∠C＝90°，BE，DF分别是∠ABC、∠ADC的平分线．求证：（1）∠1+∠2＝90°；（2）BE//DF．22．如图，小明站在乙楼BE前方的点C处恰好看到甲．乙两楼楼顶上的点A和E重合为一点，若B、C相距30米，CD相距60米，乙楼高BE为20米，小明身高忽略不计，则甲楼的高AD是多少米？（注：AD⊥DC，EB⊥DC，EF//DB，此时DF＝BE，EF＝BD）23．如图，在△ABC中，D是边AB上一点，E是边AC的中点，作CF//AB交DE的延长线于点F．（1）证明：△ADE≌△CFE；（2）若AB＝AC，CE＝5，CF＝7，求DB的长．24．如图，BD是△ABC的角平分线，DE//BC，交AB于点E，BF是△BDE的高．（1）若∠A＝48°，∠BDC＝81°，求∠BED的度数；（2）若∠C＝∠AED，求证：∠A＝2∠EBF．25．如图，CD//AB，△ABC的中线AE的延长线与CD交于点D．（1）若AE＝3，求DE的长度；（2）∠DAC的平分线与DC交于点F，连接EF，若AF＝DF，AC＝DE，请写出线段AB 与线段AF、EF之间存在的数量关系，并说明理由．。
2020-2021学年辽宁省沈阳126中八年级上学期第一次月考数学试卷(解析版)
2020-2021学年辽宁省沈阳126中八年级（上）第一次月考数学试卷一．选择题（共10小题）.1．在平面直角坐标系中，点P（﹣2，x2+1）所在的象限是（）A．第一象限B．第二象限C．第三象限D．第四象限2．下列计算正确的是（）A．2+3＝5B．＝2C．5×＝5D．＝23．下列实数，0.3，，，，，0.1010010001…（相邻两个1之间依次增加一个0），其中无理数有（）A．1个B．2个C．3个D．4个4．的算术平方根是（）A．4B．±4C．2D．±25．在△ABC中，∠A、∠B、∠C的对边分别为a、b、c，下列条件中，能判断△ABC是直角三角形的是（）A．a＝，b＝，c＝B．a＝b，∠C＝45°C．∠A：∠B：∠C＝3：4：5D．a＝，b＝，c＝26．如图，矩形ABCD中，AB＝3，AD＝1，AB在数轴上，若以点A为圆心，对角线AC的长为半径作弧交数轴的正半轴于M，则点M表示的实数为（）A．2.5B．C．D．﹣17．使代数式有意义的x的取值范围是（）A．x≠3B．x＜7且x≠3C．x≤7且x≠2D．x≤7且x≠38．已知一轮船以18海里/小时的速度从港口A出发向西南方向航行，另一轮船以24海里/小时的速度同时从港口A 出发向东南方向航行，离开港口1.5h后，两轮船相距（）A．30海里B．35海里C．40海里D．45海里9．如图，已知长方形ABCD中AB＝8cm，BC＝10cm，在边CD上取一点E，将△ADE折叠使点D恰好落在BC边上的点F，则CE的长为（）A．2cm B．3cm C．4cm D．5cm10．下列说法：①无理数就是开方开不尽的数；②满足﹣＜x＜的x的正整数有4个；③﹣3是的一个平方根；④两个无理数的和还是无理数；⑤不是有限小数的不是有理数；⑥对于任意实数a，都有＝a，其中正确的个数有（）A．1个B．2个C．3个D．4个二．填空题（共6小题）11．如图所示，圆柱体底面圆的半径是，高为1，若一只小虫从A点出发沿着圆柱体的外侧面爬行到C点，则小虫爬行的最短路程是．12．直角坐标系中，第四象限内一点P到x轴的距离为2，到y轴的距离为5，那么点P的坐标是．13．如图，每个小正方形的边长为1，剪一剪，拼成一个正方形，那么这个正方形的边长是．14．若的值在两个整数a与a+1之间，则a＝．15．在平面直角坐标系中，已知点A（﹣，0），B（，0），点C在坐标轴上，且AC+BC＝6，满足条件的点C共有个．16．在△ABC中，AB＝2，BC＝1，∠ABC＝45°，以AB为一边作等腰直角三角形ABD，使∠ABD＝90°，连接CD，则线段CD的长为．三．解答题（共9小题）17．计算①（﹣）（+）+2②﹣++（﹣3）0③+5④（﹣）2．18．计算：（1）﹣+（+1）（﹣1）．（2）（3﹣2+）÷2．19．解下列关于方程的问题（1）解方程：16（x﹣2）2＝64；（2）解方程：2x2+x﹣1＝0；（3）已知关于x的方程x2+px﹣q＝0的两个根是0和﹣3，求p、q的值．20．解方程（每小题4分，本题共8分）（1）25x2﹣36＝0（2）x2+2（﹣1）x+3﹣2＝0．21．如图，四边形ABCD中，AB⊥AD，已知AD＝3cm，AB＝4cm，CD＝13cm，BC＝12cm，求四边形ABCD的面积．22．已知2a﹣1的算术平方根是3，3a+b﹣9的立方根是2，c是的整数部分，求7a﹣2b﹣2c的平方根．23．如图，已知网格上每个小的正方形的边长为1（长度单位），点A、B、C在格点上．（1）直接在平面直角坐标系中作出△ABC关于y轴对称的图形A1B1C1（点A对应点A1，点B对应点B1，点C 对应点C1）；（2）△ABC的面积＝；点B到AC的距离＝；（3）若在x轴上有一点P，使△PBC周长值最小，此时△PBC周长最小值为．24．如图，在平面直角坐标系中，点A在x轴负半轴上，点B在y轴的正半轴上，点C在第二象限，OA＝1，AB＝BC＝，AB⊥BC．（1）A点坐标为，B点坐标为，C点坐标为．（2）过点C作直线MN平行于x轴，点P是直线MN上一点，点P在第二象限，且△ABP的面积是△ABC面积的2倍，则点P的坐标为．（3）在x轴上有一点D，使∠BDA＝∠BAD，则点D的坐标为．25．在等腰Rt△ABC中，∠BAC＝90°，AB＝AC＝6，D是射线CB上的动点，过点A作AF⊥AD（AF始终在AD上方），且AF＝AD，连接BF．（1）如图1，当点D在线段BC上时，BF与DC的关系是．（2）如图2，若D、E为线段BC上的两个动点，且∠DAE＝45°，连接EF，DC＝3，求ED的长；（3）若在点D的运动过程中，BD＝3，则AF＝；（4）如图3，若M为AB中点，连接MF，在点D的运动过程中，当BD＝时，MF的长最小？最小值是．参考答案一．选择题（共10小题）1．解：∵x2≥0，∴x2+1≥1，∴点P（﹣2，x2+1）在第二象限．故选：B．2．解：不能合并，故选项A错误，，故选项B正确，，故选项C错误，，故选项D错误，故选：B．3．解：无理数有：，，0.1010010001…（相邻两个1之间依次增加一个0），共3个．故选：C．4．解：＝4，4的算术平方根2，故选：C．5．解：A、由题意知，a2≠b2+c2，则△ABC不是直角三角形，故本选项不符合题意；B、由题意知，∠A＝∠B＝62.5°，则△ABC不是直角三角形，故本选项不符合题意；C、由题意知∠A＝45°，则∠B＝60°，∠C＝75°，△ABC不是直角三角形，故本选项不符合题意；D、由题意知，a2+c2＝b2＝7，则△ABC是直角三角形，故本选项符合题意；故选：D．6．解：∵四边形ABCD是矩形，∴∠ABC＝90°，∵AB＝3，AD＝BC＝1，∴AC＝＝＝，∵AM＝AC＝，OA＝1，∴OM＝﹣1，∴点M表示点数为﹣1．故选：D．7．解：∵代数式有意义，∴7﹣x≥0，且2x﹣6≠0，解得：x≤7且x≠3，故选：D．8．解：如图，连接BC．∵两船行驶的方向是东北方向和东南方向，∴∠BAC＝90°，两小时后，两艘船分别行驶了24×1.5＝36（海里），18×1.5＝27（海里），根据勾股定理得：BC＝＝＝45（海里）．故选：D．9．解：∵四边形ABCD是矩形，∴AD＝BC＝10cm，CD＝AB＝8cm，根据题意得：Rt△ADE≌Rt△AFE，∴∠AFE＝90°，AF＝10cm，EF＝DE，设CE＝xcm，则DE＝EF＝CD﹣CE＝（8﹣x）cm，在Rt△ABF中由勾股定理得：AB2+BF2＝AF2，即82+BF2＝102，∴BF＝6cm，∴CF＝BC﹣BF＝10﹣6＝4（cm），在Rt△ECF中，由勾股定理可得：EF2＝CE2+CF2，即（8﹣x）2＝x2+42，∴64﹣16x+x2＝x2+16，∴x＝3（cm），即CE＝3cm．故选：B．10．解：①无理数就是开方开不尽的数，说法错误，无理数是无限不循环小数；②满足﹣＜x＜的x的正整数有1，2共2个，故原说法错误；③﹣3是的一个平方根，正确；④两个无理数的和不一定是无理数，例如，故原说法错误；⑤不是有限小数的不是有理数，说法错误，无限循环小数也是有理数；⑥对于任意实数a，都有＝a，说法错误，当a为负数时不成立，正确说法为：对于任意实数a，都有＝|a|．故正确有③共1个．故选：A．二．填空题（共6小题）11．解：圆柱的侧面展开图是一个矩形，此矩形的长等于圆柱底面周长，C是边的中点，矩形的宽即高等于圆柱的母线长．∵AB＝π•＝2，CB＝1．∴AC＝＝，故答案为：．12．解：∵第四象限内一点P到x轴的距离为2，到y轴的距离为5，∴点P的横坐标是5，纵坐标是﹣2，∴点P（5，﹣2）．故答案为：（5，﹣2）．13．解：分割图形如下：，故这个正方形的边长是：．故答案为：．14．解：∵2＜＜3，∴的值在两个整数2与3之间，∴可得a＝2．故答案为：2．15．解：如图，①当点C位于y轴上时，设C（0，b）．则＝6，解得，b＝2或b＝﹣2，此时C（0，2），或C（0，﹣2）．如图，②当点C位于x轴上时，设C（a，0）．则|﹣﹣a|+|a﹣|＝6，即2a＝6或﹣2a＝6，解得a＝3或a＝﹣3，此时C（﹣3，0），或C（3，0）．综上所述，点C的坐标是：（0，2），（0，﹣2），（﹣3，0），（3，0）．故答案是4．16．解：①如图1，点A、D在BC的两侧，∵△ABD是等腰直角三角形，∴AD＝AB＝×2＝4，∵∠ABC＝45°，∴BE＝DE＝AD＝×4＝2，BE⊥AD，∵BC＝1，∴CE＝BE﹣BC＝2﹣1＝1，在Rt△CDE中，CD＝＝＝；②如图2，点A、D在BC的同侧，∵△ABD是等腰直角三角形，∴BD＝AB＝2，过点D作DE⊥BC交BC的反向延长线于E，则△BDE是等腰直角三角形，∴DE＝BE＝×2＝2，∵BC＝1，∴CE＝BE+BC＝2+1＝3，在Rt△CDE中，CD＝＝＝，综上所述，线段CD的长为或．故答案为：或．三．解答题（共9小题）17．解：（1）原式＝5﹣7+2＝0；（2）原式＝3﹣++1＝3+1；（3）原式＝2+6+5＝13；（4）原式＝5﹣4+＝．18．解：（1）﹣+（+1）（﹣1）＝3﹣2+3﹣1＝+2（2）（3﹣2+）÷2＝（6﹣+4）÷2＝3﹣+2＝19．解：（1）（x﹣2）2＝4，∴x﹣2＝±2，∴x﹣2＝2或x﹣2＝﹣2，∴x1＝4，x2＝0；（2）（2x﹣1）（x+1）＝0，∴x+1＝0或2x﹣1＝0，∴x1＝﹣1，x2＝；（3）根据根与系数的关系得：0+（﹣3）＝﹣p，0×（﹣3）＝q，∴p＝3，q＝0．20．解：（1）（5x+6）（5x﹣6）＝0，5x+6＝0，5x﹣6＝0，x1＝﹣，x2＝．（2）原方程化为：x2+2（﹣1）+（﹣1）2＝0，（x+﹣1）2＝0，x+﹣2＝0，x1＝x2＝1﹣．21．解：连接BD，∵AD＝4cm，AB＝3cm，AB⊥AD，∴BD＝＝5（cm）∴S △ABD ＝AB •AD ＝6（cm 2）．在△BDC 中，∵52+122＝132，即BD 2+BC 2＝CD 2，∴△BDC 为直角三角形，即∠DBC ＝90°，∴S △DBC ＝BD •BC ＝30（cm 2）．∴S 四边形ABCD ＝S △BDC ﹣S △ABD ＝30﹣6＝24（cm 2）．答：四边形ABCD 的面积为24cm 2．22．解：∵2a ﹣1的算术平方根是3，∴2a ﹣1＝9，∴a ＝5，∵3a +b ﹣9的立方根是2，∴3a +b ﹣9＝8，∴b ＝2，∵c 是的整数部分，，∴c ＝3，∴7a ﹣2b ﹣2c ＝35﹣4﹣6＝25，∴7a ﹣2b ﹣2c 的平方根是±5．23．解：（1）如图，A 1B 1C 1即为所求．（2）S △ABC ＝4×4﹣×3×4﹣×1×3﹣×4×1＝6.5．设点B 到AC 的距离为h ，则有××h ＝6.5，∴h ＝，故答案为：6.5，．（3）作点C关于x轴的对称点C′，连接BC′交x轴于点P，连接PC，此时△PBC的周长最小，最小值＝+＝+，故答案为：+．24．解：（1）作CD⊥y轴于D，∵OA＝1，AB＝BC＝，∴OB＝＝2，∴A（﹣1，0），B（0，2），∵AB⊥BC．∴∠CBD+∠ABO＝90°，∵∠CBD+∠BCD＝90°，∴∠BCD＝∠ABO，在△CBD和△BAO中，，∴△CBD≌△BAO（AAS），∴CD＝OB＝2，BD＝OA＝1，∴OD＝2+1＝3，∴C（﹣2，3），故答案为（﹣1，0），（0，2），（0，3）；（2）如图2，延长AB，交MN于E，∵A（﹣1，0），B（0，2），∴直线AB的解析式为y＝2x+2，∵MN∥x轴，∴直线MN为y＝3，把y＝3代入得，3＝2x+2，解得x＝，∴E（，3），∵C（﹣2，3），∴CE＝+2＝，∵△ABP的面积是△ABC面积的2倍，∴PC＝CE＝，∴P（﹣，3），故答案为（﹣，3）；（3）作A点关于y轴的对称点A′，连接A′B，∴A′B＝AB＝，OA′＝OA＝1，∠BAO＝∠BA′O，在x轴上截取A′D＝A′B＝，∴∠A′DB＝∠A′BD，∵∠BA′O＝∠A′DB+∠A′BD，∴∠BAD＝2∠ADB，∵OA′＝OA＝1，AD＝，∴OD＝+1，∴D（+1，0），故答案为（+1，0）．25．解：（1）当点D在线段BC上时，∵AF＝AD，∠BAF＝90°﹣∠BAD＝∠DAC，AB＝AC，∴△FAB≌△DAC（SAS），∴BF＝DC．故答案为：BF＝DC；（2）∵AE＝AE，∠EAF＝90°﹣∠DAE＝45°＝∠EAD，AF＝AD，∴△FAE≌△DAE（SAS），∴ED＝EF＝3；（3）BD＝3，设AG为BC边上的高，G为垂足，在等腰Rt△ABC中，G为BC的中点，∴AF＝AD＝＝＝3．故答案为：3；（4）点F运动轨迹是过点B，且垂直于BC的射线，根据垂线段最短的性质，当MF⊥BF时，线段MF最短，如图2，又因为BC⊥BF，∠ABC＝45°，∠FBD＝90°，∴△BFM为等腰直角三角形，∴MF＝BF＝＝＝＝3，由（1）知：BF＝CD＝3，∴BD＝BC﹣DC＝12﹣3＝9，此时MF＝3．故答案为：9，3．。
2020-2021年长沙湘一芙蓉、一中双语联考八年级(上)第一次月考数学试卷【附答案】
数，表示时关键要正确确定 a 的值以及 n 的值．
3.
【答案】C
【解析】ห้องสมุดไป่ตู้
试题分析：根据互为余角的两个角的和等于 90°对各选项分析判断即可得：
A、∠1=∠2，不是互为余角关系，故本选项错误；
B、∠1=∠2，是对顶角，不是互为余角关系，故本选项错误；
C、∠1 与∠2 互为余角关系，故本选项正确； D、∠1 与∠2 互为补角关系，故本选项错误． 故选 C． 考点：余角和补角 4. 【答案】D 【解析】 【分析】 多边形的每一个内角都等于 120°，则每个外角是 60°，而任何多边形的外角是 360°，则求得多边形的边数； 再根据多边形一个顶点出发的对角线＝n﹣3，即可求得对角线的条数． 【详解】解：∵多边形的每一个内角都等于 120°， ∴每个外角是 60 度， 则多边形的边数为 360°÷60°＝6， 则该多边形有 6 个顶点， 则此多边形从一个顶点出发的对角线共有 6﹣3＝3 条．
可能
10. 某种商品因换季准备打折出售，若按定价的七五折出售将赔 25 元，若按定价的九折出售将赚 20 元，
则这种商品的定价为（ ）
A 280 元
B. 300 元
C. 320 元
D. 200 元
11. 如图，△ABC≌△AEF，AB＝AE，∠B＝∠E，则对于结论：①AC＝AF；②∠FAB＝∠EAB；③EF＝
B. 60°
C. 80°
D. 100°
8. 长为 9，6，5，4 的四根木条，选其中三根组成三角形，选法有（ ）
A. 1 种
B. 2 种
C. 3 种
D. 4 种
9. 一个多边形截取一个角后，形成另一个多边形的内角和是 1620°，则原来多边形的边数是（ ）
湖北省黄冈市2023-2024学年八年级上学期月考数学试题(含答案)
∴ ACD 1 BCD 35 ， 2
∴由（1）知， 2 ACD 35 . ∴ DE AF ， AC ∥ DE ， ∴ AC AF ， ∴ CAF 90 . ∴ FAB CAF 2 55 .
22.解：
3x 2 y 2a 3 ①
（1） 2x 3y 7 7a
，
②
①＋②得： 5x 5y 10 5a ，
黄冈市 2023 年秋季八年级教学质量抽测
数学试题
黄冈市教育科学研究院命制 全卷满分 120 分，考试用时 120 分钟.
注意事项： 1.答卷前，考生务必将自己的姓名、准考证号填写在试卷卷和答题卡上，并将准考证号条形码粘 贴在答题卡上的指定位置。 2.判断题、选择题每小题选出答案后，用 2B 铅笔把答题卡上对应题目的答案标号涂黑。如需改 动，用橡皮擦干净后，再选涂其他答案标号。答在试题卷上无效。 3.非判断题、选择题的作答：用 0.5 毫米黑色墨水签字笔直接答在答题卡上对应的答题区域内。 答在试题卷上无效。 4.考生必须保持答题卡的整洁。考试结束后，请将本试题卷和答题卡一并上交。 一、选择题（每空 3 分，共 27 分）
故1800 ≤ 20a 15100 a ≤1812 ，
解得： 60 ≤ a ≤ 62.4 .
∵a 是整数，
∴ a 60 ，61，62. ∴100 a 40 ，39，38.
∴共有 3 种方案，分别如下： 方案一：购买 60 件 A 种小礼品，40 件 B 种小礼品； 方案二：购买 61 件 A 种小礼品，39 件 B 种小礼品； 方案三：购买 62 件 A 种小礼品，38 件 B 种小礼品.
如图，已知 1 BCD ， 2 3 180 .
（第 21 题图） （1）判断 AC 与 DE 的位置关系，并说明理由；
2020-2021学年河南省实验中学八年级上学期第一次月考数学试卷 (Word版 含解析)
2020-2021学年河南省实验中学八年级（上）第一次月考数学试卷一、选择题（共10小题）.1．（3分）下列各数：，3.14159265，﹣8，，π，0.，0.8080080008…（相邻两个8之间依次多一个0），其中无理数的个数为（）A．1个B．2个C．3个D．4个2．（3分）的平方根是（）A．B．﹣C．±D．3．（3分）下列四组数中，是勾股数的是（）A．0.3，0.4，0.5B．32，42，52C．3，4，5D．4．（3分）下列二次根式中是最简二次根式的是（）A．B．C．D．5．（3分）已知△ABC的三边分别为a、b、c，下列条件中，不能判定△ABC为直角三角形的是（）A．∠A＝∠B+∠C B．a：b：c＝1：1：C．∠A：∠B：∠C＝3：4：5D．b2＝a2+c26．（3分）如图，数轴上点A所表示的实数是（）A．B．C．D．27．（3分）如图，是一扇高为2m，宽为1.5m的门框，李师傅有3块薄木板，尺寸如下：①号木板长3m，宽2.7m；②号木板长2.8m，宽2.8m；③号木板长4m，宽2.4m．可以从这扇门通过的木板是（）A．①号B．②号C．③号D．均不能通过8．（3分）下列说法中，正确的个数有（）①不带根号的数一定是有理数；②任意一个实数都可以用数轴上的点表示；③无限小数都是无理数；④是17的平方根；A．1个B．2个C．3个D．4个9．（3分）已知CD是△ABC的边AB上的高，若CD＝，AD＝1，AB＝2AC，则BC的长为（）A．或B．C．D．或10．（3分）如图，在正方形ABCD纸片上有一点P，PA＝1，PD＝2，PC＝3，现将△PCD 剪下，并将它拼到如图所示位置（C与A重合，P与G重合，D与D重合），则∠APD 的度数为（）A．150°B．135°C．120°D．108°二．填空题（每小题3分，共15分）11．（3分）比较大小3（填“＞”、“＜”或“＝”）；12．（3分）若+（3﹣y）2＝0，那么y x＝．13．（3分）若一个正数x的两个平方根分别是3m+1与﹣2m﹣3，则x的值是．14．（3分）如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上．若PA＝AB＝5，点P到AD的距离是3，有一只蚂蚁要从点P爬到点B，它的最短行程是．15．（3分）如图，已知AD∥BC，AB⊥BC，AB＝3，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC 于点M，N．当点B′为线段MN的三等分点时，BE的长为．三．解下列各题（共75分）16．（10分）计算下列各题．（1）；（2）（43）2．17．（8分）先化简，再求值：（x+）（x﹣）﹣x（x﹣6）+9，其中x＝﹣1．18．（10分）在海洋上有一近似于四边形的岛屿，其平面如图甲，小明据此构造处该岛的一个数学模型（如图乙四边形ABCD），AC是四边形岛屿上的一条小溪流，其中∠B＝90°，AB＝BC＝5千米，CD＝千米，AD＝4千米．（1）求小溪流AC的长．（2）求四边形ABCD的面积．（结果保留根号）19．（10分）已知5a+2的立方根是3，3a+b﹣1的算术平方根是4，c是的整数部分．（1）求a，b，c的值；（2）求3a﹣b+c的平方根．20．（8分）问题背景：在△ABC中，AB，BC，AC三边的长分别为，求这个三角形的面积，小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图所示，这样不需要求高，而借用网格就能计算出它的面积．请将△ABC的面积直接填写在横线上．思维拓展：我们把上述求△ABC面积的方法叫做构图法，若△ABC中，AB，BC，AC三边长分别为，2（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，直接写出此三角形最长边上的高是．21．（9分）如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，求蚂蚁从外壁A处到达内壁B处的最短距离．22．（10分）阅读下列运算过程，并完成各小题：；．数学上把这种将分母中的根号去掉的过程称作“分母有理化”，如果分母不是一个无理数，而是两个无理数的和或差，此时也可以进行分母有理化，如：1；．模仿上例完成下列各小题：（1）＝；（2）＝；（3）＝；（4）请根据你得到的规律计算下题：（n 为正整数）．23．（10分）如图所示，已知△ABC中，∠B＝90°，AB＝16cm，AC＝20cm，P、Q是△ABC的边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts．（1）则BC＝cm；（2）当t为何值时，点P在边AC的垂直平分线上？此时CQ＝；（3）当点Q在边CA上运动时，直接写出使△BCQ成为等腰三角形的运动时间．参考答案一．选择题（每小题3分，共30分）1．（3分）下列各数：，3.14159265，﹣8，，π，0.，0.8080080008…（相邻两个8之间依次多一个0），其中无理数的个数为（）A．1个B．2个C．3个D．4个解：是分数，属于有理数；3.14159265是有限小数，属于有理数；﹣8，是整数，属于有理数；0.是循环小数，属于有理数；无理数有π，0.8080080008…（相邻两个8之间依次多一个0）共2个．故选：B．2．（3分）的平方根是（）A．B．﹣C．±D．解：的平方根是±；故选：C．3．（3分）下列四组数中，是勾股数的是（）A．0.3，0.4，0.5B．32，42，52C．3，4，5D．解：A、0.32+0.42＝0.52，能构成直角三角形，但不是整数，不是勾股数，故本选项不符合题意；B、（32）2+（42）2≠（52）2，不是勾股数，故本选项不符合题意；C、32+42＝52，是勾股数，故本选项符合题意；D、（）2+（）2≠（）2，不是勾股数，故本选项不符合题意．故选：C．4．（3分）下列二次根式中是最简二次根式的是（）A．B．C．D．解：A、原式为最简二次根式，符合题意；B、原式＝6，不符合题意；C、原式＝2，不符合题意；D、原式＝，不符合题意．故选：A．5．（3分）已知△ABC的三边分别为a、b、c，下列条件中，不能判定△ABC为直角三角形的是（）A．∠A＝∠B+∠C B．a：b：c＝1：1：C．∠A：∠B：∠C＝3：4：5D．b2＝a2+c2解：A、∵∠A＝∠B+∠C，∠A+∠B+∠C＝180°，∴∠A＝90°，∴△ABC为直角三角形，故此选项不合题意；B、∵（）2＝12+12，∴能构成直角三角形，故此选项不合题意；C、设∠A＝3x°，∠B＝4x°，∠C＝5x°，3x+4x+5x＝180，解得：x＝15，则5x°＝75°，∴△ABC不是直角三角形，故此选项符合题意；D、∵b2＝a2+c2，∴能构成直角三角形，故此选项不符合题意．故选：C．6．（3分）如图，数轴上点A所表示的实数是（）A．B．C．D．2解：由勾股定理，得斜线的为＝，由圆的性质得：点A表示的数为﹣1+，即﹣1．故选：B．7．（3分）如图，是一扇高为2m，宽为1.5m的门框，李师傅有3块薄木板，尺寸如下：①号木板长3m，宽2.7m；②号木板长2.8m，宽2.8m；③号木板长4m，宽2.4m．可以从这扇门通过的木板是（）A．①号B．②号C．③号D．均不能通过解：因为＝2.5，所以木板的长和宽中必须有一个数据小于2.5米．所以选③号木板．故选：C．8．（3分）下列说法中，正确的个数有（）①不带根号的数一定是有理数；②任意一个实数都可以用数轴上的点表示；③无限小数都是无理数；④是17的平方根；A．1个B．2个C．3个D．4个解：①π不带根号的数，是无理数，原来的说法错误；②任意一个实数都可以用数轴上的点表示是正确的；③无限小数0.是有理数，原来的说法错误；④是17的平方根是正确的．故选：B．9．（3分）已知CD是△ABC的边AB上的高，若CD＝，AD＝1，AB＝2AC，则BC的长为（）A．或B．C．D．或解：当△ABC是锐角三角形，如图1，∵CD⊥AB，∴∠CDA＝90°，由勾股定理得，AC＝＝＝2，∵AB＝2AC，∴AB＝4，∴BD＝4﹣1＝3，∴BC＝＝＝2，当△ABC是钝角三角形，如图2，同理得：AC＝2，AB＝4，∴BC＝＝＝2，则BC的长为2或2，故选：D．10．（3分）如图，在正方形ABCD纸片上有一点P，PA＝1，PD＝2，PC＝3，现将△PCD 剪下，并将它拼到如图所示位置（C与A重合，P与G重合，D与D重合），则∠APD 的度数为（）A．150°B．135°C．120°D．108°解：连接PG，如图所示：∵四边形ABCD是正方形，∴AD＝CD，∠ADC＝90°，AG＝PC＝3，∵PA＝1，PD＝2，PC＝3，将△PCD剪下，并将它拼到如图所示位置（C与A重合，P 与G重合，D与D重合），∴PD＝GD＝2，∠CDP＝∠ADG，∴∠PDG＝∠ADC＝90°，∴△PDG是等腰直角三角形，∴∠GPD＝45°，PG＝PD＝2，∵AG＝PC＝3，AP＝1，PG＝2，∴AP2+PG2＝AG2，∴∠GPA＝90°，∴∠APD＝90°+45°＝135°；故选：B．二．填空题（每小题3分，共15分）11．（3分）比较大小＜3（填“＞”、“＜”或“＝”）；解：∵3＝，＜，∴＜3，故答案为：＜．12．（3分）若+（3﹣y）2＝0，那么y x＝9．解：∵+（3﹣y）2＝0，∴x﹣2＝0，3﹣y＝0，解得：x＝2，y＝3，故y x＝32＝9．故答案为：9．13．（3分）若一个正数x的两个平方根分别是3m+1与﹣2m﹣3，则x的值是49．解：由题意可知：3m+1﹣2m﹣3＝0，解得：m＝2，∴3m+1＝7，∴x＝72＝49，故答案为：49．14．（3分）如图，教室的墙面ADEF与地面ABCD垂直，点P在墙面上．若PA＝AB＝5，点P到AD的距离是3，有一只蚂蚁要从点P爬到点B，它的最短行程是4．解：如图，∵AG＝3，AP＝AB＝5，∴PG＝4，∴BG＝8，∴PB＝＝4．故这只蚂蚁的最短行程应该是4．故答案为：4．15．（3分）如图，已知AD∥BC，AB⊥BC，AB＝3，点E为射线BC上一个动点，连接AE，将△ABE沿AE折叠，点B落在点B′处，过点B′作AD的垂线，分别交AD，BC 于点M，N．当点B′为线段MN的三等分点时，BE的长为或．解：如图，由翻折的性质，得AB＝AB′，BE＝B′E．①当MB′＝2，B′N＝1时，设EN＝x，得B′E＝．△B′EN∽△AB′M，＝，即＝，x2＝，BE＝B′E＝＝．②当MB′＝1，B′N＝2时，设EN＝x，得B′E＝，△B′EN∽△AB′M，＝，即＝，解得x2＝，BE＝B′E＝＝，故答案为：或．三．解下列各题（共75分）16．（10分）计算下列各题．（1）；（2）（43）2．解：（1）原式＝﹣+＝；（2）原式＝4﹣3+2＝4﹣3+4＝4+．17．（8分）先化简，再求值：（x+）（x﹣）﹣x（x﹣6）+9，其中x＝﹣1．解：原式＝x2﹣3﹣x2+6x+9＝6x+6，当x＝﹣1时，原式＝6（x+1）＝6．18．（10分）在海洋上有一近似于四边形的岛屿，其平面如图甲，小明据此构造处该岛的一个数学模型（如图乙四边形ABCD），AC是四边形岛屿上的一条小溪流，其中∠B＝90°，AB＝BC＝5千米，CD＝千米，AD＝4千米．（1）求小溪流AC的长．（2）求四边形ABCD的面积．（结果保留根号）解：（1）∵∠B＝90°，AB＝BC＝5千米，∴AC＝＝＝5（千米）；（2）∵AC2＝（5）2＝50，CD2+AD2＝（）2+（4）2＝50，∴AC2＝CD2+AD2，则∠D＝90°，S四边形ABCD＝S△ABC+S△ACD＝×5×5+××4＝（+2）平方千米．19．（10分）已知5a+2的立方根是3，3a+b﹣1的算术平方根是4，c是的整数部分．（1）求a，b，c的值；（2）求3a﹣b+c的平方根．解：（1）∵5a+2的立方根是3，3a+b﹣1的算术平方根是4，∴5a+2＝27，3a+b﹣1＝16，∴a＝5，b＝2；∵，c是的整数部分，∴c＝3；（2）3a﹣b+c＝15﹣2+3＝16，16的平方根是±4．20．（8分）问题背景：在△ABC中，AB，BC，AC三边的长分别为，求这个三角形的面积，小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点（即三个顶点都在小正方形的顶点处），如图所示，这样不需要求高，而借用网格就能计算出它的面积．请将△ABC的面积直接填写在横线上．思维拓展：我们把上述求△ABC面积的方法叫做构图法，若△ABC中，AB，BC，AC三边长分别为，2（a＞0），请利用图②的正方形网格（每个小正方形的边长为a）画出相应的△ABC，直接写出此三角形最长边上的高是a．解：问题背景：S△ABC＝3×3﹣×1×2﹣×1×3﹣×2×3＝．思维拓展：如图作BH⊥AC于H．∵S△ABC＝•AC•BH＝2a×4a﹣×2a×2a﹣×a×2a﹣×a×4a＝3a2，∴×a×BH＝3a2，∴BH＝a．21．（9分）如图，圆柱形容器高为18cm，底面周长为24cm，在杯内壁离杯底4cm的点B 处有一滴蜂蜜，此时一只蚂蚁正好在杯外壁，离杯上沿2cm与蜂蜜相对的点A处，求蚂蚁从外壁A处到达内壁B处的最短距离．解：如图：将杯子侧面展开，作A关于EF的对称点A′，连接A′B，则A′B即为最短距离，A′B＝＝20（cm）．答：蚂蚁从外壁A处到达内壁B处的最短距离是20cm．22．（10分）阅读下列运算过程，并完成各小题：；．数学上把这种将分母中的根号去掉的过程称作“分母有理化”，如果分母不是一个无理数，而是两个无理数的和或差，此时也可以进行分母有理化，如：1；．模仿上例完成下列各小题：（1）＝；（2）＝；（3）＝2﹣；（4）请根据你得到的规律计算下题：（n 为正整数）．解：（1）（1）＝；（2）＝﹣＝﹣＝；（3）＝＝2﹣；（4）原式＝﹣1+﹣+…+﹣＝﹣1．故答案为；；﹣2．23．（10分）如图所示，已知△ABC中，∠B＝90°，AB＝16cm，AC＝20cm，P、Q是△ABC的边上的两个动点，其中点P从点A开始沿A→B方向运动，且速度为每秒1cm，点Q从点B开始沿B→C→A方向运动，且速度为每秒2cm，它们同时出发，设出发的时间为ts．（1）则BC＝12cm；（2）当t为何值时，点P在边AC的垂直平分线上？此时CQ＝13cm；（3）当点Q在边CA上运动时，直接写出使△BCQ成为等腰三角形的运动时间．解：（1）∵∠B＝90°，AB＝16cm，AC＝20cm∴BC＝＝＝12（cm）．故答案为：12；（2）∵点P在边AC的垂直平分线上，∴PC＝PA＝t，PB＝16﹣t，在Rt△BPC中，BC2+BP2＝CP2，即122+（16﹣t）2＝t2解得：t＝．此时，点Q在边AC上，CQ＝（cm）；故答案为：13cm．（3）①当CQ＝BQ时，如图1所示，则∠C＝∠CBQ，∵∠ABC＝90°，∴∠CBQ+∠ABQ＝90°．∠A+∠C＝90°，∴∠A＝∠ABQ，∴BQ＝AQ，∴CQ＝AQ＝10，∴BC+CQ＝22，∴t＝22÷2＝11秒．②当CQ＝BC时，如图2所示，则BC+CQ＝24，∴t＝24÷2＝12秒．③当BC＝BQ时，如图3所示，过B点作BE⊥AC于点E，∴，∴＝．∴CQ＝2CE＝14.4，∴BC+CQ＝26.4，∴t＝26.4÷2＝13.2秒．综上所述：当t为11秒或12秒或13.2秒时，△BCQ为等腰三角形．。
2020-2021学年山东省济南市长清区八年级(上)第一次月考数学试卷 (解析版)
2020-2021学年山东省济南市长清区八年级第一学期第一次月考数学试卷一、选择题（共12小题）.1．（4分）9的平方根是（）A．±3B．±C．3D．﹣32．（4分）下列实数中是无理数的是（）A．0.38B．C．﹣D．π3．（4分）下列计算正确的是（）A．＝﹣4B．＝±4C．＝﹣4D．＝﹣4 4．（4分）下列各组数中互为相反数的一组是（）A．﹣3与B．﹣3与C．﹣3与D．|﹣3|与35．（4分）在平面直角坐标系中，点（﹣1，﹣3）位于（）A．第一象限B．第二象限C．第三象限D．第四象限6．（4分）△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（）A．∠A+∠B＝∠C B．∠A：∠B：∠C＝1：2：3C．a2＝c2﹣b2D．a：b：c＝3：4：67．（4分）|1﹣|＝（）A．1﹣B．﹣1C．1+D．﹣1﹣8．（4分）点P（1，﹣2）关于y轴对称的点的坐标是（）A．（﹣1，﹣2）B．（1，2）C．（﹣1，2）D．（﹣2，1）9．（4分）若点B（m﹣1，m+2）在x轴上，则m的值为（）A．﹣1B．1C．﹣2D．210．（4分）已知a＝，b＝，c＝，则下列大小关系正确的是（）A．a＞b＞c B．c＞b＞a C．b＞a＞c D．a＞c＞b 11．（4分）a、b在数轴上的位置如图所示，那么化简的结果是（）A．a﹣2b B．a C．﹣a D．﹣a+2b12．（4分）如图，Rt△ABC中BC＝3，AC＝4，在同一平面上把△ABC沿最长边AB翻折后得到△ABC′，则CC′的长等于（）A．B．C．D．二、填空题（共6小题）.13．（4分）的算术平方根是．14．（4分）已知一个Rt△的两边长分别为3和4，则第三边长是．15．（4分）如图，正方形ODBC中，OC＝1，OA＝OB，则数轴上点A表示的数是．16．（4分）已知实数x，y满足+（y+1）2＝0，则x y＝．17．（4分）如图，长方体的底面边长分别为2cm和4cm，高为5cm．若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为cm．18．（4分）如图，点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2019次运动后动点P的坐标是．三、解答题：（本大题共6个小题，共78分，解答应写出文字说明、证明过程或演算步骤）19．（24分）计算下列各题：（1）﹣5+；（2）﹣3；（3）；（4）（1﹣）0+|2﹣|+（﹣1）2020﹣×．20．（8分）已知2a﹣1的平方根是，3a+b﹣1的算术平方根是6，求a+4b的平方根．21．（10分）有一个小朋友拿着一根竹竿通过一个长方形的门，如果把竹竿竖放就比门高1尺，斜入恰好等于门的对角线长．已知门宽4尺，请求竹竿的长度．22．（12分）△ABC在直角坐标系内的位置如图所示（1）分别写出点A，C的坐标：A：，C：；（2）△ABC的周长为，面积为；（3）请在这个坐标系内画出△A1B1C1与△ABC关于x轴对称．23．（12分）观察下列一组等式，解答后面的问题：（+1）（﹣1）＝1，（+）（﹣）＝1，（+）（﹣）＝1，（+）（﹣）＝1，…（1）根据上面的规律，计算下列式子的值：（）（+1）．（2）利用上面的规律，比较与的大小．24．（12分）如图，△ABC中，∠C＝90°，AB＝10cm，BC＝6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．（1）出发2秒后，求△ABP的周长；（2）当t为几秒时，BP平分∠ABC；（3）问t为何值时，△BCP为等腰三角形？参考答案一、选择题（共12小题）.1．（4分）9的平方根是（）A．±3B．±C．3D．﹣3解：9的平方根是：±＝±3．故选：A．2．（4分）下列实数中是无理数的是（）A．0.38B．C．﹣D．π解：A、0.38是有理数，故A错误；B、＝2是有理数，故B错误；C、﹣是有理数，故C错误；D、π是无理数，故D正确．故选：D．3．（4分）下列计算正确的是（）A．＝﹣4B．＝±4C．＝﹣4D．＝﹣4解：A、原式没有意义，错误；B、原式＝4，错误；C、原式＝|﹣4|＝4，错误；D、原式＝﹣4，正确，故选：D．4．（4分）下列各组数中互为相反数的一组是（）A．﹣3与B．﹣3与C．﹣3与D．|﹣3|与3解：①＝3，和﹣3互为相反数，故A正确；②＝﹣3，不是﹣3的相反数，故B错误；③﹣3和﹣互为倒数，不互为相反数，故C错误；④|﹣3|和3相等，故D错误．综上可知只有A正确．故选：A．5．（4分）在平面直角坐标系中，点（﹣1，﹣3）位于（）A．第一象限B．第二象限C．第三象限D．第四象限解：∵点（﹣1，﹣3）的横纵坐标都为：﹣，∴位于第三象限．故选：C．6．（4分）△ABC中，∠A，∠B，∠C的对边分别记为a，b，c，由下列条件不能判定△ABC为直角三角形的是（）A．∠A+∠B＝∠C B．∠A：∠B：∠C＝1：2：3C．a2＝c2﹣b2D．a：b：c＝3：4：6解：A、∠A+∠B＝∠C，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；B、∠A：∠B：∠C＝1：2：3，又∠A+∠B+∠C＝180°，则∠C＝90°，是直角三角形；C、由a2＝c2﹣b2，得a2+b2＝c2，符合勾股定理的逆定理，是直角三角形；D、32+42≠62，不符合勾股定理的逆定理，不是直角三角形．故选：D．7．（4分）|1﹣|＝（）A．1﹣B．﹣1C．1+D．﹣1﹣解：|1﹣|＝﹣1．故选：B．8．（4分）点P（1，﹣2）关于y轴对称的点的坐标是（）A．（﹣1，﹣2）B．（1，2）C．（﹣1，2）D．（﹣2，1）解：∵点P（1，﹣2）关于y轴对称，∴点P（1，﹣2）关于y轴对称的点的坐标是（﹣1，﹣2）．故选：A．9．（4分）若点B（m﹣1，m+2）在x轴上，则m的值为（）A．﹣1B．1C．﹣2D．2解：∵点B（m﹣1，m+2）在x轴上，∴m+2＝0，解得：m＝﹣2，故选：C．10．（4分）已知a＝，b＝，c＝，则下列大小关系正确的是（）A．a＞b＞c B．c＞b＞a C．b＞a＞c D．a＞c＞b解：∵a＝＝，b＝＝，c＝＝，且＜＜，∴＞＞，即a＞b＞c，故选：A．11．（4分）a、b在数轴上的位置如图所示，那么化简的结果是（）A．a﹣2b B．a C．﹣a D．﹣a+2b解：由题意可知，a＞0，b＜0，所以a﹣b＞0，，原式＝（a﹣b）﹣（﹣b）＝a﹣b+b＝a．故选：B．12．（4分）如图，Rt△ABC中BC＝3，AC＝4，在同一平面上把△ABC沿最长边AB翻折后得到△ABC′，则CC′的长等于（）A．B．C．D．解：∵把△ABC沿最长边AB翻折后得到△ABC′，∴AB是CC′的对称轴，是CC′的垂直平分线，即CD＝C′D，在Rt△ABC中，BC＝3，AC＝4，由勾股定理得：AB＝5，根据三角形面积公式得：CD×AB＝AC×BC，5CD＝3×4，CD＝，即CC′＝2×＝，故选：C．二、填空题：（本大题共6个小题．每小题4分，共24分．把答案填在题中横线上．）13．（4分）的算术平方根是2．解：∵＝4，∴的算术平方根是＝2．故答案为：2．14．（4分）已知一个Rt△的两边长分别为3和4，则第三边长是5或．解：当长是3和4的两边是两条直角边时，第三边是斜边＝＝5；当长是3和4的两边一条是直角边，一条是斜边时，则长是4的一定是斜边，第三边是直角边＝＝．故第三边长是：5或．故答案是：5或．15．（4分）如图，正方形ODBC中，OC＝1，OA＝OB，则数轴上点A表示的数是﹣．解：∵OB＝＝，∴OA＝OB＝，∵点A在数轴上原点的左边，∴点A表示的数是﹣，故答案为：﹣．16．（4分）已知实数x，y满足+（y+1）2＝0，则x y＝．解：由题意得，x﹣2＝0，y+1＝0，解得x＝2，y＝﹣1，所以，x y＝2﹣1＝．故答案为：．17．（4分）如图，长方体的底面边长分别为2cm和4cm，高为5cm．若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点，则蚂蚁爬行的最短路径长为13cm．解：∵PA＝2×（4+2）＝12，QA＝5∴PQ＝13．故答案为：13．18．（4分）如图，点P在平面直角坐标系中按图中箭头所示方向运动，第1次从原点运动到点（1，1），第2次接着运动到点（2，0），第3次接着运动到点（3，2），…，按这样的运动规律，经过第2019次运动后动点P的坐标是（2019，2）．解：分析图象可以发现，点P的运动每4次位置循环一次．每循环一次向右移动四个单位．∴2019＝4×504+3当第504循环结束时，点P位置在（2016，0），在此基础之上运动三次到（2019，2）故答案为：（2019，2）三、解答题：（本大题共6个小题，共78分，解答应写出文字说明、证明过程或演算步骤）19．（24分）计算下列各题：（1）﹣5+；（2）﹣3；（3）；（4）（1﹣）0+|2﹣|+（﹣1）2020﹣×．解：（1）原式＝2﹣+＝2；（2）原式＝+﹣3＝+2﹣3＝0；（3）原式＝5﹣6＝﹣1；（4）原式＝1+﹣2+1﹣＝0．20．（8分）已知2a﹣1的平方根是，3a+b﹣1的算术平方根是6，求a+4b的平方根．解：根据题意，得2a﹣1＝17，3a+b﹣1＝62，解得a＝9，b＝10，所以，a+4b＝9+4×10＝9+40＝49，∵（±7）2＝49，∴a+4b的平方根是±7．21．（10分）有一个小朋友拿着一根竹竿通过一个长方形的门，如果把竹竿竖放就比门高1尺，斜入恰好等于门的对角线长．已知门宽4尺，请求竹竿的长度．解：设竹竿的长度为x尺，根据题意得：（x﹣1）2+42＝x2，整理得：2x﹣17＝0，解得：x＝8.5．答：竹竿的长度为8.5尺．22．（12分）△ABC在直角坐标系内的位置如图所示（1）分别写出点A，C的坐标：A：（0，3），C：（﹣2，1）；（2）△ABC的周长为2++，面积为5；（3）请在这个坐标系内画出△A1B1C1与△ABC关于x轴对称．解：（1）如图所示：A：（0，3），C：（﹣2，1）；故答案为：（0，3），（﹣2，1）；（2）如图所示：AB＝＝，BC＝＝，AC＝＝2，故△ABC的周长为：2++，面积为：3×4﹣×1×4﹣×2×2﹣×2×3＝5；故答案为：2++，5；（3）如图所示：△A1B1C1，即为所求．23．（12分）观察下列一组等式，解答后面的问题：（+1）（﹣1）＝1，（+）（﹣）＝1，（+）（﹣）＝1，（+）（﹣）＝1，…（1）根据上面的规律，计算下列式子的值：（）（+1）．（2）利用上面的规律，比较与的大小．解：（1）原式＝（﹣1+﹣+﹣+…+﹣）（+1）＝（﹣1）（+1）＝2016﹣1＝2015；（2）∵＝+，＝+，而+＜+，∴﹣＞﹣．24．（12分）如图，△ABC中，∠C＝90°，AB＝10cm，BC＝6cm，若动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm，设出发的时间为t秒．（1）出发2秒后，求△ABP的周长；（2）当t为几秒时，BP平分∠ABC；（3）问t为何值时，△BCP为等腰三角形？解：（1）∵∠C＝90°，AB＝10cm，BC＝6cm，∴有勾股定理得AC＝8cm，动点P从点C开始，按C→A→B→C的路径运动，且速度为每秒1cm∴出发2秒后，则CP＝2cm，那么AP＝6cm．∵∠C＝90°，∴由勾股定理得PB＝2cm∴△ABP的周长为：AP+PB+AB＝6+10+2＝（16+2）cm；（2）如图2所示，过点P作PD⊥AB于点D，∵BP平分∠ABC，∴PD＝PC．在Rt△BPD与Rt△BPC中，，∴Rt△BPD≌Rt△BPC（HL），∴BD＝BC＝6 cm，∴AD＝10﹣6＝4 cm．设PC＝x cm，则PA＝（8﹣x）cm在Rt△APD中，PD2+AD2＝PA2，即x2+42＝（8﹣x）2，解得：x＝3，∴当t＝3秒时，AP平分∠CAB；（3）若P在边AC上时，BC＝CP＝6cm，此时用的时间为6s，△BCP为等腰三角形；若P在AB边上时，有两种情况：①若使BP＝CB＝6cm，此时AP＝4cm，P运动的路程为12cm，所以用的时间为12s，故t＝12s时△BCP为等腰三角形；②若CP＝BC＝6cm，过C作斜边AB的高，根据面积法求得高为4.8cm，根据勾股定理求得BP＝7.2cm，所以P运动的路程为18﹣7.2＝10.8cm，∴t的时间为10.8s，△BCP为等腰三角形；③若BP＝CP时，则∠PCB＝∠PBC，∵∠ACP+∠BCP＝90°，∠PBC+∠CAP＝90°，∴∠ACP＝∠CAP，∴PA＝PC ∴PA＝PB＝5cm∴P的路程为13cm，所以时间为13s时，△BCP为等腰三角形．∴t＝6s或13s或12s或10.8s时△BCP为等腰三角形．。
吉林省名校调研卷系列(省命题)2020-2021学年八年级上学期第一次月考数学试题( 有答案)
∠ACF = 140°，∠ADE = 105°，则∠A 的大小为
（）
A．30°
B．35°
C．50°
D．75°
得 分 评卷人
二、填空题（每小题 3 分，共 24 分）
7. 如图，自行车的主框架采用了三角形结构，这样设计依据的数学道理是三角形具有
.
（第 7 题）
（第 8 题）
（第 10 题）
8．如图，△ABC ≌ △DEF，点 A 与点 D 对应，点 B 与点 E 对应，若 AB = 5，BC = 6，AC
有
个.
14．如图，B 地在 A 地的南偏西 45°方向，C 地在 A 地的南偏东 15°方向，C 地在 B 地的北
偏东 80°方向，则∠ACB =
度.
得 分 评卷人
三、解答题（每小题 5 分，共 20 分）
15．一个多边形的内角和是外角和的 2 倍，求这个多边形的边数.
16．如图，在△ABC 中，CD 平分∠ACB. 若∠A = 70°，∠B = 50°，求∠ACD 的度数. A
得 分 评卷人
六、解答题（每小题 10 分，共 20 分）
25．已知△OAB、△OCD 的顶点 O 重合. - 9 - / 14
【感知】如图①，若∠A＋∠B＋∠C＋∠D = 180°，则∠AOB＋∠DOC =
度；
【探究】如图②，连接AD、BC，若AO、BO、CO、DO 分别是四边形 ABCD 的四个内角的 平分线，∠COD = 65°，求∠AOB 的度数；
C．60°
D．90°
…
… 2．下列说法正确的是
（）
…
… …
A．周长相同的两个三角形全等
B．面积相等的两个三角形全等
2020-2021学年度第一学期八年级数学月考试卷含答案共六套
2020-2021学年八年级（上）第一次月考数学试卷一、选择题（本题共10小题，每小题4分，满分40分）1．下列函数中是一次函数的是（）A．y＝B．y＝C．y＝ax+b D．y＝x22．下列各点中位于第二象限的是（）A．（﹣2，0）B．（8，﹣2）C．（0，3）D．（﹣，4）3．已知过A（﹣1，a），B（2，﹣2）两点的直线平行于x轴，则a的值为（）A．﹣1 B．1 C．2 D．﹣24．关于函数y＝﹣﹣1，下列说法错误的是（）A．当x＝2时，y＝﹣2B．y随x的增大而减小C．若x1＞x2，则y1＞y2D．图象经过第二、三、四象限5．下面四条直线，其中直线上的每一个点的坐标都是二元一次方程2x﹣3y＝6的解的是（）A．B．C．D．6．已知y﹣1与x成正比例，当x＝3时，y＝2．则当x＝﹣1时，y的值是（）A．﹣1 B．0 C．D．7．实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加，后10秒冲刺，中间速度保持不变，则跳绳速度v（个/秒）与时间t（秒）之间的函数图象大致为（）A．B．C．D．8．一次函数y＝ax+b与y＝abx在同一个平面直角坐标系中的图象不可能是（）A．B．C．D．9．若点（﹣1，m）和（2，n）在直线y＝﹣x+b上，则m、n、b的大小关系是（）A．m＞n＞b B．m＜n＜b C．m＞b＞n D．b＜m＜n10．甲车从A地到B地，乙车从B地到A地，乙车先出发先到达，甲乙两车之间的距离y（千米）与行驶的时间x（小时）的函数关系如图所示，则下列说法中不正确的是（）A．甲车的速度是80km/hB．乙车的速度是60km/hC．甲车出发1h与乙车相遇D．乙车到达目的地时甲车离B地10km二、填空题（共4题，每题5分）11．函数中，自变量x的取值范围是．12．已知关于x的方程mx+n＝0的解是x＝﹣2，则直线y＝mx+n与x轴的交点坐标是．13．若点P的坐标是（2a+1，a﹣4），且P点到两坐标轴的距离相等，则P点的坐标是．14．直线y＝kx﹣2与直线y＝x﹣1（1≤x≤4）有交点，则k的取值范围是．三、解答题（共8题，共90分）15．已知一次函数的图象平行于y＝﹣x，且截距为1．（1）求这个函数的解析式；（2）判断点P（﹣2，）是否在这个函数的图象上．16．若函数y＝（m+1）x+m2﹣1是正比例函数．（1）求该函数的表达式．（2）将该函数图象沿y轴向上或者向下平移，使其经过（1，﹣2），求平移的方向与距离．17．如图，先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1（1）画出△A1B1C1，并写出点A1、B1、C1的坐标．（2）求△A1B1C1的面积．18．画出函数y＝﹣x+3的图象，并利用图象解下列问题：（1）求方程﹣x+3＝0的解．（2）求不等式﹣x+3＞0的解集．（3）若﹣3≤y＜6，求x的取值范围．19．如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．人体构造学的研究成果表明，一般情况下人的指距d和身高h成如下所示的关系．指距d（cm）20 21 22 23身高h（cm）160 169 178 187 （1）直接写出身高h与指距d的函数关系式；（2）姚明的身高是226厘米，可预测他的指距约为多少？（精确到0.1厘米）20．如图，直线l1：y＝2x﹣2与x轴交于点D，直线l2：y＝kx+b与x轴交于点A，且经过点B，直线l1，l2交于点C（m，2）．（1）求m的值；（2）求直线l2的解析式；（3）根据图象，直接写出1＜kx+b＜2x﹣2的解集．（4）求△ACD的面积．21．甲、乙两个工程队完成某项工程，先由甲单独做10天，乙队再加入合作．工进度满足如图所示．（1）求工作量y与工作时间x（天）之间的函数关系式；（2）这项工程全部完成需要多少天？（3）求乙队单独完成这项工程的天数．22．甲、乙两人分别安装同一种零件40个，其中乙在安装两小时后休息了2小时，后继续按原来进度工作，他们每人安装的零件总数y（个）与安装时间x（小时）的函数关系如图1所示，两人安装零件总数之差z（件）与时间x（小时）的函数关系如图2所示．（1）a＝；b＝．（2）求出甲工作2小时后的安装的零件数y与时间x的函数关系．（3）甲、乙两人在什么时间生产的零件总数相差8个？参考答案与试题解析一．选择题（共10小题）1．下列函数中是一次函数的是（）A．y＝B．y＝C．y＝ax+b D．y＝x2【分析】根据一次函数的定义解答．【解答】解：A、是正比例函数，特殊的一次函数，故本选项符合题意；B、自变量次数不为1，不是一次函数，故本选项不符合题意；C、单a＝0时，它不是一次函数，故本选项不符合题意；D、自变量次数不为1，不是一次函数，故本选项不符合题意．故选：A．2．下列各点中位于第二象限的是（）A．（﹣2，0）B．（8，﹣2）C．（0，3）D．（﹣，4）【分析】依据位于第二象限的点的横坐标为负，纵坐标为正，即可得到结论．【解答】解：∵位于第二象限的点的横坐标为负，纵坐标为正，∴位于第二象限的是（﹣，4）故选：D．3．已知过A（﹣1，a），B（2，﹣2）两点的直线平行于x轴，则a的值为（）A．﹣1 B．1 C．2 D．﹣2【分析】根据两点所在直线平行于x轴，那么这两点的纵坐标相等解答即可．【解答】解：∵过A（﹣1，a），B（2，﹣2）两点的直线平行于x轴，∴a＝﹣2，故选：D．4．关于函数y＝﹣﹣1，下列说法错误的是（）A．当x＝2时，y＝﹣2B．y随x的增大而减小C．若x1＞x2，则y1＞y2D．图象经过第二、三、四象限【分析】根据一次函数的性质判定即可．【解答】解：关于函数y＝﹣﹣1，A、当x＝2时，y＝﹣﹣1＝﹣2，说法正确，不合题意；B、∵k＝﹣，∴y随x的增大而减小，说法正确，不合题意；C、∵k＝﹣，∴y随x的增大而减小，∴若x1＞x2，则y1＜y2，说法错误，符合题意；D、图象经过第二、三、四象限，说法正确，不合题意；故选：C．5．下面四条直线，其中直线上的每一个点的坐标都是二元一次方程2x﹣3y＝6的解的是（）A．B．C．D．【分析】根据两点确定一条直线，当x＝0，求出y的值，再利用y＝0，求出x的值，即可得出一次函数图象与坐标轴交点，即可得出图象．【解答】解：∵2x﹣3y＝6，∴y＝x﹣2，∴当x＝0，y＝﹣2；当y＝0，x＝3，∴一次函数y＝x﹣2，与y轴交于点（0，﹣2），与x轴交于点（3，0），即可得出选项D符合要求，故选：D．6．已知y﹣1与x成正比例，当x＝3时，y＝2．则当x＝﹣1时，y的值是（）A．﹣1 B．0 C．D．【分析】设y﹣1＝kx（k≠0），把x＝3，y＝2代入求出k的值，把x＝﹣1代入函数关系式即可得到相应的y的值；【解答】解：设y﹣1＝kx（k≠0），则由x＝3时，y＝2，得到：2﹣1＝3k，解得k＝．则该函数关系式为：y＝x+1；把x＝﹣1代入y＝x+1得到：y＝﹣+1＝；故选：D．7．实践证明1分钟跳绳测验的最佳状态是前20秒速度匀速增加，后10秒冲刺，中间速度保持不变，则跳绳速度v（个/秒）与时间t（秒）之间的函数图象大致为（）A．B．C．D．【分析】根据前20秒匀加速进行，20秒至50秒保持跳绳速度不变，后10秒继续匀加速进行，得出速度y随时间x的增加的变化情况，即可求出答案．【解答】解：随着时间的变化，前20秒匀加速进行，所以此时跳绳速度y随时间x的增加而增加，再根据20秒至50秒保持跳绳速度不变，所以此时跳绳速度y随时间x的增加而不变，再根据后10秒继续匀加速进行，所以此时跳绳速度y随时间x的增加而增加，故选：C．8．一次函数y＝ax+b与y＝abx在同一个平面直角坐标系中的图象不可能是（）A．B．C．D．【分析】根据a、b的取值，分别判断出两个函数图象所过的象限，要注意分类讨论．【解答】解：当ab＞0，a，b同号，y＝abx经过一、三象限，同正时，y＝ax+b过一、三、二象限；同负时过二、四、三象限，当ab＜0时，a，b异号，y＝abx经过二、四象限a＜0，b＞0时，y＝ax+b过一、三、四象限；a＞0，b＜0时，y＝ax+b过一、二、四象限．故选：D．9．若点（﹣1，m）和（2，n）在直线y＝﹣x+b上，则m、n、b的大小关系是（）A．m＞n＞b B．m＜n＜b C．m＞b＞n D．b＜m＜n【分析】根据一次函数的解析式判断出其增减性，再根据点的横坐标的特点即可得出结论．【解答】解：∵直线y＝﹣x+b中，k＝﹣1＜0，∴y随x的增大而减小．∵﹣1＜0＜2，∴m＞b＞n．故选：C．10．甲车从A地到B地，乙车从B地到A地，乙车先出发先到达，甲乙两车之间的距离y（千米）与行驶的时间x（小时）的函数关系如图所示，则下列说法中不正确的是（）A．甲车的速度是80km/hB．乙车的速度是60km/hC．甲车出发1h与乙车相遇D．乙车到达目的地时甲车离B地10km【分析】根据已知图象分别分析甲、乙两车的速度，进而分析得出答案．【解答】解：根据图象可知甲用了（3.5﹣1）小时走了200千米，所以甲的速度为：200÷2.5＝80km/h，故选项A不合题意；由图象横坐标可得，乙先出发的时间为1小时，两车相距（200﹣140）＝60km，故乙车的速度是60km/h，故选项B不符合题意；140÷（80+60）＝1（小时），即甲车出发1h与乙车相遇，故选项C不合题意；200﹣（200÷60﹣1）×80＝km，即乙车到达目的地时甲车离B地km，故选项D符合题意．故选：D．二．填空题（共4小题）11．函数中，自变量x的取值范围是x＞﹣2 ．【分析】根据二次根式的性质和分式的意义，被开方数大于或等于0，分母不等于0，就可以求解．【解答】解：根据题意得：被开方数x+2≥0，解得x≥﹣2，根据分式有意义的条件，x+2≠0，解得x≠﹣2，故x＞﹣2．故答案为x＞﹣2．12．已知关于x的方程mx+n＝0的解是x＝﹣2，则直线y＝mx+n与x轴的交点坐标是（﹣2，0）．【分析】求直线与x轴的交点坐标，需使直线y＝mx+n的y值为0，则mx+n＝0；已知此方程的解为x＝﹣2．因此可得答案．【解答】解：∵方程的解为x＝﹣2，∴当x＝﹣2时mx+n＝0；又∵直线y＝mx+n与x轴的交点的纵坐标是0，∴当y＝0时，则有mx+n＝0，∴x＝﹣2时，y＝0．∴直线y＝mx+n与x轴的交点坐标是（﹣2，0）．13．若点P的坐标是（2a+1，a﹣4），且P点到两坐标轴的距离相等，则P点的坐标是（﹣9，﹣9）或（3，﹣3）．【分析】根据点到两坐标轴的距离相等列出绝对值方程求出a的值，然后求解即可．【解答】解：∵点P（2a+1，a﹣4）到两坐标轴的距离相等，∴|2a+1|＝|a﹣4|，∴2a+1＝a﹣4或2a+1＝﹣（a﹣4），解得a＝﹣5或a＝1，当a＝﹣5时，点P的坐标为（﹣9，﹣9），当a＝1时，点P的坐标为（3，﹣3），综上所述，点P的坐标为（﹣9，﹣9）或（3，﹣3），故答案为：（﹣9，﹣9）或（3，﹣3）．14．直线y＝kx﹣2与直线y＝x﹣1（1≤x≤4）有交点，则k的取值范围是≤k≤2 ．【分析】根据已知条件得到直线y＝kx﹣2与y轴的交点坐标为C（0，﹣2），求得直线y＝x﹣1过A（1，0），B（4，3），设直线AC的解析式为y＝mx+n，得到直线AC的解析式为y＝2x﹣2，设直线BC的解析式为y＝ex+f，得到直线BC的解析式为y＝x﹣2，于是得到结论．【解答】解：令x＝0，则y＝0•k﹣2＝﹣2，所以直线y＝kx﹣2与y轴的交点坐标为C（0，﹣2），∵当x＝1时，y＝x﹣1＝0，当x＝4时，y＝x﹣1＝3，∴直线y＝x﹣1过A（1，0），B（4，3），设直线AC的解析式为y＝mx+n，则，解得．所以直线AC的解析式为y＝2x﹣2，设直线BC的解析式为y＝ex+f，则，解得．所以直线BC的解析式为y＝x﹣2，若直线y＝kx﹣2与直线y＝x﹣1（1≤x≤4）有交点，则k的取值范围是≤k≤2，故答案为≤k≤2：三．解答题（共8小题）15．已知一次函数的图象平行于y＝﹣x，且截距为1．（1）求这个函数的解析式；（2）判断点P（﹣2，）是否在这个函数的图象上．【分析】（1）根据两平行直线的解析式的k值相等求出k，然后根据截距为1求出b值，即可得解；（2）把点P（﹣2，）代入解析式，检验即可．【解答】解：（1）设这个函数的解析式为y＝kx+b，∵一次函数的图象平行于y＝﹣x，且截距为1，∴k＝﹣，b＝1，∴这个函数的解析式为y＝﹣x+1；（2）当x＝﹣2时，y＝+1＝，故点P（﹣2，）不在这个函数的图象上．16．若函数y＝（m+1）x+m2﹣1是正比例函数．（1）求该函数的表达式．（2）将该函数图象沿y轴向上或者向下平移，使其经过（1，﹣2），求平移的方向与距离．【分析】（1）根据正比例函数的定义列式计算即可得解；（2）设平移后的函数的解析式为y＝2x+b，把（1，﹣2）代入求得b的值，即可求得结论．【解答】解：（1）根据题意得，m2﹣1＝0且m+1≠0，解得m＝±1且m≠﹣1，所以m＝1．所以该函数的表达式为y＝2x；（2）设平移后的函数的解析式为y＝2x+b，∵经过（1，﹣2），∴﹣2＝2+b，∴b＝﹣4，∴函数图象沿y轴向下平移4个单位，使其经过（1，﹣2）．17．如图，先将△ABC向上平移2个单位再向左平移5个单位得到△A1B1C1（1）画出△A1B1C1，并写出点A1、B1、C1的坐标．（2）求△A1B1C1的面积．【分析】（1）直接利用平移的性质得出对应点位置进而得出答案；（2）利用△A1B1C1所在矩形面积减去周围三角形面积得出答案．【解答】解：（1）如图所示：△A1B1C1，点A1（﹣1，5），B1（﹣2，3），C1（﹣4，4）；（2）△A1B1C1的面积为：2×3﹣×1×3﹣×2×1﹣×1×2＝2.5；18．画出函数y＝﹣x+3的图象，并利用图象解下列问题：（1）求方程﹣x+3＝0的解．（2）求不等式﹣x+3＞0的解集．（3）若﹣3≤y＜6，求x的取值范围．【分析】（1）先利用描点法画出一次函数图象，然后利用直线与x轴的交点坐标确定方程﹣x+3＝0的解；（2）利用x轴上方所对应的自变量的范围确定不等式的解集；（3）利用图象确定y＝﹣3和y＝6对应的自变量的值，从而得到对应的x的取值范围．【解答】解：（1）如图，∵直线与x轴的交点坐标为（2，0），∴方程﹣x+3＝0的解为x＝2，（2）如图，∵x＜2时，y＞0，∴不等式﹣x+3＞0的解集为x＜2；（3）如图，﹣2＜x≤4时，﹣3≤y＜6．19．如图，大拇指与小拇指尽量张开时，两指尖的距离称为指距．人体构造学的研究成果表明，一般情况下人的指距d和身高h成如下所示的关系．指距d（cm）20 21 22 23身高h（cm）160 169 178 187 （1）直接写出身高h与指距d的函数关系式；（2）姚明的身高是226厘米，可预测他的指距约为多少？（精确到0.1厘米）【分析】（1）运用待定系数法求解即可；（2）把h＝226代入（1）中的结论即可．【解答】解：根据表格中数据，d每增加1，身高增加9cm，故d与h是一次函数关系，设这个一次函数的解析式是：h＝kd+b，，解得，故一次函数的解析式是：h＝9d﹣20；（2）当h＝226时，9d﹣20＝226，解得d＝27.3．即姚明的身高是226厘米，可预测他的指距约为27.3厘米．20．如图，直线l1：y＝2x﹣2与x轴交于点D，直线l2：y＝kx+b与x轴交于点A，且经过点B，直线l1，l2交于点C（m，2）．（1）求m的值；（2）求直线l2的解析式；（3）根据图象，直接写出1＜kx+b＜2x﹣2的解集．（4）求△ACD的面积．【分析】（1）把C（m，2）代入y＝2x﹣2中可求出m的值；（2）利用待定系数法求直线l2的解析式；（3）结合图象写出y＝kx+b的函数值大于2且直线l1在直线l2上方对应的自变量的范围；（4）根据两直线解析式确定A、D点的坐标，然后利用三角形面积公式计算．【解答】解：（1）把C（m，2）代入y＝2x﹣2得2m﹣2＝2，解得m＝4；（2）把C（2，2），B（3，1）代入y＝kx+b得，解得，∴直线l2的解析式为y＝﹣x+4；（3）2＜x＜3；（3）当y＝0时，2x﹣2＝0，解得x＝1，则C（1，0），当y＝0时，﹣x+4＝0，解得x＝4，则A（4，0），∴S△ACD＝×（4﹣1）×2＝3．21．甲、乙两个工程队完成某项工程，先由甲单独做10天，乙队再加入合作．工进度满足如图所示．（1）求工作量y与工作时间x（天）之间的函数关系式；（2）这项工程全部完成需要多少天？（3）求乙队单独完成这项工程的天数．【分析】（1）分段函数，运用待定系数法解答即可；（2）根据（1）的结论解答即可；（3）根据（1）可得乙队的工作效率，从而计算出乙队单独完成这项工程要60天．【解答】解：（1）当x≤10时，设y＝kx，根据题意得，解得k＝，∴y＝；当x＞10时，设y＝k1x+b，根据题意得：，解得，∴y＝．（天）∴10＜x≤28，∴；（2）由（1）得，当y＝1时，，解得x＝28．答：这项工程全部完成需要28天；（3）（1﹣）÷（28﹣10）＝（天），（天），答：乙队单独完成这项工程需要60天．22．甲、乙两人分别安装同一种零件40个，其中乙在安装两小时后休息了2小时，后继续按原来进度工作，他们每人安装的零件总数y（个）与安装时间x（小时）的函数关系如图1所示，两人安装零件总数之差z（件）与时间x（小时）的函数关系如图2所示．（1）a＝ 4 ；b＝10 ．（2）求出甲工作2小时后的安装的零件数y与时间x的函数关系．（3）甲、乙两人在什么时间生产的零件总数相差8个？【分析】（1）根据题意和图象中的数据可以求得a、b的值；（2）根据函数图象中的数据可以求得甲工作2小时后的安装的零件数y与时间x的函数关系；（3）根据函数图象，利用分类讨论的方法可以求得甲、乙两人在什么时间生产的零件总数相差8个．【解答】解：（1）由图可得，a＝10﹣6＝4，b＝4+（40﹣10）÷（10÷2）＝4+30÷5＝4+6＝10，故答案为：4，10；（2）甲后来的速度为：＝6件/小时，甲做完40个需要的时间为：2+（40﹣4）÷6＝2+36÷6＝2+6＝8，设甲工作2小时后的安装的零件数y与时间x的函数关系是y＝kx+b，∵甲工作2小时后的安装的零件数y与时间x的函数图象过点（2，4），（8，40），∴，得，即甲工作2小时后的安装的零件数y与时间x的函数关系是y＝6x﹣8（2＜x≤8）；（3）设t小时时，甲、乙两人生产的零件总数相差8个，乙的速度为：10÷2＝5件/小时，当4＜t≤8时，6+（t﹣4）×（6﹣5）＝8，解得，t＝6，当8＜t＜10时，5（10﹣t）＝8，解得，t＝8.4，答：甲、乙两人在6小时或8.4小时时生产的零件总数相差8个．2020-2021学年度第一学期第一次月考八年级数学试题卷考试方式：闭卷考试时间：100 分钟满分：120 分一．选择题（共10小题，每题3分，共30分，请把正确答案写在答案卷上.）1.下列四个图案是我国几家银行的标志，其中是轴对称图形的有（）A．1个 B．2个 C．3个 D．4个2.下列各条件不能作出唯一直角三角形的是（）A．已知两直角边 B．已知两锐角C．已知一直角边和它们所对的锐角 D．已知斜边和一直角边3．下列语句中正确的有几个（）①关于一条直线对称的两个图形一定能重合；②两个能重合的图形一定关于某条直线对称；③两个轴对称图形的对应点一定在对称轴的两侧；④一个圆有无数条对称轴．A．1 B．2 C．3 D．44.如图，已知AB=AD，那么添加下列一个条件后，仍无法判定△ABC≌△ADC的（）A．CB=CD B．BAC=∠DAC C．BCA=DCA D．∠B=∠D=9005.如图，请仔细观察用直尺和圆规作一个角等于已知角AOB ∠的示意图，请你根据所学的图形的全等这一章的知识，说明画出'''A O B AOB ∠=∠的依据是（ ）A.SASB.ASAC.AASD.SSS6.如图，将三角形纸片ABC 折叠，使点C 与点A 重合，折痕为DE . 若∠B ＝80°，∠BAE ＝26°，则∠EAD 的度数为（ ）A.36°B. 37°C.38°D.45°7.如图，将一张正方形纸片对折两次，然后在上面打3个洞，则纸片展开后是( )8.如图,工人师傅做了一个长方形窗框ABCD,E,F,G,H 分别是四条边上的中点,为了使它稳固,需要在窗框上钉一根木条,这根木条不应钉在( )A. A,C 两点之间B. E,G 两点之间C. B,F 两点之间D. G,H 两点之间9.如图，在△ABC 中，AD 为∠BAC 的平分线，DE ⊥AB 于E ，DF ⊥AC 于F ，△ABC 的面积是28cm 2，AB =20cm ，AC =8cm ，则DE 的长是（ ）A ．4cmB ．3cmC ．2cmD ．1cm10.如图，在△ABC 中，∠A=∠B ，∠ACB=90°，点D 、E 在AB 上，将△ACD 、△B CE 分别沿CD 、CE 翻折，点A 、B 分别落在点A′、B′的位置，再将△A′CD 、△B′CE 分别沿A′C 、B′C 翻折，点D 与点E 恰好重合于点O ，则∠A′OB′的度数是（ ） A ．90°B ．120°C ．135°D ．150°二．填空题（共8小题，每题2分，共16分，请把结果直接填在答案卷上.）11.下列图形：①角；②直角三角形；③等边三角形；④线段；⑤等腰三角形；⑥平行四边形.其中一定是轴对称图形的有 个.AC OB DA'C O'B'DBAE DC第3题B CDA(第4题图) (第5题图)(第6题图)（第8题图） （第9题图） （第10题图）12.小明从平面镜子中看到镜中电子钟示数的像如图所示，这时的时刻应是 ．13．如图，AC=BD ，要使△ABC ≌△DCB （SAS ），只要添加一个条件 ．14．如图，△ABC 的周长为32，且BD=DC ，AD ⊥BC 于D ，△ACD 的周长为24，那么AD 的长为 ． 15．如图，已知AB ∥CF ，E 为DF 的中点，若AB ＝8 cm ，BD ＝3 cm ，则CF ＝ cm ．16．如图，点D 在边BC 上，DE ⊥AB ，DF ⊥BC ，垂足分别为点E ，D ，BD ＝CF ，BE ＝CD ．若∠AFD ＝155°，则∠EDF ＝ ．17．如图，方格纸中△ABC 的3个顶点分别在小正方形的顶点（格点）上，这样的三角形叫格点三角形，图中与△ABC 全等的格点三角形共有 个（不含△ABC ）．18．已知在△ABC 中，AB=5，BC=7，BM 是AC 边上的中线，则BM 的取值范围为 ．三．解答题（共8小题，共74分. 解答需写出必要的文字说明或演算步骤.）19．（本题满分12分）如图，在3×3的正方形网格中，有一个以格点为顶点的三角形.（1）请你在图①，图②，图③中，分别画出一个与该三角形成轴对称且以格点为顶点的三角形，并将所画三角形涂上阴影．（注：所画的三幅图不能重复）．（2）格纸中所有与该三角形成轴对称且以格点为顶点的三角形共有 个．20．（本题满分8分）如图，在所给正方形网格图中完成下列各题：①画出格点△ABC （顶点均在格点上）关于直线DE 对称的△A 1B 1C 1；FEDCB A(第15题图) (第16题图)(第17题图)(第12题图)(第13题图) (第14题图)②在DE上画出点Q，使QA+QC最小．（用直尺画图，保留痕迹）21.（本题满分8分）已知△ABC，按下列要求作图：（尺规作图，保留痕迹不写作法。
湖南省广益实验中学2020—2021学年上学期第三次月考八年级数学试题
20秋广益初二第三次月考（教师版）参考答案与试题解析一．选择题（共13小题）1．2020年全国上下抗击疫情，众志成城，下列防疫标志图形中是轴对称图形的是（）A．B．C．D．【解答】解：D、是轴对称图形，故此选项符合题意；故选：D．2．新冠病毒的直径最小大约为0.00000008米，这个数用科学记数法表示为（）A．8×10﹣8B．8×10﹣7C．80×10﹣9D．0.8×10﹣7【解答】解：∵0.00000008＝8×10﹣8；故选：A．3．如果分式2xx+y中的x和y都扩大为原来的2倍，那么分式的值（）A．扩大2倍B．扩大4倍C．不变D．缩小2倍【解答】解：分式2xx+y中的x和y都扩大为原来的2倍后可得：4x 2x+2y =4x2(x+y)=2xx+y，∴分式的值不变，故选：C．4．下列运算中正确的是（）A．√2+√3=√5B．（−√5）2＝5C．3√2−2√2=1D．√16=±4【解答】解：B、原式＝5，所以B选项正确；故选：B．5．如图，在△ABC 中，∠C ＝90°，点D 在斜边AB 上，且AD ＝CD ，则下列结论中错误的结论是（ ） A ．∠DCB ＝∠BB ．BC ＝BDC ．AD ＝BDD ．∠ACD =12∠BDC【解答】解：∵∠C ＝90°，∴∠A +∠B ＝90°，∠ACD +∠BCD ＝90°，∵AD ＝CD ， ∴∠A ＝∠ACD ，∴∠B ＝∠BCD ，A 选项结论正确，不符合题意； BC 与BD 不一定相等，B 选项结论错误，符合题意；∵∠B ＝∠BCD ， ∴BD ＝CD ，∵AD ＝CD ，∴AD ＝BD ，C 选项结论正确，不符合题意； ∵∠A ＝∠ACD ，∴∠BDC ＝∠A ＝∠ACD ＝2∠ACD ，∴∠ACD =12∠BDC ，D 选项结论正确，不符合题意；故选：B ．6．已知：a ＝﹣32，b ＝（−13）﹣2，c ＝（−13）0，a 、b 、c 的大小关系是（ ）A ．a ＜b ＜cB ．a ＜c ＜bC ．b ＜a ＜cD ．c ＜a ＜b【解答】解：∵a ＝﹣32＝﹣9，b ＝（−13）﹣2＝9，c ＝（−13）0＝1， ∴a ＜c ＜b ．故选：B ．7．分式x 2−1x+1=0，则x 的值是（ ）A ．1B ．﹣1C ．±1D ．0【解答】解：∵分式x 2−1x+1=0，∴x 2﹣1＝0且x +1≠0，解得：x ＝1．故选：A ．8．实数a ，b 在数轴上对应点得位置如图，则化简|a ﹣b |−√a 2的结果是（ ）A ．2a ﹣bB ．b ﹣2aC ．bD ．﹣b【解答】解：由数轴上a ，b 的位置可得：a ﹣b ＜0，a ＜0， 故|a ﹣b |−√a 2=−（a ﹣b ）﹣（﹣a ）＝b ．故选：C ．9．体育测试中，小进和小俊进行800米跑测试，小进的速度是小俊的1.25倍，小进比小俊少用了40秒，设小俊的速度是x 米/秒，则所列方程正确的是（ ）A ．40×1.25x ﹣40x ＝800B ．800x−8002.25x=40C ．800x−8001.25x=40D ．8001.25x−800x=40【解答】解：小进跑800米用的时间为8001.25x秒，小俊跑800米用的时间为800x秒，∵小进比小俊少用了40秒，方程是800x−8001.25x=40，故选：C ．10．等腰三角形的周长是20cm ，一边是另一边的两倍，则底边长（ ） A ．10cm 或4cmB ．10cmC ．4cmD ．无法确定【解答】解：根据题意设底边长xcm ，则腰长为2xcm ． x +2x +2x ＝20，解得 x ＝4故底边长为4cm ，故选：C ．11．如图，△ABC 是等边三角形，AD ＝6，AD 是BC 边上的高，E 是AC 的中点，P 是AD 上的一个动点，则PE +PC 的最小值为（ ） A ．3 B ．4C ．6D ．8【解答】解：如图，连接BE 交AD 于点P ′，∵，△ABC 是等边三角形，AD ＝6，AD 是BC 边上的高，E 是AC 的中点，∴AD 、BE 分别是等边三角形ABC 边BC 、AC 的垂直平分线， ∴P ′B ＝P ′C ，P ′E +P ′C ＝P ′E +P ′B ＝BE=AD=6根据两点之间线段最短，点P 在点P ′时，PE +PC 有最小值，最小值即为BE 的长． 所以P ′E +P ′C 的最小值为6．故选：C ．12．如图，∠AOB ＝120°，OP 平分∠AOB ，且OP ＝10．若点M ，N 分别在射线OA ，OB 上，且△PMN 是边长为整数的等边三角形，则满足上述条件的点M 有（参考数据：√3≈ 1.73）（ ）A ．4个以上B ．4个C ．3个D ．2个【解答】解：在OB 截取OK ＝OP ，连接PK ，则△OPK 是等边三角形．可以证明当∠MPN ＝60°时，△PMN 是等边三角形． 理由：∵∠MPN ＝∠OPB ＝60°，∴∠OPM ＝∠NPK ，∵OP ＝PK ，∠POM ＝∠PKN ，∴△POM ≌△PKN ，∴PM ＝PN ，∴△PMN 是等边三角形，当PM ⊥OA 时，PM 的值最小，最小值为5√3， PM 的最大值为10，∴5√3≤PM ≤10，∵PM 是整数， ∴PM 的值有两种可能，对应的点M 有4种可能，故选：B ． 二．填空题（共5小题）13．因式分解：a a 163-＝)4)(4(-+a a a ；【解答】解：)4)(4(-+a a a ；14．若代数式x211-在实数范围内有意义，则x 的取值范围是 21<x ．【解答】解：根据二次根式的意义，被开方数021>-x ，解得21<x ； 15．若点A （1+m ，1﹣n ）与点B （﹣3，2）关于y 轴对称，则m +n 的值是 1 ． 【解答】解：∵点A （1+m ，1﹣n ）与点B （﹣3，2）关于y 轴对称， ∴1+m ＝3、1﹣n ＝2，解得：m ＝2、n ＝﹣1，所以m +n ＝2﹣1＝1， 故答案为：1．16．已知关于x 的二次三项式x 2+2mx +4﹣m 2是完全平方式，则实数m 的值为 ±√2 ． 【解答】解：∵x 2+2mx +4﹣m 2是完全平方式，∴4﹣m 2＝m 2， 即m 2＝2，解得m ＝±√2．17．如图，在已知的△ABC 中，按以下步骤作图：①分别以B ，C 为圆心，以大于12BC 的长为半径作弧，两弧相交于两点M ，N ；②作直线MN 交AB 于点D ，连接CD ．若CD ＝AC ，∠A ＝50°，则∠ACB ＝ 105° ． 【解答】解：如图所示：∵MN 垂直平分BC ，∴CD ＝BD ，∴∠DBC ＝∠DCB ∵CD ＝AC ，∠A ＝50°，∴∠CDA ＝∠A ＝50°， ∵∠CDA ＝∠DBC +∠DCB ，∴∠DCB ＝∠DBC ＝25°，∠DCA ＝180°﹣∠CDA ﹣∠A ＝80°， ∴∠ACB ＝∠DCB +∠ACD ＝25°+80°＝105°．故答案为：105°．18．若x ≠﹣1，则把−1x+1称为x 的“和1负倒数”，如：2的“和1负倒数”为−13，﹣3的“和1负倒数”为12，若x 1=23，x 2是x 1的“和1负倒数”，x 3是x 2的“和1负倒数”，…依此类推，则x 2020的值为32【解答】解：∵x 1=23，∴x 2=−11+23=−35，x 3=−11−35=−52， x 4=−11−52=23，……∴此数列每3个数为一周期循环，∵2020÷3＝673…1，∴x 2020＝x 1=23，三．解答题（共8小题） 19．计算题（1）()02224182-+-+--π 【解答】解：（1）原式＝14122241+-+-=21-20．先化简式子221(1)2x x x x x ⎛⎫++-÷⎪⎝⎭，再从0，1-3 【解答】解：原式=11+-x x 当x ＝2时，原式=31． 21．（8分）已知关于x 的方程12111x x -=--的解比2121kx k x x--=-的解多1，求2(3)k +的值。
2020-2021学年湖南衡阳八年级上数学月考试卷及答案
2020-2021学年湖南衡阳八年级上数学月考试卷一、选择题1. 181 的平方根是( ) A.13B.19C.±13D.±192. 下列等式错误的是( ) A.√81=±9 B.±√0.04=±0.2 C. √−643=−4D.±√0.01=±0.13. 计算√25−√−83的结果是( ) A.−3 B.3 C.−7 D.74. 下列运算结果正确的是( ) A.4a 3⋅2a 2=8a 6 B.x 3+x 2=x 5 C.b ⋅b 3=b 4 D.5a 3−3a 3=25. 在实数√4，0，227，√0.1253，0.1010010001…，√3，π2中无理数有（ ）A.2个B.0个C.3个D.1个6. 我们知道√5是一个无理数，那么√5−1在哪两个整数之间？( ) A.2与3 B.1与2C.3与4D.4与57. 下列各数没有平方根的是( ) A.(−2)3 B.64C.(−3)4D.08. (−3)2的平方根是( ) A.±3 B.3C.±9D.−39. 下列说法正确的是( ) A.立方根等于本身的数是0和−1 B.平方根等于本身的数是0和1 C.实数和数轴上的点一一对应D.算术平方根等于本身的数是0和±110. 计算(a m )3⋅a n 的结果是( ) A.a 3m+n B.a m2+nC.a 3(m+n)D.a 3mn二、填空题已知3n =a ，3m =b ，则3m+n+1=________．如果√a −1有意义，那么a 的取值范围是________．2−√3的相反数是________．(−xy )7÷(−xy )2=________.−64×(−6)5=________.√64的立方根是________.若|a −b +1|与√a +2b +4互为相反数，则(a −b )2004=________.一个正数的算术平方根是a ，那么比这个正数大2的数的算术平方根是________． 三、解答题计算.(1)(−2a 2b )(ab 2−a 2b +a 2)；(2)(x +y )(x 2−xy +y 2). 化简.(1)√(−3)2−√83+√4；(2)x 3⋅(2x 3)2÷(x 4)2.已知√4−x +√x −4+3=y ，求y x 的平方根.先化简，再求值：(x−2y)(x+3y)−(2x−y)(x−4y)，其中x=−1，y=2．试说明：代数式(2x+3)⋅(6x+2)−6x(2x+13)+8(7x+2)的值与x的取值无关. 实数a，b在数轴上的位置如图所示，化简：√(a+1)2+√(b−1)2−√(a−b)2.已知x≠1，并且(1+x)(1−x)=(1−x2)，(1−x)(1+x+x2)=(1−x3)，(1−x)(1+x+x2+x3)=(1−x4)．(1)观察以上各式并猜想：(1−x)(1+x+x2+⋯+x n)=________（n为正整数）；(2)根据你的猜想计算：(1−2)(1+2+22+23+24+25)=________；(x−1)(x99+x98+x97+⋯+x2+x+1)=________．2+22+23+...+2n=________（n为正整数）．参考答案与试题解析2020-2021学年湖南衡阳八年级上数学月考试卷一、选择题1.【答案】此题暂无答案【考点】平方根【解析】此题暂无解析【解答】此题暂无解答2.【答案】此题暂无答案【考点】立方于的性术算三平最根平方根【解析】此题暂无解析【解答】此题暂无解答3.【答案】此题暂无答案【考点】实因归运算【解析】此题暂无解析【解答】此题暂无解答4.【答案】此题暂无答案【考点】同底水水的乘法单项使性单项式合较溴类项【解析】此题暂无解析【解答】此题暂无解答5.【答案】此题暂无答案【考点】无理较的识轻立方于的性术算三平最根【解析】此题暂无解析【解答】此题暂无解答6.【答案】此题暂无答案【考点】估算无于数的深小【解析】此题暂无解析【解答】此题暂无解答7.【答案】此题暂无答案【考点】平方根【解析】此题暂无解析【解答】此题暂无解答8.【答案】此题暂无答案【考点】平方根有理表的木方【解析】此题暂无解析【解答】此题暂无解答9.【答案】此题暂无答案【考点】在数轴来表示兴数立方根算三平最根平方根【解析】此题暂无解析【解答】此题暂无解答10.【答案】此题暂无答案【考点】幂的乘表与型的乘方【解析】此题暂无解析【解答】此题暂无解答二、填空题【答案】此题暂无答案【考点】同底水水的乘法【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】二次根式较意夏的条件【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】实根的冬质相反数【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】单项式验河单项式同底射空的除法【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】同底水水的乘法【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】立方于的性术算三平最根【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】非负射的纳质：算术棱方础非负数的较质：绝对值【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】算三平最根【解析】此题暂无解析【解答】此题暂无解答三、解答题【答案】此题暂无答案【考点】单项较乘多洗式多项都接多项式【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】立方于的性术同底射空的除法同底水水的乘法平方根【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】平方根【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】整式都混接运算白—化冰求值【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】整式较混合轻算多项都接多项式列使数种【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】在数轴来表示兴数绝对值数轴【解析】此题暂无解析【解答】此题暂无解答【答案】此题暂无答案【考点】规律型：因字斯变化类【解析】此题暂无解析【解答】此题暂无解答。
2020-2021学年合肥三十八中八年级上学期第一次月考数学试卷(含解析)
2020-2021学年合肥三十八中八年级上学期第一次月考数学试卷一、选择题（本大题共10小题，共40.0分）1.下列各曲线表示的y与x之间的关系中，y不是x的函数的是()A. B.C. D.2.如图，小明居住的小区内有一条笔直的小路，有一盏路灯位于小路上M、N两点的正中间，晚上，小明由点M处径直走到点N处，他在灯光照射下的影长y与行走路程x之间的变化关系用图象表示大致是()A. B.C. D.3.如图，在边长为1的正方形网格中，将△ABC向右平移两个单位长度得到△A′B′C′，则与点B′关于x轴对称的点的坐标是()A. (0,−1)B. (1,1)C. (2,−1)D. (1,−2)4.已知a、b、c为自然数，且a2+b2+c2+42<4a+4b+12c，且a2−a−2>0，则代数式1a+1 b +1c的值为()A. 1B. 76C. 10D. 115.已知点A的坐标为(2,0)，点P在直线y=x上运动，当以点P为圆心，PA的长为半径的圆的面积最小时，点P的坐标为()A. (1,−1)B. (0,0)C. (1,1)D. (√2,√2)6.下列函数中一次函数的个数为()①y=2x；②y=3+4x；③y=12；④y=ax(a≠0的常数)；⑤xy=3；⑥2x+3y−1=0．A. 3个B. 4个C. 5个D. 6个7.如图，∠AOB=α°，点P是∠AOB内任意一点，OP=6cm，点M和点N分别是射线OA和射线OB上的动点，若△PMN周长的最小值是6cm，则α的值是()A. 15B. 30C. 45D. 608.不等式组：{2x>−4x−5≤0的解集是()A. x>−2B. −2<x≤5C. x≤5D. 无解9.如图，一次函数y=−x+1的图象与两坐标轴分别交于A、B两点，点C是线段AB上一动点(不与点A、B重合)，过点C分别作CD、CE垂直于x轴、y轴于点D、E，当点C从点A开始向点B运动时，则矩形CDOE的周长()A. 不变B. 逐渐变大C. 逐渐变小D. 先变小后变大10.如图，点B、C分别在直线y=2x和y=kx上，点A，D是x轴上的两点，已知四边形ABCD是正方形，则k的值为()A. 12B. 23C. 1D. 32二、填空题（本大题共4小题，共20.0分）11.函数y=x−13+x中，自变量x的取值范围是______ ．12.如果一次函数y=kx+b的图象如图所示，那么k______0，b______0.13.已知三个非负实数a，b，c，满足3a+2b+c=5，2a+b−3c=1，若s=3a+b−7c的最大值为m，最小值为n，则mn=______ ．14.已知直线y=x−a与y=−x+b相交于点(1,0)，则不等式x−a≥−x+b的解集是______ ．三、计算题（本大题共1小题，共10.0分）15.在平面直角坐标系中，点A、B的坐标分别是(0,−2)，(0,2)，点C在x轴上，如果S△ABC=6，求点C的坐标．四、解答题（本大题共8小题，共80.0分）16.“三等分角”是数学史上一个著名的问题，但仅用尺规不可能“三等分角”.下面是数学家帕普斯借助函数给出的一种“三等分锐角”的方法(如图)：将给定的锐角∠AOB置于直角坐标系中，边OB在x轴上、边OA与函数y=1x的图象交于点P，以P为圆心、以2OP为半径作弧交图象于点R.分别过点P和R作x轴和y轴的平行线，两直线相交于点M，连接OM得到∠MOB，则∠MOB=13∠AOB.要明白帕普斯的方法，请研究以下问题：(1)设P(a,1a )、R(b,1b)，求直线OM对应的函数表达式(用含a，b的代数式表示)；(2)分别过点P和R作y轴和x轴的平行线，两直线相交于点Q.请说明Q点在直线OM上，并据此证明∠MOB=13∠AOB；(3)应用上述方法得到的结论，你如何三等分一个钝角(用文字简要说明)．17.如图1，在平面直角坐标系中，点A(0,n)，B(m,0)中的m，n满足|m+8|+(m+2n−4)2=0，点C在x轴的正半轴上，且△ABC的面积为33，AB=10，过点A作AD//x轴，过点C作CD⊥AD于点D，动点P从点D出发，以每秒2个单位长度的速度在射线DA上运动，同时另一动点Q从点B出发向终点A运动，速度是每秒3个单位长度，一点停止运动另一点也停止，设运动时间为t秒．(1)求出点A、B、C的坐标；(2)连接PC，请用含t的关系式来表示△PAC的面积S；(3)是否存在某一时刻t，使△PAC的面积等于△BOQ面积的一半？若存在请求出t值，若不存在请说明理由．18.如图，△A′B′C′是△ABC向右平移3个单位长度后得到的，且三个顶点的坐标分别为A′(2,1)，B′(5,2)，C′(4,4)(1)请画出△ABC，并写出点A，B，C的坐标；(2)画出△A′B′C′绕点O逆时针旋转180°后的图形．19.在初中阶段的函数学习中，我们经历了“确定函数的表达式−利用函数图象研究其性质−应用函数解决问题”的学习过程．在画函数图象时，我们通过描点或平移的方法画出了一个陌生函数的大致图象，结合上面经历的学习过程，现在来解决下面问题：在函数y=|√a×|x|+b中，当x=0时，y=1；当x=2时，y=√7．(1)求这函数的表达式______；(2)在给出的平面直角坐标系中画出这个函数的大致图象并写出这个函数的一条性质______；(3)结合你所画的函数图象与y=12x+32的图象，直接写出不等式组{√a×|x|+b≤12x+32x≥0的解集．20.已知：P(4,1)为平面直角坐标系中的一点，点A(a,0)，点B(0,a)(其中a>0)分别是坐标轴上的动点，若△PAB的面积为3，试求点A的坐标．21.如图，某公司组织员工假期去旅游，租用了一辆耗油量为每百公里约为25L的大巴车，大巴车出发前油箱有油100L，大巴车的平均速度为80km/ℎ，行驶若干小时后，由于害怕油箱中的油不够，在途中加了一次油，油箱中剩余油量y(L)与行驶时间x(ℎ)之间的关系如图所示，请根据图象回答下列问题：(1)汽车行驶______ h后加油，中途加油______ L；(2)求加油前油箱剩余油量y与行驶时间x的函数解析式；(3)若当油箱中剩余油量为10L时，油量表报警，提示需要加油，大巴车不再继续行驶，则该车最远能跑多远？此时，大巴车从出发到现在已经跑了多长时间？22.已知老师家20164月份用2吨，交水费71元；5月份用水28，水16．自来水销售格污水处价格每户每月用量价：元/吨单：元/吨17及以下a.80超过17不超过0吨的分b.80超过30的部分.000.0[说明：每户产生的污水量等于该户的量，=水费+水处理费]求a、的值；夏天到，用水量将大幅加，老师划把6月份水费控制在家月收入的2，老师家月收入为9200元，则按划张老家6月份最能用多少吨？x+6与x轴、y轴交于A、B两点，点C在第四象限，BC⊥AB，且BC=AB；23. 如图，直线y=34(1)如图1，求点C的坐标；(2)如图2，D是BC的中点，过D作AC的垂线EF交AC于E，交直线AB于F，连接CF，点P为射线AD上一动点，求PF2−PC2的值；(3)如图3，在(2)的条件下，在第二象限过点A作线段AM⊥AB于点A，在线段AB上取一点N，连接MN，使MN=BN，在第三象限取一点Q，使∠NMQ=90°，连接QC，若QC//AB，且QC=6AM，设点P的横坐标为t，△PMQ的面积为s，求s与t的函数关系式．【答案与解析】1.答案：C解析：解：根据函数的意义可知：对于自变量x的任何值，y都有唯一的值与之相对应，所以只有选项C不满足条件．故选：C．根据函数的意义即可求出答案．函数的意义反映在图象上简单的判断方法是：做垂直x轴的直线在左右平移的过程中与函数图象只会有一个交点．本题主要考查了函数的定义．函数的定义：在一个变化过程中，有两个变量x，y，对于x的每一个取值，y都有唯一确定的值与之对应，则y是x的函数，x叫自变量．2.答案：C解析：解：∵小路的正中间有一路灯，小明在灯光照射下的影长y与行走的路程x之间的变化关系，应为当小明走到灯下以前为：y随x的增大而减小，离开灯走到N：y随x的增大而增大∴用图象刻画出来应为C．故选：C．根据中心投影的性质得出小明在灯下走的过程中应长随路程之间的变化，进而得出符合要求的图象．此题主要考查了函数图象以及中心投影的性质，得出l随s的变化规律是解决问题的关键．3.答案：D解析：试题分析：首先根据图形，得到点B的坐标，再根据平移时，坐标的变化规律：左减右加，上加下减，求得点B′的坐标，最后再利用平面内两点关于x轴对称时：横坐标不变，纵坐标互为相反数，进行求解．∵点B(−1,2)，∴向右平移两个单位后，B′(1,2)．∴点B′(1,2)关于x轴对称点的坐标为(1,−2)．故选D4.答案：A解析：解：由a2−a−2>0，a为自然数，可知a>2，将化a2+b2+c2+42<4a+4b+12c为(a−2)2+(b−2)2+(c−6)2<2，因为(a−2)2、(b−2)2、(c−6)2都大于0，当a≥4时，上式不成立，所以自然数a只能取值为3．当a=3时，代入上式，得：(b−2)2+(c−6)2<1，所以只能使(b−2)2=0，(c−6)2=0，即b=2，c=6，所以1a +1b+1c=1．故选：A．先由a2−a−2>0得到a>2或a<−1，再变形a2+b2+c2+42<4a+4b+12c为：(a−2)2+ (b−2)2+(c−6)2<2，得到a=3，进而得到(b−2)2+(c−6)2<1，再得到b=2，c=6，故能求得1a +1b+1c的值．本题的关键是把不等式转化成平方的形式，然后分析在什么情况下小于2，从而求出a，b，c的值．5.答案：C解析：解：如图，过点A作AP与直线y=x垂直，垂足为点P，此时PA最小，则以点P为圆心，PA的长为半径的圆的面积最小．过点P作PM与x轴垂直，垂足为点M．在Rt△OAP中，∵∠OPA=90°，∠POA=45°，∴∠OAP=45°，∴PO=PA，∵PM⊥x轴于点M，∴OM=MA=12OA=1，∴PM=OM=1，∴点P的坐标为(1,1)．故选：C．本题考查了一次函数图象上点的坐标特征，垂线的性质，等腰直角三角形的判定与性质及对圆的认识，综合性较强，难度适中，得出点P的位置是解题的关键．当PA最小时，以点P为圆心，PA的长为半径的圆的面积最小．根据垂线段最短可知，过点A作AP 与直线y=x垂直，垂足为点P，此时PA最小．6.答案：B解析：解：①y=2x是一次函数；②y=3+4x是一次函数；③y=1，自变量系数为0，不是一次函数；2④y=ax(a≠0的常数)是一次函数；⑤xy=3自变量次数不为1，故不是一次函数；⑥2x+3y−1=0是一次函数．综上可得，①②④⑥是一次函数，共4个．故选：B．根据一次函数y=kx+b的定义条件是：k、b为常数，k≠0，自变量次数为1，判断各式即可．本题主要考查了一次函数的定义，难度不大，注意基础概念的掌握．7.答案：B解析：解：分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，如图所示：∵点P关于OA的对称点为D，关于OB的对称点为C，∴PM=DM，OP=OD，∠DOA=∠POA；∵点P关于OB的对称点为C，∴PN=CN，OP=OC，∠COB=∠POB，∠COD，∴OC=OP=OD，∠AOB=12∵△PMN周长的最小值是6cm，∴PM+PN+MN=6，∴DM+CN+MN=6，即CD=6=OP，∴OC=OD=CD，即△OCD是等边三角形，∴∠COD=60°，∴∠AOB=30°；故选：B．分别作点P关于OA、OB的对称点C、D，连接CD，分别交OA、OB于点M、N，连接OC、OD、PM、PN、MN，由对称的性质得出PM=DM，OP=OC，∠COA=∠POA；PN=CN，OP=OD，∠DOB=∠POB，得出∠AOB=12∠COD，证出△OCD是等边三角形，得出∠COD=60°，即可得出结果．本题考查了轴对称的性质、最短路线问题、等边三角形的判定与性质；熟练掌握轴对称的性质，证明三角形是等边三角形是解决问题的关键．8.答案：B解析：解：由2x>−4，得x>−2；由x−5≤0，得x≤5，所以−2<x≤5．选B．分别求出两个不等式的解集，再求其公共解集．本题考查一元一次不等式组的解法，属于基础题．求不等式组的解集，要遵循以下原则：同大取较大，同小取较小，小大大小中间找，大大小小解不了．9.答案：A解析：解：设点C的坐标为(m,−m+1)(0<m<1)，则CE=m，CD=−m+1，∴C矩形CDOE=2(CE+CD)=2，故选：A．根据一次函数图象上点的坐标特征可设出点C的坐标为(m,−m+1)，根据矩形的周长公式即可得出C矩形CDOE=2，此题得解．本题考查了一次函数图象上点的坐标特征以及矩形的性质，根据一次函数图象上点的坐标特征设出点C的坐标是解题的关键．10.答案：B解析：解：设正方形的边长为a，则B的纵坐标是a，把点B代入直线y=2x的解析式，设点B的坐标为(a2,a)，则点C的坐标为(a2+a,a)，把点C的坐标代入y=kx中得，a=k(a2+a)，解得k=23，故选：B．设正方形的边长为a ，根据正方形的性质分别表示出B ，C 两点的坐标，再将C 的坐标代入函数中从而可求得k 的值．本题考查的是一次函数图象上点的坐标特征、正方形的性质，掌握一次函数图象上点的坐标特征是解题的关键．11.答案：x ≠−3解析：解：由题意得，3+x ≠0， 解得，x ≠−3， 故答案为：x ≠−3．根据分式有意义的条件列出不等式，解不等式得到答案．本题考查的是函数自变量的取值范围的确定，掌握分式的分母不为0是解题的关键．12.答案：< <解析：解：∵一次函数y =kx +b 的图象经过第二、三、四象限， 又∵当k <0时，直线必经过二、四象限， ∴k <0．∵图象与y 轴负半轴相交， ∴b <0． 故答案为<，<．根据图象在坐标平面内的位置关系确定k ，b 的取值范围，从而求解．本题主要考查一次函数图象在坐标平面内的位置与k 、b 的关系．解答本题注意理解：直线y =kx +b 所在的位置与k 、b 的符号有直接的关系．k >0时，直线必经过一、三象限；k <0时，直线必经过二、四象限；b >0时，直线与y 轴正半轴相交；b =0时，直线过原点；b <0时，直线与y 轴负半轴相交．13.答案：577解析：解：联立{3a +2b =5−c2a +b =1+3c解得：{a =7c −3b =7−11c∵a 、b 、c 都是非负实数，∴{7c −3≥07−11c ≥0c ≥0解得：37≤c≤711∴s=3a+b−7c=3(7c−3)+(7−11c)−7c=3c−2∴当c=711时，s的最大值为：m=−111，当c=37时，s的最小值为：n=−57∴mn=577故答案为：577联立两等式后求出a与b，然后将a与b代入s中，化为一次函数最值问题，利用非负实数求出c的范围即可求出m与n的值．本题考查一次函数的综合问题，解题的关键是列出方程组求出a与b的表达式，然后利用一元一次不等式组求出c的范围，本题属于中等题型．14.答案：x≥1解析：解：已知直线y=x−a与y=−x+b相交于点(1,0)，直线y=x−a中y随x的增大而增大，而y=−x+b中y随x的增大而减小，因而不等式x−a≥−x+b的解集是x≥1．故答案为：x≥1．由于直线y=x−a与y=−x+b相交于点(1,0)，根据直线y=x−a和y=−x+b的图象的性质可求得不等式x−a≥−x+b的解集．本题主要考查了一次函数的性质，根据性质比较容易解决．15.答案：解：设C点的坐标是(x,0)．12×(2+2)x=6x=3．C点的坐标为(3,0)或(−3,0)．解析：点C在x轴上，所以可以在右半轴上，也可以在左半轴上，因此有两个解，根据面积为6，可求出解．本题考查三角形的面积为：12×底×高，根据坐标与图形的性质，可求出坐标．16.答案：解：(1)设直线OM的函数关系式为y=kx，P(a,1a )、R(b,1b).则M(b,1a)，∴k=1a ÷b=1ab．∴直线OM的函数关系式为y=1abx.(2)∵Q的坐标(a,1b )，满足y=1abx，∴点Q在直线OM上．∵四边形PQRM是矩形，∴SP=SQ=SR=SM=12PR．∴∠SQR=∠SRQ．∵PR=2OP，∴PS=OP=12PR．∴∠POS=∠PSO．∵∠PSQ是△SQR的一个外角，∴∠PSQ=2∠SQR．∴∠POS=2∠SQR．∵QR//OB，∴∠MOB=∠SQR．∴∠POS=2∠MOB．∴∠MOB=13∠AOB．(3)①先做出钝角的一半，按照上述方法先将此钝角的一半(锐角)三等分，进而做出再做一个角与已做得的角相等即可得到钝角的三等分角．②先作钝角的邻补角的三等分角，然后再以得到的三等分角作等边三角形可得钝角的三等分角，在钝角内作做出这个角即可．解析：(1)直线OM是正比例函数，可利用所给的坐标得到M的坐标，代入函数解析式即可；(2)根据所给的点的坐标得到Q 的坐标，看是否符合(1)中的函数解析式；运用矩形的性质，作图过程中的条件，外角与不相邻内角的关系，即可得证；(3)既然能作出锐角的三等分角，先将此钝角的一半(锐角)三等分，再作钝角的三等分角． 过某个点，这个点的坐标应适合这个函数解析式．注意使用作图过程中利用的条件．17.答案：解：(1)∵|m +8|+(m +2n −4)2=0，又∵|m +8|≥0，(m +2n −4)2≥0， ∴{m +8=0m +2n −4=0，解得{m =−8n =6，∴A(0,6).B(−8,0)，∵S △ABC =12×BC ×OA =33，∴BC =11， ∴OC =3， ∴C(3,0)．(2)由题意，D 的坐标是(3,6)， 当0≤t <32时，AP =3−2t ，则S =12⋅AP ⋅CD =12(3−2t)×6=9−6t ； 当32<t ≤103时，AP =2t −3，则S =12×(2t −3)×6=6t −9；(3)作QH ⊥OB 于点H.则BQ =3t ，△BQH∽△BAO ， 则BQAB =QHQA，即3t 10=QH 6，解得：QH =95t ， 则S △BOQ =12×8×95t =365t.当0≤t ≤32时，9−6t =12×365t ，解得：t =1516； 当32<t ≤103时，6t −9=12×365t ，解得：t =154(舍去)，综上所述，满足条件的t 的值为1516． 解析：(1)利用非负数的性质即可解决问题． (2)求得AD 的长是3，则分成0≤t ≤32和32<t ≤103两种情况求得AP 的长，利用三角形的面积公式求解；(3)作QH ⊥OB 于点H.则BQ =3t ，△BQH∽△BAO ，利用相似三角形的性质求得QH 的长，则△OBQ 的面积即可利用t 表示出来，然后分成0≤t ≤32和32<t ≤103两种情况，根据△PAC 的面积等于△BOQ面积的一半即可列方程求解．本题属于三角形综合题，考查了非负数的性质，三角形的面积，路程，速度，时间之间的关系等知识，解题的关键是学会用分类讨论的思想思考问题，属于中考常考题型．18.答案：解：(1)如图所示：A(−1,1)，B(2,2)，C(1,4)；(2)如图所示，△A″B″C″由△A′B′C′绕O 点逆时针旋转180°而得．解析：(1)直接利用平移的性质分别得出对应点位置进而得出答案；(2)直接利用旋转的性质得出对应点位置进而得出答案． 此题主要考查了旋转变换以及平移变换，根据题意得出对应点位置是解题关键．19.答案：y =√3×|x|+1 关于y 轴对称解析：解：(1)∵在函数y =√a ×|x|+b 中，当x =0时，y =1；当x =2时，y =√7． ∴{√b =1√2a +b =√7，得{a =3b =1，∴这个函数的表达式是y =√3×|x|+1， 故答案为y =√3×|x|+1； (2)∵y =√3×|x|+1， ∴y ={√3x +1(x ≥0)√−3x +1(x <0)，列表：x−5−2−10125…y4√7212√74…描点、连线画出该函数的图象如图所示：函数的性质：关于y轴对称，故答案为关于y轴对称；(3)由函数图象可得，y=√3×|x|+1是0≤x≤1．(1)根据在函数y=√a×|x|+b中，当x=0时，y=1；当x=2时，y=√7，可以求得该函数的表达式；(2)根据(1)中的表达式列表、描点，连线可以画出该函数的图象并得到函数的性质；(3)根据图象可以直接写出所求不等式组的解集．本题考查一次函数图象和性质、一元一次不等式与一次函数的关系，解答本题的关键是明确题意，利用一次函数的性质和数形结合的思想解答．20.答案：解：过点P作PC⊥x轴于C，作PD⊥y轴于D，则四边形OCPD是矩形，如图1，点C在点A的左边时，a>4，∵P(4,1)，点A(a,0)，点B(0,a)，∴AC=a−4，BD=a−1，△PAB的面积=12×4×(a−1)+12×(a−4)×1+1×4−12×a2=3，整理得，a2−5a+6=0，解得a1=2(舍去)，a2=3(舍去)，如图2，点C在点A的右边时，a<4，∵P(4,1)，点A(a,0)，点B(0,a)，∴AC=4−a，BD=a−1，△PAB的面积=12×4×(a−1)+4×1−12×(4−a)×1−12×a2=3，整理得，a2−5a+6=0，解得a1=2，a2=3，∴点A的坐标为(2,0)或(3,0)，综上所述，若△PAB的面积为3，则点A的坐标为(2,0)或(3,0)．解析：过点P作PC⊥x轴于C，作PD⊥y轴于D，可得四边形OCPD是矩形，再分点C在点A的左边和右边两种情况，表示出AC、BD，再利用梯形的面积和三角形的面积表示出△ABP的面积，然后计算即可得解．本题考查了三角形的面积，坐标与图形性质，难点在于分情况讨论并表示出△ABP的面积列出方程．21.答案：解：(1)由图象可以直接看出汽车行驶两小时后加油，汽车2小时耗油25×80×2100=40，由此可知加油量为：250−(100−40)=190；故答案为2；190；(2)y=100−80×0.25x=−20x+100；(3)由于速度相同，因此每小时耗油量也是相同的，设此时油箱剩余油量y与行驶时间x的解析式为y=kx+b，把k=−20代入，得到y=−20x+b，再把(2,250)代入，得b=290，所以y=−20x+290，当y=10时，x=14，所以14×80=1120km，因此该车从出发到现在已经跑了1120km，用时14h．解析：此题主要考查了一次函数的应用以及待定系数法求一次函数解析式等知识，根据已知图象获取正确信息是解题关键．(1)由图象可以直接看出汽车行驶两小时后加油，先计算汽车2小时耗油量，再结合函数图象可计算加油量；(2)根据每百公里耗油量约为25L ，可知每公里耗油0.25L ，根据余油量=出发前油箱油量−耗油量列出函数表达式即可；(3)由于速度相同，因此每小时耗油量也是相同的，可知k 不变，设加油后的函数为y =−20x +b ，代入(2,250)求出b 的值，然后计算剩余油量为10时的行驶时间，计算行驶路程即可．22.答案：解：由题意得{7a +b +21×0.8=117a +11b +0.8=106，设张老师家6用水量为x ，当用量为30时水费为：17×2.+13×4.292元，92%=184元， 由题意：172.234.2+6(x −30)+.x ≤194， ∴老师家六月的用水量超过3吨， 解得：{=2.2b =42，张老师月份最多用水41吨．解析：根据表格收标准，及张45两用水量、水费，可得出程组，解出可； 先判断用量超过30吨，继而再费超过94，可出不等式，解出即．本题考查了元一次方程组及元一次不等式的识答的键是细审题，将实际问题转为数学模型求解．23.答案：解：(1)如图1中，在y = 34 x +6中，令y =0，得x =−8；令x =0，得y =6∴A(−8,0)，B(0,6)， ∴OA =8，OB =6，过C 作CH ⊥y 轴于H ，则∠BCH +∠CBH =90°， ∵BC ⊥AB ，∴∠ABO +∠CBH =90°， ∴∠BCH =∠ABO ，又∠BHC =∠AOB =90°，BC =AB ，∴△BHC≌△AOB(AAS)，∴HC=OB=6，BH=OA=8，OH=8−6=2，∴C(6,−2)．(2)如图2中，设射线AD交CF于G．∵BC⊥AB，BC=AB，∴∠BAC=45°∵EF⊥AC，∴∠AFE=45°∴△BDF是等腰直角三角形，∴BD=BF，又∠ABD=∠CBF=90°，AB=CB∴△ABD≌△CBF(SAS)，∴∠BAD=∠BCF，∵∠BDA=∠CDG，∴∠CGD=∠ABD=90°，即AD⊥CF，∵OA=8，OB=6，∴AB= √62+82=10，∴BC=10，∴BF=BD=5，∴PF 2−PC 2=( PG 2+FG 2 )−( PG 2+CG 2 )=FG 2−CG 2=( DF 2−DG 2 )−( DC 2−DG 2 )=DF 2−DC 2=DF 2−BD 2=BF 2=25(3)如图3中，连接BM，BQ，过B作BK⊥QM延长线于点K，延长MA交QC于点T，可得正方形ABCT．∵MN=BN，∴∠NMB=∠NBM，∵BK⊥QK，NM⊥QK，∴BK//MN，∴∠KBM=∠BMN，∴∠KBM=∠MBA，∵MB=MB，∠K=∠BAM=90°∴△BKM≌△BAM(ASA)，∴BA=BK=BC，MK=MA，∴Rt△BKQ≌Rt△BCQ(HL)，∴QK=QC，设AM=a，则QK=QC=6a，在Rt△QMT中，MQ=5a，MT=a+10，QT=6a−10，勾股定理可得a=103，∵tan∠MNA=tan∠QMT=tan∠BAO=34，∴QT=10，MQ=503，MT=403∴MN//x轴，MQ//y轴，作PS⊥MQ于点S，∴S△PMQ=12MQ⋅PS，设MQ与x轴交于点I，Rt△MAI中，AI=2，作AL⊥PS于点L，得矩形ALSI，∴PS =PL +LS =t +10，∴S △PMQ =12×503×(t +10)，∴s =253t +2503．解析：(1)过C 作CH ⊥y 轴于H ，则∠BCH +∠CBH =90°，证明△BHC≌△AOB(AAS)即可解决问题．(2)(2)如图2中，设射线AD 交CF 于G.证明△ABD≌△CBF(SAS)，利用勾股定理解决问题即可．(3)如图3中，连接BM ，BQ ，过B 作BK ⊥QM 延长线于点K ，延长MA 交QC 于点T ，可得正方形ABCT.证明△BKM≌△BAM(ASA)，推出BA =BK =BC ，MK =MA ，证明Rt △BKQ≌Rt △BCQ(HL)，推出QK =QC ，设AM =a ，则QK =QC =6a ，在Rt △QMT 中，MQ =5a ，MT =a +10，QT =6a −10，勾股定理可得a =103，由tan∠MNA =tan∠QMT =tan∠BAO =34，推出QT =10，MQ =503，MT =403，作PS ⊥MQ 于点S ，根据S △PMQ =12MQ ⋅PS ，计算即可．本题属于一次函数综合题，考查了全等三角形的判定和性质，等腰直角三角形的判定和性质，勾股定理，正方形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造全等三角形解决问题，学会利用参数构建方程解决问题，属于中考压轴题．。
2020-2021学年四川省成都市双流中学实验学校八年级(上)月考数学试卷(12月份) (解析版)
2020-2021学年四川省成都市双流中学实验学校八年级第一学期月考数学试卷（12月份）一、选择题（共10小题，每题3分，共30分）.1．下列实数中，属于无理数的是（）A．0B．3.14C．D．2．使代数式有意义的x的取值范围是（）A．x≥﹣1B．x＞﹣1C．x≥1D．x＞13．已知A，B两点在y＝2x+1上，A的坐标为（1，m），B的坐标为（3，n），则（）A．m＝n B．m＜n C．m＞n D．无法确定4．在平面直角坐标系中，一次函数y＝kx﹣3（k＜0）的图象大致是（）A．B．C．D．5．在平面直角坐标系xOy中，点P（x，y）在第二象限，且点P到横轴的距离等于3，到纵轴的距离等于4，则点P坐标是（）A．（﹣3，4）B．（3，﹣4）C．（﹣4，3）D．（4，﹣3）6．将函数y＝﹣4x的图象沿y轴向下平移2个单位后，所得到的函数图象对应的函数表达式（）A．y＝﹣4x+2B．y＝﹣6x C．y＝﹣4x﹣2D．y＝﹣2x7．学习了《数据的分析》后，小王同学对其学习小组内甲、乙、丙、丁四名同学的三次数学单元考试成绩的平均分（）、方差（s2）统计如下表，则数学成绩最好、最稳定的同学是（）甲乙丙丁平均分（）1009510095方差（s2）0.890.89 1.01 1.01A．甲B．乙C．丙D．丁8．如图所示，数轴上点A所表示的数为a，则a的值是（）A．+1B．C．﹣1D．﹣+19．某公司去年的利润（总产值﹣总支出）为200万元．今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元．如果去年的总产值x万元、总支出y 万元，则下列方程组正确的是（）A．B．C．D．10．如图所示，边长分别为1和2的两个正方形靠在一起，其中一边在同一水平线上．大正方形保持不动，小正方形沿该水平线自左向右匀速运动，设运动时间为t，大正方形内去掉小正方形重叠部分后的面积为s，那么s与t的大致图象应为（）A．B．C．D．二、填空题（本大题共4小题，每小题4分，共16分）11．比较大小：2；﹣5﹣5．12．已知：如图，∠1＝∠2＝∠3＝55°，则∠4的度数是．13．如图所示，一根长为7cm的吸管放在一个圆柱形杯中，测得杯的内部底面直径为3cm，高为4cm，则吸管露出在杯外面的最短长度为cm．14．如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组的解是．三、解答题（本大题共6小题，共54分）15．计算：（1）×﹣（1﹣）2；（2）（π﹣2020）0+6﹣|5﹣|﹣（）﹣2．16．解方程组：．17．为了提高学生阅读能力，“双中实验校”倡议八年级学生利用双休日加强课外阅读，为了解同学们阅读的情况，学校随机抽查了部分同学周末阅读时间，并且得到数据绘制了不完整的统计图，根据图中信息回答下列问题：（1）将条形统计图补充完整：被调查的学生周末阅读时间众数是小时，中位数是小时．（2）计算被调查学生阅读时间的平均数．（3）我校八年级共有1200人，试估计周末阅读时间不低于1.5小时的人数．18．某旅馆的客房有三人间和两人间两种，三人间每人每天25元，两人间每人每天35元，一个50人的旅游团到该旅馆住宿，租住了若干客房，且每个客房正好住满，一天花去住宿费1510元，两种客房各租住多少间？19．如图，在平面直角坐标系xOy中，直线y＝﹣x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．（1）求AB的长；（2）求点C和点D的坐标；（3）y轴上是否存在一点P，使得S△PAB＝S△OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．20．在等腰Rt△ABC中，∠ABC＝90°，AB＝BC．（1）如图1，D为线段BC的延长线上一点，连接AD，过点B作BE⊥AD，已知AB＝8，AD＝17，求CD和BE的长．（2）如图2，点F是线段AC上一点，连接BF，过点B作BG⊥AC于点G，过点C作CH⊥BF于点H，连接GH．①若＝，AC＝5，求S△BCH的值．②求证：CH﹣BH＝HC．四、填空题（本大题共5小题，每小题4分，共20分）21．若（a﹣2）+3y b﹣2＝2是关于x，y的二元一次方程，则a﹣b＝．22．已知关于x，y的二元一次方程组的解满足x﹣y＝3，则m的值为23．如图，已知直线上l：y＝x，过点A（0，1）作y轴的垂线交直线l于点B，过点B 作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线的垂线交轴于点A2；按此作法继续下去，则A1的坐标为，A2020的坐标．24．如图，已知a，b，c分别Rt△ABC是的三条边长，∠C＝90°，我们把关于x的形如y ＝x+的一次函数称为“勾股一次函数”．若点P（1，）在“勾股一次函数”的图象上，且Rt△ABC的面积是10，则c的值是．25．如图，已知x轴上一点A（4，0），B为y轴上的一动点，连接AB，以B为直角顶点，AB为腰作等腰直角△ABC，连接OC，则AC+OC的最小值是．五、解答题（本大题共3小题，共30分）26．甲、乙两个仓库要向A、B两地运送水泥，已知甲库可调出水泥100吨，乙库可调出水泥80吨；A地需水泥70吨，B地需水泥110吨，两仓库到A、B两地的路程和运费如下表：路程（千米）运费（元/吨•千米）甲库乙库甲库乙库A地20151212B地2520108（1）设甲库运往A地水泥x吨，求总运费y（元）关于x（吨）的函数关系式及x的取值范围；（2）当甲、乙两个仓库各运往A、B两地水泥多少吨时总运费最少？最少运费是多少？27．已知：直线m∥n，点A，B分别是直线m，n上任意两点，在直线m上取一点C，使AC＝AB，连接BC，在直线BC上任取一点E，作∠AEF＝∠BAC，EF交直线n于点F．（1）如图1，当点E在线段BC上，目∠BFE＝20°时，求∠BAE的度数．（2）若点E是线段BC上任意一点，求证：EF＝AE．（3）如图2，当点E在线段BC的延长线上时，若∠BAC＝90°，请判断线段EF与AE 的数量关系，并说明理由．28．如图，直线y＝kx+k分别交x轴、y轴于点A，C，直线BC过点C交x轴于点B，且OA＝OC，∠CBA＝45°，点P是直线BC上的一点．（1）求直线BC的解析式；（2）若动点P从点B出发沿射线BC方向匀速运动，速度为个单位长度/秒，连接AP，设△PAC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，并写出t的取值范围；（3）若点Q是直线AC上且位于第三象限图象上的一个动点，点M是y轴上的一个动点，当以点B、M、Q为顶点的三角形为等腰直角三角形时，求点Q和点M的坐标．参考答案一、选择题（共10小题，每题3分，共30分）.1．下列实数中，属于无理数的是（）A．0B．3.14C．D．【分析】根据无限不循环小数叫无理数，可得答案．解：A.0是整数，属于有理数；B.3.14是有限小数，属于有理数；C.是分数，属于有理数；D.是无理数．故选：D．2．使代数式有意义的x的取值范围是（）A．x≥﹣1B．x＞﹣1C．x≥1D．x＞1【分析】根据二次根式的被开方数是非负数列出不等式，解不等式得到答案．解：使代数式有意义，则x﹣1≥0，解得，x≥1，故选：C．3．已知A，B两点在y＝2x+1上，A的坐标为（1，m），B的坐标为（3，n），则（）A．m＝n B．m＜n C．m＞n D．无法确定【分析】利用一次函数图象上点的坐标特征可得出m，n的值，比较后即可得出结论．解：∵点A（1，m），B（3，n）在y＝2x+1上，∴m＝3，n＝7．∵3＜7，∴m＜n．故选：B．4．在平面直角坐标系中，一次函数y＝kx﹣3（k＜0）的图象大致是（）A．B．C．D．【分析】根据题目中的函数解析式和一次函数的性质，可以得到该函数图象经过哪几个象限，本题得以解决．解：∵一次函数y＝kx﹣3（k＜0），b＝﹣3，∴该函数图象经过第二、三、四象限，故选：C．5．在平面直角坐标系xOy中，点P（x，y）在第二象限，且点P到横轴的距离等于3，到纵轴的距离等于4，则点P坐标是（）A．（﹣3，4）B．（3，﹣4）C．（﹣4，3）D．（4，﹣3）【分析】P在第二象限，那么点P的横纵坐标的符号为负，正；进而根据P到x轴的距离为纵坐标的绝对值．到y轴的距离为横坐标的绝对值判断出具体坐标．解：∵点P在第二象限，且第二象限内的点横坐标小于0，纵坐标大于0；∴点P的横坐标小于0，纵坐标大于0∵点P到x轴的距离等于3，到y轴的距离等于4，∴点P的坐标是（﹣4，3）．故选：C．6．将函数y＝﹣4x的图象沿y轴向下平移2个单位后，所得到的函数图象对应的函数表达式（）A．y＝﹣4x+2B．y＝﹣6x C．y＝﹣4x﹣2D．y＝﹣2x【分析】直接利用一次函数平移规律，“上加下减”得出即可．解：将函数y＝﹣4x的图象沿y轴向下平移2个单位后，所得图象对应的函数关系式为：y＝﹣4x﹣2．故选：C．7．学习了《数据的分析》后，小王同学对其学习小组内甲、乙、丙、丁四名同学的三次数学单元考试成绩的平均分（）、方差（s2）统计如下表，则数学成绩最好、最稳定的同学是（）甲乙丙丁平均分（）1009510095方差（s2）0.890.89 1.01 1.01A．甲B．乙C．丙D．丁【分析】此题有两个要求：①成绩较好，②最稳定．于是应选平均数大、方差小的运动员参赛．解：由于甲的平均数较大且方差较小，故选甲．故选：A．8．如图所示，数轴上点A所表示的数为a，则a的值是（）A．+1B．C．﹣1D．﹣+1【分析】根据勾股定理，可得圆的半径，根据圆的性质，可得答案．解：如图，在Rt△BCD中，由勾股定理，得BD＝＝＝，由圆的性质，得AD＝BD＝，1﹣a＝，∴a＝1﹣，故选：D．9．某公司去年的利润（总产值﹣总支出）为200万元．今年总产值比去年增加了20%，总支出比去年减少了10%，今年的利润为780万元．如果去年的总产值x万元、总支出y 万元，则下列方程组正确的是（）A．B．C．D．【分析】根据：①去年总产值﹣去年总支出＝200，②今年总产值﹣今年总支出＝780，可列方程组．解：设去年的总产值x万元、总支出y万元，根据题意，可列方程：，故选：A．10．如图所示，边长分别为1和2的两个正方形靠在一起，其中一边在同一水平线上．大正方形保持不动，小正方形沿该水平线自左向右匀速运动，设运动时间为t，大正方形内去掉小正方形重叠部分后的面积为s，那么s与t的大致图象应为（）A．B．C．D．【分析】根据题意和函数图象可以得到各个过程中S随着t的变化如何变化，注意选项A 和选项D中的区别是一个变化比较大，一个变化比较小，这个可以根据两个正方形的面积进行判断正误．解：由题意可得，小正方形的面积为：1×1＝1，大正方形的面积为：2×2＝4，∴刚开始小正方形从左向右运动，到小正方形正好完全进入大正方形的过程中，S随t的增大而减小，面积由4减小到3；当小正方形刚好完全进入大正方形到一边刚好要出大正方形的过程中，S随t的增大不变，一直是S＝3，从小正方形刚好出大正方形到完全出大正方形的过程中，S随t的增大而增大，S由3增加到4，故选项A、B、C不符合题意，选项D符合题意，故选：D．二、填空题（本大题共4小题，每小题4分，共16分）11．比较大小：＜2；﹣5＜﹣5．【分析】根据算术平方根估算大小，然后利用实数的大小比较法则进行比较．解：∵，∴，∵，∴5＞5，∴﹣5＜﹣5．故答案为：＜，＜．12．已知：如图，∠1＝∠2＝∠3＝55°，则∠4的度数是125°．【分析】由∠1＝∠2及对顶角相等可得出∠1＝∠5，利用“同位角相等，两直线平行”可得出l1∥l2，利用“两直线平行，同旁内角互补”可求出∠6的度数，再利用对顶角相等可得出∠4的度数．解：给各角标上序号，如图所示．∵∠1＝∠2，∠2＝∠5，∴∠1＝∠5，∴l1∥l2，∴∠3+∠6＝180°．∵∠3＝55°，∴∠6＝180°﹣55°＝125°，∴∠4＝∠6＝125°．故答案为：125°．13．如图所示，一根长为7cm的吸管放在一个圆柱形杯中，测得杯的内部底面直径为3cm，高为4cm，则吸管露出在杯外面的最短长度为2cm．【分析】吸管露出杯口外的长度最少，即在杯内最长，可用勾股定理解答．解：设在杯里部分长为xcm，则有：x2＝32+42，解得：x＝5，所以露在外面最短的长度为7cm﹣5cm＝2cm，故吸管露出杯口外的最短长度是2cm，故答案为：2．14．如图，已知函数y＝x+1和y＝ax+3图象交于点P，点P的横坐标为1，则关于x，y的方程组的解是．【分析】先把x＝1代入y＝x+1，得出y＝2，则两个一次函数的交点P的坐标为（1，2）；那么交点坐标同时满足两个函数的解析式，而所求的方程组正好是由两个函数的解析式所构成，因此两函数的交点坐标即为方程组的解．解：把x＝1代入y＝x+1，得出y＝2，函数y＝x+1和y＝ax+3的图象交于点P（1，2），即x＝1，y＝2同时满足两个一次函数的解析式．所以关于x，y的方程组的解是．故答案为．三、解答题（本大题共6小题，共54分）15．计算：（1）×﹣（1﹣）2；（2）（π﹣2020）0+6﹣|5﹣|﹣（）﹣2．【分析】（1）根据二次根式的乘法法则和完全平分公式计算；（2）利用零指数幂、负整数指数幂和绝对值的意义计算．解：（1）原式＝﹣（1﹣2+3）＝2﹣4+2＝4﹣4；（2）原式＝1+2+5﹣3﹣4＝2﹣．16．解方程组：．【分析】方程组利用加减消元法求出解即可．解：，①×3得：6x﹣3y＝9③，②+③得：7x＝7，解得：x＝1，将x＝1代入①得：2﹣y＝3，解得：y＝﹣1，则方程组的解为．17．为了提高学生阅读能力，“双中实验校”倡议八年级学生利用双休日加强课外阅读，为了解同学们阅读的情况，学校随机抽查了部分同学周末阅读时间，并且得到数据绘制了不完整的统计图，根据图中信息回答下列问题：（1）将条形统计图补充完整：被调查的学生周末阅读时间众数是 1.5小时，中位数是 1.5小时．（2）计算被调查学生阅读时间的平均数．（3）我校八年级共有1200人，试估计周末阅读时间不低于1.5小时的人数．【分析】（1）根据众数，中位数的定义解决问题即可．（2）根据平均数的定义求解即可．（3）用样本估计总体的思想解决问题即可．解：（1）由题意可得，本次调查的学生数为：30÷30%＝100（人），阅读时间1.5小时的学生数为：100﹣12﹣30﹣18＝40（人），补全的条形统计图如图所示：由补全的条形统计图可知，抽查的学生阅读时间的众数是1.5小时，中位数是1.5小时．故答案为：1.5；1.5．（2）所有被调查同学的平均阅读时间为：（小时），即所有被调查同学的平均阅读时间为1.32小时．（3）不低于1.5小时所占比例；，∴1200×58%＝696（人），故我校八年级阅读不低于1.5小时的人数696人．18．某旅馆的客房有三人间和两人间两种，三人间每人每天25元，两人间每人每天35元，一个50人的旅游团到该旅馆住宿，租住了若干客房，且每个客房正好住满，一天花去住宿费1510元，两种客房各租住多少间？【分析】设租住三人间x间，租住两人间y间，就可以得出3x+2y＝50，3×25x+2×35y ＝1510，由这两个方程构成方程组求出其解就可以得出结论．解：设租住三人间x间，租住两人间y间，由题意，得，解得：．答：租住三人间8间，租住两人13间．19．如图，在平面直角坐标系xOy中，直线y＝﹣x+4与x轴、y轴分别交于点A、点B，点D在y轴的负半轴上，若将△DAB沿直线AD折叠，点B恰好落在x轴正半轴上的点C处．（1）求AB的长；（2）求点C和点D的坐标；（3）y轴上是否存在一点P，使得S△PAB＝S△OCD？若存在，直接写出点P的坐标；若不存在，请说明理由．【分析】（1）先求得点A和点B的坐标，则可得到OA、OB的长，然后依据勾股定理可求得AB的长，（2）依据翻折的性质可得到AC的长，于是可求得OC的长，从而可得到点C的坐标；设OD＝x，则CD＝DB＝x+4．，Rt△OCD中，依据勾股定理可求得x的值，从而可得到点D（0，﹣6）．（3）先求得S△PAB的值，然后依据三角形的面积公式可求得BP的长，从而可得到点P 的坐标．解：（1）令x＝0得：y＝4，∴B（0，4）．∴OB＝4令y＝0得：0＝﹣x+4，解得：x＝3，∴A（3，0）．∴OA＝3．在Rt△OAB中，AB＝＝5．（2）∵AC＝AB＝5，∴OC＝OA+AC＝3+5＝8，∴C（8，0）．设OD＝x，则CD＝DB＝x+4．在Rt△OCD中，DC2＝OD2+OC2，即（x+4）2＝x2+82，解得：x＝6，∴D（0，﹣6）．（3）存在，理由如下：∵S△PAB＝S△OCD，∴S△PAB＝××6×8＝12．∵点P在y轴上，S△PAB＝12，∴BP•OA＝12，即×3BP＝12，解得：BP＝8，∴P点的坐标为（0，12）或（0，﹣4）．20．在等腰Rt△ABC中，∠ABC＝90°，AB＝BC．（1）如图1，D为线段BC的延长线上一点，连接AD，过点B作BE⊥AD，已知AB＝8，AD＝17，求CD和BE的长．（2）如图2，点F是线段AC上一点，连接BF，过点B作BG⊥AC于点G，过点C作CH⊥BF于点H，连接GH．①若＝，AC＝5，求S△BCH的值．②求证：CH﹣BH＝HC．【分析】（1）先利用勾股定理求出BD，CD，再利用S△ABD＝•AB•BD＝•AD•BE，求出BE，即可解决问题；（2）①如图2中，设BH＝x，CH＝2x，利用勾股定理可得x，求出BH，CH可得结论；②如图3，在CH上截取CM＝BH，连接GM，证明△GCM≌△GBH，根据线段的差可得结论．解：（1）在Rt△ABD中，AB＝8，AD＝17，∠ABC＝90°，∴，∵AB＝BC＝8，∴CD＝BD﹣BC＝15﹣8＝7，∵．∴BE＝＝＝．（2）①∵AB＝BC，∠ABC＝90°，∴，∴BC＝5，∵，设BH＝x，则HC＝2x，在Rt△BCH中，BC2＝BH2+HC2＝5x2，∴5x2＝52，∴，∴，∴．②在CH上截取CM＝BH，连接GM，∵AB＝BC，BG⊥AC，∠ABC＝90°，∴BG＝AG＝CG，∵BH⊥CH，∴∠BHC＝∠BGC＝90°，由8字模型倒角得∠GCM＝∠GBH，在△GCM和△GBH中，，∴△GCM≌△GBH（SAS），∴CM＝CH，∠CGM＝∠BGH，∴∠CGM+∠BGM＝∠BGH+∠BGM＝90°，∴∠HGM＝90°，∴△HGM是等腰直角三角形，∴，∴，∴．四、填空题（本大题共5小题，每小题4分，共20分）21．若（a﹣2）+3y b﹣2＝2是关于x，y的二元一次方程，则a﹣b＝﹣5．【分析】根据二元一次方程的定义得到且a﹣2≠0，联立方程组并解答．解：依题意得且a﹣2≠0，解得，则a﹣b＝﹣2﹣3＝﹣5．故答案为：﹣5．22．已知关于x，y的二元一次方程组的解满足x﹣y＝3，则m的值为1【分析】②﹣①得到x﹣y＝4﹣m，代入x﹣y＝3中计算即可求出m的值．解：，②﹣①得：x﹣y＝4﹣m，∵x﹣y＝3，∴4﹣m＝3，解得：m＝1，故答案为：123．如图，已知直线上l：y＝x，过点A（0，1）作y轴的垂线交直线l于点B，过点B 作直线l的垂线交y轴于点A1；过点A1作y轴的垂线交直线l于点B1，过点B1作直线的垂线交轴于点A2；按此作法继续下去，则A1的坐标为（0，4），A2020的坐标（0，24040）．【分析】根据所给直线解析式可得l与x轴的夹角，进而根据所给条件依次得到点A1，A2的坐标，通过相应规律得到A2020坐标即可．解：∵直线l的解析式为上，当y＝1，时，代入上式x＝，即AB＝，AO＝1，∴tan∠AOB＝＝，∴∠AOB＝60°，∵A（0，1），AB⊥y轴，∴OB＝2，∵A1B⊥l，∴OA1＝4，∴A1（0，4），同理可得A2（0，16）...A n（0，22n），∴A2020的纵坐标为24040，∴A2021（0，24040），故答案为：A2020（0，24040）．24．如图，已知a，b，c分别Rt△ABC是的三条边长，∠C＝90°，我们把关于x的形如y ＝x+的一次函数称为“勾股一次函数”．若点P（1，）在“勾股一次函数”的图象上，且Rt△ABC的面积是10，则c的值是．【分析】依据题意得到三个关系式：，ab＝20，a2+b2＝c2，运用完全平方公式即可得到c的值．解：∵点在“勾股一次函数”乌的图象上，∴把代入得，，即，∵a，b，c分别是Rt△ABC的三条边长，∠C＝90°，Rt△ABC的面积为10，∴，a2+b2＝c2，故ab＝20，∴（a+b）2﹣2ab＝c2，∴，∴，解得：，故答案为：．25．如图，已知x轴上一点A（4，0），B为y轴上的一动点，连接AB，以B为直角顶点，AB为腰作等腰直角△ABC，连接OC，则AC+OC的最小值是4．【分析】过C作CH⊥y轴于H，根据等腰直角三角形，的性质得到AB＝BC，∠ABC＝90°．根据全等三角形的性质得到OB＝HC，OA＝BH．设B点坐标为（0，n），得到OB＝HC＝n，推出点C在直线y＝x+4上．设直线y＝x+4与x轴交于点P，与y轴交于点Q，令y＝0，得到P（﹣4，0），Q（0，4），过O点作直线y＝x+4的对称点M，连结PM，AM，CM，根据轴对称的性质得到PO＝PM，CO＝CM，∠OPQ＝∠MPQ＝45°，求得M点坐标为（﹣4，4）．当且仅当A，M，C三点共线时，AC+OC取得最小值，根据勾股定理即可得到结论．解：过C作CH⊥y轴于H，∴△ABC是等腰直角三角形，∴AB＝BC，∠ABC＝90°．∵∠AOB＝∠CHB＝90°，∴∠OBA+∠OAB＝90°，∠0BA+∠HBC＝90°，∴∠OAB＝∠HBC，在△AOB和△BHC中，∴△AOB≌△BHC（AAS），∴OB＝HC，OA＝BH．∵A点坐标为（4，0），∵OA＝4，∴BH＝4，设B点坐标为（0，n），∴OB＝HC＝n，∴OH＝OB+BH＝4+n，∴C点坐标为（n，4+n），∴点C在直线y＝x+4上．设直线y＝x+4与x轴交于点P，与y轴交于点Q，令y＝0，x+4＝0，解得x＝﹣4，令x＝0，y＝4，∴P（﹣4，0），Q（0，4），∴OP＝OQ＝4．∵∠POQ＝90°，∴∠OPQ＝45°，过O点作直线y＝x+4的对称点M，连结PM，AM，CM，由对称性可知，PO＝PM，CO＝CM，∠OPQ＝∠MPQ＝45°，∴∠MPO＝90°，∴M点坐标为（﹣4，4）．∵AC+OC＝AC+CM≥AM，∴当且仅当A，M，C三点共线时，AC+OC取得最小值，∴AC+OC的最小值即为线段AM的长度．∴，∴AC+OC的最小值为．故答案为：．五、解答题（本大题共3小题，共30分）26．甲、乙两个仓库要向A、B两地运送水泥，已知甲库可调出水泥100吨，乙库可调出水泥80吨；A地需水泥70吨，B地需水泥110吨，两仓库到A、B两地的路程和运费如下表：路程（千米）运费（元/吨•千米）甲库乙库甲库乙库A地20151212B地2520108（1）设甲库运往A地水泥x吨，求总运费y（元）关于x（吨）的函数关系式及x的取值范围；（2）当甲、乙两个仓库各运往A、B两地水泥多少吨时总运费最少？最少运费是多少？【分析】（1）由甲库运往A地水泥x吨，根据题意首先求得甲库运往B地水泥（100﹣x）吨，乙库运往A地水泥（70﹣x）吨，乙库运往B地水泥（10+x）吨，然后根据表格求得总运费y（元）关于x（吨）的函数关系式；（2）根据（1）中的一次函数解析式的增减性，即可知当x＝70时，总运费y最省，然后代入求解即可求得最省的总运费．解：（1）设甲库运往A地水泥x吨，依题意得y＝12×20x+10×25×（100﹣x）+12×15×（70﹣x）+8×20×（10+x）＝﹣30x+39200 （0≤x≤70）（2）上述一次函数中k＝﹣30＜0∴y的值随x的增大而减小，∴x＝70时，总运费y最少，最少的总运费为37100元．27．已知：直线m∥n，点A，B分别是直线m，n上任意两点，在直线m上取一点C，使AC＝AB，连接BC，在直线BC上任取一点E，作∠AEF＝∠BAC，EF交直线n于点F．（1）如图1，当点E在线段BC上，目∠BFE＝20°时，求∠BAE的度数．（2）若点E是线段BC上任意一点，求证：EF＝AE．（3）如图2，当点E在线段BC的延长线上时，若∠BAC＝90°，请判断线段EF与AE 的数量关系，并说明理由．【分析】（1）由三角形的内角和定理可求解；（2）由“AAS”可证△EMF≌△EBA，可得EF＝AE；（3）由“SAS”可证△ABE≌△NBE，可得AE＝EN，∠EAB＝∠ENB，由补角的性质可证EF＝EN＝AE．【解答】证明：（1）如图1，设AB与EF交于点O，∵m∥n，∴∠BAC＝∠ABF，∵∠BAC＝∠ABF，∴∠AEF＝∠ABF，∵∠AOE＝∠BOF，∠OAE＝180°﹣∠AEF﹣∠AOE，∠BFE＝180°﹣∠ABF﹣∠BOF，∴∠OAE＝∠BFE＝20°．（2）如图1﹣1，以E为圆心，BE为半径画弧交直线n于点M，连接EM，∴EM＝EB，∴∠EMB＝∠EBM，∵m∥n，∴∠ACB＝∠EBM，∵AC＝AB，∴∠ACB＝∠ABC，∴∠EMF＝∠ABC，由（1）可知，∠EAB＝∠EFB，在△EMF和△EBA中，，∴△EMF≌△EBA（AAS），∴EF＝AE．（3）EF＝AE，理由如下：如图2，在BF上截取BN＝AB，连接EN，∴AB＝AC，∴∠ACB＝∠ABC，∵m∥n，∴∠ACB＝∠NBC，∴∠ABC＝∠NBC，在△ABE和△NBE中，，∴△ABE≌△NBE（SAS），∴AE＝EN，∠EAB＝∠ENB，∵∠AEF＝∠BAC＝90°，∠BAC＝∠ABF＝90°，∴∠EAB+∠EFB＝180°，∵∠ENB+∠ENF＝180°，∴∠EFB＝∠ENF，∴EF＝EN，∴EF＝AE．28．如图，直线y＝kx+k分别交x轴、y轴于点A，C，直线BC过点C交x轴于点B，且OA＝OC，∠CBA＝45°，点P是直线BC上的一点．（1）求直线BC的解析式；（2）若动点P从点B出发沿射线BC方向匀速运动，速度为个单位长度/秒，连接AP，设△PAC的面积为S，点P的运动时间为t秒，求S与t之间的函数关系式，并写出t的取值范围；（3）若点Q是直线AC上且位于第三象限图象上的一个动点，点M是y轴上的一个动点，当以点B、M、Q为顶点的三角形为等腰直角三角形时，求点Q和点M的坐标．【分析】（1）点A（﹣1，0），且OA＝OC，则点C（0，3），则k＝3，∠CBA＝45°，则OB＝OC＝3，即可求解；（2）利用S＝S△ABC﹣S△ABP或S＝S△ABP﹣S△ABC，即可求解；（3）分∠BMQ＝90°、∠MQB＝90°、∠QBM＝90°三种情况，分别求解即可．解：（1）直线y＝kx+k分别交x轴、y轴于点A，C，则点A（﹣1，0），且OA＝OC，则点C（0，3），则k＝3，故直线AC的表达式为：y＝3x+3，∵∠CBA＝45°，∴OB＝OC＝3，∴点B（3，0），∵点C（0，3）、点B（3，0），则直线BC的表达式为：y＝﹣x+3；（2）当点P在线段BC时，过点P作PH⊥x轴于点H，∵∠CBA＝45°，PH＝PB sin45°＝t×＝t，S＝S△ABC﹣S△ABP＝×BA×（OC﹣PH）＝4×（3﹣t）＝6﹣2t，（0≤t≤3）；当点P在y轴右侧的射线BC上时，同理可得：S＝S△ABP﹣S△ABC＝2t﹣6，（t＞3）；故S＝；（3）设点M（0，m），点Q（n，3n+3），①如图2（左侧图），当∠BMQ＝90°时，（点M在x轴上方），分别过点Q、P作y轴的平行线QG、BH，过点M作x轴的平行线分别交GQ、BH于点G、H，∵∠GMQ+∠MQG＝90°，∠GMQ+∠HMB＝90°，∴∠HMB＝∠GQM，∠MHB＝∠QGM＝90°，MB＝MQ，∴△MHB≌△QGM（AAS），∴GQ＝MH，BH＝GM，即：m＝﹣n，m﹣3n﹣3＝3，解得：m＝，n＝﹣；故点M（0，）、点Q（﹣，﹣）；同理当点M在x轴下方时，3n+3﹣m＝3且﹣m＝﹣n，解得：m＝n＝0（舍去）；②当∠MQB＝90°时，同理可得：﹣n＝﹣3n﹣3，3n+3﹣m＝3﹣n，解得：m＝﹣6，n＝﹣，故点M（0，﹣6）、点Q（﹣，﹣）；③当∠QBM＝90°时，同理可得：﹣3n﹣3＝3，m＝3﹣n解得：m＝5，n＝﹣2，点M（0，5）、点Q（﹣2，﹣3）；综上，M（0，）、Q（﹣，﹣）或M（0，﹣6）、Q（﹣，﹣）或M（0，5）点Q（﹣2，﹣3）．。
郑中国际学校2020-2021学年上期八年级月考试题数学试卷(定稿)
郑中国际学校2020—2021学年上期八年级月考试题数学试卷（满分：100分，时长：90分钟）一、选择题（每题2分，共20分）1.在下列各数()，，，，，，1415.35333.0-982-30 0，，6.1010010001…(1之间逐次增加一个0)中，无理数的个数是（ ）A ．1B ．2C ．3D ．42.若一个数的立方根等于这个数的算术平方根，则这个数是（ ）A ．0B ．0和1C ．1D ．±1和03.满足下列条件的△ABC ，不是直角三角形的是（ ）A ．b 2=c 2﹣a 2B ．a ：b ：c=3：4：5C ．∠C=∠A ﹣∠BD ．∠A ：∠B ：∠C=12：13：154.直角三角形斜边的平方等于两直角边乘积的2倍，这个直角三角形有一个锐角是（ ）A.15°B.30°C.45°D.75°5. 132202）. Ａ．6到7之间 Ｂ．7到8之间Ｃ．8到9之间 Ｄ．9到10之间 6.下列说法正确的是（ ）A.若a a -=2，则a<0B.0,2>=a a a 则若C ．4284b a b a =D ．5的平方根是57.已知点M 在第四象限内到x 轴的距离为3，到y 轴距离为2，则点M 的坐标为（ ）A.（2，3）B.（2，－3）C.（3，2）D.不能确定8.如果x x -+-91有意义，那么代数式2)9(1-+-x x 的值为（ ）A ．8B ．±8C ．与x 的值无关D ．无法确定9.如果m 是任意实数，则点P （m-1，m+3）一定不在（ ）A.第一象限B.第二象限C.第三象限D.第四象限10.如图所示，A （-3，0）、B （0，1）分别为x 轴、y 轴上的点，△ABC 为等边三角形，点P （3，a ）在第一象限内，且满足2S △ABP =S △ABC ，则a 的值为( )A.47 B.2 C.3 D.2 二、填空题（每题3分，共30分）11.16的平方根是 ．12.若代数式21--x x 有意义，则x 的取值范围是 . 13.比较31-3 31(填“＜”“＞”“=”） 14.已知55+的小数部分是a ，5-5的整数部分是b ，则a+b 的值为 ．15.已知16x x +=（0＜x ＜1），则1x x -= ． 16.如图是由“赵爽弦图”变化得到的，它由八个全等的直角三角形拼接而成，记图中正方形ABCD 、正方形EFGH 、正方形MNPQ 的面积分别为S 1、S 2、S 3．若S 1+S 2+S 3＝60，则S 2的值是 .17.如图，把一张长方形纸片ABCD 折叠起来，使其对角顶点A 与C 重合，D 与G 重合，若长方形的长BC 为8，宽AB 为4，求=GED ΔS .18.在平面直角坐标系中，已知A （4，1），B （0，3），请在x 轴上找一点P ，使得点P 到点A 、B 两点距离之和最小，则点P 的坐标是 ．19.如图，在平面直角坐标系中，A （1，1），B （﹣1，1），C （﹣1，﹣2），D （1，﹣2）．把一条长为2012个单位长度且没有弹性的细线（线的粗细忽略不计）的一端固定在点A 处，并按A ﹣B ﹣C ﹣D ﹣A ﹣…的规律紧绕在四边形ABCD 的边上，则细线另一端所在位置的点的坐标是 .20.在平面直角坐标系中，已知A （2，-2），在y 轴上确定点P ，使△AOP 为等腰三角形，则符合条件的点P 坐标为 ．第16题 第17题 第19题三. 解答题（共50分）21.(16分)计算(1)22)3(25)6(-+-- (2)1221348⨯⨯÷(3)3248312123÷⎪⎪⎭⎫ ⎝⎛+- (4)()()220202019)21(814322322----+22．（8分）(1)已知23211a a -=-,求a 的值;(2)若√1−2x 3与√3x −53互为相反数,求√x -1的平方根.23．(6分)如图,△ABC在正方形网格中，若点A的坐标为(0，3)，点B的坐标为(－3，－1)，按要求回答下列问题：(1)在图中建立正确的平面直角坐标系；(2)根据所建立的直角坐标系,写出点C的坐标；(3)作出△ABC关于x轴的对称图形△A'B'C'(不用写作法)．24.（6分）如图,已知A(－4,0),B(6,0),C(2,4),D(－3,2).(1)求四边形ABCD的面积;(2)在y轴上找一点P,使△APB的面积等于四边形ABCD面积的一半,求点P的坐标.25．（6分）勾股定理神秘而美妙，它的证法多样，其巧妙各有不同，其中的“面积法”给了小聪以灵感，他惊喜的发现，当两个全等的直角三角形如图1或图2摆放时，都可以用“面积法”来证明，下面是小聪利用图1证明勾股定理的过程：将两个全等的直角三角形按图1所示摆放，其中∠DAB=90°，求证：a2+b2=c2证明：连结DB，过点D作BC边上的高DF，则DF =EC=b﹣a．∵S四边形ADCB=S△ACD+S△ABC=b2+ab．又∵S四边形ADCB=S△ADB+S△DCB=c2+a（b﹣a）∴b2+ab=c2+a（b﹣a）∴a2+b2=c2请参照上述证法，利用图2完成下面的证明．将两个全等的直角三角形按图2所示摆放，其中∠DAB=90°．求证：a2+b2=c2。
2020-2021学年黑龙江哈工大附中八年级(上)月考数学试卷(12月份)(五四学制)(附答案详解)
2020-2021学年黑龙江省哈尔滨工大附中八年级（上）月考数学试卷（12月份）（五四学制）1.在x2y ，−m2−1π，3xy10，m+nm，b−c5+a，x2−1x−1中，分式有( )A. 2个B. 3个C. 4个D. 5个2.下列计算正确的是( )A. a2⋅a3=a6B. (−a−1b−3)−2=−a2b6C. (a−b)4=−(b−a)4D. 3a−3=3a33.下列因式分解正确的是( )A. a2−2=(a+4)(a−4)B. 25x2−1=(5x−1)(1−5x)C. 4−12x+9x2=(−3x+2)2D. x2−27=(x−3)(x−9)4.已知x2+mx+25是完全平方式，则m的值为( )A. 10B. ±10C. 20D. ±205.如图，在Rt△ABC中，∠ACB=90∘，∠A=60∘，CD是斜边AB上的高，若AD=3cm，则斜边AB的长为( )A. 3cmB. 6cmC. 9cmD. 12cm6.如果把分式x+y5xy中的x、y都扩大到原来的5倍，则分式的值( )A. 扩大到原来的25倍B. 扩大到原来的5倍C. 不变D. 缩小到原来的157.甲、乙两人同时从A地出发，骑自行车行30千米到B地，甲比乙每小时少走3千米，结果乙先到40分钟．若设乙每小时走x千米，则可列方程( )A. 30x−3−30x=23B. 30x−30x+3=23C. 30x+3−30x=23D. 30x−30x−3=238.如图，在四边形ABCD中，∠A=58∘，∠C=100∘，连接BD，E是AD上一点，连接BE，∠EBD=36∘.若点A，C分别在线段BE，BD的中垂线上，则∠ADC的度数为( )A. 75∘B. 65∘C. 63∘D. 61∘9.当n是整数时，两个连续奇数的平方差(2n+1)2−(2n−1)2是_____的倍数．( )A. 3B. 5C. 7D. 810.下列说法正确的是( )A. 任何数的0次幕都等于1B. 等腰三角形是关于一条边上的中线成轴对称的图形C. 等腰三角形两腰上的高相等D. 如果三角形一条边上的中线等于这条边的一半，则这个三角形是等腰直角三角形11.−0.00000015用科学记数法表示为______.12.分解因式3x(m+n)−6y(m+n)=______.13.当x为______时，分式3x−62x+1的值为0.14.分式12x2y2，13xy3的最简公分母是______.15.若a+b=7，ab=12，则a2−ab+b2的值是______.16.已知1x −1y=3，则5x+xy−5yx−xy−y的值为______.17.A、B两种机器人都被用来搬运化工原料，A型机器人比B型机器人每小时多搬运30kg，A型机器人搬运900kg所用的时间与B型机器人搬运600kg所用时间相等，两种机器人每小时分别搬运多少化工原料？若设A型机器人每小时搬运xkg，可列方程：______.18.如图，在△ABC中，∠ABC=50∘，∠ACB=80∘，延长CB至D，使DB=BA，延长BC至E，使CE=AC，则∠DAE=______.19.△ABC中，AB的垂直平分线与∠ACB的外角平分线交于点D，DE垂直直线BC于E，若AC=7，CE=2，则BC的长是______.20.如图，在△ABC中，点D在边BC上，点E在边AC上，AB=AE，连接AD，DE，过点A作AF⊥BC于点F，若∠BAC=∠ADE=60∘，BD=5，DE=3，则BF的长是______.21.计算．(1)(2m2n−2)2⋅3m−3n3；(2)a−bb÷(a−2ab−b2a).22.解下列方程：(1)3x−2−x2−x=−2(2)x+1x−1−4x2−1=123.先化简，再求值：x2−1x2−2x+1÷x+1x−1⋅1−x1+x，其中x=12.24.如图，BF⊥AC于F，CE⊥AB于E，BF交CE于点D，BD=CD，连接AD.(1)求证：AD平分∠BAC；(2)当BD=AD，∠BAD=30∘时，直接写出图中度数是120∘的角．25.哈工大图书馆新进一批图书，张强和李明两位图书员负责整理图书，已知张强3小时清点完这批图书的一半，李明加入清点另一半图书的工作，两人合作1.2小时清点完另一半图书；(1)如果李明单独清点这批图书需要几小时？(2)经过一段时间，这批图书破损严重，哈工大图书馆决定在致知书店购买甲、乙两种图书共120本进行补充，该书店每本甲种图书的售价为25元，进价20元；每本乙种图书的售价为40元，进价30元．如果此批图书全部售出后所得利润不低于950元，那么该书店至少需要卖出乙种图书多少本？26.在等边三角形ABC中，D为直线BC上一点，连接AD，在射线BC上取一点E，使AD=DE，连接AE，在射线AC上取点F，连接EF.(1)如图1，当点D在BC边上，∠CAD=2∠FEC时，求∠AEF的度数；(2)在(1)的条件下，求证：AD=AF；(3)在(1)的条件下，如图2，若点D在BC延长线上，过点A作AK⊥EF交EF的延长线于点K，过点F作BE的平行线交AK于点H，连接DH，若FH=2，DH=4，求线段AF的长度．27.如图，在平面直角坐标系中，点A(t,0)为x轴负半轴上一动点，等腰△ABC的底边AC在x轴上，AB=BC，∠ACB=30∘，点B(t+3,√3)在第一象限．(1)如图1，求点C的坐标；(用含t的代数式表示)(2)如图2，在y轴负半轴上分别取点D和点E，连接BD，CD，BE，BE与CD交于点F，若BD=DE=AB，请猜想∠BFC的度数是否发生变化？若变化，请说明理由；若不变，请求出∠BFC的度数；(3)如图3，在(2)的条件下，过点D作DG//BE交x轴于点G，连接AD，若AD=DF，OA=5OG，2请求出点A的坐标．答案和解析1.【答案】C【解析】解：在x 2y ，−m2−1π，3xy10，m+nm，b−c5+a，x2−1x−1中，x2y，m+nm，b−c5+a，x2−1x−1的分母中含有字母，是分式，共有4个．故选：C.利用分式定义可得答案．此题主要考查了分式的定义，关键是掌握分式的分母必须含有字母，而分子可以含字母，也可以不含字母．2.【答案】D【解析】解：A.根据同底数幂的乘法，a2⋅a3=a5，那么A错误，故A不符合题意．B.根据积的乘方与幂的乘方，(−a−1b−3)−2=(−1)−2a2b6=a2b6，那么B错误，故B不符合题意．C.根据乘方的定义，(a−b)4=[−(b−a)]4=(b−a)4，那么C错误，故C不符合题意．D.根据负整数指数幂，3a−3=3a3，那么D正确，故D符合题意．故选：D.根据同底数幂的乘方、积的乘方与幂的乘方、负整数指数幂解决此题．本题主要考查同底数幂的乘方、积的乘方与幂的乘方、负整数指数幂，熟练掌握同底数幂的乘方、积的乘方与幂的乘方、负整数指数幂是解决本题的关键．3.【答案】C【解析】解：A.根据平方差公式，a2−2=(a+√2)(a−√2)，那么A错误，故A不符合题意．B.根据平方差公式，25x2−1=(5x+1)(5x−1)，那么B错误，故B不符合题意．C.根据完全平方公式，4−12x+9x2=(−3x+2)2，那么C正确，故C符合题意．D.根据平方差公式，x2−27=(x+3√3)(x−3√3)，那么D错误，故D不符合题意．故选：C.根据平方差公式以及完全平方公式解决此题．本题主要考查因式分分解，熟练掌握公式法进行因式分解是解决本题的关键．4.【答案】B【解析】解：∵x2+mx+25是完全平方式，∴m=±10，故选：B.利用完全平方公式的结构特征判断即可确定出m的值．此题考查了完全平方式，熟练掌握完全平方公式是解本题的关键．5.【答案】D【解析】【分析】本题考查了三角形内角和定理和含30∘角的直角三角形的性质，能根据含30∘角的直角三角形的性质得出AC=2AD和AB=2AC是解此题的关键，注意：在直角三角形中，如果有一个角等于30∘，那么这个角所对的直角边等于斜边的一半．根据三角形内角和定理求出∠ACD=30∘，∠B=30∘，根据含30∘角的直角三角形的性质得出AC= 2AD，AB=2AC，代入求出即可【解答】解：∵CD是斜边AB上的高，∴∠ADC=90∘，∵∠A=60∘，∠ACB=90∘，∴∠B=180∘−∠ACB−∠A=30∘，∠ACD=180∘−∠ADC−∠A=30∘，∵AD=3cm，∴AC=2AD=6cm，∴AB=2AC=12cm，故选：D..6.【答案】D【解析】解：5x+5y5×5x×5y=5(x+y) 125xy=x+y 25xy=x+y5xy ⋅1 5，所以如果把分式x+y5xy 中的x、y都扩大到原来的5倍，那么分式的值缩小原来的15，故选：D.先根据题意列出算式，再根据分式的基本性质进行化简，最后根据求出的结果得出选项即可．本题考查了分式的基本性质，能正确根据分式的基本性质进行化简是解此题的关键．7.【答案】A【解析】解：设乙每小时走x千米，则甲每小时走(x−3)千米，由题意得：30 x−3−30x=23，故选：A.首先根据题意可设乙每小时走x千米，则甲每小时走(x−3)千米，根据题意可得等量关系：甲走30千米的时间-乙走30千米的时间=40分钟，由等量关系列出方程即可．此题主要考查了由实际问题抽象出分式方程，关键是根据题意，找出等量关系，设出未知数，列出方程．8.【答案】B【解析】解：∵点A，C分别在线段BE，BD的中垂线上，∴AE=AB，BC=DC.∵∠A=58∘，∠C=100∘，∴∠ABE=180∘−58∘2=61∘，∠CBD=180∘−100∘2=40∘.∵∠EBD=36∘，∴∠ABC=∠ABE+∠EBD+∠CBD=61∘+36∘+40∘=137∘，∴∠ADC=360∘−∠A−∠C−∠ABC=360∘−58∘−100∘−137∘=65∘.故答案为：65∘.故选B.先根据线段垂直平分线的性质得出AE=AB，BC=DC，再由∠A=58∘，∠C=100∘得出∠ABE及∠CBD的度数，根据∠EBD=36∘得出∠ABC的度数，由四边形内角和定理即可得出结论．本题考查的是线段垂直平分线的性质，熟知线段垂直平分线上任意一点，到线段两端点的距离相等是解答此题的关键．9.【答案】D【解析】解：∵(2n+1)2−(2n−1)2=[(2n+1)+(2n−1)][(2n+1)−(2n−1)]=4n×2=8n.又∵n是整数，∴(2n+1)2−(2n−1)2是8的倍数．故选：D.利用平方差公式把式子(2n+1)2−(2n−1)2进行因式分解后，得到结果再进行判断．本题考查了平方差公式的应用，熟练掌握平方差公式的结构特点是解题的关键．10.【答案】C【解析】解：A.任何非零数的0次幕都等于1，原说法错误，故本选项不合题意；B.等腰三角形是关于底边上的中线所在的直线成轴对称的图形，原说法错误，故本选项不合题意；C.等腰三角形两腰上的高相等，说法正确，故本选项符合题意；D.如果三角形一条边上的中线等于这条边的一半，则这个三角形是直角三角形，原说法错误，故本选项不合题意；故选：C.选项A根据零指数幂的定义判断即可；选项B、C根据等腰三角形的性质判断即可；选项D根据直角三角形的判定方法判断即可．本题考查了等腰三角形，轴对称图形以及直角三角形斜边上的中线，掌握等腰三角形的性质是解答本题的关键．11.【答案】−1.5×10−7【解析】解：−0.00000015=−1.5×10−7.故答案为：−1.5×10−7.绝对值小于1的负数也可以利用科学记数法表示，一般形式为a×10−n，与较大数的科学记数法不同的是其所使用的是负整数指数幂，指数由原数左边起第一个不为零的数字前面的0的个数所决定．本题考查用科学记数法表示较小的数，一般形式为a×10−n，其中1≤|a|<10，n为由原数左边起第一个不为零的数字前面的0的个数所决定．12.【答案】3(m+n)(x−2y)【解析】解：原式=3(m+n)(x−2y)，故答案为：3(m+n)(x−2y)原式提取公因式即可得到结果．此题考查了因式分解-提公因式法，熟练掌握提取公因式的方法是解本题的关键．13.【答案】2【解析】【分析】本题考查的是分式的值为零的条件，即分式值为零的条件是分子等于零且分母不等于零．根据分式的值为0的条件进行解答即可．【解答】解：∵3x−6=0，∴x=2，当x=2时，2x+1≠0.∴当x=2时，分式的值是0.故答案为2.14.【答案】6x2y3【解析】解：分式12x2y2，13xy3的最简公分母是6x2y3.故答案为：6x2y3.根据最简公分母的概念解答即可．本题考查了最简公分母：通常取各分母系数的最小公倍数与字母因式的最高次幂的积作公分母，这样的公分母叫做最简公分母．15.【答案】13【解析】解：∵a+b=7，ab=12，∴原式=(a+b)2−3ab=49−36=13，故答案为：13原式利用完全平方公式变形，将各自的值代入计算即可求出值．此题考查了完全平方公式，熟练掌握完全平方公式是解本题的关键．16.【答案】72【解析】解：∵1x −1y=y−xxy=3，∴y−x=3xy，即x−y=−3xy，则5x+xy−5yx−xy−y =5(x−y)+xy(x−y)−xy=−15xy+xy−3xy−xy=−14xy−4xy=72.故答案为：72将已知等式左边通分并利用同分母分式的减法法则计算，得出x−y=−3xy，将所求式子分子第一、三项结合，提取5分解因式，分母第一、三项结合，把x−y=−3xy代入化简，即可求出值．此题考查了分式的化简求值，分式的加减运算关键是通分，通分的关键是找最简公分母；分式的乘除运算关键是约分，约分的关键是找公因式，约分时，分式的分子分母出现多项式，应将多项式分解因式后再约分．17.【答案】900x =600x−30【解析】解：设A种机器人每小时搬运x千克化工原料，则B种机器人每小时搬运(x−30)千克化工原料，由题意得900 x =600x−30，故答案为：900x =600x−30.设A种机器人每小时搬运x千克化工原料，则B种机器人每小时搬运(x−30)千克化工原料，根据A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等建立方程求出其解就可以得出结论．本题考查了列分时方程解实际问题的运用，分式方程的解法的运用，解答时根据A型机器人搬运900kg原料所用时间与B型机器人搬运600kg原料所用时间相等建立方程是关键．18.【答案】115∘【解析】解：∵∠ABC=50∘，DB=BA，∴∠D=∠DAB=12∠ABC=25∘；同理可得∠CAE=12∠ACB=40∘；∵在△ABC中，∠ABC=50∘，∠ACB=80∘，∴∠BAC=50∘，∴∠DAE=∠DAB+∠BAC+∠CAE=115∘，故答案为：115∘由∠ABC=50∘，DB=BA，据三角形外角性质可得∠D=∠DAB=12∠ABC=25∘；同理可得∠CAE= 40∘；由三角形内角和定理可得∠BAC=50∘，即可得∠DAE的度数．此题考查等腰三角形的性质，关键是根据三角形内角和定理和三角形外角的性质解答．19.【答案】11或3【解析】解：如图，当点E在BC上时．过点D作DF⊥AC，交AC的延长线于F，连接AD=BD，∵AB的垂直平分线与∠ACB的外角平分线交于点D，∴AD=BD，DE=DF，在Rt△ADF和Rt△BDE中，{AD=BDDF=DE，∴Rt△ADF≌Rt△BDE(HL)，∴BE=AF，同理可得CE=CF，∴AF=7+2=9，∴BC=BE+CE=9+2=11，当点E在BC的延长线上时，如图，同理可得AF=BE=AC−CF=7−2=5，∴BC=BE−CE=5−2=3，综上：BC=11或3，故答案为：11或3.分点E在BC上或点E在BC的延长线上两种情形，分别利用HL证明Rt△ADF≌Rt△BDE，得BE=AF，同理可得CE=CF，从而解决问题．本题主要考查了线段垂直平分线的性质，角平分线的性质，全等三角形的判定与性质等知识，运用分类讨论思想是解题的关键．20.【答案】1【解析】解：延长DE至点G，使DE=AD，∵∠ADE=60∘，∴△ADG是等边三角形，∴∠DAG=∠BAC=60∘，AG=AD，∴∠BAD=∠EAG，在△BAD和△EAG中，{AB=AE∠BAD=∠EAG AD=AG，∴△BAD≌△EAG(SAS)，∴BD=EG=5，∠ADB=∠G=60∘，∴AD=DG=8，∵∠DAF=30∘，∴DF=12AD=4，∴BF=1，故答案为：1.延长DE至点G，使DE=AD，则△ADG是等边三角形，再利用SAS证明△BAD≌△EAG，得BD= EG=5，∠ADB=∠G=60∘，进而解决问题．本题主要考查了全等三角形的判定与性质，等边三角形的判定与性质，含30∘角的直角三角形的性质等知识，作辅助线构造全等三角形是解题的关键．21.【答案】解：(1)原式=4m4n−4⋅3m−3n3=12mn−1=12mn；(2)原式=a−bb ÷a2−(2ab−b2)a=a−bb⋅aa2−2ab+b2=a−bb⋅a(a−b)2=ab(a−b)=aab−b2.【解析】(1)先根据积的乘方与幂的乘方的运算法则得到原式=4m4n−4⋅3m−3n3，再进行同底数幂的乘法运算，然后把n−1化为1n即可；(2)先把括号内通分，再把括号内合并，接着把除法运算化为乘法运算，然后约分即可．本题考查了分式的混合运算：分式的混合运算，一般按常规运算顺序，但有时应先根据题目的特点，运用乘法的运算律进行灵活运算．也考查了幂的运算．22.【答案】解：(1)化为整式方程得：3=x =−2x +4，解得：x =13，经检验x =13是分式方程的解， 所以原方程的解是：x =13；(2)化为整式方程得：x 2+2x +1−4=x 2−1，解得：x =1，经检验x =1不是分式方程的解，所以原方程无解．【解析】(1)分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解；(2)分式方程去分母转化为整式方程，求出整式方程的解得到x 的值，经检验即可得到分式方程的解．此题考查了解分式方程，解分式方程的基本思想是“转化思想”，把分式方程转化为整式方程求解．解分式方程一定注意要验根．23.【答案】解：(x+1)(x−1)(x−1)2⋅x−1x+1⋅1−x 1+x =1−x 1+x ，当x =12时，原式=1−121+12=13. 【解析】先根据分式的混合运算法则化简，然后代入计算即可．本题考查分式的混合运算，解题的关键是记住分式的混合运算，先乘方，再乘除，然后加减，有括号的先算括号里面的．24.【答案】(1)证明：∵BF ⊥AC ，CE ⊥AB ，∴∠BED =∠DFC =90∘，在△BDE 和△CDF 中，{∠BED =∠CFD ∠BDE =∠CDF BD =CD，∴△BDE ≌△CDF(AAS)，∴DE =DF ，又∵BF ⊥AC ，CE ⊥AB ，∴AD 平分∠BAC ；(2)解：∵BD =AD ，∠BAD =30∘，∵AD平分∠BAC，∴∠BAD=∠CAD=30∘，∵BD=CD=AD，∴∠DAC=∠C=30∘，∵BF⊥AC，CE⊥AB，∴∠ADF=∠CDF=∠ADE=∠BDE=60∘，∴∠ADB=∠EDF=∠ADC=120∘.【解析】(1)由“AAS”可证△BDE≌△CDF，可得结论；(2)由等腰三角形的性质可得∠BAD=∠B=30∘，∠DAC=∠C=30∘，由余角的性质可得∠ADF=∠CDF=∠ADE=∠BDE=60∘，即可求解．本题考查了全等三角形的判定和性质，等腰三角形的性质，角平分线的性质等知识，证明三角形全等是解题的关键．25.【答案】解：(1)设李明单独清点这批图书需要x小时，根据题意得：1.22×3+1.2x=12，解得x=4，经检验，x=4是原方程的解，也符合题意，∴x=4，答：李明单独清点这批图书需要4小时；(2)设书店卖出乙种图书m本，根据题意得(25−20)(120−m)+(40−30)m≥950，解得m≥70，答：该书店至少需要卖出乙种图书70本．【解析】(1)设李明单独清点这批图书需要x小时，知李明1小时清点1x，根据张强3小时清点完这批图书的一半，可得张强1小时清点12×3=16，由两人合作1.2小时清点完另一半图书列方程可解得答案；(2)设书店卖出乙种图书m本，根据此批图书全部售出后所得利润不低于950元，列不等式可解得答案．本题考查分式方程和一元一次不等式的应用，解题的关键是读懂题意，列出方程和不等式．26.【答案】(1)解：∵AD=DE，∴∠AED=∠EAD，设∠CEF=α，∠AEF=β，∵AD=DE，∴∠AED=∠EAD=β−α，∴∠EAC=2α+β−α=α+β，∵△ABC是等边三角形，∴∠ACB=60∘=∠CAE+∠AEC=2β，∴β=30∘，∴∠AEF=30∘；(2)证明：延长EF交∠CDA的角平分线于点M，连接DF，AM，∵MD=MD，∠EDM=∠ADM，ED=AD，∴△EDM≌△ADM(SAS)，∴∠EMD=∠AMD，EM=AM，∴∠AEM=∠EAM=30∘，∴∠EMA=∠EMD=∠AMD=120∘，∵∠EAF+∠DEF=30∘，∠EAF+∠FAM=30∘，∴∠FAM=∠DEF，∴∠FAM=∠MAD，∴△FAM≌△DAM(ASA)，∴AF=AD；(3)如图2中，延长DH交EF于点Q，延长FH交AB的延长线于点J，连接DJ，交AK于点T，连接AQ.∵FJ//CB，∴∠AJF=∠ABC=60∘，∠AFJ=∠ACB=60∘，∵∠CAB=60∘，∴△AFJ是等边三角形，∴FJ=AF=AJ，∵AD=AF=DE，∴DE=FJ，DE//FJ，∴四边形DEFJ是平行四边形，∴QE//DJ，∵AK⊥FQ，∴AK⊥DJ，∵AD=AJ，∴AK垂直平分线段DJ，∴HD=JH，∴∠HDJ=∠HJD，∵FQ//DJ，∴∠HFQ=∠HJD，∠HQF=∠HDJ，∴∠HFQ=∠HQF，∴HF=HQ=2，∴DQ=DH+HQ=4+2=6，∴AF=AQ，∴∠FAK=∠KAQ，∵AD=AJ，AT⊥DJ，∴∠DAT=∠JAT，∴△DAF=∠QAJ，∴∠DAQ=∠CAB=60∘∴△ADQ是等边三角形，∴AD=DQ=6，∴AF=AD=6.【解析】(1)设∠CEF=α，∠AEF=β，则∠CAD=2∠FEC=2α，∠EAC=α+β，再由∠ACB=60∘= 2β，可求∠AEF；(2)延长EF交∠DCA的角平分线于点M，连接DF，AM，证明△EDM≌△ADM(SAS)，再证明△FAM≌△DAM(ASA)，即可求解；(3)如图2中，延长DH交EF于点Q，延长FH交AB的延长线于点J，连接DJ，交AK于点T，连接AQ.想办法证明FH=HQ，推出DQ=6，再证明△ADQ是等边三角形，可得结论．本题属于三角形综合题，考查了等边三角形的判定和性质，全等三角形的判定和性质，等腰三角形的性质，平行四边形的判定和性质等知识，解题的关键是学会添加常用辅助线，构造特殊四边形解决问题，属于中考压轴题．27.【答案】解：(1)如图1，过B作BD⊥x轴于点M，∵B(t+3,√3)，A(t,0)，∴AM=(t+3)−t=3，∵AB=BC，∴CM−AM=3，∴OC=OM+CM=t+3+3=t+6，∴C(t+6,0)；(2)如图2，连接AD，设∠DAC=α，∴∠BAD=∠DAC+∠BAC=α+30∘，∵AB=BD=DE，∴∠BDA=∠BAD=α+30∘，∠DEB=∠DBE，∵∠ADO=90∘−∠DAC=90∘−α，∴∠ODB=∠BDA−∠ODA=(α+30∘)−(90∘−α)=2α−60∘，∵∠DEB+∠DBE=∠ODB，∴2∠DBE=2α−60∘，∴∠DBE=α−30∘，∵BD=BC=AB，∠CBD=∠ABC−∠ABD=120∘−(120∘−2α)=2α，∴∠BDC=∠BCD=180∘−∠CBD2=180∘−2α2=90∘−α，∴∠BFC=∠DBE+∠BDC=(α+30∘)+(90∘−α)=60∘；(3)如图3，延长AD交BE于Q，作BR⊥y轴于R，作BW⊥AC于W，由(2)知：∠ADB=α+30∘，∠BDC=90∘−α，∠BFC=60∘，∴∠ADC=∠ADB+∠BDC=120∘，∠DFQ=∠BFC=60∘，∴∠FDQ=180∘−∠ADC=60∘，∴△DFQ是等边三角形，∴DF=DQ，∵AD=DF，∴AD=DQ，∵DG//BE，∴AGGT =ADDQ=1，∠ODG=∠DEB，∴GT=AG，∵BW//OE，∴∠TBW=∠DEB，∴∠ODG=∠TBW，∵∠BWT=∠DOG=90∘，∴△BWT∽△DOG，∴ODOG =BWTW，设OG=2a，则OA=5a，∴GT=AG=7a，∴AT=GT+AG=14a，OT=OG+GT=9a，∵AW=3，∴WT=AW−AT=3−14a，∴OD2a =√33−14a，∴OD=2√3a3−14a，∴OE=DE+OD=2√3+2√3a3−14a，ER=OE+OR=3√3+2√3a3−14a，∵OT//BR，∴△EOT∽△ERB，∴OTBR =OERE，∵BR=OW−OA=3−5a，∴9a3−5a =2√3+2√3a3−14a3√3+2√3a3−14a，化简得，490a 2−189a +18=0，∴(14a −3)⋅(35a −6)=0，∴a 1=314，a 2=635， 当a =314时，AT =14a =3=AW ，不符合题意，故舍去，∴a =635，∴OA =5a =67，∴A(−67,0).【解析】(1)过B 作BD ⊥x 轴于点D ，根据点A 、B 坐标可以计算线段OD ，AD 的长，再根据AB =BC ，所以DA =DC =3，即可解答；(2)连接AD ，设∠DAC =α，依次计算出∠ADO ，∠ADB ，进而求得∠ODB ，∠DBE ；表示出∠DBC ，进而表示出∠BDC ，进而求得结果；(3)延长AD 交BE 于Q ，作BR ⊥y 轴于R ，作BW ⊥AC 于W ，可证得△DFQ 是等边三角形，设OG =2a ，OA =5a ，进而得出GT =7a ，AT =14a ，TW =3−14a ，进而证明△BWT ∽△DOG ，进而表示出OD ，根据△EOT ∽△ERB ，列出比例式，从而求得a 的值，进一步得出结果．本题考查了等腰三角形的性质，等边三角形的判定和性质，相似三角形的判定和性质等知识，解决问题的关键是作辅助线，转化条件，发现图形的特殊性．。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
江苏省兴化市顾庄学区2020-2021学年八年级上学期12月月考抽测数学试题学校:___________姓名：___________班级：___________考号：___________一、单选题1．下列四个图形中轴对称图形的个数是（ ）A ．1B ．2C ．3D ．42．已知点P （0，a ）在y 轴的负半轴上，则点Q （﹣a 2﹣1，﹣a+1）在（ ） A ．第一象限B ．第二象限C ．第三象限D ．第四象限3．下列实数0，23π，其中，无理数共有（ ） A ．1个 B ．2个 C ．3个 D ．4个 4．下列等式正确的是（ ）A ．712=±B ．32=-C ．3=-D ．4=5．等腰三角形两边长分别是2 cm 和5 cm ，则这个三角形周长是（ ）A ．9 cmB ．12 cmC ．9 cm 或12 cmD ．14 cm6．6月1日起，我国将全面试行居民阶梯式电价，某市出台了实施细则，具体规定如下： 设用电量为a 度，当a ≤150时，电价为现行电价，每度0.51元；当150＜a ≤240时，在现行电价基础上，每度提高0.05元；当a ＞240时，在现行电价基础上，每度提高0.30元．设某户的月用电量为x （度），电费为y （元）．则y 与x 之间的函数关系的大致图像是（ ）A ．B ．C ．D ．二、填空题7．a的平方根是±3，那么a= ．8．函数y=x的取值范围是_____．9．已知点P(2a+b，b)与P1(8，﹣2)关于y轴对称，则a+b＝_____．10．近似数13.7万精确到_____位．11．已知一次函数的图象与直线y=﹣x+1平行，且过点（8，2），那么此一次函数的解析式为．12．已知在△ABC中，∠C＝90°，AC＝3，BC＝4，分别以AC、BC、AB为直径作半圆，如图所示，则阴影部分的面积是_____．13．在平面直角坐标系中，若点M（2，4）与点N（x，4）之间的距离是3，则x的值是_____．14．如图，在平面直角坐标系中，点P(﹣1，a)在直线y＝2x+2与直线y＝2x+4之间，则a的取值范围是_____．15．已知：如图△ABC中，∠B＝50°，∠C＝90°，在射线BA上找一点D，使△ACD为等腰三角形，则∠ACD的度数为_____．16．如图，已知直线AB与x轴交于点A（4，0）、与y轴交于点B（0，3），直线BD 与x轴交于点D，将直线AB沿直线BD翻折，点A恰好落在y轴上的C点，则直线BD对应的函数关系式为______ ．三、解答题17．计算：()2301(2018)312π-⎛⎫-+--+- ⎪⎝⎭. 18．求下列各式中x 的值：(1)2x 2－32＝0；(2)(x ＋4)3＋64＝0.19．已知2m+2的平方根是±4，3m+n+1的平方根是±5，求m+2n 的立方根．20．如图，已知 AB =DC ，AC =DB ，AC 和 DB 相交于点 O ． 求证：OB =OC ．21．如图，在一棵树CD 的10m 高处的B 点有两只猴子，它们都要到A 处池塘边喝水，其中一只猴子沿树爬下走到离树20m 处的池塘A 处，另一只猴子爬到树顶D 后直线跃入池塘的A 处．如果两只猴子所经过的路程相等，试问这棵树多高？22．（1）在网格中画ABC ，使AB 、BC 、AC （2）判断三角形的形状:_______________(直接填结论)．（3）求ABC 的面积．23．已知一次函数y=kx+b的图象经过点（﹣2，﹣4），且与正比例函数12y x的图象相交于点（4，a），求：（1）a的值；（2）k、b的值；（3）画出这两个函数图象，并求出它们与y轴相交得到的三角形的面积．24．某厂家在甲、乙两家商场销售同一商品所获得的利润分别为y甲，y乙（单位：元），y甲，y乙与销售数量x（单位：件）的函数关系如图所示，试根据图象解决下列问题：（1）分别求出y甲，y乙关于x的函数关系式；（2）现厂家分配该商品800件给甲商场，400件给乙商场，当甲、乙商场售完这批商品后，厂家可获得的总利润是多少元？25．已知等腰Rt△ABC中，∠BAC＝90°．点D从点B出发在线段BC移动，以AD为腰作等腰Rt△ADE，∠DAE＝90°．连接CE．⑴如图，求证：△ACE≌△ABD；⑵求证：BD2＋CD2＝2AD2；⑶若AB＝4，试问：△DCE的面积有没有最大值，如没有请说明理由，如有请求出最大值．26．一列快车从甲地驶往乙地，一列慢车从乙地驶往甲地，两车同时出发，设慢车行驶的时间为x(h)，两车之间的距离．．．．．．．为y(km)，图中的折线表示y与x之间的函数关系．根据图象进行以下探究：⑴请问甲乙两地的路程为；⑵求慢车和快车的速度；⑶求线段BC所表示的y与x之间的函数关系式，并写出自变量x的取值范围；⑷如果设慢车行驶的时间为x(h),快慢两车到乙地的距离分别为y1(km)、y2(km)，请在右图中画出y1、y2与x的函数图像．参考答案1．C【解析】【分析】根据轴对称图形的概念求解．【详解】解：根据轴对称图形的定义可知：第1，2，3个图形为轴对称图形，第4个图形不是轴对称图形，轴对称图共3个，故选：C．【点睛】本题考查了轴对称图形的概念，轴对称图形的关键是寻找对称轴，图形两部分沿对称轴折叠后可重合．2．B【分析】根据y轴负半轴上点的纵坐标是负数求出a的取值范围，再求出点Q的横坐标与纵坐标的正负情况，然后求解即可．【详解】解：∵点P（0，a）在y轴的负半轴上，∴a＜0，∴﹣a2﹣1＜0，﹣a+1＞0，∴点Q在第二象限．故选B．【点睛】本题考查了各象限内点的坐标的符号特征，记住各象限内点的坐标的符号是解决的关键，四个象限的符号特点分别是：第一象限（+，+）；第二象限（﹣，+）；第三象限（﹣，﹣）；第四象限（+，﹣）．3．B【分析】根据无理数的概念可判断出无理数的个数．【详解】，π.故选B.本题主要考查了无理数的定义，注意带根号的要开不尽方才是无理数，无限不循环小数为无理数．4．D【分析】原式各项利用立方根及算术平方根定义计算即可得到结果．【详解】A、原式=712，错误；B、原式=-（-32）=32，错误；C、原式没有意义，错误；D、原式=4，正确，故选D．【点睛】此题考查了立方根，以及算术平方根，熟练掌握各自的定义是解本题的关键．5．B【解析】当腰长是2 cm时，因为2+2<5，不符合三角形的三边关系，排除；当腰长是5 cm 时，因为5+5>2，符合三角形三边关系，此时周长是12 cm．故选B．6．D【分析】根据阶梯电价的收费标准知：电费随着用电量的增加而增加，而且用电量越大，增加的越快，据此可以得到答案．【详解】解：根据当a≤150时，电价为现行电价，每度0.51元；当150＜a≤240时，在现行电价基础上，每度提高0.05元；当a＞240时，在现行电价基础上，每度提高0.30元可知：电费随着用电量的增加而增加，而且用电量越大，增加的越快．故选：D．【点睛】本题考查的是实际生活中函数的图象变化，属于基础题．解决本题的主要方法是根据题意判断函数图象的大致走势，然后再下结论．【分析】利用平方根定义计算即可确定出a 的值．【详解】已知a 的平方根是±3，根据平方根定义可得a=9． 8．2x ≥【分析】根据被开方式是非负数列式求解即可.【详解】依题意，得20x -≥，解得：2x ≥，故答案为2x ≥．【点睛】本题考查了函数自变量的取值范围，函数有意义时字母的取值范围一般从几个方面考虑：①当函数解析式是整式时，字母可取全体实数；②当函数解析式是分式时，考虑分式的分母不能为0；③当函数解析式是二次根式时，被开方数为非负数．④对于实际问题中的函数关系式，自变量的取值除必须使表达式有意义外，还要保证实际问题有意义．9．﹣5．【解析】试题解析：由题意可得:282,a b b +=-⎧⎨=-⎩解得：32,a b =-⎧⎨=-⎩5.a b ∴+=-故答案为 5.-点睛：关于y 轴对称的点的特征：纵坐标不变，横坐标互为相反数.10．千．【分析】根据最后一个数所在的位置就是精确度，即可得出答案.近似数13.7万中的3，表示3万，是万位，因而13.7最后的数字7应是千位，则13.7万是精确到千位.故近似数13.7万是精确到千位.【点睛】本题考查的是近似数和有效数字，找准最后一位数所在的位置，并知道最后一位数所在的位置就是精确度是解决本题的关键.11．y=－x+10【解析】由函数的图象与直线y=-x+1平行，可得斜率，将点（8，2）代入即可人求解．解：设所求一次函数的解析式为y=kx+b，∵函数的图象与直线y=-x+1平行，∴k=-1，又过点（8，2），有2=-1×8+b，解得b=10，∴一次函数的解析式为y=-x+10，故答案为y=-x+10．12．6【分析】先利用勾股定理列式求出AB，再根据阴影部分面积等于以AC、BC为直径的两个半圆的面积加上直角三角形ABC的面积减去以AB为直径的半圆的面积，列式计算即可得解．【详解】解：∵在Rt△ABC中，∠ACB＝90°，∴AC2+ BC2＝AB2，∵BC＝4，AC＝3，∴AB＝5，S阴影＝直径为AC的半圆的面积＋直径为BC的半圆的面积＋S△ABC−直径为AB的半圆的面积＝12π（2AC）2＋12π（2BC）2＋12AC×BC−12π（2AB）2，。