高等数学ch12第九节
高等数学ch12_3_112.3.2 电子教案

而
xn
x
x
x
xn1 dx xn1 dx
dx
n1 n n1 0
0 n1
01 x
ln(1 x)
故
S 1
2
S(x)
x
xn
1
xn
2 n1 n 2x n3 n
内容小结
1. 求幂级数收敛域的方法 1) 对标准型幂级数
发散 .
收敛;
例2. 求下列幂级数的收敛域 : 规定: 0 ! = 1
解: (1)
1
R lim an lim n an1 n
n! 1
(n 1)!
所以收敛域为 ( , ) .
(2) R lim an
n an1
lim
n
n! (n 1)
!
所以级数仅在 x = 0 处收敛 .
n0n 1 x n0 n 1
1 x
x
0
xn
n0
dx
1 x
x1
0
1
x
dx
(0 x 1 及
)
S(x)
(0 x 1 及
)
而
x
=
0
时级数收敛于1,
lim
x0
ln
(1 x
x)
1
,
因此由和函数的连续性得:
S(x)
1 ln(1 x) , x [1,0) (0,1) x
an xn (为常数) x R1
n0
中国政法大学《高等数学》课件——第十二章

u 4 (sin t 1 sin 3t 1 sin 5t)
3
5
u
1
2 3
2
2
O
3
2
2
2
t
1
©
傅里叶(Fourier)级数
u 4 (sin t 1 sin 3t 1 sin 5t 1 sin 7t)
3
5
7
u
1
2 3
2
2
O
3
2
2
2
t
1
©
傅里叶(Fourier)级数
45
1 sin7t,
47
1 sin 9t,
49
©
傅里叶(Fourier)级数
u 4 sin t
u
1
2 3
O 3 2
t
2
2 1
2
2
©
傅里叶(Fourier)级数
u 4 (sin t 1 sin 3t)
3
u
1
2
3
2
2
O
3
2
2
2
t
1
©
傅里叶(Fourier)级数
2
©
傅里叶(Fourier)级数
例
将函数
x,
f (x)
x,
x 0 0 x
展开为傅氏级数.
解 所给函数在区间 [ , ]上满足狄氏充要条件,
傅里叶(Fourier)级数
例
函数f ( x)以2为周期,且 f
将 f (x) 展开为傅里叶级数.
(
x)
x, 0,
x 0, 0 x,
解 f (x) 的图象
y
高等数学同济第七版第十二章课后习题答案

…I I
半径为 I,收敛区间为(-1 J).
(4)lim %" = lim —= 0 ,故收敛半在为+8,收敛区间是(-8 , ♦ 8 ). …14 | …2 (门♦ I)
第十二童无穷级数
221
由此可知.对任意给定的正数£ .取正整数 A m 岫十,当〃 >投时,对一切正整数 p, 都有 S--
力 < £ ,按柯西收敛原理.该级数收敛•
(4)本题与(2)类同.因 4 =丁\ + (
故对 3/1 ♦ 1 \3n +2 3n + 3) 3〃 ♦ I An
% = + .不论/!取什么正整数.取 p = 〃时.就有 1〃.,・h1 =%八+U..2 ।…+
219
解(D 此级数为公比 g =-5 的等比级数.因|°| < 1 ,故该级数收敛.
(2)此级数的部分和
即该级数发散.
lim sA = + oc , 冬■一
(3)此级数的一股项% =*,有 要条 忖% = lim(y), = 1 ,不满足级数收敛的必
件,故该级数发散. (4)此级数为公比 4 二方的等比级数,因|q| > 1 ,故该级数发散. (5)此级数的一般项% =3.二注意到与£ 上分别是公比”;
•
・a
散,故各项乘;志的级数 Ej 也发放,由比较审敛法知原级数 s 二二■? 发散.
1 解法二 因=1,而 y 1 发故.故由极限形式的比较审敛法知原 … I 2 1n
级数发散 (2) u = Lt: >二而 f L 发散.由比较审敛法知原级数 ・
1 > n2 n n2 n Sf”
222
一• 《高等数学》(第七版)下册习咫全解
12-9 高等数学课件

yxkexQ m (x);
( 2 ) f ( x ) e x [ P l ( x ) cx o P n ( x ) s sx i ]n ,
y x k e x [ R m ( 1 ) ( x ) cx o R m ( 2 ) ( s x ) sx i ]n ;
x;
4、
y
C1e x
C
2e
x
1 10
cos
2
x
1 2
.
二 、 1 、 y 1 (11 5e 4 x ) 5 x ;
16
4
2 、 y [ 2 1 ( 1 1 ) x ]e x x 3 e x x 2 e x ;
e6 2e
6
2
3 、 y 1 sin 2 x 1 x (1 sin 2 x ) .
(1x4j)(c 2x ojssi2x n ) 39
1 x c2 x o 4 s s2 i x n ( 4 c2 x o 1 x s s2 i x ) j n , 3 9 93
所求非齐方程特解为 y1xco 2xs4si2n x,
3
9 (取实部)
原方程通解为 y C 1 cx o C 2 s sx i n 1 3 x c2 o x 9 4 s s2 ix .n
2pq0, 2p0,
可 Q (x 设 )xm (Q x ),yxm Q (x)ex;
(3) 若是特征方程的重根,
2pq0, 2p0,
可Q (设 x)x2Q m (x), yx2Q m (x)ex.
综上讨论
0 不是根
设 y x k e x Q m (x ), k 1 是单根,
2 是重根
注意 上述结论可推广到n阶常系数非齐次线性 微分方程(k是重根次数).
《高等数学(下册)》 第12章

n
0 时, (i ,i )si 的极限即为曲线形构件的质量,即 i 1
n
M
lim 0
i 1
(i
,i )si .
上述例子是通过“分割、近似、求和、取极限”的方法来计算密度不均匀的曲
线形构件质量,对该过程进行提炼,便可得到对弧长的曲线积分的概念.
12.1.1 对弧长的曲线积分的概念与性质
2.概念与性质
定义 设 L 为 xOy 面内的一条光滑曲线弧,函数 f (x ,y) 在 L 上有界.在 L 上用任
意的 点 M1 ,M2 , ,Mn1 把曲线弧 L 分 割成 n 个小 弧段,记第 i 个 小弧段的 长度为
si (i 1,2 , ,n) ,并在 si 上任取一点 (i ,i ) si ,作乘积 f (i ,i )si ,并作和
x y
(t) , (t) ,(
t
),
若(t) , (t) 在[ , ] 上具有一阶连续导数且不同时为零,则曲线积分 f (x ,y)ds 存在, L
且
f (x ,y)ds f [(t) , (t)] 2 (t) 2(t)dt ( ) .
L
(12-1)
由以上定理可知,在计算对弧长的曲线积分时,只要将被积表达式中的 x ,y ,ds 依
12.1.1 对弧长的曲线积分的概念与性质
1.引例——曲线形构件的质量 为了方便理解,曲线形构件可理解为一根弯曲的金属细丝.若曲线形构件为均 匀质体,即其线密度为常数,则构件的质量就等于线密度与构件长度的乘积.若构 件为非均匀质体,则不能直接用上述方法来计算.一般情况下,由于工艺制造的原 因,曲线形构件多为非均匀质体,因此,可认为曲线形构件的线密度是变量.
最后,要取得功 W 的精确值,只需对上述式子求极限即可,即
高等数学 课后习题答案第九章
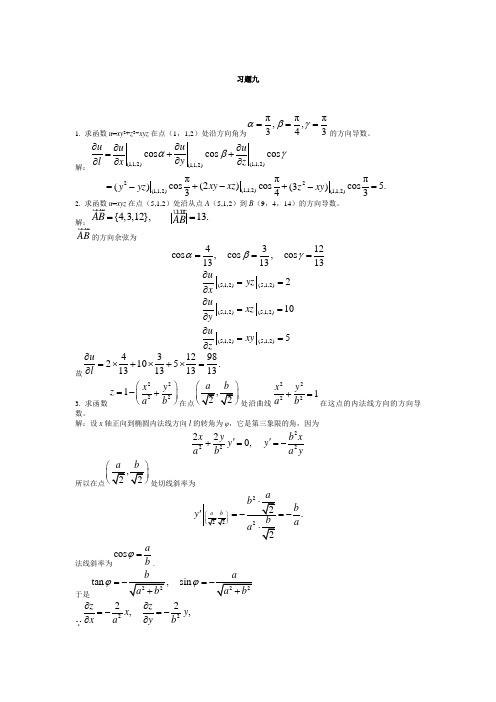
习题九1. 求函数u =xy 2+z 3-xyz 在点(1,1,2)处沿方向角为πππ,,343αβγ===的方向导数。
解:(1,1,2)(1,1,2)(1,1,2)cos cos cos u u u uy l x z αβγ∂∂∂∂=++∂∂∂∂22(1,1,2)(1,1,2)(1,1,2)πππcoscos cos 5.(2)()(3)343xy xz y yz z xy =++=---2. 求函数u =xyz 在点(5,1,2)处沿从点A (5,1,2)到B (9,4,14)的方向导数。
解:{4,3,12},13.AB AB ==AB的方向余弦为4312cos ,cos ,cos 131313αβγ=== (5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)(5,1,2)2105uyz x uxz yuxy z ∂==∂∂==∂∂==∂故4312982105.13131313u l∂=⨯+⨯+⨯=∂ 3. 求函数22221x y z a b ⎛⎫=-+ ⎪⎝⎭在点处沿曲线22221x y a b +=在这点的内法线方向的方向导数。
解:设x 轴正向到椭圆内法线方向l 的转角为φ,它是第三象限的角,因为2222220,x y b x y y a b a y ''+==-所以在点处切线斜率为2.b y a a '==-法线斜率为cos ab ϕ=.于是tan sin ϕϕ== ∵2222,,z z x y x a y b ∂∂=-=-∂∂∴2222zl a b⎛∂=--=∂⎝4.研究下列函数的极值:(1)z=x3+y3-3(x2+y2); (2)z=e2x(x+y2+2y);(3)z=(6x-x2)(4y-y2); (4)z=(x2+y2)22()e x y-+;(5)z=xy(a-x-y),a≠0.解:(1)解方程组22360360xyz x xz y y⎧=-=⎪⎨=-=⎪⎩得驻点为(0,0),(0,2),(2,0),(2,2).z xx=6x-6, z xy=0, z yy=6y-6在点(0,0)处,A=-6,B=0,C=-6,B2-AC=-36<0,且A<0,所以函数有极大值z(0,0)=0.在点(0,2)处,A=-6,B=0,C=6,B2-AC=36>0,所以(0,2)点不是极值点.在点(2,0)处,A=6,B=0,C=-6,B2-AC=36>0,所以(2,0)点不是极值点.在点(2,2)处,A=6,B=0,C=6,B2-AC=-36<0,且A>0,所以函数有极小值z(2,2)=-8.(2)解方程组222e(2241)02e(1)0xxxyz x y yz y⎧=+++=⎪⎨=+=⎪⎩得驻点为1,12⎛⎫-⎪⎝⎭.22224e(21)4e(1)2exxxxxyxyyz x y yz yz=+++=+=在点1,12⎛⎫-⎪⎝⎭处,A=2e,B=0,C=2e,B2-AC=-4e2<0,又A>0,所以函数有极小值e1,122z⎛⎫=--⎪⎝⎭. (3) 解方程组22(62)(4)0(6)(42)0xyz x y yz x x y⎧=--=⎪⎨=--=⎪⎩得驻点为(3,2),(0,0),(0,4),(6,0),(6,4).Z xx=-2(4y-y2),Z xy=4(3-x)(2-y)Z yy=-2(6x-x2)在点(3,2)处,A=-8,B=0,C=-18,B2-AC=-8×18<0,且A<0,所以函数有极大值z(3,2)=36. 在点(0,0)处,A=0,B=24,C=0,B2-AC>0,所以(0,0)点不是极值点.在点(0,4)处,A=0,B=-24,C=0,B2-AC>0,所以(0,4)不是极值点.在点(6,0)处,A=0,B=-24,C=0,B2-AC>0,所以(6,0)不是极值点.在点(6,4)处,A=0,B=24,C=0,B2-AC>0,所以(6,4)不是极值点.(4)解方程组2222()22()222e(1)02e(1)0x yx yx x yy x y-+-+⎧--=⎪⎨--=⎪⎩得驻点P0(0,0),及P(x0,y0),其中x02+y02=1,在点P0处有z=0,而当(x,y)≠(0,0)时,恒有z>0,故函数z在点P0处取得极小值z=0.再讨论函数z=u e-u由de(1)duzuu-=-,令ddzu=得u=1,当u>1时,ddzu<;当u<1时,ddzu>,由此可知,在满足x 02+y 02=1的点(x 0,y 0)的邻域内,不论是x 2+y 2>1或x 2+y 2<1,均有2222()1()e e x y z x y -+-=+≤.故函数z 在点(x 0,y 0)取得极大值z =e -1(5)解方程组(2)0(2)0x y z y a x y z x a y x =--=⎧⎨=--=⎪⎩ 得驻点为12(0,0),,33a a P P ⎛⎫⎪⎝⎭z xx =-2y , z xy =a -2x -2y , z yy =-2x .故z 的黑塞矩阵为222222ya x y H a x y x ---⎡⎤=⎢⎥---⎣⎦ 于是122033(),().0233aa a H P H P a a a ⎡⎤--⎢⎥⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥--⎢⎥⎣⎦ 易知H (P 1)不定,故P 1不是z 的极值点,H (P 2)当a <0时正定,故此时P 2是z 的极小值点,且3,2733a a a z ⎛⎫=⎪⎝⎭,H (P 2)当a >0时负定,故此时P 2是z 的极大值点,且3,2733a a a z ⎛⎫=⎪⎝⎭.5. 设2x 2+2y 2+z 2+8xz -z +8=0,确定函数z =z (x ,y ),研究其极值。
12高等数学课件详细

发散 .
例4.
判别级数
ln
n1
1
1 n2
的敛散性.
ln(1
1 n2
)
~
1 n2
解:
lim n2
n
ln
1
1 n2
lim
n
n
2
1 n2
1
根据比较审敛法的极限形式知 ln1
n1
1 n2
收敛 .
定理4 . 比值审敛法 ( D’ALEMBERT
判别法)
设 un 为正项级数, 且 lim n (1) 当 1 时, 级数收敛 ;
un1 un
,
则
(2) 当 1 或 时, 级数发散 .
(3) 当 1 时, 级数可能收敛可能发散 ;
说明: 当 lim un1 1 时,级数可能收敛也可能发散.
n un
例如, p – 级数
1 n1 n p
:
lim un1 n un
1
lim
.
事实上 , 假设调和级数收敛于 S , 则
lim (S2n Sn ) 0
n
但
S2n
Sn
1 n 1
1 n2
1 n3
1 n 1 2n 2n 2
矛盾! 所以假设不真 .
第二节 常数项级数的审敛法
一、正项级数及其审敛法 二、交错级数及其审敛法 三、绝对收敛与条件收敛
n1
un 也收敛 ;
n1
vn 也发散 .
n1
例1.
讨论
P
高等数学习题册 第十二章 参考答案

1第十二章 无穷级数第一节 常数项级数的概念与性质1.填空: (1)1+1(-1)n n n -.(2)__0__.(3)111+-n , _1_. (4)11+-n a a ,1a a -.(5) 收敛 ,12-s u .(6) 发散_. 2.根据级数收敛与发散的定义判断下列级数的敛散性,如果收敛,则求级数的和:(1)解:级数的部分和为...n s +++1-.因为lim 1)n n n s →∞→∞=-=+∞,即部分和数列不存在极限,所以原级数发散. (2)解:将级数的一般项进行分解得211111()(1)(1)2111n u n n n n n ===-+--+-, 所以,级数的部分和为111111111[()+()()...()]213243511n s n n =--+-++--+1111(1)221n n =+--+. 因为11113lim lim (1)2214n n n s n n →∞→∞=+--=+, 即部分和数列存在极限,且极限值为34,根据定义可得,原级数收敛,且收敛于34.(3)解: 因为lim lim sin 6n n n n u π→∞→∞=不存在,根据收敛级数的必要性条件可知,级数的一般项极限不为零,则原级数必定发散.3.判断下列级数的敛散性,如果收敛,则求级数的和: (1)解:这是一个公比为34-的等比级数,因为314-<,所以收敛.其和为13343171()4u s q-===----. (2)解:这是公比为32-的等比级数,因为3>12-,所以发散.(3)解:因为1lim lim=0100+1100n n n n u n →∞→∞=≠,根据收敛级数的2必要性条件可知,原级数发散. (4)解:因为级数123nnn ∞=∑是公比为23的等比级数,所以收敛,而级数1131=3n n n n∞∞==∑∑是发散级数,根据收敛级数的性质可知,原级数发散.(5)解:原级数的一般项ln (1)-ln n u n n =+,所以原级数的部分和(ln 2-ln1)(ln 3-ln 2)...[(ln(1)-ln ]n s n n =++++ln(1)-ln1ln(1)n n =+=+,因为lim limln(1)n n n s n →∞→∞=+不存在,所以原级数发散.(6)解:原级数变形为111[()()]32n n n ∞=+∑,因为级数11()3nn ∞=∑和11()2n n ∞=∑均为公比1q <的等比级数,所以原级数收敛. 其和为113321121132s =+=--.(7)解:因为313lim =3lim()3lim011+(1+)(1+)n nn n n n nn n n e n n→∞→∞→∞==≠,根据收敛级数的必要条件可知,原级数发散.第二节 常数项级数的审敛法1.填空: (1) 收敛 .(2) 发散 ; 收敛 ;可能收敛也可能发散 . (3)1k <;1k >时,1k =.(4)1p >;1p ≤时.(5)发散 . (6)可能发散也可能收敛 . 2.选择:(1)D .(2)C .(3)B .(4)C .3.用比较审敛法及其极限形式判断下列级数的敛散性:(1)解:因为222+1++2lim lim 11+2n n n n n n n n→∞→∞==,而级数11n n∞=∑发散,根据比较审敛法的极限形式(或者极限审敛法),原级数一定发散.(2)解:因为2211(1)(21)limlim 1(1)(21)2n n n n n n n n →∞→∞++==++,而3 级数211n n∞=∑收敛,根据比较审敛的极限形式(或者极限审敛法),原级数一定收敛.(3)解:因为0sin 22n n ππ≤≤,而12n n π∞=∑是公比为12的等比级数,根据比较审敛法,原级数一定收敛.(4)解:当>1a 时,110<1n na a ≤+而11n n a∞=∑是公比为1<1a 的等比级数,根据比较审敛法,级数111nn a ∞=+∑一定收敛; 当0<1a <时,因为1lim=101nn a →∞≠+,根据级数收敛的必要性条件,级数111nn a ∞=+∑发散; 当=1a 时,原级数即112n ∞=∑,发散. (5*)解:因为ln (1+)(0,1)x x x x <≠-<<+∞,所以111ln =ln(1+)n n n n +<,即原级数为正项级数; 同时,111ln =ln ln(1)111n n n n n n +-=-->+++, 则:21111110<ln 1(1)n n n n n n n n+-<-=<++, 而211n n∞=∑收敛,所以原级数也收敛. 4.用比值审敛法判断下列级数的敛散性:(1)解:2+122(1)1113lim lim(1)1333n n n nn n n →∞→∞+=+=<,根据比值审敛法,原级数收敛.(2)解:135(2+1)2+1(+1)!limlim 2>1135(21)+1!n n n n n n n n →∞→∞⋅⋅⋅⋅⋅==⋅⋅⋅⋅⋅-,根据比值审敛法,原级数发散.4(3)解:+2+2+1+1(+1)tan+1122limlim 12tan 22n n n n n n n n n n ππππ→∞→∞=⋅=<,根据比值审敛法,原级数收敛.(4)解:1+12(1)!12(+1)lim 2lim()2lim <1112!(1+)n n n n n n n nnn n n n e n n n +→∞→∞→∞+===+, 根据比值审敛法,原级数收敛.5.用根值审敛法判别下列级数的敛散性:(1)解:1lim 12+12n n n n →∞=<,根据根值审敛法,原级数收敛. (2)解:1lim 01ln(+1)n n n →∞=<,根据根值审敛法,原级数收敛. (3)解:n b a, 当1ba<,即>a b 时,原级数收敛; 当>1ba ,即ab <时,原级数发散; 当1ba=,即=a b 时,原级数可能收敛也可能发散. 6.判别下列级数的敛散性: (1)解:10n n ==≠,根据收敛级数的必要条件可知,原级数发散.(2)解:原级数显然为正项级数,根据比较审敛法的极限形式,111lim =lim 1n n na b b aa n n→∞→∞+=+,所以原级数发散. (3)解:因为11lim 1>122nn n e n →∞⎛⎫+= ⎪⎝⎭, 所以原级数发散.7.判别级数的敛散性,若收敛,指出条件收敛还是绝对收敛: (1)解:因为11111(1)=33n n n n n n n ∞∞---==-∑∑,而1+11+113lim =lim <1333n n n n n n n n →∞→∞-=,所以级数113n n n ∞-=∑收敛,5因此原级数绝对收敛.(2)解:因为22(21)(21)cos 22n nn n n π++≤,又因为: 22+122(23)(23)12lim =lim 12(21)2(21)2n n n nn n n n →∞→∞++=<++,所以级数21(21)2nn n ∞=+∑收敛,因此原级数绝对收敛. (3)解:级数的一般项为:11(1)(1)10n n n u -=-+,因为1lim||lim(1)1010n n n n u →∞→∞=+=≠,所以原级数的一般项不趋近 于0,原级数发散. (4*)解:这是一个交错级数11(1)n n n u ∞-=-∑,因为级数1n ∞=-∑发散(见第一节习题2(1)),所以原级数不是绝对收敛,又因为:0n n =,1n n u u +-=---==-,根据莱布尼兹定理可知,原级数收敛且是条件收敛.8*.解:先讨论0x >的情形. 当=1x 时,级数为112n ∞=∑,显然发散;当0<<1x 时,级数为正项级数,利用比值审敛法,1221+122221lim =lim lim 111n n n n n n n n n n nu x x x x x u x x x ++++→∞→∞→∞++⋅==<++, 所以此时级数211+n nn x x ∞=∑收敛且是绝对收敛; 当1x >时,同样利用比值审敛法,2121+12222111lim =lim lim1111n n n n n n n nn u x x x x u x x x +++→∞→∞→∞+++==<++,6 所以此时级数211+nnn x x∞=∑收敛且是绝对收敛; 再看<0x 的情形.当1x =-,级数为1(1)2nn ∞=-∑,显然发散;当10x -<<和1x <-时,级数为21()(1)1nn n n x x ∞=--+∑,这是一个交错级数,对其一般项取绝对值得到正项级数21()1nnn x x ∞=-+∑,按照同样的方法可知21()1nnn x x∞=-+∑收敛,也即原级数绝对收敛; 而当0x =时,级数显然收敛且绝对收敛;综合得,原级数在1x =±时发散,其他均为绝对收敛. 9*.证明:设111(1)n n n a S ∞-=-=∑,若∑∞=-112n n a 收敛,设2121n n aS ∞-==∑,则122121111(1)n n n n n n n a a a S S ∞∞∞--====--=-∑∑∑,即21nn a∞=∑收敛,所以22-111(+)nn n n n aa a ∞∞===∑∑收敛,与11(1)n n n a ∞-=-∑条件收敛矛盾,所以∑∞=-112n n a 发散.因为11(1)n n n a ∞-=-∑条件收敛,所以∑∞=1n n a 发散.10*证明:因为222||0nnn n a b a b +≥≥,所以∑∞=1n nnba 收敛;因为2220()2||n n n nn n a b a b a b ≤+≤++,所以∑∞=+12)(n n nb a收敛;令1n b n =,因为∑∞=12n n b 收敛,所以∑∞=1n n n b a 收敛,即∑∞=1n n na 收敛.第三节 幂级数1.填空:(1)绝对收敛 ; 绝对收敛 .(2)1ρ;+∞;_0_.(3)_1_,7 (-1,1).(4)12=R R ;(5) (),R R -.2.选择:(1)B .(2)B . (3)A . (4)C . (5*)B (提示:令=1y x -,则1111(1)n n n n n n na x na y ∞∞++==-=∑∑21211=()n n n n n n yna yy a y ∞∞-=='=∑∑).(6)B .(7)D .3. 求下列幂级数的收敛域:(1)解:因为+11=lim lim 02(1)n n n na a n ρ→∞→∞==+,收敛半径为R =+∞,收敛域为(,)-∞+∞.(2)解:因为12121(1)(1)limlim 11(1)n n n n n na n a nρ++→∞→∞-+===-, 所以收敛半径1R =,收敛区间为(1,1)-;当1x =时,级数为211(1)nn n ∞=-∑,这是一个绝对收敛级数; 当1x =-时,级数为211n n∞=∑,这是一个收敛的正项级数; 综合得原级数的收敛域为[1,1]-.(3)解:121limlim 121n n n n a n a n +→∞→∞-==+1R ⇒=, 故当231x -<,即12x <<时级数绝对收敛,当1x =时,11(1)(1)12121n n n n n n ∞∞==--=--∑∑,级数发散,当2x =时, 1(1)21nn n ∞=--∑为收敛的交错级数,所以原级数的收敛域为(1,2].(4)解:这是一个缺奇次项的幂级数,直接使用比值审敛法得:1()lim ()n n n nu x u x +→∞=2222n x x =⋅=,8 所以当22<1x,即x <<时,级数绝对收敛;当22>1x时,即x >或<x -时,原级数发散;当x =时,级数为1n ∞=∑,发散;当x =时,级数为21(1)nn ∞=--∑,发散(见第一节习题2(1));所以,级数的收敛域为(-.(5*)解:因为+111111+231=limlim 111123n n n na n n a nρ→∞→∞+++⋅⋅⋅++=+++⋅⋅⋅+11lim(1)111123n n n→∞+=++++⋅⋅⋅+,因为正项级数11n n ∞=∑发散,因此111lim(1)23n n →∞+++⋅⋅⋅+=+∞,所以上述的=1ρ,即级数的收敛半径为1,收敛区间为(1,1)-.当1x =±时,级数为∑∞=+⋅⋅⋅+++1)131211(n n x n,因为 111=1()23n u n n+++⋅⋅⋅+→∞→∞, 所以发散,综合得原级数的收敛域为(1,1)-. 4.求下列幂级数的收敛域与和函数:(1)解:先求收敛域:利用比值审敛法可得454141()45lim lim =()41n n n n n nx u x n x u x x n +++→∞→∞+=+, 因此,当41x <,即||1x <时,级数收敛; 当1x =时,级数为141n n ∞=+∑,发散;当1x =-时,级数为1()41n n ∞=-+∑,发散,所以级数的收敛域为(1,1)-.9为求和函数,令410()=41n n x s x n +∞=+∑,两端同时求导得:4141440001()==,(1,1)41411-n n n n n n x x s x x x n n x ++∞∞∞===''⎛⎫⎛⎫'==∈- ⎪ ⎪++⎝⎭⎝⎭∑∑∑再两端同时积分得:400111+1()(0)=()==ln arctan 4121-xxx s x s s x dx dx x x x '-+-⎰⎰, 显然(0)=0s ,所以原级数的和函数为11+1()=ln arctan ,(1,1)412x s x x x x +∈--.(2)解:212121(22)lim lim 2n n n n n nu x n x u x n ++-→∞→∞+==, 故当211x x <⇒<时级数绝对收敛,当||1x >时,级数发散. 当1x =-时,21112(1)2n n n n n ∞∞-==-=-∑∑发散,当1x =时,12n n ∞=∑发散,⇒ 收敛域为(1,1)-.令211()2(0)0n n S x nxS ∞-==⇒=∑2212211()21xxn nn n x S t dt ntdt xx ∞∞-==⇒===-∑∑⎰⎰22222()(||1)1(1)x x S x x xx '⎛⎫⇒==< ⎪--⎝⎭. (3)解:先求收敛域:因为1(+1)(+2)limlim 1(+1)n n n n a n n a n n ρ+→∞→∞===, 所以收敛半径为1,明显当1x =±原级数发散,故级数的收敛域为(1,1)-;令1()(1)(0)0nn S x n n xS ∞==+⇒=∑,121111()(1)xx nn n n n n S t dt n n t dt nxxnx∞∞∞+-===⇒=+==∑∑∑⎰⎰222211(1)n n x x x x x x x ∞=''⎛⎫⎛⎫=== ⎪ ⎪--⎝⎭⎝⎭∑ 2232()(||1)(1)(1)x x S x x x x '⎛⎫⇒==< ⎪--⎝⎭.10(4)解:212121(21)lim lim (21)n n n n n nu x n x u x n ++-→∞→∞-==+,故当211x x <⇒<时级数绝对收敛, 当||1x >时,级数发散.当1x =-时, 12111(1)(1)(1)2121n n n n n n n +∞∞-==---=--∑∑为收敛的交错级数,当1x =时, 11(1)21n n n +∞=--∑为收敛的交错级数,⇒ 收敛域为[1,1]-.令1211(1)()(0)021n n n x S x S n +-∞=-=⇒=-∑, 122211()(1)1n n n S x x x∞+-='⇒=-=+∑ 201()(0)arctan 1xS x S dt x t ⇒-==+⎰()arctan (11)S x x x ⇒=-≤≤.第四节 函数展开成幂级数1.将下列函数展开成x 的幂级数,并求展开式成立的区间:(1)解:利用间接展开法.因为=0=,(,)!nxn x e x n ∞∈-∞+∞∑,所以ln ln 00(ln )(ln ),(,)!!xn n xa x ann n x a a a eex x n n ∞∞======∈-∞+∞∑∑.(2)解:利用间接展开法.因为1(1)ln(1)=,(1,1]1n n n x x x n ∞+=-+∈-+∑,所以 ln()=ln[(1)]ln ln(1)x xa x a a a a++=++110(1)ln ,(,](1)nn n n a x x a a n a∞++=-=+∈-+∑. (3*)解:利用间接展开法.因为2(1)(1)...(1)(1)1...,||12!!m nm m m m m n x mx x x x n ---++=++++<122(1)x x -=⋅+11357113135...,(1,1]224246x x x x x ⋅⋅⋅=-+-+∈-⋅⋅⋅. 注:当1=2m -时,在右端点处收敛.(4)解:利用间接展开法.因为20(1)cos =,(,)(2)!n nn t t x n ∞=-∈-∞+∞∑,所以22100000(1)(1)cos d =[]d d (2)!(2)!n nxxx n n n n t t t t t t t t n n ∞∞+==--=∑∑⎰⎰⎰ 212200(1)(1)=d ,(,)(2)!(2)!(22)n nxn n n n t t t x n n n ∞∞++==--=∈-∞+∞+∑∑⎰. 2. 解:111(1)=,(,)!nx x x x x e ee e e x n ∞-+-=-=⋅=∈-∞+∞∑.3.解:011111(2),(0,4)2422212n n n x x x x ∞==⋅=-∈---∑. 4.解:将sin x 变形为:1sin sin[()])cos()662626x x x x ππππ=-+=-+-, 利用sin x 和cos x 的展开式可得2-121211sin ()()...221!622!6(1))(),(,)622n!6n n n x x x x x x ππππ-=+---++⋅⋅--+-∈-∞+∞⋅.5.解:211=()34154x x x x x x ----+5(5)111=()531(5)414x x x +--⋅-+-+111005111=(1)(1)(5)(1)(1)(5)3344n n nn n n n n x x ∞∞+++==---+---∑∑, 其中第一个展开式的收敛域为|5|<1x -,第二个展开式的收敛域为|5|<14x -,所以原函数的展开式的收敛域为|5|<1x -,即46x <<.第五节 函数的幂级数展开式的应用1.利用函数的幂级数的展开式求下列各数的近似值: (1)解:根据ln (1+)x 的展开式可得:35111ln2(...)(11)135x x x x x x +=+++-<<-(见教材)12令1=51x x +-,解得2(1,1)3x =∈-,带入上述展开式可得 35793579212121212ln 52(...)335793333=+⋅+⋅+⋅+⋅,如果取前五项作为其近似值,则1113151751113151712121212||=2(...)111315173333r ⋅+⋅+⋅+⋅+1123112312114114114=2(1...)111391517399⋅⋅+⋅+⋅+⋅+1123112322444(1...)119399<⋅++++ 111111112212290.00384111153319<⋅⋅=⋅⋅≈-,符合误差要求,因此取前五项作为其近似值,即35793579212121212ln 52() 1.61335793333≈+⋅+⋅+⋅+⋅≈.(2)解:根据cos x 的幂级数展开式可得246111cos18cos1()()() (10)2!104!106!10ππππ==-+-+, 6-61() 1.335106!10π≈⨯,所以取前四项作为近似值,即 246111cos181()()()0.950992!104!106!10πππ=-+-≈.(3)解:根据cos x 的幂级数展开式可得2621cos 111...2!4!6!x x x x -=-++, 于是可得0.50.5262001cos 111d =(...)d 2!4!6!x x x x x x--++⎰⎰ 3511111111=()()...0.123272!24!326!52⋅-⋅⋅+⋅⋅+≈. 2.解:因为sin arctan x x 、的展开式分为可以写为:33sin ()3!x x x o x =-+,33arctan ()3x x x o x =-+,所以3333001()sin arctan 16lim lim 6x x x o x x x x x→→+-==.第七节 傅里叶级数1.填空:(1)其中的任何两个不同函数的乘积在区间[,]ππ-上的积分为130,相同函数的乘积在此区间上积分不为0 . (2)1()d f x x πππ-⎰,1()cos d (1,2,...)f x nx x n πππ-=⎰,1()sin d (1,2,...)f x nx x n πππ-=⎰. (3)02=0,()sin d n n a b f x nx x ππ=⎰.(4)1+π.(5)在一个周期内连续或者只有有限个第一类间断点 , 在一个周期内至多有有限个极值点 , 收敛 ,()f x , 左右极限均值.2.下列函数以π2为周期,且在[,)ππ-上取值如下,试将其展开成傅里叶级数:(1)解:先利用系数公式得出傅里叶级数.2220111()d d ()2x xx a f x x e x e e πππππππ---===-⎰⎰, 22212()(1)()cos ,( 1.2 (4)n e ea f x nxdx n n ππππππ----==⋅=+⎰, 2-2121(1)()sin ,(n=1,2...)4n n e e nb f x nxdx nππππππ+---==⋅+⎰, 所以,函数的傅里叶级数为2-22221(1)()(2cos sin )44nn e e e e f x nx n nx nππππππ-∞=---+-+∑. 再考虑其收敛性.易知函数满足收敛性定理的条件,其不连续点为(21)(0,1,2,...)x k k π=+=±±,在这些点处,上述的傅里叶级数收敛于左右极限的均值,即22(0)(0)22f x f x e e ππ-++-+=,在连续点处,傅里叶级数收敛于函数2()=xf x e ,因此2-22221(1)()(2cos sin )44nn e e e e f x nx n nx nππππππ-∞=---=+-+∑(,),(21)(0,1,2,...)x x k k π∈-∞+∞≠+=±±.(2)解:先根据系数公式求傅里叶级数.40113()d sin d 4a f x x x x ππππππ--===⎰⎰, 41131sin cos (2cos2cos4)cos 422n a x nxdx x x nxdx ππππππ--==-+⎰⎰, 根据三角函数系的正交性,仅当=2,=4n n 时,0n a ≠,易得142411,28a a =-=,由于4()sin f x x =是[,]ππ-的偶函数,故0n b =; 又因为函数4()sin f x x =是连续函数,所以可得:311()cos 2cos 4,<<828f x x x x =-+-∞∞.3.解:(1) ()()f x x x ππ=-<<作周期延拓的图象如下:其分段光滑,故可展开为傅里叶级数. 由系数公式得.当时,,,所以 11sin ()2(1)()n n nxf x x xππ∞+==--<<∑,为所求. (2)()(02)f x x x π=<<作周期延拓的图象如下:其分段光滑,故可展开为傅里叶级数. 由系数公式得.当时,011()d d 0a f x x x x ππππππ--===⎰⎰1n ≥11cos d d(sin )n a x nx x x nx n ππππππ--==⎰⎰11sin sin d 0|x nx nx x n n ππππππ--=-=⎰11sin d d(cos )n b x nx x x nx n ππππππ---==⎰⎰1112cos cos d (1)|n x nx nx x n n n ππππππ+---=+=-⎰220011()d d 2a f x x x x πππππ===⎰⎰1n ≥22011cos d d(sin )n a x nx x x nx n ππππ==⎰⎰15 ,,所以1sin ()2(02)n nxf x x x ππ∞==-<<∑,为所求. 4.解:要展开为余弦级数,需对函数进行偶延拓,即定义函数1cos 02()cos ,02x x f x x x ππ⎧≤≤⎪⎪=⎨⎪-≤≤⎪⎩,,并将1()f x 以2π周期延拓到整个数轴,得到偶函数()g x . 对()g x 进行傅里叶展开,显然有0n b =,且0024cos d 2x a x πππ==⎰,2024(1)cos cos d ()(=1,2,...)241nn x a nx x n n πππ-==--⎰,根据上述系数即可得到()g x 在整个数轴上的傅里叶展开式,由于()g x 连续,所以其傅里叶均收敛于()g x ,最后将展开式限制在[0,]π,既得()cos2xf x =的傅里叶展开式 2124(1)()cos ,[0,]41nn f x nx x n πππ∞=-=--∈-∑.4.解:将函数进行奇延拓,并求傅里叶系数:0(0,1,2,...)n a n ==,021sin [(1)1](1,2,...)42n n b nxdx n nπππ==---=⎰,因此函数()4f x π=的正弦级数展开式为11sin +sin 3sin 5...(0,)435x x x x ππ=++∈, 根据收敛性定理,在端点=0,=x x π处傅里叶级数收敛于零.令上式中的=2x π,即可得到1111 (4357)π=-+-+.第八节 一般周期函数的傅里叶级数1.填空:220011sin sin d 0|x nx nx x n n ππππ=-=⎰220011sin d d(cos )n b x nx x x nx n ππππ-==⎰⎰2200112cos cos d |x nx nx x n n n ππππ--=+=⎰16(1)-1()cos (0,1,2...)l n l n xa f x dx n l lπ==⎰-1()sin (1,2...)l n l n x b f x dx n l l π==⎰.(2)02()sin(n=1,2...)l n xf x dx l lπ⎰. 2.解:为展开为正弦级数,先将函数()f x 做奇延拓,其傅里叶系数为0(0,1,2,...)n a n ==;20222sin +(-)sin ll l n n x n xb x dx l x dx l l l lππ=⎰⎰224=sin2l n n ππ, 所以1()=sinn n n xf x b lπ∞=∑ 22224131517=(sin sin +sin sin +...)357l x x x xl l l l πππππ--, 由于()f x 连续,上述展开式对于任意的[0,]x l ∈均成立. 3.解:()2+||f x x =为偶函数,所以展为余弦级数,其系数为0(1,2,...)n b n ==,1002(2)d 5a x x =+=⎰,1222(cos 1)2(2)cos()(1,2,...)n n a x n x dx n n πππ-=+==⎰, 因为函数()2+||f x x =满足狄氏收敛定理,所以22152(cos 1)2||cos 2n n x n x n πππ∞=-+=+∑ 2225411(cos cos3cos5...)()235x x x x ππππ=-+++-∞≤≤∞. 令上式中的=0x ,可得2222111 (8135)π+++=,又2222222=11111111(...)(...)135246n n ∞=+++++++∑ 2222221111111(...)(...)4135123=+++++++所以22222=114111=(...)=36135n nπ∞+++∑.第十二章 自测题1.填空:17 (1)仍收敛于原来的和s .(2) 均收敛 ; 均发散 . (3)_1_;_2__.(4)34, 12, 34. 2.选择:(1)C .(2)A (提示:使用阿贝尔定理).(3)D (提示:ln ln ln 2ln ln 2ln 22()n n n e e n λλλλ--⋅--===). (4)B .(5)A . (6)C .3.判别下列级数的敛散性,若收敛指出绝对收敛或条件收敛: (1)解:根据正项级数的根值审敛法,有(!)lim n n n n →∞=+∞, 所以,原级数发散.(2)解:因为2211sin 4n n n π≤,而211n n∞=∑收敛, 所以原级数收敛且绝对收敛.(3)解:这是一个交错级数,由于(1)11=-ln -ln n n n n n n-≥,所以不是绝对收敛.因为111ln(1)ln n n n n-+-+-1ln(1)10(ln )[1ln(1)]n n n n n +-=<-+-+,且1lim=0ln n n n→∞-,根据莱布尼兹定理,级数收敛,即原级数条件收敛.(4*)解:根据比值审敛法,有1(1)lim ||lim ||1n pp n n n pa n n a a n a n +→∞→∞+⎛⎫== ⎪+⎝⎭, 所以,当||<1a 时,即11a -<<时,级数绝对收敛; 当||1a >,根据罗比达法则可知212+++ln (ln )lim lim lim(1)x x x p p p x x x a a a a a x px p p x --→∞→∞→∞=-, 因为p 是常数,有限次使用罗比达法则,可求出上述极限为无穷,因此lim np n a n→∞=∞,所以原级数发散;当1a =时,级数既为11pn n∞=∑,此时若01p <≤时,原级数18 发散,若1p >原级数收敛且绝对收敛;当1a =-时,级数既为1(1)npn n∞=-∑,此时,若01p <≤时,根据莱布尼兹定理可知,原级数条件收敛,若1p >时,根据比较审敛法可知,原级数绝对收敛.4.解:因为11113+(2)[3+(2)]1lim lim 3+(2)(1)[3+(2)]n n n n n nn n n n n n n n++++→∞→∞--+=-+-12[1+()]3lim 3112(1)[1+()]33n n nn +→∞-==+⋅⋅-,所以,级数的收敛半径为13,收敛区间为42(,)33--;在端点4=3x -处,级数为12(1)+()3nnn n ∞=-∑,因为级数11(1)21,()3n n n n n n ∞∞==-⋅∑∑均收敛,所以在此点处,原级数收敛; 在端点2=3x -处,级数为121+()3nn n ∞=-∑,因为级数11,n n ∞=∑发散,而121()3nn n∞=-⋅∑收敛,所以在此端点处,原级数发散; 综合得,原级数的收敛域为42[,)33--. 5.解:先利用比值审敛法求幂级数的收敛域.因为2+222(2+2)!lim =lim (2+2)(2+1)(2)!n n n n x x n n n xn →∞→∞=+∞, 所以级数的收敛域为(,)-∞+∞;令22420()1......(2)!2!4!(2)!n nn x x x x s x n n ∞===+++++∑, 则3521()+......3!5!(21)!n x x x s x x n -'=++++-,所以 234()()1......2!3!4!!nx x x x x s x s x x e n '+=+++++++=,19 即()()x s x s x e '+=,这是一个一阶线性微分方程,解之得1()+2x x s x ce e -=.又因为(0)1s =,带入求得常数12c =,所以幂级数的和函数为11()(,)22x xs x e e x -=+∈-∞+∞,.6.解:因为2ln(12)ln(1)ln(12)x x x x +-=-++,而11(1)ln(1)(11)n nn x x x n -∞=-+=-<≤∑,所以,=1ln(1)(11)nn x x x n∞-=--≤<∑,1=1(1)211ln(12)()22n n n n x x x n -∞-+=-<≤∑,于是得出原函数的展开式为12=1(1)2111ln(12)=()22n n n n x x x x n -∞--+--<≤∑.7.解:为展开为正弦级数,先将函数()f x 在[,0)π-上做奇延拓,再延拓到整个数轴,并求傅里叶系数0(0,1,2...)n a n ==, 02()sin d n b f x nx x ππ=⎰202sin d x nx x ππ=⎰221sincos (1,2,...)22n n n n n πππ=-=, 因此可得函数()f x 在[0,)π的傅里叶级数2=121()(sincos )sin ([0,),)222n n n f x nx x x n n πππππ∞=-∈≠∑, 由于3=2x π-为函数的不连续点,根据狄氏收敛性定理,和函数在3=2x π-处的值3()2s π-为左右极限的均值,即31()=24s ππ-,而5=4x π是函数的连续点,在此点处,收敛于(延拓后的)函数()f x ,即5()=04s π.8.考研题练练看:(1)C .解析:幂级数1(1)k kk ax ∞=-∑的收敛域中心为1x =,而20 =1(1,2,...)n n k k S a n ==∑无界表明1(1)k k k a x ∞=-∑在2x =发散,因此幂级数的收敛半径1R ≤,同时,根据莱布尼兹定理,数列{}n a 单减且收敛于0,表明1(1)kkk ax ∞=-∑在0x =收敛,因此幂级数的收敛半径1R ≥,综合得收敛半径为=1R ,因此选C . (2)A .解析:若1n n u ∞=∑收敛,则对其任意项加括号后仍收敛,其逆命题不一定成立,所以选A . (3)D .解析:=11(1)a n n ∞-∑绝对收敛,即1=121a n n∞-∑收敛,所以32α>,又由2=1(1)n a n n ∞--∑条件收敛可知12α≤<,所以选D .(4)C .解析:根据题意,将函数在[]1,1-展开成傅里叶级数(只含有正弦,不含余弦),因此将函数进行奇延拓:1,(0,1)2()1,(1,0)2x x f x x x ⎧-∈⎪⎪=⎨⎪-+∈-⎪⎩,其傅里叶级数以2为周期,则当()1,1x ∈-且()f x 在x 处连续时,()()S x f x =,所以 91111()()()()44444S S S f -=-=-=-=-.(5)D .解析:因为1P >时,=11P n n ∞∑收敛,且lim =lim 1Pn n n n Pa n a n →∞→∞存在,所以=1nn a∞∑收敛.(6)解:先求收敛域.222212(1)212+1lim lim 12+1(1)21n n n n n nxn n x x n x n +-→∞→∞--==<--,即11x -<<时级数绝对收敛;当=1x ±时,级数为1=1(1)21n n n -∞--∑,根据莱布尼兹定理,可知21此级数收敛,因此原级数的收敛域为[1,1]-.为求和函数,设112211=1(1)(1)()2121n n n n n n s x x x xn n --∞∞-=--==--∑∑, 令1211=1(1)()21n n n s x xn -∞--=-∑,则 1212112=1=1(1)1()=() (11)211n n n n n s x x x x n x -∞∞--'⎛⎫-'=-=-<< ⎪-+⎝⎭∑∑, 两端同时积分,得11201()(0)d arctan (11)1xs x s x x x x -==-<<+⎰,明显1(0)0s =,所以1()arctan (11)s x x x =-<<,既得()arctan (11)s x x x x =-<<,又因为=1x ±时,()arctan s x x x ,都有定义,且连续,所以()arctan (11)s x x x x =-≤≤.(7)B.(8)解:先求收敛域.22224(+1)4(+1)321lim 12(1)1443n n n n x x n n n →∞+++⋅⋅=<++++, 即11x -<<时级数绝对收敛;当=1x ±时,级数为2=044321n n n n ∞+++∑,发散,因此幂级数的收敛域为11x -<<.为求和函数,设2222=0=0443(21)2()==2121n nn n n n n S x x x n n ∞∞++++++∑∑,所以22=0=02()=(21)21nn n n S x n xx n ∞∞+++∑∑,令2212=0=02()=(21)()21nn n n S x n x S x x n ∞∞+=+∑∑,,对1()S x 两端积分得210=0()d =(21)d xx nn S x x n x x ∞+∑⎰⎰212=0= (11)1n n xx x x∞+=-<<-∑, 两端求导得212221()= (11)1(1)xx S x x xx '+⎛⎫=-<< ⎪--⎝⎭;22因为212=02()21n n xS x x n ∞+=+∑,两边求导得 222=02[()]2 (11)1n n xS x x x x ∞'==-<<-∑, 再对两端积分得22021()0(0) ln (11)11xxxS x S dx x xx +-⋅==-<<--⎰,所以211()ln((1,0)(0,1))1xS x x x x+=∈-⋃-, 又因为=0x 时,12(0) 1.(0)2S S ==,综合可得和函数为222111ln ,(1,0)(0,1)()1(1)3, 0x xx S x x xx x ⎧+++∈-⋃⎪=--⎨⎪=⎩. (9)(i)证明:由题意得1=1()n nn S x na x∞-'=∑,22=2=0()(1)(1)(2)n nn n n n S x n n a xn n a x ∞∞-+''=-=++∑∑,2(1)0n n a n n a ---=,2=(1)(2)(0,1,2...)n n a n n a n +∴++=, ()=()S x S x ''∴,即()()0S x S x ''-=.(ii) 解:()()0S x S x ''-=为二阶常系数齐次线性微分方程,其特征方程为210λ-=,从而特征根为1λ=±,于是其通解为12()x xS x C e C e -=+,由0(0)3S a ==,1(0)1S a '==得1212123121C C C C C C +=⎧⇒==⎨-+=⎩,,所以()2x x S x e e -=+. (10)解:(1)证明:由cos cos n n n a a b -=,及0,022n n a b ππ<<<<可得0cos cos 2n n n a a b π<=-<,所以02n n a b π<<<,由于级数1nn b∞=∑收敛,所以级数1nn a∞=∑也收敛,由收敛的必要条件可得lim 0n n a →∞=.(2)证明:由于0,022n n a b ππ<<<<,23 所以sin ,sin 2222n n n n n n n na b a b b a b a ++--≤≤2222sin sin cos cos 22222222n n nnn n n n n nn n n nn n n nn n n a b b a a a b b b b a b b a b a b b b b b +--==+--≤=<=由于级数1nn b∞=∑收敛,由正项级数的比较审敛法可知级数1nn na b ∞=∑收敛. (11)解:由于1lim1n n na a +→∞=,所以得到收敛半径1R =. 当1x =±时,级数的一般项不趋于零,是发散的,所以收敛域为()1,1-.令和函数)(x S =0(1)(3)n n n n x ∞=++∑,则2111()(43)(2)(1)(1)nn n nn n S x n n x n n x n x ∞=∞∞===++=++++∑∑∑211123"'3"'11(1)n n n n x x x x x x x x ∞∞++==⎛⎫⎛⎫=+ ⎪ ⎪⎝⎭⎝⎭⎛⎫-⎛⎫=+= ⎪ ⎪---⎝⎭⎝⎭∑∑。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
bn1202ksin n2xdxnk(1cons)
n2k
当n1,3,5, ,
0 当n2,4,6,
f ( x ) k 2 k (s x i1 s n 3 i x n 1 s5 i x n ) 2 23 25 2
( x ; x 0 , 2 , 4 , )
例 2将 函 数 f(x)1 0 x5x1展 5开 成 傅
a n 0 ,( n 0 ,1 ,2 , ) y F(z)
bn5 205(z)sin n2 zdz 5 0 5 10
15
x
(1)n 10, (n 1 ,2 , )
n
F(z)10(1)nsin nz,
n1 n
5
(5z5)
1 0x1 0( 1)nsin n (x [1)0] n 1 n 5
f
(x)
x,2
x,
x
x
2
3
展开成
2
2
傅里叶级数 .
练习题答案
一、 f (x) 4
n1
[1
(1)n n22
2sinn 2 ]cosnx
n
1
2cosn 2
n
sinnx
(x 2k, x 2k 1 ,k 0,1,2,).
2
二、
f
( x)
4l 2
n1
1 n2
sinn 2
10 (1)nsinnx.
n1 n
5
(5x1)5
另解 an1 55 1(51 0x)co n 5sxdx 2 5 1c 5 o n 5 x s d x 1 55 1x 5co n 5 x s dx 0, (n 1 ,2 , ) a015515(10x)dx 0,
bn1 55 1(51 0x)sin n 5xdx(1)n n10, (n 1 ,2 , )
氏 级 数 .
解 作变量z代 x换 1,0
5x15 5 z 5 , f(x)f(z1)0 zF(z), 补充 F (z) 函 z( 5 数 z 5 )的,定义 令 F(5)5, 然后 F(z)将 作周期 (T1 延 )0 拓
这拓广的周期函 收数 敛满 定足 理的 , 条件
且展(开 5,5)内 式收 在 F(z敛 ). 于
高等数学ch12第九节
二、典型例题
例1 设f(x)是周期为4的周期函数,它在[2,2)
上的表达式为f(x)k0
2x0
,
0x2
将其展
成傅氏级数.
y
k
解 l2,满足狄氏.充分条件
a012020dx1202kdxk,
4 2 0 2
x 4
an
1 2kconsxdx 0,
20
2
(n 1 ,2 , )
故 f(x )1 0 x1 0( 1 )nsin n x n 1 n 5 (5x1)5
三、小结
以2l为周期的傅氏系数; 利用变量代换求傅氏展开式; 求傅氏展开式的步骤; 1.画图形验证是否满足狄氏条件(收敛域,奇偶性); 2.求出傅氏系数; 3.写出傅氏级数,并注明它在何处收敛于f (x).
练习题
一 、设 周 期 为2 的 周 期 函 数 f ( x )在 一 个 周 期 内 的 表 达 式
x ,1 x 0
为
f (x)
1
,
0
x
1 2
,试将其展开成傅里叶级 数 .
1
,1 2
x
1
二、试将函数
f (x)
x
,
0
l
x
x l 2
,l x 2
展开成正弦级数和 l
余
弦级数 .
三、将函数
sinnx l
(0 x l
