《高等数学》教学大纲(Syllabus of advanced mathematics)
《高等数学I》教学大纲
《高等数学》教学大纲课程名称:高等数学 Advanced Mathematics课程性质:通识课公共必修课学分:11总学时:170学时理论学时:170学时适用专业:本(工)科各专业先修课程:教学目的与要求:高等数学是高等院校本科学生数学教育都应达到的合格要求,也是选学工科各专业学生的基本要求,因此该课程不仅是高等院校本科数学教育的一门通识课程,也是工科本科各专业的一门重要基础理论课程与核心课程,它的教学目的与要求是:1. 使学生获得高等数学的基本概念、基本理论与基本运算技能,为学习后续课程和进一步获得数学知识奠定必要的数学基础;2. 使学生具有一定的抽象思维能力、逻辑推理能力和空间想象能力;具有较强的自学能力;3. 使学生学习体会研究问题解决问题的一般科学方法,培养学生用数学方法解决实际问题的意识、兴趣和能力。
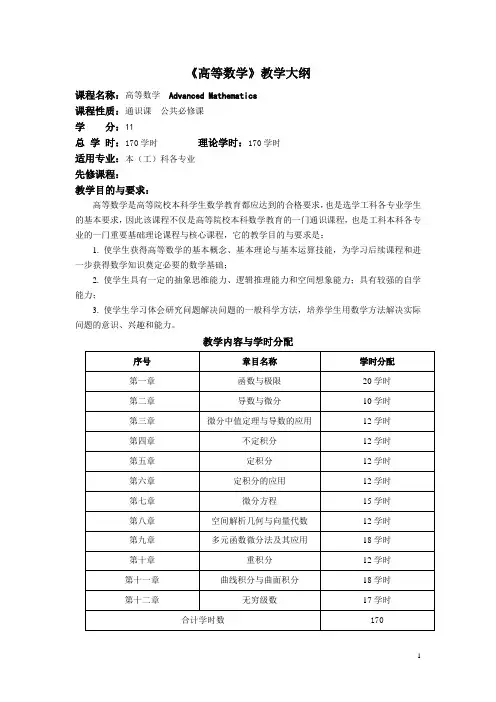
教学内容与学时分配各章节主要知识点与教学要求第一章函数与极限(20学时)第一节映射与函数第二节数列的极限第三节函数的极限第四节无穷小与无穷大,第五节极限运算法则第六节极限存在准则两个重要极限第七节无穷小的比较第八节函数的连续性与间断点第九节连续函数的运算与初等函数的连续性第十节闭区间上连续函数的性质本章重点:函数与复合函数的概念,初等函数,实际问题中的函数关系;极限概念与极限运算法则;无穷小与无穷小的比较;两个重要极限;函数连续的概念与初等函数的连续性;间断点的分类;闭区间上连续函数的性质。
本章难点:复合函数的复合过程;极限定义的理解;两个重要极限的灵活运用;极限存在的两个准则的应用;闭区间上连续函数性质的应用。
教学要求:(1)掌握函数的概念、表示方法与性质,并会建立简单应用问题中的函数关系式;(2)掌握基本初等函数的性质及其图形,掌握复合函数的复合过程;(3)了解函数极限的概念,会用极限定义证明一些极简单的极限,理解和掌握极限的运算性质;(4) 理解函数左极限与右极限的概念,以及极限存在与左、右极限之间的关系;(5) 了解极限存在的两个准则,并会利用它们求极限;(6)掌握利用两个重要极限求极限的方法;(7)掌握无穷小的有关理论,会用等价无穷小求极限;(8)掌握函数连续的定义,会判别函数间断点的类型;(9)了解连续函数的性质和初等函数的连续性,会用闭区间上连续函数的性质解决一些简单的有关问题。
高等数学教学大纲

高等数学教学大纲《高等数学?》教学大纲一、课程基本信息课程代码课程类别公共基础课中文名称高等数学英文名称 Advanced Mathematics 适用专业农林类各专业开课单位数学与统计学院总学时 (理论:81 实验实习: 0 ) 学分 4.5学分先修课程初等数学后续课程概率论二、课程性质、地位和任务高等数学是研究现实世界的空间形式和数量关系的科学,是高等学校农林类各专业学生的一门必修的重要基础理论课,通过本课程的学习,使学生系统地获得微积分及常微分方程的基础理论知识,掌握数学的基本方法,培养学生的抽象思维能力、逻辑推理能力、自学能力、综合运用所学知识分析问题和解决实际问题的能力,能建立一些简单的数学模型,并为后续课程以及进一步获得数学知识奠定必要的数学基础,使学生掌握数学的思维方式和特点,培养学生应用数学的意识,为终身学习打下扎实的基础。
三、课程基本要求理论和知识方面:通过本课程的学习,要使学生获得:一元、二元函数微积分学方面的基本概念、基本性质和定理,并掌握一元、二元函数微积分学的基本运算技能;掌握常微分方程的基本概念、基本理论和基本求解方法;为学习后继课程和解决实际问题提供必不可少的数学知识及常用的数学方法基础;具体要求如下:1、要正确理解以下概念:函数、极限、连续性、导数、微分、偏导数、全微分、极值, 不定积分、定积分、二重积分及常微分方程的基本概念;2、要理解下列基本理论、定理和公式:基本初等函数的性质及图形,基本初等函数的导数公式,微分中值定理(罗尔定理、拉格朗日定理),极值存在的必要条件,不定积分基本积分公式,变上限积分函数及其求导定理、牛顿,莱布尼兹公式,二阶线性常微分方程解的结构;3、要掌握下列运算法则和方法:数列、函数极限的运算法则与计算方法,导数和微分的运算法则,复合函数、隐函数及参数方程求导法,高阶导数的求法,用导数判断函数的单调性及求极值的方法,用二阶导数判断曲线的凹凸性及求拐点的方法,多元函数偏导数的求法,不定积分、定积分的换元与分部积分法,二重积分的计算方法,一阶可分离变量微分方程的求解,二阶常系数齐次线性微分方程的解法。
《高等数学》教学大纲(Syllabus of advanced mathematics).doc

《高等数学》教学大纲(Syllabus of advanced mathematics)People do a Book slaves, then living with dead....... Put the book as a tool, the books of knowledge will live. It's alive. -- Hua LuogengSyllabus of advanced mathematicsAdvanced MathematicsCourse Code: 070A1012 for professional: tube each professional class Polytechnic: 186 Credits: 12Content introductionThe research object of this course is a function (dependence change process quantity). The content includes the function, limit, continuity, unary function calculus, vector algebra and space analytic geometry, multivariate function differential, multi function calculus, infinite series (Fourier Series) and ordinary differential equations etc..Two, the purpose and task of this courseThrough the study of this course, we should make students master the basic concepts, basic theory and basic operation skills of calculus, so as to lay the necessary mathematical foundation for learning subsequent courses and further acquiring mathematical knowledge. Through each teaching link to cultivate students' abstract thinking ability, logical reasoning ability, spatial imagination ability andself-learning ability, but also pay special attention to thecultivation of students' skilled operation ability and comprehensive use of the knowledge to the ability to analyze and solve problems.Three, the relationship between this course and other coursesThis course is the first basic course in science, engineering, management and other related professional. The study of this course is closely related to the learning of students' subsequent courses, which is related to the determination of students' learning goals and the future trend of students. This course after the end of the study, as a starting point, students can enter the relevant courses.This course is a basic course of the University for four years to learn must learn.The course is basic and theoretical, and closely related to the related courses. It is the subject of national postgraduate entrance examination, which is related to the cultivation of students' comprehensive ability. This course directly affects the school teaching level.Four, the basic requirements of the courseA basic understanding of the basic theory of calculus; fully understand the background of thought and mathematical thought of calculus. Master the basic methods, means, skills of calculus, and have certain ability of analysis and demonstration and strong calculation ability. The thought method can skillfully applied calculus to solve applicationproblems.Five, the course content and the distribution of class hours Teaching content of theoryChapter 1 function and limit (14 hours)Understanding the concept of function, compound function and piecewise function; understanding of the concept of limit, limit on the left and right limit; understand the concept of infinity and infinitesimal; understanding the concept of function continuity (including left and right continuous continuous); graphic properties and grasp the basic elementary function; and the properties of palm grip limit four operations rule; master two criteria on the existence of limit; grasp the method of two important limits; grasp the method of infinitesimal; understand the function of parity, monotonicity, periodicity and boundedness; understand the concept of inverse function and implicit function, and the relationship between the existence of the limit and the left and right limit understanding; the nature of continuous function and continuity of elementary functions, understand the nature of continuous function on a closed interval (boundedness, maximum and minimum value theorem and intermediate value theorem); a simple stress By using the functional relation in the problem, the limit of the two criteria of the limit can be used; the limit of equivalent infinitesimal is used; the type of the discontinuous point of the function is distinguished; the properties of the continuous function on the closed interval can be applied.The second chapter, derivative and differential (12 hours)To understand the concept of derivative and differential; understand the relation between derivative and differential geometry; understanding of derivative; understand the function of the relationship between the derivation and continuity; derivation rule master derivative four arithmetic operations and composite function; derivative formula master basic elementary function; understand the physical meaning of derivative; understanding four differential algorithm and first-order differential form invariance; understand the application of differential in approximation; understand the concept of high order derivative; tangent equation and normal equation for the plane curve will;Describe some physical quantity with the derivative; differential will function; n derivative will ask simple function; one order and two order derivative will ask piecewise function; one order and two order derivative function for implicit function and is determined by the parameter equation of the derivative of the inverse function of the will.The third chapter is the application of mean value theorem and the derivative (12 hours)The extreme value of understanding the function of judgment; grasp the monotonicity of the function and method of the extremal function with the derivative, grasp the function of maximum value and minimum value method and simple method for application; grasp the limits with the Cauchy theorem ofl'Hopital's rule; understand; understand the concept of curvature and radius of curvature; will use Rolle's theorem, the Lagrange theorem and Taylor theorem; judgment function graph convexity and inflection point with derivative function graph will ask the level, vertical and oblique asymptote, will describe the function of the graphics; calculate the curvature and radius of curvature, angle will seek two curve.The fourth chapter is indefinite integral (8 hours)Understanding the original function, the concept of indefinite integral grasp; indefinite integral properties; master the basic formula of indefinite integral; grasp the changing integral method and integral method; integral rational function, will seek the rational formula of trigonometric function and simple irrational function.The fifth chapter is definite integral (8 hours)Understanding the concept of definite integral; understand the function of variable upper limit definite integral definition and derivation; grasp the nature of definite integral and definite integral mean value theorem, grasp the Newton Leibniz formula; master element integral method and integral method of definite integral; understand the concept of generalized integral and generalized integral calculation.The application of definite integral in the sixth chapter (6 hours)Master the definite integral element method; master by integralexpression and calculation of some geometrical and physical quantities (plane graphics area, the length of plane curve, volume and side area, the rotating body parallel section area, average volume of a solid known variable work, gravity, pressure and function value etc.).The seventh chapter of space analytic geometry and vector algebra (12 hours)To understand the spatial Cartesian coordinate system, and understand the concept of vector representation; concept surface equation; master vector (linear operation, the number of product, vector product, mixed product), grasp the coordinate expression of unit vector and direction number and direction cosine, vector, and method of coordinate expression vector operations; control plane equation and linear equation and its solution; to understand the two vector vertical and parallel conditions; understand the equation and the common figures of two surface; understand the plane curve parameter equation and general equation; understand; use the relationship between plane and straight line (parallel, vertical, intersecting etc.) to solve the problem will ask for the cylinder; equation is parallel to the axis of the rotation axis of rotation surface and bus to the axis; projection curve will space curve on coordinate plane equation.The eighth chapter of multivariate function differential method and its application (18 hours)To understand the concept of multivariate function, geometric meaning of function of two variables; understanding multifunction partial derivative and differential concept; concept of directional derivative and gradient and master the calculation method; understand the concept of multiple function extremum and conditional extremum; grasp the method for multiple function partial derivative; master the calculation method of directional derivative and gradient; master the necessary condition for the existence of extremum of multivariate function; understand the partial derivative function of two variables and total differential concept, and the bounded property of continuous function in closed area; understand the necessary conditions and sufficient conditions for the existence of differential; understand the invariance of differential form, understand the application of differential in approximation; understand the concept of curve and the tangent plane and the tangent plane and surface normals; understand the sufficient conditions for the existence of two yuan would blame the extremum of function; differential; Will find the implicit function (including the implicit function determined by equations) of the partial derivative; will find the curve and the tangent plane and the surface of the tangent plane and normal equation; extreme for two yuan function, using Lagrange multiplier method; will ask simple multivariate function of the maximum and minimum,And it will solve some simple application problems.The ninth chapter is the multiple integral (10 hours)Understanding the concept of double integral, triple integral three; grasp the double integral (Cartesian coordinates and polar coordinates) calculation method; understand the natureof the double integral concept of double integral, triple integral three, understand the nature of the double integral to the mean value theorem of double integral; triple integral calculation three (rectangular coordinate and cylindrical coordinate and spherical coordinates).The tenth chapter of curvilinear integral and surface integral (14 hours)Understand the concept of two kinds of curve integral; master the calculation method of two kinds of curve integral; master Green formula and use plane curve integral is path independent of the conditions; grasp the method of calculation of two types of surface integral relations; to understand the nature of two curvilinear integral and two curvilinear integral; understand the concept of two types of surface integral the nature of the relationship, and two kinds of surface integral; understand the Gauss formula, Stokes Gong;; calculate the surface integral with Gauss formula; with triple integral, curve integral and surface integral for some geometrical and physical quantities (graphic area, volume, surface area, arc length, mass, center of gravity and moment of inertia gravity power and flow rate); calculate the divergence and curl.The eleventh chapter infinite series (14 hours)Understanding of constant series convergence, divergence and convergence of a series of necessary conditions and concepts; grasp the basic properties and convergence series; grasp the convergence and divergence of geometric series and series of conditions; grasp the positive series comparison test and ratiotest; master class number theorem Leibniz staggered; master method the radius of convergence, convergence and convergence interval of power series; master, McLaughlin, expansion and understanding; concept of absolute convergence and conditional convergence of a series of arbitrary items, as well as the relationship between the absolute convergence and conditional convergence; understand the concept of function series convergence domain and function; to understand some of the basic properties of power series in the convergence interval; understand the function necessary and sufficient conditions for the Taylor series; understand the power series in a simple approximate calculation of the understanding of the Fu Liye series; The concept and function to the de Lickley theorem of Fourier series; will law root; will seek some power series in the convergence region and function; some simple function will be indirectly expanded in power series; will be defined in the function is expanded into Fourier series, will be defined in the function sine and cosine series series, Fourier series and the expression will write function.The twelfth chapter of ordinary differential equations (12 hours)Understanding the properties of solutions of linear differential equations and structure theorems of solutions; grasp the solution variable separation equation and linear equation; grasp the two order constant coefficient homogeneous linear differential equation solution; differential equation and its solution, in order to understand the general solution, and the initial condition and the solution concept; understand the power series solution of differential equation the will;solutions of homogeneous equations, Bernoulli equation and differential equation, the solution will be some differential equations with simple variable substitution; will solve the following equations by reduction method, and the solution will be:; some higher than two order linear homogeneous differential equation with constant coefficients; be polynomial, exponential function, sine function and cosine function for the free term is two, and their sum and product of constant coefficient non homogeneous linear differential equations special solution and general solution of Euler equations; will, will first order solution contains two unknown functions with constant coefficients Linear differential equations; using differential equations (or equations) to solve some simple application problems.Practice teaching content1. Exercise classThe first chapter arranges three exercise classes, the sixth, seventh chapter arranges an exercise class, and the remaining chapters arrange two exercise classes each chapter,A total of 23 times, accounting for 46 hours.Six, teaching materials and reference books"Higher mathematics" (upper and lower) Mathematics Education Department of Tongji University, higher education press.The "guiding learning of higher mathematics Harbin Universityof Science and Technology mathematics" (upper and lower)."Higher mathematics" (upper, middle and lower volumes) edited by Wen Li, Cambridge University Press.Seven, the teaching methods of this courseThe characteristics of this course are theoretical, ideological, and related basic courses and specialized courses more contacts, should pay attention to inspire and guide students to master the important concept of ideological background teaching, ideological essence of important concepts, avoid rote learning. To be good at the relevant disciplines or life often encountered in terms of the concept of concepts and calculus combined, so that students understand the necessity of learning calculus. Pay attention to various aspects of teaching (theoretical teaching, exercise class, homework, counseling) the organic links, especially to strengthen the operation and guidance link, deepen the students' understanding of the content of classroom teaching, improve the ability of analyzing and solving problems and operation ability. In teaching, the relationship between learning mathematics and learning specialized courses is introduced to students in a planned and purposeful way. Learning advanced mathematics is the key subject to obtain further learning opportunities. Due to the characteristics of the subject, the teaching should highlight the central position of the teacher, and through the efforts of teachers, fully mobilize the students' interest in learning.Eight. Distribution of teaching hoursChapterClassroom teaching Exercise class SubtotalChapter one FourteenSixTwentySecond chapters TwelveFourSixteenThird chapters TwelveFourSixteenFourth chapters EightFourTwelveFifth chapters EightFourTwelveSixth chapters SixTwoEightSeventh chapters TwelveTwoFourteenEighth chapters EighteenFourTwenty-twoNinth chapters TenFourFourteenTenth chapters FourteenFourEighteenEleventh chapters FourteenFourEighteenTwelfth chaptersTwelveFourSixteenTotalOne hundred and fortyForty-sixOne hundred and eighty-sixNine, should pay attention to the implementation of the outlineThis syllabus is based on the basic requirements of the undergraduate basic course issued by the Higher Education Department of the State Education Commission, and is formulated in accordance with the teaching plan of our university. In the process of development, the demand for mathematics knowledge based on the management profession is taken into consideration, and the physics specialty and the relatively few professional needs of mathematics are dealt with separately. The syllabus specifies four aspects: understanding, mastering,understanding and meeting, and should pay attention to the implementation. The ratio of hours to hours is 1:2. Exercise course is an important teaching link to complete the basic requirements of teaching. Exercise class hours should not be less than the total class hours of 1/6, and the small class is appropriate. In the teaching process, teachers should according to the students' situation, according to the requirements of the outline, in each part in the review guide book for students to indicate different grades ofextra-curricular self-study content.People do a Book slaves, then living with dead....... Put the book as a tool, the books of knowledge will live. It's alive. -- Hua Luogeng。
高等数学教学大纲

高等数学教学大纲《高等数学》课程教学大纲一、《高等数学》课程说明(一)课程代码:(二)课程英文名称:Advanced Mathematics(三)开课对象:非数学专业专科学生(理科)(四)课程的性质:高等数学是高等教育专科重要的基础理论课之一。
通过本课程的学习,使学生获得微积分、空间解析几何、级数及常微分方程的基础知识和常用的运算方法。
通过各教学环节逐步培养学生分析问题和解决问题的能力。
为学习后继课程及今后的专业工作奠定必要的数学基础。
(五)教学目的:通过本课程的教学,提高学生的逻辑推理的能力,空间想象的能力,使学生具有比较熟练的运算能力和综合运用所学知识去分析问题、解决问题的能力。
(六)教学内容:1 要正确了解和理解以下概念:函数、极限、连续性、导数、微分、偏导数、全微分、函数的极值。
不定积分、定积分、二重积分、三重积分、无穷级数的敛散性、有关空间解析几何及常微分方程的基本概念。
2 要了解和掌握下列基本理论、基本定理和公式:基本初等函数的性质及图形,基本初等函数的导数公式,微分中值定理(罗尔定理、拉格朗日定理),不定积分基本公式,变上限积分及其求导定理、牛顿,莱伯尼兹公式,偏导数的几何意义,极值存在的必要条件,几何级数和P级数的收敛性,级数敛散性的判定条件,直线与平面的方程,典型的二次曲面、二阶线性常微分方程解的结构。
3掌握下列运算法则和方法:求函数和数列极限的方法与运算法则,导数和微分的运算法则,复合函数求导法,初等函数一阶、二阶导数的求法,用导数判断函数的单调性及求极值方法,多元函数复合函数的偏导数求法,不定积分、定积分的换元与分部积分法,正项级数的比值审敛法,求幂级数的收敛半径和收敛区间,函数展开成幂级数的间接展开法,一阶变量可分离变量微分方程的求解,二阶常系数线性微分方程的解法。
4 应用方面:用定积分和常微分方程方法求解一些简单的几何和物理问题,用极值方法求解最大值最小值的应用问题。
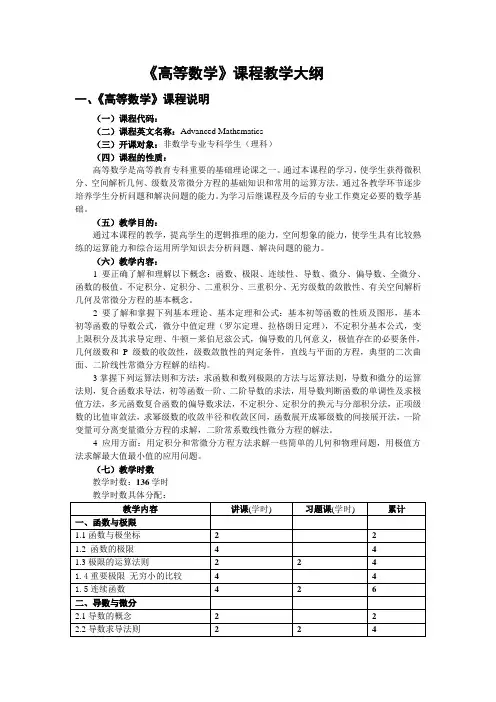
(七)教学时数教学时数:136学时教学时数具体分配:教学内容讲课(学时) 习题课(学时) 累计一、函数与极限 1.1函数与极坐标2 2 1.2 函数的极限 4 4 1.3极限的运算法则 2 2 4 1.4重要极限无穷小的比较4 4 1.5连续函数 4 2 6 二、导数与微分 2.1导数的概念 2 2 2.2导数求导法则2 2 4 too busy to come over, this is very responsible. Next to the sanitation department signed removal contracts, in strict accordance with the provisions of the contract. The back street alleys and suburban , to do a good job in environmental health at the same time, do a good job in a timely public facilities maintenance, repair, install, completely solve the piles of garbage, sewage crosscurrent, heidengxiahuo, potholes and other phenomena, do the streets clean, orderly, the convenience of the public life. To some five on the improvement of the urban river construction site. Now our urban river environment really let people see not bottom go to, than the works ofLao She's "Longxugou ditch" is not strong to where to go. The next step, we should insist on treating the symptoms, the strict implementation of the "long river" responsibility system, strengthen the river daily cleaning, planting a number of decomposition and green vegetation, so that Hanoi no garbage, riverside, no debris, the river no smell. At the same time, it is necessary to focus on the effect a permanent cure, accelerate the rain sewage diversion, to carry out the system of comprehensive remediation, accomplish treat a river, into a piece of landscape. The building housing the departments should strengthen the construction site construction supervision, supervise the implementation of construction dust dust measures, the public security traffic police department To2.3隐函数及参数方程所确定的函4 2 6数的导数2.4高阶导数 2 2 2.5函数的微分 2 2 4 三、中值定理与导数的应用3.1微分中值定理 2 2 3.2洛必达法则 2 2 4 3.3函数的单调性与极值 2 2 4 3.4曲线的凹凸性与拐点、绘图 2 2 四、不定积分 4.1不定积分的概念和性质 2 2 4.2换元积分法 4 2 6 4.3分部积分法 4 2 6 五、定积分及其应用 5.1定积分的概念与性质 2 2 5.2微积分基本公式 2 2 4 5.3定积分的换元积分法和分部积4 2 6 分法5.4广义积分 2 2 5.5定积分的应用 2 2 六、常微分方程6.1微分方程的概念 2 2 6.2一阶微分方程 4 2 6 6.3可降阶的高阶微分方程 4 4 6.4二阶常系数线性微分方程 4 2 6 七、空间解析几何与向量代数 7.1空间直角坐标系与向量 2 2 7.2向量的数量积与向量积 2 2 4 7.3空间平面与直线 4 4 7.4空间中点、线、面的关系 4 4 7.5空间曲面与空间曲线 2 2 4 八、多元函数微分学 8.1多元函数的基本概念 2 2 8.2偏导数与全微分 4 4 8.3链锁规则与隐函数求导 4 2 68.4高阶偏导数 2 2 8.5多元函数的应用 4 2 6 合计 102 34 136(八)教学方式课堂讲授,课外习作及批改.(九)考核方式和成绩记载说明考核方式为考试。
《高等数学》课程教学大纲

《高等数学》课程教学大纲英文名称:Advanced Mathematics课程代码:课程类别:专业基础课课程性质:必修开课学期:第一、二学期总学时:90学时总学分:5考核方式:闭卷适用专业:经济学专业一、课程简介数学向社会科学渗透及社会的数字化是当今科技发展的一般趋势。
它是一门研究客观世界数量关系和空间形式的科学,也是一种思维模式和文化素养。
数学教育在培养高素质经济管理人才中具有独特的、不可替代的重要作用。
高等数学是高等学校经济学专业的一门专业基础课。
通过本课程的学习,使学生获得一元函数微积分、多元函数微积分、常微分方程及其经济应用方面的基本概念、基本理论、基本方法和运算技能,为学习各类后续课程和今后从事科研活动、阅读或撰写论文奠定必要的数学基础,提供常用的数学方法。
在能力培养上,在传授知识的同时通过各教学环节逐步培养学生用极限的方法解决问题的能力,培养学生具有一定的逻辑思维能力,初步的抽象概括问题的能力和综合运用所学知识分析问题、解决问题的能力。
学生在进入本课程学习之前,应具备初等数学的理论基础,为本课程提供了必须的数学基础知识。
本课程学习结束后,学生可具备进一步学习相关课程的理论基础。
本课程总90学时,其中第一学期36学时,第二学期54学时。
考核方式为闭卷考试,根据平时考勤成绩、习题作业成绩、阶段性单元检测成绩及闭卷期末考试成绩综合给予最终成绩评定。
二、课程目标及其对毕业要求的支撑目标1-人文素养目标:教育学生认真学习马克思列宁主义、毛泽东思想、邓小平理论、“三个代表”、科学发展观和新时代中国特色社会主义的重要思想;忠诚党的教育事业和体育事业,培养学生互教互学、团结友爱、共同提高的集体主义精神;培养学生有严格组织纪律性,吃苦耐劳和勇敢顽强的意志品质。
目标2-理论知识培养目标:使学生掌握高等数学的基本理论和基础知识,初步掌握微分学和积分学的基本思想和方法,进一步学习用微积分学的思想理论分析解决各种应用问题。
高等数学教学大纲
《高等数学》课程教学大纲一、《高等数学》课程说明(一)课程代码:(二)课程英文名称:Advanced Mathematics(三)开课对象:非数学专业专科学生(理科)(四)课程的性质:高等数学是高等教育专科重要的基础理论课之一。
通过本课程的学习,使学生获得微积分、空间解析几何、级数及常微分方程的基础知识和常用的运算方法。
通过各教学环节逐步培养学生分析问题和解决问题的能力。
为学习后继课程及今后的专业工作奠定必要的数学基础。
(五)教学目的:通过本课程的教学,提高学生的逻辑推理的能力,空间想象的能力,使学生具有比较熟练的运算能力和综合运用所学知识去分析问题、解决问题的能力。
(六)教学内容:1 要正确了解和理解以下概念:函数、极限、连续性、导数、微分、偏导数、全微分、函数的极值。
不定积分、定积分、二重积分、三重积分、无穷级数的敛散性、有关空间解析几何及常微分方程的基本概念。
2 要了解和掌握下列基本理论、基本定理和公式:基本初等函数的性质及图形,基本初等函数的导数公式,微分中值定理(罗尔定理、拉格朗日定理),不定积分基本公式,变上限积分及其求导定理、牛顿-莱伯尼兹公式,偏导数的几何意义,极值存在的必要条件,几何级数和P级数的收敛性,级数敛散性的判定条件,直线与平面的方程,典型的二次曲面、二阶线性常微分方程解的结构。
3掌握下列运算法则和方法:求函数和数列极限的方法与运算法则,导数和微分的运算法则,复合函数求导法,初等函数一阶、二阶导数的求法,用导数判断函数的单调性及求极值方法,多元函数复合函数的偏导数求法,不定积分、定积分的换元与分部积分法,正项级数的比值审敛法,求幂级数的收敛半径和收敛区间,函数展开成幂级数的间接展开法,一阶变量可分离变量微分方程的求解,二阶常系数线性微分方程的解法。
4 应用方面:用定积分和常微分方程方法求解一些简单的几何和物理问题,用极值方法求解最大值最小值的应用问题。
(七)教学时数教学时数:136学时教学时数具体分配:(八)教学方式课堂讲授,课外习作及批改.(九)考核方式和成绩记载说明考核方式为考试。
高等数学教学大纲
高等数学教学大纲课程概述高等数学是大学数学教育的基础课程,旨在为学生提供数学知识和技能,培养其逻辑思维能力、分析问题和解决问题的能力。
本大纲详细说明了高等数学课程的教学目标、教学内容、教学方法和评估方式。
教学目标1.理解高等数学的基本概念和理论,如函数、极限、连续性、微积分等。
2.掌握高等数学的基本方法和技能,包括微分学、积分学及其应用,能够运用数学知识解决实际问题。
3.培养学生的数学素养和逻辑思维能力,提高其分析问题和解决问题的能力。
4.使学生具备初步的研究能力,为后续课程的学习和研究打下基础。
教学内容1.函数与极限:包括函数的定义与性质,数列的极限,函数的极限与连续性。
2.导数与微分:包括导数的定义与性质,求导法则,微分及其应用。
3.积分学:包括不定积分与定积分的定义、性质和计算方法,以及积分的应用。
4.多元函数微积分:包括多元函数的极限、连续性、偏导数与全微分,以及二重积分。
5.无穷级数与常微分方程:包括无穷级数的概念与性质,常微分方程的基本概念与求解方法。
教学方法1.课堂讲解:通过讲解基本概念、理论和例题,使学生了解和掌握高等数学的知识和方法。
2.习题练习:通过大量的习题练习,加深学生对知识的理解,提高其解题能力。
3.案例分析:通过分析实际问题中的数学应用,培养学生的数学应用能力和解决问题的能力。
4.课堂讨论:通过讨论式教学,引导学生主动参与学习,提高其自主学习和合作学习能力。
评估方式1.平时作业:通过定期布置和批改平时作业,了解学生的学习情况,以便及时调整教学策略。
2.期中考试:通过期中考试检查学生对知识的掌握情况,为后续教学提供参考。
3.期末考试:通过期末考试全面评估学生对高等数学知识的掌握情况和应用能力。
4.课堂表现:通过观察学生的课堂表现,了解其学习状态和参与度,及时给予指导和帮助。
教学资源1.教材:选用适合学生学习的高等数学教材,保证教学内容的准确性和系统性。
2.教学辅导材料:提供相应的教学辅导材料,如习题集、案例集等,以便学生巩固和提高。
《高等数学》教学大纲
《高等数学》教学大纲一、课程基本信息课程名称:高等数学课程类别:公共基础课课程学分:_____课程总学时:_____授课对象:_____先修课程:_____二、课程性质与任务高等数学是高等院校各专业学生必修的一门重要基础理论课,它不仅为学生学习后续课程和解决实际问题提供了必不可少的数学基础知识和数学方法,而且在培养学生的创新思维能力、逻辑推理能力、空间想象能力以及分析问题和解决问题的能力等方面都起着重要的作用。
本课程的主要任务是使学生掌握高等数学的基本概念、基本理论和基本方法,培养学生运用数学知识解决实际问题的能力,为学生学习后续课程以及今后从事科学研究和实际工作打下坚实的数学基础。
三、课程教学目标1、知识目标使学生掌握函数、极限、连续、一元函数微积分学、多元函数微积分学、无穷级数、常微分方程等方面的基本概念、基本理论和基本方法。
了解数学建模的基本思想和方法,能够运用所学的数学知识建立简单的数学模型,并求解实际问题。
2、能力目标培养学生的逻辑推理能力、抽象思维能力和空间想象能力。
提高学生的运算能力和综合运用所学知识分析问题、解决问题的能力。
培养学生的创新意识和创新能力。
3、素质目标培养学生的科学态度和严谨的治学精神。
提高学生的数学素养和文化素质。
培养学生的团队合作精神和沟通能力。
四、课程教学内容与要求(一)函数、极限与连续1、函数理解函数的概念,掌握函数的表示方法。
了解函数的单调性、奇偶性、周期性和有界性。
掌握基本初等函数的性质和图形,了解初等函数的概念。
2、极限理解数列极限和函数极限的概念。
掌握极限的性质和运算法则,会求数列和函数的极限。
了解无穷小量和无穷大量的概念,掌握无穷小量的性质和比较方法。
3、连续理解函数连续的概念,掌握函数在一点连续的充要条件。
了解函数的间断点及其类型,会判断函数的间断点。
掌握初等函数的连续性,会利用连续性求函数的极限。
(二)一元函数微分学1、导数与微分理解导数的概念,掌握导数的几何意义和物理意义。
《 高等数学》教学大纲
(1)了解微分方程、方程的阶、解、通解、初始条件、特解等概念。
(2)熟练掌握可分离变量微分方程及一阶线性微分方程的解法。
、重要的不是知识的数量,而是知识的质量,有些人知道很多很多,但却不知道最有用的东西。 —— 托尔斯泰
(3)知道特殊的高阶微分方程的降阶法。
教学重点:向量的概念,向量的坐标表示及运算,两个向量平行与垂直的充要条件。简单的平面方程与直线方程的确定,常用二次曲面的方程及其图形。多元函数的概念, 偏导数、全微分的概念, 复合函数的求导法则, 曲面的切平面与法线, 多元函数极值及一些简单的最大值和最小值的应用。二重积分的概念,二重积分的计算方法(直角坐标,极坐标)。
2.平面方程(点法式、一般式)与直线方程(点向式、一般式)。(2学时)
3.常用二次曲面,以坐标轴为旋转轴的旋转曲面及母线平行于坐标轴的柱面方程及其图形。空间曲面关于坐标面的投影柱面及投影曲线。(2学时)
4.习题课:向量的点积与叉积,平面方程与直线方程。(2学时)
5.多元函数概念,二元函数极限与连续的概念,偏导数概念。(2学时)
(11)会求隐函数的偏导数。
(12)会求曲线的切线和法平面及曲面的切平面与法线。
(13)了解多元函数极值的概念,会求函数的极值。会解一些简单的最大值和最小值的应用。
(14)理解二重积分的概念,知道二重积分的性质。
(15)掌握二重积分的计算方法(直角坐标、极坐标)。
(16)会用二重积分解决简单的应用题(体积、质量、曲面面积)。
4.掌握线性方程组解判定方法;解的结构,通解的求法;掌握线性方程组的消元法。(4学时)
*(八)无穷级数(14学时)
1.无穷级数收敛、发散的概念,无穷级数性质。正项级数比较、比值审敛法。交错级数审敛法,绝对收敛与条件收敛。(6学时)
高等数学教学大纲
高等数学教学大纲高等数学》是一门必修的基础理论课程,适用于高等院校工程造价等专业学生。
其目的是培养高层次人才所需的基本课程,通过研究使学生掌握函数极限和连续、一元函数微分学、一元函数积分学、多元函数微积分、微分方程等方面的基本概念,为学生提供必不可少的数学基础知识和常用的数学方法。
同时,在能力培养上,通过各教学环节逐步培养学生用极限的方法分析的方法解决问题的能力,培养学生具有一定的逻辑思维能力,初步的抽象概括问题的能力和综合运用所学知识分析问题、解决问题的能力。
第一章为函数极限连续,包括理解函数的概念、会求函数的定义域、了解函数有界性、单调性、奇偶性和周期性、理解复合函数的概念、会写复合函数的复合结构、了解反函数的概念、掌握基本初等函数的性质及其图形、会建立简单实际问题中的函数关系式等内容。
教学重点为理解函数的定义,会求不同类型的函数的定义域,理解复合函数的概念,会写复合函数的复合结构。
教学难点为理解复合函数的概念,写出复合函数的复合结构。
教学方法为讲授为主。
第二章为一元函数微分学及其应用,包括了解导数的物理意义,并会用导数描述一些物理量等内容。
教学重点为掌握几种求极限的方法,利用函数在某点处连续的概念判断函数在这点处的连续性,了解间断点的概念,并会判别间断点的类型。
教学难点为利用两个重要极限的第二个求极限。
教学方法为启发讲授、讲练结合。
总体来说,《高等数学》课程教学大纲是为了培养学生的数学基础知识和常用的数学方法,同时也注重学生的能力培养,通过各教学环节逐步培养学生的分析问题和解决问题的能力。
理解导数的概念及几何意义,以及函数的可导性与连续性之间的关系。
重点介绍导数在物理上的应用。
掌握导数的四则运算法则,复合函数的求导法,以及基本初等函数的求导公式。
理解高阶导数的概念,会计算高阶导数,特别是一阶和二阶导数的求法。
理解微分的概念,会求函数的微分,并了解微分在近似计算中的应用。
理解罗尔中值定理、拉格朗日中值定理和柯西中值定理的主要内容,会用拉格朗日中值定理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
《高等数学》教学大纲(Syllabus of advanced mathematics)People do a Book slaves,then living with dead......Put the book as a tool,the books of knowledge will live.It's alive. --Hua LuogengSyllabus of advanced mathematicsAdvanced MathematicsCourse Code:070A1012for professional:tube each professional class Polytechnic:186Credits:12Content introductionThe research object of this course is a function(dependence change process quantity).The content includes the function, limit,continuity,unary function calculus,vector algebra and space analytic geometry,multivariate function differential, multi function calculus,infinite s eries(Fourier Series)and ordinary differential equations etc..Two,the purpose and task of this courseThrough the study of this course,we should make students master the basic concepts,basic theory and basic operation skills of calculus,so as to lay the necessary mathematical foundation for learning subsequent courses and further acquiring mathematical knowledge.Through each teaching link to cultivate students'abstract thinking ability,logical reasoning ability,spatial imagination ability andself-learning ability,but also pay special attention to thecultivation of students'skilled operation ability and comprehensive use of the knowledge to the ability to analyze and solve problems.Three,the relationship between this course and other coursesThis course is the first basic course in science,engineering, management and other related professional.The study of this course is closely related to the learning of students' subsequent courses,which is related to the determination of students'learning goals and the future trend of students.This course after the end of the study,as a starting point,students can enter the relevant courses.This course is a basic course of the University for four years to learn must learn.The course is basic and theoretical,and closely related to the related courses.It is the subject of national postgraduate entrance examination,which is related to the cultivation of students'comprehensive ability.This course directly affects the school teaching level.Four,the basic requirements of the courseA basic understanding of the basic theory of calculus;fully understand the background of thought and mathematical thought of calculus.Master the basic methods,means,skills of calculus,and have certain ability of analysis and demonstration and strong calculation ability.The thought method can skillfully applied calculus to solve applicationproblems.Five,the course content and the distribution of class hours Teaching content of theoryChapter1function and limit(14hours)Understanding the concept of function,compound function and piecewise function;understanding of the concept of limit, limit on the left and right limit;understand the concept of infinity and infinitesimal;understanding the concept of function continuity(including left and right continuous continuous);graphic properties and grasp the basic elementary function;and the properties of palm grip limit four operations rule;master two criteria on the existence of limit;grasp the method of two important limits;grasp the method of infinitesimal;understand the function of parity,monotonicity, periodicity and boundedness;understand the concept of inverse function and implicit function,and the relationship between the existence of the limit and the left and right limit understanding;the nature of continuous function and continuity of elementary functions,understand the nature of continuous function on a closed interval(boundedness,maximum and minimum value theorem and intermediate value theorem);a simple stress By using the functional relation in the problem, the limit of the two criteria of the limit can be used;the limit of equivalent infinitesimal is used;the type of the discontinuous point of the function is distinguished;the properties of the continuous function on the closed interval can be applied.The second chapter,derivative and differential(12hours)To understand the concept of derivative and differential; understand the relation between derivative and differential geometry;understanding of derivative;understand the function of the relationship between the derivation and continuity; derivation rule master derivative four arithmetic operations and composite function;derivative formula master basic elementary function;understand the physical meaning of derivative;understanding four differential algorithm andfirst-order differential form invariance;understand the application of differential in approximation;understand the concept of high order derivative;tangent equation and normal equation for the plane curve will;Describe some physical quantity with the derivative; differential will function;n derivative will ask simple function;one order and two order derivative will ask piecewise function;one order and two order derivative function for implicit function and is determined by the parameter equation of the derivative of the inverse function of the will.The third chapter is the application of mean value theorem and the derivative(12hours)The extreme value of understanding the function of judgment; grasp the monotonicity of the function and method of the extremal function with the derivative,grasp the function of maximum value and minimum value method and simple method for application;grasp the limits with the Cauchy theorem ofl'Hopital's rule;understand;understand the concept of curvature and radius of curvature;will use Rolle's theorem, the Lagrange theorem and Taylor theorem;judgment function graph convexity and inflection point with derivative f unction graph will ask the level,vertical and oblique asymptote,will describe the function of the graphics;calculate the curvature and radius of curvature,angle will seek two curve.The fourth chapter is indefinite integral(8hours)Understanding the original function,the concept of indefinite integral grasp;indefinite integral properties;master the basic formula of indefinite integral;grasp the changing integral method and integral method;integral rational function,will seek the rational formula of trigonometric function and simple irrational function.The fifth chapter is definite integral(8hours)Understanding the concept of definite integral;understand the function of variable upper limit definite integral definition and derivation;grasp the nature of definite integral and definite integral mean value theorem,grasp the Newton Leibniz formula;master element integral method and integral method of definite integral;understand the concept of generalized integral and generalized integral calculation.The application of definite integral in the sixth chapter(6 hours)Master the definite integral element method;master by integralexpression and calculation of some geometrical and physical quantities(plane graphics area,the length of plane curve, volume and side area,the rotating body parallel section area, average volume of a solid known variable work,gravity, pressure and function value etc.).The seventh chapter of space analytic geometry and vector algebra(12hours)To understand the spatial Cartesian coordinate system,and understand the concept of vector representation;concept surface equation;master vector(linear operation,the number of product,vector product,mixed product),grasp the coordinate expression of unit vector and direction number and direction cosine,vector,and method of coordinate expression vector operations;control plane equation and linear equation and its solution;to understand the two vector vertical and parallel conditions;understand the equation and the common figures of two surface;understand the plane curve parameter equation and general equation;understand;use the relationship between plane and straight line(parallel, vertical,intersecting etc.)to solve the problem will ask for the cylinder;equation is parallel to the axis of the rotation axis of rotation surface and bus to the axis;projection curve will space curve on coordinate plane equation.The eighth chapter of multivariate function differential method and its application(18hours)To understand the concept of multivariate function,geometric meaning of function of two variables;understanding multifunction partial derivative and differential concept;concept of directional derivative and gradient and master the calculation method;understand the concept of multiple function extremum and conditional extremum;grasp the method for multiple function partial derivative;master the calculation method of directional derivative and gradient; master the necessary condition for the existence of extremum of multivariate function;understand the partial derivative function of two variables and total differential concept,and the bounded property of continuous function in closed area; understand the necessary conditions and sufficient conditions for the existence of differential;understand the invariance of differential form,understand the application of differential in approximation;understand the concept of curve and the tangent plane and the tangent plane and surface normals; understand the sufficient conditions for the existence of two yuan would blame the extremum of function;differential;Will find the implicit function(including the implicit function determined by equations)of the partial derivative;will find the curve and the tangent plane and the surface of the tangent plane and normal equation;extreme for two yuan function,using Lagrange multiplier method;will ask simple multivariate function of the maximum and minimum,And it will solve some simple application problems.The ninth chapter is the multiple integral(10hours)Understanding the concept of double integral,triple integral three;grasp the double integral(Cartesian coordinates and polar coordinates)calculation method;understand the natureof the double integral concept of double integral,triple integral three,understand the nature of the double integral to the mean value theorem of double integral;triple integral calculation three(rectangular coordinate and cylindrical coordinate and spherical coordinates).The tenth chapter of curvilinear integral and surface integral (14hours)Understand the concept of two kinds of curve integral;master the calculation method of two kinds of curve integral;master Green formula and use plane curve integral is path independent of the conditions;grasp the method of calculation of two types of surface integral relations;to understand the nature of two curvilinear integral and two curvilinear integral;understand the concept of two types of surface integral the nature of the relationship,and two kinds of surface integral;understand the Gauss formula,Stokes Gong;;calculate the surface integral with Gauss formula;with triple integral,curve integral and surface integral for some geometrical and physical quantities (graphic area,volume,surface area,arc length,mass,center of gravity and moment of inertia gravity power and flow rate); calculate the divergence and curl.The eleventh chapter infinite series(14hours)Understanding of constant series convergence,divergence and convergence of a series of necessary conditions and concepts; grasp the basic properties and convergence series;grasp the convergence and divergence of geometric series and series of conditions;grasp the positive series comparison test and ratiotest;master class number theorem Leibniz staggered;master method the radius of convergence,convergence and convergence interval of power series;master,McLaughlin,expansion and understanding;concept of absolute convergence and conditional convergence of a series of arbitrary items,as well as the relationship between the absolute convergence and conditional convergence;understand the concept of function series convergence domain and function;to understand some of the basic properties of power series in the convergence interval; understand the function necessary and sufficient conditions for the Taylor series;understand the power series in a simple approximate calculation of the understanding of the Fu Liye series;The concept and function to the de Lickley theorem of Fourier series;will law root;will seek some power series in the convergence region and function;some simple function will be indirectly expanded in power series;will be defined in the function is expanded into Fourier series,will be defined in the function sine and cosine series series,Fourier series and the expression will write function.The twelfth chapter of ordinary differential equations(12 hours)Understanding the properties of solutions of linear differential equations and structure theorems of solutions; grasp the solution variable separation equation and linear equation;grasp the two order constant coefficient homogeneous linear differential equation solution;differential equation and its solution,in order to understand the general solution, and the initial condition and the solution concept;understand the power series solution of differential equation the will;solutions of homogeneous equations,Bernoulli equation and differential equation,the solution will be somedifferential equations with simple variable substitution;will solve the following equations by reduction method,and the solution will be:;some higher than two order linear homogeneous differential equation with constant coefficients;be polynomial, exponential function,sine function and cosine function for the free term is two,and their sum and product of constant coefficient non homogeneous linear differential equations special solution and general solution of Euler equations;will, will first order solution contains two unknown functions with constant coefficients Linear differential equations;using differential equations(or equations)to solve some simple application problems.Practice teaching content1.Exercise classThe first chapter arranges three exercise classes,the sixth, seventh chapter arranges an exercise class,and the remaining chapters arrange two exercise classes each chapter,A total of23times,accounting for46hours.Six,teaching materials and reference books"Higher mathematics"(upper and lower)Mathematics Education Department of Tongji University,higher education press.The"guiding learning of higher mathematics Harbin Universityof Science and Technology mathematics"(upper and lower)."Higher mathematics"(upper,middle andlower volumes)edited by Wen Li,Cambridge University Press.Seven,the teaching methods of this courseThe characteristics of this course are theoretical, ideological,and related basic courses and specialized courses more contacts,should pay attention to inspire and guide students to master the important concept of ideological background teaching,ideological essence of important concepts, avoid rote learning.To be good at the relevant disciplines or life often encountered in terms of the concept of concepts and calculus combined,so that students understand the necessity of learning calculus.Pay attention to various aspects of teaching(theoretical teaching,exercise class,homework, counseling)the organic links,especially to strengthen the operation and guidance link,deepen the students' understanding of the content of classroom teaching,improve the ability of analyzing and solving problems and operation ability. In teaching,the relationship between learning mathematics and learning specialized courses is introduced to students in a planned and purposeful way.Learning advanced mathematics is the key subject to obtain further learning opportunities.Due to the characteristics of the subject,the teaching should highlight the central position of the teacher,and through the efforts of teachers,fully mobilize the students'interest in learning.Eight.Distribution of teaching hoursChapterClassroom teaching Exercise class SubtotalChapter one FourteenSixTwentySecond chapters TwelveFourSixteenThird chapters TwelveFourSixteenFourth chapters EightFourTwelveFifth chapters EightFourTwelveSixth chapters SixTwoEightSeventh chapters TwelveTwoFourteenEighth chapters EighteenFourTwenty-twoNinth chapters TenFourFourteenTenth chapters FourteenFourEighteenEleventh chapters FourteenFourEighteenTwelfth chaptersTwelveFourSixteenTotalOne hundred and fortyForty-sixOne hundred and eighty-sixNine,should pay attention to the implementation of the outlineThis syllabus is based on the basic requirements of the undergraduate basic course issued by the Higher Education Department of the State Education Commission,and is formulated in accordance with the teaching plan of our university.In the process of development,the demand for mathematics knowledge based on the management profession is taken into consideration, and the physics specialty and the relatively few professional needs of mathematics are dealt with separately.The syllabus specifies four aspects:understanding,mastering,understanding and meeting,and should pay attention to the implementation.The ratio of hours to hours is1:2.Exercise course is an important teaching link to complete the basic requirements of teaching.Exercise class hours should not be less than the total class hours of1/6,and the small class is appropriate.In the teaching process,teachers should according to the students'situation,according to the requirements of the outline,in each part in the review guide book for students to indicate different grades ofextra-curricular self-study content.People do a Book slaves,then living with dead......Put the book as a tool,the books of knowledge will live.It's alive. --Hua Luogeng。
