11-卷积码
合集下载
卷积码
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25
可以看出交织可能会造成独立错误变成突发错误的特殊情况
级联码
级联码的最初想法是为了进一步降低残余误码率，但事实上它同 级联码的最初想法是为了进一步降低残余误码率， 样可以提高较低信噪比下的性能。 样可以提高较低信噪比下的性能。这是由较好构造的短码进一步 构造性能更好的长码的一种途径
纠正突发错误的码
分组码、循环码均可以检测、纠正突发错误 分组码、循环码均可以检测、 对于一个能纠正l个错误的( 对于一个能纠正l个错误的(n, k)分组码，要求： 分组码，要求： r = n – k ≥ 2l 2l 即一个( 即一个(n, k)分组码最多能纠正(n – k)/2个突发错误 分组码最多能纠正( )/2个突发错误 若再要求该( 若再要求该(n, k)分组码能够检测d个突发错误，则要求： 分组码能够检测d个突发错误，则要求： r=n–k≥l+d
下面是未进行交织处理的序列
x1 x2 x3 x4 x5 x6 x7 x8 x9 x10 x11 x12 x13 x14 x15 x16 x17 x18 x19 x20 x21 x22 x23 x24 x25
假设在信道上发送时，产生了2个突发错误，如下红色部分所示： 假设在信道上发送时，产生了2个突发错误，如下红色部分所示：
10 11(1) 00 11(0) c 01 00(1)
b 01(1)
10(0)
a
11 d 01(0)
10(1)
卷积码的图解表示— 卷积码的图解表示—树状图
观察卷积码的状态迁移图，可知根据输入值的不同，编码器只向两种状态迁移， 观察卷积码的状态迁移图，可知根据输入值的不同，编码器只向两种状态迁移， 因此也可以用二叉树来描述卷积码 树状图绘制方法： 树状图绘制方法： 1）先假设其从某一状态开始； 先假设其从某一状态开始； 2）输入为0时，树状图向上延伸；输入为1时，向下延伸； 输入为0 树状图向上延伸；输入为1 向下延伸； 3）按照状态图在时间上的迁移顺序依次绘制，分支上的数字为编码器的输出 按照状态图在时间上的迁移顺序依次绘制， 编码方法： 编码方法： 1）从树根开始编码，每一节点为码元输入点； 从树根开始编码，每一节点为码元输入点； 2）到达每一节点时按照下一输入的码元向上（0）或向下（1）走； 到达每一节点时按照下一输入的码元向上（ 或向下（ 3）编码完毕后，将行走路径上的依次进行排列，即可得到卷积码序列 编码完毕后，将行走路径上的依次进行排列，
2012.卷积码
信息组i-1对当前输出的贡献 g1=[m1, m1+Dm1,m1+D2m1]=m1［1, 1+D, 1+D2］=[0,1,0] 信息组i-2对当前输出的贡献 g2=[m2, m2+Dm2,m2+D2m2]=m2［1, 1+D, 1+D2］=[0,0,1]
输入 … i ＋ 1m i m p i,1 mi p i,2 输出
12
我们称G∞为该卷积码的生成矩阵。 由此矩阵看出,
这是一个半无限矩阵。 它有无限多的行和列。 但是,仔 细观察G∞ 可知，它的每一行都是前一行右移n0(3)位的 结果,也就是说它完全由第一行决定。 若第一行决定了, 则该码的G∞矩阵也就完全决定了。 我们把决定G∞的第 一行取出,并表示成 g∞=［111,010,001,000,000,…］=［g0,g1,g2,0,0,…］ (10.2.2)
7
一、 卷积码的生成矩阵
卷积码的一般编码器如图 10 - 3所示。 在某一时刻i,
输入到编码器的是由k0个信息元组成的信息组mi,相应地输 出序列是由n0 个码元组成的子码ci 。 若输入的信息序列
m0,m1,…,mi,…是一个半无限序列,则由卷积码编码器输出的
序列,也是一个由各子码c0,c1,…,ci,…组成的半无限长序列,称 此序列为卷积码的一个码序列。
c i(3)
(3,2,2)卷积码编码器
G (D) 1 0
g
0 1
2 1 D 1 D
101 000 001 000 011 001 000 000 g 0 , g 1 , g 2 , 0, ...
... ...
26
101 011 C M G M
输入 … i ＋ 1m i m p i,1 mi p i,2 输出
12
我们称G∞为该卷积码的生成矩阵。 由此矩阵看出,
这是一个半无限矩阵。 它有无限多的行和列。 但是,仔 细观察G∞ 可知，它的每一行都是前一行右移n0(3)位的 结果,也就是说它完全由第一行决定。 若第一行决定了, 则该码的G∞矩阵也就完全决定了。 我们把决定G∞的第 一行取出,并表示成 g∞=［111,010,001,000,000,…］=［g0,g1,g2,0,0,…］ (10.2.2)
7
一、 卷积码的生成矩阵
卷积码的一般编码器如图 10 - 3所示。 在某一时刻i,
输入到编码器的是由k0个信息元组成的信息组mi,相应地输 出序列是由n0 个码元组成的子码ci 。 若输入的信息序列
m0,m1,…,mi,…是一个半无限序列,则由卷积码编码器输出的
序列,也是一个由各子码c0,c1,…,ci,…组成的半无限长序列,称 此序列为卷积码的一个码序列。
c i(3)
(3,2,2)卷积码编码器
G (D) 1 0
g
0 1
2 1 D 1 D
101 000 001 000 011 001 000 000 g 0 , g 1 , g 2 , 0, ...
... ...
26
101 011 C M G M
第七章卷积码
3
Cl ( j) mlt (1) gt (1, j) t0
j 1,2
输入信息序列：M m0(1)m1(1)m2(1)m3(1) 输出码序列：C C0(1)C0(2)C1(1)C1(2)C2(1)C2(2)C3(1)C3(2)
19
卷积码的矩阵描述
(1) 卷积码的生成矩阵(2,1,3) 码的生成矩阵是如何得到的？
7
卷积码的基本概念
(1) 卷积码的生成序列、约束度和约束长度
(2,1,3)码
信息序列 M=[m0(1)m1(1)…]；
ml(1)表示第 l 个时刻的第 k=1个信息元； 卷积码的生成序列
– 生成序列：给定 g(i,j) 后，就可以生成编码器输出的码元。称g(1,1) 和 g(1,2) 为 (2,1,3) 卷积码的生成序列。
非系统码：在码序列 C 中的每个子码不是系统码字结构。（本例是非系统
码）
11
卷积码的基本概念
(1) 卷积码的生成序列、约束度、约束长度和码率
推论：(n,k,m) 码完全由 (nk) 个生成序列所生成，每个生成序列中含有 (N =m+1) 个元素。
– 码序列：C=[C0(1)C0(2)…C0(n) C1(1)C1(2)…C1(n) … Cl(1)Cl(2)…Cl(n)…]
• 序列译码：译码延时是随机的。 • 维特比译码：译码延时是固定的。
3
卷积码的基本概念
(1) 卷积码的生成序列、约束度、约束长度和码率 (2) 系统码形式的卷积码
4
卷积码的基本概念
(1) 卷积码的生成序列、约束度和约束长度
(2,1,3)码
5
卷积码的基本概念
(1) 卷积码的生成序列、约束度和约束长度
卷积码 交织 网格编码
交织器有两种结构，一种为伪随机交织器，一般应用于 扩频通信系统中，设计比较复杂，但性能较好。另一种为周 期性交织，周期性交织又可分为矩阵交织和卷积交织。本文 主要介绍矩阵交织结构 矩阵交织器是最早应用于信道编码中的，他是行读列出 或列读行出的交织器。解交织的操作与交织相反，接收端接 收到交织帧后，按列写入按行读出。交织与解交织是一个互 逆的过程。交织器的设计要考虑数据的长度，因为交织不可 避免的会引入延时，所以在满足系统延迟的前提下，交织矩 阵的规划是重中之重。
C1 1 0 1 ， C2 1 0 0 1 C1 0 ， C2 1 C1 0 ， C2 0
11
10
3 4 5 6 7 8 9
0 1 1 1 0 0 0
01 00 10 01 10 11 00
01 10 11 11 01 00 00
4
C1 1 ， C2 0
7
（2）卷积译码 卷积码的译码方式基本上分为两大类：代数译码和概率 译码。此处主要介绍概率译码，它是实际应用中最常采 用的译码方法。 Viterbi 引入了一种卷积码的译码算法，就是 1967年， 著名的 Viterbi 算法，之后被证明此算法等价于通过一个 加权图的最短路径问题的动态规划解，实际上就是卷积 码的最大似然译码算法。即译码器的输出总是能给出对 数似然函数值为最大码的码字。 依照上文的思想，论述 Viterbi 译码过程。假设输入 序列 U 1011100 ，输出码字 C 11,10,00,01,10,01,11 ， 经过信道传输之后出现了两个误码，送到译码器的序列 变为 R 10,10,00,01,11,01,11 ，下面就用 Viterbi 算法 来纠正错误。
8
从初始状态 S0 开始接收第一个码元，栅格图往后延 伸到下一个节点时有两条路径，输入0到 S1 和输入1 到 S0 ，然后比较接受到的码元序列与状态转移时的估 S0 到 S0 状态的估计序列是00， 计序列，本例中接收到10， S0 到 S1 的估计序列是11，然后求出两个序列的最小汉 明距离 d ，保留一条具有最大似然值的路径。如果到 达同一节点的两条路径具有相同的最大似然值，则选择 任意一条路径均可，不影响最后的译码。第一个码元译 码结束后开始比较第二个码元，同样按照“比较-保留舍弃”的算法找出最优路径，依次接收完毕全部码元信 息。如图 1-4 所示，展示了译码的完整过程。
C1 1 0 1 ， C2 1 0 0 1 C1 0 ， C2 1 C1 0 ， C2 0
11
10
3 4 5 6 7 8 9
0 1 1 1 0 0 0
01 00 10 01 10 11 00
01 10 11 11 01 00 00
4
C1 1 ， C2 0
7
（2）卷积译码 卷积码的译码方式基本上分为两大类：代数译码和概率 译码。此处主要介绍概率译码，它是实际应用中最常采 用的译码方法。 Viterbi 引入了一种卷积码的译码算法，就是 1967年， 著名的 Viterbi 算法，之后被证明此算法等价于通过一个 加权图的最短路径问题的动态规划解，实际上就是卷积 码的最大似然译码算法。即译码器的输出总是能给出对 数似然函数值为最大码的码字。 依照上文的思想，论述 Viterbi 译码过程。假设输入 序列 U 1011100 ，输出码字 C 11,10,00,01,10,01,11 ， 经过信道传输之后出现了两个误码，送到译码器的序列 变为 R 10,10,00,01,11,01,11 ，下面就用 Viterbi 算法 来纠正错误。
8
从初始状态 S0 开始接收第一个码元，栅格图往后延 伸到下一个节点时有两条路径，输入0到 S1 和输入1 到 S0 ，然后比较接受到的码元序列与状态转移时的估 S0 到 S0 状态的估计序列是00， 计序列，本例中接收到10， S0 到 S1 的估计序列是11，然后求出两个序列的最小汉 明距离 d ，保留一条具有最大似然值的路径。如果到 达同一节点的两条路径具有相同的最大似然值，则选择 任意一条路径均可，不影响最后的译码。第一个码元译 码结束后开始比较第二个码元，同样按照“比较-保留舍弃”的算法找出最优路径，依次接收完毕全部码元信 息。如图 1-4 所示，展示了译码的完整过程。
信息论与编码第六章
编码矩阵的第i行第j列元素表示由一个状态转移到
下一个状态时发送的码字。“.”表示该状态转移 不可能。
信息论与编码-卷积码
还可以用状态流图（状态转移图）来表示，如下图所示。
1/111
S2
1/100
S0
1/110
0/011
S3
0/000 0/001
S1
0/010
1/101
所以当输入信息序列是10110…时，输出码字为：
码流首先经串并转换送入移位寄存器中，移位寄 存器的一列存放一个信息组。由于约束长度为 L+1，所以共有k行L+1列。这L+1个信息码组 的k(L+1)个码元信息送入线性组合器，得到线性
组合后的n个码元 c0 i、 c1i、 、 cn i1 ，经并串
转换后作为编码器的输出。
信息论与编码-卷积码
S 1/111
0
……。
S 0/011
2
S S S 1/110 1
S 1/100
0/010
2
3
1
信息论与编码-卷积码
从例题中可以看出，编码矩阵C比较好地展示了 状态转移规律，但不足之处在于没有状态随时 刻变化的状态转移轨迹。网格图解决了这一问 题。
网格图分两部分：一部分实际上就是状态转移图， 即在某移时刻从某一状态可能转移到下一时刻 的哪些状态，输入/输出信息是什么；另一部 分是对编码过程的纪录，即状态随时刻变化的 轨迹。通过一个例题来说明。
解：本题 n=3，k=1，L=2，可以得到编码器的状态 定义、不同状态和输入时的输出以及不同状态和 输入时的下一个状态，如下表所示。
信息论与编码-卷积码
信号入
m
i 0
卷积码文档
卷积码引言卷积码是一种常用的纠错编码方法，经常用于数字通信中。
它是一种线性块码，通过将输入数据和码字的历史信息进行卷积操作，生成输出码字。
卷积码具有优秀的纠错性能和高效的解码算法，在实际应用中得到了广泛的使用。
原理卷积码的编码过程主要由两个部分组成：移位寄存器和更新寄存器。
移位寄存器用于存储输入数据的历史信息，更新寄存器用于更新码字。
卷积码的编码可以用一个状态机来表示，状态机的每个状态对应于一个码字。
通过状态转移矩阵来描述状态之间的转移关系。
卷积码的具体编码步骤如下： 1. 将输入数据放入移位寄存器。
2. 根据移位寄存器中的数据和更新寄存器的状态，计算输出码字。
3. 将输出码字发送给接收端。
卷积码的解码过程主要是一个估计问题，通过找到最有可能的原始输入数据来进行解码。
特点卷积码具有以下几个特点： - 纠错能力强：卷积码通过引入冗余信息，即码字的历史信息，可以检测和纠正数据传输中的错误。
不同的卷积码可以提供不同的纠错能力。
- 高效的解码算法：卷积码的解码算法相对简单，常用的解码算法有迭代译码算法和软判决译码算法。
这些算法能够以较低的复杂度实现可靠的解码。
- 码率灵活：卷积码的码率可以根据需求进行调整。
常用的卷积码有1/2、1/3、2/3等码率，通过调整码率可以在保证一定的纠错性能的同时，提高数据传输的效率。
应用卷积码在数字通信中有着广泛的应用，常用于以下方面：1. 移动通信：在移动通信系统中，卷积码常用于物理信道的编码和解码，提高信号的抗干扰能力和传输质量。
2. 数字广播：数字广播系统中，卷积码用于提供高质量的音视频传输，保证数据在无线环境下的实时性和可靠性。
3. 卫星通信：卫星通信系统中，卷积码被广泛应用于数据传输和媒体分发，确保数据在不同地区之间的可靠传输。
结论卷积码是一种常用的纠错编码方法，具有优秀的纠错性能和高效的解码算法。
它在数字通信中发挥着重要的作用，广泛应用于移动通信、数字广播和卫星通信等领域。
卷积码
引言卷积码是深度空间通信系统和无线通信系统中常用的一种差错控制编码。
在编码过程中,卷积码充分利用了各码字间的相关性。
在与分组码同样的码率和设备复杂性的条件下,无论从理论上还是从实践上都证明,卷积码的性能都比分组码具有优势。
而且卷积码在实现最佳译码方面也较分组码容易。
因此卷积码广泛应用于卫星通信，CDMA数字移动通信等通信系统，是很有前途的一种编码方式。
对其进行研究有很大的现实意义。
1 、(2.1.2)卷积码的基本概念1.1(2.1.2)卷积码的结构图(2.1.2)卷积码的编码器由两级移位寄存器组成，它的存数(Q0，Q1)有四种可能：00，10，01和11，相应于编码器的四个状态S0, S1, S2和S3。
(2.1.2)卷积码编码器如图1：由图可知，该卷积码的生成多项式为于是，得到的码多项式是1.2(2.1.2)卷积码的网格图表示为了表示卷积码编码器在不同输入的信息序列下，编码器各状态之间的转移关系，以及状态转移与时间的关系，须画出编码器的网格图。
网格图是一种能清楚显示状态转移的时间依赖性状态图，因而用网格图来表示编码器的操作是很有用的。
图2表示了(2.1.2)卷积码的网格图。
图中四行小圆圈表示移位寄存器的四种状态，虚线表示输入是0时的状态转移，实线表示输入是1时的状态转移，支路上标注的码元为输出比特。
2 、(2.1.2)卷积码编码器的编程实现与仿真波形由以上分析可以发现，(2.1.2)编码器由两个模二加法器组成，分别生成、。
而此时输出的是并行数据，须经过并串转换才能输出，在用VHDL编程时，用LOAD和CLK来控制信息的输入与卷积码的产生，当LOAD为底电平时，在每个CLK的上升沿输入一位信息，并进行异或运算;当LOAD为高电平时，在CLK 的上升沿时刻，把生成的卷积码经过并串转换之后输出。
经过编译调试之后，仿真波形如图3：图中，D-IN为输入的信息位，D-OUT为输出的串行卷积码，Q为移位寄存器的内容。
循环码BCH码卷积码
7
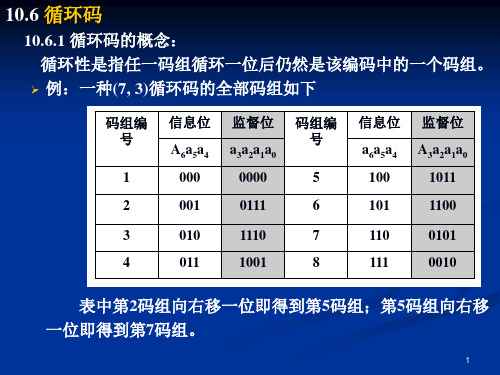
生多项式的性质： 生多项式的性质： g(x)是一 -k)次多项式 是一(n 次多项式； （1）g(x)是一(n-k)次多项式； g(x)的常数项不为 的常数项不为0 （2） g(x)的常数项不为0； g(x)必须是 必须是（ +1）的一个因子。 （3） g(x)必须是（xn+1）的一个因子。
8
因此，循环码的生成矩阵 可以写成 因此，循环码的生成矩阵G可以写成
x k −1 g ( x ) k−2 x g ( x) G ( x ) = ⋮ xg ( x ) g (x)
信息位 a6a5a4 监督位 A3a2a1a0 1011 1100 0101 0010
例：
码组编号
信息位 A6a5a4
监督位 a3a2a1a0 0000 0111 1110 1001
5
循环码的生成 有了生成矩阵G，就可以由k个信息位得出整个码组 个信息位得出整个码组： 有了生成矩阵 ，就可以由 个信息位得出整个码组： 例： A = [a 6 a 5 a 4 a 3 a 2 a 1 a 0 ] = [a 6 a 5 a 4 a 3 ]G 式中， 式中， 1000 ⋮111
x i ⋅ T ( x ) ≡ T ′( x ) （模 ( x n + 1) ）
可知， 在模(x 运算下也是一个码组， 可知，xk T ′(x)在模 n + 1)运算下也是一个码组，所以有 在模 运算下也是一个码组
x k T ′( x) T ( x) = Q( x) + n xn +1 x +1
上式左端分子和分母都是n次多项式，故相除的商式 上式左端分子和分母都是 次多项式，故相除的商式Q(x) = 1。 次多项式 。 因此， 因此，上式可以写成
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
例：设卷积码为(n, k, m) = (3, 1, 2)码
现在的发送信息位为1101
了3个“0”，即1101000
为了使移存器中的信息位全部移出，在信息位后面加入
编码后的发送序列：111 接收序列：111
110 010 100 001 011 000
010 010 110 001 011 000 (红色为错码)
000 111 001 100 010 101 011 100 010 101 101 d 011 001 000 011 a b c
a b
001
c d
110
13
若已知这3个码元是（为结尾而补充的）“0”，则在解码时 就预先知道在接收这3个“0”码元后，路径必然应该回到状 态a。而由图可见，
000 111 001 100 010 101 011 100 010 101 101 d 001 011 001 011 000 a b c
按照上表中的幸存路径画出的网格图示于下图中。
a
b
111 001
a 011 100 110 110 010 101 010 d b
100
c d
c
图中粗线路径是距汉明离最小（等于2）的路径。
12
在编码时，信息位后面加了3个“0”。若把这3个“0”仍然 看作是信息位，则可以按照上述算法继续解码。这样得到 的幸存路径网格图示于下图中。图中的粗线仍然是汉明距 离最小的路径。
3
4 5 6
aaab
abcb aabc abdc
000 000 111
111 001 100 000 111 001 111 110 010
6
4 7 1
否
是 否 是
7
8
aabd
abdd
000 111 110
111 110 101
6
4
否
是
比较到达每个状态的两条路径的汉明距离，将距离小的
一条路径保留，称为幸存路径。这样，就剩下4条路径 了，即表中第2, 4, 6和8条路径。
比较网格图中的这8条路径和接收序列之间的汉明距离。
011 011 011 b 100 100 100 001 001 001 001 c 110 110 110 110 010 010 010 d 101 101 101
9
将这8个比较结果列表如下：
序 号 1 2 路径 aaaa abca 对应序列 000 000 000 111 001 011 汉明距离 5 3 幸存否？ 否 是
例如，由出发点状态a经过3级路径后到达状态a的两条 路径中上面一条为“000 000 000”。它和接收序列“111 010 010”的汉明距离等于5；下面一条为“111 001 011”, 它和接收序列的汉明距离等于3。
a b c d 000 111 000 111 000 111 000 111 000 111 a
编码器的工作状态
b1 b3b2 状态
1 00 a
1 01 110 b
1 10 c
1 11 d
0 00 000 a
0 01 001 b
0 10 011 c
0 11 010 d
4
c1c2 c3 111
100 101
卷积码的解码 码树搜索法：(3, 1, 2)卷积码的码树图
c000c c c000c3 a 1 2 3 a c2 1 111 b c000c3 c2 1 a 001 c 111
19
维特比译码的特点
维特比算法是最大似然的序列译码算法 译码复杂度与信道质量无关 运算量与序列长度呈线性关系 存贮量与序列长度呈线性关系 运算量和存贮量都与状态数呈线性关系 状态数随分组大小k及编码深度m呈指数关系
20
维特比译码算法的演示
21
a b c d
110
只有两条路径可以回到a状态。所以，这时上图可以简化成：
a b
000 111 001 100 011 100 010 001 011 001
000 011
a b c
c d
110
010
14
d
在上例中卷积码的约束长度为N = 3，需要存储和计算8条
路径的参量。 由此可见，维特比算法的复杂度随约束长度N按指数形式 2N增长。故维特比算法适合约束长度较小（N 10）的编 码。
10
解码第2步：继续考察接收序列中的后继3个比特“110” 计算4条幸存路径上增加1级后的8条可能路径的汉明距 离。计算结果列于下表中。
路径
abca+a abdc+a abca+b abdc+b abcb+c
序号
1 2 3 4 5
原幸存路径的 距离
3 1 3 1 4
新增 路径段
aa ca ab cb bc
卷积码
1
卷积码的特点：
监督码元不仅和当前的k比特信息段有关，而且还同前面m = (N – 1)个信息段有关。
将N称为码组的约束长度。
将卷积码记作(n, k, m)，其码率为k/n。
2
卷积码的编码 一般原理方框图
每次输入 k比特
1 … k … 2k … 3k 1 … k 1 … k 1 … k … … … … … … … Nk 1 … k
15
维特比译码——收尾
最大似然序列译码要求序列有限，因此对卷积码 来说，要求能收尾。 收尾的原则：在信息序列输入完成后，利用输入 一些特定的比特，使M个状态的各残留路径可以 到达某一已知状态（一般是全零状态）。这样就 变成只有一条残留路径，这就是最大似然序列。
16
卷积码收尾的实现
非递归卷积码：约束长度为m+1的卷积码，只要 在信息序列输入完成后连续送入m个0，即可使任 一路径都到达最终的状态0。 递归卷积码：可通过将输入值置成反馈值，而使 m个时钟后的状态到达0。
17
卷积码收尾
非系统非递归码
D D
递归系统码
D D
18
维特比译码的复杂度
对信息序列长度为L，信息符号取自GF(p)，R=k/n， 约束长度为m+1的卷积码。状态数为pkm，因此对 每个时刻要做pkm次加比选得到pkm个状态的残留路 径，每次加比选包括pk次加法和pk-1次比较。因此 总运算量约为Lpkm次加比选。同时要能保存pkm条 残留路径，因此需要Lpkm个存贮单元。
Nk级 移存器
1
2
… … … …
n
n个模2 加法器
每输入k比特 旋转1周
编码输出
3
卷积码编码器的实例方框图：(n, k, m) =（3, 1, 2）
输入 1 b1 2 b2 3 b3
c3 c2 c1
编码输出
每当输入1比特时，此编码器输出3比特c1c2 c3：
c1 b1
c2 b1 b3 c3 b1 b2 b3
信息位
000 111 001 110 011 100 010 101 1
下 半 部
1
1
d
此法不实用：因为随信息位增多，分支数目按指数规律增长 5
卷积码的状态图 移存器状态和输入输出码元的关系
输入 1 b1 2 b2 3 b3
c1 b1
c3 c2 c1 编码输出
c2 b1 b3 c3 b1 b2 b3
前一状态 b3 b2 a (00) b (01) c (10) d (11)
当前输入 b1 0 1 0 1 0 1 0 1
输出 c1c 2c3 000 111 001 110 011 100 010 101
下一状态 b3 b2 a (00) b (01) c (10) d (11) a (00) b (01) c (10) d (11) 000 a 111 100 011 c
新增距离
2 2 1 1 3
总距离
5 3 4 2 7
幸存否？
否 是 否 是 否
6
7 8
abdd+c
abcb+d abdd&#dd
1
0 2
5
4 6
是
是 否
表中总距离最小为2，其路径是abdc+b，相应序列为
111 110 010 100。它和发送序列相同，故对应发送信息 位1101。 11
由于这是一个 (3, 1, 2)卷积码，发送序列的约束长度为N = m + 1 ＝ 3，所以首先需考察3个信息段，即考察3n ＝ 9比 特，即接收序列前9位“111 010 010”。
8
解码第1步
由网格图可见，沿路径每一级有4种状态a,
b, c和d。每 种状态只有两条路径可以到达。故4种状态共有8条到达 路径。
000 111 011 100 001
110 010
000 111
011 100 001 110 010 101
000 111
a
001 c d
a
b 111
110
101
011 b 100 001 c 110 010 d 101
a b
100
001 c
c
d
110
010
d
7
维特比算法
基本原理：将接收到的序列和所有可能的发送序列作比较， 选择其中汉明距离最小的序列当作是现在的发送序列
b
110 001 010 d 101
状态图
6
(3, 1, 2)卷积码的网格图 网格图中的编码路径举例 输入信息位为11010时 输出编码序列是： 111 110 010 100 001…
现在的发送信息位为1101
了3个“0”，即1101000
为了使移存器中的信息位全部移出，在信息位后面加入
编码后的发送序列：111 接收序列：111
110 010 100 001 011 000
010 010 110 001 011 000 (红色为错码)
000 111 001 100 010 101 011 100 010 101 101 d 011 001 000 011 a b c
a b
001
c d
110
13
若已知这3个码元是（为结尾而补充的）“0”，则在解码时 就预先知道在接收这3个“0”码元后，路径必然应该回到状 态a。而由图可见，
000 111 001 100 010 101 011 100 010 101 101 d 001 011 001 011 000 a b c
按照上表中的幸存路径画出的网格图示于下图中。
a
b
111 001
a 011 100 110 110 010 101 010 d b
100
c d
c
图中粗线路径是距汉明离最小（等于2）的路径。
12
在编码时，信息位后面加了3个“0”。若把这3个“0”仍然 看作是信息位，则可以按照上述算法继续解码。这样得到 的幸存路径网格图示于下图中。图中的粗线仍然是汉明距 离最小的路径。
3
4 5 6
aaab
abcb aabc abdc
000 000 111
111 001 100 000 111 001 111 110 010
6
4 7 1
否
是 否 是
7
8
aabd
abdd
000 111 110
111 110 101
6
4
否
是
比较到达每个状态的两条路径的汉明距离，将距离小的
一条路径保留，称为幸存路径。这样，就剩下4条路径 了，即表中第2, 4, 6和8条路径。
比较网格图中的这8条路径和接收序列之间的汉明距离。
011 011 011 b 100 100 100 001 001 001 001 c 110 110 110 110 010 010 010 d 101 101 101
9
将这8个比较结果列表如下：
序 号 1 2 路径 aaaa abca 对应序列 000 000 000 111 001 011 汉明距离 5 3 幸存否？ 否 是
例如，由出发点状态a经过3级路径后到达状态a的两条 路径中上面一条为“000 000 000”。它和接收序列“111 010 010”的汉明距离等于5；下面一条为“111 001 011”, 它和接收序列的汉明距离等于3。
a b c d 000 111 000 111 000 111 000 111 000 111 a
编码器的工作状态
b1 b3b2 状态
1 00 a
1 01 110 b
1 10 c
1 11 d
0 00 000 a
0 01 001 b
0 10 011 c
0 11 010 d
4
c1c2 c3 111
100 101
卷积码的解码 码树搜索法：(3, 1, 2)卷积码的码树图
c000c c c000c3 a 1 2 3 a c2 1 111 b c000c3 c2 1 a 001 c 111
19
维特比译码的特点
维特比算法是最大似然的序列译码算法 译码复杂度与信道质量无关 运算量与序列长度呈线性关系 存贮量与序列长度呈线性关系 运算量和存贮量都与状态数呈线性关系 状态数随分组大小k及编码深度m呈指数关系
20
维特比译码算法的演示
21
a b c d
110
只有两条路径可以回到a状态。所以，这时上图可以简化成：
a b
000 111 001 100 011 100 010 001 011 001
000 011
a b c
c d
110
010
14
d
在上例中卷积码的约束长度为N = 3，需要存储和计算8条
路径的参量。 由此可见，维特比算法的复杂度随约束长度N按指数形式 2N增长。故维特比算法适合约束长度较小（N 10）的编 码。
10
解码第2步：继续考察接收序列中的后继3个比特“110” 计算4条幸存路径上增加1级后的8条可能路径的汉明距 离。计算结果列于下表中。
路径
abca+a abdc+a abca+b abdc+b abcb+c
序号
1 2 3 4 5
原幸存路径的 距离
3 1 3 1 4
新增 路径段
aa ca ab cb bc
卷积码
1
卷积码的特点：
监督码元不仅和当前的k比特信息段有关，而且还同前面m = (N – 1)个信息段有关。
将N称为码组的约束长度。
将卷积码记作(n, k, m)，其码率为k/n。
2
卷积码的编码 一般原理方框图
每次输入 k比特
1 … k … 2k … 3k 1 … k 1 … k 1 … k … … … … … … … Nk 1 … k
15
维特比译码——收尾
最大似然序列译码要求序列有限，因此对卷积码 来说，要求能收尾。 收尾的原则：在信息序列输入完成后，利用输入 一些特定的比特，使M个状态的各残留路径可以 到达某一已知状态（一般是全零状态）。这样就 变成只有一条残留路径，这就是最大似然序列。
16
卷积码收尾的实现
非递归卷积码：约束长度为m+1的卷积码，只要 在信息序列输入完成后连续送入m个0，即可使任 一路径都到达最终的状态0。 递归卷积码：可通过将输入值置成反馈值，而使 m个时钟后的状态到达0。
17
卷积码收尾
非系统非递归码
D D
递归系统码
D D
18
维特比译码的复杂度
对信息序列长度为L，信息符号取自GF(p)，R=k/n， 约束长度为m+1的卷积码。状态数为pkm，因此对 每个时刻要做pkm次加比选得到pkm个状态的残留路 径，每次加比选包括pk次加法和pk-1次比较。因此 总运算量约为Lpkm次加比选。同时要能保存pkm条 残留路径，因此需要Lpkm个存贮单元。
Nk级 移存器
1
2
… … … …
n
n个模2 加法器
每输入k比特 旋转1周
编码输出
3
卷积码编码器的实例方框图：(n, k, m) =（3, 1, 2）
输入 1 b1 2 b2 3 b3
c3 c2 c1
编码输出
每当输入1比特时，此编码器输出3比特c1c2 c3：
c1 b1
c2 b1 b3 c3 b1 b2 b3
信息位
000 111 001 110 011 100 010 101 1
下 半 部
1
1
d
此法不实用：因为随信息位增多，分支数目按指数规律增长 5
卷积码的状态图 移存器状态和输入输出码元的关系
输入 1 b1 2 b2 3 b3
c1 b1
c3 c2 c1 编码输出
c2 b1 b3 c3 b1 b2 b3
前一状态 b3 b2 a (00) b (01) c (10) d (11)
当前输入 b1 0 1 0 1 0 1 0 1
输出 c1c 2c3 000 111 001 110 011 100 010 101
下一状态 b3 b2 a (00) b (01) c (10) d (11) a (00) b (01) c (10) d (11) 000 a 111 100 011 c
新增距离
2 2 1 1 3
总距离
5 3 4 2 7
幸存否？
否 是 否 是 否
6
7 8
abdd+c
abcb+d abdd&#dd
1
0 2
5
4 6
是
是 否
表中总距离最小为2，其路径是abdc+b，相应序列为
111 110 010 100。它和发送序列相同，故对应发送信息 位1101。 11
由于这是一个 (3, 1, 2)卷积码，发送序列的约束长度为N = m + 1 ＝ 3，所以首先需考察3个信息段，即考察3n ＝ 9比 特，即接收序列前9位“111 010 010”。
8
解码第1步
由网格图可见，沿路径每一级有4种状态a,
b, c和d。每 种状态只有两条路径可以到达。故4种状态共有8条到达 路径。
000 111 011 100 001
110 010
000 111
011 100 001 110 010 101
000 111
a
001 c d
a
b 111
110
101
011 b 100 001 c 110 010 d 101
a b
100
001 c
c
d
110
010
d
7
维特比算法
基本原理：将接收到的序列和所有可能的发送序列作比较， 选择其中汉明距离最小的序列当作是现在的发送序列
b
110 001 010 d 101
状态图
6
(3, 1, 2)卷积码的网格图 网格图中的编码路径举例 输入信息位为11010时 输出编码序列是： 111 110 010 100 001…