专升本《信息论与编码》_试卷_答案
信息论与编码习题参考答案(全)
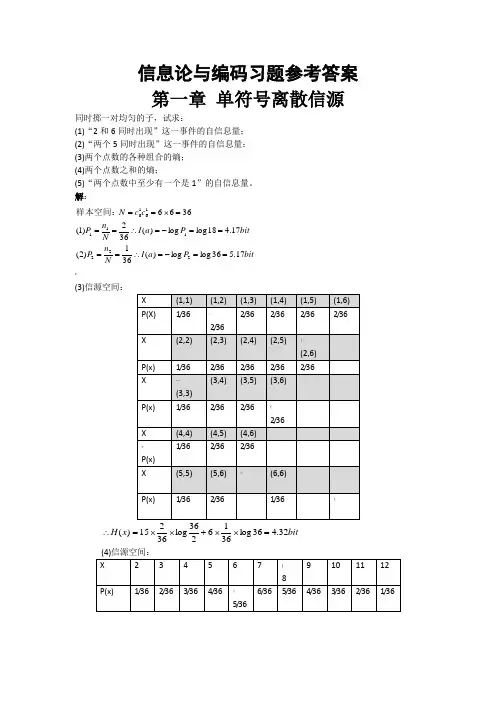
信息论与编码习题参考答案第一章 单符号离散信源同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。
解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：* (3)信源空间：bit x H 32.436log 3616236log 36215)(=⨯⨯+⨯⨯=∴bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==?如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格内，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格内。
（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。
解： ！bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率bitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知 bitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为%.如果你问一位男士：“你是否是红绿色盲”他的回答可能是：“是”，也可能“不是”。
信息论与编码试卷及答案2
篇一：信息论与编码期末题(全套)〔一〕7、某二元信源一、判断题共 10 小题，总分值 20 分.1. 当随机变量X和Y相互独立时，条件熵H(X|Y)等于信源熵H(X). 〔〕2. 由于构成同一空间的基底不是唯一的，所以不同的基1X0P(X)1/21/2，其失真矩阵0a，那么该信源的Dmax= Da0三、此题共 4 小题，总分值 50 分.1、某信源发送端有2种符号xi(i1,2),p(x1)a；接收端底或生成矩阵有可能生成同一码集.符号 y( j 1 ,2) ，转移概率矩阵为有3 种,3〔〕3.一般情况下，用变长编码得到的平均码长比定长编码大得多. 〔〕4. 只要信息传输率大于信道容量，总存在一种信道编译码，可以以所要求的任意小的误差概率实现可靠的通信〔〕 5. 各码字的长度符合克拉夫特不等式，是唯一可译码存在的充分和必要条件. 〔〕 6. 连续信源和离散信源的熵都具有非负性. 〔〕7. 信源的消息通过信道传输后的误差或失真越大，信宿收到消息后对信源存在的不确定性就越小，获得的信息量就越小. 8. 汉明码是一种线性分组码. 〔〕 9. 率失真函数的最小值是0. 〔〕10.必然事件和不可能事件的自信息量都是0. 〔〕二、填空题共 6 小题，总分值 20 分.1、码的检、纠错能力取决于 .2、信源编码的目的是的目的是 .3、把信息组原封不动地搬到码字前k位的(n,k)码就叫做 .4、香农信息论中的三大极限定理是、、. 5、设信道的输入与输出随机序列分别为X和Y，那么I(XN,YN)NI(X,Y)成立的条件6、对于香农-费诺编码、原始香农-费诺编码和哈夫曼编码，编码方法惟一的是 . iP1/21/201/21/41/4.〔1〕计算接收端的平均不确定度H(Y)；〔2〕计算由于噪声产生的不确定度H(Y|X)；〔3〕计算信道容量以及最正确入口分布. 2、一阶马尔可夫信源的状态转移图2-13图如右图所示，信源X的符号集为{0,1,2}. 〔1〕求信源平稳后的概率分布；〔2〕求此信源的熵；〔 3 〕近似地认为此信源为无记忆时，符号的概率分布为平 X )稳分布.求近似信源的熵H(并与H进行比拟.4 、设二元( 7 , 4 ) 线〔1〕给出该码的一致校验矩阵，写出所有的陪集首和与之相对应的伴随式；)，试计算出其对应的伴随式S并按照最小距离译码准那么试着对其译码. 〔二〕一、填空题〔共15分，每空1分〕1、信源编码的主要目的是，信道编码的主要目的是。
信息论与编码习题参考答案(全)
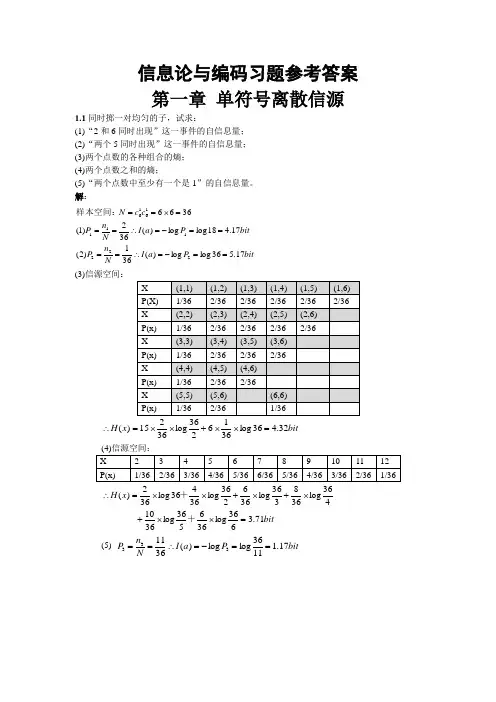
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。
解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格。
（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。
解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士：“你是否是红绿色盲？”他的回答可能是：“是”，也可能“不是”。
信息论与编码习题参考答案(全)
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。
解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格。
（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。
解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士：“你是否是红绿色盲？”他的回答可能是：“是”，也可能“不是”。
信息论与编码试题集与答案
一填空题（本题20分，每小题2分）1、平均自信息为表示信源的平均不确定度，也表示平均每个信源消息所提供的信息量。
平均互信息表示从Y获得的关于每个X的平均信息量，也表示发X前后Y的平均不确定性减少的量，还表示通信前后整个系统不确定性减少的量。
2、最大离散熵定理为：离散无记忆信源，等概率分布时熵最大。
3、最大熵值为。
4、通信系统模型如下：5、香农公式为为保证足够大的信道容量，可采用（1）用频带换信噪比；（2）用信噪比换频带。
6、只要，当N足够长时，一定存在一种无失真编码。
7、当R＜C时，只要码长足够长，一定能找到一种编码方法和译码规则，使译码错误概率无穷小。
8、在认识论层次上研究信息的时候，必须同时考虑到形式、含义和效用三个方面的因素。
9、1948年，美国数学家香农发表了题为“通信的数学理论”的长篇论文，从而创立了信息论。
按照信息的性质，可以把信息分成语法信息、语义信息和语用信息。
按照信息的地位，可以把信息分成 客观信息和主观信息 。
人们研究信息论的目的是为了 高效、可靠、安全 地交换和利用各种各样的信息。
信息的 可度量性 是建立信息论的基础。
统计度量 是信息度量最常用的方法。
熵 是香农信息论最基本最重要的概念。
事物的不确定度是用时间统计发生 概率的对数 来描述的。
10、单符号离散信源一般用随机变量描述，而多符号离散信源一般用 随机矢量 描述。
11、一个随机事件发生某一结果后所带来的信息量称为自信息量，定义为 其发生概率对数的负值 。
12、自信息量的单位一般有 比特、奈特和哈特 。
13、必然事件的自信息是 0 。
14、不可能事件的自信息量是 ∞ 。
15、两个相互独立的随机变量的联合自信息量等于 两个自信息量之和 。
16、数据处理定理：当消息经过多级处理后，随着处理器数目的增多，输入消息与输出消息之间的平均互信息量 趋于变小 。
17、离散平稳无记忆信源X 的N 次扩展信源的熵等于离散信源X 的熵的 N 倍 。
信息论与编码考试题(附答案版)
1.按发出符号之间的关系来分，信源可以分为（有记忆信源）和（无记忆信源）2.连续信源的熵是（无穷大），不再具有熵的物理含义。
3.对于有记忆离散序列信源，需引入（条件熵）描述信源发出的符号序列内各个符号之间的统计关联特性3.连续信源X,平均功率被限定为P时，符合（正态）分布才具有最大熵，最大熵是（1/2ln（2 ⅇ 2））。
4.数据处理过程中信息具有（不增性）。
5.信源冗余度产生的原因包括（信源符号之间的相关性）和（信源符号分布的不均匀性）。
6.单符号连续信道的信道容量取决于（信噪比）。
7.香农信息极限的含义是（当带宽不受限制时，传送1bit信息，信噪比最低只需-1.6ch3）。
8.对于无失真信源编码，平均码长越小，说明压缩效率（越高）。
9.对于限失真信源编码，保证D的前提下，尽量减少（R(D)）。
10.立即码指的是（接收端收到一个完整的码字后可立即译码）。
11.算术编码是（非）分组码。
12.游程编码是（无）失真信源编码。
13.线性分组码的（校验矩阵）就是该码空间的对偶空间的生成矩阵。
14.若（n，k）线性分组码为MDC码，那么它的最小码距为（n-k+1）。
15.完备码的特点是（围绕2k个码字、汉明矩d=[（d min-1）/2]的球都是不相交的每一个接受吗字都落在这些球中之一，因此接收码离发码的距离至多为t，这时所有重量≤t的差错图案都能用最佳译码器得到纠正，而所有重量≤t+1的差错图案都不能纠正）。
16.卷积码的自由距离决定了其（检错和纠错能力）。
（对）1、信息是指各个事物运动的状态及状态变化的方式。
（对）2、信息就是信息，既不是物质也不是能量。
（错）3、马尔可夫信源是离散无记忆信源。
（错）4、不可约的马尔可夫链一定是遍历的。
（对）5、单符号连续信源的绝对熵为无穷大。
（错）6、序列信源的极限熵是这样定义的：H(X)=H(XL|X1,X2,…,XL-1)。
（对）7、平均互信息量I(X;Y)是接收端所获取的关于发送端信源X的信息量。
信息论与编码考试题(附答案版)
1.按发出符号之间的关系来分，信源可以分为（有记忆信源）和（无记忆信源）2.连续信源的熵是（无穷大），不再具有熵的物理含义。
3.对于有记忆离散序列信源，需引入（条件熵）描述信源发出的符号序列内各个符号之间的统计关联特性3.连续信源X,平均功率被限定为P时，符合（正态）分布才具有最大熵，最大熵是（1/2ln （2πⅇσ2））。
4.数据处理过程中信息具有（不增性）。
5.信源冗余度产生的原因包括（信源符号之间的相关性）和（信源符号分布的不均匀性）。
6.单符号连续信道的信道容量取决于（信噪比）。
7.香农信息极限的含义是（当带宽不受限制时，传送1bit信息，信噪比最低只需-1.6ch3）。
8.对于无失真信源编码，平均码长越小，说明压缩效率（越高）。
9.对于限失真信源编码，保证D的前提下，尽量减少（R(D)）。
10.立即码指的是（接收端收到一个完整的码字后可立即译码）。
11.算术编码是（非）分组码。
12.游程编码是（无）失真信源编码。
13.线性分组码的（校验矩阵）就是该码空间的对偶空间的生成矩阵。
14.若（n，k）线性分组码为MDC码，那么它的最小码距为（n-k+1）。
15.完备码的特点是（围绕2k个码字、汉明矩d=[（d min-1）/2]的球都是不相交的每一个接受吗字都落在这些球中之一，因此接收码离发码的距离至多为t，这时所有重量≤t的差错图案都能用最佳译码器得到纠正，而所有重量≤t+1的差错图案都不能纠正）。
16.卷积码的自由距离决定了其（检错和纠错能力）。
（对）1、信息是指各个事物运动的状态及状态变化的方式。
（对）2、信息就是信息，既不是物质也不是能量。
（错）3、马尔可夫信源是离散无记忆信源。
（错）4、不可约的马尔可夫链一定是遍历的。
（对）5、单符号连续信源的绝对熵为无穷大。
（错）6、序列信源的极限熵是这样定义的：H(X)=H(XL|X1,X2,…,XL-1)。
（对）7、平均互信息量I(X;Y)是接收端所获取的关于发送端信源X的信息量。
信息论与编码习题参考答案(全)
信息论与编码习题参考答案 第一章 单符号离散信源1.1同时掷一对均匀的子，试求：(1)“2和6同时出现”这一事件的自信息量； (2)“两个5同时出现”这一事件的自信息量； (3)两个点数的各种组合的熵； (4)两个点数之和的熵；(5)“两个点数中至少有一个是1”的自信息量。
解：bitP a I N n P bit P a I N n P c c N 17.536log log )(361)2(17.418log log )(362)1(36662221111616==-=∴====-=∴===⨯==样本空间：(3)信源空间：bit x H 32.436log 3662log 3615)(=⨯⨯+⨯⨯=∴ bitx H 71.3636log 366536log 3610 436log 368336log 366236log 36436log 362)(=⨯⨯+⨯+⨯+⨯⨯=∴＋＋ (5) bit P a I N n P 17.11136log log )(3611333==-=∴==1.2如有6行、8列的棋型方格，若有两个质点A 和B ，分别以等概落入任一方格，且它们的坐标分别为（Xa ，Ya ）, （Xb ，Yb ）,但A ，B 不能同时落入同一方格。
（1） 若仅有质点A ，求A 落入任一方格的平均信息量； （2） 若已知A 已落入，求B 落入的平均信息量； （3） 若A ，B 是可辨认的，求A ，B 落入的平均信息量。
解：bita P a P a a P a I a P A i 58.548log )(log )()(H 48log )(log )(481)(:)1(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率Θbitb P b P b b P b I b P A i 55.547log )(log )()(H 47log )(log )(471)(:B ,)2(481i i i i i ==-=∴=-=∴=∑=落入任一格的概率是落入任一格的情况下在已知ΘbitAB P AB P AB H AB P AB I AB P AB i i i i i i i 14.11)4748log()(log )()()(log )(471481)()3(47481=⨯=-=-=∴⨯=∑⨯=是同时落入某两格的概率1.3从大量统计资料知道,男性中红绿色盲的发病率为7%,女性发病率为0.5%.如果你问一位男士：“你是否是红绿色盲？”他的回答可能是：“是”，也可能“不是”。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
专升本《信息论与编码》一、（共48题,共150分）1. H(X)____________0，小概率事件对熵的贡献____________，确定事件的信息量____________0。
（6分）.标准答案：1. >= ;2. 小;3. =;2. 确定信道的H(Y/X) ____0，H(X/Y) ____0。
（4分）.标准答案：1. =;2. ;3. 霍夫曼编码可以编出不同的码，这些码的平均码长________，.编码效率________，码长方差________。
（6分）.标准答案：1. 一样;2. 一样;3. 不一定一样;4. N个独立并联的信道，每个信道的信道容量为C，为了达到总的信道容量NC，所有信道的输入要________________，.所有信道的输入概率分布是各自信道的________________。
（4分）.标准答案：1. 相互独立;2. 最佳分布;5. 通信系统中的编码器包括____________________，____________________，____________________。
（6分）.标准答案：1. 信源编码器;2. 纠错编码器;3. 调制器;6. 率失真函数R（D）的最大值为________________，最小值为________________。
（4分）.标准答案：1. H(X);2. 0;7. 某事件的概率为p(x)，则自信息量为（）。
（2分）A.-p(x)B.1/ p(x)C.-log p(x)D.log p(x).标准答案：C8. 有事件x，y，I(x)=2 bit，I(x/y)=1 bit，则互信息量I(x；y)的值为（）。
（2分）A.1 bitB.2 bitC.3 bitD.4 bit.标准答案：A9. 下列关于条件熵的结论，不成立的是（）（2分）A.H(X/Y)C.H(X/Y).标准答案：B10. 使I(X;Y)=0成立的条件是（）: （2分）A.X和Y相互独立B.H (X) =H(Y)C.X和Y的概率分布相同.标准答案：A 11. 以下关于离散无记忆信源（熵为H(X)）的结论，不正确的是（）: （2分）A.是平稳信源B.其N次无记忆扩展信源的熵是NH(X)C.其极限熵大于H(X).标准答案：C12. 以下关于信道容量C和信息传输率R间的关系，正确的是（）: （2分）A.C RB.C=RC.C R.标准答案：A13. 某信源有8个符号，其信源熵为2.4 bit，进行二元定长编码（不扩展），则其编码效率至少可达（）（2分）A.80%B.85%C.90%D.95%.标准答案：A14. 在准对称信道中，要达到信道容量，要求（）: （2分）A.信源和信宿的概率分布一致B.信源为等概分布C.信宿为等概分布.标准答案：B15. 在信道编码中，简单重复编码可以（）: （2分）A.减小但降低了信息传输率B.提高了信息传输率，但增大了PEC.减小并提高了信息传输率.标准答案：A16. 二元码C={(000),(011),(101),(110)，该码的最小码距是（）:。
（2分）A.1B.2C.3D.4.标准答案：B17. 率失真函数R(D)的取值与（）无关（2分）A.信源的概率分布B.保真度DC.失真函数D.信道转移矩阵.标准答案：D18. 熵函数是信源概率分布的________函数，函数值________0。
（4分）.标准答案：1. 上凸;2. ;19. I(x i,y j) ____ I(y j,x i)，I(x i,y j) ____ I(x i)，I(x i,y j) ____ I(y j)。
（6分）.标准答案：1. =;2. ;3. ;20. 信源编码的目的是提高系统的____________，纠错编码的目的是提高系统的____________。
（4分）.标准答案：1. 有效性;2. 可靠性;21. 无噪信道的H（X/Y）____0，收到Y可完全确定____，其最佳输入分布为____。
（6分）.标准答案：1. =;2. X;3. 等概分布;22. 有m个输入符号的离散无损信道的信道容量为________________bit，其最佳输入分布为________________。
（4分）.标准答案：1. logm;2. 等概分布;23. 一个(n,k)线性分组码的最小汉明距离为5，则其校验矩阵中任意____个列向量线性无关，可检测____个错误，可纠正____个错误。
（6分）.标准答案：1. 4;2. 4;3. 2;24. 两个事件A和B，P(A)>P(B)，则两者包含的自信息量I(A)和I(B)的关系是（）。
（2分）A.I(A)>I(B)B.I(A)=I(B)C.I(A).标准答案：C25. 信源X包含n个不同的离散消息，其信源熵的最大值为（）。
（2分）A.nB.1C.log nD.n+1.标准答案：C26. 离散无记忆信源X的熵为2，则其三次扩展信源的熵为（）: （2分）A.2B.4C.6D.8.标准答案：C27. 对马尔科夫信源来说，下列结论不正确的是（）: （2分）A.是有记忆信源B.其记忆长度是无限的C.是平稳信源.标准答案：B28. 对有n个输入符号、m个输出符号的确定信道来说，其信道容量为（）: （2分）A.log nB.log mC.H(X)D.H(Y).标准答案：B29. 对一个两级串联信道，要使串联传输不增加信息损失，信道需满足（）: （2分）A.两个信道都是对称信道B.两个信道的信道矩阵相同C.两个信道的信道容量相等D.总的信道矩阵等于第一级信道矩阵.标准答案：D30. 为了正确译码，信源编码必须是（）: （2分）A.奇异码B.非奇异码C.唯一可译码.标准答案：C31. 信源X的熵为2，信源Y的熵为3，X、Y相互独立，则其联合熵H(XY)=（）（2分）A.2B.3C.6D.5.标准答案：D32. 费诺编码在（）的情况下，编码效率最高（2分）A.信源为等概分布B.概率分布极不平均C.编码时每次分组的概率相等.标准答案：C33. 香农信息论中，概率小的事件，信息量____，确定事件____信息量。
（4分）.标准答案：1. 大;2. 不含;34. H(X/Y) ________H(X) 0；H(XY) ________H(X)；H(XY) ________H(X/Y)。
（6分）.标准答案：1.35. 对串联信道，如果串联信道的总的信道矩阵等于第一级信道矩阵，则________增加信息的损失；信息在传输中损失后，后续系统________恢复。
（4分）.标准答案：1. 不会;2. 不能;36. 率失真函数R(D)是D的________、________下凸函数，当D>=Dmax时，R(D)= ________。
（6分）.标准答案：1. 递减;2. 下凸;3. 0;37. 无记忆信源____平稳信源，马尔科夫信源____平稳信源，.平稳信源的极限熵____H(X)。
（6分）.标准答案：1. 是;2. 是;3.38. 香农编码、费诺编码和霍夫曼编码的共同点是编出的码都是____________，大概率符号对应的码字码长____________。
（4分）.标准答案：1. 即时码;2. 短;39. 一下关于条件自信息量的结论，不正确的是（）。
（2分）A.条件自信息量不大于联合自信息量B.条件自信息量不能为负数C.条件自信息量不大于自信息量.标准答案：C40. 互信息量为负值的条件是（）:（2分）A.见图B.见图C.见图D.见图.标准答案：D41. 信源X有三个消息符号，当概率分布为（），H(X)的值最大: （2分）A.{1,0,0B.{1/3,1/3,/1/3C.{0,1/2,1/2.标准答案：B42. 对信源X和Y来说，下列值中最小的是（）: （2分）A.I(X;Y)B.H(X)C.H(Y)D.H(X,Y).标准答案：A43. 信道容量C是（）对信源分布的最大值: （2分）A.I(X;Y)B.H(X)C.H(Y)D.H(X,Y).标准答案：A44. 实现离散准对称无记忆信道信道容量的信源应满足（）: （2分）A.信源为等概分布B.信源符号和信宿符号个数相等C.信源和信宿概率分布相同D.信宿为等概分布.标准答案：A45. 一个小型字库有220个汉字，要进行二元定长编码，为了保证唯一可译性，则码长至少是（）。
（2分）A.5B.6C.7D.8.标准答案：D46. 选择译码规则总的原则是（）: （2分）A.使平均错误概率PE最小B.使噪声熵最小C.使信道损失最小.标准答案：A47. 对连续信源和连续信道来说，下列结论不正确的是（）（2分）A.条件熵可正可负B.无条件熵可正可负C.联合熵可正可负D.平均互信息可正可负.标准答案：D 48. 在线性分组码中，生成矩阵G和校验矩阵H的关系是:（2分）A.见图B.见图C.见图D.见图.标准答案：A。