对勾函数最值的十种求法

合集下载

对勾函数绝对经典

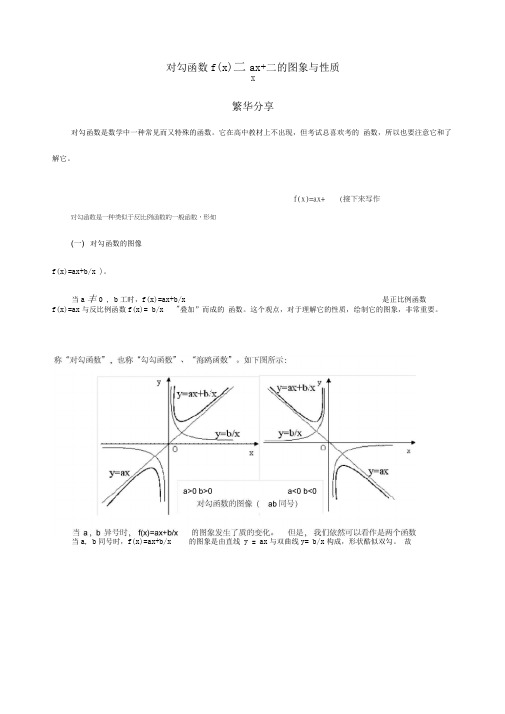
对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+ (接下来写作对勾函数f(x)二ax+二的图象与性质X繁华分享对勾函数是数学中一种常见而又特殊的函数。

它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。

(一) 对勾函数的图像f(x)=ax+b/x )。

当a丰0 , b工时，f(x)=ax+b/x 是正比例函数f(x)=ax与反比例函数f(x)= b/x "叠加”而成的函数。

这个观点，对于理解它的性质，绘制它的图象，非常重要。

当a, b同号时，f(x)=ax+b/x 的图象是由直线y = ax与双曲线y= b/x构成，形状酷似双勾。

故加”而成。

(请自己在图上完成：他是如何叠加而成的。

ab异号）般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。

接下来，为了研究方便，我们规定a>0，b>0。

之后当a<0，b<0时，根据对称就很容易得出结论了。

（二）对勾函数的顶点对勾函数性质的研究离不开均值不等式。

利用均值不等式可以得到：当x>0时，g = 是2耐当且黯心扌时取等号），此时卞=卡。

当x<0时，f（£ = 3龙十g玉一2耳旺律且尽当= £时IR等号卜此时耳=-皆。

即对勾函数的定点坐标：ulr2,-2 vabA;（三）对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。

定义域：図£ = 0% 值域；｛y|y >厶飯或v< -2VaS）（四）对勾函数的单调性对于函数f(x)= ax-1-单调增区间’fl U 卡卄）；单调减2>（五）对勾函数的渐进线由图像我们不难得到:对于函它的渐进线有两離"Xiy = is；F =0；X（六）对勾函数的奇偶性对勾函数在定义域内是奇函数,利用对号函数以上性质，在解某些数学题时很简便，下面举例说明:1、求函数yx2 2x 4 .x22x 的最小值。

对勾函数的顶点

对勾函数的顶点一、什么是对勾函数呢？对勾函数啊，就是那种形状像个对勾的函数啦。

它的一般形式是y = ax + b/x（a、b同号）。

这个函数在数学里可有趣了呢。

二、对勾函数顶点的求法1. 咱们可以用求导的方法来求顶点哦。

先对函数y = ax + b/x求导，根据求导公式（x^n的导数是nx^(n - 1)），y' = a - b/x²。

然后令y' = 0，也就是a - b/x² = 0。

通过这个方程就能解出x的值啦，解出来x = ±√(b/a)（这里要注意哦，a、b同号这个条件很重要呢）。

再把x的值代回到原函数y = ax + b/x中，就能求出对应的y值啦。

这样就得到了对勾函数的顶点坐标哦。

2. 还有一种方法呢，就是利用均值不等式。

对于正数m和n，有m + n ≥ 2√(mn)。

对于y = ax + b/x（a、b同号，这里假设a>0，b>0），当ax = b/x的时候，函数能取得最值。

也就是x = √(b/a)的时候，y = 2√(ab)。

这个点其实就是对勾函数的顶点啦。

不过要记住，这里只是简单的情况，要是a<0，b<0的时候，分析起来就有点不一样啦，但原理是差不多的哦。

三、对勾函数顶点的意义对勾函数的顶点可是很重要的呢。

它就像是这个函数的一个关键特征点。

从图像上看，顶点就是对勾函数的最低点或者最高点（取决于a、b的正负）。

在实际问题里，比如说在经济学里计算成本和利润的关系之类的问题，如果可以用对勾函数来建模，那这个顶点可能就代表着最优解，比如成本最低或者利润最高的情况呢。

(完整版)对勾函数详细分析

对勾函数的性质及应用一、对勾函数b y ax x =+)0,0(>>b a 的图像与性质：1. 定义域：),0()0,(+∞⋃-∞2. 值域：),2[]2,(+∞⋃--∞ab ab3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即0)()(=-+x f x f 4. 图像在一、三象限, 当0x >时，by ax x=+≥ab 2（当且仅当b x a ，即)(x f 在x=a b 时，取最小值ab 2由奇函数性质知：当x<0时，)(x f 在x=ab -时，取最大值ab 2-5. 单调性：增区间为（∞+,ab ），（a b -∞-,）,减区间是（0，a b ），（a b -,0）二、对勾函数的变形形式类型一：函数by ax x=+)0,0(<<b a 的图像与性质 1.定义域：),0()0,(+∞⋃-∞ 2.值域：),2[]2,(+∞⋃--∞ab ab3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，)(x f 在x=ab 时，取最小值ab 2；当0x >时，)(x f 在x=ab -时，取最大值ab 2-5.单调性：增区间为（0，a b ），（a b -,0）减区间是（∞+,ab ），（a b -∞-,）,类型二：斜勾函数by ax x =+)0(<ab①0,0<>b a 作图如下1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-∞，0），（0，+∞）.②0,0><b a 作图如下：1.定义域：),0()0,(+∞⋃-∞2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-∞，0），（0，+∞）.类型三：函数)0()(2>++=ac xcbx ax x f 。

一类“对勾函数”型函数最值求法

教学信息新教师教学近年来高考对函数求最值问题一直都是热点，特别有一类“对勾函数”型的函数的最值越来越明显，对勾函数是一种类似于反比例函数的一般函数。

所谓的对勾函数，函数，是一种教材上没有但考试老喜欢考的函数意和学习。

而函数的最值求法必须注意其定义域，同时其最值求解及研究也离不开均值不等式，所以本文先简单介绍一下对勾函数图像与性质，再通过举例来说明对勾函数最值求解的方法。

对勾函数，的函数，此函数的图像与其参数a ，b ab >0时图像，其图像如下：在本文的例题当中只对参数a >0，b >0时进行研究，当a >0，为单调递增，在特别地当a =b =1时，：即x=1时取等号）；当即x上为单调递增，在递减。

一、例题讲解例1（1）数最大值；（2）的最值解（1）令，由对勾函数的性质可知：即t =1，也即x =0时取等号），于是有（2）（x >0，x ≠1）可令，当时，当时所以当时，即f （x ）取极大值-1；当时，即f （x ）取极小值7。

从上例可知求解函数最值时要注意函数定义域，函数的最值也即函数值域，因此注意函数定义域是必须的。

练习1　已知x >1求下列函数最值：（1（2；（3答案：（18，无最大值；（2）f (x )=3x+无最大值；（3）f （x ）最小值为3，无练习2。

（答案：f （x ）最小值为。

二、小结本文主要介绍了一下对勾函数型函数最值求解方法，对于对勾函数型函数是指可以通过转化化成对勾函数，所以在求解时首先是先把函数转化成对函数，再利用对勾函数的图像用及性质求解，当然在求解过程中，有些问题可以利用均值不等式来解，但利用均值不等式求解时要注意取等号时是否能成立，若不能成立，文中采用了函数的单调性来求解，如文中的例题3就说明了这一些问题的处理方法。

对勾函数专题讲解

对勾函数专题讲解专题：对勾函数及其应用1.对勾函数定义对勾函数是指形如 y = ax + (a>0.b>0) 的一类函数，因其图像形态极像对勾，因此被称为“对勾函数”。

2.对勾函数 y = ax + (a>0，b>0) 的性质1) 定义域：(-∞。

0) ∪ (0.+∞)。

2) 值域：(-∞。

-2ab] ∪ [2ab。

+∞)。

3) 奇偶性：在定义域内为奇函数。

4) 单调性：(-∞。

-a/b)，(a/b。

+∞) 上是增函数；(-a/b。

0)，(0.a/b) 上是减函数。

3.对勾函数 y = ax + (a>0，b>0) 的单调区间的分界点：±a/b。

求分界点方法：令 ax = 0，即可得到 x = ±a/b。

特殊的，当 a>0 时，y = x + 的单调区间的分界点为 ±a。

4.对勾函数应用时主要是利用其单调性求其最值，解题时要先找出对应的单调区间，然后求解。

5.利用对勾函数求最值，常常用到如下的重要不等式：若 a>0，b>0，则 x>0 时，ax + b ≥ 2ab。

当且仅当 ax = b，x = a/b 时取等号。

例1：已知 f(x) = x + (x>0)，求 f(x) 在下列区间的最小值：(1) [1,2]。

(2) [3,4]。

(3) [-3,-1]。

变式训练：已知函数 f(x) = x^2 - 2x - 1，求其值域。

例2：求函数 f(x) = (x+2)/((1+x^2)(x^2+5)) 的最小值，并求此时 x 的值。

变式训练：求函数 f(x) = (x-1)/(x-1) 的值域。

强化训练：1.下列函数中最小值是 4 的是 ()。

A。

y = x^4 + x^2B。

y = x^4 + xC。

y = x^4 - xD。

y = x^2 + 42.函数 y = x/(x^2+1)。

x∈(1,3] 的值域为 ()。

对勾函数详细分析

一、对勾函数 y ax bx 1. 定义域： ( ,0)对勾函数的性质及应用( a 0, b 0) 的图像与性质：(0,)2. 值域： (, 2 ab ] [ 2 ab ,)3. 奇偶性：奇函数，函数图像整体呈两个“对勾” 的形状，且函数图像对于原点呈中心对称，即 f (x) f ( x) 04. 图像在一、三象限 , 当 x0 时， y ax b 2 ab （当x且仅当 xb取等号），即 f (x) 在 x=b时，取最小值 2 abaa由奇函数性质知：当 x<0 时， f ( x) 在 x=b时，取最大值2 aba5. 单一性：增区间为（b ），（,b） ,减区间是（ 0，b），（b,0）, aaaa二、对勾函数的变形形式种类一：函数 y axb(a 0, b 0) 的图像与性质x1.定义域： ( ,0) (0, )2. 值域： (, 2 ab ] [ 2 ab ,)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状 .4.图像在二、四象限 , 当 x<0 时， f (x) 在 x= b时，取 a最小值 2 ab ；当 x时， f (x) 在 x= b时，取最大值 2 aba5.单一性：增区间为（ 0， b ），（b,0）减区间是（b , ），（,b） ,a aaa种类二：斜勾函数 yax b(ab 0)x① a 0, b 0 作图以下 1.定义域： (,0) (0, ) 2. 值域： R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值 .5.单一性：增区间为（ -， 0），（0， +） .② a 0, b 0 作图以下：1.定义域： ( ,0) (0, )2. 值域： R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单一性：减区间为（ -， 0），（0， + ） .种类三：函数 f ( x) ax2bx c(ac 0) 。

x此类函数可变形为f ( x)axc b ，可由对勾函数 y axc上下平移获得xx练习 1. 函数 f ( x)x2x 1的对称中心为x种类四：函数f ( ) x a ( a 0, k 0)x x kaa 此类函数可变形为f (x) ( x k) k ，则 f ( x) 可由对勾函数 y xx左右平移，上下平移获得1kx练习 1. 作函数 f ( x)x 与 f ( x)x 3x 2 xx 的草图22.求函数f ( x)x 1在 ( 2,) 上的最低点坐标2x43.求函数f (x)xx 的单一区间及对称中心x 1种类五：函数f ( x)ax(a 0,b 0) 。

对勾函数

其他解法
面对这个函数 f(x)=ax+b/x, 我们应该想得更多，需要我们深入探究：（1）它的单调性与奇偶性有何应用？而值域问题恰好与单调性密切相关，所以命题者首先想到的问题应该与值域有关；（2）函数与方程之间有密切的联系，所以命题者自然也会想到函数与方程思想的运用；（3）众所周知，双曲线中存在很多定值问题，所以很容易就想到定值的存在性问题。因此就由特殊引出了一般结论；继续拓展下去，用所猜想、探索的结果解
其实用导数也可以研究对勾函数的性质。不过首先要会负指数幂的换算，这也很简单，但要熟练掌握。举几个例子：1/x=x^-1，4/x^2=4x^-2。明白了吧，x为分母的时候可以转化成负指数幂。那么就有f(x)=ax+b/x=ax+bx-1，求导方法一样，求的的导函数为a+(-b)x^-2，令f'(x)=0，计算得到b=ax2，结果仍然是x=sqrt(b/a)，如果需要的话算出f(x)就行了。平时做题的时候用导数还是均值定理，就看你喜欢用那个了。不过注意均值定理最后的讨论，有时ax≠b/x，就不能用均值定理了。上述研究都是建立在x>0的基础上的，不过对勾函数是奇函数，所以研究出正半轴图像的性质后，自然能补出对称的图像。如果出现平移了的问题（图像不再规则），就先用平移公式或我总结出的平移规律还原以后再研究，这个能力非常重要，一定要多练，争取做到特别熟练的地步。对勾函数实际是反比例函数的一个延伸，至于它是不是双曲线还众说不一
极值不等式
对勾函数性质的研究离不开均值不等式。
说到均值不等式，其实也是根据二次函数得来的。
我们都知道，(a-b)^2≥0，展开就是a^2-2ab+b^2≥0，
有a^2+b^2≥2ab，两边同时加上2ab，整理得到(a+b)^2≥4ab，同时开根号，

对勾函数详细分析

对勾函数的性质及应用一.对勾函数的图像与性质：1.定义域：（-∞，0）∪（0，+∞）2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即4.图像在一、三象限, 当时，2√ab（当且仅当取等号），即在x=时，取最小值由奇函数性质知：当x<0时，在x=时，取最大值5.单调性：增区间为（），（）,减区间是（0，），（,0）1、对勾函数的变形形式类型一：函数的图像与性质1.定义域：2.值域：(-∞,-√ab]U[√ab,+∞)3.奇偶性：奇函数，函数图像整体呈两个“对勾”的形状.4.图像在二、四象限, 当x<0时，在x=时，取最小值；当时，在x=时，取最大值5.单调性：增区间为（0，），（,0）减区间是（），（）,类型二：斜勾函数①作图如下1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：增区间为（-，0），（0，+）.②作图如下：1.定义域：2.值域：R3.奇偶性：奇函数4.图像在二、四象限，无最大值也无最小值.5.单调性：减区间为（-，0），（0，+）.类型三：函数。

此类函数可变形为，可由对勾函数上下平移得到练习1.函数的对称中心为类型四：函数此类函数可变形为，则可由对勾函数左右平移，上下平移得到练习 1.作函数与的草图2.求函数在上的最低点坐标3. 求函数的单调区间及对称中心类型五：函数。

此类函数定义域为，且可变形为a.若，图像如下：1．定义域： 2. 值域：3. 奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最大值，当x<0时，在x=时，取最小值5. 单调性：减区间为（），（）；增区间是练习1.函数的在区间上的值域为b. 若，作出函数图像：1．定义域： 2. 值域：3. 奇偶性：奇函数.4. 图像在一、三象限.当时，在时，取最小值，当x<0时，在x=时，取最大值5. 单调性：增区间为（），（）；减区间是练习1.如，则的取值范围是类型六：函数.可变形为，则可由对勾函数左右平移，上下平移得到练习1.函数由对勾函数向（填“左”、“右”）平移单位，向（填“上”、“下”）平移单位.2.已知，求函数的最小值；3.已知，求函数的最大值类型七：函数练习1.求函数在区间上的最大值；若区间改为则的最大值为2.求函数在区间上的最大值类型八：函数.此类函数可变形为标准形式：练习1.求函数的最小值；2．求函数的值域；3.求函数的值域类型九：函数。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

关于求函数()01>+=x x
x y 最小值的十种解法一、均值不等式
Θ0>x ，∴21≥+=x x y ，当且仅当x
x 1=，即1=x 的时候不等式取到“=”。

∴当1=x 的时候，2min =y
二、∆法
0112=+-⇒+=yx x x
x y 若y 的最小值存在，则042≥-=∆y 必需存在，即2≥y 或2-≤y （舍）
找到使2=y 时，存在相应的x 即可。

通过观察当1=x 的时候，2min =y
三、单调性定义
设210x x <<
()()()⎪⎪⎭
⎫ ⎝⎛--=-+-=-21212121211111x x x x x x x x x f x f ()2121211x x x x x x --= 当对于任意的21,x x ，只有21,x x (]1,0∈时，()()21x f x f -0>，∴此时()x f 单调递增；当对于任意的21,x x ，只有21,x x ()+∞∈,1时，()()21x f x f -0<，∴此时()x f 单调递减。

∴当1=x 取到最小值，()21min ==f y
四、复合函数的单调性
2112
+⎪⎪⎭
⎫ ⎝⎛-=+=x x x x y x x t 1
-=在()+∞,0单调递增，22+=t y 在()0,∞-单调递减；在[)+∞,0单调递增又Θ∈x ()1,0()0,∞-∈⇒t ∈x [)+∞,1[)+∞∈⇒,0t
∴原函数在()1,0上单调递减；在[)+∞,1上单调递增
即当1=x 取到最小值，()21min ==f y
五、求一阶导 2'111x y x x y -=⇒+= 当()1,0∈x 时，0'<y ，函数单调递减；当[)+∞∈,1x 时，0'>y ，函数单调递增。

∴当1=x 取到最小值，()21min ==f y
六、三角代换
令αtan =x ，⎪⎭
⎫ ⎝⎛∈2,0πα，则αcot 1=x α
αα2sin 2cot tan 1=+=+=x x y ⎪⎭⎫ ⎝
⎛∈2,0πα()πα,02∈⇒ ∴当4π
α=，即22π
α=时，()12sin max =α，2min =y ，显然此时1=x
七、向量
b a x x x x y ⋅=⋅+⋅=+=1111，
()1,1,1,=⎪⎭
⎫ ⎝⎛=b x x a b a ⋅θcos b a ⋅=θcos 2a
根据图象，a 为起点在原点，终点在x
y 1=()0>x 图象上的一个向量，θcos a 的几何意义为a 在b 上
的投影，显然当b a =时，θcos a 取得最小值。

此时，1=x ，222min =⋅=y
八、图象相减
⎪⎭
⎫ ⎝⎛--=+=x x x x y 11，即y 表示函数x y =和x y 1-=两者之间的距离求min y ，即为求两曲线竖直距离的最小值
平移直线x y =，显然当x y =与x y 1-=相切时，两曲线竖直距离最小。

x y 1-=关于直线x y -=轴对称，若x y =与x
y 1-=在1>x 处有一交点，根据对称性，在10<<x 处也必有一
个交点，即此时x y =与x
y 1-
=相交。

显然不是距离最小的情况。

所以，切点一定为()1,1-点。

此时，1=x ，2min =y 九、平面几何
依据直角三角形射影定理，设x EB x AE 1,=
=，则x x AD AB 1+== 显然，x
x 1+为菱形的一条边，只用当AD AB ⊥，即AD 为直线AB 和CD 之间的距离时，x
x 1+
取得最小值。

即四边形ABCD 为矩形。

此时，x x 1=，即1=x ，2min =y 十、对应法则
设()[]t x f =min
()=2x f 221x
x + Θ()+∞∈,0x ，()+∞∈,02x ，对应法则也相同
∴()[]t x f =min 2
()()2112
22++=⇒+=x x x f x x x f Θ左边的最小值=右边的最小值
∴122-=⇒+=t t t （舍）或2=t
当2
x P x ==，即1=x 时取到最小值，且2min =y。