基本不等式—最值—对勾函数耐克函数(学案 附答案)
基本不等式精讲+对勾函数暴力讲解
第2讲 基本不等式精讲+对勾函数暴力讲解【学习目标】1.了解基本不等式的证明过程.2.会用对勾函数的性质求特定函数的最值3.会用基本不等式解决简单的最大(小)值问题.【要点梳理】要点1 对勾函数()0,0by ax a b x=+>>的图像与性质 （1） 定义域：()(),00,-∞+∞；（2） 值域：(),2,ab ⎡-∞-+∞⎣； （3） 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称；（4） 图像在一、三象限，当0x >时，by ax x=+≥x =等号），即()f x 在x =0x <时，()f x 在x =-；（5） 单调性：增区间⎫+∞⎪⎪⎭，,⎛-∞ ⎝，减区间是⎛ ⎝，⎛⎫⎪ ⎪⎝⎭要点2 基本不等式 基本不等式：ab ≤a ＋b 2(1)基本不等式成立的条件：a >0，b >0.(2)等号成立的条件：当且仅当a ＝b 时取等号． 要点3 几个重要的不等式 (1)a 2＋b 2≥2ab (a ，b ∈R )． (2)b a ＋ab ≥2(a ，b 同号)． (3)ab ≤⎝⎛⎭⎪⎫a ＋b 22(a ，b ∈R )．(4)a 2＋b 22≥⎝⎛⎭⎪⎫a ＋b 22(a ，b ∈R )． 以上不等式等号成立的条件均为a ＝b . 要点4 利用基本不等式求最值问题 已知x >0，y >0，则(1)如果积xy 是定值p ，那么当且仅当x ＝y 时，x ＋y 有最小值2p .(简记：积定和最小)(2)如果和x ＋y 是定值p ，那么当且仅当x ＝y 时，xy 有最大值p 24.(简记：和定积最大) 【经典例题】 题型1 基本公式套用例1 【★】已知a ，b ，0c >，且222412a ab ac bc +++=，则a b c ++的最小值为________．例2 【★•2019秋•徐汇区校级期中】设0x >，0y >，下列不等式中等号能成立的有（ ）． ①114x yx y ⎛⎫⎛⎫++ ⎪ ⎪⎝⎭⎝⎭；②()114x y x y ⎛⎫++ ⎪⎝⎭；24；④4x y ++；A ．1个B ．2个C ．3个D ．4个例3 【★•2019秋•历下区校级月考】设,a b +∈R ，则下列各式中不一定成立的是（ ）． A ．2a b ab + B ．2b aa b+C 222abD ．2ab ab a b+例4 【★•2019秋•迎泽区校级月考】已知实数1x >，则91x x +-的最小值为（ ）． A ．4B ．6C ．7D ．10例5 【★★】设a ，0b >，5a b +=+________．例6 【★★•2019秋•梅河口市校级期末】已知a ，b 为正数，2247a b +=，则大值为（ ）．A B C ．D ．2题型2 对勾函数例1【★★•2019秋•淮安期末】函数22(1)1y x x x =+>-的最小值是( ) A ．2B ．4C ．6D ．8例2【★★•2020春•龙华区校级月考】若1x >，则1411x x ++-的最小值等于( ) A ．6B ．9C ．4D ．1例3【★★•2019春•河北月考】若1x <，则2471x x x -+-的( )A ．最小值为2B ．最大值为2C ．最小值为6-D ．最大值为6-例4【★★•2019春•东湖区校级月考】函数24(0)1x x y x x ++=>+的最小值是( )A ．3B ．4C ．103D ．6例5【★★•2019秋•常熟市期中】若2x >，则函数42y x x =+-的最小值为( ) A ．3B ．4C ．5D ．6题型3 “1”的代换例1．【★★•2020•韶关二模】已知0x >，0y >，且121x y+=，则2x y +的最小值是( ) A ．7B ．8C ．9D ．10例2．【★★•2020•辽阳二模】已知0a >，0b >，32a b ab +=，则23a b +的最小值为()A ．20B ．24C ．25D ．28例3．【★★•2020春•九龙坡区校级期中】若x ，y R +∈，且315x y+=，则34x y +的最小值是( )A ．5B ．245C D ．195例4．【★★•2020春•昌吉市期中】若0a >，0b >，23a b +=，则36a b+的最小值为( ) A ．5 B ．6C ．8D ．9题型4 x ，y ，xy 型例1【★★•2019春•江岸区校级期末】已知223a b ab ++=，0a >，0b >，则2a b +的取值范围是( )A ．(0,3)B ．[33)C ．[2，)+∞D ．[2，3)例2【★★•2020春•浙江期中】已知0x >，0y >，3236x y xy ++=，则3x y +的最小值为 ．例3【★★•2020春•定海区校级月考】已知实数a ，b 满足1a >，0b >且2220a b ab +--=，那么2a b +的最小值是 ．例4【★★•2020•红桥区模拟】已知0x >，0y >，35x y xy +=，则2x y +的最小值是 ． 例5【★★•2020•河西区二模】已知x ，y 为正实数，且2441xy x y ++=，则x y +的最小值为例6【★★•2020•锡山区校级模拟】已知01a <<，01b <<，且44430ab a b --+=，则12a b+的最小值是 ．题型5 2x ，2y ，xy 型例1【★★•2020•浙江模拟】对于0c >，当非零实数a ，b 满足224240a ab b c -+-=，且使|2|a b +最大时，345a b c-+的最小值为( ) A ．12-B ．12C ．2-D ．2例2【★★•2019秋•聊城期末】若实数x ，y 满足221x y xy ++=，则x y +的最大值是()A ．6B ．4C D ．23例3【★★•2020春•浙江期中】若正数x ，y 满足2249330x y xy ++=，则xy 的最大值是() A ．43B ．53C ．2D ．54例4【★★•2020•南通模拟】（2020•南通模拟）已知实数x ，y 满足22210x xy y ---=，则222522x yx xy y +++的最大值为 ．【课后练习】1．【★2020春•福州期中】以下结论，正确的是（ ） A ．y ＝x +≥4 B ．e x +＞2C ．x （1﹣x ）≤（）2＝D ．sin x +（0＜x ＜π）的最小值是22．【★★2020•湖北模拟】直线2ax +by ﹣2＝0（a ＞0，b ＞0）过函数图象的对称中心，则的最小值为（ ） A ．9B ．4C ．8D ．103．【★★2020•滨海新区模拟】已知正实数a ，b 满足a +b ＝1，则的最小值为（ ） A ．13B ．11C ．10D ．94．【★★2020•河东区一模】已知实数a 、b ，ab ＞0，则的最大值为（ ）A．B．C．D．6。
高考数学复习专题系列学案：基本不等式对勾函数
基本不等式与对勾函数b、对勾函数y = ax • b (a . 0,b .0)的图像与性质x性质： 1.定义 '*_f(x) =aj+ —>C.A A 0) 当孟a 0*. == 3 + —2石瓦f 当 且仅当站=—)」AX当孟= —(iix + —｝台 2-Jab,X所臥得到血点坐标A (£.2加)』,_2石咬一41 I I 1*iI I i i| I I5-—_—M —— —三 <_ — ■. ■■ ■■ ■ ■“ ■ ■■ tM' — —' "W— ■* ~ — 1(-=,0) (0,二)2. 值域：(-：：,-2 . ab) (2、ab,：：)3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即 f(x) f(-x) =0 4. 图像在一、三象限当x =0时，由基本不等式知 yuax + PzzJab (当且仅当x = J 匕取等号)，xV a由奇函数性质知: 当x<0时，f (x)在x= — 时，取最大值 -^ab\ a一、对勾函数的变形形式 类型一：函数y =ax • b (a ：：： 0, b ：：： 0)的图像与性质 x此函数与对勾函数 y =(-a)x • J?关于原点对称，故函数图像为x即f (x)在x=—时，取最小值a2 . ab5.单调性：增区间为( 减区间是(0，性质: 类型二：斜勾函数y = ax • b (ab ：：： 0)xf(x)二2ax bx c(ac 0)此类函数可变形为cc f(x)二ax b ，贝y f(x)可由对勾函数 y 二ax上下平移得到xx性质： ②a 0,b . 0作图 如下： 类型三：函数例1作函数f (x) x2 x 1的草图解：f(x)二匚x1f(x)=x 1作图如下:x类型四：函数f(x)=x・a(a 0,k") x k此类函数可变形为a t af(x)=(x，k )-k ,则f (x)可由对勾函数y = x 左右平移,x上下平移得到例2作函数f (x)的草图x -2解：f (x) 例3作函数f(x)=x-2 12作图如下:x — 2=xx -2x 3x 2x 3x「f(x)二x的作图:x 2 1 1 1 f (x) x=1 x=x 2 1 x+2 x+2 x+21 练习：1.求函数f(x) =x 在(2/ ::)上的最低点坐标2x —4 解：f (x)X2.求函数f(X )= X的单调区间及对称中心X —1a.若a • 0 ,则f (x)的单调性和对勾函数 y = x •巴的单调性相反，图像如下: x1 .定义域：(一匚片•：：)由奇函数性质知: 当x<0时，f (x)在x= - b 时，取最小值-—a _2Jb5.单调性：减区间为( Jb, +30 ), (一00，-Jb )增区间是[- b, b]类型五： ax函数 f (X )二 2(a = 0,b . 0)f (x)二x 2 b3.奇偶性：奇函数，函数图像整体呈两个倒着的“对勾”的形状，且函数图像关于原点呈 中心对称，即f(x) f (-x) =04.图像在一、三象限 当x 0时，由基本不等式知f (x) V ——a 二a (当且仅当X 二• b 取等号2"： 2"即f (x)在x - b 时，取最大值a2“b此类函数定义域为R ，且可变形为性质:3当 x=1 时，f(x)二X-12(x —1)23(xT) 4 (X-1)3(xT) 4 x 〔4x — 1问：若区间改为［4,则f (x)的最大值为2x 7x 10类型七：函数f(x)2x max +bx+cx 1x例4作函数f(x)二—X x 解：f(x)二: x +1 11 x - xb.若acO ,作出函数图像： 2x r 的草图 x 2 4 例5作函数f (x)二类型六：函数 f (x)二 ax bx c(a = 0) x 十m 2 此类函数可变形为f(xH a(X m) S(X m)=a(x m) —t — s(at 0)x+ m则f (x)可由对勾函数 y 二ax •丄左右平移，上下平移得到 xx 2+x +1 1 例6说明函数f(x) 由对勾函数y=x 如何变换而来 ■ x 解：f(x)= (x 1)2 -(x 1) ^x . 1 1 X 十1 故 此函数f (x)可由对勾函数 (填“上”、“下”)平移*1宀 y = x 向 __________ x单位.草图如下:(填 “左”、“右”)平移 单位,2.已知x 1 ，求函数f (X )口x 2 9x -10x-1的最大值练习：1.已知x ^ -1，求函数f(x)=的最小值例7求函数f ( X )工 在区间(1, •二)上的最大值解：当x =1时，f (1)=0x + b 类型八：函数f (x)=Jx + a此类函数可变形为标准形式：f(x^x a ^^./xb-a (b_a.O) v x + ax + 3例8求函数f(x)的最小值 <x 解:f(x) =x "4Jx —1x + 5 •求函数f(x)的值域J x +1函数 f(x)=—— v'x 十此类函数可变形为标准形式：解: y =x…x 2 aa2xf (x )= ( X 2 * * a)2 b-ax 2 a二 x 2 a 「Tag °〉工的最小值4x 2 5 =解：f(x) = x 2 4x 2 4 1 f (x)' = lx 2 +4 十 1 Jx 2 +4 lx 2+4练习：1.求函数f (X )例10已知a 0,求函数y= X 2 1、—2 的值域X 2 17x 2a 1 .X 2—a 的最小值。
高中数学专题7-1 基本不等式和对钩函数(解析版)
4
4
无法直接使用基本不等式，需要凑配位和定：
f (x) 4x(3 2x) 22x(3 2x) 2( 2x 3 2x)2 9 ；
2
2
再如：f (x) 4x 2 1 直接使用基本不等式，则 f (x) 4x 2 1 2 (4x 2) 1 ，
4x 5
4x 5
4x 5
发现积不定，则需要凑配为积定：
【答案】1
【详解】因为 a 1，所以 a 2 a 1 2 1 2 a 1 2 1 2 2 1，
a 1
a 1
a 1
当且仅当 a 1 2 时取等号．故 m 2 2 1， n 2 1，所以， 2n m 1． 故答案为：1. 2．（2022·云南·屏边苗族自治县第一中学高一阶段练习）（ 若 x 2 ，求： x 2 的最小值.
【答案】(1) 9
【详解】（1）由题得 y 4x 1 1 4(x 1) 1 5，
x 1
x 1
因为 x 1，所以 x 1 0 ，
所以 4(x 1) 1 5 2 4(x 1) 1 5 9 ，
x 1
x 1
当且仅当 4(x 1) 1 ，即 x 3 时取得等号，
x 1
2
所以 y 4x 1 1 的最小值为 9 . x 1
y
4x2
9 x2
2
4x2
9 x2
12 ，
当且仅当 4x2
9 x2
，即 x
6 时取等号，
2
所以 ymin 12 ， 故选：C.
2．（2022·黑龙江·哈尔滨工业大学附属中学校高二学业考试）若 x 0 ，则 x 1 1的最小 x
值是（ ）
A．0 【答案】B
B．1
C． 3 2
公开课教案3——耐克函数的最值
形如
()(0)a f x x a x
=+>的最值 一、教学目标： 掌握利用基本不等式求最值须满足的条件；利用单调性求函数的最值。
二、教学重点和难点：
①分类讨论能力，使学生掌握分类的依据，当含有字母时应对其对应区间特别是区间两
端点的位置关系进行讨论。
②数形结合能力，利用函数的单调性求最值。
三、教学过程：
1、复习提问： 复习()(0)a f x x a x
=+>的图像与性质： （1）图像：（通过几何画板演示得出）
（2）性质：
①定义域：()(),00,-∞+∞；
②值域： ()
,2,a ⎡-∞-+∞⎣； ③奇偶性：奇函数；
④单调性：当()f x 在(,-∞及)
+∞上是增函数；
当()f x 在)⎡⎣及(上是减函数； 2、新课讲解：
例1、设4()f x x x
=+，试求()f x 的最小值。
（1）(]0,1x ∈；（2）(]0,3x ∈；
思考1、（3）当(]()0,0x n n ∈>，
例2、设函数(),0a f x x a x =+
>，[]1,2x ∈；试求()f x 的最小值。
（1）14
a =；（2）5a =；（3）2a =；
思考2：设函数()a f x x x =+，0a >，[]1,2x ∈，试求()f x 的最小值。
课堂小结：
思考3：设函数(),0a f x x a x =+
>，[]1,2x ∈；试求()f x 的最大值。
（1）14
a =
；（2）5a =；（3）2a =；
3、作业：练习册37页。
耐克函数
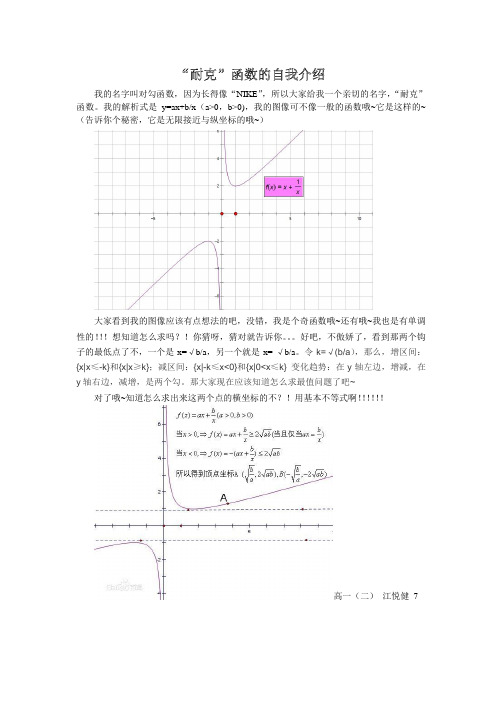
我的名字叫对勾函数，因为长得像“NIKE”，所以大家给我一个亲切的名字，“耐克”函数。
我的解析式是y=ax+b/x（a>0，b>0)，我的图像可不像一般的函数哦~它是这样的~（告诉你个秘密，它是无限接近与纵坐标的哦~）
大家看到我的图像应该有点想法的吧，没错，我是个奇函数哦~还有哦~我也是有单调性的！！！想知道怎么求吗？！你猜呀，猜对就告诉你。
好吧，不傲娇了，看到那两个钩子的最低点了不，一个是x=√b/a，另一个就是x=-√b/a。
令k=√(b/a），那么，增区间：{x|x≤-k}和{x|x≥k}；减区间：{x|-k≤x<0}和{x|0<x≤k} 变化趋势：在y轴左边，增减，在y轴右边，减增，是两个勾。
那大家现在应该知道怎么求最值问题了吧~ 对了哦~知道怎么求出来这两个点的横坐标的不？！用基本不等式啊！！！！！！
高一（二）江悦健7。
对勾函数讲解与例题解析
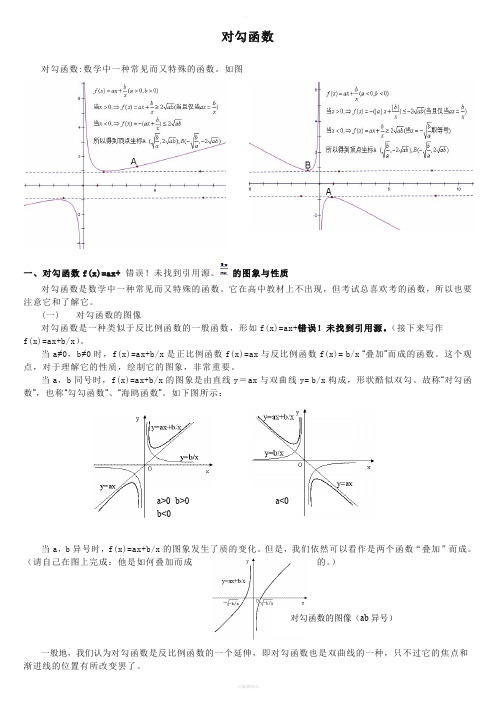
对勾函数对勾函数:数学中一种常见而又特殊的函数。
如图一、对勾函数f(x)=ax+错误！未找到引用源。
的图象与性质对勾函数是数学中一种常见而又特殊的函数。
它在高中教材上不出现，但考试总喜欢考的函数，所以也要注意它和了解它。
(一) 对勾函数的图像对勾函数是一种类似于反比例函数的一般函数，形如f(x)=ax+错误！未找到引用源。
（接下来写作f(x)=ax+b/x ）。
当a ≠0，b ≠0时，f(x)=ax+b/x 是正比例函数f(x)=ax 与反比例函数f(x)= b/x “叠加”而成的函数。
这个观点，对于理解它的性质，绘制它的图象，非常重要。
当a ，b 同号时，f(x)=ax+b/x 的图象是由直线y ＝ax 与双曲线y= b/x 构成，形状酷似双勾。
故称“对勾函数”，也称“勾勾函数”、“海鸥函数”。
如下图所示：当a ，b 异号时，f(x)=ax+b/x 的图象发生了质的变化。
但是，我们依然可以看作是两个函数“叠加”而成。
（请自己在图上完成：他是如何叠加而成的。
）一般地，我们认为对勾函数是反比例函数的一个延伸，即对勾函数也是双曲线的一种，只不过它的焦点和渐进线的位置有所改变罢了。
a>0 b>0 a<0 b<0 对勾函数的图像（ab 同号）对勾函数的图像（ab 异号）接下来，为了研究方便，我们规定a>0，b>0。
之后当a<0，b<0时，根据对称就很容易得出结论了。
(二) 对勾函数的顶点对勾函数性质的研究离不开均值不等式。
利用均值不等式可以得到：当x>0时，错误！未找到引用源。
当x<0时，错误！未找到引用源。
即对勾函数的定点坐标：(三) 对勾函数的定义域、值域由（二）得到了对勾函数的顶点坐标，从而我们也就确定了对勾函数的定义域、值域等性质。
(四) 对勾函数的单调性(五) 对勾函数的渐进线 由图像我们不难得到： (六) 对勾函数的奇偶性 ：对勾函数在定义域内是奇函数，二、均值不等式(基本不等式） 对勾函数性质的研究离不开均值不等式。
对勾函数
对勾函数是一种类似于反比例函数的一般函数，又被称为“双勾函数”、"勾函数"等。
也被形象称为“耐克函数”或“耐克曲线”所谓的对勾函数（双曲线函数），是形如f(x)=ax+b/x（a>0)的函数。
由图像得名。
图像对勾函数：图像，性质，单调性第三行为f（x）=-（ax+b/y）大于等于2√ab对勾函数是数学中一种常见而又特殊的函数，见图示，在作图时最好画出渐近线，y=ax。
奇偶性与单调性当x>0时，f(x)=ax+b/x有最小值（这里为了研究方便，规定a>0，b>0），也就是当x=sqrt(b/a）的时候（sqrt表示求二次方根）奇函数。
令k=sqrt(b/a），那么：增区间：{x|x≤-k}和{x|x≥k}；减区间：{x|-k≤x<0}和{x|0<x≤k} 变化趋势：在y轴左边，增减，在y轴右边，减增，是两个勾。
渐近线对勾函数的图像是分别以y轴和y=ax为渐近线的两支双曲线。
均值不等式(基本不等式）对勾函数性质的研究离不开均值不等式。
说到均值不等式，其实也是根据二次函数得来的。
我们都知道，（a-b)^2≥0，展开就是a^2-2ab+b^2≥0，有a^2+b^2≥2ab，两边同时加上2ab，整理得到（a+b)^2≥4ab，同时开根号，就得到了平均值定理的公式：a+b≥2 sqrt(ab）。
把ax+b/x套用这个公式，得到ax+b/x≥2sqrt(axb/x)=2sqrt(ab），这里有个规定：当且仅当ax=b/x时取到最小值，解出x=sqrt(b/a），对应的f(x)=2sqrt(ab）。
我们再来看看均值不等式，它也可以写成这样：（a+b)/2≥sqrt(ab），前式大家都知道，是求平均数的公式。
那么后面的式子呢？也是平均数的公式，但不同的是，前面的称为算术平均数，而后面的则称为几何平均数，总结一下就是算术平均数绝对不会小于几何平均数。
这些知识点也是非常重要的。
必修二对数函数对勾函数教案及训练题
专题：对数教学目标理解对数的概念；能够说明对数与指数的关系；掌握对数式与指数式的相互转化，并能运用指对互化关系研究一些问题.知识梳理1. 定义：一般地，如果x a N =(0,1)a a >≠，那么数 x 叫做以a 为底 N 的对数（logarithm ）.记作 log a x N =，其中a 叫做对数的底数，N 叫做真数2. 我们通常将以10为底的对数叫做常用对数（common logarithm ），并把常用对数10log N 简记为lg N 在科学技术中常使用以无理数e=2.71828……为底的对数，以e 为底的对数叫自然对数，并把自然对数log e N 简记作ln N3. 根据对数的定义，得到对数与指数间的互化关系：当0,1a a >≠时，log b a N b a N =⇔=.4. 负数与零没有对数；log 10a =， log 1a a =典例精讲【例1】将下列指数式化为对数式，对数式化为指数式： （1）712128-=； （2）327a =； （3）1100.1-=；（4）12log 325=-； （5）lg 0.0013=-； （6）ln100=4.606.解：（1）21log 7128=-； （2）3log 27a =； （3）lg 0.11=-；（4）51()322-=； （5）3100.001-=； （6） 4.606100e =.【例2】计算下列各式的值：（1）lg 0.001； （2）4log 8； （3）ln e .解：（1）设lg 0.001x =，则100.001x =，即31010x -=，解得3x =-. 所以，lg 0.0013=-. （2）设4log 8x =，则48x =，即2322x =，解得32x =. 所以，43log 82=. （3）设ln e x =，则xe e =，即12xe e =，解得12x =. 所以，1ln 2e =.【例3】求证：（1）log n a a n =； （2）log log log a a a M M N N-=.证明：（1）设log n a a x =，则n x a a =，解得x n =. 所以log n a a n =.（2）设log a M p =，log a N q =，则p a M =，q a N =. 因为p p qqM a aN a-==，则log log log aa a M p q M N N=-=-.所以，log log log a a aM M N N-=.点评：对数运算性质是对数运算的灵魂，其推导以对数定义得到的指对互化关系为桥梁，结合指数运算的性质而得到. 我们需熟知各种运算性质的推导.【例4】试推导出换底公式：log log log c a c b b a=（0a >，且1a ≠；0c >，且1c ≠；0b >）.证明：设log c b m =，log c a n =，log a b p =，则m c b =，n c a =，pa b =.从而()n p m c b c ==，即np m =. 由于log log 10c c n a =≠=，则m p n=.所以，log log log c a c b b a=.点评：换底公式是解决对数运算中底数不相同时的核心工具. 其推导也密切联系指数运算性质，牢牢扣住指对互化关系.巩固练习1．log (0,1,0)b N a b b N =>≠>对应的指数式是（ ）. A. b a N = B. a b N = C. N a b = D. N b a = 2．下列指数式与对数式互化不正确的一组是（ ）. A. 01ln10e ==与 B. 1()381118log 223-==-与C. 123log 9293==与 D. 17log 7177==与 3．设lg 525x =，则x 的值等于（ ）.A. 10B. 0.01C. 100D. 1000 4．设13log 82x=，则底数x 的值等于（ ）.A. 2B. 12C. 4D.145．已知432log [log (log )]0x =，那么12x -等于（ ）.A.13B.123C.122D.1336．若21log 3x =，则x = ； 若log 32x =-，则x = .7．计算：3log 81= ； 6lg 0.1= .※能力提高8．求下列各式的值：（1）22log8； （2）9log 3.9．求下列各式中x 的取值范围：（1）1log (3)x x -+； （2）12log (32)x x -+.※探究创新10．（1）设log 2a m =，log 3a n =，求2m n a +的值.（2）设{0,1,2}A =,{log 1,log 2,}a a B a =，且A B =，求a 的值.回顾总结专题:对数函数的性质教学目标通过具体实例，直观了解对数函数模型所刻画的数量关系，初步理解对数函数的概念，体会对数函数是一类重要的函数模型；能借助计算器或计算机画出具体对数函数的图像，探索并了解对数函数的单调性与特殊点.掌握对数函数的性质，并能应用对数函数解决实际中的问题. 知道指数函数y =a x 与对数函数y =log a x 互为反函数. （a > 0, a ≠1）知识梳理1. 定义：一般地，当a ＞0且a ≠1时，函数a y=log x 叫做对数函数(logarithmic function). 自变量是x ； 函数的定义域是（0，+∞）.2. 由2log y x =与12log y x =的图象，可以归纳出对数函数的性质：定义域为(0,)+∞，值域为R ；当1x =时，0y =，即图象过定点(1,0)；当01a <<时，在(0,)+∞上递减，当1a >时，在(0,)+∞上递增.3.当一个函数是一一映射时, 可以把这个函数的因变量作为一个新函数的自变量, 而把这个函数的自变量新的函数的因变量. 我们称这两个函数为反函数（inverse function ）. 互为反函数的两个函数的图象关于直线y x =对称.4. 函数(0,1)x y a a a =>≠与对数函数log (0,1)a y x a a =>≠互为反函数.5. 复合函数(())y f x ϕ=的单调性研究，口诀是“同增异减”，即两个函数同增或同减，复合后结果为增函数；若两个函数一增一减，则复合后结果为减函数. 研究复合函数单调性的具体步骤是：（i ）求定义域；（ii ）拆分函数；（iii ）分别求(),()y f u u x ϕ==的单调性；（iv ）按“同增异减”得出复合函数的单调性.典例精讲【例1】比较大小：（1）0.9log 0.8，0.9log 0.7，0.8log 0.9； （2）3log 2，2log 3，41log 3.解：（1）∵ 0.9log y x =在(0,)+∞上是减函数，且0.90.80.7>>， ∴ 0.90.91log 0.8log 0.7<<. 又 0.80.8log 0.9log 0.81<=， 所以0.80.90.9log 0.9log 0.8log 0.7<<. （2）由 333log 1log 2log 3<<，得30log 21<<. 又22log 3log 21>=，441log log 103<=，所以4321log log 2log 33<<.【例2】求下列函数的定义域：（1）2log (35)y x =-；（2）0.5log (4)3y x =-.解：（1）由22log (35)0log 1x -≥=，得351x -≥，解得2x ≥.所以原函数的定义域为[2,)+∞.（2）由0.5log (4)30x -≥，即30.50.5log (4)3log 0.5x ≥=，所以3040.5x <≤，解得1032x <≤. 所以，原函数的定义域为1(0,]32.【例3】已知函数()log (3)a f x x =+的区间[2,1]--上总有|()|2f x <，求实数a 的取值范围. 解：∵ [2,1]x ∈--， ∴ 132x ≤+≤当1a >时，log 1log (3)log 2a a a x ≤+≤，即0()log 2a f x ≤≤. ∵ |()|2f x <， ∴{1log 22a a ><， 解得2a >.当01a <<时，log 2log (3)log 1a a a x ≤+≤，即log 2()0a f x ≤≤. ∵ |()|2f x <， ∴{01log 22a a <<>-， 解得202a <<.综上可得，实数a 的取值范围是2(0,)(2,)2+∞ .点评：先对底数a 分两种情况讨论，再利用函数的单调性及已知条件，列出关于参数a 的不等式组，解不等式（组）而得到参数的范围. 解决此类问题的关键是合理转化与分类讨论，不等式法求参数范围.【例4】求不等式log (27)log (41)(0,1)a a x x a a +>->≠且中x 的取值范围.解：当1a >时，原不等式化为2704102741x x x x +>⎧⎪->⎨+>-⎪⎩，解得144x <<.当01a <<时，原不等式化为 2704102741x x x x +>⎧⎪->⎨+<-⎪⎩，解得4x >.所以，当1a >时，x 的取值范围为1(,4)4；当01a <<时，x 的取值范围为(4,)+∞.点评：结合单调性，将对数不等式转化为熟悉的不等式组，注意对数式有意义时真数大于0的要求. 当底数a 不确定时，需要对底数a 分两种情况进行讨论【例1】讨论函数0.3log (32)y x =-的单调性.解：先求定义域，由320x ->, 解得32x <. 设332,(,)2t x x =-∈-∞，易知为减函数.又∵ 函数0.3log y t =是减函数，故函数0.3log (32)y x =-在3(,)2-∞上单调递增. 【例2】（05年山东卷.文2）下列大小关系正确的是（ ）. A. 30.440.43log 0.3<< B. 30.440.4log 0.33<< C. 30.44log 0.30.43<< D. 0.434log 0.330.4<<解：在同一坐标系中分别画出40.4,3,log x x y y y x ===的图象，分别作出当自变量x 取3，0.4，0.3时的函数值.观察图象容易得到：30.44log 0.30.43<<. 故选C.【例3】指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象有何关系？ 解：在指数函数x y a =的图象上任取一点00(,)M x y ，则00x y a =. 由指对互化关系，有00log a y x =.所以，点00'(,)M y x 在对数函数log a y x =的图象上. 因为点00(,)M x y 与点00'(,)M y x 关于直线y x =对称，所以指数函数(0,1)x y a a a =>≠的图象与对数函数log (0,1)a y x a a =>≠的图象关于直线y x =对称.点评：两个函数的对称性，由任意点的对称而推证出来. 这种对称性实质是反函数的图象特征，即函数x y a =与log (0,1)a y x a a =>≠互为反函数，而互为反函数的两个函数图象关于直线y x =对称.巩固练习1．下列各式错误的是（ ）.A. 0.80.733>B. 0.10.10.750.75-<C. 0..50..5log 0.4log 0.6>D. lg1.6lg1.4>.2．当01a <<时,在同一坐标系中,函数log x a y a y x -==与的图象是（ ）.A B C D3．下列函数中哪个与函数y =x 是同一个函数（ ） A.log (0,1)a xy a a a =>≠ B. y =2xxC. log (0,1)x a y a a a =>≠D. y =2x4．函数12log (1)y x =-的定义域是（ ）.A. (1,)+∞B. (,2)-∞C. (2,)+∞D. (1,2]5．若log 9log 90m n <<，那么,m n 满足的条件是（ ）.A. 1 m n >>B. 1n m >>C. 01n m <<<D. 01m n <<< 6．函数3log y x =的定义域为 . （用区间表示）7．比较两个对数值的大小：ln 7 ln 12 ； 0.5log0.7 0.5log 0.8.※能力提高8．求下列函数的定义域：（1） ()()34log 11x f x x x -=++-； （2）21log (45)y x =--.9．已知函数2()3log ,[1,4]f x x x =+∈，22()()[()]g x f x f x =-，求： （1）()f x 的值域； （2）()g x 的最大值及相应x 的值.※探究创新10．若,a b 为不等于1的正数，且a b <，试比较log a b 、1log ab、1log bb.1．函数1lg1x y x+=－的图象关于（ ）. A. y 轴对称B. x 轴对称C. 原点对称D. 直线y ＝x 对称2．函数212log (617)y x x =-+的值域是（ ）.A. RB. [8,)+∞C. (,3]-∞-D. [3,)+∞xy1 1oxy o 1 1oy x11 oy x1 13．（07年全国卷.文理8）设1a >，函数()log a f x x =在区间[]2a a ，上的最大值与最小值之差为12，则a =（ ）.A.2B. 2C. 22D. 44．图中的曲线是log a y x =的图象，已知a 的值为2，43，310，15，则相应曲线1234,,,C C C C 的a 依次为（ ）.A. 2，43，15，310B.2，43，310，15 C.15，310，43，2 D. 43，2，310，155．下列函数中，在(0,2)上为增函数的是（ ）. A. 12log (1)y x =+ B. 22log 1y x =- C. 21log y x= D.20.2log (4)y x =-6． 函数2()lg(1)f x x x =+-是 函数. （填“奇”、“偶”或“非奇非偶”） 7．函数x y a =的反函数的图象过点(9,2)，则a 的值为 . ※能力提高 8．已知6()log ,(0,1)af x a a x b=>≠-，讨论()f x 的单调性.※探究创新10． 已知函数()log (1),()log (1)a a f x x g x x =+=-其中(01)a a >≠且．（1）求函数()()f x g x -的定义域； （2）判断()()f x g x -的奇偶性，并说明理由；（3）求使()()0f x g x ->成立的x 的集合.对数与对数运算（2）教学目标通过阅读材料，了解对数的发现历史以及对简化运算的作用；理解对数的概念及其运算性质，知道用换底公式能将一般对数转化成自然对数或常用对数；理解推导这些运算性质的依据和过程；能较熟练地运用运算性质解决问题知识梳理1. 对数的运算法则：log ()log log a a a M N M N =+ ，log log log aa a M M N N=-，log log na a M n M =，其中0,1a a >≠且，0,0,M N n R >>∈. 三条法则是有力的解题工具，能化简与求值复杂的对数式.2. 对数的换底公式log log log b a b N N a=. 如果令b =N ，则得到了对数的倒数公式1log log a b b a=. 同样，也可以推导出一些对数恒等式，如log log nna a N N =，log log mn a a n N N m=，log log log 1a b c b c a = 等.0 x C 1C 2C 4C 3 1y典例精讲【例1】化简与求值：（1）221(lg 2)lg 2lg 5(lg 2)lg 212++-+ ；（2）2log (4747)++-.解：（1）原式=2211(lg 2)lg 2lg 5(lg21)22++- =211lg 2lg 2lg 5(lg21)42+--=2111lg 2lg 2lg 5lg 21422+-+ =1lg 2(lg 22lg 52)14+-+=1lg 2(lg 1002)10114-+=+=.（2）原式=1222log (4747)⨯++-=221log (4747)2++-=221log (4747247)2++-+-=21log 142.【例2】若2510a b ==，则11a b+= . （教材P 83 B 组2题）解：由2510a b ==，得2log 10a =，5log 10b =. 则251111lg 2g 5lg 101log 10log 10a b +=+=+==.【例3】 （1）方程lg lg(3)1x x ++=的解x =________；（2）设12,x x 是方程2lg lg 0x a x b ++=的两个根，则12x x 的值是 . 解：（1）由lg lg(3)1x x ++=，得lg[(3)]lg10x x +=， 即(3)10x x +=，整理为23100x x +-=.解得x =－5或x =2. ∵ x ＞0， ∴ x =2.（2）设lg x t =，则原方程化为20t at b ++=，其两根为1122lg ,lg t x t x ==. 由121212lg lg lg()lg10b t t x x x x b +=+=== ，得到1210b x x = .点评：同底法是解简单对数方程的法宝，化同底的过程中需要结合对数的运算性质. 第2小题巧妙利用了换元思想和一元二次方程根与系数的关系.【例4】（1）化简：532111log 7log 7log 7++；（2）设23420052006log 3log 4log 5log 2006log 4m ⋅⋅⋅= ，求实数m 的值. 解：（1）原式=77777log 5log 3log 2log (532)log 30++=⨯⨯=. （2）原式左边=2222222222log 4log 5log 2006log log 3log log 3log 4log 2005log 2006mm ⋅⋅⋅=, ∴ 422log 4log 2m ==， 解得16m =.点评：换底时，一般情况下可以换为任意的底数，但习惯于化为常用对数. 换底之后，注意结合对数的运算性质完成后阶段的运算.巩固练习1．1logn n++（1n n ＋－）等于（ ）. A. 1B. －1C. 2D. －2 2．25log()(5)a -（a ≠0）化简得结果是（ ）. A. －aB. a 2C. ｜a ｜D. a3．化简3lg 2lg 5log 1++的结果是（ ）.A.12B. 1C. 2D.104．已知32()log f x x =, 则(8)f 的值等于（ ）. A. 1 B. 2 C. 8 D. 125．化简3458log 4log 5log 8log 9⋅⋅⋅的结果是 （ ）. A .1 B.32C. 2D.36．计算2(lg 5)lg 2lg 50+⋅＝ . 7．若3a ＝2，则log 38－2log 36＝ . ※能力提高 8．（1）已知18log 9a =，185b =，试用a 、b 表示18log 45的值； （2）已知1414log 7log 5a b ==，，用a 、b 表示35log 28.※探究创新10．（1）设,,x y z 均为实数，且34x y =，试比较3x 与4y 的大小.（2）若a 、b 、c 都是正数，且至少有一个不为1，1x y z y z x z x y a b c a b c a b c ===，讨论x 、y 、z 所满足的幂函数¤学习目标：通过实例，了解幂函数的概念；结合函数y=x, y=x 2, y=x 3, y =1/x , y=x 1/2 的图像，了解它们的变化情况. 知识要点：1. 幂函数的基本形式是y x α=，其中x 是自变量，α是常数. 要求掌握y x =，2y x=，3y x =，1/2y x=，1y x -=这五个常用幂函数的图象.2. 观察出幂函数的共性，总结如下：（1）当0α>时，图象过定点(0,0),(1,1)；在(0,)+∞上是增函数.（2）当0α<时，图象过定点(1,1)；在(0,)+∞上是减函数；在第一象限内，图象向上及向右都与坐标轴无限趋近.3. 幂函数y x α=的图象，在第一象限内，直线1x =的右侧，图象由下至上，指数α由小到大. y 轴和直线1x =之间，图象由上至下，指数α由小到大.¤例题精讲：【例1】已知幂函数()y f x =的图象过点(27,3)，试讨论其单调性.解：设y x α=，代入点(27,3)，得327α=，解得13α=，所以13y x =，在R 上单调递增.【例2】已知幂函数6()m y x m Z -=∈与2()m y x m Z -=∈的图象都与x 、y 轴都没有公共点，且2()m y xm Z -=∈的图象关于y 轴对称，求m 的值．解：∵ 幂函数图象与x 、y 轴都没有公共点，∴{6020m m -<-<，解得26m <<.又 ∵ 2()m y x m Z -=∈的图象关于y 轴对称， ∴ 2m -为偶数，即得4m =. 【例3】幂函数m y x =与n y x =在第一象限内的图象如图所示，则（ ）. A ．101n m -<<<< B ．1,01n m <-<<C ．10,1n m -<<>D ．1,1n m <->解：由幂函数图象在第一象限内的分布规律，观察第一象限内直线1x =的右侧，图象由下至上，依次是n y x =，1y x -=，0y x =，m y x =，1y x =，所以有101n m <-<<<. 选B.点评：观察第一象限内直线1x =的右侧，结合所记忆的分布规律. 注意比较两个隐含的图象1y x =与0y x =.【例4】本市某区大力开展民心工程，近几年来对全区2a m 的老房子进行平改坡（“平改坡”是指在建筑结构许可条件下，将多层住宅平屋面改建成坡屋顶，并对外墙面进行整修粉饰，达到改善住宅性能和建筑物外观视觉效果的房屋修缮行为），且每年平改坡面积的百分比相等. 若改造到面积的一半时，所用时间需10年. 已知到今年为止，平改坡剩余面积为原来的22.（1）求每年平改坡的百分比；（2）问到今年为止，该平改坡工程已进行了多少年？ （3）若通过技术创新，至少保留24a m 的老房子开辟新的改造途径. 今后最多还需平改坡多少年？解：（1）设每年平改坡的百分比为(01)x x <<，则 101(1)2a x a -=，即11011()2x -=，解得11011()0.0670 6.702x =-≈=%.（2）设到今年为止，该工程已经进行了n 年，则2(1)2na x a -=，即110211()()22n =，解得n =5.所以，到今年为止，该工程已经进行了5年. （3）设今后最多还需平改坡m 年，则 51(1)4m a x a +-=，即521011()()22m +=，解得m =15. 所以，今后最多还需平改坡15年.点评：以房屋改造为背景，从中抽象出函数模型，结合两组改造数据及要求，通过三个等式求得具有实际意义的底数或指数. 体现了代入法、方程思想等数学方法的运用.第18练 §2.3 幂函数※基础达标1．如果幂函数()f x x α=的图象经过点2(2,)2，则(4)f 的值等于（ ）.A. 16B. 2C.116D.122．下列函数在区间(0,3)上是增函数的是（ ）. A. 1y x=B. 12y x = C. 1()3x y = D. 2215y x x =--3．设120.7a =，120.8b =，c 3log 0.7=，则（ ）. A. c <b <a B. c <a <b C. a <b <c D. b <a <c12±四个值，与曲线4．如图的曲线是幂函数ny x =在第一象限内的图象. 已知n 分别取2±，1c 、2c 、3c 、4c 相应的n 依次为（ ）.42510c 4c 3c 2c 1A ．112,,,222-- B. 112,,2,22--C. 11,2,2,22-- D. 112,,,222--5．下列幂函数中过点(0,0)，(1,1)的偶函数是（ ）.A.12y x = B. 4y x = C. 2y x-= D.13y x =6．幂函数()y f x =的图象过点1(4,)2，则(8)f 的值为 .7．比较下列各组数的大小： 32(2)a + 32a ； 223(5)a -+ 235-； 0.50.4 0.40.5.※能力提高8．幂函数273235()(1)t tf x t t x +-=-+是偶函数，且在(0,)+∞上为增函数，求函数解析式.一、对勾函数b y ax x=+)0,0(>>b a 的图像与性质性质：1. 定义域：),0()0,(+∞⋃-∞2. 值域：),2[]2,(+∞⋃--∞ab ab3. 奇偶性：奇函数，函数图像整体呈两个“对勾”的形状，且函数图像关于原点呈中心对称，即0)()(=-+x f x f4. 图像在一、三象限当0x >时，由基本不等式知b y ax x=+≥ab 2（当且仅当b x a=取等号），即)(x f 在x=ab 时，取最小值ab 2由奇函数性质知： 当x<0时，)(x f 在x=ab -时，取最大值ab 2-5. 单调性：增区间为（∞+,a b），（a b-∞-,）减区间是（0，a b ），（a b -,0）。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
基本不等式——形式一：a b +≥(a>0,b>0)____a b +（ ）——形式二：2a b+≥ (a__0,b__0)__(a >0,b >0)2a b + ——形式三：22a b ab +⎛⎫≤ ⎪⎝⎭（ ）(a>0,b>0)2a b+≤2a b+？ 用分析法证明：要证2a b+ （1） 只要证 a b +≥ （2）要证（2），只要证____0a b +-≥ （3） 要证（3），只 要证2(__________)0-≥ （4）显然（4）是成立的. 当且仅当a=b 时，（4）中的等号成立.探究3：使用基本不等式的三个条件：一正二定三相等思考：（1）已知y=x+x1 ( x>0 ) ，求y 的范围.（2）已知y=x+x1( x≠0 ) ，求y 的范围.例题拓展【例1 】已知0x >，则xx 432++的最小值是________。
【 例2 】下列不等式一定成立的是 （ ）A ．xy y x 2≥+B ．21≥+xx C ．xy y x 222≥+ D ．xyxy y x 12≥+【 例3 】下列结论中，错用基本不等式做依据的是（ ）基础回顾1、对于____ _ ,a b ,有22____2a b ab +,当且仅当____ _ 时，等号成立.2、基本不等式：对于____ _,a b ,则2a b+___ _时，不等式取等号.注意：使用基本不等式时，应具备三个条件：____ _ ____ _【例1 】（1）已知x >0，且y = x ＋81x，x =_________时，y 取最小值 （2）已知0x >，则xx 432++的最小值是________。
（3）y x x=++23122的最小值是（4）a+b=2，则3a +3b 的最小值是______________（5）a+2b=4，则3a +9b 的最小值是______________【 例2】设x ，y 为正数， 求14()()x y x y++的最小值【例4 】若0,0,x y >>且211x y+=，则2x y +的最小值为________练兵场：1、函数y =31-x + x (x>3) 的最小值是_________。
2、y =xx sin 22sin +(0<x <π)的最小值是__________。
3、已知0<x ，则xx 432++的最大值是________。
4、下列函数中最小值是4的是（ ） A ．x x y 4+= B ．xx y sin 4sin += C ．xx y -++=1122 D ．)0(,31122≠+++=x x x y5、已知a,b 为正实数，且ba b a 11,12+=+则的最小值为_______6、已知0,0x y >>且满足281x y+=,求x y +的最小值。
【例4】已知y x ,都是正数（1）若积xy 是定值p ，求y x +的最小值；（2）若和y x +是定值s ，求xy 的最大值。
【例5】一段长为36 m 的篱笆围成一个一边靠墙的矩形菜园，问这个矩形的长、宽各为多少时，菜园的面积最大，最大面积是多少?【例6】已知x >0，y >0，且3x +4y =12，求lgx +lgy 的最大值及此时x 、y 的值。
变式1、已知xy y x R y x ，则，且14,=+∈+的最大值是 。
拓展归纳：最值定理设,0,2x y x y xy >+≥由（1）若积xy 是定值p ，则当y x =时和y x +有___________ （2）若和y x +是定值s ，则当y x =时积xy 有___________变式2、设x ＞0，y ＞0且3x +2y =12，则xy 的最大值是___________。
【小秘书】分离系数法是处理参数取值范围的常用方法。
试一试：1、当x ＞2时，使不等式a x x ≥-+21恒成立的实数a 的取值范围是 。
2、已知0,0x y >>,且211x y+=, 若222x y m m +>+ 恒成立, 则实数m 的取值范围是_____实例思考分析思考1：反比例函数(0)ky k x=≠，x 的范围，图象特征，y 的范围？思考2：已知y=x+x4( x≠0 ) ，y 的范围，图象特征？思考3：已知y=2x+x4( x≠0 ) ，y 的范围，图象特征？归纳总结拓展应用备注：“值域”，即y 的范围，用区间或集合形式表示【例1】（1）函数xx y 4+= 1x >（） 的值域为_________________（2）函数x x y 4+=,30,2x ⎛⎤∈ ⎥⎝⎦的值域为_________________（3）函数xx y 4+=,(],1x ∈-∞-的值域为_________________（4）函数xx y 4+=,[]13x ∈，的值域为_________________（5）函数xx y 4+=,04x x <>或的值域为_________________【例2】（1）函数x x x y 342++=,30,2x ⎛⎤∈ ⎥⎝⎦的值域为_________________（2）函数14++=x x y ,30,2x ⎛⎤∈ ⎥⎝⎦的值域为_________________（3）函数314+-+-=xx y ,[)-10x ∈，的值域为_________________【例3】当(1,2)x ∈，不等式240x mx ++<恒成立，求实数m 的范围．练习：已知不等式022>+⋅-x a x 对于+∞∈,21[x ）恒成立，求实数a 的取值范围.补充练习（基本不等式）1.在下列函数中，最小值为2的是( ) A ．y ＝x ＋1xB ．y ＝3x ＋3－xC ．y ＝lg x ＋1lg x (0＜x ＜1)D ．y ＝sin x ＋1sin x ⎝⎛⎭⎪⎫0＜x ＜π22．若a ＋b ＝2，则3a ＋3b的最小值是( )A ．18B ．6C ．2 3D ．243 每一天都是全新的一天，每一天都是进步的一天。
从今天起步，在明天收获！3．已知x <12，则函数y ＝2x ＋12x －1的最大值是( ) A ．2 B ．1 C ．－1 D ．－24. 若a >0，b >0，a ，b 的等差中项是12，且α＝a ＋1a ，β＝b ＋1b，则α＋β的最小值为( )A ．2B ．3C ．4D ．55．已知圆x 2＋y 2＋2x －4y ＋1＝0关于直线2ax －by ＋2＝0(a >0，b >0)对称，则4a ＋1b的最小值是( )A ．4B ．6C ．8D ．96．已知x ，y ∈R ＋，且x ＋4y ＝1，则x ·y 的最大值为________．7．当a >0，a ≠1时，函数f (x )＝log a (x －1)＋1的图象恒过定点A ，若点A 在直线mx－y ＋n ＝0上，则4m ＋2n 的最小值是________．8.如下图，某药店有一架不准确的天平(其两臂长不相等)和一个10克的砝码，一个患者想要买20克的中药，售货员先将砝码放在左盘上，放置药品于右盘上，待平衡后交给患者；然后又将砝码放在右盘上，放置药品于左盘上，待平衡后再交给患者．设患者一次实际购买的药量为m(克)，则m________20克．(请选择填“>”或“<”或“＝”)9．(2008年高考广东卷)某单位用2160万元购得一块空地，计划在该地块上建造一栋至少10层、每层2000平方米的楼房．经测算，如果将楼房建为x(x≥10)层，则每平方米的平均建筑费用为560＋48x(单位：元)．为了使楼房每平方米的平均综合费用最少，该楼房应建为多少层？(注：平均综合费用＝平均建筑费用＋平均购地费用，平均购地费用＝购地总费用)建筑总面积参考答案1．B 2.解析：选B.3a ＋3b ≥23a ·3b ＝23a ＋b ＝6.3.解析：选C.y ＝2x ＋12x －1＝－[(1－2x )＋11－2x]＋1， 由x <12可得1－2x >0，根据基本不等式可得(1－2x )＋11－2x ≥2，当且仅当1－2x ＝11－2x 即x ＝0时取等号，则y max ＝－1.正确答案为C.4. 解析：选D.因为a ＋b ＝1，所以α＋β＝a ＋1a ＋b ＋1b ＝1＋1a ＋1b ＝1＋1＋b a ＋1＋a b≥5， 故选D.5.解析：选D.由圆的对称性可得，直线2ax －by ＋2＝0必过圆心(－1,2)，所以a ＋b ＝1.所以4a ＋1b ＝4(a ＋b )a ＋a ＋b b ＝4b a ＋a b ＋5≥24b a ·a b＋5＝9， 当且仅当4b a ＝a b，即a ＝2b 时取等号，故选D.6.1167.解析：A (2,1)，故2m ＋n ＝1. ∴4m ＋2n ≥24m ·2n ＝222m ＋n ＝2 2.当且仅当4m ＝2n ，即2m ＝n ，即n ＝12，m ＝14时取等号． ∴4m ＋2n 的最小值为2 2. 答案：2 28.解析：设两次售货员分别在盘中放置m 1、m 2克药品，则⎩⎪⎨⎪⎧ 10a ＝m 1b ，10b ＝m 2a ，m ＝m 1＋m 2，前两个式子相乘，得100ab ＝m 1m 2·ab ，得m 1m 2＝100，因为m 1≠m 2，所以m ＝m 1＋m 2>2m 1m 2＝20，所以填“>”．答案：> 9.解：设将楼房建为x 层，则每平方米的平均购地费用为2160×1042000x ＝10800x. ∴每平方米的平均综合费用y ＝560＋48x ＋10800x ＝560＋48(x ＋225x )． 当x ＋225x取最小值时，y 有最小值．∵x >0， ∴x ＋225x ≥2x ·225x＝30， 当且仅当x ＝225x， 即x ＝15时，上式等号成立．所以当x ＝15时，y 有最小值2000元．因此该楼房建为15层时，每平方米的平均综合费用最小．。