高考数学考点专题总复习12
考点巩固卷12 等差、等比数列(七大考点)(学生版) 2025年高考数学一轮复习考点通关卷(新高考
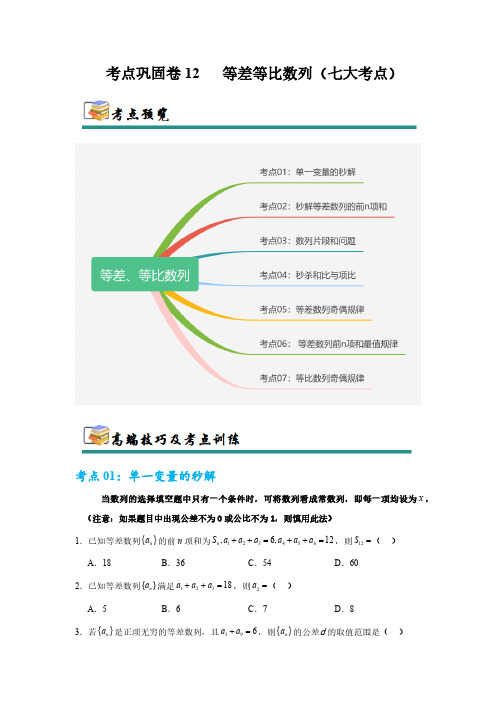
考点巩固卷12 等差等比数列(七大考点)考点01:单一变量的秒解当数列的选择填空题中只有一个条件时,可将数列看成常数列,即每一项均设为x ,(注意:如果题目中出现公差不为0或公比不为1,则慎用此法)1.已知等差数列{}n a 的前n 项和为123456,6,12n S a a a a a a ++=++=,则12S =( )A .18B .36C .54D .602.已知等差数列{}n a 满足12318a a a ++=,则2a =( )A .5B .6C .7D .83.若{}n a 是正项无穷的等差数列,且396a a +=,则{}n a 的公差d 的取值范围是( )A .[)12,B .305æöç÷èø,C .35¥æö+ç÷èø,D .305éö÷êëø,4.等差数列{}n a 前n 项和为7,4n S a =,则13S =( )A .44B .48C .52D .565.已知等差数列{}n a 满足25815a a a ++=,记{}n a 的前n 项和为n S ,则9S =( )A .18B .24C .27D .456.在等差数列{}n a 中,若354a a +=,则其前7项和为( )A .7B .9C .14D .187.已知等差数列{}n a 的前n 项和为n S ,若91S =,则37a a +=( )A .2-B .73C .1D .298.在等比数列{}n a 中,25,a a 是方程2780x x --=的两个根,则16a a =( )A .7B .8C .8-或8D .8-9.已知等差数列{}n a 的前n 项和为S n ,若5414a a a +=+,则15S =( )A .4B .60C .68D .13610.设等差数列{}n a 的前n 项和为n S ,已知2410268a a a ++=,则9S =( )A .272B .270C .157D .153考点02:秒解等差数列的前n 项和等差数列中,有()⇒-=-n n a n S 1212奇偶有适用.()()()()nn n n an n a n a a 12212221212112-=-=-+=--⇒将12-n 换为n 11.在等差数列{}n a 中,公差3d =,n S 为其前n 项和,若89S S =,则17S =( )A .2-B .0C .2D .412.已知n S 是等差数列{}n a 的前n 项和,且7287026S a a =+=,,则{}n a 的公差d =( )A .1B .2C .3D .4.13.已知等差数列{}n a 的公差为d ,前n 项和为n S ,若12413,22a a S +==,则d =( )A .7B .3C .1D .1-14.等差数列 {}n a 中,n S 是其前 n 项和,53253S S -=,则公差 d 的值为( )A .12B .1C .2D .315.记n S 为等差数列{}n a 的前n 项和,已知510S S =,51a =,则1a =( )A .72B .73C .13-D .711-16.已知等差数列{}n a 的前15项之和为60,则313a a +=( )A .4B .6C .8D .1017.已知等差数列{}n a 的前n 项和为n S ,23a =,221n n a a =+,若1100n n S a ++=,则n =( )A .8B .9C .10D .1118.n S 是等差数列{}n a 的前n 项和,若1236a a a ++=,7916+=a a ,则9S =( )A .43B .44C .45D .4619.已知n S 是等差数列{}n a 的前n 项和,若23a =,525S =,则442S a a =-( )A .1B .2C .3D .420.已知n S 为等差数列{}n a 的前n 项和,已知848,16S S =-=,则56223839a a a a a ++++=( )A .215B .185C .155D .135考点03:数列片段和问题k k k k k S S S S S 232,,--这样的形式称之为“片段和”①当}{n a 是等差数列时:k k k k k S S S S S 232,,--也为等差数列,且公差为d k 2.②当}{n a 是等比数列时:k k k k k S S S S S 232,,--也为等比数列,且公比为kq .21.已知等差数列{}n a 的前n 项和为n S ,36S =,()*3164,n S n n -=³ÎN ,20n S =,则n 的值为( )A .16B .12C .10D .822.已知等差数列{}n a 的前n 项和为n S ,若330S =,651S =,则9S =( )A .54B .63C .72D .13523.已知等差数列{}n a 的前n 项和为n S ,且365,15S S ==,则9S =( )A .35B .30C .20D .1524.记n S 为等差数列{}n a 的前n 项和,若4127,45S S ==.则8S =( )A .28B .26C .24D .2225.已知等差数列{}n a 的前n 项和为n S ,若42S =,812S =,则20S =( )A .30B .58C .60D .9026.在等差数列{}n a 中,若363,24S S ==,则12S =( )A .100B .120C .57D .1827.等差数列{}n a 的前n 项和为n S .若10111012101310148a a a a +++=,则2024S =( )A .8096B .4048C .4046D .202428.若正项等比数列{}n a 的前n 项和为n S ,且8426S S -=,则9101112a a a a +++的最小值为( )A .22B .24C .26D .2829.设n S 是等比数列{}n a 的前n 项和,若23S =,346a a +=,则108S S =( )A .157B .3115C .2D .633130.在正项等比数列{}n a 中,n S 为其前n 项和,若301010303,80S S S S =+=,则20S 的值为( )A .10B .20C .30D .40考点04:秒杀和比与项比结论1:若两个等差数列}{n a 与}{n b 的前n 项和分别为n n T S ,,若DCn B An T S n n ++=,则()()Dn C B n A T S b a n n n n +-+-==--12121212结论2:若两个等差数列}{n a 与}{n b 的前n 项和分别为n n T S ,,若DCn B An T S n n ++=,则()()Dm C B n A b a m n +-+-=121231.已知等差数列{}n a 与{}n b 的前n 项和分别为,n n S T ,且231n n S n T n +=+,则19119a ab b ++的值为( )A .1311B .2110C .1322D .212032.已知等差数列{}n a 和{}n b 的前n 项和分别为n S 和n T ,且335n n S n T n +=+,则526a b b =+( )A .1417B .417C .313D .1533.已知数列{}{}n n a b ,均为等差数列,其前n 项和分别为n n S T ,,满足(23)(31)n n n S n T +=-,则789610a a ab b ++=+( )A .2B .3C .5D .634.设数列{}n a 和{}n b 都为等差数列,记它们的前n 项和分别为n S 和n T ,满足21n n n a b n =+,则55S T =( )A .12B .37C .59D .3535.已知等差数列{}n a 和{}n b 的前n 项和分别为,n n S T ,若342n n S n T n +=+,则58211a a b b +=+( )A .1713B .3713C .207D .37736.等差数列{}{},n n a b 的前n 项和分别是,n n S T ,若542n n S n T n +=+,则44a b = .37.设等差数列{}n a ,{}n b 的前n 项和分别为n S ,n T ,若对任意正整数n 都有2343n n S n T n -=-,则839457a ab b b b +=++ .38.已知n S ,n T 分别是等差数列{}n a ,{}n b 的前n 项和,且2131n n S n T n +=-,那么44a b = .39.两个等差数列{}n a 和{}n b 的前n 项和分别为n S 、n T,且523n n S n T n +=+,则220715a a b b ++等于40.已知等差数列{}n a , {}n b 的前n 项和分别为n S ,n T ,且214n nS n T n +=,则537a b b =+ .考点05:等差数列奇偶规律结论()*ÎNn n 2则1,+==-n n a aS S nd S S 偶奇奇偶n 2,则它的奇数项分别为135721,,,......n a a a a a -则它的偶数项分别为24682,,,......na a a a a 则奇数项之和()1212=22n nnn a a n a S na -+×==奇则偶数项之和()22+1+12=22n n n n a a n a S na +×==偶代入公式得1-S =n( )n n S a a nd +-=奇偶,11=S n n n n S na ana a ++=奇偶()*Î+Nn n 12则()()111,11,+++=+=+==-n n n na S a n S nn S S a S S 偶奇偶奇偶奇∵12-n 项,则它的奇数项为127531,,,+n a a a a a 则它的偶数项分别为na a a a 2642,, 则奇数项之和()()()1121112+++=+×+=n n an n a a S 奇则偶数项之和()1222+=×+=n n nan a a S 偶代入公式得()1111+++=-+=-n n n a na a n S S 偶奇()nn na a n S S n n 1111+=+=++偶奇说明:偶奇,S S 分别表示所有奇数项与所有偶数项的和41.已知等差数列{}n a 的项数为()21Ν,m m *+Î其中奇数项之和为140, 偶数项之和为 120,则m =( )A .6B .7C .12D .1342.一个等差数列共100项,其和为80,奇数项和为30,则该数列的公差为( )A .14B .2C .13D .2543.已知等差数列{}n a 的前30项中奇数项的和为A ,偶数项的和为B ,且45B A -=,2615A B =+,则n a =( )A .32n -B .31n -C .31n +D .32n +44.已知数列{}n a 的前n 项和为n S ,且11a =,22a =,13++=n n a a n ,则( )A .45a =B .20300S =C .31720S =D .n 为奇数时,2314+=n n S 45.已知等差数列{}n a 共有21n -项,奇数项之和为60,偶数项之和为54,则n =.46.已知数列{}n a 满足11a =,12,3,n n na n a a n ++ì=í+î为奇数为偶数,则{}n a 的前40项和为.47.已知等差数列{}n a 的项数为21m +()*m ÎN ,其中奇数项之和为140,偶数项之和为120,则数列{}n a 的项数是 .48.数列{}n a 满足:2212212121,2,2n n n na a a a a a ++-==-==,数列{}n a 的前n 项和记为n S ,则23S = .49.在等差数列{}n a 中,已知公差12d =,且1359960+++×××+=a a a a ,求12399100a a a a a +++×××++的值.50.已知{}n a 是等差数列,其中222a =,610a =.(1)求{}n a 的通项公式;(2)求24620a a a a ++++ 的值.考点06: 等差数列前n 项和最值规律方法一:函数法⇒利用等差数列前n 项和的函数表达式,通过配方或借助图象求二次函数最值的方法求解.bn an S n +=2模型演练()n d a n d S d n n na S n n ×÷øöçèæ-+=⇒×-+=222112121122222÷÷÷÷øöççççèæ--÷÷÷÷øöççççèæ-+=⇒d d a d d d a n d S n 2121212212÷øöçèæ--⎥⎦⎤êëé÷øöçèæ--=⇒d a d d a n d S n 由二次函数的最大值、最小值可知,当n 取最接近da 121-的正整数时,n S 取到最大值(或最小值)注意:最接近da 121-的正整数有时1个,有时2个51.已知等差数列{}n a 的前n 项和为n S ,10a >,且316=S S ,则n S 取最大值时,n =( ).A .9B .10C .9或10D .10或1152.已知等差数列{}n a 的前n 项和为n S ,若50a <,380a a +>,则当n S 取得最小值时,n =( )A .4B .5C .6D .753.设数列{}n a 的前n 项和为11,1,321n nn S S S S n n+-=-=+,则下列说法正确的是( )A .{}n a 是等比数列B .36396,,S S S S S --成等差数列,公差为9-C .当且仅当17n =时,n S 取得最大值D .0n S ³时,n 的最大值为3354.数列{}n a 的前n 项和211n S n n =-,则( )A .110a =B .32a a >C .数列{}n S 有最小项D .n S n ìüíýîþ是等差数列55.已知等差数列{}n a 的首项为1a ,公差为d ,前n 项和为n S ,若1089S S S <<,则下列说法正确的是( )A .1a d>B .使得0n S >成立的最大正整数18n =C .891011a a a a +<+D .n n S a ìüíýîþ中最小项为1100S a 56.等差数列 {}n a 的前 n 项和为 1214,0,0n S a a a >+=,则( )A .80a =B .1n na a +<C .79S S <D .当 0n S < 时, n 的最小值为 1657.已知无穷数列{}n a 满足:110a =-,12n n a a +=+()*N n Î.则数列{}n a 的前n 项和最小值时n 的值为 .58.设等差数列{}n a 的公差为d ,其前n 项和为n S ,且满足991,27a S =-=.(1)求d 的值;(2)当n 为何值时n S 最大,并求出此最大值.59.已知数列{}n a 是公差不为零的等差数列,111a =-,且256,,a a a 成等比数列.(1)求{}n a 的通项公式;(2)设n S 为{}n a 的前n 项和,求n S 的最小值.60.记n S 为等差数列{}n a 的前n 项和,已知17a =-,315S =-.(1)求{}n a 的通项公式;(2)求n S ,并求n S 的最小值.考点07:等比数列奇偶规律结论()*ÎNn n 2则qS S =奇偶n 2,则它的奇数项分别为135721,,,......n a a a a a -则它的偶数项分别为24682,,,......na a a a aq a a q a a q a a ×=×=×=342312,,∵()q a a a a a a a a a a q a a a a a a a a a a n n n n n n n n =++++++++=++++++++∴-------123253112325311232531222642()*Î+Nn n 12则q S a S =-偶奇112+n ,则它的奇数项分别为13572+1,,,......n a a a a a 则它的偶数项分别为24682,,,......na a a a a q a a q a a q a a ×=×=×=453423,,∵q S a S q a a a a a a a a a a a a a a a a a a a n n n n n n n n =-⇒=+++++++=++++++++∴-+--+-偶奇12226421212532226421212531 说明:偶奇,S S 分别表示所有奇数项与所有偶数项的和61.已知等比数列{}n a 有21n +项,11a =,所有奇数项的和为85,所有偶数项的和为42,则n =( )A .2B .3C .4D .562.已知等比数列{}n a 的前n 项和为n S ,其中10a >,则“31a a >”是“n S 无最大值”的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件63.已知一个等比数列的项数是是偶数,其奇数项之和1011,偶数项之和为2022,则这个数列的公比为( ).A .8B .2-C .4D .264.已知等比数列{}n a 的公比为13-,其前n 项和为n S ,且1a ,243a +,3a 成等差数列,若对任意的*n ÎN ,均有2nnA SB S £-£恒成立,则B A -的最小值为( )A .2B .76C .103D .5365.已知一个项数为偶数的等比数列{}n a ,所有项之和为所有偶数项之和的4倍,前3项之积为64,则1a =( )A .1B .4C .12D .3666.已知数列}{n a 的前n 项和121n n S -=+,则数列}{n a 的前10项中所有奇数项之和与所有偶数项之和的比为( )A .12B .2C .172341D .34117267.等比数列{}n a 的首项为2,项数为奇数,其奇数项之和为8532,偶数项之和为2116,则这个等比数列的公比q = .68.等比数列的性质已知{}n a 为等比数列,公比为q ,n S 为其前n 项和.(1)若()0,0,1n n S Aq B A q q =+¹¹¹,则A B += ;(2)当0n S ¹时,n S , ,32,n n S S - 为等比数列;(3)若等比数列{}n a 共2k 项,记S 奇为诸奇数项和,S 偶为诸偶数项和,则S S =奇偶 ;69.已知首项均为32的等差数列{}n a 与等比数列{}n b 满足32a b =-,43a b =,且{}n a 的各项均不相等,设n S 为数列{}n b 的前n 项和,则n S 的最大值与最小值之差为 .70.(1)在等比数列{}n a 中,已知248,60n n S S ==,求3n S ;(2)一个等比数列的首项是1,项数是偶数,其奇数项的和为85,偶数项的和为170,求此数列的公比和项数.。
考点12 零点定理——2021年高考数学专题复习真题练习

考点12:零点定理【题组一 求零点】1.函数f (x )2120810x x log x x ⎧-≤⎪=⎨⎪-+⎩(),()(>)的零点为_____.2.若函数()()2log a f x x =+的零点为2-,则a =________.3.设函数[)()222,1,()2,,1x x f x x x x ⎧-∈+∞⎪=⎨-∈-∞⎪⎩,则函数()y f x =的零点是________________.【题组二 零点区间】1.函数3()log (2)1f x x x =++-的零点所在的一个区间是( ) A .(0,1) B .(1,2) C .(2,3) D .(3,4)2.已知函数()26log 21f x x x =--+.在下列区间中,包含()f x 零点的区间是( ) A .()0,1 B .()1,3C .()3,5D .()5,73.函数1()sin 2f x x x =-在下列哪个区间必有零点( ) A .0,2π⎛⎫⎪⎝⎭B .,2ππ⎛⎫⎪⎝⎭C .3,2ππ⎛⎫ ⎪⎝⎭D .3,22ππ⎛⎫⎪⎝⎭【题组三 零点个数】1.函数()231xf x log x =-的零点个数为 .2.函数()22xf x e x =+-在区间()21-,内零点的个数为 .3.函数f (x )=cosπx ﹣(12)x+1在区间[﹣1,2]上的零点个数为 .4.函数()2ln f x x x =+的零点个数是 .5.函数()3f x x =,则()f x 的零点个数为________.6.定义在R 上的偶函数()f x 满足()(4)f x f x =-,且当[0,2]x ∈时,()cos f x x =,则()()lg g x f x x =-的零点个数为____________.7.函数25()sin log ||22f x x x π⎛⎫=- ⎪⎝⎭的零点个数为_______________.8.f(x)是R 上的偶函数,f(x +2)=f(x),当0≤x≤1时,f(x)=x 2,则函数y =f(x)-|log 5x|的零点个数为 .9.若偶函数()f x 的图像关于32x =对称,当30,2x ⎡⎤∈⎢⎥⎣⎦时,()f x x =,则函数()()20log g x f x x =-在[]20,20-上的零点个数是 .10.定义在R 上的奇函数()f x 满足()()22f x f x -=-+,且在区间[)2,4上,()2,234,34x x f x x x -≤<⎧=⎨-≤<⎩,则函数()3log y f x x =-的零点的个数为______.11.函数()f x 对于任意实数x ,都()()f x f x -=与(1)(1)f x f x -=+成立,并且当01x ≤≤时,()2f x x =.则方程()02019xf x -=的根的个数是 .12.已知定义在R 上,且最小正周期为4的函数()f x ,满足()()f x f x -=-,则在区间()10,10-内函数()y f x =的零点个数的最小值是______【题组四 根据零点求参数】1.方程24(2)50x m x m +-+-=的一根在区间()1,0-内,另一根在区间()02,内,则m 的取值范围是 .2.已知函数()()2log 13f x x x m =+++的零点在区间(]0,1上,则m 的取值范围为 .3.若函数()3()1x f x x a =--在(﹣∞,0)上有零点,则实数a 的取值范围为 .4.若函数2()log ()f x x x k k z =+-∈在区间(2,3)上有零点,则k = .5.函数1()lg 1f x x m x =-++在区间()0,9上有零点,则实数m 的取值范围为____________.6.已知函数()ln f x x m =-的零点位于区间()1,e 内,则实数m 的取值范围是________.7.设函数f (x )=log 32x x+-a 在区间(1,2)内有零点,则实数a 的取值范围是________.8.若函数()()21xf x x a =+-在区间[]0,1上有零点,则实数a 的取值范围是 .9.已知函数22log (),0()3,0x a x f x x ax a x +≤⎧=⎨-+>⎩有三个不同的零点,则实数a 的取值范围是________.10.已知函数()226f x x ax =+--,若存在a R ∈,使得()f x 在[]2,b 上恰有两个零点,则实数b 的最小值是______.11.函数f (x)=∣4x -x 2∣-a 的零点的个数为3,则a = .12.设(0,1)m ∈,若函数2log ,02()(4),24x m x f x f x x ⎧-<≤=⎨-<<⎩有4个不同的零点1234,,,x x x x ,且1234x x x x <<<,则22341225x x x x +-+的取值范围是 .13.已知直线y mx =与函数()211,0212,03xx x f x x ⎧+>⎪⎪=⎨⎛⎫⎪-≤ ⎪⎪⎝⎭⎩的图象恰好有3个不同的公共点,则实数m 的取值范围是 .14.已知m R ∈,函数221,1()log (1),1x x f x x x ⎧+<=⎨->⎩,2()221g x x x m =-+-,若函数[()]y f g x m =-有6个零点,则实数m 的取值范围是 .15.已知定义在R 上的偶函数()f x ,且0x ≥时,()31,0153,13x x x f x x -⎧+≤≤⎪=⎨+>⎪⎩,方程()f x m =恰好有4个实数根,则实数m 的取值范围是 .【题组四 二分法】1.已知函数f(x)=x 3+2x −8的零点用二分法计算,附近的函数值参考数据如下表所示:则方程x 3+2x −8=0的近似解可取为(精确度0.1) .2.下列函数中,不能用二分法求函数零点的是( ) A .()21f x x =- B .()221f x x x =-+C .()2log f x x =D .()2xf x e =-3.用二分法求方程的近似解,求得3()29f x x x =+-的部分函数值数据如下表所示:则当精确度为0.1时,方程3290x x +-=的近似解可取为4.用二分法研究函数()321f x x x =--的零点时,若零点所在的初始区间为()12,,则下一个有解区间为( ) A .()12, B .()1.752, C .()1.52, D .()1 1.5,5.若函数()3222f x x x x =+--的—个正数零点附近的函数值用二分法逐次计算,参考数据如下表:2)1.250.984=-那么方程32220x x x +--=的一个近似根(精确度为0.05)为 .6.已知函数f (x )的图象如图,其中零点的个数与可以用二分法求解的个数分别为 .A .4,4B .3,4C .5,4D .4,37.某同学求函数()ln 26f x x x =+-的零点时,用计算器算得部分函数值如表所示:则方程ln 260x x +-=的近似解(精确度0.1)可取为( ) A .2.52 B .2.625C .2.47D .2.758.用“二分法”求26y x =-的零点时,初始区间可取 ( ) A .0,1B .1,2C .()2,3D .()3,4如何学好数学1.圆锥曲线中最后题往往联立起来很复杂导致k 算不出,这时你可以取特殊值法强行算出k 过程就是先联立,后算代尔塔,用下伟达定理,列出题目要求解的表达式,就ok 了2.选择题中如果有算锥体体积和表面积的话,直接看选项面积找到差2倍的小的就是答案,体积找到差3倍的小的就是答案,屡试不爽!3.三角函数第二题,如求a(cosB+cosC)/(b+c)coA之类的先边化角然后把第一题算的比如角A等于60度直接假设B和C都等于60°带入求解。
考点12 零点定理——2021年高考数学专题复习讲义附解析

考点12:零点定理【思维导图】【常见考法】考点一:求零点1.若幂函数()f x x α=的图象过点(,则函数()()3g x f x =-的零点是 。
2.函数()234f x x x =+-的零点是____________.3.若函数()2,01,0x e x f x x x ⎧≤=⎨->⎩,则函数()1y f x =-的零点是___________.4.函数y =11x-的图象与函数y =2sinπx(-2≤x≤4)的图象所有交点的横坐标之和等于 .考点二:零点区间1.函数()42xxf x -=-的零点所在区间是( ) A .(1,0)- B .1(0,)4 C .11(,)42D .1(,1)22.函数()2312x f x x -⎛⎫=- ⎪⎝⎭的零点所在的区间为( )A .()0,1B .()1,2C .()2,3D .()3,43.函数()ln 3f x x x =+-的零点所在的区间为( ) A .()0,1B .()1,2C .()2,3D .()3,44.已知()f x 是定义在()0,∞+上的单调函数,满足()()2ln 21xf f x ex e --+=-,则函数()f x 的零点所在区间为( ) A .210,e ⎛⎫ ⎪⎝⎭B .211,e e ⎛⎫⎪⎝⎭ C .1,1e ⎛⎫⎪⎝⎭D .()1,e考点三:零点个数1.函数f(x)=|x-2|-lnx 在定义域内零点的个数为 。
2.方程20181log 2019xx ⎛⎫= ⎪⎝⎭的解的个数是 。
3.方程2sin(2)103x π+-=在区间[0,4)π上的解的个数为 。
4.若函数()f x 是定义在R 上的偶函数,(4)()f x f x +=,且22,01()42,12x x f x x x ⎧≤<=⎨-≤≤⎩,则函数1()()13g x f x x =--的零点个数为___________.5.已知函数()()()ln 000x x f x x ⎧≠⎪=⎨=⎪⎩,则方程()()20f x f x -=的不相等的实根个数为______.6.已知定义在R 上的函数()y f x =对任意x 都满足()()1f x f x +=-,且当01x ≤<时,()f x x =,则函数()()ln ||g x f x x =-的零点个数为 。
高考数学复习考点知识与结论专题讲解12 幂的运算及幂函数

高考数学复习考点知识与结论专题讲解第12讲幂的运算及幂函数通关一、五种常见幂函数的图像与性质知识通关通关二、幂函数的性质1. 幕函数在(0,)+∞上都有定义;2. 幕函数的图像过定点(1,1);3. 当0α>时, 幕函数的图像都过点(1,1)和(0,0) , 且在(0,)+∞上单调递增;4. 当0α<时, 幕函数的图像都过点(1,1) , 且在(0,)+∞上单调递减;5. 幕函数在第四象限无图像.结论一、幂函数的图像特征1. 当0α<时, 函数图像与坐标轴没有交点, 类似于1y x -=的图像, 且在第一象限内,逆时针方向指数在增大;2. 当0α>时,函数图像倾向x 轴, 类似于y =的图像;3. 当1α>时, 函数图像倾向y 轴, 类似于3y x =的图像,而且逆时针方向指数在增大,再结合函数的奇偶性可得一般幂函数的图像及性质.【例1】以下命题正确的是(),①幂函数的图像都经过(0,0);②幂函数的图像不可能出现在第四象限;③当0n =时,函数n y x =的图像是两条射线;④若n y x =(0n <)是奇函数,则n y x =在定义域内为减函数.A. ①②B. ②④C. ②③D. ①③【答案】C【解析】①幂函数的图像不都经过(0,0) ,比如1y x=,因此错误; ②因为当0x >时, 0x α>, 幂函数的图像不可能出现在第四象限,因此正确;③当0n =时,函数0x α>的图像是一条直线,但是去掉(0,1), 因此正确;④若n y x =(0n <)是奇函数,则n y x =在定义域内不具有单调性, 例如1y x=, 不正确. 综上,故选 C. 【变式】如图所示的曲线是幂函数y x α=在第一象限的图像,已知11{4,,,4}44α∈-- , 相应曲线1234,,,C C C C 对应的α值依次为().A. 114,444--,,B. 114,444,-,- C. 11444-,-,4, D. 114,444,-,- 【答案】B【解析】结合幂函数的单调性及图像,易知曲线1234,,,C C C C 对应的α值依次为114,444,-,-, . 故选 B.结论二、幂函数比较大小1. 当幂的底数相同,指数不同时,可以利用指数函数的单调性比较;2. 当幂的底数不同,指数相同时,可以利用幂函数的单调性比较;3. 当幂的底数和指数都不相同时,一种方法是作商,通过商与1的大小关系确定两个幂值的大小;另一种方法是运用媒介法,即找到一个中间值,通过比较两个幂值与中间值的大小,确定两个幂值的大小;4. 比较多个幂值的大小,一般也采用媒介法,即先判断这组数中每个幂值与0,1,等数的大小关系,据此将它们分成若干组,然后将同一组内的各数再利用相关方法进行比较,最终确定各数之间的大小关系.【例2】已知01m n <<<且1a b <<,则下列各式中一定成立的是()A.m n b a >B. m n b a <C.b a m n >D.b am n <【答案】D【解析】因为()(1)a f x x a =>在(0,)+∞上为单调递增函数,且01m n <<<,所以.a m n α< 又()(01)x g x m m =<<在R 上为单调递减函数,且1a b <<,所以.b a m m <综上,b a m n <.故选D.【变式】当01a b <<<,下列不等式正确的是()A.1(1)(1)b b a a ->-B.(1)(1)a b a b +>+C. 2(1)(1)b b a a ->-D.(1)(1)a b a b ->-【答案】D【解析】因为0(1)(1)1a b <-<-<,又函数(1)x y b =-为减函数,ay x =在(0,1)上为增函数, 所以(1)(1)(1).b a a b b a -<-<-故选D. 结论三、幂函数单调性若0,y x αα>=在(0,)+∞上是增函数;若0,y x αα<=在(0,)+∞上是减函数.【例3】幂函数223()(1)m m f x m m x+-=--在(0,)+∞上是减函数,则实数m 的值为() A.2或-1B.-1C.-2D.-2或1【答案】B【解析】由于幂函数223()(1)m m f x m m x +-=--在(0,)+∞上是减函数,故有221130m m m m ⎧--=⎨+-<⎩,解得 1.m =-故选B. 【变式】已知幂函数221()(1)m f x m m x--=--在(0,)+∞上单调递增. (1)求实数m 的值;(2)若(1)(32)m m k k +<-,求实数k 的取值范围.【答案】(1)1-;(2)23(,1)(,)32-∞-⋃【解析】(1)由题意得211m m --=,解得1m =-或2m =.因为()f x 在(0,)+∞上 单调递增,所以210m -->,即12m <-,所以1m =-. (2)由于1y x=在区间(,0),(0,)-∞+∞上都是减函数,分三种情况讨论: ①当1032k k +<<-,即1k <-时,原不等式成立;②当10k +<且320k -<时,有132k k +>-,即13223k k k ⎧⎪<-⎪⎪>⎨⎪⎪>⎪⎩,解集为空集; ③当10k +>,且,320k ->时,有,132k k +>-解得2332k <<. 综上可知,k 的取值范围是23(,1)(,).32-∞-⋃。
新高考数学复习考点知识提升专题训练12---基本不等式的应用

新高考数学复习考点知识提升专题训练(十二) 基本不等式的应用(一)基础落实1.下列等式中最小值为4的是( ) A .y =x +4xB .y =2t +1tC .y =4t +1t(t >0)D .y =t +1t解析:选C A 中x =-1时,y =-5<4;B 中t =-1时,y =-3<4;C 中y =4t +1t ≥24t ·1t=4,当且仅当t =12时,等号成立;D 中t =-1时,y =-2<4.2.已知0<x <1,则x (3-3x )取得最大值时x 的值为( ) A.13 B.12 C.34D.23解析:选B 由x (3-3x )=13×3x (3-3x )≤13×94=34,当且仅当3x =3-3x ,即x =12时取等号.3.函数y =3x 2+6x 2+1的最小值是( ) A .32-3 B .3 C .62 D .62-3 解析:选D y =3(x 2+1)+6x 2+1-3≥23(x 2+1)·6x 2+1-3=218-3=62-3,当且仅当x 2=2-1时等号成立,故选D.4.(多选)设y =x +1x -2,则( )A .当x >0时,y 有最小值0B .当x >0时,y 有最大值0C .当x <0时,y 有最大值-4D .当x <0时,y 有最小值-4解析:选AC 当x >0时,y =x +1x -2≥2x ·1x -2=2-2=0,当且仅当x =1x,即x =1时,等号成立,故A 正确,B 错误;当x <0时,y =-⎣⎢⎡⎦⎥⎤-x +1-x -2≤-2-2=-4,当且仅当-x =1-x,即x =-1时,等号成立,故C 正确,D 错误.故选A 、C.5.已知x >0,y >0,且x +y =8,则(1+x )(1+y )的最大值为( ) A .16 B .25 C .9D .36解析:选B (1+x )(1+y )≤⎣⎢⎡⎦⎥⎤(1+x )+(1+y )22=⎣⎢⎡⎦⎥⎤2+(x +y )22=⎝ ⎛⎭⎪⎫2+822=25,当且仅当1+x =1+y ,即x =y =4时,等号成立. 6.如果a >0,那么a +1a +2的最小值是________.解析:因为a >0,所以a +1a +2≥2a ·1a+2=2+2=4,当且仅当a =1时等号成立. 答案:47.若正数m ,n 满足2m +n =1,则1m +1n的最小值为________.解析:∵2m +n =1,∴1m +1n =⎝⎛⎭⎫1m +1n (2m +n )=3+2m n +nm ≥3+22,当且仅当n =2m ,即m =1-22,n =2-1时,等号成立,即最小值为3+2 2. 答案:3+2 28.某公司购买一批机器投入生产,据市场分析,每台机器生产的产品可获得的总利润y (单位:万元)与机器运转时间x (单位:年)的关系为y =-x 2+18x -25(x ∈N *),则当每台机器运转________年时,年平均利润最大,最大值是________万元.解析:每台机器运转x 年的年平均利润为y x =18-⎝⎛⎭⎫x +25x ,且x >0,故yx≤18-225=8,当且仅当x =5时,等号成立,所以,当每台机器运转5年时,年平均利润最大,最大值为8万元.答案:5 89.(1)已知x <3,求4x -3+x 的最大值;(2)已知x ,y 是正实数,且x +y =4,求1x +3y 的最小值.解:(1)∵x <3,∴x -3<0, ∴4x -3+x =4x -3+(x -3)+3 =-⎣⎢⎡⎦⎥⎤43-x +(3-x )+3≤-243-x·(3-x )+3 =-1,当且仅当43-x =3-x ,即x =1时,等号成立,∴4x -3+x 的最大值为-1. (2)∵x ,y 是正实数,x +y =4,∴1x +3y =⎝⎛⎭⎫1x +3y ·x +y 4=14⎝⎛⎭⎫4+y x +3x y ≥1+234=1+32,当且仅当y x =3x y ,即x =2(3-1),y =2(3-3)时等号成立.故1x +3y 的最小值为1+32.10.某农业科研单位打算开发一个生态渔业养殖项目,准备购置一块1 800平方米的矩形地块(如图所示),中间挖三个矩形池塘养鱼,挖出的泥土堆在池塘四周形成基围(阴影部分所示)种植桑树,鱼塘周围的基围宽均为2米,池塘所占面积为S 平方米,其中a ∶b =1∶2.(1)试用x ,y 表示S ;(2)若要使S 最大,则x ,y 的值分别为多少?解:(1)由题意得,xy =1 800,b =2a , 则y =a +b +6=3a +6,S =a (x -4)+b (x -6)=a (x -4)+2a (x -6) =(3x -16)a =(3x -16)×y -63=xy -6x -163y +32=1 832-6x -163y ,其中6<x <300,6<y <300.(2)由(1)可知,6<x <300,6<y <300,xy =1 800,6x +163y ≥26x ·163y =26×16×600=480,当且仅当6x =163y 时等号成立,∴S =1 832-6x -163y ≤1 832-480=1 352,此时9x =8y ,xy =1 800,解得x =40,y =45,即x 为40,y 为45.(二)综合应用1.(多选)一个矩形的周长为l ,面积为S ,则下列四组数对中,可作为数对(S ,l )的有( ) A .(1,4) B .(6,8) C .(7,12)D.⎝⎛⎭⎫3,12 解析:选AC 设矩形的长和宽分别为x ,y ,则x +y =12l ,S =xy .由xy ≤⎝ ⎛⎭⎪⎫x +y 22知,S ≤l 216,故A 、C 成立.2.已知a >0,b >0,则1a +1b +2ab 的最小值是( )A .2B .2 2C .4D .5解析:选C1a +1b+2ab ≥21a ·1b+2ab ≥41ab·ab =4,当且仅当1a =1b 且1ab=ab ,即a =b =1时取等号.3.已知x >-1,则(x +10)(x +2)x +1的最小值为________.解析:(x +10)(x +2)x +1=(x +1+9)(x +1+1)x +1=(x +1)2+10(x +1)+9x +1=(x +1)+9x +1+10,∵x >-1,∴x +1>0,∴(x +1)+9x +1+10≥29+10=16,当且仅当x +1=9x +1,即x =2时,等号成立.答案:164.若a >0,b >0,且a 2+b 22=1,求a 1+b 2的最大值. 解:∵a >0,b >0,a 2+b 22=1, ∴a 1+b 2=a 2(1+b 2)=2a 2·1+b 22=2a 2·1+b 22≤2⎝ ⎛⎭⎪⎫a 2+12+b 2222 =2⎝ ⎛⎭⎪⎫1+1222=324,当且仅当正数a ,b 满足a 2=1+b 22且a 2+b 22=1,即a =32,b =22时等号成立.∴a 1+b 2的最大值为324.(三)创新发展1.若不等式ax 2+1x 2+1≥2-3a 3(a >0)恒成立,则实数a 的取值范围是________.解析:原不等式可转化为a (x 2+1)+1x 2+1≥23,又a >0,则a (x 2+1)+1x 2+1≥2a (x 2+1)·1x 2+1=2a ,当且仅当a (x 2+1)=1x 2+1,即a =1(x 2+1)2时,等号成立,则根据恒成立的意义可知2a ≥23,解得a ≥19.答案:⎩⎨⎧⎭⎬⎫a|a ≥192.某单位决定投资3 200元建一仓库(长方体状),高度恒定,它的后墙利用旧墙不花钱,正面用铁栅,每米长造价40元,两侧墙砌砖,每米长造价45元,顶部每平方米造价20元,设铁栅长为x 米,一堵砖墙长为y 米.(1)写出x 与y 的关系式;(2)求出仓库面积S 的最大允许值.为使S 达到最大,而实际投资又不超过预算,那么正面铁栅应设计为多长?解:(1)由于铁栅长为x 米,一堵砖墙长为y 米,由题意可得40x +2×45y +20xy =3 200,即4x +9y +2xy =320,解得y =320-4x2x +9,由于x >0且y >0,可得0<x <80,所以,x 与y 的关系式为y =320-4x2x +9(0<x <80).(2)S =xy =x ·320-4x2x +9=x ·338-2(2x +9)2x +9=x ·⎝ ⎛⎭⎪⎫3382x +9-2=338x 2x +9-2x =169(2x +9)-169×92x +9-2x =169-2x -169×92x +9=178-(2x +9)-169×92x +9=178-⎣⎢⎡⎦⎥⎤(2x +9)+169×92x +9≤178-2(2x +9)×169×92x +9=100,当且仅当2x +9=169×92x +9,即⎩⎨⎧x =15,y =203时,等号成立,因此,仓库面积S 的最大允许值是100平方米,此时正面铁栅长应设计为15米.。
专题12-1 参数方程与极坐标归类-2023年高考数学一轮复习热点题型(全国通用)(原卷版)

【提分秘籍】
基本规律
极坐标一线两点(一般直线或射线过极点):
| AB | |2 -1|=|B A(| 若是韦达定理型,则= 2 +1 2 -421)
【变式演练】
在平面直角坐标系中,曲线
C1
的参数方程为
x y
3 cos 2 sin
(
为参数),以
O
为极点,x
,求
AB
.
【题型二】参数方程难点 1:万能代换型消参
【典例分析】
在直角坐标系
xOy
中,曲线
C
的参数方程为
x
1 1
t t
2 2
,
(t
为参数).以坐标原点
O
为极点,x
轴的
y
1
4t t
2
正半轴为极轴建立极坐标系,直线 l 的极坐标方程为 2 cos 3 sin 11 0 .
(1)求 C 和 l 的直角坐标方程;(2)求 C 上的点到 l 距离的最小值.
三、极坐标体系弦长公式
(1)一线两点(一般直线(射线)过极点
| AB | |2 -1|=|B A(| 若是韦达定理型,则= 2 +1 2 -421)
(2)两线两点:余弦定理 | AB |2 =22 +12 -221 co(s 2 -1)
【变式演练】
在直角坐标系
xOy
中,曲线 C1 的参数方程为
l
的极坐标方程为
sin
3
2
.
(1)求曲线 C 的普通方程和直线 l 的直角坐标方程; (2)设直线 l 与 y 轴的交点为 P,经过点 P 的动直线 m 与曲线 C 交于 A,B 两点,证明: PA PB 为定值.
高考数学总复习:第十二篇 第3讲 数学归纳法
(m∈N*)能被3整除.
证明 (1)当m=1时,a4m+1=a5=a4+a3=(a3+a2)+(a2+a1) =(a2+a1)+2a2+a1=3a2+2a1=3+0=3.
即当m=1时,第4m+1项能被3整除.故命题成立.
抓住2个考点
突破4个考向
揭秘3年高考
(2)假设当m=k时,a4k+1能被3整除,则当m=k+1时, a4(k+1)+1=a4k+5=a4k+4+a4k+3=2a4k+3+a4k+2 =2(a4k+2+a4k+1)+a4k+2=3a4k+2+2a4k+1.
(2)由假设n=k成立证n=k+1时,要推导详实,并且一定
要运用n=k成立的结论. (3)要注意n=k到n=k+1时增加的项数.
抓住2个考点
突破4个考向
揭秘3年高考
考点自测
1 1.在应用数学归纳法证明凸 n 边形的对角线为 n(n-3)条 2 时,第一步检验第一个值 n0 等于 ( ).
A.1 解析 答案 C
即Tk+1+12=-2ak+1+10bk+1.
因此n=k+1时等式也成立. 由①②可知,对任意n∈N*,Tn+12=-2an+10bn成立.
抓住2个考点
突破4个考向
揭秘3年高考
法二
由(1)得 Tn=2an+22an-1+23an-2+„+2na1,
① ②
2Tn=22an+23an-1+„+2nan+2n+1a1. ②-①,得
则当n=k+1时有
抓住2个考点 突破4个考向 揭秘3年高考
Tk+1=ak+1b1+akb2+ak-1b3+…+a1bk+1 =ak+1b1+q(akb1+ak-1b2+…+a1bk) =ak+1b1+qTk
=ak+1b1+q(-2ak+10bk-12)
高考数学复习考点突破专题讲解12 圆锥曲线的方程与性质
高考数学复习考点突破专题讲解第12讲圆锥曲线的方程与性质一、单项选择题1.(2022·广东惠州一模)若抛物线y2=2px(p>0)上一点P(2,y0)到其焦点的距离为4,则抛物线的标准方程为()A.y2=2xB.y2=4xC.y2=6xD.y2=8x2.(2022·山东临沂二模)已知双曲线C:=1(a>0,b>0)的焦距为4,实轴长为4,则C的渐近线方程为()A.y=±2xB.y=±xC.y=±xD.y=±x3.(2022·广东肇庆二模)已知F1,F2分别是椭圆C:=1(a>b>0)的左、右焦点,A是椭圆上一点,O 为坐标原点,若|OA|=|OF1|,直线F2A的斜率为-3,则椭圆C的离心率为()A. B. C. D.4.(2022·河北保定高三期末)为了更好地研究双曲线,某校高二年级的一位数学老师制作了一个如图所示的双曲线模型.已知该模型左、右两侧的两段曲线(曲线AB与曲线CD)为某双曲线(离心率为2)的一部分,曲线AB与曲线CD中间最窄处间的距离为30 cm,点A与点C,点B与点D均关于该双曲线的对称中心对称,且|AB|=36 cm,则|AD|=()A.12 cmB.6 cmC.38 cmD.6 cm5.(2022·全国甲·文11)已知椭圆C:=1(a>b>0)的离心率为,A1,A2分别为C的左、右顶点,B为C的上顶点.若=-1,则C的方程为()A.=1B.=1C.=1D.+y2=16.(2022·广东执信中学模拟)已知双曲线C的离心率为,F1,F2是C的两个焦点,P为C上一点,|PF1|=3|PF2|,若△PF1F2的面积为,则双曲线C的实轴长为()A.1B.2C.3D.47.(2022·江西宜春期末)已知抛物线E:y2=8x的焦点为F,P是抛物线E上的动点,点Q与点F关于坐标原点对称,当取得最小值时,△PQF的外接圆半径为()A.1B.2C.2D.48.(2022·山东滨州二模)已知椭圆C1和双曲线C2有相同的左、右焦点F1,F2,若C1,C2在第一象限内的交点为P,且满足∠POF2=2∠PF1F2,设e1,e2分别是C1,C2的离心率,则e1,e2的关系是()A.e1e2=2B.=2C.+e1e2+=2D.=2二、多项选择题9.(2022·湖北武昌高三期末)已知双曲线C:=1,下列对双曲线C判断正确的是()A.实轴长是虚轴长的2倍B.焦距为8C.离心率为D.渐近线方程为x±y=010.(2022·新高考Ⅱ·10)已知O为坐标原点,过抛物线C:y2=2px(p>0)的焦点F的直线与C交于A,B两点,点A在第一象限,点M(p,0),若|AF|=|AM|,则()A.直线AB的斜率为2B.|OB|=|OF|C.|AB|>4|OF|D.∠OAM+∠OBM<180°11.(2022·山东临沂三模)2022年4月16日9时56分,神舟十三号返回舱成功着陆,返回舱是宇航员返回地球的座舱,返回舱的轴截面可近似看作是由半圆和半椭圆组成的“曲圆”,如图,在平面直角坐标系中,半圆的圆心在坐标原点,半圆所在的圆过椭圆的焦点F(0,2),椭圆的短轴与半圆的直径重合,下半圆与y轴交于点G.若过原点O的直线与上半椭圆交于点A,与下半圆交于点B,则()A.椭圆的长轴长为4B.线段AB长度的取值范围是[4,2+2]C.△ABF的面积最小值是4D.△AFG的周长为4+412.(2022·江苏南通高三检测)已知椭圆C1:=1(m>n>0)的上焦点为F1,双曲线C2:=1的左、右焦点分别为F2,F3,直线F1F2与C2的右支相交于点A,若AF3⊥F2F3,则()A.C1的离心率为B.C2的离心率为C.C2的渐近线方程为y=±xD.△AF1F3为等边三角形三、填空题13.(2021·全国乙·理13)已知双曲线C:-y2=1(m>0)的一条渐近线为x+my=0,则C的焦距为.14.(2022·河北保定模拟)已知椭圆C的中心为坐标原点,焦点在y轴上,F1,F2为C的两个焦点,C的短轴长为4,且C上存在一点P,使得|PF1|=6|PF2|,写出椭圆C的一个标准方程:.15.(2022·山东威海高三期末)已知抛物线C1:y2=8x,圆C2:x2+y2-4x+3=0,点M(1,1),若A,B分别是C1,C2上的动点,则|AM|+|AB|的最小值为.16.(2022·河北石家庄二模)已知椭圆C1和双曲线C2有公共的焦点F1,F2,曲线C1和C2在第一象限内相交于点P,且∠F1PF2=60°.若椭圆C1的离心率的取值范围是,则双曲线C2的离心率的取值范围是.高考数学复习考点突破专题讲解12圆锥曲线的方程与性质1.D解析∵抛物线y2=2px上一点P(2,y0)到其焦点的距离等于到其准线的距离,∴+2=4,解得p=4,∴抛物线的标准方程为y2=8x.2.C解析由已知得,双曲线的焦点在y轴上,双曲线的焦距2c=4,解得c=2,双曲线的实轴长为2a=4,解得a=2,则b=--=4,故双曲线C的渐近线方程为y=±x=±x.3. D解析如图,由|OA|=|OF1|,得|OA|=|OF1|=|OF2|=c,故∠F1AF2=90°.因为直线F2A的斜率为-3,所以tan∠F1F2A=3,所以|AF1|=3|AF2|.又|AF1|+|AF2|=2a,所以|AF1|=,|AF2|=.又|AF1|2+|AF2|2=|F1F2|2,即a2+a2=4c2,得,所以.4. D解析以双曲线的对称中心为坐标原点,建立平面直角坐标系xOy,因为双曲线的离心率为2,所以可设双曲线的标准方程为=1(a>0),依题意可得2a=30,则a=15,即双曲线的标准方程为=1.因为|AB|=36cm,所以点A的纵坐标为18.由=1,得|x|=3,故|AD|=6cm.5.B解析由题意知,A1(-a,0),A2(a,0),B(0,b),则=(-a,-b)·(a,-b)=-a2+b2=-1,①由e=,得e2=-=1-,即b2=a2.②联立①②,解得a2=9,b2=8.故选B.6.B解析根据双曲线的定义,可得|PF1|-|PF2|=2a,又|PF1|=3|PF2|,解得|PF1|=3a,|PF2|=a.因为双曲线C的离心率为,所以c= a.在△PF1F2中,由余弦定理,可得cos∠F1PF2=-=-,则sin∠F1PF2=.由△PF1F2的面积为,可得|PF1||PF2|sin∠F1PF2=a2=,解得a=1.故双曲线C的实轴长为2.7. C解析过点P作准线的垂线,垂足为M,由抛物线的定义知|PF|=|PM|,所以=cos∠QPM=cos∠PQF,要使取得最小值,则cos∠PQF取得最小值,即tan∠PQF取得最大值0<∠PQF<,此时直线PQ与抛物线相切.设直线PQ的方程为y=k(x+2),由得k2x2+(4k2-8)x+4k2=0,所以Δ=(4k2-8)2-4k2·4k2=64(1-k2)=0,即k2=1,解得k=±1,不妨取k=1,此时直线PQ的倾斜角∠PQF=,且有x2-4x+4=0,所以x=2,所以P(2,4),所以|PF|=4.设△PQF的外接圆半径为R,在△PQF中,由正弦定理知,2R==4.所以此时△PQF的外接圆半径R=2.8. D解析因为∠POF2=∠PF1F2+∠F1PO,∠POF2=2∠PF1F2,所以∠PF1F2=∠F1PO,所以|OF1|=|OP|=|OF2|=c,所以PF1⊥PF2.记椭圆长半轴长为a1,双曲线实半轴长为a2,椭圆和双曲线的半焦距为c,|PF1|=m,|PF2|=n,则由椭圆和双曲线定义可得,m+n=2a1,①m-n=2a2,②①2+②2可得2(m2+n2)=4().由勾股定理知,m2+n2=4c2,代入上式可得2c2=,整理得=2,即=2,所以=2.9.BD解析由双曲线C:=1,可得a2=12,b2=4,则c2=a2+b2=16,所以a=2,b=2,c=4,故A不正确,B正确;e=,故C不正确;易知渐近线方程为y=±x,即x±y=0,故D正确.10.ACD解析选项A,由题意知,点A为FM的中点,设A(x A,y A),则x A=p,所以=2px A=2p·p=p2(y A>0).=2,故选项A正确;所以y A=p,故k AB=-选项B,由斜率为2可得直线AB的方程为x=y+,联立抛物线方程得y2-py-p2=0,设B(x B,y B),则p+y B=p,则y B=-,代入抛物线方程得-=2p·x B,解得x B=.∴|OB|=,故选项B错误;选项C,|AB|=p++p=p>2p=4|OF|,故选项C正确;选项D,由选项A,B知,A p,p,B,-p,所以=p,p·,-p=-p2=-p2<0,所以∠AOB为钝角.又=-p·-,-p=-p2=-p2<0,所以∠AMB为钝角.所以∠OAM+∠OBM<180°.故选项D正确.故选ACD.11. ABD解析由题知,椭圆中b=c=2,则a=2,则2a=4,故A正确;|AB|=|OB|+|OA|=2+|OA|,由椭圆性质可知2≤|OA|≤2,所以4≤|AB|≤2+2,故B正确;若A,B,F能构成三角形,则AB不与y轴重合,此时2≤|OA|<2,记∠AOF=θ,则S△ABF=S△AOF+S△OBF=|OA||OF|sinθ+OB·OF sin(π-θ)=|OA|·sinθ+2sinθ=(|OA|+2)sinθ,取θ=,则S△ABF=1+|OA|<1+×2<4,故C错误;由椭圆定义知,|AF|+|AG|=2a=4,所以△AFG的周长L=|FG|+4=4+4,故D正确.12. ACD解析易知F1(0,-),F2(-,0),F3(,0),将x=代入双曲线C2的方程得=1,可得y2=,则点A.因为O为F2F3的中点,且OF1∥AF3,所以OF1为△F2AF3的中位线,所以-,整理可得m4=4m2n2-4n4,即m2=2n2.椭圆C1的离心率为e1=-,故A正确;双曲线C2的离心率为e2=,故B错误;双曲线C2的渐近线方程为y=±x=±x,故C正确;易知点A(n,2n),F2(-n,0),则,则∠AF2F3=30°,故∠F2AF3=60°.因为|AF3|=2n,|AF1|=|AF2|=(|AF3|+2n)=2n,所以△AF1F3为等边三角形,故D正确.13.4解析由双曲线方程可知其渐近线方程为±y=0,即y=±x,得-=-,解得m=3.可得C 的焦距为2=4.14.=1(答案不唯一)解析因为|PF1|=6|PF2|,所以|PF1|+|PF2|=7|PF2|=2a,则|PF2|=.又因为a-c≤|PF2|≤a+c,所以≥a-c,即.根据题意可设C的标准方程为=1(a>b>0),因为椭圆C的短轴长为4,所以2b=4,b=2.又由,可得--,解得a2≥,所以椭圆C的一个标准方程为=1.15. 2解析由抛物线C1:y2=8x得焦点F(2,0),准线方程为x=-2.由圆C2:x2+y2-4x+3=0,得(x-2)2+y2=1,所以圆C2是以F(2,0)为圆心,以r=1为半径的圆.所以|AM|+|AB|≥|AM|+|AF|-1,所以当|AM|+|AF|取得最小值时,|AM|+|AB|取得最小值.又根据抛物线的定义得|AF|等于点A到准线的距离,所以过点M作准线的垂线,垂足为N,且与抛物线C1:y2=8x相交,当点A为此交点时,|AM|+|AF|取得最小值,最小值为|1-(-2)|=3.所以此时|AM|+|AB|≥|AM|+|AF|-1≥3-1=2,所以|AM|+|AB|的最小值为2.16.解析设椭圆C1:=1(a>b>0),双曲线C2:=1,椭圆与双曲线的半焦距为c,椭圆的离心率e=,双曲线的离心率e1=,|PF1|=s,|PF2|=t,如图,由椭圆的定义可得s+t=2a,由双曲线定义可得s-t=2a1,联立可得s=a1+a,t=a-a1.由余弦定理可得4c2=s2+t2-2st cos∠F1PF2=(a+a1)2+(a-a1)2-2(a+a1)(a-a1)cos60°=a2+3,即4=,解得.-因为e∈,所以≤e2≤,2≤≤3,可得≤3,故≤e1≤.。
高考数学二轮复习考点十二《数列综合练习》课件
数列,当 n 为偶数时,bn+2=bn+1,数列为以 1 为公差的等差数列,∴S23
1-212
11×(11-1)
=(b1+b3+…+b23)+(b2+b4+…+b22)= 1-2 +11×4+
2
×1=212-1+44+55=4194.
2.等差数列{an}中,a1+a2=152,a2+a5=4,设 bn=[an],[x]表示不超 过 x 的最大整数,[0.8]=0,[2.1]=2,则数列{bn}的前 8 项和 S8=( )
A.12<a2<1
B.{an}是递增数列
C.12<a3<34
D.34<a2022<1
答案 ABD
解析 由 an+1=an+ln (2-an),0<a1<12,设 f(x)=x+ln (2-x),则 f′(x) =1-2-1 x=12- -xx,所以当 0<x<1 时,f′(x)>0,即 f(x)在(0,1)上单调递增, 所以 f(0)<f(x)<f(1),即12=ln e<ln 2<f(x)<1+ln 1=1,所以12<f(x)<1,即12 <an<1(n≥2),故 A 正确;因为 f(x)在(0,1)上单调递增,0<an<1(n∈N*),所 以 an+1-an=ln (2-an)>ln (2-1)=0,所以{an}是递增数列,故 B项中,只有一项符合题目要求) 1.已知数列{bn}满足 b1=1,b2=4,bn+2=1+sin2n2πbn+cos2n2π,则该 数列的前 23 项和为( ) A.4194 B.4195 C.2046 D.2047
答案 A
解析 由题意,得当 n 为奇数时,bn+2=2bn,数列为以 2 为公比的等比
高考数学总复习考点知识专题讲解12 离散型随机变量的数字特征
高考数学总复习考点知识专题讲解专题12 离散型随机变量的数字特征知识点一离散型随机变量的均值1.离散型随机变量的均值的概念一般地,若离散型随机变量X的分布列为则称E(X)=x1p1+x2p2+…+x i p i+…+x n p n=∑=ii ip x1,为随机变量X的均值或数学期望.2.离散型随机变量的均值的意义均值是随机变量可能取值关于取值概率的加权平均数,它综合了随机变量的取值和取值的概率,反映了随机变量取值的平均水平.3.离散型随机变量的均值的性质若Y=aX+b,其中a,b均是常数(X是随机变量),则Y也是随机变量,且有E(aX+b)=aE(X)+b.证明如下:如果Y=aX+b,其中a,b为常数,X是随机变量,那么Y也是随机变量.因此P(Y=ax i+b)=P(X=x i),i=1,2,3,…,n,所以Y的分布列为于是有E(Y)=(ax1+b)p1+(ax2+b)p2+…+(ax i+b)p i+…+(ax n+b)p n=a(x1p1+x2p2+…+x i p i+…+x n p n)+b(p1+p2+…+p i+…+p n)=aE(X)+b,即E(aX+b)=aE(X)+b .知识点二 两点分布的均值如果随机变量X 服从两点分布,那么E (X )=0×(1-p )+1×p =p .【例1】(2023•岳阳楼区校级开学)甲乙两人进行乒乓球比赛,每人各局取胜的概率均为12,现采用五局三胜制,胜3局者赢得全部奖金800元.若前两局比赛均为甲胜,此时因某种原因比赛中止,为使奖金分配合理,则乙应得奖金()元 A .700B .600C .200D .100【例2】(2023•宝山区期末)设0a b <…,随机变量X 的分布是124()a b a b+,则()E X 的取值范围是()A .3(1,)2B .11[,3)4C .11(1,]4D .53[,)22【例3】(2023•多选•扬州期中)乒乓球()tabletennis ,被称为中国的“国球”,是一种世界流行的球类体育项目,是推动外交的体育项目,被誉为“小球推动大球”.某次比赛采用五局三胜制,当参赛甲、乙两位中有一位赢得三局比赛时,就由该选手晋级而比赛结束.每局比赛皆须分出胜负,且每局比赛的胜负不受之前已赛结果影响.假设甲在任一局赢球的概率为(01)p p 剟,实际比赛局数的期望值记为()f p ,下列说法正确的是() A .三局就结束比赛的概率为33(1)p p +-B .()f p 的常数项为3 C .14()()35f f <D .133()28f =知识点三 离散型随机变量的方差、标准差 设离散型随机变量X 的分布列如表所示.我们用X 所有可能取值x i 与E (X )的偏差的平方(x 1-E (X ))2,(x 2-E (X ))2,…,(x n -E (X ))2,关于取值概率的加权平均,来度量随机变量X 取值与其均值E (X )的偏离程度.我们称D (X )=(x 1-E (X ))2p 1+(x 2-E (X ))2p 2+…+(x n -E (X ))2p n =i ni i p X E x ∑=-12))((为随机变量X 的方差(variance),有时也记为Var (X )X 的标准差(standard deviation),记为σ(X ). 知识点四 离散型随机变量方差的性质 1.设a ,b 为常数,则D (aX +b )=a 2D (X ). 2.D (c )=0(其中c 为常数). 均值、方差在决策中的作用(1)均值:均值反映了离散型随机变量取值的平均水平,均值越大,平均水平越高. (2)方差:方差反映了离散型随机变量取值的离散波动程度,方差越大越不稳定. (3)在决策中常结合实际情形依据均值、方差做出决断.【例4】(2023•巴中模拟)若一组样本数据1y ,2y ,⋯⋯,n y 的期望和方差分别为2,0.04,则数据151y +,251y +,351y +,⋯⋯,51n y +的期望和方差分别为() A .3,1B .11,1C .3,0.2D .11,0.2【例5】(2023•多选•重庆期中)若随机变量X 服从两点分布,且1(0)4P X ==,则()A .(1)()P X E X ==B .(41)3E X +=C .3()16D X =D .(41)4D X +=【例6】(2023•多选•南山区期中)设离散型随机变量X 的分布列为若离散型随机变量Y 满足21Y X =+,则下列结果正确的有() A .0.5q =B .()3E X =,() 1.4D X =C .()3E X =,() 1.8D X =D .()7E Y =,() 5.6D Y =【例7】(2022•浙江)现有7张卡片,分别写上数字1,2,2,3,4,5,6.从这7张卡片中随机抽取3张,记所抽取卡片上数字的最小值为ξ,则(2)P ξ==,()E ξ=.【例8】(2023•湖南月考)长沙市有橘子洲,岳麓山,天心阁,开福寺四个景点,一位游客来长沙市游览.已知该游客游览橘子洲的概率为23,游览其他景点的概率都是12.该游客是否游览这四个景点相互独立,用随机变量X 记录该游客游览的景点数,下列说法正确的是()A .游客至多游览一个景点的概率为14B .3(2)8P X ==C .1(4)24P X ==D .13()6E X =【例9】(2023•多选•南京模拟)在10件产品中,其中有3件一等品,4件二等品,3件三等品,现从这10件产品中任取3件,记X 为取出的3件产品中一等品件数,事件A为取出的3件产品中一等品件数等于一等品件数,事件B 为取出的3件产品中一等品件数等于三等品件数,则下列命题正确的是() A .7(2)40P X ==B .29(1)30P X =…C .9()10E X =D .A ,B 相互独立【例10】(2022•多选•张家口期末)一种疾病需要通过核酸检测来确定是否患病,检测结果呈阴性即没患病,呈阳性即为患病,已知7人中有1人患有这种疾病,先任取4人,将他们的核酸采样混在一起检测.若结果呈阳性,则表明患病者为这4人中的1人,然后再逐个检测,直到能确定患病者为止;若结果呈阴性,则在另外3人中逐个检测,直到能确定患病者为止.则()A .最多需要检测4次可确定患病者B .第2次检测后就可确定患病者的概率为27C .第3次检测后就可确定患病者的概率为27D .检测次数的期望为227【例11】(2023•河源期末)某工厂有甲、乙、丙三条生产线同时生产同一产品,这三条生产线生产产品的次品率分别为6%,5%,4%,假设这三条生产线产品产量的比为5:7:8,现从这三条生产线上共任意选取100件产品,则次品数的数学期望为4.85.【例12】(2022•甲卷)甲、乙两个学校进行体育比赛,比赛共设三个项目,每个项目胜方得10分,负方得0分,没有平局.三个项目比赛结束后,总得分高的学校获得冠军.已知甲学校在三个项目中获胜的概率分别为0.5,0.4,0.8,各项目的比赛结果相互独立.(1)求甲学校获得冠军的概率;(2)用X表示乙学校的总得分,求X的分布列与期望.【例13】(2021•新高考Ⅰ)某学校组织“一带一路”知识竞赛,有A,B两类问题.每位参加比赛的同学先在两类问题中选择一类并从中随机抽取一个问题回答,若回答错误则该同学比赛结束;若回答正确则从另一类问题中再随机抽取一个问题回答,无论回答正确与否,该同学比赛结束.A类问题中的每个问题回答正确得20分,否则得0分;B 类问题中的每个问题回答正确得80分,否则得0分.已知小明能正确回答A类问题的概率为0.8,能正确回答B类问题的概率为0.6,且能正确回答问题的概率与回答次序无关.(1)若小明先回答A类问题,记X为小明的累计得分,求X的分布列;(2)为使累计得分的期望最大,小明应选择先回答哪类问题?并说明理由.同步训练1.(2019•浙江)设01<<.随机变量X的分布列是a则当a在(0,1)内增大时,()A.()D X减小D X增大B.()C.()D X先减小后增大D X先增大后减小D.()2.(2023•多选•从化区期中)袋内有大小完全相同的2个黑球和3个白球,从中不放回地每次任取1个小球,直至取到白球后停止取球,则()A .抽取2次后停止取球的概率为35B .停止取球时,取出的白球个数不少于黑球的概率为910C .取球次数ξ的期望为2D .取球3次的概率为1103.(2022•多选•南关区开学)已知随机变量ξ的分布列如下表;记“函数()3sin()2x f x x R π+=∈是偶函数”为事件A ,则下列结论正确的有() A .3()4E m ξ=-B .34m n +=C .3()4P A =D .1()4P A =4.(2023•多选•城厢区期末)设01m <<,随机变量的分布列为:则当m 在(0,1)上增大时,() A .()E ξ减小B .()E ξ增大C .()D ξ先增后减,最大值为16D .()D ξ先减后增,最小值为165.(2021•浙江)袋中有4个红球,m 个黄球,n 个绿球.现从中任取两个球,记取出的红球数为ξ,若取出的两个球都是红球的概率为16,一红一黄的概率为13,则m n -=,()E ξ=.6.(2020•浙江)盒中有4个球,其中1个红球,1个绿球,2 个黄球.从盒中随机取球,每次取1个,不放回,直到取出红球为止.设此过程中取到黄球的个数为ξ,则(0)Pξ==,Eξ=.()7.(2022•全国)甲、乙两名运动员进行五局三胜制的乒乓球比赛,先赢得3局的运动员获胜,并结束比赛.设各局比赛的结果相互独立,每局比赛甲赢的概率为2,乙赢的3.概率为13(1)求甲获胜的概率;(2)设X为结束比赛所需要的局数,求随机变量X的分布列及数学期望.8.(2022•北京)在校运动会上,只有甲、乙、丙三名同学参加铅球比赛,比赛成绩达到9.50m以上(含9.50)m的同学将获得优秀奖.为预测获得优秀奖的人数及冠军得主,收集了甲、乙、丙以往的比赛成绩,并整理得到如下数据(单位:):m甲:9.80,9.70,9.55,9.54,9.48,9.42,9.40,9.35,9.30,9.25;乙:9.78,9.56,9.51,9.36,9.32,9.23;丙:9.85,9.65,9.20,9.16.假设用频率估计概率,且甲、乙、丙的比赛成绩相互独立.(Ⅰ)估计甲在校运动会铅球比赛中获得优秀奖的概率;(Ⅱ)设X是甲、乙、丙在校运动会铅球比赛中获得优秀奖的总人数,估计X的数学期望EX;(Ⅲ)在校运动会铅球比赛中,甲、乙、丙谁获得冠军的概率估计值最大?(结论不要求证明)9.(2021•新高考Ⅱ)一种微生物群体可以经过自身繁殖不断生存下来,设一个这种微生物为第0代,经过一次繁殖后为第1代,再经过一次繁殖后为第2代,⋯⋯,该微生物每代繁殖的个数是相互独立的且有相同的分布列,设X 表示1个微生物个体繁殖下一代的个数,()(0i P X i p i ===,1,2,3).(Ⅰ)已知00.4p =,10.3p =,20.2p =,30.1p =,求()E X ;(Ⅱ)设p 表示该种微生物经过多代繁殖后临近灭绝的概率,p 是关于x 的方程:230123p p x p x p x x +++=的一个最小正实根,求证:当()1E X …时,1p =,当()1E X >时,1p <;(Ⅲ)根据你的理解说明(2)问结论的实际含义.10.(2020•江苏)甲口袋中装有2个黑球和1个白球,乙口袋中装有3个白球.现从甲、乙两口袋中各任取一个球交换放入另一口袋,重复n 次这样的操作,记甲口袋中黑球个数为n X ,恰有2个黑球的概率为n p ,恰有1个黑球的概率为n q . (1)求1p ,1q 和2p ,2q ;(2)求2n n p q +与112n n p q --+的递推关系式和n X 的数学期望()n E X (用n 表示).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1. 在△ABC 中,∠C=90°,),3,2(),1,(==k 则k 的值是
A 5
B -5
C 23
D 2
3- 2.已知a 、均为单位何量,它们的夹角为60°,那么| a + 3 | =
A 7
B 10
C 13
D 4
3. 已知点A (3,1),B (0,0)C (3,0).设∠BAC 的平分线AE 与BC 相交于E ,那么有λλ其中,=等于
A 2
B 21
C -3
D -31
4. 已知向量a ≠e ,|e |=1,对任意t ∈R ,恒有|a -t e |≥|a -e |,则 A a ⊥e B a ⊥(a -e ) C e ⊥(a -e ) D (a +e )⊥(a -e )
5.已知向量(,12),(4,5),(,10)OA k OB OC k ===-,且A 、B 、C 三点共线,则k=___
6..已知向量a 与的夹角为120°,且|a |=2, ||=5,则
(2a -b )·a = . 7..已知向量
b a x f x x b x x a ⋅=-+=+=)()),4
2tan(),42sin(2()),42tan(,2cos 2(令πππ. 是否存在实数?))()((0)()(],,0[的导函数是其中使x f x f x f x f x '='+∈π若存在,则求出x 的值;若不存在,则证明之.
8.如图,在Rt △ABC 中,已知BC=a ,若长为2a 的线段PQ 以点A 为中点,问PQ 最大值. 与的夹角θ取何值时,·的值最大?并求出这个
A B
C
a
参考答案
1.A [解析]: ∠C=90°,),3,2(),1,(==AC k AB 则
)2,2(k BC -=∵∠C=90°
∴506)2(20=∴=+-∴=⋅k k BC AC
2.C [解析]:已知a 、均为单位何量,它们的夹角为60°,那么a •b =2
1 ∴| a + 3 |2=13962
2=+⋅+
3.C [解析]:设∠BAC 的平分线AE 与BC 相交于E , 那么31
12=+=+=∴=AC AC AB AC AB EC BE λ 4.C[解析]:已知向量a ≠e ,|e |=1,对任意t ∈R ,恒有|a -t e |≥|a -e |
即 |a -t e |2≥|a -e |2 ∴01222≥-⋅+⋅-t t
即
01010)12(4)2(22=-⋅∴≤-⋅≤-⋅-⋅=∆)即(
002=-⋅∴=-⋅( 5. 23-[解析]:向量(,12),(4,5),(,10)OA k OB OC k ===-,
∴ )2,2(),7,4(--=--=k k 又A 、B 、C 三点共
线
故(4-k,- 7)= λ(- 2k,- 2) ∴k=2
3
-
6 13 [解析]: (2a -)·a =2a 2- a ·=213)2
1(5222=-⨯⨯-⨯ 7. 已知向量)),42tan(),42sin(2()),42tan(,2cos 2(πππ-+=+=x x x x . )2
sin 2(cos 2cos )2cos 2(sin 2sin )(,1)2cos 2(sin 2cos 2)(|x x x x x x x f x x x x f -++-=∴-+=⋅=∴ 当0)()(='+x f x f 则2cosx=0 答:2
x π=时,()()0f x f x '+=. 8.解法一:∵AB ⊥AC ,∴AB ·
AC =0. ∵= -,=-,=-AC , ∴BP ·=(AP -AB )·
(-AC ) =·AQ -·-·AQ +·
= -a 2-AP ·AC +AB ·AP
= -a 2-·(-)
= -a 2+2
1PQ · = -a 2+ a 2cos θ. 故当cosθ=1,即θ=0 (与BC 方向相同)时, BP ·最大,最大值为0.
解法二:以直角顶点为坐标原点,两直角边所在直线为坐标轴建立如图所示的平面直角
坐标系.
设|AB|=c,|AC|=b,则A(0,0),B(0,0),C(0,0).
且|PQ|=2a,|BC|=a.
设点P 的坐标为(x,y),则Q(-x, -y),
∴=(x-c, y),=( -x, -y- b). BC =(-c, b), =(-2x, -2y). BP ·=( x-c)(-x)+ y(-y- b)= - (x 2+y 2)+ c x- b y .
∵cos θ
2
a by cx -=, ∴c x-
b y= a 2 cos θ.
∴·CQ = -a 2+ a 2cos θ.
故当cos θ=1,即θ=0 (与方向相同)时, ·最大,最大值为0.。
