现代控制理论第3章答案
(完整word版)现代控制理论习题解答(第三章)
第三章 线性控制系统的能控性和能观性01010（ 1） A10 1B( 2) A 0 0 1 ,B 011024311113 10 1 1（ 3） A0 10 1 0 3 0 , B00 ( 4) AB0 0 11 001211【解】：(1)11U c B AB 1 1, rankU c n 2 ，所以系统完全能控。
c 0 1 c(2)10 0 1 2U c B AB A 2B1 1 11 1 17前三列已经可使 rankU c n 3 ，所以系统完全能控（后续列元素不必计算） 。
（3）A 为约旦标准型， 且第一个约旦块对应的B 阵最后一行元素全为零， 所以系统不完全 能控。
（4）A 阵为约旦标准型的特殊结构特征， 所以不能用常规标准型的判别方法判系统的能控 性。
同一特征值对应着多个约旦块，只要是单输入系统，一定是不完全能控的。
可以求一下能控判别阵。
1213 1223B AB A 2B A 3B2 3 U c1 1 12 13 1 11 12 31111rankU c 2 ，所以系统不完全能控。
3 1110 10 0 x0 3 0x 0 0ux0 01x 0u (1)0 0 12(2)61161101yxy10 0x1 10解】：1）311 已知 A 0 30,B0 001220 0 D CB CAB CA 2B 0 0 前两列已经使 rank D CBCAB110 1 0 00 ， C ，D1 1 0 0 031112CA B m2， 所以系统输出能控。
（2） 系统为能控标准型，所以状态完全能控。
又因输出矩阵 状态维数 n ，所以状态能控则输出必然能控。
C 满秩，且输出维数 m 小于1 0x0 01xx1 1 (1)2 43 ； (2) 1 x 0；011y1 1xyx12 12 1 0 4 0 0x0 20xx4 0x(3)；（4）0 030 1y0 1 1x y11 4x解】：1）已知 A01 00 242-3-3 判断下列系统的能观性。
《现代控制理论》课后习题全部答案(最完整打印版)
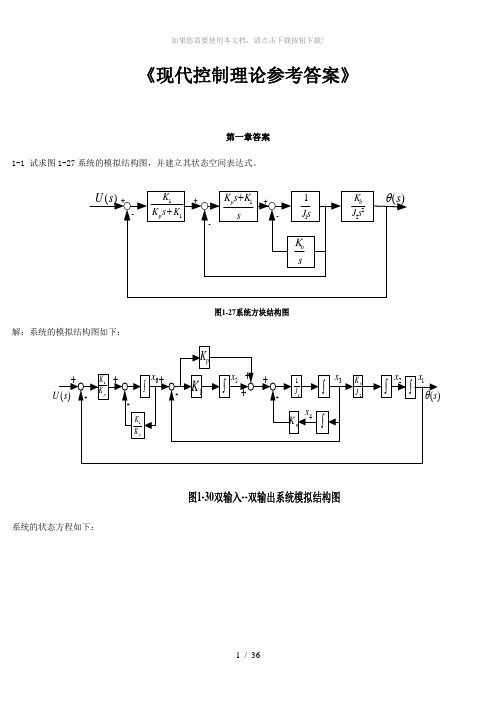
第一章习题答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
11K s K K p +sK s K p 1+s J 11sK n 22s J K b -++-+-)(s θ)(s U 图1-27系统方块结构图解：系统的模拟结构图如下：)(s U )(s θ---+++图1-30双输入--双输出系统模拟结构图1K pK K 1pK K 1+++pK n K ⎰⎰⎰11J ⎰2J K b ⎰⎰-1x 2x 3x 4x 5x 6x系统的状态方程如下：u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n p b1611166131534615141313322211+--=+-==++--===∙∙∙∙∙∙阿令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙∙∙654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp npb1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
R1L1R2L2CU---------Uc---------i1i2图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：∙∙∙+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=∙∙∙写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
《现代控制理论》第3版(刘豹-唐万生)课后习题答案
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下：uK K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x p p pp n p b1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
L1L2U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论第三章答案 舒欣梅
可能是因为第三章的内容相对比较简单，总得情况比上两次都要好。
3-1（研究能控性，只需知道系统的内部结构和外部输入对状态的影响，因此只需要A 和B 阵）(1)能控性矩阵[]1100c Q BA B -⎡⎤==⎢⎥⎣⎦()12c rank Q =<，系统不能控(2) 能控性矩阵2120201001026c Q BABAB ⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥-⎣⎦()3c rank Q =，系统能控3-2（需要知道所有的矩阵） (1) 输出能控性判别矩阵[][]11S CBCAB ==()1rank S =，系统输出能控3-3(3) 能观性矩阵213005645054o C Q C A C A -⎡⎤⎡⎤⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥--⎣⎦⎣⎦()3o rank Q =，系统能观(4) 系统为对角标准形，其输出矩阵C 中不存在全零列，因此系统能观。
3-6（计算出错） (1) 能控性矩阵[]1117c Q BAB -⎡⎤==⎢⎥⎣⎦，()2c rank Q =，系统能控 写出系统的特征多项式：2det()510I A λλλ-=-+ 变换矩阵[]11111516110171021a PBAB ----⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦⎣⎦⎣⎦⎣⎦1116188211344P -⎡⎤-⎢⎥-⎡⎤==⎢⎥⎢⎥⎣⎦⎢⎥⎢⎥⎣⎦11105A PAP-⎡⎤==⎢⎥-⎣⎦，01B P B ⎡⎤==⎢⎥⎣⎦则系统的能控标准形为0101051x x u ⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦3-7（将P 和P 非弄反）(1) 能观性矩阵1102o C Q C A -⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦，()2o rank Q =，系统能观 写出系统的特征多项式：2det()22I A λλλ-=-+变换矩阵1121112010100211a C P C A --⎡⎤⎡⎤⎡⎤⎡⎤⎡⎤===⎢⎥⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦⎣⎦⎣⎦111020211112P--⎡⎤⎢⎥⎡⎤==⎢⎥⎢⎥-⎣⎦⎢⎥⎢⎥⎣⎦10212A PAP--⎡⎤==⎢⎥⎣⎦，41B PB ⎡⎤==⎢⎥-⎣⎦，[]101C CP -==则系统的能观标准形为[]02412101x x u y x-⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦= 3-8(2)首先对分式化简为225()143yu s G s s s +=+++012013,4,1,5,2,1a a a b b d ======，根据式(3-26)与(3-31)写出系统的能控标准形为：[]01034152xx u y x u⎡⎤⎡⎤=+⎢⎥⎢⎥--⎣⎦⎣⎦=+ 根据对偶关系，写出系统的能观标准形为：[]03514201xx u y x u-⎡⎤⎡⎤=+⎢⎥⎢⎥-⎣⎦⎣⎦=+ 计算系统的特征根为121,3λλ=-=-，根据()0i i I A P λ-=，求得相应的特征向量为：1211,13P P ⎡⎤⎡⎤==⎢⎥⎢⎥--⎣⎦⎣⎦得到转移矩阵11113P -⎡⎤=⎢⎥--⎣⎦，31221122P ⎡⎤⎢⎥=⎢⎥⎢⎥--⎢⎥⎣⎦，此处可根据友矩阵的特性，直接写出转移矩阵（范德蒙矩阵）11003A PAP--⎡⎤==⎢⎥-⎣⎦，1212B PB ⎡⎤⎢⎥==⎢⎥⎢⎥-⎢⎥⎣⎦，[]131C CP -==-系统的对角标准形为： []1102031231xx u y x u⎡⎤⎢⎥-⎡⎤=+⎢⎥⎢⎥-⎣⎦⎢⎥-⎢⎥⎣⎦=-+3-9(不能化简，能控型分解是换列，能观性是换行)能控性矩阵23061311013c Q BABA B -⎡⎤⎢⎥⎡⎤==-⎣⎦⎢⎥⎢⎥-⎣⎦，()23c rank Q =<，系统不能控取c Q 的前两列，再补充一列与其他列线性无关的列，得到1301130010cP -⎡⎤⎢⎥=⎢⎥⎢⎥⎣⎦，013001139c P -⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦12113003c cA P AP --⎡⎤⎢⎥==-⎢⎥⎢⎥-⎣⎦，100cB P B ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦，[]1010c C CP -==则能控子系统动态方程为[]0211130001c c c x x x u y x-⎡⎤⎡⎤⎡⎤=++⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦⎣⎦= 不能控子系统动态方程为：30c c x x y =-=。
大连理工大学 现代控制理论 王金城 第三章 答案
第3章习题参考答案：3-1 (1)1101 0221rank[] 2 rank[]2c o c o ⎡⎤⎡⎤==⎢⎥⎢⎥⎣⎦⎣⎦==Q Q Q Q 能控，能观测(2) 1979818100139155153 rank[] 3 201618139153c c ⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦Q Q 100210123 rank[] 33812913363550141o o ⎡⎤⎢⎥⎢⎥⎢⎥==⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦Q Q 能控，能观测(3) 根据能控/能观测判别准则二知，系统能控，但不能观测 (4) 00()()1t t ⎡⎤==⎢⎥⎣⎦M b1001d()(t)()()d t t t t t -⎡⎤=-+=⎢⎥-⎣⎦M A M M [][][]010*******()() rank[]21()()01d()()()()0d ()01 rank[]2()0c c o o t t t t t t t t t t tt t t -⎡⎤===⎢⎥-⎣⎦===+=-⎡⎤⎡⎤==<⎢⎥⎢⎥⎣⎦⎣⎦Q M M Q N c N N A N N Q Q N能控但不能观测(5) 02()()t t e t t e --⎡⎤==⎢⎥⎣⎦M b1000d()(t)()()0d t t t t ⎡⎤=-+=⎢⎥⎣⎦M A M M[]0120100010()() rank[]20()()1d ()()()()13d ()1rank[]2()13tc c tt tt o o t e t t e t t e t t t t e tt e t e ------⎡⎤==<⎢⎥⎣⎦⎡⎤==⎣⎦⎡⎤=+=--⎣⎦⎡⎤⎡⎤==<⎢⎥⎢⎥--⎣⎦⎣⎦Q M M Q N c N N A N N Q Q N能观测但不能控3-2 (1) 矩阵A 为约当标准形，对应于唯一特征值12λ=-共有3个约当块。
系统完全能控的充要条件是矩阵B 中对应于三个约当小块的末行为行线性无关。
《现代控制理论》第三版_.习题答案
1 0 0 3 1 0 5 2 1 52 7 1 5 2 70 125 3 5 7 5 0 0 1 1 B 2 ； 2 5 5
1 0 a1 0 0 1 0 1 0 0 1 a2 3 7 5
0 B 0 1
C (b0 a0bn ) (bn1 an1bn ) 2 1 0
3 1 a 或者 2 2 1 a1 0 a0
e At I At 1 22 1 33 A t A t 2! 3! t2 t4 t6 t3 t5 1 4 16 64 , 4 16 t 2! 4! 6! 3! 5! 3 5 2 4 6 t t t t t t 4 16 64 , 1 4 16 64 3! 5! 2! 4! 6!
0 0 1 B M 1 0 0 0 0 1 M2
1 0 B 1 M1 B1 M2
1 B1 M1 B1 B2 M2
0
0 0 1 0 C 0 0 0 1
1－5. 根据微分方程， 写状态方程， 画模 拟结构图。
1 a2 a2 2 a1 3 2 a a a 1 2 2 a0
1 a2 a1
1 a2
12 b1 b0
b3 b 2 b1 1 b0
凯莱哈密顿法： 1,2 2 j
0 (t ) 1 1 e1t 1 2(e 2 jt e 2 jt ) (t ) 1 2t 4 2 jt 2 jt e j ( e e ) 2 1
《现代控制理论》第3版课后习题答案
《现代控制理论参考答案》第一章答案1-1 试求图1-27系统的模拟结构图，并建立其状态空间表达式。
图1-27系统方块结构图解：系统的模拟结构图如下：图1-30双输入--双输出系统模拟结构图系统的状态方程如下： )u K K x K K x K K x X K x K x x x x J K x J x J K x J K x x J K x x x pp p p n pb1611166131534615141313322211+--=+-==++--===••••••令y s =)(θ，则1x y =所以，系统的状态空间表达式及输出方程表达式为[]⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡-----=⎥⎥⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡••••••654321165432111111112654321000001000000000000010010000000000010x x x x x x y uK K x x x x x x K K K K K K J K J J K J K J K x x x x x x p p pp n p b1-2有电路如图1-28所示。
以电压)(t u 为输入量，求以电感中的电流和电容上的电压作为状态变量的状态方程，和以电阻2R 上的电压作为输出量的输出方程。
U图1-28 电路图解：由图，令32211,,x u x i x i c ===，输出量22x R y =有电路原理可知：•••+==+=++3213222231111x C x x x x R x L ux x L x R 既得22213322222131111111111x R y x C x C x x L x L R x u L x L x L R x =+-=+-=+--=•••写成矢量矩阵形式为： `[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡32121321222111321000*********x x x R y u L x x x CCL L R L L R x x x 。
现代控制理论第三章习题解答
第三章习题答案3-1判断下列系统的状态能控性和能观测性。
系统中a,b,c,d 的取值对能控性和能观性是否有关，若有关，其取值条件如何？ （1）系统如图3.16所示：图3.16 系统模拟结构图解：由图可得：343432112332211x y dx x x cx x x x x cx x bx x u ax x =-=-+=++-=-=+-=∙∙∙∙状态空间表达式为：[]xy ux x x x d c b a x x x x 0100000110001100000043214321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙由于∙2x 、∙3x 、∙4x 与u 无关，因而状态不能完全能控，为不能控系统。
由于y 只与3x 有关，因而系统为不完全能观的，为不能观系统。
（3）系统如下式：x d c y ub a x x x x x x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∙∙∙00000012200010011321321 解：如状态方程与输出方程所示，A 为约旦标准形。
要使系统能控，控制矩阵b 中相对于约旦块的最后一行元素不能为0，故有0,0≠≠b a 。
要使系统能观，则C 中对应于约旦块的第一列元素不全为0，故有0,0≠≠d c 。
3-2时不变系统X y u X X ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=∙111111113113试用两种方法判别其能控性和能观性。
解：方法一：[]⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=2-2-112-2-11AB B M 1111,1111,3113C B A系统不能控。
,21<=rankM ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎦⎤⎢⎣⎡=44221111CA C N 系统能观。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章习题3-1判断下列系统的状态能控性和能观测性。
系统中a,b,c,d 的取值对能控性和能观性是否有关，若有关，其取值条件如何？ （1）系统如图3.16所示：图3.16 系统模拟结构图解：由图可得：343432112332211x y dx x x cx x x x x cx x bx x u ax x =-=-+=++-=-=+-=∙∙∙∙状态空间表达式为：[]xy ux x x x d c b a x x x x 0100000110001100000043214321=⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡+⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎣⎡∙∙∙∙由于∙2x 、∙3x 、∙4x 与u 无关，因而状态不能完全能控，为不能控系统。
由于y 只与3x 有关，因而系统为不完全能观的，为不能观系统。
（3）系统如下式：x d c y ub a x x x x x x ⎥⎦⎤⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎣⎡∙∙∙00000012200010011321321 解：如状态方程与输出方程所示，A 为约旦标准形。
要使系统能控，控制矩阵b 中相对于约旦块的最后一行元素不能为0，故有0,0≠≠b a 。
要使系统能观，则C 中对应于约旦块的第一列元素不全为0，故有0,0≠≠d c 。
3-2时不变系统X y u X X ⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡--=∙111111113113试用两种方法判别其能控性和能观性。
解：方法一：[]⎥⎦⎤⎢⎣⎡==⎥⎦⎤⎢⎣⎡-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=2-2-112-2-11AB B M 1111,1111,3113C B A系统不能控。
,21<=rankM ⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎣⎡----=⎥⎦⎤⎢⎣⎡=44221111CA C N 系统能观。
,2=rankN方法二：将系统化为约旦标准形。
()420133113A I 212-=-==-+=+--+=-λλλλλλ，⎥⎦⎤⎢⎣⎡=⇒=⎥⎦⎤⎢⎣⎡=⇒=1-1P P P A 11P P P A 2222211111λλ则状态矢量：⎥⎦⎤⎢⎣⎡=1-111T ，⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=21212121T 1- ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=4-002-1-1113-113-21212121AT T 1- ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=0011111121212121B T 1- ⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡⎥⎦⎤⎢⎣⎡=20021-1111-111CT B T -1中有全为零的行，系统不可控。
CT 中没有全为0的列，系统可观。
3-3确定使下列系统为状态完全能控和状态完全能观的待定常数i i βα和[]11,11,01)1(21-=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡=C b A αα 解：构造能控阵：[]⎥⎦⎤⎢⎣⎡+==21111ααAb bM 要使系统完全能控，则211αα≠+，即0121≠+-αα 构造能观阵：⎥⎦⎤⎢⎣⎡--=⎥⎦⎤⎢⎣⎡=21111CA C ααN 要使系统完全能观，则121αα-≠-，即0121≠+-αα 3-4设系统的传递函数是182710)()(23++++=s s s as s u s y（1）当a 取何值时，系统将是不完全能控或不完全能观的？ （2）当a 取上述值时，求使系统的完全能控的状态空间表达式。
（3）当a 取上述值时，求使系统的完全能观的状态空间表达式。
解：(1) 方法1 ：)6)(3)(1()()()(++++==s s s as s u s y s W 系统能控且能观的条件为W(s)没有零极点对消。
因此当a=1,或a=3或a=6时，系统为不能控或不能观。
方法2：6s 156-a 3631s 101-a )6)(3)(1()()(+++--+=++++=s a s s s as s u s y 631321-=-=-=λλλ，，X a a a y u X X ⎥⎦⎤⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=∙156631011116000301系统能控且能观的条件为矩阵C 不存在全为0的列。
因此当a=1,或a=3或a=6时，系统为不能控或不能观。
（2）当a=1, a=3或a=6时，系统可化为能控标准I 型[] x01a y u 100x 102718100010 =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x（3）根据对偶原理，当a=1, a=2或a=4时，系统的能观标准II 型为[] x 100y u 01a x 101027011800 =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x3-6已知系统的微分方程为：u y y y y 66116...=+++ 试写出其对偶系统的状态空间表达式及其传递函数。
解：63611603210=====b a a a a ，，，， 系统的状态空间表达式为[] x 006y u 100x 611610001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x 传递函数为[]6116610061161001006A)-C(sI )(2311-+++=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+--==-s s s s s s B s W 其对偶系统的状态空间表达式为：[] x100y u 006x 6101101600 =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=x 传递函数为61166)(23+--=s s s s W 3-9已知系统的传递函数为348622++++=s s s s )s (W试求其能控标准型和能观标准型。
解：345213486)(222++++=++++=s s s s s s s s W系统的能控标准I 型为[]u x 25y u 10x 4-3-10 +=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=x 能观标准II 型为[]ux 10y u 25x 4-13-0 +=⎥⎦⎤⎢⎣⎡+⎥⎦⎤⎢⎣⎡=x 3-10给定下列状态空间方程，试判别其是否变换为能控和能观标准型。
[] x 100y u 210x 311032010 =⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡+⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=x 解：[]100210311032010=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=C b A ，， []⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---==11527213102b A Ab bM 。
不能变换为能控标准型，系统为不能控系统，32<=rankM⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡----=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=9713111002CA CA C N 以变换为能观标准型。
，系统为能观系统，可3=rankN3-11试将下列系统按能控性进行分解（1）[]111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 解：[]⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==9310004102b A Ab bM rankM=2<3，系统不是完全能控的。
构造奇异变换阵c R ：⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-==⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==010*********R Ab R b R ，，，其中3R 是任意的，只要满足c R 满秩。
即⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=031100010c R 得⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=-010*******c R ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--==-1002412301c c AR R A ⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡==-0011b R b c []121-==c cR c 3-12 试将下列系统按能观性进行结构分解（1） []111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 解： 由已知得[]111,100,340010121-=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡--=C b A 则有⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=4742321112CA CA C N rank N=2<3，该系统不能观构造非奇异变换矩阵10R -，有10111232001R --⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦ 则0311210001R --⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦11000010123027321x R AR x R bu x u --⎡⎤⎡⎤⎢⎥⎢⎥=+=-+⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦[]0100y cR xx == 3-13 试将下列系统按能控性和能观性进行结构分解（1）[]211,221,102322001=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡=⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-=C b A解：由已知得211121226202M A Ab Ab ⎡⎤⎢⎥⎡⎤==⎣⎦⎢⎥⎢⎥-⎣⎦rank M=3，则系统能控21121257411c N c A cA ⎡⎤⎡⎤⎢⎥⎢⎥==-⎢⎥⎢⎥⎢⎥⎢⎥-⎣⎦⎣⎦ rank N=3，则系统能观所以此系统为能控并且能观系统取211121226202c T ⎡⎤⎢⎥=⎢⎥⎢⎥-⎣⎦，则1217344173215344c T -⎡⎤-⎢⎥⎢⎥⎢⎥=--⎢⎥⎢⎥⎢⎥-⎢⎥⎣⎦则002105014A ⎡⎤⎢⎥=-⎢⎥⎢⎥⎣⎦，12100c B T b -⎡⎤⎢⎥==⎢⎥⎢⎥⎣⎦，[]271323c c cT ==3-14求下列传递函数阵的最小实现。
（1） ()111111w s s ⎡⎤=⎢⎥+⎣⎦解： 01α=，01111B ⎡⎤=⎢⎥⎣⎦，1001c A -⎡⎤=⎢⎥-⎣⎦ 1001c B ⎡⎤=⎢⎥⎣⎦，1111c C ⎡⎤=⎢⎥⎣⎦，0000c D ⎡⎤=⎢⎥⎣⎦ 系统能控不能观取101101R -⎡⎤=⎢⎥⎣⎦，则01101R -⎡⎤=⎢⎥⎣⎦ 所以10010ˆ01A R AR --⎡⎤==⎢⎥-⎣⎦，1011ˆ01c B R B -⎡⎤==⎢⎥⎣⎦ 010ˆ10c C C R ⎡⎤==⎢⎥⎣⎦，00ˆ00D ⎡⎤=⎢⎥⎣⎦所以最小实现为ˆ1m A =，[]ˆ11m B =，1ˆ1m C ⎡⎤=⎢⎥⎣⎦，00ˆ00m D ⎡⎤=⎢⎥⎣⎦ 验证：()()1111ˆˆˆ111m mm C sI A B w s s -⎡⎤-==⎢⎥+⎣⎦3-15设1∑和2∑是两个能控且能观的系统[]1121210431022221111==-=∑=⎥⎦⎤⎢⎣⎡=⎥⎦⎤⎢⎣⎡--=∑C b A C b A ，，：，，： （1）试分析由1∑和2∑所组成的串联系统的能控性和能观性，并写出其传递函数； （2）试分析由1∑和2∑所组成的并联系统的能控性和能观性，并写出其传递函数。