分治法实现快速排序与两路合并排序
c语言分治法实现合并排序算法
c语言分治法实现合并排序算法分治法是一种重要的算法思想，它将原问题分解成若干个子问题来解决，最终将子问题的解合并为原问题的解。
其中，合并排序算法就是分治法的一个典型应用。
合并排序算法是一种基于比较的排序算法，它将待排序的序列不断地分割成更小的子序列，直到每个子序列只有一个元素为止，然后将这些子序列合并起来，直到整个序列有序为止。
在C语言中，实现合并排序算法的分治法思想非常简单，可以通过递归调用函数来实现。
具体来说，可以将待排序序列分为左右两个子序列，分别对其进行排序，最后将左右两个有序序列进行合并。
下面是C语言实现合并排序算法的示例代码：```void merge(int arr[], int l, int m, int r){int i, j, k;int n1 = m - l + 1;int n2 = r - m;/* 创建临时数组 */int L[n1], R[n2];/* 拷贝数据到临时数组 L[] 和 R[] */for (i = 0; i < n1; i++)L[i] = arr[l + i];for (j = 0; j < n2; j++)R[j] = arr[m + 1 + j];/* 合并临时数组到 arr[l..r]*/i = 0; /* 初始化左子数组的索引 */ j = 0; /* 初始化右子数组的索引 */ k = l; /* 初始归并子数组的索引 */ while (i < n1 && j < n2) {if (L[i] <= R[j]) {arr[k] = L[i];i++;}else {arr[k] = R[j];j++;}k++;}/* 拷贝 L[] 的剩余元素 */while (i < n1) {arr[k] = L[i];i++;k++;}/* 拷贝 R[] 的剩余元素 */while (j < n2) {arr[k] = R[j];j++;k++;}}void mergeSort(int arr[], int l, int r){if (l < r) {/* 找到中间点 */int m = l + (r - l) / 2;/* 分治排序左子数组和右子数组 */mergeSort(arr, l, m);mergeSort(arr, m + 1, r);/* 合并已排序的左子数组和右子数组 */merge(arr, l, m, r);}}```上述代码中，首先定义了一个函数 `merge()` 用于将两个已排序的子序列合并成一个有序序列。
分治算法及其典型应用
分治算法及其典型应用
分治算法是一种重要的算法设计策略，它将一个大问题分解成若干个规模较小的子问题，然后递归地解决这些子问题，最后将它们的解合并起来，得到原问题的解。
分治算法在计算机科学和算法设计中有着广泛的应用，可以解决许多实际问题，下面将介绍一些典型的应用。
1. 排序算法。
分治算法在排序算法中有着重要的应用。
其中最著名的就是归并排序和快速排序。
在归并排序中，算法将数组分成两个子数组，分别进行排序，然后合并这两个有序的子数组。
而在快速排序中，算法选择一个基准值，将数组分成两个子数组，分别小于和大于基准值，然后递归地对这两个子数组进行排序。
2. 搜索算法。
分治算法也可以用于搜索问题，例如二分搜索算法。
在这种算法中，将搜索区间分成两个子区间，然后递归地在其中一个子区间中进行搜索，直到找到目标元素或者子区间为空。
3. 求解最大子数组问题。
最大子数组问题是一个经典的动态规划问题，也可以用分治算法来解决。
算法将数组分成两个子数组，分别求解左右子数组的最大子数组，然后再考虑跨越中点的最大子数组，最后将这三种情况的最大值作为整个数组的最大子数组。
4. 矩阵乘法。
分治算法也可以用于矩阵乘法。
在矩阵乘法中，算法将两个矩阵分成四个子矩阵，然后递归地进行矩阵乘法，最后将四个子矩阵的结果合并成一个矩阵。
总的来说，分治算法是一种非常重要的算法设计策略，它在许多实际问题中有着广泛的应用。
通过将一个大问题分解成若干个规模较小的子问题，然后递归地解决这些子问题，最后将它们的解合并起来，我们可以高效地解决许多复杂的问题。
分治法解决问题的步骤
分治法解决问题的步骤一、基础概念类题目（1 - 5题）题目1：简述分治法解决问题的基本步骤。
解析：分治法解决问题主要有三个步骤：1. 分解（Divide）：将原问题分解为若干个规模较小、相互独立且与原问题形式相同的子问题。
例如，对于排序问题，可将一个大的数组分成两个较小的子数组。
2. 求解（Conquer）：递归地求解这些子问题。
如果子问题规模足够小，则直接求解（通常是一些简单的基础情况）。
对于小到只有一个元素的子数组，它本身就是有序的。
3. 合并（Combine）：将各个子问题的解合并为原问题的解。
在排序中，将两个已排序的子数组合并成一个大的有序数组。
题目2：在分治法中，分解原问题时需要遵循哪些原则？解析：1. 子问题规模更小：分解后的子问题规模要比原问题小，这样才能逐步简化问题。
例如在归并排序中，不断将数组对半分，子数组的长度不断减小。
2. 子问题相互独立：子问题之间应该尽量没有相互依赖关系。
以矩阵乘法的分治算法为例，划分后的子矩阵乘法之间相互独立进行计算。
3. 子问题与原问题形式相同：方便递归求解。
如二分查找中，每次查找的子区间仍然是一个有序区间，和原始的有序区间查找问题形式相同。
题目3：分治法中的“求解”步骤，如果子问题规模小到什么程度可以直接求解？解析：当子问题规模小到可以用简单的、直接的方法（如常量时间或线性时间复杂度的方法）解决时，就可以直接求解。
例如，在求数组中的最大最小值问题中，当子数组只有一个元素时，这个元素既是最大值也是最小值，可以直接得出结果。
题目4：分治法的“合并”步骤有什么重要性？解析：1. 构建完整解：它将各个子问题的解组合起来形成原问题的解。
例如在归并排序中，单独的两个子数组排序好后，只有通过合并操作才能得到整个数组的有序排列。
2. 保证算法正确性：如果合并步骤不正确，即使子问题求解正确，也无法得到原问题的正确答案。
例如在分治算法计算斐波那契数列时，合并不同子问题的结果来得到正确的斐波那契数是很关键的。
分治法-合并排序和快速排序
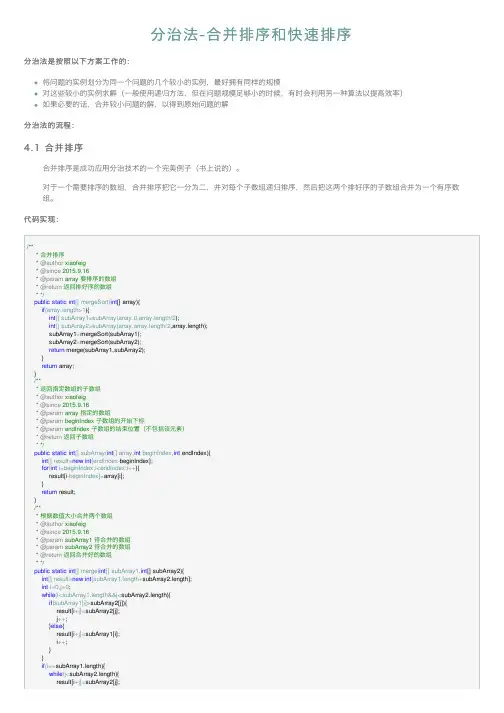
分治法-合并排序和快速排序分治法是按照以下⽅案⼯作的：将问题的实例划分为同⼀个问题的⼏个较⼩的实例，最好拥有同样的规模对这些较⼩的实例求解（⼀般使⽤递归⽅法，但在问题规模⾜够⼩的时候，有时会利⽤另⼀种算法以提⾼效率）如果必要的话，合并较⼩问题的解，以得到原始问题的解分治法的流程：4.1 合并排序合并排序是成功应⽤分治技术的⼀个完美例⼦（书上说的）。
对于⼀个需要排序的数组，合并排序把它⼀分为⼆，并对每个⼦数组递归排序，然后把这两个排好序的⼦数组合并为⼀个有序数组。
代码实现：/*** 合并排序* @author xiaofeig* @since 2015.9.16* @param array 要排序的数组* @return返回排好序的数组* */public static int[] mergeSort(int[] array){if(array.length>1){int[] subArray1=subArray(array,0,array.length/2);int[] subArray2=subArray(array,array.length/2,array.length);subArray1=mergeSort(subArray1);subArray2=mergeSort(subArray2);return merge(subArray1,subArray2);}return array;}/*** 返回指定数组的⼦数组* @author xiaofeig* @since 2015.9.16* @param array 指定的数组* @param beginIndex ⼦数组的开始下标* @param endIndex ⼦数组的结束位置（不包括该元素）* @return返回⼦数组* */public static int[] subArray(int[] array,int beginIndex,int endIndex){int[] result=new int[endIndex-beginIndex];for(int i=beginIndex;i<endIndex;i++){result[i-beginIndex]=array[i];}return result;}/*** 根据数值⼤⼩合并两个数组* @author xiaofeig* @since 2015.9.16* @param subArray1 待合并的数组* @param subArray2 待合并的数组* @return返回合并好的数组* */public static int[] merge(int[] subArray1,int[] subArray2){int[] result=new int[subArray1.length+subArray2.length];int i=0,j=0;while(i<subArray1.length&&j<subArray2.length){if(subArray1[i]>subArray2[j]){result[i+j]=subArray2[j];j++;}else{result[i+j]=subArray1[i];i++;}}if(i==subArray1.length){while(j<subArray2.length){result[i+j]=subArray2[j];}}else{while(i<subArray1.length){result[i+j]=subArray1[i];i++;}}return result;}算法分析：当n>1时，C(n)=2C(n-2)+C merge(n)，C(1)=0C merge(n)表⽰合并阶段进⾏键值⽐较的次数。
分治算法的实验报告
一、实验背景分治算法是一种常用的算法设计方法，其基本思想是将一个复杂问题分解成若干个相互独立的小问题，然后将小问题递归求解，最终将子问题的解合并为原问题的解。
分治算法具有高效性、可扩展性和易于实现等优点，被广泛应用于各个领域。
本实验旨在通过实现分治算法解决实际问题，掌握分治算法的设计思想，并分析其时间复杂度。
二、实验目的1. 理解分治算法的基本思想；2. 掌握分治算法的递归实现方法；3. 分析分治算法的时间复杂度；4. 应用分治算法解决实际问题。
三、实验内容本实验选择两个分治算法：快速排序和合并排序。
1. 快速排序快速排序是一种高效的排序算法，其基本思想是将待排序序列分为两个子序列，其中一个子序列的所有元素均小于另一个子序列的所有元素，然后递归地对两个子序列进行快速排序。
（1）算法描述：① 选择一个基准值（pivot），通常取序列的第一个元素；② 将序列分为两个子序列，一个子序列包含所有小于基准值的元素，另一个子序列包含所有大于基准值的元素；③ 递归地对两个子序列进行快速排序。
（2）代码实现：```cvoid quickSort(int arr[], int left, int right) {if (left < right) {int pivot = arr[left];int i = left;int j = right;while (i < j) {while (i < j && arr[j] >= pivot) {j--;}arr[i] = arr[j];while (i < j && arr[i] <= pivot) {i++;}arr[j] = arr[i];}arr[i] = pivot;quickSort(arr, left, i - 1);quickSort(arr, i + 1, right);}}```2. 合并排序合并排序是一种稳定的排序算法，其基本思想是将待排序序列分为两个子序列，分别对两个子序列进行排序，然后将排序后的子序列合并为一个有序序列。
快速排序（QuickSort）
快速排序（QuickSort）⼀、思路快速排序是⼀种分治排序算法。
快速排序先把数组重新整理分割两个⼦数组，然后对两个⼦数组进⾏排序。
快速排序和归并排序是互补的：归并排序中，算法先将数组分为两个⼦数组进⾏排序，再将两个⼦数组进⾏归并成⼀个有序的数组。
快速排序中，算法先对数组进⾏重新整理分割成两个⼦数组，再对两个⼦数组进⾏排序，当两个⼦数组是有序时，整个数组即为有序的。
归并排序中，递归调⽤发⽣在处理整个数组之前。
快速排序中，递归调⽤发⽣在处理整个数组之后。
归并排序数组是对半平分的，快速排序数组切分位置取决于数组的内容。
归并排序代码： private static void sort(Comparable[] input, int lo, int hi) {if(lo >= hi)//just one entry in arrayreturn;int mid = lo + (hi-lo)/2;sort(input, lo, mid);sort(input, mid+1, hi);merge(input, lo, mid, hi);}快速排序代码： private static void sort(Comparable[] a, int lo, int hi) {if(hi <= lo)return;int j = partition(a, lo, hi);sort(a, lo, j-1);sort(a, j+1, hi);}快速排序的关键在于partition⽅法，执⾏完partition⽅法之后应该达到，a[j]就是最终位置，a[lo~(j-1)]都要⼩于或等于a[j]，a[j+1~hi]都要⼤于或等于a[j]。
策略：1、选a[lo]作为切分元素2、从数组左端开始查找⼤于或等于a[lo]的元素（下标i<=hi）3、从数组右端开始查找⼩于或等于a[lo]的元素（下标j>=lo）4、交换这两个元素。
分治算法举例范文
分治算法举例范文分治算法是一种很重要的算法思想，它将一个大的问题划分成较小的子问题，然后分别求解这些子问题，最后将子问题的解合并起来得到原问题的解。
下面我将详细介绍分治算法的几个经典例子。
1. 快速排序（Quick Sort）快速排序是一种经典的使用分治算法的排序算法。
它首先选择一个基准元素，然后将数组划分成两个子数组：小于基准元素的和大于基准元素的。
然后对这两个子数组分别递归地进行快速排序，最后将两个子数组合并起来即可得到有序的数组。
快速排序的时间复杂度为O(nlogn)。
2. 归并排序（Merge Sort）归并排序也是一种利用分治思想的排序算法。
它将待排序的数组划分成两个子数组，然后分别对这两个子数组进行归并排序，最后将两个有序的子数组合并成一个有序的数组。
归并排序的时间复杂度也是O(nlogn)。
3. 汉诺塔问题（Tower of Hanoi）汉诺塔问题是数学领域中一个经典的问题，也可以通过分治算法来解决。
问题的规模是将n个圆盘从一个柱子移动到另一个柱子上，移动时需要遵守以下规则：每次只能移动一个盘子，移动过程中不能将较大的盘子放在较小的盘子上。
可以将问题划分成三个子问题：将前n-1个盘子从起始柱子移动到中间柱子上，将最后一个盘子从起始柱子移动到目标柱子上，最后将前n-1个盘子从中间柱子移动到目标柱子上。
这样就可以递归地求解子问题，最后合并起来得到原问题的解。
4. 最大子数组和问题（Maximum Subarray）最大子数组和问题是求解给定数组中连续子数组的最大和的问题。
可以使用分治算法来解决这个问题。
首先将数组划分成两个子数组，然后分别求解这两个子数组中的最大子数组和。
接下来，需要考虑跨越中点的情况，即包含中点的子数组的最大和。
最后，将这三种情况中的最大值作为最终的结果。
最大子数组和问题的时间复杂度为O(nlogn)。
5. 矩阵乘法（Matrix Multiplication）矩阵乘法也可以通过分治算法来实现。
c语言分治法实现合并排序算法
c语言分治法实现合并排序算法在计算机科学中，分治算法是一种将问题划分为较小子问题，然后将结果合并以解决原始问题的算法。
其中，合并排序算法就是一种常见的分治算法。
C语言可以使用分治法实现合并排序算法。
该算法的基本思想是将原始数组递归地分成两半，直到每个部分只有一个元素，然后将这些部分合并起来，直到形成一个完整的已排序的数组。
具体实现过程如下：1.首先，定义一个函数merge，该函数将两个已排序的数组合并成一个已排序的数组。
2.然后，定义一个函数merge_sort，该函数使用递归的方式将原始数组分成两个部分，并对每个部分调用merge_sort函数以进行排序。
3.最后，将已排序的两个数组合并到一起，使用merge函数。
以下是C语言代码：void merge(int arr[], int left[], int left_count, int right[], int right_count) {int i = 0, j = 0, k = 0;while (i < left_count && j < right_count) {if (left[i] < right[j]) {arr[k++] = left[i++];} else {arr[k++] = right[j++];}}while (i < left_count) {arr[k++] = left[i++];}while (j < right_count) {arr[k++] = right[j++];}}void merge_sort(int arr[], int size) { if (size < 2) {return;}int mid = size / 2;int left[mid];int right[size - mid];for (int i = 0; i < mid; i++) {left[i] = arr[i];}for (int i = mid; i < size; i++) {right[i - mid] = arr[i];}merge_sort(left, mid);merge_sort(right, size - mid);merge(arr, left, mid, right, size - mid);}int main() {int arr[] = {3, 8, 1, 6, 9, 4, 5, 7, 2};int size = sizeof(arr) / sizeof(arr[0]);merge_sort(arr, size);for (int i = 0; i < size; i++) {printf('%d ', arr[i]);}return 0;}以上代码可以将数组{3, 8, 1, 6, 9, 4, 5, 7, 2}排序成{1, 2, 3, 4, 5, 6, 7, 8, 9}。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
实验报告（2015 / 2016 学年第二学期）课程名称实验名称分治法实现快速排序与两路合并排序实验时间年月日指导单位计算机学院计算机科学与技术系指导教师学生姓名班级学号学院(系) 专业实验报告三、实验原理及内容实验原理：分治法：即分而治之。
将问题分解为规模较小，相互独立，类型相同的问题进行求解。
对于无序数组的有序排序也就是按某种方式将序列分成两个或多个子序列，分别进行排序，再将已排序的子序列合并成一个有序序列。
实验内容：两路合并排序算法的基本思想是：将待排序元素序列一分为二，得到两个长度基本相等的子序列，其过程类似于对半搜索；然后将子序列分别排序，如果子序列较长，还可以继续细分，知道子序列长度不超过1为止。
以上的实现由下列代码执行：void SortableList::MergeSort(){MergeSort(0,n-1);}void SortableList::MergeSort(int left,int right){if (left<right){int mid=(left+right)/2;MergeSort(left,mid);MergeSort(mid+1,right);Merge(left,mid,right);}}函数MergeSort是类SortableList上的公有成员函数。
mid=(left+right)/2;将函数划分为两个长度基本相等的子序列，用递归来执行两个子序列的内部排序。
而Merge函数是将有序的子序列合并，通过合并过程将自问题的解组合成元问题的解。
通过比较两个序列中的最小者，输出其中的较小者，重复此过程，直到一个序列为空，如果还有元素为输出则输出即可。
其中对于Merge函数代码如下：void SortableList::Merge(int left,int mid,int right)//将两个长度之和为n的有序子序列合并一个有序序列{int *temp=new int[right-left+1];int i=left,j=mid+1,k=0;while((i<=mid)&&(j<=right))if (l[i]<=l[j]) temp[k++]=l[i++];else temp[k++]=l[j++];while (i<=mid) temp[k++]=l[i++];while (j<=right) temp[k++]=l[j++];for (i=0,k=left;k<=right;) l[k++]=temp[i++];}快速排序算法的基本思想是：在待排序序列 K[left:right]上选择一个基准元素（通常是最左边的元素），通过一趟分划操作将序列分成左右两个子序列，左子序列中所有元素都小于等于该基准元素，有子序列中所有元素都大于等于该基准元素。
划分操作如下：int SortableList::Partition(int left,int right){int i=left,j=right+1;do{do i++; while (l[i]<l[left]);do j--; while (l[j]>l[left]);if (i<j) Swap(i,j);}while (i<j);Swap(left,j);return j;}则当前基准元素所在的位置位于左、右子序列的中间，即是其排序完成后的最终位置。
通过递归调用，对左子序列和右子序列再分别进行快速排序算法的调用。
由于每一趟分划结束后，左子序列中的元素均不大于基准元素，右子序列中的元素均不小于基准元素。
而每次分划后，对分划得到的左、右子序列的快速排序又均是就地进行，所以一旦左、右两个子序列都已分别排好序后，无需再执行任何计算，整个序列就是所要求的有序序列了。
因此类中应定义成员函数 QuickSort来完成递归快速排序算法的调用和成员函数。
快速排序操作如下：void SortableList::QuickSort(){QuickSort(0,n-1);}void SortableList::QuickSort(int left,int right){if (left<right){int j=Partition(left,right);QuickSort(left,j-1);QuickSort(j+1,right);}}比较合并排序和快速排序的异同。
合并排序——将序列一分为二即可。
快速排序——需调用 Partition函数将一个序列划分为子序列。
子问题解合并得到原问题解的过程：合并排序——需要调用 Merge函数来实现。
（Merge 函数时间复杂度为O(n)）..快速排序——一旦左、右两个子序列都已分别排序，整个序列便自然成为有序序列。
程序中的其他函数：输入输出函数：void SortableList::Input(){for(int i=0;i<maxSize;i++){cin>>l[i];n++;}}void SortableList::Output(){for(int i=0;i<maxSize;i++){cout<<l[i]<<" ";}}主函数：void main(){int n;int i;cout <<"***************************************"<<endl<<endl;cout <<" 1 两路合并排序"<<" "<<"2 快速排序"<< endl<<endl; cout <<"***************************************"<<endl<<endl;while(1){cout <<"************请选择排序方式*************"<<endl;cin>>i;if(i!=1&&i!=2){ cout<<"fault"<<endl;break;}cout <<"*********** 请输入比较个数 ************"<<endl;cin >> n;SortableList l(n);cout<<"************ 请输入"<<n<<"个数：*************"<<endl;l.Input();if(i=1)l.MergeSort();elsel.QuickSort();cout<<"************ 排序后序列是： ***********"<<endl;l.Output();cout<<endl;}}实验结果：实验用例（1）72 26 57 88 42 80 72 48 60（2）0 0 0 0 0完整实验代码：#include<iostream.h>class SortableList{public:SortableList(int mSize)//构造函数{maxSize=mSize;l=new int[maxSize];n=0;}~SortableList()//析构函数{delete []l;}void MergeSort();void QuickSort();void Input();void Output();private:int *l;int maxSize;int n;void MergeSort(int left,int right);void Merge(int left,int mid,int right); void Swap(int i,int j);void QuickSort(int left,int right);int Partition(int left,int right);};void SortableList::Swap(int i,int j) {int c=l[i];l[i]=l[j];l[j]=c;}int SortableList::Partition(int left,int right) {int i=left,j=right+1;do{do i++; while (l[i]<l[left]);do j--; while (l[j]>l[left]);if (i<j) Swap(i,j);}while (i<j);Swap(left,j);return j;}void SortableList::QuickSort(){QuickSort(0,n-1);}void SortableList::QuickSort(int left,int right) {if (left<right){int j=Partition(left,right);QuickSort(left,j-1);QuickSort(j+1,right);}}void SortableList::MergeSort(){MergeSort(0,n-1);}void SortableList::MergeSort(int left,int right) {if (left<right){int mid=(left+right)/2;MergeSort(left,mid);MergeSort(mid+1,right);Merge(left,mid,right);}}void SortableList::Merge(int left,int mid,int right)//将两个长度之和为n的有序子序列合并一个有序序列{int *temp=new int[right-left+1];int i=left,j=mid+1,k=0;while((i<=mid)&&(j<=right))if (l[i]<=l[j]) temp[k++]=l[i++];else temp[k++]=l[j++];while (i<=mid) temp[k++]=l[i++];while (j<=right) temp[k++]=l[j++];for (i=0,k=left;k<=right;) l[k++]=temp[i++];}void SortableList::Input(){for(int i=0;i<maxSize;i++){cin>>l[i];n++;}}void SortableList::Output(){for(int i=0;i<maxSize;i++){cout<<l[i]<<" ";}}void main(){int n;int i;cout <<"***************************************"<<endl<<endl;cout <<" 1 两路合并排序"<<" "<<"2 快速排序"<< endl<<endl; cout <<"***************************************"<<endl<<endl;while(1){cout <<"************请选择排序方式*************"<<endl;cin>>i;if(i!=1&&i!=2){ cout<<"fault"<<endl;break;}cout <<"*********** 请输入比较个数 ************"<<endl;cin >> n;SortableList l(n);cout<<"************ 请输入"<<n<<"个数：*************"<<endl;l.Input();if(i=1)l.MergeSort();elsel.QuickSort();cout<<"************ 排序后序列是： ***********"<<endl;l.Output();cout<<endl;}}实验报告。