14、勾股定理、逆定理及证明
勾股定理(毕达哥拉斯定理)及各类证明方式

勾股定理(毕达哥拉斯定理)是一个,是人类初期发觉并证明的重要数学定理之一,用思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
是的一个特例。
约有400种证明方式,是数学定理中证明方式最多的之一。
“”是勾股定理最大体的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)确实是。
也确实是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 若是的两条直角边长别离为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 若是的三边长a ,b ,c 知足,那么那个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,那么每一个直角三角形的面积等于21ab. 把这四个直角三角形拼成如下图形状. ∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º, ∴ ABCD 是一个边长为c 的正方形,它的面积等于c2. ∵ EF = FG =GH =HE = b―a ,∠HEF = 90º. ∴ EFGH 是一个边长为b―a 的正方形,它的面积等于.∴ ∴.【证法2】(讲义的证明)做8个全等的直角三角形,设它们的两条直角边长别离为a 、b ,斜边长为c ,再做三个边长别离为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上能够看到,这两个正方形的边长都是a + b ,因此面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,那么每一个直角三角形的面积等于. 把这两个直角三角形拼成如下图形状,使A 、E 、B 三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴ AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的黄昏,在美国华盛顿的郊外,有一名中年人正在散步,欣赏黄昏的美景,他确实是那时美国俄亥俄州共和党议员伽菲尔德。
勾股定理

板块一 勾股定理1.勾股定理的内容:如果直角三角形的两直角边分别是a 、b ,斜边为c ,那么a 2+b 2=c 2.即直角三角形中两直角边的平方和等于斜边的平方。
注:勾——最短的边、股——较长的直角边、 弦——斜边。
CAB cba勾股定理3.勾股定理的逆定理:如果三角形中两边的平方和等于第三边的平方,那么这个三角形是直角三角形。
即 222,,ABC AC BC AB ABC ∆+=∆在中如果那么是直角三角形。
4.勾股数:满足a 2 +b 2=c 2的三个正整数,称为勾股数.勾股数扩大相同倍数后,仍为勾股数.常用勾股数:3、4、5; 5、12、13;7、24、25;8、15、17。
板块一、勾股定理【例1】 下列说法正确的是( )A. 若a b c ,,是ABC ∆的三边,则222a b c +=B. 若a b c ,,是Rt ABC ∆的三边,则222a b c +=C. 若 a b c ,,是Rt ABC ∆的三边,90A ∠=︒,则222a b c +=D. 若 a b c ,,是Rt ABC ∆的三边,90C ∠=︒,则222a b c +=【例2】 在Rt ABC ∆中, 90C ∠=︒,(1)如果34a b ==,,则c = ; (2)如果68a b ==,,则c = ; (3)如果512a b ==,,则c = ; (4)如果1520a b ==,,则c = .【例3】 若一个直角三角形三边的长分别是三个连续的自然数,则这个三角形的周长为【例4】 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .【例5】 已知直角三角形的两边长分别为3、4,求第三边长.【例6】 已知直角三角形两边x ,y 的长满足240x -,则第三边长为______________.【例7】 一个直角三角形中,两直角边长分别为3和4,下列说法正确的是( )A .斜边长为25B .三角形周长为25C .斜边长为5D .三角形面积为20【例8】 如果梯子的底端距离墙根的水平距离是9m ,那么15m 长的梯子可以达到的高度为【例9】 如图,梯子AB 斜靠在墙面上,AC BC AC BC ⊥=,,当梯子的顶端A 沿AC 方向下滑x 米时,梯足B 沿CB 方向滑动y 米,则x 与y 的大小关系是( ) A .x y = B .x y > C .x y < D .不确定CA【例10】 如图,一个长为10米的梯子,斜靠在墙上,梯子的顶端距离地面的垂直距离为8米,如果梯子的顶端下滑1米,那么,梯子底端的滑动距离 米(填“大于”、“等于”、“小于”)68【例11】 三角形的三边长分别为6,8,10,它的最短边上的高为( )A. 6B. 4.5C. 2.4D.8【例12】 若ABC ∆的三边a b c ,,满足条件:222338102426a b c a b c +++=++,则这个三角形最长边上的高为【例13】 如果把直角三角形的两条直角边同时扩大到原来的2倍,那么斜边扩大到原来的( )A. 1倍B. 2倍C. 3倍D. 4倍【例14】 如图,一根高8米的旗杆被风吹断倒地,旗杆顶端A 触地处到旗杆底部B 的距离为6米,则折断点C到旗杆底部B 的距离为CBA【例15】 已知,如图所示,折叠长方形的一边AD ,使点D 落在BC 边的点F 处,•如果8cm AB =,10cm BC =,求EC 的长.【例16】 如图,有一个直角三角形纸片,两直角边6cm 8cm AC BC ==,,现将直角边AC 沿直线AD 折叠,使它落在斜边AB 上,且与AE 重合,那么CD 的长为多少?EDCBA【例17】 如图,正方形网格中,每个小正方形的边长为1,则网格上的三角形ABC 中,边长为无理数的边数是( )A. 0B. 1C. 2D. 3CBA【例18】 如图所示,在ABC ∆中,三边a b c ,,的大小关系是( )cbaCBAA. a b c <<B. c a b <<C. c b a <<D. b a c <<【例19】 设,,,a b c d 都是正数。
初二勾股定理逆定理证明方法

初二勾股定理逆定理证明方法
初二勾股定理逆定理是指在已知三角形三边长度的情况下,判断该三角形是否为直角三角形。
其逆定理为:若三边的长度满足勾股定理条件,即a+b=c,则该三角形为直角三角形。
为了证明初二勾股定理逆定理,我们可以采用以下方法:
方法一:通过计算
1. 已知三角形的三边边长为a、b、c,且满足a+b=c。
2. 计算a、b和c的值。
3. 判断a+b是否等于c。
- 若等于,说明三角形满足勾股定理,是直角三角形。
- 若不等于,说明三角形不满足勾股定理,不是直角三角形。
方法二:利用勾股定理的性质
1. 已知三角形的三边边长为a、b、c,且满足a+b=c。
2. 假设三角形不是直角三角形。
3. 根据假设,评估三角形的类型:锐角三角形或钝角三角形。
4. 假设三角形是锐角三角形,根据锐角三角形的特点,有a+b>c。
5. 假设三角形是钝角三角形,根据钝角三角形的特点,有a+b<c。
6. 可以看到,无论假设三角形是锐角三角形还是钝角三角形,都与已知条件(a+b=c)相矛盾。
7. 因此,根据反证法,假设不成立,说明三角形必定是直角三角形。
以上是初二勾股定理逆定理的证明方法。
通过计算三边长度或利用勾股定理的性质,我们可以判断一个三角形是否为直角三角形。
这个逆定理的应用可以帮助我们在解决实际问题时,更准确地判断三角形的类型。
勾股定理逆定理八种证明方法

勾股定理逆定理八种证明方法集团标准化小组:[VVOPPT-JOPP28-JPPTL98-LOPPNN]证法1作四个的直角三角形,把它们拼成如图那样的一个多边形,使D、E、F在一条上(设它们的两条直角边长分别为a、b ,斜边长为c.)。
过点C作AC的延长线交DF于点P.∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD,∴ ∠EGF = ∠BED,∵ ∠EGF + ∠GEF =90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180°―90°= 90°又∵ AB = BE = EG = GA = c,∴ ABEG是一个边长为c的正方形。
∴ ∠ABC + ∠CBE = 90°∵ RtΔABC ≌ RtΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90° 即∠CBD= 90°又∵ ∠BDE = 90°,∠BCP = 90°,BC = BD = a.∴ BDPC是一个边长为a的正方形。
同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则证法2作两个的直角三角形,设它们的两条直角边长分别为a、b(b>a),做一个边长为c的正方形。
斜边长为c. 再把它们拼成如图所示的多边形,使E、A、C 三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N.∵ ∠BCA = 90°,QP∥BC,∴ ∠MPC = 90°,∵ BM⊥PQ,∴ ∠BMP = 90°,∴ BCPM是一个矩形,即∠MBC =90°。
∵ ∠QBM + ∠MBA = ∠QBA = 90°,∠ABC + ∠MBA = ∠MBC = 90°,∴ ∠,又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c,∴ RtΔBMQ ≌ RtΔBCA. 同理可证RtΔQNF ≌ RtΔAEF.即证法3作两个全等的直角三角形,同证法2,再作一个边长为c的正方形。
勾股定理逆定理符号语言

勾股定理逆定理符号语言勾股定理是初中数学中极为基础的一条定理,它有着广泛的应用和重要的意义。
而勾股定理的逆定理同样也有着很高的实用价值,在实际生活中起到重要的作用。
本文将对勾股定理逆定理进行详细的解释和阐述,探讨其应用领域和数学意义。
首先,我们来复习一下勾股定理的内容。
勾股定理是指在直角三角形中,直角边的平方等于两条直角边的平方和。
用符号语言表示为:a² + b² = c²。
其中,a和b为直角边的长度,c为斜边的长度。
那么,勾股定理的逆定理就是:如果一个三角形的三边的边长符合a² + b² = c²的关系,那么这个三角形一定是一个直角三角形。
在证明勾股定理逆定理之前,我们首先来看一下为什么勾股定理成立。
勾股定理可以通过几何方法和代数方法进行证明。
在几何方法中,我们可以用三个正方形的面积之和来证明勾股定理。
具体来说,我们可以将三角形分别取为三个正方形的内切圆,然后计算三个正方形的面积。
在代数方法中,我们可以利用坐标系的方法,将三角形的顶点设为某个点,然后利用勾股定理设立方程来证明勾股定理。
接下来,我们来证明勾股定理的逆定理。
假设有一个三角形,已知三个边的长度为a、b、c,且符合a² + b² = c²的关系。
我们需要证明这个三角形一定是直角三角形。
我们可以假设反证法,假设这个三角形不是直角三角形,而是一个锐角三角形或者钝角三角形。
首先,我们假设这个三角形是一个锐角三角形。
根据锐角三角形的性质,三个内角都是锐角,即都小于90°。
那么根据余弦定理,我们可以得到:c² = a² + b² - 2ab·cosC。
由于c² = a² + b²,可以得到2ab·cosC = 0。
由于a和b都大于0,所以cosC = 0。
但是在三角函数表中,我们知道cos90° = 0,意味着C = 90°,与假设的锐角三角形相矛盾。
勾股定理(毕达哥拉斯定理)及各种证明方法
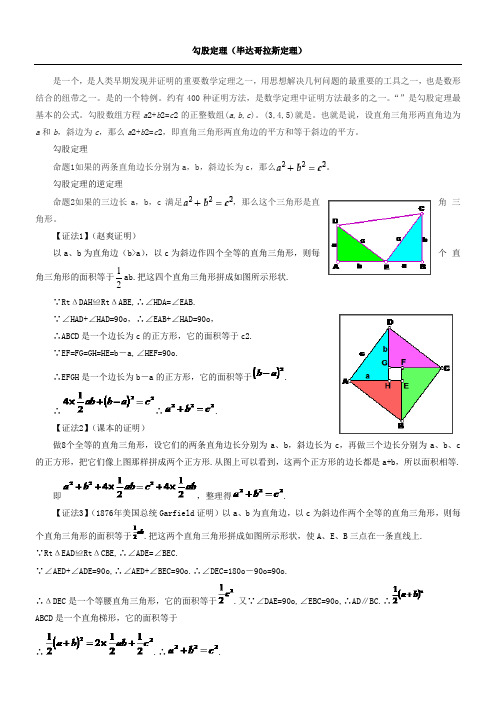
勾股定理(毕达哥拉斯定理) 是一个,是人类早期发现并证明的重要数学定理之一,用思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
是的一个特例。
约有400种证明方法,是数学定理中证明方法最多的之一。
“”是勾股定理最基本的公式。
勾股数组方程a 2+b 2=c 2的正整数组(a ,b ,c )。
(3,4,5)就是。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a 2+b 2=c 2,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1如果的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2如果的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ),以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab.把这四个直角三角形拼成如图所示形状. ∵RtΔDAH≌RtΔABE,∴∠HDA=∠EAB.∵∠HAD+∠HAD=90o,∴∠EAB+∠HAD=90o,∴ABCD 是一个边长为c 的正方形,它的面积等于c2.∵EF=FG=GH=HE=b―a,∠HEF=90o.∴EFGH 是一个边长为b―a 的正方形,它的面积等于.∴∴.【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a+b ,所以面积相等.即,整理得.【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于.把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上. ∵RtΔEAD≌RtΔCBE,∴∠ADE=∠BEC.∵∠AED+∠ADE=90o,∴∠AED+∠BEC=90o.∴∠DEC=180o―90o=90o.∴ΔDEC 是一个等腰直角三角形,它的面积等于.又∵∠DAE=90o,∠EBC=90o,∴AD∥BC.∴ABCD 是一个直角梯形,它的面积等于 ∴.∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理(毕达哥拉斯定理)及各种证明方法

勾股定理(毕达哥拉斯定理) 勾股定理是一个初等几何定理,是人类早期发现并证明的重要数学定理之一,用代数思想解决几何问题的最重要的工具之一,也是数形结合的纽带之一。
勾股定理是余弦定理的一个特例。
勾股定理约有400种证明方法,是数学定理中证明方法最多的定理之一。
“勾三股四弦五”是勾股定理最基本的公式。
勾股数组方程a ² + b ²= c ²的正整数组(a ,b ,c )。
(3,4,5)就是勾股数。
也就是说,设直角三角形两直角边为a 和b ,斜边为c ,那么a ²+b ²=c ² ,即直角三角形两直角边的平方和等于斜边的平方。
勾股定理命题1 如果直角三角形的两条直角边长分别为a ,b ,斜边长为c ,那么。
勾股定理的逆定理命题2 如果三角形的三边长a ,b ,c 满足,那么这个三角形是直角三角形。
【证法1】(赵爽证明)以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于21ab. 把这四个直角三角形拼成如图所示形状.∵ RtΔDAH ≌ RtΔABE,∴ ∠HDA = ∠EAB.∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c2.∵ EF = FG =GH =HE = b―a ,∠HEF = 90º.∴ EFGH 是一个边长为b―a 的正方形,它的面积等于. ∴ ∴.【证法2】(课本的证明) 做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等.即, 整理得 .【证法3】(1876年美国总统Garfield证明)以a、b 为直角边,以c为斜边作两个全等的直角三角形,则每个直角三角形的面积等于. 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上.∵ RtΔEAD ≌ RtΔCBE,∴ ∠ADE = ∠BEC.∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º.∴ ∠DEC =180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形,它的面积等于.又∵ ∠DAE = 90º, ∠EBC = 90º,∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于∴ .∴.【趣闻】:在1876年一个周末的傍晚,在美国华盛顿的郊外,有一位中年人正在散步,欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德。
勾股定理逆定理八种证明方法

证法1作四个全等的直角三角形,把它们拼成如图那样的一个多边形,使D、E、F在一条直线上(设它们的两条直角边长分别为a、b ,斜边长为c.)。
过点C作AC 的延长线交DF于点P.∵ D、E、F在一条直线上,且RtΔGEF ≌ RtΔEBD,∴∠EGF = ∠BED,∵ ∠EGF + ∠GEF = 90°,∴ ∠BED + ∠GEF = 90°,∴ ∠BEG =180°―90°= 90°又∵ AB = BE = EG = GA = c,∴ ABEG是一个边长为c的正方形。
∴ ∠ABC + ∠CBE = 90°∵ RtΔABC ≌ RtΔEBD,∴ ∠ABC = ∠EBD.∴ ∠EBD + ∠CBE = 90° 即∠CBD= 90°又∵ ∠BDE = 90°,∠BCP = 90°,BC = BD = a.∴ BDPC是一个边长为a的正方形。
同理,HPFG是一个边长为b的正方形. 设多边形GHCBE的面积为S,则证法2作两个全等的直角三角形,设它们的两条直角边长分别为a、b(b>a),做一个边长为c的正方形。
斜边长为c. 再把它们拼成如图所示的多边形,使E、A、C三点在一条直线上. 过点Q作QP∥BC,交AC于点P. 过点B作BM⊥PQ,垂足为M;再过点F作FN⊥PQ,垂足为N.∵ ∠BCA = 90°,QP∥BC,∴ ∠MPC = 90°,∵ BM⊥PQ,∴ ∠BMP = 90°,∴ BCPM是一个矩形,即∠MBC = 90°。
∵ ∠QBM + ∠MBA = ∠QBA = 90°,∠ABC + ∠MBA = ∠MBC = 90°,∴ ∠,又∵ ∠BMP = 90°,∠BCA = 90°,BQ = BA = c,∴ RtΔBMQ ≌ RtΔBCA. 同理可证RtΔQNF ≌ RtΔAEF.即证法3作两个全等的直角三角形,同证法2,再作一个边长为c的正方形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
勾股定理、逆定理及证明
一、勾股定理
二、勾股定理逆定理
三、勾股定理的证明
1、勾股定理的证明方法很多,常见的是拼图的方法,用拼图的方法验证勾股定理的思路是:①图形进过割补拼接后,只要没有重叠,没有空隙,面积就不会改变;②根据同一种图形的面积不同的表示方法,列出等式,推导出勾股定理.
2、常见证法如下:
(1)方法一:△正方形正方形S S S EFGH ABCD 4+=,
即)2
1(4)(2
2
ab a b c ⨯+-=化简可证.
(2)方法二:△
正方形正方形S S S EFGH ABCD 4+=即)2
1(4)(2
2
ab c b a ⨯+=+化简可证.
直角三角形两条直角边a 、b 的平方和等于斜边c 的平方,即:a 2
+b 2
=c 2
.
如果三角形的三边长分别为a 、b 、c ,且a 2
+b 2
=c 2
,
那么这个三角形是直角三角形.
(3)方法三:AEB
BCE ADE ABCD S S S S △△△梯形++=即
2
21212
1))((21
c ab ab b a b a ++=++
化简可证.
真题精炼
一、勾股定理及逆定理
1、(16-17学年二十九中期中)如图,以直角三角形一边向外作正方形,
其中两个正方形的面积为100和64,则正方形A 的边长为______.
2、(16-17学年致远期中)如图,△ABC 中,∠ACB =90°,分别以AC 、AB 为边向外作正方形,面积分别为1S ,2S ,
若25921==S S ,,则=BC ______.3、(16-17学年玄武区期中)如图,四边形ABCD 和四边形AEFG 都是正方形,点B 在EF 上,12414021==S S ,,EB 的长为______.
4、(16-17学年树人期中)如图,直线l 上有三个正方形a 、b 、c ,若a 、c 的面积分别为3和4,则b 的面积为_______.
5、(16-17学年玄武区期中)如图,△ABC 中,∠ABC =45°,AC =10,对
折使点B 与点A 重合,折痕与BC 交于点D ,BD :DC =4:3,则DC 的长为().
A .4
B .6
C .8
D .10
6、(16-17学年秦淮区期中)如图,在△ABC 中,∠C=90°,已知a+b=14,ab=48,则c=______.
7、(15-16学年鼓楼区期中)已知直角三角形斜边长为10cm ,周长为22cm ,则此直角三角形的面积为
.
8、(16-17学年南外期中)如图是2002年在北京召开的国际数学家大会的会标,它是由四个全等的直角三角形和一个小正方形拼成的大正方形,若大正方形的面积是9,小正方形的面积是1,直角三角形的较短边为a ,较长边为b ,则2
)(b a =______.
9、(16-17学年秦淮区期中)如图,∠ABC=∠ADC=90°,M 、N 分别是AC 、BD 的中点,AC=10,BD=8,则MN 为()
A.3
B .4
C .5
D .6
10、(16-17学年汇文期中)下列长度的三条线段能组成直角三角形的是().
A .2,3,4
B .3,4,6
C .5,12,13
D .3,4,7
11、(2016年南京中考)下列长度的三条线段能组成钝角三角形的是()
A 、3、4、4
B 、3、4、5
C 、3、4、6
D 、3、4、7
12、(15-16学年秦淮区期中)一块钢板的形状如图所示,已知AB =12cm ,BC =13cm ,CD =4cm ,AD =3cm ,∠ADC =90°,则这块钢板的面积是______cm 2.
13、(17-18学年建邺区期末)如图,有四个三角形,各有一边长为6,一边长为8,若第三边分别为6,8,10,12,则面积最大的三角形是(
)
A B C
D
6
88
6
8
6
810
6
8
12
6
14、(16-17学年二十九中期中)如图,在四边形ABCD 中,已知AB =AD =2,BC =3,CD =1,
90A ∠=︒.
(1)求2
BD .
(2)求ADC ∠.
15、(15-16学年鼓楼区期中)如图,将边长为a 与b 、对角线长为c 的长方形纸片ABCD ,绕点C 顺时针旋转90°得到长方形EFCG ,连接AE .通过用不同方法计算梯形ABGE 的面积可验证
勾股定理,请你写出验证的过程.
A B C G
E F
D
a a
b b c
c
16、
(16-17学年致远期中)勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,其中的“面积法”给了小明以灵感,他惊喜的发现,当四个全等的直角三角形如图摆放时,可以用“面积法”来推导明222a b c +=.请你写出推导过程.
17、(16-17学年汇文期中)如图,在Rt ABC △中,90ACB ∠=︒,E 为AC 上一点,
且AE BC =,过点A 作AD CA ⊥,垂足为A ,且AD AC =,AB 、DE 交于点F .(1)判断线段AB 与DE 的数量关系和位置关系,并说明理由.
(2)连接BD 、BE .若设BC a =,AC b =,AB c =,请利用四边形ADBE 的面积证明勾股定理.
18、(16-17学年十三中期中)在《3.1勾股定理》这一节课,我们运用拼图的方式,利用两种不同的方法计算方形的面积,通过正方形面积相等,验证了勾股定理.
小明和小红在学习完这一节课之后,利用4张全等的直角三角形纸片(如图所示,直角边长分别为a、b,斜边为c).在边长为a b 的两个正方形硬纸板上(如图(1)、图(2)所示),采取不同的拼图方法,分别计算图(1)、图(2)中空余部分的面积,也验证了勾股定理,请你完善他们的验证过程.
(1)在图(1)、(2)中分别画出两种拼法的示意图.
(2)利用图(1)、图(2),写出验证勾股定理的过程.。
