悬链线方程
系泊系统悬链线方程
系泊系统悬链线方程引言系泊系统是一个用于固定船只或其他浮动物体的装置。
在海洋工程中，悬链线常被用作系泊系统的一部分，用于支撑和固定船只。
了解悬链线方程可以帮助工程师更好地设计和计算系泊系统，以确保船只的安全。
本文将介绍悬链线的概念以及如何推导悬链线的方程。
我将向您解释悬链线的基本原理，并提供一个简单的数学推导，从而得出悬链线的方程。
悬链线的基本原理悬链线是指在自由悬挂的条件下所呈现的线形。
当在自由空间中的两个点之间拉起悬链线时，其形状与悬链线的长度和两个拉力有关。
悬链线形成的原因是张力与重力在平衡状态下相互作用。
在船只的系泊系统中，悬链线呈现出类似于倒钟的形状。
这是因为船只的重力在悬链线上形成一个上向的张力，而风力和浪力则在悬链线上形成一个下向的张力。
这种平衡状态使船只能够固定在一个位置，并抵抗外部的力量。
推导悬链线的方程为了推导悬链线的方程，我们可以使用悬链线微元的分析方法。
假设有一段长度为ds的悬链线，在这段悬链线上的张力为T，重力为dF。
考虑到悬链线的长度非常小，我们可以使用近似的方法进行推导。
首先，我们可以将悬链线微元的受力分解为水平方向和垂直方向的分量。
垂直方向的受力平衡可以表示为：T * cosθ = dF其中，θ表示悬链线微元的倾角。
我们可以将dF表示为悬链线微元的重力分量dm乘以重力加速度g，即dF = dm * g。
然后，我们可以将水平方向的受力平衡表示为：T * sinθ = T * dθ悬链线微元的弧长长度可以表示为：ds = R * dθ其中，R表示悬链线微元与悬链线中心线的距离，也就是悬链线的半径。
将上述方程联立解得：T * cosθ = dm * gT * sinθ = R * dθ我们可以进一步将cosθ与sinθ之间的关系表示为：sinθ = √(1 - cos²θ)将这个关系带入前面的方程，我们可以得到：dm * g = R * dθ * √(1 - cos²θ)对上述方程进行微分运算，并将dm表示为dM/dθ：g * dM/dθ = R * dθ * √(1 - cos²θ)将上述方程进行变量分离和积分运算，得到：∫dθ/√(1 - cos²θ) = ∫g * R / M dM其中，M表示总质量等效值。
悬链线方程的推导过程
悬链线方程的推导过程嘿，朋友们！今天咱就来聊聊悬链线方程的推导过程，这可有意思啦！咱先来说说啥是悬链线。
你看那悬挂起来的链条，它自然下垂形成的那个曲线，就是悬链线啦。
就好像咱平时看到的晾衣绳，或者那种古老的吊桥的铁链，它们垂下来的样子。
那为啥要研究它的方程推导呢？这可重要啦！它在好多地方都有用武之地呢，比如建筑设计呀，桥梁工程呀。
要是咱能搞清楚它，那不是能让好多东西建得更漂亮更稳固嘛！那怎么推导呢？咱先从最基本的开始。
想象一下，把这个悬链分成一小段一小段的。
每一小段都受到重力的作用，对吧？然后呢，再考虑这些小段之间的相互关系。
这就好像拼图一样，一块一块地拼起来，慢慢地就能看出整个图案啦。
咱再深入一点。
这些小段之间的力呀，得平衡才行。
这就好比拔河比赛，两边的力量得差不多，不然不就被拉跑啦。
通过研究这些力的平衡，就能找到一些规律。
然后呢，咱就可以用一些数学知识啦。
什么微积分呀，函数呀，都可以派上用场。
就好像是给这个悬链线穿上了一件数学的外衣，让它变得更加清晰明了。
你说这是不是很神奇？从一个看起来普普通通的链条，通过一点点的分析和推导，就能得出一个那么复杂又那么有用的方程。
这就好比是从一粒小小的种子，最后长成了一棵参天大树。
而且啊，这个推导过程可不是一帆风顺的哟！有时候会遇到难题，就好像爬山的时候遇到了陡峭的山坡。
但咱可不能退缩呀，得鼓起勇气往上爬。
当我们终于推导出来的时候，那种成就感呀，简直无与伦比！就好像是解开了一道超级难的谜题，心里那叫一个痛快！所以说呀，悬链线方程的推导过程虽然有点复杂，但真的很值得我们去研究。
它让我们看到了数学和现实世界的紧密联系，也让我们感受到了探索的乐趣和成就感。
大家不妨也去试试，说不定你也能发现其中的奥秘呢！。
悬链线方程
通常任何材料包括导线在内，都具有一定的刚性，但由于悬挂在杆塔上的一档导线相对较长，因此导线材料的刚性对其几何形状的影响很小，故在计算中假定：（1）导线为理想的柔索。
因此，导线只承受轴向张力（或拉力），任意一点的弯矩为零。
这样导线力学计算可应用理论力学中的柔索理论进行计算。
（2）作用在导线上的荷载均指同一方向，且沿导线均匀分布。
一、悬链线方程及曲线弧长1.悬链线方程为了分析方便，我们先从悬挂点等高，即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上，导线悬在空中的曲线形态，从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索，则可按照理论力学中的悬链线关系来进行分析，即将导线架设在空中的几何形态视为悬链形态，而由此导出的方程式为悬链线方程。
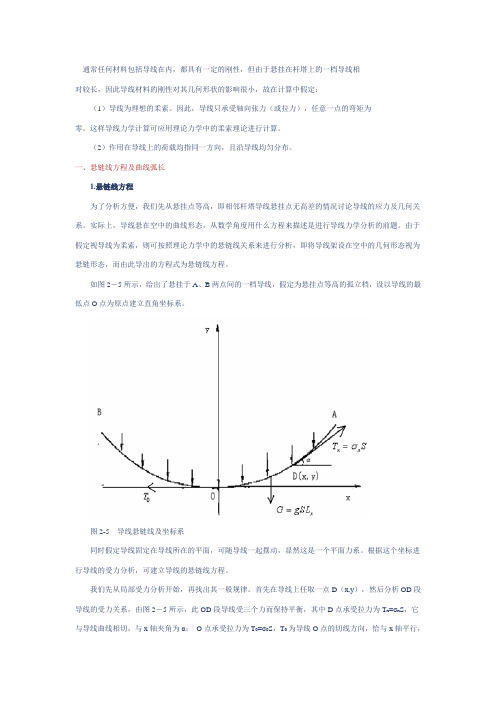
如图2－5所示，给出了悬挂于A、B两点间的一档导线，假定为悬挂点等高的孤立档，设以导线的最低点O点为原点建立直角坐标系。
图2-5导线悬链线及坐标系同时假定导线固定在导线所在的平面，可随导线一起摆动，显然这是一个平面力系。
根据这个坐标进行导线的受力分析，可建立导线的悬链线方程。
我们先从局部受力分析开始，再找出其一般规律。
首先在导线上任取一点D（x,y），然后分析OD段导线的受力关系，由图2－5所示，此OD段导线受三个力而保持平衡，其中D点承受拉力为T x=σx S，它与导线曲线相切，与x轴夹角为α；O点承受拉力为T0=σ0S，T0为导线O点的切线方向，恰与x轴平行，故又称水平张力；此外还有OD段导线自身的荷载为G=gSL x，其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示，如图2－6所示，图2-6导线受力情况由静力学平衡条件可知，在平面坐标系中，其水平分力，垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
关于悬链线计算公式的讨论
关于悬链线计算公式的讨论
悬链线计算公式是用于计算架空线路中导线长度的一种方法。
在实际工程应用中，悬链线法是一种较为精确的计算方法，尽管它也是一种近似计算。
接下来，我们将讨论悬链线计算公式及其应用。
悬链线法的基本原理是将架空线路的导线视为一条理想的无刚度、无自重的链条，根据链条的自然形态来计算导线长度。
在实际工程中，导线受到水平张力H、每米自重W以及高差的影响。
因此，悬链线计算公式需要考虑这些因素。
悬链线计算公式如下：
L = 2 * √(H * f / W)
其中，L表示导线长度，f表示导线的弧垂。
在实际应用中，我们还需根据导线的档距l和高差角来计算弧垂f。
高差角α的计算公式为：
α= arcsin(√((H^2 + l^2) - 2 * H * cos(θ)))
其中，θ表示导线与水平方向的夹角。
有了高差角α和档距l，我们可以计算出弧垂f，然后代入悬链线计算公式，求得导线长度L。
值得注意的是，悬链线法虽然考虑了导线的自重、水平张力以及高差等因素，但仍然是一种近似计算。
在实际工程中，根据工程需要和精度要求，我们可以选择合适的方法进行导线长度的计算。
对于精度要求较高的工程，可以考虑采用更为精确的数值模拟方法或其他近似计算方法。
总之，悬链线计算公式是一种应用于架空线路工程中的常用计算方法。
在实际工程中，我们需要根据具体情况选择合适的计算方法，以确保计算结果的精度和可靠性。
悬链线公式范文
悬链线公式范文悬链线曲线可以通过悬链线公式来描述，该公式是一种二次积分方程。
悬链线公式的推导可以追溯到17世纪，最早由数学家伽利略提出。
早期的研究主要关注两个重要参数，悬链线的弧长和张力。
在此基础上，经过长期的发展和改进，悬链线公式逐渐完善起来。
y = a * cosh(x/a)其中，y表示曲线上其中一点的纵坐标，x表示该点距离对称轴的横坐标，a是曲线的挂链长度。
这个公式可以用来计算悬链线上任意一点的位置。
在特定的条件下，可以通过解析法或数值计算的方法，确定悬链线上任意一点的坐标。
首先，我们考虑悬链线上其中一点的切线斜率。
根据物理学知识，悬链线上任意一点处切线的斜率等于该点处曲线的斜率。
而曲线的斜率可以通过曲线的微分方程来表示。
因此，我们可以通过微分方程计算出悬链线上其中一点的切线斜率。
接下来，我们将斜率表示为dy/dx的形式，并对其进行积分得到y关于x的函数表达式。
为了求解这个积分方程，我们使用变量代换来简化计算。
最后，我们对积分方程进行求解，得到了悬链线公式。
悬链线公式的应用非常广泛。
在物理学中，它可以用来描述悬链线的形状和张力分布。
在工程学中，悬链线公式可以应用于吊桥、电线杆、挂钟和索道等结构设计。
悬链线的形状对于这些结构的稳定性和载荷分布具有重要影响。
总之，悬链线公式是一种描述悬链线形状的数学公式。
它的推导过程比较复杂，需要运用高等数学知识。
悬链线公式的应用涵盖了物理学和工程学等领域，对于研究结构的稳定性和计算载荷分布非常重要。
悬链线方程的推导
1 悬链线方程的推导 锚链一端受到水平预张力()0T KN ，并在其均匀分布的自重力作用下产生下垂。
设锚链水中 单位重力为()/W KN m ，建立如图1所示的直角坐标系，并设锚链曲线对应的函数为()y f x =。
对于横坐标上0至x 这段锚链，长度为L ，则G wL =，顶端拉力为T ，该力倾角为θ，水平张力0T ,根据力学原理可知，T ，G 和0T 三力平衡。
可知0tan /G T θ=(图2). 图1图2假定该水平张力在锚链上处处相等，对于任意一段锚链L ，该平衡均成立，0tan wL T θ=，而tan dy dxθ=，对该式取微分，则有()()00tan x w d d L T θ===（1） 弧长微分ds=1）分离变量后并积分： 0tan d w dx T =⎰（2） 对式（2）积分后得到：10tan w sh x c T θ⎛⎫=+ ⎪⎝⎭（3）对式（3）再次分离变量后，得10w dy sh x c dx T ⎛⎫=+ ⎪⎝⎭（4）并积分，10w y sh x c dx T ⎛⎫=+ ⎪⎝⎭⎰（5）查积分公式可得：0120T w y ch x c c w T ⎛⎫=++ ⎪⎝⎭（6） 式（6）即为锚链悬链线的一般方程。
假设锚链末端拖地，并设拖地点为原点，则对于拖地点有，0,0,tan 0x y θ===，代入式（3）和（6），联立方程后，可解得：10c =，2T c w=,代入式（6）得: 001T w y ch x w T ⎛⎫=- ⎪⎝⎭（7） 式（5）即为拖地点为原点的悬链线一般方程。
而对于悬挂点为原点的悬链线方程，仅系数有所变化，如下式表示，推导过程不再叙述。
该方程对于有悬锤的悬链线更适用。
0,0,tan wL x y Tθ===，代入式（3）,（6）可解得： 002cosh sinh wL T a T c w⎡⎤⎛⎫⎢⎥ ⎪⎝⎭⎣⎦=（8） 式（8）即是以悬挂点为原点的悬链线一般方程。
悬链线方程及曲线弧长
第二章导线应力弧垂分析第三节悬点等高时导线弧垂、线长和应力关系一、悬链线方程及曲线弧长1.悬链线方程为了分析方便，我们先从悬挂点等高，即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上，导线悬在空中的曲线形态，从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索，则可按照理论力学中的悬链线关系来进行分析，即将导线架设在空中的几何形态视为悬链形态，而由此导出的方程式为悬链线方程。
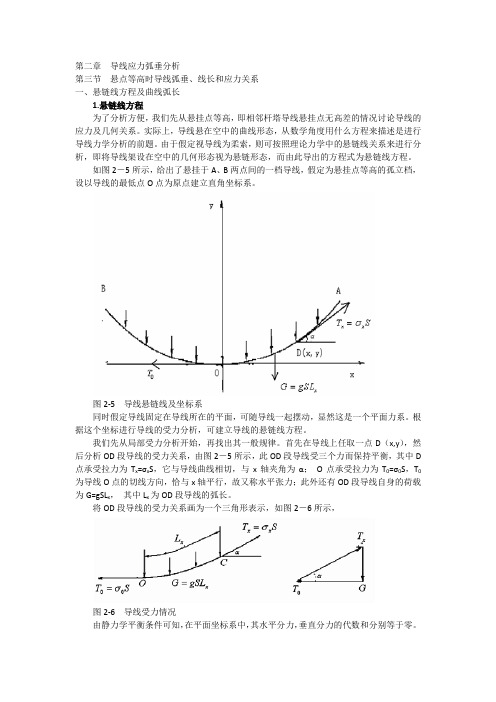
如图2－5所示，给出了悬挂于A、B两点间的一档导线，假定为悬挂点等高的孤立档，设以导线的最低点O点为原点建立直角坐标系。
图2-5导线悬链线及坐标系同时假定导线固定在导线所在的平面，可随导线一起摆动，显然这是一个平面力系。
根据这个坐标进行导线的受力分析，可建立导线的悬链线方程。
我们先从局部受力分析开始，再找出其一般规律。
首先在导线上任取一点D（x,y），然后分析OD段导线的受力关系，由图2－5所示，此OD段导线受三个力而保持平衡，其中D 点承受拉力为T x=σx S，它与导线曲线相切，与x轴夹角为α；O点承受拉力为T0=σ0S，T0为导线O点的切线方向，恰与x轴平行，故又称水平张力；此外还有OD段导线自身的荷载为G=gSL x，其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示，如图2－6所示，图2-6导线受力情况由静力学平衡条件可知，在平面坐标系中，其水平分力，垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
其中σ0、T0为导线最低点的应力和张力，σx、T x为导线任一点的应力和张力，S、g为导线截面和比载。
将上述二式相比，则可求得导线任意一点D的斜率为：(2-10)由微分学知识可知，曲线上任一点的导数即为切线的斜率。
式（2－10）是悬链曲线的微分方程。
我们要用坐标关系表示出导线受力的一般规律，还需要将不定量L x消去，因此，将式对x微分得：（微分学中弧长微分公式为dS2=(dx)2+(dy)2）将上式移项整理后，两端进行积分这是个隐函数，因此，再进行分离变量积分，查积分公式有：（2－11）再进行分离变量积分，有于是，导线任一点D的纵坐标为：（2－12）式（2－12）是悬链方程的普通形式，其中C1和C2为积分常数，其值可根据取坐标原点的位置及初始条件而定。
悬链线方程的推导过程
悬链线方程的推导过程悬链线是一种曲线，其形状类似于悬链。
悬链线最早由德国数学家焦若贝利在1725年所提出，也被称为Catenary（猫enary）曲线。
这条曲线具有许多独特的性质和应用领域，因此悬链线的推导过程也非常有趣。
悬链线的推导涉及到一些微积分和几何的知识。
在这里，我将尽量简明扼要地介绍悬链线方程的推导过程。
第一步：设定问题和坐标系我们假设有一根不可伸长、重力平均作用于其上的悬链线。
我们希望找到这条悬链线的方程。
为此，我们首先将悬链线放在一个笛卡尔坐标系中。
设悬链线的轴线为x轴，y轴垂直于轴线。
第二步：表示悬链线的参数方程为了表示悬链线，我们引入参数t，表示悬链线上任意一点的位置。
我们假设悬链线的最低点为原点O(0, 0)，则悬链线的参数方程可以表示为：x = at， y = bch(a)，其中a和b是任意的正数，c是一个常数，表示悬链线的形状。
第三步：应用欧拉－积分方程为了求解悬链线的参数方程，我们需要应用欧拉－积分方程。
欧拉－积分方程是描述弹性形体的自平衡状态的一个重要方程。
我们令L表示悬链线的弧长，则有：L = ∫√(1 + (dy/dx)²)dx将悬链线的参数方程带入上式，可以得到：L = ∫√(1 + (a² + b²ch²(a)²)dt第四步：求解悬链线弧长的积分通过对上式中的积分进行变量替换和一些微积分的技巧可以求得L的积分形式。
最终我们得到：L = ∫csch(a)da，其中csch(a)是双曲正弦函数的倒数，定义为csch(a) = 1/sinh(a) = (2e^a)/(e^2a - 1)第五步：应用数值积分方法由于上述积分无法通过标准的解析方法求解，我们可以应用数值积分方法来计算L。
一种常用的数值积分方法是龙格－库塔法则，它可以在较高精度下计算复杂的积分。
第六步：求解悬链线方程通过数值积分得到L后，我们可以尝试通过方程L=c来求解a。
悬链线方程的推导过程
悬链线方程的推导过程悬链线 (Catenary) 是一种曲线，它的形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名。
适当选择坐标系后，悬链线的方程是一个双曲余弦函数，其公式为：y = a*cosh(x/a)其中 a 是一个常数。
最低点处受水平向左的拉力H ，右悬挂点处受一个斜向上的拉力T ，设T 和水平方向夹角为θ，绳子一半的质量为m,受力分析有：Tsin Tcos θθ=mg,=H并且对于绳上任意一点有tan θ=dy/dx=mg/H ，ρmg=s其中s 是右半段绳子的长度, ρ是绳子密度,认为绳子截面积是1,带入得微分方程 ρdy/dx=s/H 利用弧长公式ds=(1+dy^2/dx^2)dx所以有，实际上就是弧长积分公式：⎰s=1+dy^2/dx^2dx所以把s 带入微分方程得ρ⎰dy/dx=1+dy^2/dx^2dx/H （1）对于(1)设p =dy/dx 并做微分处理可得：ρ=dp p'=/H 1+p^2dx（2） 对（2）分离常量求积分 dp ρ=⎰⎰1/Hdx 1+p^2 （3）得：ln()p x ρ+=1+p^2/H+C边界条件：x=0，dy/dx=0，代入后可得C 0=，整理后为：ln()p x ρ+=1+p^2/H （4）由))p p xρ==-=/H （5） 即得x x ρρ⎡⎤⎣⎦p=e^(/H)-e^(-/H)/2=dy/dx （6）x x ρρρ⎡⎤⎣⎦y=p=H/2e^(/H)+e^(-/H) （7）如果令ρa=H/的话，则有/(2)cosh(/)x a x a a a x a =⎡⎤⎣⎦y=p=e^(/)+e^(-/) （8） 即为双曲函数。
悬链线方程
通常任何材料包括导线在内，都具有一定的刚性，但由于悬挂在杆塔上的一档导线相对较长，因此导线材料的刚性对其几何形状的影响很小，故在计算中假定：（1）导线为理想的柔索。
因此，导线只承受轴向张力（或拉力），任意一点的弯矩为零。
这样导线力学计算可应用理论力学中的柔索理论进行计算。
（2）作用在导线上的荷载均指同一方向，且沿导线均匀分布。
一、悬链线方程及曲线弧长1.悬链线方程为了分析方便，我们先从悬挂点等高，即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上，导线悬在空中的曲线形态，从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索，则可按照理论力学中的悬链线关系来进行分析，即将导线架设在空中的几何形态视为悬链形态，而由此导出的方程式为悬链线方程。
如图2－5所示，给出了悬挂于A、B两点间的一档导线，假定为悬挂点等高的孤立档，设以导线的最低点O点为原点建立直角坐标系。
图2-5导线悬链线及坐标系同时假定导线固定在导线所在的平面，可随导线一起摆动，显然这是一个平面力系。
根据这个坐标进行导线的受力分析，可建立导线的悬链线方程。
我们先从局部受力分析开始，再找出其一般规律。
首先在导线上任取一点D（x,y），然后分析OD段导线的受力关系，由图2－5所示，此OD段导线受三个力而保持平衡，其中D点承受拉力为T x=σx S，它与导线曲线相切，与x轴夹角为α；O点承受拉力为T0=σ0S，T0为导线O点的切线方向，恰与x轴平行，故又称水平张力；此外还有OD段导线自身的荷载为G=gSL x，其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示，如图2－6所示，图2-6导线受力情况由静力学平衡条件可知，在平面坐标系中，其水平分力，垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
悬链线 相对论
悬链线相对论悬链线是一种特殊的曲线，其形状类似于一条悬挂在两点之间的链条所形成的形状。
相对论是一种物理学理论，它描述了时间和空间的相对性和统一性，以及物质和能量的相对性和分布。
首先，我们来了解一下悬链线。
悬链线是一种非均匀曲线，其形状取决于两个点的高度和两点之间的距离。
在数学上，悬链线的方程为y = kx + b/x，其中k为曲率，b为原点到曲线上某一点的距离。
这种曲线在自然界中可以应用于许多场景，如河流的流动、弹簧的振动等。
悬链线的形状也暗示了物理学的某些特性，如引力、速度和时间的相对性。
接下来，我们来谈谈相对论。
相对论是现代物理学的一个重要理论，它试图通过将时间和空间看作是相对的和可变的来统一牛顿力学和电磁学。
相对论的基本原理包括光速不变、相对速度、时间和空间的相对性等。
这些原理对于理解许多自然现象，如黑洞、引力波和宇宙学等至关重要。
当我们将悬链线和相对论结合起来时，我们可以得出一些有趣的结论。
首先，悬链线可以被视为一种相对论的几何表现形式，因为它涉及到时间和空间的相对性和变化。
其次，悬链线的形状和相对论的原理相结合，可以暗示物质和能量的相对性和分布，以及引力、速度和时间的相对性。
最后，这种结合可以用于解释一些物理学现象，如黑洞的几何形状、引力波的产生等。
总的来说，悬链线和相对论之间存在着一种内在的联系。
悬链线可以被视为一种相对论的几何表现形式，它涉及到时间和空间的相对性和变化。
而相对论的基本原理则可以与悬链线的形状相结合，来解释一些物理学现象。
这种结合不仅可以加深我们对物理学原理的理解，还可以为未来的科学研究提供新的思路和方法。
基于python的悬链线数学模型
基于Python的悬链线数学模型悬链线是一个物理现象，当一条不可伸长的、均匀的、柔软的链条或绳索在重力作用下悬挂时，它呈现出的曲线就是悬链线。
在数学上，悬链线可以用双曲余弦函数来表示。
假设悬链线的最低点位于原点(0, 0)，且其两端固定于高度为h的平面上，水平距离为2a。
那么悬链线的数学模型可以用以下公式表示：y = a * (cosh(x/a) - 1)其中，y是链条上任意一点的垂直坐标，x是该点的水平坐标，a是链条在最低点的水平张力与重力之比的一个常数，cosh是双曲余弦函数。
在Python中，你可以使用math库中的cosh函数来计算悬链线的y值。
下面是一个简单的示例代码：pythonimport mathimport matplotlib.pyplot as plt# 定义参数a = 1.0 # 可以根据实际需要调整x_values = [-5*a, -4*a, -3*a, -2*a, -a, 0, a, 2*a, 3*a, 4*a, 5*a] # x的取值范围# 计算y值y_values = [a * (math.cosh(x/a) - 1) for x in x_values]# 绘制悬链线plt.plot(x_values, y_values)plt.xlabel('x')plt.ylabel('y')plt.title('Catenary Curve')plt.grid(True)plt.show()这段代码首先定义了悬链线模型中的参数a，然后定义了一系列x值。
接着，它使用列表推导式来计算每个x值对应的y值。
最后，它使用matplotlib库来绘制悬链线。
你可以根据需要调整参数a和x的取值范围来观察不同的悬链线形状。
悬链线
悬链线科技名词定义中文名称：悬链线英文名称：catenary定义：两端悬挂的理想柔性软索的曲线。
工程计算中，可近似用抛物线计算。
应用学科：电力（一级学科）；输电线路（二级学科）以上内容由全国科学技术名词审定委员会审定公布目录悬链线等高悬链线数学表达式的证明工程中的应用悬链线悬链线(Catenary) 是一种曲线，它的形状因与悬在两端的绳子因均匀引力作用下掉下来之形相似而名。
适当选择坐标系后，悬链线的方程是一个双曲余弦函数，其公式为：y = a*cosh(x/a) 其中a 是一个常数。
等高悬链线数学表达式的证明注释如右图，设最低点A处受水平向左的拉力H，右悬挂点处表示为C点，在AC弧线区段任意取一段设为B点，则B受一个斜向上的拉力T，设T 和水平方向夹角为θ，绳子的质量为m,受力分析有：Tsinθ=mg；Tcosθ=H，tanθ=dy/dx=mg/H，mg=ρs，，其中s是右段AB 绳子的长度，ρ是绳子线重量密度，代入得微分方程dy/dx=ρs/H;利用弧长公式ds=√(1+dy^2/dx^2)*dx;所以s=∫√(1+dy^2/dx^2)*dx; 所以把s 带入微分方程得dy/dx=ρ∫√(1+dy^2/dx^2)*dx/H;.....(1) 对于(1)设p=dy/dx微分处理得p'=ρ/H*√(1+p^2)......(2) p'=dp/dx; 对（2）分离常量求积分∫dp/√(1+p^2)=∫ρ/H*dx 得ln[p+√(1+p^2)]=ρx/H+C，即asinhp（反双曲正弦）=ρx/H+C 当x=0时，dy/dx=p=0；带入得C=0；整理得asinhp=ρx/H 另祥解：（ln[p+√(1+p^2)]=ρx/H）；p=sh(ρx/H) （1+p^2=e^(2ρx/H)-2pe^(ρx/H)+p^2）；(p=[e^(ρx/H)-e^(-ρx/H)]/2=dy/dx)；y=ch (ρx/H)* H / ρ（y=H/(2ρ)*[e^(ρx/H)+e^(-ρx/H)] ）；令a=H/ρ：y=a*cosh (x/a) (y=a[e^(x/a)+e^(-x/a)]/(2)= a*cosh(x/a))。
悬链线方程——数学史上的难题之一，伽利略没能求出，难在哪里？
悬链线方程——数学史上的难题之一，伽利略没能求出，难在哪里？一个完美均匀且灵活的平衡链被它的两端悬挂，并只受重力的影响，这个链子形成的曲线形状被称为悬链线。
1690年，荷兰物理学家、数学家、天文学家、发明家克里斯蒂安·惠更斯（Christiaan Huygens）在给德国著名博学家戈特弗里德·莱布尼茨（Gottfried Leibniz）的一封信中创造了这个名字。
悬链线与抛物线相似。
意大利伟大的天文学家、物理学家和工程师伽利略是第一个研究悬链线的人，并错误地将其形状认定为抛物线。
1691年，莱布尼茨、惠根斯和瑞士数学家约翰·伯努利分别得出了正确的形状。
他们都是为了响应瑞士数学家雅各布·伯努利（约翰的哥哥）提出的一项挑战，即得到“悬链线”方程。
•图1：从左到右分别是雅各布·伯努利，戈特弗里德·莱布尼茨，克里斯蒂安·惠更斯和约翰·伯努利莱布尼茨和惠更斯发给雅各布·伯努利的图如下所示。
他们发表在《博学学报》上，这是欧洲德语国家的第一份科学期刊。
•图1：莱布尼茨和惠更斯提交给雅各布·伯努利的答案。
约翰·伯努利很高兴，他成功地解决了他哥哥雅各布没能解决的问题。
27年后，他在一封信中写道：我哥哥的努力没有成功。
就我而言，我更幸运，因为我发现了这个问题的答案。
对于我当时的年龄和经验来说，这是一个巨大的成就。
……我满心欢喜地跑到哥哥那里，他一直在苦苦地与这个难题作斗争，却没有任何进展，总是像伽利略一样认为这个链线是一个抛物线。
我对他说，不要再折磨自己了，不要再试图用抛物线来寻求悬链的方程了，因为那是完全错误的。
——约翰·伯努利求悬链线方程为求悬链线方程，作以下假设：•悬链悬挂在两点之间，靠自身重量悬挂。
•悬链是灵活的，有一个统一的线性重量密度（等于w_0）。
为了简化代数上的繁琐，我们让y轴通过曲线的最小值。
悬链式方程
悬链式方程
摘要：
一、悬链式方程的定义与背景
1.悬链式方程的概念
2.悬链式方程的来源和发展
二、悬链式方程的数学模型
1.悬链式方程的一般形式
2.悬链式方程的物理意义
三、悬链式方程的求解方法
1.分离变量法
2.矩方法
3.数值解法
四、悬链式方程在工程中的应用
1.桥梁工程
2.输电塔工程
3.其他工程领域
正文：
悬链式方程是一种描述绳索、链条、电线等受力平衡问题的数学方程。
它的名字来源于悬链这个形象的概念，就像悬在空中的链条一样。
悬链式方程广泛应用于桥梁工程、输电塔工程等领域，对于分析和预测这些工程结构的安全性能具有重要意义。
悬链式方程的数学模型一般形式为：
u/t = cu/x
其中，u 表示绳索或链条的位移，t 表示时间，x 表示绳索或链条的长度，c 表示绳索或链条的传播速度。
悬链式方程的求解方法有分离变量法、矩方法、数值解法等。
其中，分离变量法是一种较为直观且易于实现的求解方法，但仅适用于一维问题。
矩方法则可以解决多维问题，但计算过程较为复杂。
数值解法则可以处理更复杂的问题，但精度受到数值方法的选取和计算步长的限制。
悬链式方程在工程中的应用十分广泛。
在桥梁工程中，悬链式方程可以用于分析桥梁的挠度、位移等受力性能，为桥梁设计提供理论依据。
在输电塔工程中，悬链式方程可以用于分析输电塔的挠曲变形和风振响应，以确保输电塔的安全稳定。
悬链线方程
通常任何材料包括导线在内,都具有一定得刚性,但由于悬挂在杆塔上得一档导线相对较长,因此导线材料得刚性对其几何形状得影响很小,故在计算中假定:ﻫ(１)导线为理想得柔索。
因此,导线只承受轴向张力(或拉力),任意一点得弯矩为ﻫ零。
这样导线力学计算可应用理论力学中得柔索理论进行计算。
ﻫ(2)作用在导线上得荷载均指同一方向,且沿导线均匀分布。
一、悬链线方程及曲线弧长1。
悬链线方程为了分析方便,我们先从悬挂点等高,即相邻杆塔导线悬挂点无高差得情况讨论导线得应力及几何关系。
实际上,导线悬在空中得曲线形态,从数学角度用什么方程来描述就是进行导线力学分析得前题、由于假定视导线为柔索,则可按照理论力学中得悬链线关系来进行分析,即将导线架设在空中得几何形态视为悬链形态,而由此导出得方程式为悬链线方程。
如图2－5所示,给出了悬挂于A、B两点间得一档导线,假定为悬挂点等高得孤立档,设以导线得最低点Ｏ点为原点建立直角坐标系。
ﻫ图２—5导线悬链线及坐标系同时假定导线固定在导线所在得平面,可随导线一起摆动,显然这就是一个平面力系。
根据这个坐标进行导线得受力分析,可建立导线得悬链线方程、ﻫ我们先从局部受力分析开始,再找出其一般规律、首先在导线上任取一点D(x,y),然后分析ＯD段导线得受力关系,由图2—5所示,此OD段导线受三个力而保持平衡,其中D点承受拉力为T x=σｘS,它与导线曲线相切,与x轴夹角为α; O点承受拉力为Ｔ０=σ0Ｓ,T0为导线O点得切线方向,恰与x轴平行,故又称水平张力;此外还有OD段导线自身得荷载为G＝gSL x, 其中L x为OＤ段导线得弧长。
ﻫ将OD段导线得受力关系画为一个三角形表示,如图2－6所示,ﻫﻫ图2-６导线受力情况ﻫ由静力学平衡条件可知,在平面坐标系中,其水平分力,垂直分力得代数与分别等于零。
或沿x 轴或y轴上分力代数与分别等于零。
垂直方向分力G＝T x siｎα=gSLｘ;水平方向分为Ｔ0=T xｃosα=σ0Ｓ、其中σ0、T0为导线最低点得应力与张力,σx、T x为导线任一点得应力与张力,S、g为导线截面与比载。
悬链线方程的推导
悬链线方程的推导一根无比柔软的绳子，两固定，自然静止状态下，它的形状是悬链线。
其实曲线是以绳子命名的。
如何根据绳子的受力来推导出悬链线方程呢？用高等数学所学的知识就够了。
第一步：背景知识 ㈠我们熟悉如何将)2sin(πα⋅+n 转化成余弦的形式，口诀是奇变偶不变，符号看象限。
现在扩展一下，研究正切、余切，正割、余割的转化口诀。
tanx cotx 转换：奇变号变偶不变。
也就是说，n 为奇数时，要转化成相反形式，且要补一个负号，n 为偶数时就不用变了。
secx cscx 转换：奇变偶不变，符号看象限。
我正弦、余弦非常相似。
㈡不定积分C x x C x x x x d x dx xdx C x x C x x x d x x d x x x dx x dx xdx ++=++-+=++==+-=+=====⎰⎰⎰⎰⎰⎰⎰⎰tan sec ln )2cot()2csc(ln )2sin()2(cos sec cot csc ln 2tan ln 2tan 2tan 2tan 22sec 2cos 2sin 2sin csc 2ππππ求⎰+22ax dx，令t a x tan =，22ππ<<-t aC C C a x x C ax a a x C t t tdt a t a tdt a ln )ln(ln tan sec ln sec tan sec 1122222222-=+++=+++=++==+=⎰⎰㈢双曲余弦 chx e e y x x =+=-2 双曲正弦 shx e e y xx =-=-2反双曲余弦 x>0时，archy y y x =-+=)1ln(2； 反双曲正弦 arshy y y x =++=)1ln(2； 求导：shxchx chx shx ='=')()( 第二步：微分方程平衡方程：,0cos ,0sin =-⋅=-⋅H T gs T θρθ 解得：gH a dx y a y a s H gsx ρρθ='+='===⎰,11tan 02 边界条件：x=0 y=a ； x=0 y'=0。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
通常任何材料包括导线在内，都具有一定的刚性，但由于悬挂在杆塔上的一档导线相
对较长，因此导线材料的刚性对其几何形状的影响很小，故在计算中假定：
（1）导线为理想的柔索。
因此，导线只承受轴向张力（或拉力），任意一点的弯矩为
零。
这样导线力学计算可应用理论力学中的柔索理论进行计算。
（2）作用在导线上的荷载均指同一方向，且沿导线均匀分布。
一、悬链线方程及曲线弧长
1.悬链线方程
为了分析方便，我们先从悬挂点等高，即相邻杆塔导线悬挂点无高差的情况讨论导线的应力及几何关系。
实际上，导线悬在空中的曲线形态，从数学角度用什么方程来描述是进行导线力学分析的前题。
由于假定视导线为柔索，则可按照理论力学中的悬链线关系来进行分析，即将导线架设在空中的几何形态视为悬链形态，而由此导出的方程式为悬链线方程。
如图2－5所示，给出了悬挂于A、B两点间的一档导线，假定为悬挂点等高的孤立档，设以导线的最低点O点为原点建立直角坐标系。
图2-5 导线悬链线及坐标系
同时假定导线固定在导线所在的平面，可随导线一起摆动，显然这是一个平面力系。
根据这个坐标进行导线的受力分析，可建立导线的悬链线方程。
我们先从局部受力分析开始，再找出其一般规律。
首先在导线上任取一点D（x,y），然后分析OD段导线的受力关系，由图2－5所示，此OD段导线受三个力而保持平衡，其中D点承受拉力为T x=σx S，它与
导线曲线相切，与x轴夹角为α； O点承受拉力为T0=σ0S，T0为导线O点的切线方向，恰与x轴平行，故又称水平张力；此外还有OD段导线自身的荷载为G=gSL
x，其中L x为OD段导线的弧长。
将OD段导线的受力关系画为一个三角形表示，如图2－6所示，
图2-6 导线受力情况
由静力学平衡条件可知，在平面坐标系中，其水平分力，垂直分力的代数和分别等于零。
或沿x轴或y轴上分力代数和分别等于零。
垂直方向分力G=T x sinα=gSL x;水平方向分为T0=T x cosα=σ0S。
其中σ0、T0为导线最低点的应力和张力，σx、T x为导线任一点的应力和张力，S、g为导线截面和比载。
将上述二式相比，则可求得导线任意一点D 的斜率为：
(2-10)
由微分学知识可知，曲线上任一点的导数即为切线的斜率。
式（2－10）是悬链曲线的微分方程。
我们要用坐标关系表示出导线受力的一般规律，还需要将不定量L x消去，因此，将式对x微分得：
（微分学中弧长微分公式为dS2=(dx)2+(dy)2）将上式移项整理后，两端进行积分
这是个隐函数，因此，再进行分离变量积分，查积分公式有：
（2－11）
再进行分离变量积分，有
于是，导线任一点D的纵坐标为：
（2－12）
式（2－12）是悬链方程的普通形式，其中C1和C2为积分常数，其值可根据取坐标原点的位置及初始条件而定。
如果将坐标原点于导线最低点处，则有下述初始条件：
x=0, dy/dx=tgα=0
代入式（2－11）则C1＝0，将x=0,y=0,C1＝ 0 代入式（2－12），，如此，求得坐标原点最低点O处的悬链方程为：
（2－13）
式中σ0—水平应力(即导线最低点应力)，MPa;
g—导线的比载，N/m.mm2。
当坐标原点选在其它点（例如选在悬挂点处）时，悬链线方程的常数项将有所不同，可以得到不同的公式。
若式（2－13）中x代表档距的时候，则y即为导线的弧垂，因此悬链线方程描述了导线弧垂与应力、比载及档距之间的基本关系，此式称为精确式。
实际上导线的悬链线方程还可以从另一种方式进行推导,下面介绍如下：
由式,对其求导得：
变换为,为找原函数进行积分,
由积分式两边积分，
则有：变为指数形式为
这是个隐函数，为解出，对应有式：
将两式相减则有：
因为双曲正弦函数为：
双曲余弦函数为：
又因为：
最后积分有：
定积分常数,因在坐标原点则，其结果是一样的，即
在线路设计中，为了计算上的方便，一般不使用精确式方程，而是将其展开为泰勒级数形式。
将悬链线方程式（2－13）展开成无穷级数（在x=0点），可得：
（2－14）
2．曲线弧长（或弧长方程）
导线最低点O至任一点的曲线长度叫做弧长，用Lx表示。
将式（2－11）代入式（2－10）中，且积分常数C1＝0，得导线的弧长方程为
（2－15）
根据式（2－15）可以计算一个档距内导线的曲线长度（也叫一档线长）将弧长方程式（2－15）展开成无穷级数可得：
（2－16）
一质量均匀分布的绳两端悬挂时绳子所表示的曲线为悬链线。
关于悬链线解析方程的求解，我很早就知道其方程为双曲余弦函数。
然而当时数学水平尚未满足要求。
后来学会关于双曲函数的相关内容后，又由于坚信绳中张力处处相等而推出悖论，本研究就此搁浅。
直到7
月初，我又想起了该曲线的方程求解问题。
需要说明的一点是，绳中张力处处相等要求绳子无质量、绷紧，对于悬链显然不适用。
但受力方向沿着绳是正确的，所以必须结合力的方向来求解。
假设一个无限长的质量均匀分布的绳子在重力作用下自然下垂。
设绳底端受到拉力为T0，线密度为ρ，重力加速度g。
如图所示建立直角坐标系，设绳对应的函数为y=f(x)
对于横坐标从0至x这一段的绳，设质量为m，长度L，受重力为G，受顶端拉力大小为T，该力倾斜角为θ
该段绳受三力平衡：T、G、T0，画出受力示意图，有G/T0=tanθ
由导数的几何意义，tanθ=dy/dx，而G=mg=ρgL，故ρgL/T0=dy/dx，ρgL=T0*dy/dx
对上式取微分，得ρg*dL=T0*d2y/dx，而dL=(dx2+dy2)1/2=[1+(dy/dx)2]1/2*dx，代入得
ρg[1+(dy/dx)2]1/2=T0*d2y/dx2=T0*d(dy/dx)/dx，令dy/dx=P，则
ρg(1+P2)1/2=T0*dP/dx，ρg/T0*dx=dP/(1+P2)1/2
对两侧取积分得∫ρg/T0*dx=∫dP/(1+P2)1/2
ρgx/T0=sinh-1P+C1，P=sinh(ρgx/T0-C1)，dy/dx=sinh(ρgx/T0-C1)
当x=0时，dy/dx=0，代入得sinh(-C1)=0,C1=0，故dy=sinh(ρgx/T0)*dx
再次积分，得y=T0/ρg*cosh(ρgx/T0)+C2
当x=0时，y=0，故0=T0/ρg*cosh0+C2,C2=-T0/ρg
设k=T0/ρg，则y=kcosh(x/k)-k，若只考虑其形状可忽略常数项，故悬链线方程为
y=kcosh(x/k)-k，其中k=T0/ρg
关于双曲函数的一些说明：双曲正弦函数sinhx=(e x-e-x)/2，双曲余弦函数coshx=(e x+e-x)/2由其定义可得d(sinhx)/dx=coshx，d(coshx)/dx=sinhx，cosh2x-sinh2x=1
其反函数分别为反双曲正弦函数sinh-1x=ln[x+(x2+1)1/2]，反双曲余弦函数
cosh-1x=ln[x+(x2-1)1/2]
涉及的一步积分：在∫dP/(1+P2)1/2中，令P=sinht
∫dP/(1+P2)1/2=∫d(sinht)/(1+sinh2t)1/2=∫cosht*dt/cosht=∫dt=t+C=sinh-1P+C
（注：专业文档是经验性极强的领域，无法思考和涵盖全面，素材和资料部分来自网络，供参考。
可复制、编制，期待你的好评与关注）。