一元一次方程解法复习课程
一元一次方程(复习课教案)

一元一次方程(单元复习课)【复习目标】1.系统了解一元一次方程的知识框架;2.知道解一元一次方程的步骤,熟练掌握一元一次方程的解法;3.知道列一元一次方程解应用题的步骤,会列方程解应用题;4.在小组合作交流的过程中培养学生学习数学的习惯和复习的方法.【复习重点】形成一元一次方程章节知识框架图.【活动设计】活动一、一元一次方程知识复习1.(1)已知关于x 的方程150k x -+=是一元一次方程,则k = .(2)已知关于x 的方程()250k x -+=是一元一次方程,则k .(3)已知关于x 的方程()1250k k x --+=是一元一次方程,则k = .说明:本题引导学生回忆一元一次方程的概念.2.已知3x =是关于x 的方程8203x a -=的解,则a = . 说明:本题引导学生回忆方程的解的概念.3.下列运用等式的性质进行的变形,不正确...的是( ) A.如果a b =,那么55a b +=+ B.如果a b =,那么ma mb =C.如果a b =,那么a b c c = D.如果a b c c=,那么a b = 说明:本题引导学生回忆等式的性质. 4.若2260x y --=,则2635y x --的值为 .说明:本题引导学生回忆方程的解的概念.5.解方程:211135x x ++-=. 说明:本题引导学生回忆解一元一次方程的步骤,及每一步骤的注意点. 6.如果方程()()322212x x ---=-也是关于x 的方程203m x --=的解,求m 的值. 说明:本题引导学生回忆方程的解的概念.【课堂小结】(1)一元一次方程、方程的解的概念?等式的基本性质?(2)解一元一次方程的步骤有哪些?每一步骤变形的依据是什么?活动二、利用一元一次方程知识解决实际问题思考:我们在这一章中重点学习了哪几种类型的应用题?(1)引导学生回忆类型:调配问题、行程问题、工程问题、数字问题、方案问题、盈亏问题; (2)引导学生回忆典型问题中的数量关系:如行程问题中:速度、时间、路程的关系;工程问题中:工作效率、工作时间、工作总量的关系;工作效率、工作时间、工作人数、工作总量之间的关系.盈亏问题中:利润=售价—进价=进价×利润率折数售价=标价×10……解决下列问题:1.某种长方体包装盒的表面展开图如图所示,如果该长方体包装盒的长比宽多4cm,求这种长方体包装盒的体积.2.小王逛超市看到如下两个超市的促销信息:(1)当一次性购物标价总额是300元时,甲乙超市实际付款分别是多少?(2)当标价总额是多少时,甲、乙超市实付款一样?(3)小王两次到乙超市分别购物付款198元和466元,若他只去一次该超市购买同样多的商品,可以节省多少元?【课堂小结】列方程解应用题的步骤?教师总结:审.题,设.未知数,列.方程,解.方程,检验.,写出答.案.“审”是关键,“验”是保证,“设、列、解、答”是过程.附:板书设计:。
一元一次方程解法的复习课市公开课一等奖省优质课获奖课件

2
1 x 0.2
第6页
1、 x取何值时,2x-3与-5x+6值
(1)相等
x
9
7
(2)互为相反数
x 1
2x-3=-5x+6 (2x-3)+(-5x+6)=0
第7页
2、方程13-5(4x-3)=8(4x-3)
解是x=____1.
13 5A 8A
第8页
3、解方程: 1 [1 (x 1) 1] 1 22
第12页
第9页
右图是一个长方形,被分隔成6个正方形, 已知中间最小一个正方形边长为1, 正方 形F边长为6,那么这个大长方形面积是多 少?
FB
A
E DC
第10页
第11页
必做题:书上124页 目标与评定 1-7 题 选做题(每日一题): 已知p、q都是质数,而且以x为未 知数一元一次方程px+5q=97解是 x=1,求代数式40p+101q+4值
第3页
甲、乙两位同学对,都正确吗?
甲做法: 方程两边同乘以24,得
乙做法:
6(1 2x) 214 4(1 x) 方程两边同乘以12,得 3(1 2x) 121 2(1 x)
第4页
解方程:
1 (2x 3) x 5
3
37
第5页
解方程:1 2x 0.5
老师将出示10张写有代数式和符号 卡片,请选取其中部分卡片结构任 意你想要方程.
2x y2 1 2x y 5(x 1)
x
6 2
第2页
解方程 5(x 1) 2x 6
解:去括号,得 5x+5=2x+6
移项,得 5x 2x 6 5
合并同类项,得 3x 1
一元一次方程的概念与解法(复习)
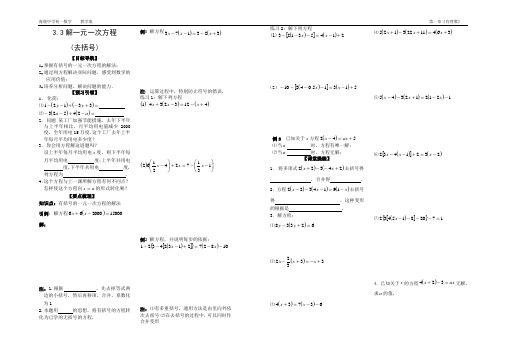
3.3解一元一次方程(去括号)【目标导航】1.掌握有括号的一元一次方程的解法;2.通过列方程解决实际问题,感受到数学的应用价值;3.培养分析问题、解决问题的能力.【预习引领】1. 化简:⑴()()=+-+--33121y y ⑵()()=-+--a a 24523 2.问题 某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度.这个工厂去年上半年每月平均用电多少度? 3.你会用方程解这道题吗?设上半年每月平均用电x 度,则下半年每月平均用电 度;上半年共用电 度,下半年共用电 度. 列方程为 . 4.这个方程与上一课所解方程有何不同点?怎样使这个方程向a x =的形式转化呢?【要点梳理】知识点: 有括号的一元一次方程的解法引例:解方程()15000200066=-+x x 解:注:1.根据 ,先去掉等式两边的小括号,然后再移项、合并、系数化为12.本题用 的思想,将有括号的方程转化为已学的无括号的方程.例1 解方程()()323173+-=--x x x注:运算过程中,特别防止符号的错误. 练习1:解下列方程()()()41232341+-=-+x x x()⎪⎭⎫ ⎝⎛--=+⎪⎭⎫ ⎝⎛-1317242162x x x例2 解方程,并说明每步的依据:()[]{}()1082721324321--=+---x x注:⑴有多重括号,通用方法是由里向外依次去括号.⑵在去括号的过程中,可以同时作合并变形.练习2:解下列方程(1)()[]()21453123+-=---x x(2)()[]()51315.04210+-=----x x例3 已知关于x 方程()542+=-ax x ⑴当a 时,方程有唯一解; ⑵当a 时,方程无解;【课堂操练】 1. 将多项式()()24322+--+x x 去括号得 ,合并得 . 2.方程()()()x x x -=---1914322去括号得 ,这种变形的根据是 . 3.解方程: ⑴()62338=+-y y ⑵()33322+-=+-x x x⑶()()63734--=+x x⑷()()()36411223125+=+-+x x x⑸()()()121212345--=+--x x x⑹()[]()2321432-=+--x x x⑺()[]{}1720815432=----x4.已知关于x 的方程()ax x =-+324无解,求a 的值.【课后盘点】1.若关于x 的方程b x x a 3746-=+的解是1=x ,则a 和b 满足的关系式是 . 2.当=x 时,式子()23-x 和()434-+x 的值相等.3.比方程()472=+x 的解的3倍小5的数是 . 4.已知公式()h b a S +=21中,60=S ,6=a ,6=h ,则=b .5.化简下列各式⑴()()223248y xy y xy +-+---⑵()[]a b a b a +----22⑶()[]()y x y x +----25⑷()[]152322+---x x x x6.方程()113=--x x 的根是( ) A .2=x B .1=x C .0=x D .1-=x 7.下列去括号正确的是( )A .()1123=--x x 得4123=--x xB .()x x =++-314得x x =++-344C .()59172+-=-+x x x 得59772+-=--x x x D .()[]21423=+--x x 得24423=++-x x8.解下列方程 ⑴()212-=--t⑵()()32523-=+x x⑶()()23341+=+-x x⑷()()x x x 3234248--+=+⑸()()()x x x -=---1914322 ⑹()x x 415126556=-⎥⎦⎤⎢⎣⎡++9.已知关于x 的方程()3245-=-x ax 无解,求a 的值.10.若x A 34-=,x B 45+=,且B A 3202+=.求x 的值.【课外拓展】1.已知关于x 的方程()251-=-x x m 有唯一解,求m 的值.2.已知关于x 的方程()()b x a x a 3512+-=-有无数多个解,求a 、b 的值.3.三年前父亲的年龄是儿子年龄的4倍,三年后父亲的年龄是儿子年龄的3倍,求父子两人现在的年龄各是多少岁?(设计人:江云桂)No .4一元一次方程的概念与解法(复习)【目标导航】1.复习一元一次方程的概念、等式的性质、一元一次方程的解法;2.能根据题意列一元一次方程解决实际问题;【预习引领】1. 方程,一元一次方程,方程的解; 2. 等式性质;3. 解一元一次方程的步骤及每一步的依据。
一元一次方程的解法复习课件公开课

移项,得:8 x - 10 x - 6 x = -3 - 1 + 4 - 1
合并同类项,得: - 8x = -1
化系数为1,得: x
=
1 8
判断
3、下列方程变形有没有错,若错, 错在哪里?
4方程:3z - 4 - 3.5 = 0.01- 3z ,
0.02
0.03
去分母得:
3003z - 4- 350 6 = 200(0.01 - 3z)
(1)5y+8=9y移项得5y-9y=8; (2)2x+3=x-1移项得2x-x=3-1; (3)3x-12-2x=4x-3移项得 3x-2x+4x=-12-3.
判断
2、下列方程变形有没有错,若错,错在哪里?
(1)5(y+8)-2 =4y 去括号得 5y+8-2=4y; (2)2x-3(3x-2)=x-1 去括号2x-9x-2=x-1;
3、去分母时(1)勿漏乘不含分母的 项(2)分子是多项式时,去掉分母要 添上括号
4、勿跳步,勿忘判断符号,常检验
比一比,谁正确 解方程
15x - 1- 3 + 2x = 7
2y - y -1 = 2 - y + 3
2
4
3 2 y +1 + 10 y +1 = 1- 1- 2 y
4
6
3
(4) 1 (x +15) = 1 - 1 (x - 7)
5
23
(5) x + 5 - x + 5 = x + 3 - x - 2
5
32
(6) 2x - 1.6 - 3x = 31x + 8
0.3 0.6
3
拓展:
第五章一元一次方程及其解法专题复习(教案)

3.成果展示:每个小组将向全班展示他们的讨论成果和实验操作的结果。
(四)学生小组讨论(用时10分钟)
1.讨论主题:学生将围绕“一元一次方程在实际生活中的应用”这一主题展开讨论。他们将被鼓励提出自己的观点和想法,并与其他小组成员进行交流。
2.引导与启发:在讨论过程中,我将作为一个引导者,帮助学生发现问题、分析问题并解决问题。我会提出一些开放性的问题来启发他们的思考。
3.成果分享:每个小组将选择一名代表来分享他们的讨论成果。这些成果将被记录在黑板上或投影仪上,以便全班都能看到。
(五)总结回顾(用时5分钟)
今天的学习,我们了解了一元一次方程及其解法的基本概念、重要性和应用。同时,我们也通过实践活动和小组讨论加深了对这些知识点的理解。我希望大家能够掌握这些知识点,并在日常生活中灵活运用。最后,如果有任何疑问或不明白的地方,请随时向我提问。
五、教学反思
在本次一元一次方程及其解法专题复习的教学中,我注意到几个关键点。首先,学生们在理解方程的概念和解法上普遍表现良好,他们能够迅速掌握基本的代入法、消元法等解法技巧。然而,我也发现,当涉及到将实际问题抽象成方程模型时,部分学生感到困惑。这让我意识到,我们需要在今后的教学中加强对这类问题的训练,帮助学生建立起实际情境与数学模型之间的联系。
在讲授重点难点时,我发现通过具体的案例分析和逐步解题过程,学生们的理解程度有所提高。但是,我也发现个别学生在面对复杂题目时,仍然难以独立解题。这提示我,可能需要在课后提供更多的辅导和练习机会,让学生有更多的机会巩固所学知识。
一元一次方程复习教案设计

一元一次方程复习教案设计一、教学目标1. 知识与技能:(1)理解一元一次方程的概念及其一般形式;(2)掌握一元一次方程的解法,包括加减法、乘除法、换元法等;(3)能够应用一元一次方程解决实际问题。
2. 过程与方法:(1)通过复习,巩固一元一次方程的基本概念和解法;(2)培养学生运用一元一次方程解决实际问题的能力;(3)提高学生自主学习、合作交流、归纳总结的能力。
3. 情感态度与价值观:(1)培养学生对数学的兴趣和自信心;(2)培养学生勇于探究、积极思考的精神;(3)培养学生合作交流、归纳总结的良好习惯。
二、教学内容1. 一元一次方程的概念及其一般形式;2. 一元一次方程的解法,包括加减法、乘除法、换元法等;3. 应用一元一次方程解决实际问题。
三、教学重点与难点1. 重点:一元一次方程的概念及其一般形式,一元一次方程的解法;2. 难点:一元一次方程的解法在实际问题中的应用。
四、教学过程1. 复习导入:(1)回顾一元一次方程的概念及其一般形式;(2)引导学生回忆一元一次方程的解法。
2. 课堂讲解:(1)讲解一元一次方程的解法,包括加减法、乘除法、换元法等;(2)通过例题演示和解题思路分析,让学生熟练掌握一元一次方程的解法;(3)引导学生运用一元一次方程解决实际问题,如购物问题、行程问题等。
3. 课堂练习:(1)设计具有代表性的练习题,让学生独立完成;(2)引导学生相互讨论、交流解题思路,培养合作精神;(3)对学生的练习结果进行点评,及时纠正错误,巩固知识点。
4. 归纳总结:(1)引导学生总结一元一次方程的概念、解法及实际应用;(2)强调一元一次方程在实际生活中的重要性;(3)鼓励学生在日常生活中发现和提出一元一次方程问题。
五、课后作业1. 请列出五个一元一次方程,并求解;2. 选择一个实际问题,运用一元一次方程进行解答;3. 总结一元一次方程的解法,并谈谈自己在解决实际问题中的心得体会。
教学评价:通过课后作业的完成情况,了解学生对一元一次方程的掌握程度及实际应用能力。
一元一次方程的解法复习课课件

含有未知数的等式叫做方程 定记得!)
(1)一元:只含有一个未知数
(2)一次:未知数的最高次数是一次 (3)方程的两边都是整式 3、什么是方程的解? 方程的解是指能使方程 左右两边相等的未知数 的值。
挑战记忆
4.等式的性质:
1在下列各式中?
(1) 5x=0 (2)1+3x
1 4x (5) x
挑战记忆
(3)y² =4+y
(4)x+y=5
(6) 3m+2=1–m
其中方程有( 5 )个,一元一次方程有( 2 )个
2.若关于x的方程
2x
2 m 3
2 m 0 是一元一次方程,则m=_____
3、若x=-3是方程x+a=4的解,则a的 值是 7 .
火眼金睛
下面方程的解法对吗?若不对,请改正 。 解方程
3x 1 4x 1 1 3 6
不对
去分母得 去括号,得
解:去分母,得
2(3x 1) 1 4 x 1
6 x 2 1 4 x 1
2(3x 1) 6 (4 x 1)
6x 2 6 4x 1
6x 4x 6 1 2
10 x 9
合并同类项
系数化为1
即 学 即 练 解下列方程
(1) 2(x+3)-5(1-x)=3(x-1)
2x 1 x 2 (2) 1 3 2
3 y 12 5y 7 (3) 2 4 3
简单应用1
简单应用2
简单应用3
拓展提升1
拓展提升2
9 x 10
去括号,得
移项,得
6 x 4 x 1 1 2
一元一次方程复习课教学设计(正确的)房友营

一元一次方程复习课一元一次方程单元测试卷一、选择题1. 已知下列方程:①22x x-=; ②0.31x =; ③512x x =+; ④243x x -=;⑤6x =;⑥20x y +=.其中一元一次方程的个数是 ( ).A .2B .3C .4D .52.已知关于x 的方程5(21)a x a x +=-+的解是1x =-,则a 的值是 ( ). A .-5 B .-6 C .-7D .83.方程3521x x +=-移项后,正确的是 ( ). A .3251x x +=-B . 3215x x -=-+C .3215x x -=-D . 3215x x -=--4.方程2412332x x -+-=-,去分母得 ( ). A .22(24)33(1)x x --=-+ B . 123(24)183(1)x x --=-+ C .12(24)18(1)x x --=-+ D . 62(24)9(1)x x --=-+5.甲、乙两人骑自行车同时从相距65 km 的两地相向而行,2小时相遇,若甲比乙每小时多骑2.5 km ,则乙的时速是 ( ). A .12.5 km B .15 km C .17.5 km D .20 km6.某商店卖出两件衣服,每件60元,其中一件赚25%,另一件赔25%,那么这两件衣服售出后商店是 ( ).A .不赚不赔B . 赚8元C .亏8元D . 赚15元 7.如果等式ax=bc 成立,则下列等式成立的是( D ) A .abx=abc ; B .x= bca; C .b-ax=a-bc D .b+ax=b+bc8.某种商品的标价为120元,若以九折降价出售,相对于进货价仍获利20%,该商品的进货价为( C )。
A .80元;B .85元;C .90元 ;D .95元 二.填空题9.使(1)60a x --=为关于x 的一元一次方程的a =______(写出一个你喜欢的数即可). 10.当m =______ 时,式子273m -的值是-3. 11.若3122m xy -与224n x y 在某运算中可以合并,则_____m =,_____n =.12.设某数为x ,根据下列条件列出方程: (1)某数的23比它的相反数大5.______________________________; (2)某数的13与12的差刚好等于这个数的2倍.________________________. 13.某次数学竞赛共出了15道选择题,选对一题得4分,选错一题扣2分.若某同学得36分,他选对了________道题(不选算错).14.某商场对某种商品作调价,按原价8折出售,此时商品的利润率为10%,此商品的进价是1000元,则商品的原价是________.15.某人将1000元存入银行,定期两年,若年利率为2.27%,则两年后利息为________元,若扣除20%的利息税,则实际得到的利息为________元,银行应付给该储户本息共____________元.16. 根据你们班男、女生人数编一道应用题:_________________________________________________________________ _______________________________________.假设适当的未知数,列出方程 _______________________________________.17.国家规定个人发表文章、出版图书获得稿费的纳税计算办法是:⑴稿费不高于800元的不纳税;⑵稿费高于800元,又不高于4000元,应纳超过800元的那一部分稿费14%的税;⑶稿费高于4000元,应缴纳全部稿费的11%的税。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解:设船在静水中的平均速度为x km/h,则顺流 的速度为(x+3) km/h,逆流速度为(x-3) km/h.
根据顺流速度_×__顺流时间_=__逆流速度 _×__逆流时间
列出方程,得 2 ( x + 3 )ቤተ መጻሕፍቲ ባይዱ= 2.5 ( x - 3 )
去括号,得 2x+ 6= 2.5x- 7.5
移项及合并同类项,得 0.5x=13.5
练一练
解下列方程 (1) 6x =-2(3x-5) +10; (2) -2(x+5)=3(x-5)-6
解: (1) 6x=-2(3x-5)+10 6x=-6x+10+10
(2) -2(x+5)=3(x-5)-6 -2x-10=3x-15-6
6x +6x=10+10
-2x-3x=-15-6+10
12x=20
合并同类项
注意:(1)为什 么同乘各分母 的最小公倍数6; (2)小心漏乘, 记得添括号
16x 7
系数化为1
x 7 16
典例精析
例1.解下列方程:
(1)x1122x
2
4
解:去分母(方程两边乘4),得
2(x+1) -4=8+ (2 -x)
去括号,得
2x+2 -4=8+2 -x
移项,得
2x+x =8+2 -2+4
接近“x =a”的形式.
典例精析
例1 解方程 3 x73 2 2x.
解:移项,得
3x2x327.
合并同类项 ,得
5x 25.
系数化为1,得
x 5.
移项实际上是利用等 式的性质1,但是解 题步骤更为简捷!
移项时需要移哪些项?为什么?
练一练
1.下列移项正确的是( C ) A.由2+x=8,得到x=8+2 B.由5x=-8+x,得到5x+x= -8 C.由4x=2x+1,得到4x-2x=1 D.由5x-3=0,得到5x=-3
2.去分母时要注意什么问题?
3x123x22x.
2
10 5
去分母(方程两边同乘 各分母的最小公倍数)
5 ( 3 x 1 ) 1 0 2 ( 3 x 2 ) 2 ( 2 x 3 )
去括号
1 5 x 5 2 0 3 x 2 4 x 6
移项
1 5 x 3 x 4 x 2 6 5 2 0
例1 解下列方程:
( 1 )2 x - (x + 1 0 ) = 5 x + 2 (x - 1 )
解:去括号,得
2 x - x - 1 0 = 5 x + 2 x - 2 .
移项,得 2 x - x - 5 x - 2 x = - 2 + 1 0 .
合并同类项,得
6x=8.
系数化为1,得 x= - 4 . 3
一元一次方程解法
练一练
解下列方程:
1 5x2x9
解:(1)合并同类项,得
3x9
系数化为1,得
x3
2 1x3x7
22
(2)合并同类项,得
2x7
系数化为1,得
x 7 2
二 根据“总量=各部分量的和”列方程解决问题
例2.有一列数,按一定规律排列成1,-3,9,-27,
81,-243 ,···.其中某三个相邻数的和是-1701,
系数化为1,得
x 27.
答:船在静水中的平均速度为 27 km/h.
做一做
一架飞机在两城之间航行,风速为24 km/h,顺风
飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中
的速度为(x+24) km/h ,在逆风中的速度为(x-24) km/h.
当堂练习
1.解下列一元一次方程:
(1)72x34x (2)1.8t300.3t
(3)1x13x 2
(4)5x411x8 3 33 3
答案:(1) x=-2 (2) t=20
(3) x=-4 (4) x=2
2.有一人问老师,他所教的班级有多少学生,老师说: “一半学生在学数学,四分之一的学生在学音乐,七 分之一的学生在学外语,还剩六位学生正在操场踢足 球.”你知道这个班有多少学生吗?
2. 去括号: (1) a + (– b + c ) = a-b+c (2) ( a – b ) – ( c + d ) = a-b-c-d (3) – (– a + b ) – c = a-b-c (4) – (2x – y ) – ( – x2 + y2 ) = -2x+y+x2-y2
典例精析
合并同类项,得
x 5 3
-5x=-11 x 11 5
二 去括号解方程的应用
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从 乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度 是3 km/h,求船在静水中的速度?
分析:等量关系:这艘船往返的路程相等,即 顺流速度_×__顺流时间_=__逆流速度_×__逆流时间
这三个数各是多少?
解:设所求的三个数分别是 x,3x,9x
由三个数的和是-1701,得
后面一个数 是前面一个 数乘以-3
x 3 x 9 x 1 7 0 1 .
合并同类项,得 7x1701.
系数化为1,得 x243.
3x 729,
9x 2187.
答:这三个数是 -243, 729,-2 187.
➢移项定义 一般地,把方程中的某些项改变符号 后,从方程的一边移到另一边,这种变形叫做移项.
注:移项要变号
4x –15 = 9
2x = 5x – 21
4x = 9 +15 ➢移项目的
2x –5x = – 21
一般地,把所有含有未知数的项移到方程的左边, 把所有常数项移到方程的右边,使得一元一次方程更
根据题意,得 17(x+24)=3(x-24) 6
解得
x=840.
两城市的距离为 3(8 4 0 - 2 4)= 24 4 8 .
答:两城市之间的距离为2 448 km.
讲授新课
一 解含分母的一元一次方程
合作探究
解方程:3x123x22x.
2
10 5
想一想 1.若使方程的系数变成整系数方程,方程 两边应该同乘以什么数?
答案:这个班有56个学生.
去括号法则: 去掉“+( )”,括号内各项的符号不变. 去掉“–( )”,括号内各项的符号改变.
用三个字母a、b、c表示去括号前后的变化规律:
a+(b+c) = a+b+c a–(b+c) = a–b–c
讲授新课
一 利用去括号解一元一次方程
合作探究
1.利用乘法分配律计算下列各式: (1) 2(x+8)= 2x+16 (2) -3(3x+4)= -9x-12 (3) -7(7y-5)= -49y+35
