北航高数期末考试试题43页PPT
北航高数07-08试题 答案

sin x
x3
lim x0
2 x2 cos x 2 sin2 x 3x2
2[1 1 x2 o( x2 )] [1 1 x2 o( x2 )] 2[1 1 x2 o( x2 )]
lim
2
x0
2
2
3x2
2
6
4
四、求导数(每小题5 分, 共 10 分)
x0 )
f
(1 2!
) (0
x0
)2
,1
(0,
x0
),
f (1)
f (x0 )
f ( x0 )(1
x0 )
f (2 ) (1 2!
x0 )2 ,2 ( x0 ,1),
于是f
(1
)
2 x2
,
0
f
( 2
)
(1
2 x0
)2
.
故 min{ 0 x1
f
( x)}
min{
f
(1 ),
f
(2 )}
min {
0 x01
2 x2
0
,
(1
2 x0 )2
}
8.
13
高等数学期末考试试题 2008-1-24
一、填空(每小题 4 分,共 20 分)
11
1. lim x sin cos __________.
x
xx
2. 1 (sin 5 x 1 x 2 )dx 1
.
3.曲线 y 2 ( x )3 (0 x 1) 的弧长为
.
3
2-习题课 北京航空航天大学高等数学期末模考复习
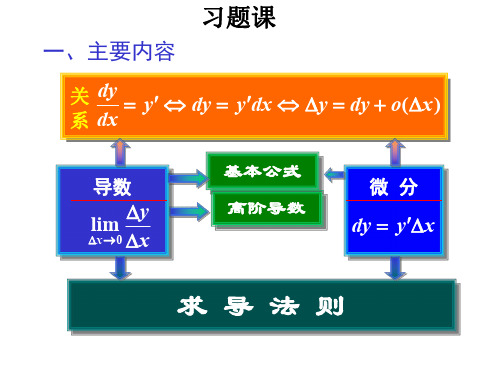
x
y
(1 ln y) y ln x 1,
y
ln x 1 ln
1 y
,
1 (ln y 1) (ln x 1) 1 y
y x
y (1 ln y)2
y(ln y 1)2 x(ln x 1)2 xy(ln y 1)3
例5 设f ( x) x x( x 2) ,求 f ( x).
f (x0 ) x0
lim
x 0
f (x0
x) x
f (x0 );
2.右导数:
f( x0 )
lim
x x0 0
f (x) x
f (x0 ) x0
lim
x 0
f (x0
x) x
f (x0 );
函数 f ( x)在点 x0处可导 左导数 f( x0 )和右 导数 f( x0 )都存在且相等.
(C)a 1, b 0; (D)a 0, b 1.
6、已知函数 f ( x)具有任意阶导数,且
f ( x) f ( x)2,则当n为大于 2 的正整数时,
f ( x)的 n 阶导数 f (n) ( x)是( )
(A)n![ f ( x)]n1;
(B) n[ f ( x)]n1;
(C) [ f ( x)]2n;
习题课
一、主要内容
关 系
dy y dy ydx y dy o(x)
dx
导数
lim y x0 x
基本公式 高阶导数
微分
dy yx
求导法则
1、导数的定义
定义
y
xx0
lim y x0 x
lim
x0
f
(x0
x) x
f
(x0
4-1不定积分 北京航空航天大学高等数学期末模考复习

5、若 f ( x)在某区间上______,则在该区间上 f ( x)的
原函数一定存在;
6、 x xdx ______________________;
7、
dx x2
x
_______________________;
8、 ( x 2 3x 2)dx _________________;
9、 ( x 1)( x 3 1)dx _____________;
显然,求不定积分得到一积分曲线族.
由不定积分的定义,可知
d
dx
f (x)dx
f
( x),
d[ f (x)dx] f (x)dx,
F ( x)dx F ( x) C , dF ( x) F ( x) C .
结论:微分运算与求不定积分的运算是 的.
二、 基本积分表
实例
x 1
1
6、 2
x
5 2
C;
7、
2
x
3 2
C;
5
3
8、 x 3 3 x 2 2 x C ; 32
9、 x 3
2
5
x2
2
3
x2
x
C、
35 3
10、2
x
4
3
x2
2
5
x2
C.
35
二、1、 x arctan x C ; 3、 x sin x C ; 2 5、4( x 2 7) C ; 74 x
5
解 x2 xdx x 2dx
根据积分公式(2)
x dx
x 1
1
C
51
x2 51
C
2 7
7
x2
C.
航空航空数学期末考试试题及答案

航空《航空数学》期末考试试题及答案基本信息:[矩阵文本题] *1. 下列语句是命题的是(). [单选题] *A. 4大于3吗?B. 请关门C. x大于yD. 4>3(正确答案)2. 下列命题是真命题的是() [单选题] *A. 正方形是矩形,且正方形是菱形(正确答案)B. -1<0,且-1是正数C. π>3,且π是有理数D. 3是偶数,且2是奇数3. 下列命题是假命题的是() [单选题] *A. 5>4,或5=4B. 5>5,或5=5C. 5<4,或5=4(正确答案)D. 实数a的绝对值等于a或-a.4.下列命题不是简单命题的是() [单选题] *A. 5>4B. 5=5C. 5<4D. 4≤5(正确答案)5. 下列不是复合命题的联结词的是() [单选题] *A. 且B. 或C. 不是D. 联结(正确答案)6. 当p为真,q为假时,下列复合命题是真命题的是() [单选题] *A. p且qB. p或q(正确答案)C. 非pD. 以上都不是7. 设p和q是两个命题,如果p q,那么称p是q的()[单选题] *A. 充分条件(正确答案)B. 必要条件C. 充分必要条件D.等价条件8. ab>0是a>0且b>0的() [单选题] *A. 充分条件B. 必要条件(正确答案)C. 充分必要条件D.等价条件9. (1) 如果p,那么q;(2) 如果q,那么p,则(2)叫做(1)的() [单选题] *A. 逆命题(正确答案)B. 否命题C. 逆否命题D.假命题10.如果原命题是真,下列正确的是() [单选题] *A. 逆命题一定真B.否命题一定假C. 逆否命题一定真(正确答案)D.逆命题一定假11. (1) 如果p,那么q; (2) 如果非q,那么非P。
则 (2)叫做(1)的() [单选题] *A. 逆命题B. 否命题C. 逆否命题(正确答案)D.假命题12. (1) 如果p,那么q; (2) 如果非p,那么非q; 则 (2)叫做(1)的() [单选题] *A. 逆命题B. 否命题(正确答案)C. 逆否命题D.假命题13. 若植树这件事的算法表示为:挖坑→栽树苗→填土→浇水,这种算法结构为() [单选题] *A. 顺序结构.(正确答案)B. 条件结构C. 循环结构.D.模块结构14.不属于算法的三种结构的是() [单选题] *A. 顺序结构.B. 条件结构C. 循环结构.D.模块结构(正确答案)15.有关数组,下列叙述不正确的是() [单选题] *A. 两个数组之和即两个数组的对应分量相加,得到的新数组B. 两个数组之差即两个数组的对应分量相减,得到的新数组C. 数组中分量的个别数叫做数组的维数D. 数组的加、减运算的维数不必相同.(正确答案)16. 有关数乘,下列说法不正确的是() [单选题] *A. 数乘就是一个实数乘一个数组B.数乘的法则就是把实数分别与分量相乘C.数乘后还是一个数组D.数乘后数组的维数会改变.(正确答案)17.有关数组的内积,下列说法正确的是() [单选题] *A. 内积即是数乘,即一个实数与数组的乘积B. 不同维数的数组可以求内积C. 两数组的内积还是一个数组D.内积的结果是一个实数(正确答案)18.对编制计划的理解下列不正确的是() [单选题] *A.编制计划就是对工作进行合理的安排B. 一个合理的计划不需考虑工期。
20030121_北京航空航天大学高等数学期末试题 含答案

C. 不存在;D. 存在性与n有关
2. 下列广义积分中,收敛的是_A__.
A.
1
1
1 dx ; 1 x2
B.
1
ex x2
dx
;
C.
1 x3
dx
;
D.
1 0
1
dx .
x ln(1 x)
1
3.
设f
(x)
1
2e x
1
arctan
1 x
,则x
0是f
( x)的 _B_间断点
1 ex
A. 可去; B. 跳跃;C. 无穷;D. 振荡.
2. 下列广义积分中,收敛的是___.
A.
1
1
1 dx ; 1 x2
B.
1
ex x2
dx
;
C.
1 x3
dx
;
D.
1 0
1
dx .
x ln(1 x)
1
3.
设f
(x)
1
2e x
1
arctan
1 x
,则x
0是f
( x)的 __间断点
1 ex
A. 可去; B. 跳跃;C. 无穷;D. 振荡.
高等数学
________ .
二.单项选择 (每小题4分,共20分)
高等数学
1. 设 lim f ( x)不存在,lim g( x) A 0,n为正整数,
x x0
x x0
则 lim [ f ( x)]n ____ . A. 存在; B. 存在性与n无关; xx0 g( x)
C. 不存在;D. 存在性与n有关
C .依赖于t和x,不依赖于s. D.依赖于s,不依赖于t.
第一学期期末复习4 北京航空航天大学高等数学期末模考复习
向量 1. 定义及表示;
2. 计算 向量的模; 向量加减、数乘、向量积、数量积;
向量夹角,方向余弦;平行两来自量的条件;垂直
三向量共面的条件;
例:期末模拟题1 二5;期末模拟题2 一5;期末 模拟题3一5;2008一5
空间解析几何 直线夹角公式;
1. 空间直线方程; 直线位置判断;平面与直线
平面夹角公式;夹角和位置关系; 2. 空间平面方程;
平面位置判断;
点到平面距离;
3. 空间曲线方程; 平面束;解题时需要验证平面
束所排除的平面是否也
4. 空间曲面方程;
符合题目条件.
旋转曲面方程求解的两个不变性: 点到旋转轴距离不变;和旋转轴垂直方向的坐标值不变;
例:2008 七;模拟7一5,七;模拟5一5,二5,六; 期末模拟题4 二5,七;期末模拟题1 一5
北航-工科数学分析2010-2011期末试题

A一、计算题(每小题6分,共60分)1、已知函数2u x yz =+,求梯度grad u 及其梯度的散度().div grad u 解:,2,,u u u x z y x y z∂∂∂===∂∂∂{2,,},grad u x z y =---------------------------------------------------------3分()()()() 2.grad u grad u grad u div grad u x y z∂∂∂=++=∂∂∂--------------------3分2、设曲线22:=14x L y +的周长为l ,求2(2).Lx y ds +⎰ 解:222(2)(4)444.LLLLx y ds x y ds xyds ds l +=++==⎰⎰⎰⎰ 3、设D 是由1,0==y x 及x y =围成的区域,计算22.y Dx e dxdy -⎰⎰解:因为2_y e dy ⎰无法用初等函数表示,所以积分时必须考虑次序,2222321112_2200..3312(1).3yy y y y Dy y x edxdy dy x edx ee dy e---====-⎰⎰⎰⎰⎰⎰4、设222:,r D x y r +≤求22201lim cos().rx y r D ex y dxdy r+-→+⎰⎰解:由积分中值定理,存在(,),r D ξη∈使得22222cos()cos().rx y D e x y dxdy e r ξηξηπ--+=+⎰⎰于是原式=2220lim cos()..r e r ξηξηππ+-→+=5、设Ω为椭球体,1222222≤++c z b y a x 计算2().x y z dxdydz Ω++⎰⎰⎰解法一:作广义极坐标变换:Asin cos :sin sin cos x ar T y br z cr ϕθϕθϕ=⎧⎪=⎨⎪=⎩则T 的Jacobi 行列式为2J(,,)sin r abcr ϕθϕ=所以2222222()[()222]()x y z dxdydzx y z xy xz yz dxdydz x y z dxdydzΩΩΩ++=+++++=++⎰⎰⎰⎰⎰⎰⎰⎰⎰2122222222402222222222002222220222(sin cos sin sin cos )sin 2(sin cos sin sin cos )sin 52(2cos 2sin )54().15d d a b c abcr drabc d a b c d abc a b c d abc a b c πππππθϕϕθϕθϕϕθϕθϕθϕϕϕθθθπ=++=++=++=++⎰⎰⎰⎰⎰⎰解法二因为2222()()222,x y z x y z xy xz yz ++=+++++且,,xy xz yz 分别关于,,x y z 的奇函数,所以20,20,20.xydxdydz xzdxdydz yzdxdydz ΩΩΩ===⎰⎰⎰⎰⎰⎰⎰⎰⎰于是2222222()[()222]()x y z dxdydzx y z xy xz yz dxdydz x y z dxdydzΩΩΩ++=+++++=++⎰⎰⎰⎰⎰⎰⎰⎰⎰又因为22zccD z dxdydz z dz dxdy-Ω=⎰⎰⎰⎰⎰⎰其中222222{(,)|1}.z x y z D x y a b c=+≤-于是2222324(1),15zccc c D z z dxdydz z dz dxdy ab z dz abc c ππ--Ω==-=⎰⎰⎰⎰⎰⎰⎰同理,232344,1515x dxdydz a bc y dxdydz ab c ππΩΩ==⎰⎰⎰⎰⎰⎰故22224()().15x y z dxdydz abc a b c πΩ++=++⎰⎰⎰6、计算积分22(),x y dxdydz Ω+⎰⎰⎰其中Ω是由2z z ==围成的区域.解:作柱面坐标变换:cos ,sin ,T x r y r z zθθ===则积分区域Ω的表达式变为{(,,)|2,02,02},r z r z r θθπΩ=≤≤≤≤≤≤因此222223016().5rx y dxdydz dr d r dz πθπΩ+==⎰⎰⎰⎰⎰⎰7、计算22,Lxydx x dy +⎰其中L 为有向折线OAB ,这里,,O A B 依次是点(0,0),(1,0),(1,1).解:222222LOAABxydx x dy xydx x dy xydx x dy+=+++⎰⎰⎰100(2.01)1.y dy=++=⎰8、设Ω是由球面2224x y z ++=和平面0,0,0x y z ===所围成的在第一卦限的空间区域,则三重积分222()d f x y z V Ω++⎰⎰⎰在球坐标系下的累次积分为解222220()sin d d f r r drππϕθθ⎰⎰⎰9、计算曲面积分222,x dydz y dzdx z dxdy ∑++⎰⎰其中∑是球面2222(0)x y z R z ++=≥的上侧.解法一:因为∑是关于Oyz 平面对称的上半球面,所以∑上关于Oyz 平面对称的元素i ∆∑在Oyz 平面上的有向投影i σ∆正好抵消,被积函数关于x 是偶函数,故由定义可得,20.x dydz ∑=⎰⎰同理,20.y dzdx ∑=⎰⎰所以原式=22222222224()().2Rx y R z dxdy R x y dxdy d R r rdr R π∑πθ+≤=--=-=⎰⎰⎰⎰⎰⎰解法二222222224()().2xyxyD D Rz dxdy z dxdy R x y dxdyd R r rdr R ∑ππθ==--=-=⎰⎰⎰⎰⎰⎰⎰⎰又2222222()()0,yzyzD D x dydz R z y dydz R z y dydz ∑=-----=⎰⎰⎰⎰⎰⎰同理,2222222()()0,zxzxD D x dydz R z x dydz R z x dydz ∑=-----=⎰⎰⎰⎰⎰⎰所以,原式4.2R π=解法三原式=22222222222240{((}00()().2xyD Rx y Rx y z dxdyR x y dxdy d R r rdr ππθ+≤+-+=++--=-=⎰⎰⎰⎰⎰⎰10求向量场222(,,)A x yz xy z xyz =的旋度.解:222222222((),(),())ij k rotA x z y y x z z y x x y z x yzx y zx yz ∂∂∂==---∂∂∂二、(本题满分10分)设(,)f x y 在2214x y +≤上具有连续的二阶偏导数,L 是椭圆2214x y +=的顺时针方向,求[3(,)](,)xyLy f x y dx fx y dy ++⎰的值.(利用Green 公式)解:(,)3(,),(,)(,),x y P x y y f x y Q x y f x y =+=---------------------------------------2分则(,)(,)3(,),(,),xy yx P x y Q x y f x y f x y yx∂∂=+=∂∂----------------------------4分由Green 公式得,[3(,)](,)36.xyLDy f x y dx fx y dy dxdy π ++=--=⎰⎰⎰-----------------------10分三、(本题满分10分)利用Gauss 公式计算32222cos cos cos ,()x y z dS x y z αβγ∑++++⎰⎰其中∑是包含原点的曲面222(1)(2)(3)191625x y z ---++=的外侧,cos ,cos ,cos αβγ是其外法线向量的方向余弦.解:332222222232222(,,)(,,),()()(,,)()x y P x y z Q x y z x y z x y z z R x y z x y z ==++++=++-----------------------2分对充分小的0,ε>取22221:x y z ε∑++=(取内侧),-------------------------------4分使1∑位于∑内的内区域中,记Ω为∑与1∑所围有界区域,则11332222222232222cos cos cos cos cos cos ()()cos cos cos ()x y z x y z dS dSx y z x y z x y z dS x y z αβγαβγαβγ∑∑+∑∑++++=++++++-++⎰⎰⎰⎰⎰⎰-------7分1222233++10(cos cos cos )134.x y z dV x y z dSdV εαβγεπεΩ∑≤=-++==⎰⎰⎰⎰⎰⎰⎰⎰---------------------------------------------10分四、(本题满分10分)利用Stokes 公式计算积分222222()()()I y z dx z x dy x y dz Γ=-+-+-⎰ ,其中Γ为平面1x y z ++=与三个坐标平面的交线,从第一卦限向原点看逆时针方向.四、解:222222P(,,)=,(,,)R(,,)=,x y z y z Q x y z x z x y z y x +=++,且cos αβγ===---------------------------------------------4分则222222cos cos cos 3().2SSI dS x y z dS dS xyzy z z x x yαβγ∂∂∂==-++=-=-∂∂∂---⎰⎰-------10分或222222Sdydzdzdx dxdyI x y z y z z x x y∂∂∂∴=∂∂∂---⎰⎰2()()()...S y z dydz z x dzdx x y dxdy =-+++++=⎰⎰.五、(本题满分10分)设曲线积分2()Lxy dx yf x dy +⎰与路径无关,其中()f x 具有连续导数,且(0)0,f =求()f x 的表达式并计算(2,2)2(0,0)()xy dx yf x dy +⎰的值.解:令2P(,)=,(,)()x y xy Q x y yf x =则'P(,)(,)2,()x y Q x y xy y f x y x∂∂==∂∂------------------------------------2分因为P(,)(,),x y Q x y y x∂∂=∂∂所以有'2(),x f x =-------------------------------------------------4分解得,2(),f x x C =+又由于(0)0,f =知20,().C f x x ==----------------------------------------------------------6分(2,2)(2,2)222(0,0)(0,0)222()(..)8.xy dx yf x dy xy dx yx dyx x x x dx +=+=+=⎰⎰⎰-------------------------------------------10分六、(附加题满分10分)设22:0L x y x y +++=的方向为逆时针方向,证明:22sin +cos 2L y x dx x y dy π≤-≤⎰证明:令由22:0L x y x y +++=围成的区域为,D 由GREEN 公式得222222sin +cos (sin cos )sin cos LDDDy x dx x y dy x y dxdyx dxdy x dxdy-=+=+⎰⎰⎰⎰⎰⎰⎰---------4分2),4Dx dxdy π=+⎰⎰-----------------------------------------6分又(,),x y D ∈于是有1||,2x ≤从而2,2x π≤所以23,444x πππ<+≤------------------------------------------------------8分于是2sin(1,24x π<+≤且2(),2S D ππ==---------------------------------------10分故命题得证.。
北京北航附属中学高三数学文下学期期末试题含解析

北京北航附属中学高三数学文下学期期末试题含解析一、选择题:本大题共10小题,每小题5分,共50分。
在每小题给出的四个选项中,只有是一个符合题目要求的1. 已知 (>0 , ) , A、B为图象上两点,B是图象的最高点,C为B在x轴上的射影,且点C的坐标为则·( ).A. B. C. 4 D.参考答案:D略2. 若为虚数单位,已知,则点与圆的关系为 ( ) A.在圆外 B.在圆上 C.在圆内 D.不能确定参考答案:A略3. 已知一个几何体的三视图如图所示,则该几何体是( )A.圆柱B.三棱柱C.球D.四棱柱参考答案:C4. 圆O1:x2+y2﹣2x=0和圆O2:x2+y2﹣4y=0的位置关系是()A.相离B.相交C.外切D.内切参考答案:B【考点】圆与圆的位置关系及其判定.【分析】求出半径,求出圆心,看两个圆的圆心距与半径的关系即可.【解答】解:圆O1:x2+y2﹣2x=0,即(x﹣1)2+y2=1,圆心是O1(1,0),半径是r1=1圆O2:x2+y2﹣4y=0,即x2+(y﹣2)2=4,圆心是O2(0,2),半径是r2=2∵|O1O2|=,故|r1﹣r2|<|O1O2|<|r1+r2|∴两圆的位置关系是相交.故选 B5. 如图,过抛物线的焦点F的直线交抛物线于A,B两点,交其准线于点C,若,且,则p=(A)1 (B)2 (C)(D) 3参考答案:B6.曲线3x2-y + 6 = 0在x =-处的切线的倾斜角是()A.B.- C. D.-参考答案:答案:C7. 阅读如图所示的程序框图,则该算法的功能是()A.计算数列{2n﹣1}前5项的和B.计算数列{2n﹣1}前6项的和C.计算数列{2n﹣1}前5项的和D.计算数列{2n﹣1}前6项的和参考答案:D【考点】E7:循环结构.【分析】根据算法流程,依次计算运行结果,由等比数列的前n项和公式,判断程序的功能.【解答】解:由算法的流程知,第一次运行,A=2×0+1=1,i=1+1=2;第二次运行,A=2×1+1=3,i=2+1=3;第三次运行,A=2×3+1=7,i=3+1=4;第四次运行,A=2×7+1=15,i=5;第五次运行,A=2×15+1=31,i=6;第六次运行,A=2×31+1=63,i=7;满足条件i>6,终止运行,输出A=63,∴A=1+2+22+…+25==26﹣1=64﹣1=63.故选D.8. 某校高三一班有学生54人,二班有学生42人,现在要用分层抽样的方法从这两个班随机选出16人参加军训表演,则一班和二班分别选出的人数是(A)8人,8人(B)15人,1人(C)9人,7人(D)12人,4人参考答案:C略9. 设函数与的图象的交点为,则所在的区间是()A.B.C.D.参考答案:答案:B.解析:令,可求得:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
谢谢!
北航高数期末试试题
26、机遇对于有准备的头脑有特别的 亲和力 。 27、自信是人格的核心。
28、目标的坚定是性格中最必要的力 量泉源 之一, 也是成 功的利 器之一 。没有 它,天 才也会 在矛盾 无定的 迷径中 ,徒劳 无功。- -查士 德斐尔 爵士。 29、困难就是机遇。--温斯顿.丘吉 尔。 30、我奋斗,所以我快乐。--格林斯 潘。
21、要知道对好事的称颂过于夸大,也会招来人们的反感轻蔑和嫉妒。——培根 22、业精于勤,荒于嬉;行成于思,毁于随。——韩愈
23、一切节省,归根到底都归结为时间的节省。——马克思 24、意志命运往往背道而驰,决心到最后会全部推倒。——莎士比亚
