计量经济学-虚拟变量模型估计-Eviews6
计量经济学EViews操作
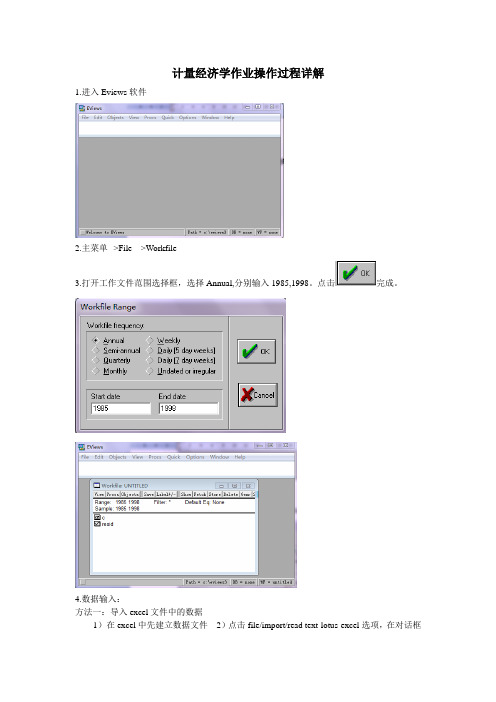
计量经济学作业操作过程详解1.进入Eviews软件2.主菜单-->File--->Workfile3.打开工作文件范围选择框，选择Annual,分别输入1985,1998。
点击完成。
4.数据输入：方法一：导入excel文件中的数据1）在excel中先建立数据文件2）点击file/import/read text-lotus-excel选项，在对话框中选择已建立的excel文件4）打开后，在新的对话框中输入想要分析的变量名称，然后点击OK即可。
此时工作文件中出现变量图标。
方法二：手工数据输入主菜单--->Quick----->Empty Group分别输入变量Y、GDP的数据。
点击obs后面的灰色格子中分别输入Y、GDP。
（方法一：一个一个输入方法二：在Excel中输入完再复制粘贴）5.主菜单---->Quick----->Estimate Equation打开估计模型对话框，输入Y C GDP ，（如上图所示，注意字母之间要有空格）点击OK键。
得出Eviews的估计结果：β（上面还要带个帽子，电脑打不出来），26.95415为1β。
其中12596.27为0第五步可以直接输入LS Y C GDP 等出结果6.一元线性回归模型的预测1）在工作文件主窗口点击procs/change workfile range(改变范围)，弹出对话框，在对话框的end date栏中输入预测值的时间或序号，点击OK2）在工作文件窗口中双击解释变量文件，在变量窗口中点击edit+/-键，进入编辑模式，在变量窗口底端输入新序号的数值，再点击edit+/-键，关闭编辑模式3）再次进行估计，点击quick/estimate equation，在对话框中输入方程，注意样本范围应不包括新序号，点击OK得到估计结果4）点击结果窗口中的forecast键，产生对话框，在对话框中选择样本范围，点击OK可得预测曲线图。
计量经济学EVIEWS教程
计量经济学软件包Eviews 教程一、启动软件包假定用户有Windows95/98的操作经验，我们通过一个实际问题的处理过程，使用户对EViews 的应用有一些感性认识，达到速成的目的。
（一）Eviews 的启动步骤：1．进入Windows/双击Eviews 快捷方式，进入EViews 窗口；2．点击开始 /程序/EViews5/Eviews ，进入EViews 窗口。
（二）EViews 窗口介绍1．标题栏：窗口的顶部是标题栏，标题栏的右端有三个按钮：最小化、最大化（或复原）和关闭，点击这三个按钮可以控制窗口的大小或关闭窗口。
当EVIEWS 处于活动状态时，标题栏将呈深蓝色，如果其处于非活动状态时，标题栏就呈灰色。
菜单栏 标题栏命令窗口控制按钮信息栏 路径状态栏主显示窗口（图一）2．菜单栏：标题栏下是主菜单栏。
主菜单栏上共有9个选项： File，Edit，Objects，View，Procs，Quick，Options，Window，Help。
用鼠标点击可打开下拉式菜单（或再下一级菜单，如果有的话），点击某个选项电脑就执行对应的操作响应（File，Edit的编辑功能与Word, Excel中的相应功能相似）。
（1）File菜单（2）Edit菜单（3）Objects菜单（4）View菜单（5）Procs菜单（6）Quick菜单（7）Options菜单（8）Window菜单（9）Help菜单3．命令窗口：主菜单栏下是命令窗口，窗口最左端一竖线是提示符，允许用户在提示符后通过键盘输入EViews（TSP风格）命令。
如果熟悉MicroTSP（DOS）版的命令可以直接在此键入，如同DOS版一样地使用EViews。
按F1键（或移动箭头），键入的历史命令将重新显示出来，供用户选用。
4．主显示窗口：命令窗口之下是Eviews的主显示窗口，以后操作产生的窗口（称为子窗口）均在此范围之内，不能移出主窗口之外。
5．状态栏：主窗口之下是状态栏，左端显示信息，中部显示当前路径，右下端显示当前状态，例如有无工作文件等。
计量经济学-多元线性回归分析;eviews6操作
E(i ) 0
V(a i)rE (i2)2
C( o i,v j) E (ij) 0
i j i,j 1 ,2 , ,n
假设5，解释变量与随机项不相关
Co(Xvji,i)0
j1,2 ,k
假设6，随机项满足正态分布
i ~N(0,2)
2021/6/4
7
上述假设的矩阵符号表示 式：
假设1，nk矩阵X是非随机的，且X的秩=k，即X满
五、样本容量问题
六、估计实例
2021/6/4
10
一、普通最小二乘估计
对于随机抽取的n组观测值 ( Y i,X j) ii , 1 , 2 , ,n ,j 0 , 1 , 2 , k
如果样本函数的参数估计值已经得到，则有：
Y ˆ i ˆ 1 ˆ 2 X 2 i ˆ 3 X 3 i ˆ k X kii=1,2…n
1、线性性
β ˆ(X X )1X Y CY
其中,C=(X’X)-1 X’ 为一仅与固定的X有关的行向量
2021/6/4
18
2、无偏性
E(βˆ) E((XX)1 XY) E((XX)1 X(Xβ μ)) β (XX)1 E(Xμ) β
这里利用了假设: E(X’)=0
3、有效性（最小方差性）
习惯上：把常数项看成为一虚变量的系数，该 虚变量的样本观测值始终取1。这样：
模型中解释变量的数目为（k）
2021/6/4
3
模 型 ： Y t 1 2 t X 2 t k X k t u t
也被称为总体回归函数的随机表达形式。它 的
非随机表达式为: E ( Y i | X 2 i , X 3 i , X k ) i 1 2 X 2 i 3 X 3 i k X ki
如何用EViews进行计量经济学分析
如何用EViews进行计量经济学分析EViews是一个功能强大的计量经济学软件，广泛应用于经济学和金融学领域。
本文将介绍如何使用EViews进行计量经济学分析。
一、EViews的基本功能和特点EViews是一款广泛用于经济学分析的软件，具有以下几个特点：1. 数据管理：EViews可以方便地导入、处理和管理各种类型的数据，包括时间序列数据和截面数据。
2. 统计分析：EViews提供了丰富的统计分析和计量经济学方法，如描述统计、回归分析、时间序列分析等。
3. 模型建立：EViews支持各种经济模型的建立和估计，如线性回归模型、ARMA模型、VAR模型等。
4. 图表展示：EViews具有强大的图表绘制功能，可以帮助用户直观地展示数据和分析结果。
二、使用EViews进行计量经济学分析的步骤下面将以线性回归模型为例，介绍如何使用EViews进行计量经济学分析。
1. 导入数据首先，将需要分析的数据导入EViews。
通过点击"File"菜单，选择"Import"，然后选择合适的数据文件类型进行导入。
2. 创建工作文件在导入数据后，可以创建一个新的工作文件，以便进行后续的分析和建模操作。
点击"File"菜单，选择"New"，然后选择"Workfile"创建一个新的工作文件。
3. 创建方程在工作文件中，可以创建一个回归模型方程。
点击"Quick"菜单，选择"Estimate Equation"，然后在弹出的对话框中输入回归方程的表达式和变量。
4. 估计模型在创建回归方程后，可以进行模型的估计。
点击"EViews"菜单，选择"Estimate Equation"，然后选择适当的估计方法和设置。
5. 解释结果估计模型后，EViews将显示回归结果的详细报告。
计量经济学(第四版)3.6 虚拟变量模型
以模型结果对定性变量的各种状态赋值。但需要更多的信息 支持。
• 赋值的方法等于是对虚变量方法中的各个虚变量的参 数施加了约束，而这种约束经常被检验为错误的。
– 模型含常数项
– 模型不含常数项
讨论：定序定性变量可否按照状态赋值？
• 例如：表示居民对某种服务的满意程度，分5种状态： 非常不满意、一般不满意、无所谓、一般满意、非常 满意。在模型中按照状态分别赋值0、1、2、3、4或 者－2、－1、0、1、2。
• 被经常采用，尤其在管理学、社会学研究领域。
• 正确的方法：
三、虚拟变量的设置原则
• 每一定性变量(qualitative variable)所需的虚 拟变量个数要比该定性变量的状态类别数 (categories)少1。即如果有m种状态，只在模 型中引入m-1个虚拟变量。
• 例如，季节定性变量有春、夏、秋、冬4种状 态，只需要设置3个虚变量：
1 春季
1 夏季
• 对于一元模型，有两组样本，则有可能出现下 述四种情况中的一种：
– 1=1 ，且2=2 ，即两个回归相同，称为重合回 归（Coincident Regressions）；
– 11 ,但2=2 ，即两个回归的差异仅在其截距， 称为平行回归（Parallel Regressions）;
– 称1=为汇1 合，回但归2(Co2n，cu即rre两nt个R回eg归re的ss差ion异s)仅；在其斜率，
年薪 Y
2 0
男职工 女职工
工龄 X
• 将上例中的性别换成教育水平，教育水平考虑 三个层次：高中以下、高中、大学及其以上。
计量经济学课件虚拟变量
通过引入虚拟变量，可以更准确地刻画经济现象的非线性特征，从而提高计量经济学模型 的精度和预测能力。
拓展应用领域
虚拟变量的引入使得计量经济学模型能够应用于更多的领域，如金融、环境、社会等，进 一步拓展了计量经济学的应用范围。
未来研究方向和趋势
深入研究虚拟变量的理论 和方法
未来研究将进一步深入探讨虚 拟变量的理论和方法，包括虚 拟变量的选择、设定和估计方 法等，以更准确地刻画经济现 象。
https://
未来研究将积极推动虚拟变量 在交叉学科领域的应用，如环 境经济学、金融经济学等，以 促进不同学科之间的交流和合 作。
WENKU DESIGN
WENKU DESIGN
2023-2026
END
THANKS
感谢观看
KEEP VIEW
WENKU DESIGN
WENKU DESIGN
WENKU
REPORTING
要点二
虚拟变量的设置原则
在设置虚拟变量时，需要遵循完备性 和互斥性的原则。完备性要求虚拟变 量的取值能够覆盖所有可能的情况， 而互斥性则要求不同虚拟变量之间不 能存在重叠或交叉的情况。
要点三
虚拟变量的回归系数 解释
在线性回归模型中，虚拟变量的回归 系数表示该定性因素对因变量的影响 程度。当虚拟变量取值为1时，其对 应的回归系数表示该水平与参照水平 相比对因变量的影响；当虚拟变量取 值为0时，则表示该水平对因变量没 有影响。
参数估计与假设检验
参数估计
采用最小二乘法等估计方法，对引入虚拟变量后的模型进行参数估计，得到各 解释变量的系数估计值。
假设检验
根据研究问题和假设，构建相应的原假设和备择假设，通过t检验、F检验等方 法对参数进行假设检验，判断虚拟变量对模型的影响是否显著。
计量经济学虚拟变量模型课件
计量经济学虚拟变量模型
21
1 正常年份 D1i 0 非正常年份
式(5.2)也可表示为
1 非正常年份 D2i 0 正常年份
Y i 0 X 1 i 1 X 2 i 2 X 3 i 3 X i u i （5.3）
其中，X 1i1 ,X 2iD 1i,X 3iD 2i，显然如下等式成立。
X1i X2i X3i
计量经济学虚拟变量模型
3
例如，性别可表现为男或女；人种可表 现为白种人和非白种人；宗教信仰可表 现为教徒和非教徒；政府的经济政策可 表现为改革开放前和改革开放后，如此 等等。
Hale Waihona Puke 计量经济学虚拟变量模型4
显然，这种不同的具体形式是无法直接引 入经济计量模型中去的。但由于这类变量 通常表现为品质、属性、种类的出现或者 未出现，所以我们可以根据质量变量的这 一特征将其数量化。
Y i1 D 1 i2 D 2 i3 X i u i （5.5）
显然模型(5.5)中，解释变量D1,D2和X之间 无完全的多重共线性。可以使用普通最小二乘 法估计式（5.5）的参数。
第五章 虚拟变量模型
在经济计量模型中除了有量的因素外 还有质的因素，质的因素包括被解释变量 为质的因素和解释变量为质的因素。如果 被解释变量为质的因素，主要是逻辑回归 要涉及的内容。
计量经济学虚拟变量模型
1
第一节 虚拟变量的概念与设定
一、虚拟变量的概念 在经济计量分析中， 经常会碰到所建模
型的被解释变量不仅受诸如收入、产量 、价格、 成本、需求、投资等数量变量
（5.4）
计量经济学虚拟变量模型
22
式(5.4)表明模型(5.3)即原模型(5.2)中有 完全的多重共线性，将导致最小二乘估计无 解。我们称该情景为掉入虚拟变量陷阱。所 以，在有截距项的情况下，如果一个质的因 素有多少个特征就引入多少个虚拟变量是行 不通的。
计量经济学-一元线性回归预测模型-Eviews6完整
数学与统计学院实验报告院（系）：数学与统计学学院学号：姓名：实验课程：计量经济学指导教师:实验类型（验证性、演示性、综合性、设计性）：综合性实验时间：2017年 3 月 1 日一、实验课题一元线性回归预测模型二、实验目的和意义用回归模型预测木材剩余物（1）用Eviews软件建立y关于x的回归方程，并对模型和参数做假设检验；（2）求y t的点预测和平均木材剩余物产出量E(y t)的置信区间预测。
（3）假设乌伊岭林业局2000年计划采伐木材20万m3，求木材剩余物的点预测值。
三、解题思路1、录非结构型的数据；2、进行描述性统计，列出回归模型；通过看t、f等统计量，检验回归模型是否正确3、运用forecast进行内预测（1-16样本），可以得到yf的点预测；再运用[yf+se]、[yf-se]进行区间估计（运用excel操作）4、将样本范围改到17个，令x=20，运用forecast进行外预测（17-17）四、实验过程记录与结果1、原始数据：乌伊岭26.1361.4东风23.4948.3新青21.9751.8红星11.5335.9五营7.1817.8上甘岭 6.817友好18.4355翠峦11.6932.7乌马河 6.817美溪9.6927.3大丰7.9921.5南岔12.1535.5带岭 6.817朗乡17.250桃山9.530双丰 5.5213.82、用Eviews软件建立y关于x的回归方程，并对模型和参数做假设检验；模型为：y=0.404280x-0.762928通过上表t、f统计量的p值<0.05，以及残差图基本在两倍标准差的范围内波动，可以得出该模型通过原假设。
3、求yt的点预测和平均木材剩余物产出量E(yt)的置信区间预测。
Yt的点估计：E（yt）的置信区间：4、假设乌伊岭林业局2000年计划采伐木材20万m3，求木材剩余物的点预测值。
空心点为预测值，上下两个红点是预测值的范围。
所以当x=20时，y的点预测值为7.322668五、结果的讨论和分析通过以上的实验，可知：模型为：y=0.404280x-0.762928，根据相关的统计量，可以得出该模型通过参数假设检验；yt的点预测运用内预测完成，而当2000年计划采伐木材20万立方米，运用外预测，可得木材剩余物的量为7.322668万立方米的六、实验小结通过这次实验，对eviews操作界面更加熟悉；掌握了如何建立数据的回归方程，以及参数的假设检验是否正确；运用eviews进行yt的点预测以及E（yt）的区间预测；当解释变量确定时，被解释变量应该为多少。
计量经济学软件Eviews6.0基本操作
计量经济学软件EVIEWS6.0基本操作一、什么是EVIEWSEVIEWS (ECONOMETRIC VIEWS)软件是QMS（QUANTITATIVE MICRO SOFTWARE）公司开发的、基于Windows平台下的应用软件，其前身是DOS操作系统下的TSP软件。
EVIEWS软件主要应用在经济学领域，可用于回归分析与预测(REGRESSION AND FORECASTING)、时间序列(TIME SERIES)以及横截面数据(CROSS-SECTIONAL DATA )分析。
与其他统计软件（如EXCEL、SAS、SPSS、stata、R）相比，EVIEWS功能优势是菜单操作简单明了，使用方法，非常适用计量经济学初级学员。
本手册对EVIEWS软件6.0版本进行简单介绍，目的是让初级学员通过本章介绍，能够对学过的计量经济理论和方法进行简单应用，以便完成本书所述的相关实验项目。
二、EVIEWS安装EVIEWS6.0文件安装包大小约190MB，可在网上下载①。
下载完毕后，按照包中安装文件所述安装方法安装该软件。
安装完毕后，将快捷键发送的桌面，电脑桌面显示有EVIEWS6.0图标，整个安装过程就结束了。
双击EVIEWS按钮即可启动该软件（图1），图1所示界面称为EVIEWS软件主窗口，主窗口中的菜单，如File菜单称为EVIEWS主菜单。
图1三、Eviews工作特点初次使EVIEWS6.0计量经济学软件，必须了解其工作过程。
如，想要完成一个校准一元线性回归模型的参数估计，必须要完成两大步工作。
第一大步工作就是在建立一个工作文档（即EVIEWS6.0中的Workfile文档）、建立变量、导入数据；第二大步工作是在第一大步工作的基础上，根据模型特征，选用适当的参数估计方法，完成参数估计及相关检验。
四、具体示例在这里，我们通过一个简单的标准一元线性回归模型的估计过程来说明Eviews软件完成回归分析的基本过程。
计量经济学6虚拟变量模型
年薪 Y
2 0
男职工 女职工
工龄 X
又例：在横截面数据基础上，考虑个人保健支出 对个人收入和教育水平的回归。
教育水平考虑三个层次：高中以下， 高中， 大学及其以上
这时需要引入两个虚拟变量：
1 D1 0
高中 其他
1 D2 0
大学及其以上 其他
模型可设定如下：
Yi 0 1 X i 2 D1 3 D2 i
例。已知冷饮的销售量Y除受k种定量变量Xk的影 响外，还受春、夏、秋、冬四季变化的影响，要考察 该四季的影响，只需引入三个虚拟变量即可：
1 春季 D1t 0 其他
1 夏季 D2t 0 其他
1 秋季 D3t 0 其他
则冷饮销售量的模型为：
Yt 0 1 X1t k X kt 1D1t 2 D2t 3 D3t t
90年前 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990
表 5.1.1
储蓄 281 399.5 523.7 675.4 892.5 1214.7 1622.6 2237.6 3073.3 3801.5 5146.9 7034.2
于是，不同性别、不同学历职工的平均薪金分别为： •女职工本科以下学历的平均薪金：
E(Yi | X i , D1 0, D2 0) 0 1 X i
•男职工本科以下学历的平均薪金：
E(Yi | X i , D1 1, D2 0) (0 2 ) 1 X i
•女职工本科以上学历的平均薪金：
X k1 X k2 X k3 X k4 X k5 X k6
1 0 0 0 0 1 0 0
0
0
1
0
0 0 0 1
计量经济学软件EViews的使用简介
SHOW（打开对象窗口） （打开对象窗口） 格式： 格式： SHOW 对象名 CLOSE （关闭对象窗口） 关闭对象窗口） 格式： 格式： CLOSE 对象名
（4）估计方法命令
• LS普通最小二乘法 LS普通最小二乘法 格式： 格式： LS 被解释变量 • TSLS二阶段最小二乘法 TSLS二阶段最小二乘法
（2）工作文件（Workfile） ）工作文件（ ）
在启动软件包以后，必须在内存RAM中建立工作文件，工作方作中 中建立工作文件， 在启动软件包以后，必须在内存 中建立工作文件 可以包括的对象有序列、 方程、图形、系统、模型及系数向量等。 可以包括的对象有序列、组、方程、图形、系统、模型及系数向量等。
计量经济学软件EViews的使用简介 的使用简介 计量经济学软件
• 一、EViews的基本概念 的基本概念
• 二、 EViews的使用简介 的使用简介
1、创建工作文件 、 2、输入与编辑数据 、 3、图形分析 、 4、用OLS估计模型中的求知参数 、 估计模型中的求知参数 5、模型检验 、 6、预测 、
格式： 格式： GENR
数据序列对象表达式 SERIES（创建数据序列对象）。 SERIES不需要赋值。 不需要赋值。 （创建数据序列对象）。 不需要赋值 格式： 格式： SERIES 数据序列名
EQUATION（创建估计式对象） （创建估计式对象） 格式： 格式： EQUATION 估计式对象
EQUATION 估计式对象 及估计表达式
（6）剪切板 ） 先使用主菜单上的Edit Copy，再使用 先使用主菜单上的 ，再使用Edit Paste 将保存在剪切板上的内容粘贴到其他地方。 将保存在剪切板上的内容粘贴到其他地方。 （7）窗口间切换 ） （8）数据文件（Data bank） ）数据文件（ ） 2、方程、指数平滑、标签、程序、残差、t统计量 、方程、指数平滑、标签、程序、残差、 统计量 (1)方程 方程(Equation) 方程 新建方程方法一： 新建方程方法一：New Object Equation后打开一个对 后打开一个对 话框，然后列出包含在方程里的变量名， 话框，然后列出包含在方程里的变量名，因变量之后排 列回归解释变量。例如，设定一个y关于 关于x和截距进行归 列回归解释变量。例如，设定一个 关于 和截距进行归 的线性消费的例子如下： 的线性消费的例子如下：y c x 新建方程方法二：例如：道格拉斯生产函数： 新建方程方法二：例如：道格拉斯生产函数： Y=c(1)*(L^c(2))*(k^c(3))
EViews6.0在面板数据模型估计中的操作
EViews 6.0在面板数据模型估计中的实验操作1、进入工作目录cd d:\nklx3，在指定的路径下工作是一个良好的习惯2、建立面板数据工作文件workfile（1）最好不要选择EViews默认的blanaced panel 类型Moren_panel（2）按照要求建立简单的满足时期周期和长度要求的时期型工作文件3、建立pool对象（1）新建对象（2）选择新建对象类型并命名（3）为新建pool对象设置截面单元的表示名称，在此提示下（Cross Section Identifiers: (Enter identifiers below this line )输入截面单元名称。
建议采用汉语拼音，例如29个省市区的汉语拼音，建议在拼音名前加一个下划线“_”，如图关闭建立的pool对象，它就出现在当前工作文件中。
4、在pool对象中建立面板数据序列双击pool对象，打开pool对象窗口，在菜单view的下拉项中选择spreedsheet （展开表）在打开的序列列表窗口中输入你要建立的序列名称，如果是面板数据序列必须在序列名后添加“?”。
例如，输入GDP?，在GDP后的?的作用是各个截面单元的占位符，生成了29个省市区的GDP的序列名，即GDP后接截面单元名，再在接时期，就表示出面板数据的3维数据结构（1变量2截面单元3时期）了。
请看工作文件窗口中的序列名。
展开表（类似excel）中等待你输入、贴入数据。
（1）打开编辑（edit）窗口（2）贴入数据（3）关闭pool窗口，赶快存盘见好就收6、在pool窗口对各个序列进行单位根检验选择单位根检验设置单位根检验单位根检验结果注意检验方法和两种检验的零假设：Null: Unit root (assumes common unit root process)各截面有相同的单位根Null: Unit root (assumes individual unit root process)允许各截面有不同单位根其中，Levin, Lin & Chu t*检验拒绝含有单位根的零假设，即拒绝非平稳7、在pool窗口对面板数据组合进行协整检验选择进行协整检验协整检验设置对话框，注意有3种检验方法（test type）协整检验结果，同样要注意两种假定（含有AR，即含有单位根，非协整），两种零假设都是非协整，小概率事件发生拒绝非协整。
虚拟变量eviews操作
虚拟变量eviews操作⼀、研究1978-2008年城乡居民储蓄存款随收⼊的变化规律是否有变化，已引⼊虚拟变量。
从上图中⽆法得到居民的储蓄⾏为发⽣明显改变的详尽信息。
做居民储蓄增量的时序图。
如下：可以看到，城乡居民的储蓄⾏为表现出了明显的阶段特征：在1996年、2000年、2005年和2007年有四个明显的转折点。
再从城乡居民储蓄存款增量与国民总收⼊之间关系的散布图看，也呈现了相同的阶段特征.为了分析居民储蓄⾏为在1996年、2000年、2005年以及2007年等不同时期的数量关系，引⼊虚拟变量D1、D2、D3、D4。
⼆、建⽴模型12314253541234(70142.5)(98000.5)(184088.6)(251483.2)t 1996t 0t 19960t t 0t t t t t t t t t t t tt t t YY GNI GNI D GNI D GNI D GNI D u ββββββ=++-+-+-+-+??===??1，为年以后1，为2000年以后其中，D D ，为年及以前，为2000年及以前1，为2005年以后 D D ，为2005年及以前t 20070t t ?=??1，为年以后，为2007年及以前三、回归估计模型series year 粘贴年份（edit ）series d1=(year>1996)series d2=(year>2000)series d3=(year>2005)series d4=(year>2007)ls yy c gni (gni-70142.5)*d1 (gni-98000.5)*d2 (gni-184088.6)*d3 (gni-251483.2)*d4四、根据上述估计结果写出模型702.31640.1330,199612687.88690.0579,1996200024467.43760.3755,2000200563121.20120.2137,20052007204856.37820.9448,2007t t t t t t t t t t GNI e t GNI e t YY GNI e t GNI e t GNI e t Λ-++≤??-+<≤??=-++<≤??-+<≤?-++>??。
Eviews：虚拟变量模型
分段回归
要判断1991年是否为一个分界点，我们可以通过分别对1991 年前的数据和1991年后的数据进行回归，分析两个回归结果中的 参数估计量，来对是否发生了结构变化进行判断。令1991年前模 型为
令1991年后模型为
Y=α1+α2X+μi1
Y=β1+β2X+μi2
可能出现回归结果
按照上述方法进行回归有可能产生下列四种情况之一：
0 1 B ; k
0 1 a k
案例分析
• 我们以中国1908-2001年城乡储蓄存款 新增额代表的居民当年储蓄Y及以GNP 代表的居民当年收入X为例。我们先以 1991年为界，判断1991年前后两个时 期中国居民的储蓄-收入关系是否已经 发生变化。
虚拟变量模型
虚拟变量及虚拟变量方程的定义
• 在经济变量的讨论中，经常要考虑属性因素的影响， 例如职业、地区、季节、战争、文化程度、自然灾害 等，它们的特点不能直接度量。为了在模型中反映这 些属性因素的影响，必须将它们“量化”。根据其属 性类型，构造只取“0”或“1”的人工变量，这就是虚 拟变量，通常记为变量D。 • 一般地，在虚拟变量的设置中，基础类型，肯定类型 取值为1，否定类型取值为0。引入虚拟变量之后，回 归方程中同时含有一般解释变量和虚拟变量，这种结 构的回归方程称为虚拟变量模型。
说 明
在引入虚拟变量时，往往容易对虚拟变量 值应该取1还是取0产生混淆。对于是非、发生 或未发生，是或者发生了就取1，非或者没有 发生即取0. 比如我们分析二战是否对1930年 到1945年间经济有影响，那么1930到1938二 战未发生时期我们取虚拟变量值为0，1939到 1945二战发生时期我们取1. 即是，肯定时为1， 否定时为0.
EVIEWS虚拟变量模型
虚拟变量【实验目的】掌握虚拟变量的设置方法。
【实验内容】一、试根据表7-1的1998年我国城镇居民人均收入与彩电每百户拥有量的统计资料建立我国城镇居民彩电需求函数；资料来源：据《中国统计年鉴1999》整理计算得到二、试建立我国税收预测模型（数据见实验一）；三、试根据表7-2的资料用混合样本数据建立我国城镇居民消费函数。
资料来源：据《中国统计年鉴》1999－2000整理计算得到【实验步骤】一、我国城镇居民彩电需求函数⒈相关图分析；键入命令：SCAT X Y，则人均收入与彩电拥有量的相关图如7-1所示。
从相关图可以看出，前3个样本点（即低收入家庭）与后5个样本点（中、高收入）的拥有量存在较大差异，因此，为了反映“收入层次”这一定性因素的影响，设置虚拟变量如下：⎩⎨⎧=低收入家庭中、高收入家庭1D图7-1 我国城镇居民人均收入与彩电拥有量相关图⒉构造虚拟变量；方式1：使用DATA 命令直接输入； 方式2：使用SMPL 和GENR 命令直接定义。
DATA D1 GENR XD=X*D1 ⒊估计虚拟变量模型： LS Y C X D1 XD再由t 检验值判断虚拟变量的引入方式，并写出各类家庭的需求函数。
按照以上步骤，虚拟变量模型的估计结果如图7-2所示。
图7-2 我国城镇居民彩电需求的估计我国城镇居民彩电需求函数的估计结果为：i i i i XD D x y 0088.08731.310119.061.57ˆ-++==t (16.249)(9.028) (8.320) (-6.593)2R ＝0.9964 2R ＝0.9937 F ＝366.374 S.E ＝1.066虚拟变量的回归系数的t 检验都是显著的，且模型的拟合优度很高，说明我国城镇居民低收入家庭与中高收入家庭对彩电的消费需求，在截距和斜率上都存在着明显差异，所以以加法和乘法方式引入虚拟变量是合理的。
低收入家庭与中高收入家庭各自的需求函数为：低收入家庭：i i x y0119.061.57ˆ+= 中高收入家庭：()()i i x y0088.00119.08731.3161.57 ˆ-++=i x 003.048.89+= 由此可见我国城镇居民家庭现阶段彩电消费需求的特点：对于人均年收入在3300元以下的低收入家庭，需求量随着收入水平的提高而快速上升，人均年收入每增加1000元，百户拥有量将平均增加12台；对于人均年收入在4100元以上的中高收入家庭，虽然需求量随着收入水平的提高也在增加，但增速趋缓，人均年收入每增加1000元，百户拥有量只增加3台。
计量经济学eviews操作
计量经济学实验指导系部：基础部专业：计算与信息科学教师：仓定帮I.实验一多元线性回归模型 (3)II.实验二异方差的检验与处理 (16)III.实验三序列相关的检验与处理 (24)IV.实验四多重共线性的检验与处理 (32)V.实验五虚拟变量模型 (39)VI.实验六分布滞后模型 (45)VII.实验七联立方程模型 (51)VIII.实验八时间序列模型分析 (58)IX.实验九V AR模型的建立与分析 (77)A. ADF检验 (78)B. VAR模型的建立 (79)C. 协整检验 (80)D. GRANGER因果检验 (81)E. 脉冲响应分析 (81)实验内容注：必做实验课堂时间完成，选做实验由学生课后选择时间完成。
每次实验后学生上交实验分析结果。
I.实验一多元线性回归模型【实验目的】通过本实验，了解Eviews软件，熟悉软件建立工作文件，文件窗口操作，数据输入与处理等基本操作。
掌握多元线性回归模型的估计方法，学会用Eiews 软件进行多元回归分析。
通过本实验使得学生能够根据所学知识，对实际经济问题进行分析，建立计量模型，利用Eiews软件进行数据分析，并能够对输出结果进行解释说明。
【实验内容及步骤】本实验选用美国金属行业主要的27家企业相关数据，如下表，其中被解释变量Y表示产出，解释变量L表示劳动力投入，K表示资本投入。
试建立三者之间的回归关系。
7 2427.89 452 3069.91 21 5159.31 835 5206.368 4257.46 714 5585.01 22 3378.4 284 3288.729 1625.19 320 1618.75 23 592.85 150 357.3210 1272.05 253 1562.08 24 1601.98 259 2031.9311 1004.45 236 662.04 25 2065.85 497 2492.9812 598.87 140 875.37 26 2293.87 275 1711.7413 853.1 154 1696.98 27 745.67 134 768.5914 1165.63 240 1078.79【实验内容及步骤】1.数据的输入STEP1：双击桌面上Eviews快捷图标，打开Eviews，如图1.图1STEP2：点击Eviews主画面顶部按钮file/new/Workfile ，如图2，弹出workfile create对话框如图3。
EViews统计分析在计量经济学中的应用--第6章-时间序列模型
1
在图6.9中，有两个选 择：一是针对何种数 据生成相关图，主要 分为原变量（level）、 一阶差分变量（1st difference）及二阶 差分变量（2st difference），这里 选择level；二是确定 相关图的滞后期 （Lags to include）， 这里选择36。
15
自相关、偏自相关图
图6.26 图示对话框
2021/2/4
1
30
自相关函K”按钮， 可得自相关 函数和偏自 相关函数， 如图6.27 所示。
图6.27 对数二阶差分自相关函数
2021/2/4
1
31
自相关函数和偏自相关函数
对数二阶差分序列自相关和偏自相关函数，如图 6.27所示，由两部分组成，左半部分为自相关 （Autocorrelation）与偏自相关（Partial Correlation）分析图，右半部分为自相关系数 （AC）、偏自相关系数（PAC）、Q统计量（QStat）与相伴概率（Prob）。由图6.27可知，自 相关和偏自相关函数的峰值同为滞后1期，自相关 函数1阶截尾，偏自相关函数2阶截尾，可初步判 定p=1，2，q=1，即可能适合的模型有 ARMA(2,1)，ARMA(1,1)，AR(1)，AR(2)， MA(1)。
2021/2/4
如图6.15所示，单位根检验选项有四个选择 区域： Test type（检验方法）：包括6种检验方法， 主要为ADF检验、DF检验、PP检验、KPSS 检验、ERSPO检验及NP检验，系统默认选择 ADF检验； Test for unit in（所检验的序列），有三种 可供选择： ◆Level：表示对水平序列进行单位根检验； ◆1st difference：表示对序列的一阶差分 序列进行单位根检验； ◆2nd difference：表示对序列的二阶差分 序列进行单位根检验；
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
12
69 6.83 87 41.86
步骤提示：
（1）做变量 fin 的散点图，观察规律，看在不同时期是否有结构性
变化。
（2）建立时间变量 t=1，2，…，做 Fin 关于 t 的线性回归模型，并对
其做参数结构稳定性检验（Chow 检验或 Chow 预测检验）（建立变量 t
的方法是：t=@trend()+1）
三、解题思路 录入数据—做散点图. 建立虚拟变量，观察模型是否显著（加法、乘法、混合模型） 利用 chow 检验该模型是否具有结构性变化 四、实验过程记录与结果 1、做变量 fin 的散点图
2、受约束模型（1952~2004）
3、不受约束模型 第一段：1952~1996
第二段：1997~2004 4、加法模型（fin c t d1）
五、结果的讨论和分析
引入虚拟变量，三种模型显著，参数也显著，模型显著有效
0，
加法模型
D
（19521-，1997） FIN = -42.56 + 34.13*T1+= 2261.44*D1，
（1998-2004）
0，
乘法模型
D
（19521-，199（71）998FIN = -21.31+ 32.93*T + 14=6.91*D1*T，
表1
ob
Fi
ob
Fi
ob
Fi
s
n
s
n
s
n
19
17
19
56
19
11
52 3.94 70 3.59 88 22.88
19
20
19
63
19
10
53 6.23 71 8.01 89 77.92
19
23
19
65
19
11
54
1.7
72 8.23 90 63.19
19
23
19
69
19
12
55 3.21 73
1
91 12.51
5、乘法模型：(fin c t t*d1)
6、混合模型：(fin c t t*d1 d1)
7、chow 检验：
F= 31807606 -（517268.9 311512.8）* 45 8 - 2 *（1 1）=915.7683
517268.9 311512.8
11
（Chow 检验中的 F 检验），1996 是断点。
19
39
19
98
20
38
65 3.14 83 2.17 01 34.16
19
46
19
11
20
44
66 5.45 84 47.95 02 81.4
19
35
19
12
20
51
67 1.99 85 87.41 03 53.4
19
30
19
12
20
60
68 2.98 86 85.16 04 92.99
19
44
19
93
19
16
60 9.06 78 1.47 96 13.19
19
27
19
92
19
18
61
0.8
79 4.71 97 68.98
19
22
19
88
19
21
62 9.72 80 2.78 98 90.3
19
26
19
87
19
26
63 6.46 81 4.02 99 16.46
19
32
19
88
20
31
64 2.98 82 4.14 00 09.61
数学与统计学院实验报告
院（系）：数学与统计学学院 学号：
姓名：
实验课程： 计量经济学 指导教师:
实验类型（验证性、演示性、综合性、设计性）： 验证性
实验时间：2017 年 3 月 29 日
一、实验课题
虚拟变量模型估计
二、实验目的和意义
1 建立财政支出模型
表 1 给出了 1952-2004 年中国财政支出（Fin）的年度数据（以 1952 年为基期，用消费价格指数进行平减后得数据）。试根据财政支出随 时间变化的特征建立相应的模型。
19
26
19
66
19
12
56 2.14 74 4.81 92 72.68
19
27
19
69
19
14
57 9.45 75 1.32 93 03.62
19
34
19
65
19
13
58 9.03 76 6.25 94 83.74
19
44
19
72
19
14
59 3.85 77 4.18 95 42.19
19
41
19
（3）若有结构性变化，建立虚拟变量，对模型进行回归。假设要建
立虚拟变量 D1 为（这里的断点时间 1996 是我随意给定的，你可以根据
实际情况进行调整）
0， D
（19521-，1996） 1= 用 EViews 生成虚拟变（量199D71-2序00列4），采用的方法为： 在工作文件窗口点击 Quick/Generate Series，在弹出的由方程生 成序列的窗口，输入 D1=0，同时更改下面的样本范围为 1952-1996，这 时只生成了第一段（1952-1996）中的 D1=0。采用同样的方法，再点击 Quick/Generate Series，在弹出的由方程生成序列的窗口，输入 D1=1， 同时更改下面的样本范围为 1997-2004 （4）建立含有虚拟变量（加法、乘法或混合）的回归模型，并对模型 及参数进行检验。 （5）比较 Chow 检验和虚拟变量模型检验的异同。
2004）
0，
混合模型
D （19521-，1997）
FIN = 7.29 + 32.01*T - 28499.21*D11=+ 616.34*D1*T，
（1998-2004）
六、实结构性变化，且断点处在 1996.利用虚拟变量对模型进行处理时，发现混合模型具有很好的显 著性效果。