实验三-利用matlab程序设计语言完成某工程导线网平差计算
基于MATLAB的水准网和测边网平差程序设计

基于MATLAB的水准网和测边网平差程序设计摘要MATLAB是目前在研究机构广泛应用的一种数值计算及图形工具软件,它的特点是语法结构简明、数值计算高效、图形功能完备,特别适合非专业编程员完成数值计算、科学试验处理等任务。
以往的测量数据处理方法需要编制特定的处理矩阵运算程序,而且程度复杂,难度大。
本文介绍一种基于MATLAB的水准网和测边网的程序设计方法,与其它算法语言相比,具有编程简单,运算速度快的特点。
文中分别阐述了水准网和测边网程序的理论基础、实现步骤和运行结果。
通过实例的分析,总结出利用MATLAB对测量数据处理有很大的应用价值,它缩短了编程的时间,提高工作效率。
关键词:MATLAB;水准网;测边网;程序设计ABSTRAC TMATLAB is one species of numerical-values calculation and graphic tools software which is widely used to apply at research institutions at present. The particularities are: concise grammar-structure、highly efficient in numerical values calculating、complete function of graphs、especially it is adapted to evildoing professional programmer to accomplish the tasks that are numerical-values calculating and scientific experiments treating. The ancient methods of measured data-processing need establishing special proceedings of treating matrices operation, moreover, it is complex and greatly difficult.This article introduces one programming method dealing with leveling and measuring edge network based on MATLAB. Compared with other algorithm language, it has particularities which are simply programming and quickly operating. The article separately expatiate the theories basics、realizing steps and running results at leveling and measuring edge network. With the analysis of examples, it has prodigious application value in measured data-processing by use of MATLAB. Moreover, it shortens programming time and improves working effectiveness.Key words:MATLAB;leveling network;measuring edge network;programming目录绪论 (4)1. MATLAB软件简介 (5)2.MATLAB 在测量平差中的应用 (6)2.1测量平差原理的概述 (6)2.2平差程序总体方案 (7)3.1程序的功能 (8)3.2水准模型网的间接平差 (8)3.2.1 “权”值的确定 (8)3.2.2 水准路线的平差计算 (9)3.2.3 精度评定 (11)3.3水准网间接平差程序信息设计 (11)3.4 水准网程序与使用说明 (12)3.4.1 水准网程序流程图 (12)3.4.2 水准网程序的使用 (12)3.5案例 (13)4. 测边网平差程序设计 (15)4.1数学模型 (15)4.1.1 误差方程和法方程的组成 (15)4.1.2 边长观测的权 (15)4.1.3 解算法方程 (16)4.1.4 精度评定 (19)4.2 测边网平差信息设计 (20)4.2.1 主要的技术要求 (21)4.3利用MATLAB的绘图语句绘制网图 (21)4.4测边网程序和使用说明 (22)4.5 程序代码说明: (23)4.6程序的使用算例 (25)结论 (29)致谢 (30)参考文献 (31)附录一 (32)附录二 (36)附录三 (46)绪论作为一名测量技术人员,如果不掌握一门PC机编程语言与便携计算工具,要想提高测量工作的效率几乎寸步难行。
MatLab平差计算实习报告

MatLab平差计算实习报告(1)实验目的和内容实验目的:1、掌握条件平差原理和计算条件方程的建立误差方程的建立误差方程的求解精度计算2、掌握MatLab平差计算实验内容:条件平差计算不同条件方程计算计算结果比较条件方程一:h1-h2+h5=0 v1-v2+v5+7=0h3-h4+h5=0 v3-v4+v5+8=0h3+h6+h7=0 v3+v6+v7+6=0hA+h2-h4=hB v2-v4-3=0将上述方程用矩阵表达为:A =1 -1 0 0 1 0 00 0 1 -1 1 0 00 0 1 0 0 1 10 1 0 -1 0 0 0W =786-3权:P =0.9091 0 0 0 0 0 00 0.5882 0 0 0 0 00 0 0.4348 0 0 0 00 0 0 0.3704 0 0 00 0 0 0 0.4167 0 00 0 0 0 0 0.7143 00 0 0 0 0 0 0.3846权逆阵:Q=inv(P)= 1.1000 0 0 0 0 0 00 1.7000 0 0 0 0 00 0 2.3000 0 0 0 00 0 0 2.7000 0 0 00 0 0 0 2.4000 0 00 0 0 0 0 1.4000 00 0 0 0 0 0 2.6000法方程系数阵:Naa=A*Q*A'= 5.2000 2.4000 0 -1.70002.4000 7.4000 2.3000 2.70000 2.3000 6.3000 0-1.7000 2.7000 0 4.4000解联系数:K=-inv(Naa)*W= -0.2206-1.4053-0.43931.4589求改正数:V=Q*A'*K=-0.24272.8552-4.2427-0.1448-3.9021-0.6151-1.1423求平差值:LL=L+V=1.11634.8642-3.87970.8672-3.2451-0.3771-1.7373单位权中误差:sigma0=sqrt(V'*P*V/r)= 2.2248求改正数协因数:QVV=Q*A'*inv(Naa)*A*Q=0.5693 -0.1608 -0.5307 -0.1608 0.3699 0.1857 0.3450 -0.1608 0.9242 -0.1608 -0.7758 -0.6151 0.0563 0.1045 -0.5307 -0.1608 1.7693 -0.1608 0.3699 0.1857 0.3450 -0.1608 -0.7758 -0.1608 1.9242 -0.6151 0.0563 0.10450.3699 -0.6151 0.3699 -0.6151 1.4150 -0.1295 -0.24040.1857 0.0563 0.1857 0.0563 -0.1295 0.4250 0.78930.3450 0.1045 0.3450 0.1045 -0.2404 0.7893 1.4658求高差平差值协因数:QLL=Q-QVV=0.5307 0.1608 0.5307 0.1608 -0.3699 -0.1857 -0.34500.1608 0.7758 0.1608 0.7758 0.6151 -0.0563 -0.10450.5307 0.1608 0.5307 0.1608 -0.3699 -0.1857 -0.34500.1608 0.7758 0.1608 0.7758 0.6151 -0.0563 -0.1045-0.3699 0.6151 -0.3699 0.6151 0.9850 0.1295 0.2404 -0.1857 -0.0563 -0.1857 -0.0563 0.1295 0.9750 -0.7893 -0.3450 -0.1045 -0.3450 -0.1045 0.2404 -0.7893 1.1342条件方程二:hA+h1-h3=hB v1-v3-4=0hA+h1+h5-h4=hB v1+v5-v4-4=0hA+h1+h6+h7=hB v1+v6+v7+2=0h6+h7+h4-h5=0 v6+v7+v4-v5-2=0将上述方程用矩阵表达为:A =1 0 -1 0 0 0 01 0 0 -1 1 0 01 0 0 0 0 1 10 0 0 1 -1 1 1W =-4-42-2权:P =0.9091 0 0 0 0 0 00 0.5882 0 0 0 0 00 0 0.4348 0 0 0 00 0 0 0.3704 0 0 00 0 0 0 0.4167 0 00 0 0 0 0 0.7143 00 0 0 0 0 0 0.3846权逆阵:Q=inv(P)= 1.1000 0 0 0 0 0 00 1.7000 0 0 0 0 00 0 2.3000 0 0 0 00 0 0 2.7000 0 0 00 0 0 0 2.4000 0 00 0 0 0 0 1.4000 00 0 0 0 0 0 2.6000法方程系数阵:Naa=A*Q*A'= 3.4000 1.1000 1.1000 01.1000 6.2000 1.1000 -5.10001.1000 1.1000 5.1000 4.00000 -5.1000 4.0000 9.1000解联系数:K=-inv(Naa)*W= 0.00004.5036-4.50364.5036求改正数:V=Q*A'*K=- 1.0000-2.9849-2.00002.0000-1.0000-2.0000求平差值:LL=L+V=2.35902.0090-2.6219-0.98802.6570-0.7620-2.5950单位权中误差:sigma0=sqrt(V'*P*V/r)= 1.5956求改正数协因数:QVV=Q*A'*inv(Naa)*A*Q= 0.5541 0 -0.5837 -0.3375 0.3000 0.1750 0.32500 0 0 0 0 0 0-0.5837 0 1.7163 -0.1941 0.1725 0.2012 0.3737-0.1822 0 -0.1941 1.3500 -1.2000 0.3500 0.65000.1925 0 0.1725 -1.3500 1.2000 -0.3500 -0.65000.1788 0 0.2012 0.3375 -0.3000 0.5250 0.97500.3713 0 0.3737 0.6750 -0.6000 1.0500 1.9500求高差平差值协因数:QLL=Q-QVV=0.5459 0 0.5837 0.3375 -0.3000 -0.1750 -0.32500 1.7000 0 0 0 0 00.5837 0 0.5837 0.1941 -0.1725 -0.2012 -0.37370.1822 0 0.1941 1.3500 1.2000 -0.3500 -0.6500-0.1925 0 -0.1725 1.3500 1.2000 0.3500 0.6500-0.1788 0 -0.2012 -0.3375 0.3000 0.8750 -0.9750-0.3713 0 -0.3737 -0.6750 0.6000 -1.0500 0.6500(2)实习工具软件介绍1、MATLAB语言的发展matlab语言是由美国的Clever Moler博士于1980年开发的设计者的初衷是为解决“线性代数”课程的矩阵运算问题取名MATLAB即Matrix Laboratory 矩阵实验室的意思➢它将一个优秀软件的易用性与可靠性、通用性与专业性、一般目的的应用与高深的科学技术应用有机的相结合➢MATLAB是一种直译式的高级语言,比其它程序设计语言容易2、MATLAB功能•强大的数值(矩阵)运算功能•广泛的符号运算功能•高级与低级兼备的图形功能(计算结果的可视化功能)•可靠的容错功能•应用灵活的兼容与接口功能•信息量丰富的联机检索功能3、MATLAB界面MATLAB操作1.创建矩阵的方法•直接输入法规则:矩阵元素必须用[ ]括住矩阵元素必须用逗号或空格分隔在[ ]内矩阵的行与行之间必须用分号分隔2、数据的保存与获取•把matlab工作空间中一些有用的数据长久保存下来的方法是生成mat数据文件。
实验三-利用matlab程序设计语言完成某工程导线网平差计算

实验三-利用m a t l a b程序设计语言完成某工程导线网平差计算(总11页)本页仅作为文档封面,使用时可以删除This document is for reference only-rar21year.March实验三利用matlab程序设计语言完成某工程导线网平差计算实验数据;某工程项目按城市测量规范(CJJ8-99)不设一个二级导线网作为首级平面控制网,主要技术要求为:平均边长200cm,测角中误差±8,导线全长相对闭合差<1/10000,最弱点的点位中误差不得大于5cm,经过测量得到观测数据,设角度为等精度观测值、测角中误差为m=±8秒,鞭长光电测距、测距中误差为m=±√smm,根据所学的‘误差理论与测量平差基础’提出一个最佳的平差方案,利用matlab完成该网的严密平差级精度评定计算;平差程序设计思路:1采用间接平差方法,12个点的坐标的平差值作为参数.利用matlab进行坐标反算,求出已知坐标方位角;根据已知图形各观测方向方位角;2计算各待定点的近似坐标,然后反算出近似方位角,近似边.计算各边坐标方位角改正数系数;3确定角和边的权,角度权Pj=1;边长权Ps=100/S;4计算角度和边长的误差方程系数和常数项,列出误差方程系数矩阵B,算出Nbb=B’PB,W=B’Pl,参数改正数x=inv(Nbb)*W;角度和边长改正数V=Bx-l;6 建立法方程和解算x,计算坐标平差值, 精度计算;程序代码以及说明:s10=;s20=;s30=;s40=;s50=;s60=;s70=;s80=;s90=;s100=;s110=;s120=;s130=;s140=; %已知点间距离Xa=;Ya=;Xb=;Yb=;Xc=;Yc=;Xd=;Yd=;Xe=;Ye=;Xf=;Yf=; %已知点坐标值a0=atand((Yb-Ya)/(Xb-Xa))+180;d0=atand((Yd-Yc)/(Xd-Xc));f0=atand((Yf-Ye)/(Xf-Xe))+360; %坐标反算方位角a1=a0+(163+45/60+4/3600)-180a2=a1+(64+58/60+37/3600)-180;a3=a2+(250+18/60+11/3600)-180;a4=a3+(103+57/60+34/3600)-180;a5=d0+(83+8/60+5/3600)+180;a6=a5+(258+54/60+18/3600)-180-360;a7=a6+(249+13/60+17/3600)-180;a8=a7+(207+32/60+34/3600)-180;a9=a8+(169+10/60+30/3600)-180;a10=a9+(98+22/60+4/3600)-180;a12=f0+(111+14/60+23/3600)-180;a13=a12+(79+20/60+18/3600)-180;a14=a13+(268+6/60+4/3600)-180;a15=a14+(180+41/60+18/3600)-180; %推算个点方位角aa=[a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a12 a13 a14 a15]'X20=Xb+s10*cosd(a1);X30=X20+s20*cosd(a2);X40=X30+s30*cosd(a3);X50a=X40+s40*cosd(a4);X60=Xd+s50*cosd(a5);X70=X60+s60*cosd(a6);X80=X70+s70*cosd(a7);X90=X80+s80*cosd(a8);X100=X90+s90*cosd(a9);X50c=X100+s100*cosd(a10);X130=Xf+s110*cosd(a12);X140=X130+s120*cosd(a13);X150=X140+s130*cosd(a14);X50e=X150+s140*cosd(a15); %各点横坐标近似值X0=[X20 X30 X40 X60 X70 X80 X90 X100 X130 X140 X150 X50a X50c X50e]'Y20=Yb+s10*sind(a1);Y30=Y20+s20*sind(a2);Y40=Y30+s30*sind(a3);Y50a=Y40+s40*sind(a4);Y60=Yd+s50*sind(a5);Y70=Y60+s60*sind(a6);Y80=Y70+s70*sind(a7);Y90=Y80+s80*sind(a8);Y100=Y90+s90*sind(a9);Y50c=Y100+s100*sind(a10);Y130=Yf+s110*sind(a12);Y140=Y130+s120*sind(a13);Y150=Y140+s130*sind(a14);Y50e=Y150+s140*sind(a15); %个点从坐标近似值Y0=[Y20 Y30 Y40 Y60 Y70 Y80 Y90 Y100 Y130 Y140 Y150 Y50a Y50c Y50e]'P=[X0 Y0];X50=(X50a+X50c+X50e)/3Y50=(Y50a+Y50c+Y50e)/3s4=sqrt((Y40-Y50)^2+(X40-X50)^2);s1=sqrt((Y100-Y50)^2+(X100-X50)^2);s14=sqrt((Y150-Y50)^2+(X150-X50)^2);A1=[cosd(a1) cosd(a2) cosd(a3) cosd(a4) cos(a5) cosd(a6) cosd(a7) cosd(a8) cosd(a9) cosd(a10) cosd(a12) cosd(a13) cosd(a14)cosd(a15)]';B11=[sind(a1) sind(a2) sind(a3) sind(a4) sin(a5) sind(a6) sind(a7) sind(a8) sind(a9) sind(a10) sind(a12) sind(a13) sind(a14) sind(a15)]'; s=blkdiag(s10,s20,s30,s4,s50,s60,s70,s80,s90,s10',s110,s120,s130,s 14);a=*inv(s)*B11b=*inv(s)*A1ab4=atand((Y50-Y40)/(X50-X40))+180;ab10=atand((Y50-Y100)/(X50-X100));ab14=atand((Y50-Y150)/(X50-X150))+360;m4=ab4-a3+180;m10=ab10-a9+180;m11=ab4-ab10;m15=ab14-a14+180;m16=ab10-ab14+360;m04=103+57/60+34/3600;m010=98+22/60+4/3600;m011=94+53/60+50/3600;m015=180+41/60+18/3600;m016=ab10-ab14+360;l=[0 0 0 m4-103-57/60-34/3600 0 0 0 0 0 m10-98-22/60-4/3600m11-94-53/60-50/3600 0 0 0 m15-180-41/60-18/3600 m16-103-23/60-8/3600 0 0 0 s40-s4 0 0 0 0 0 s100-s1 0 0 0 s140-s14]';e1=(abs(X20-Xb))/s10;e2=(abs(X30-X20))/s20;e3=(abs(X40-X30))/s30;e4=(abs(X50-X40))/s4;e5=(abs(X60-Xd))/s50;e6=(abs(X70-X60))/s60;e7=(abs(X80-X70))/s70;e8=(abs(X90-X80))/s80;e9=(abs(X100-X90))/s90;e10=(abs(X50-X100))/s1;e11=(abs(X130-Xf))/s110;e12=(abs(X140-X130))/s120;e13=(abs(X150-X140))/s130;e14=(abs(X50-X150))/s14; e=[e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14]'m1=(abs(Y20-Yb))/s10;m2=(abs(Y30-Y20))/s20;m3=(abs(Y40-Y30))/s30;m4=(abs(Y50-Y40))/s4;m5=(abs(Y60-Yd))/s50;m6=(abs(Y70-Y60))/s60;m7=(abs(Y80-Y70))/s70;m8=(abs(Y90-Y80))/s80;m9=(abs(Y100-Y90))/s90;m10=(abs(Y50-Y100))/s1;m11=(abs(Y130-Yf))/s110;m12=(abs(Y140-Y130))/s120;m13=(abs(Y150-Y140))/s130;m14=(abs(Y50-Y150))/s14; m=[m1 m2 m3 m4 m5 m6 m7 m8 m9 m10 m11 m12 m13 m14]' %以上为求得误差方程系数B=[ 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0] %系数矩阵BP=blkdiag(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,100/s10,100/s20,100/s30,1 00/s40,100/s50,100/s60,100/s70,100/s80,100/s90,100/s100,100/s 110,100/s120,100/s130,100/s140); %定义权矩阵Nbb=B'*P*BW=B'*P*l;x=inv(Nbb)*WV=B*x-l;inv(Nbb);Y=V'*P*V;O=sqrt(Y/6)*3600 %精度评定计算结果:平差值坐标X: +003 *Qx1= Qy1= Qx2= Qy2= ……Qx15= Qy15=。
数据结构课程设计——导线网平差程序的设计与实现

数据结构课程设计——导线网平差程序的设计与实现设计二:导线网平差程序的设计与实现一、设计目的立足于《数据结构与测绘软件开发》这一课程的课堂教学及其实验课程设计,为着实提高学生基于计算机辅助的方式切实解决工程实际问题的动手能力,通过本实习,一方面,使学生深入了解课堂所学知识,另一方面,通过实践掌握测绘行业软件设计与开发的基本方法,深刻掌握矩阵运算、曲线/曲面拟合的数值解法,掌握不同类型的典型测绘软件设计方法,使得学生初步具备编写测绘软件常用算法的能力以及开发中小规模测绘专业软件的能力。
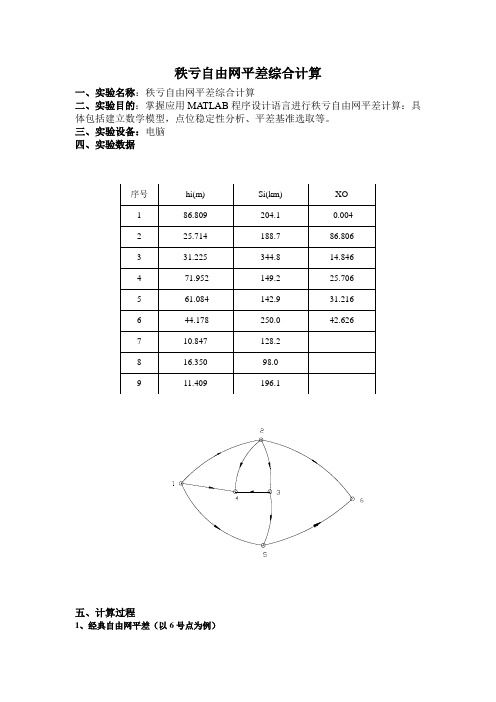
有导线网如图,观测了14条边长和16个转折角,已知测角精度10βδ''=,测边精度为1.0()()S S m mm δ=。
已知A 、B 、C 、D 、E 、F 点的坐标(无误差),如下表:表1 已知点数据点号 X(m) Y(m)A 5256.953 4520.068B 5163.752 4281.277C 3659.371 3621.210D 4119.879 3891.607E 4581.150 5345.292F 4851.5545316.953表2 角度观测值编号角度观测值(° ′ ″)编号角度观测值(° ′ ″)1 163 45 04 9 169 10 302 64 58 37 10 98 22 043 250 18 11 11 94 53 50 4 103 57 34 12 111 14 235 83 08 05 13 79 20 18三、关键问题描述3.1 未知点近似坐标计算平面控制网进行平差计算时需要计算未知点的近似坐标1.坐标计算公式1、2点的坐标已知,并观测了1-2、1-3的夹角,根据这些数据可以求出3号点坐标根据1、2两点的坐标,可以反算出1、2方向的方位角T12,3号点的坐标为++=++=)sin()cos(121313121313ααT S y y T S x x式子中S13为观测边长,α为观测角度 2.计算流程从读入的数据循环计算未知点的坐标,已计算出的坐标当做已知坐标的点处理参加下次计算,以此类推,逐步计算出未知点的坐标3.实现算法CMatrix CPlaneNetAdjust::XYJS() { CMatrix _XYJS(Pnumber,2); double T12; for(int i=0;i0&&xy[k2].Y>0) { T12=GetT12(k1,k2); } double s12=Gets12(k1,k2); double s13=Gets12(k1,k3); double T13=T12+guancejiao[i].Guancezhi; double dx=s13*cos(T13); double dy=s13*sin(T13); xy[k3].X=xy[k1].X+dx; xy[k3].Y=xy[k1].Y+dy; } for(int i=0;i<="" bdsfid="103" double="" p="" temp1="xy[i].X;" temp2="xy[i].Y;" {="">}return _XYJS;}3.2 误差方程列立1.理论分析平面控制网的误差方程都是非线性方程,必须引入参数近似值将误差方程线性化,取X的充分近似值 0X ,x ?是微小量,在按台劳公式展开时可以略去二次和二次以上的项,而只取至一次项,于是可对非线性平差值观测方程式线性化,于是有如下的式子对于观测角的改正数有对于边长观测值的改正数有2.实现算法如下:CMatrix CPlaneNetAdjust::B() { CMatrix _B1(Lnumber,Pnumber*2); double a; double b; double c; double d; double m; double n; double m1; double n1; for(int i=0;i<="">D A D A D B D B DA DB X X Y Y X X Y Y L ??arctan ??arctan 1-----=-=αα()()22??S AD A D Y Y X X -+-=kjkjk k jk jk j jk jkj jk jk jk y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200200200200"??+??-??-??+=ρρρραδh jhjh h jh jh j jh jh j jh jh jh y S Y x S Y y S X x S Y ?)(?)(?)(?)(?200 200200200"??+??-??-??+=ρρρραδ)(?)("?)("?)("?)("?)("?)("?)(" )("00200200200200200200200200i jk jh h jh jhh jh jh j jh jh j jh jh k jk jkk jk jk j jk jk j jk jk i L y S X x S Y y S X x S Y y S X x S Y y S X xS Y v ---??+?-?-?-+?-?-?-=ααρρρρρρρρi k jkjkk jk jk j jk jk j jk jk i l y S Y x S X y S Y x S X v -?+?+?-?-=000000000jki i S L l -=2002000)()(j k j k jk Y Y X X S -+-=_B1.setValue(i,2*k1,0);_B1.setValue(i,2*k1+1,0);}else{_B1.setValue(i,2*k1,a);_B1.setValue(i,2*k1+1,b);}if(k2<knpnumber)< bdsfid="148" p=""></knpnumber)<> {_B1.setValue(i,2*k2,0);_B1.setValue(i,2*k2+1,0);}else{_B1.setValue(i,2*k2,-a);_B1.setValue(i,2*k2+1,-b);}}for(int i=0;i<tnumber;i++)< bdsfid="160" p=""></tnumber;i++)<>{const double p=206.265;int k1=cezhan[i];int k3=huoshi[i];int k2=qianshi[i];double dx12=xy[k2].X-xy[k1].X;double dy12=xy[k2].Y-xy[k1].Y;double dx13=xy[k3].X-xy[k1].X;double dy13=xy[k3].Y-xy[k1].Y;c=(p*dx13/Gets12(k1,k3)/Gets12(k1,k3)-p*dx12/Gets12(k1,k2)/Gets12(k1,k2));c=-c;d=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3)+p*dy12/Gets12(k1,k2)/Get s12(k1,k2);d=-d;m=-p*dy13/Gets12(k1,k3)/Gets12(k1,k3);m=-m;n=p*dx13/Gets12(k1,k3)/Gets12(k1,k3);n=-n;m1=p*dy12/Gets12(k1,k2)/Gets12(k1,k2);m1=-m1;n1=-p*dx12/Gets12(k1,k2)/Gets12(k1,k2);n1=-n1;if(k1<knpnumber)< bdsfid="183" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k1,0);_B1.setValue(i+Snumber,2*k1+1,0);}else if(k1>=knPnumber){_B1.setValue(i+Snumber,2*k1,c);_B1.setValue(i+Snumber,2*k1+1,d);}if(k2<knpnumber)< bdsfid="194" p=""></knpnumber)<> {_B1.setValue(i+Snumber,2*k2,0);_B1.setValue(i+Snumber,2*k2+1,0);}else if(k2>=knPnumber){ _B1.setValue(i+Snumber,2*k2,m1); _B1.setValue(i+Snumber,2*k2+1,n1); } if(k3=knPnumber) { _B1.setValue(i+Snumber,2*k3,m); _B1.setValue(i+Snumber,2*k3+1,n); } }CMatrix _B(Lnumber,2*(Pnumber-knPnumber)); for(int i=0;i<_B1.getRow();i++) { for(int j=2*knPnumber;j<2*Pnumber;j++) { double temp=_B1.getValue(i,j); _B.setValue(i,(j-2*knPnumber),temp); } } return _B;}3.3 法方程构建与解算1.理论分析误差方程系数构成法方程2.实现代码①计算LCMatrix CPlaneNetAdjust::L() { CMatrix _L(Lnumber,1); double l; double s; double s0; for(int i=0;i<="" bdsfid="209" const="" cout<<l<l x B V -=?0?=-Pl B x PB B TTmin =PV V T V L L +=?20σ20?σPV V T double A13; double A;int k1=cezhan[i]; int k2=huoshi[i]; int k3=qianshi[i];A12=GetT12(k1,k2); A13=GetT12(k1,k3); A=GetA(k1,k2,k3); l=A13-A12; if(l<0) { l=pi+l; }if(l>=pi) { l=l-pi; }l=l-A;//cout<<rad_dms(a12)<<" "<<rad_dms(a)<<"<="" "<<rad_dms(a13)<<"="" bdsfid="220" p=""></rad_dms(a12)<<">"<<rad_dms(l)<<endl;< bdsfid="222" p=""></rad_dms(l)<<endl;<>_L.setValue(i+Snumber,0,rad_dms(l));} return _L; }②计算权阵PCMatrix CPlaneNetAdjust::P() { CMatrix _P(Lnumber,Lnumber); for(int i=0;i<="" p="" {="">temp=temp=Cjwucha*Cjwucha/(1*sqrt(bianchang[i].Len))/( 1*sqrt(bianchang[i].Len)); _P.setValue(i,i,temp); } for(int i=Snumber;i<="">3.4 精度估计1.单位权中误差间接平差与条件平差虽采用了不同的函数模型,但它们是在相同的最小乘原理下进行的,所以两法的平差结果总是相等的,这是因为在满足条件下的V 是唯一确定的,故平差值不因方法不同而异。
平差实验报告及完整matlab程序
%------------------从文本框输入数据-------------------------------
%m=get(findobj('tag','edit1'),'string');
%l1=str2num(m);
七、MATLAB程序代码
1、经典自由网平差
[f,p1]=uigetfile('*.txt','选择高差文件')
fnal=strcat(p1,f);fpath=p1;
fm=fopen(fnal,'r');
while (~feof(fm))
l1=fscanf(fm,'%f',inf);
end
[f,p1]=uigetfile('*.txt','选择距离文件')
(3-2)
其中
(3-3)
(3-4)
得出
(3-5)
求得参数 的最佳估值为
参数 的协因数阵为
六、综合分析
从结果中我们可以看出,三种平差方法所得高差的改正数是相同的,所得参数 的最佳估值是不同的。
经典自由网平差适用于起算数据充足的情况,而秩亏自由网平差适用于起算数据不足,需要加一个基准条件才能进行平差计算。拟稳平差则是选择一些相对稳定的点进行平差,是那些不稳定的点不参与平差。根据实际情况我们选择适宜的平差方法。
%s=str2num(n);
%s=s';
%------------------从文本框输入数据--------------------------------------------
测绘 matlab 编程 程序

导线网严密平差 完整程序代码及注释已知数据已知点坐标:XA=730.024 ,YA=126.040 ,111.855=XB,232.172=Y B应得结果 = 5.30表七:实际结果点号X(m) Y(m) 中误差X(mm) 中误差Y(mm) 点位中误差1 678.1641 287.3411 3.3868 5.8737 7.60782 564.6919 446.8827 6.0102 7.5137 9.19373 533.8468 629.2749 8.7985 7.3927 10.05964 475.6776 535.8728 7.3949 8.4987 9.96675 499.1408 374.4231 5.8076 7.6840 9.18276 594.6190 176.7976 5.2308 3.4068 7.34757 826.3848 305.7569 2.7439 5.4473 7.15518 767.8778 401.8510 4.8371 6.3810 8.37349 745.7230 531.0410 6.8992 6.6276 9.194710 671.6256 650.8637 9.0695 6.0533 9.722011 794.2833 600.4688 8.4994 6.1800 9.578412 859.0528 511.5349 6.7399 6.6874 9.160813 898.2695 399.0763 4.7580 6.4207 8.358614 919.3459 276.9409 3.1903 4.8006 7.0670单位权中误差: 5.3393详细代码% 贡XX导线严密平差程序clear;clc;% 从文件中输入数据% S1 观测角度数据% 【角号度分秒左点角点右点】-1为已知点B,0为已知点A fid1=fopen('S1.txt','rt');[S1,~]=fscanf(fid1,'%f ',[7 24]);fclose(fid1);S1=S1';% S2 边长观测值% 【边号距离测边中误差对应角号】fid2=fopen('S2.txt','rt');[S2,~]=fscanf(fid2,'%f ',[5 17]);fclose(fid2);S2=S2';% S3:度分秒到角度[S3]=dfm2jd(S1);% 计算坐标近似值% X0=[x1 y1 x2 y2 ......][X0]=zbjs(S2,S3);% 循环,未知参数改正量最大值mx<0.01mm停止mx=100;while mx>0.01% 计算B,l,P 矩阵[B,l,P]=BBll(X0,S2,S1,S3);% P68页x=(B'*P*B)\B'*P*l;% 改正量mx=max(x);v=B*x+l;[rr,cc]=size(B);m0=sqrt((v'*P*v)/(rr-cc));% 单位权中误差Q=inv(B'*P*B);% 协因数阵M=m0^2*Q;% 未知数方差矩阵% 平差后坐标X=X0'+x/1000;X0=X';end% 坐标中误差for i=1:28det(i)=sqrt(M(i,i));end% 点位中误差for i=1:14ddet(i)=2.5*sqrt(det(i*2-1)+det(i*2));endddet=ddet';% 整理数据,输出最终结果for i=1:14XX(i,1)=X(2*i-1);XX(i,2)=X(2*i);DD(i,1)=det(2*i-1);DD(i,2)=det(2*i);endjieguo(:,1)=1:14;jieguo(:,2)=XX(:,1);jieguo(:,3)=XX(:,2);jieguo(:,4)=DD(:,1);jieguo(:,5)=DD(:,2);jieguo(:,6)=ddet;disp('计算完成!')fid=fopen('输出结果.txt','wt');fprintf(fid,'点号 X(m) Y(m) 中误差X(mm) 中误差Y(mm) 点位中误差 \n');fprintf(fid,' %2d %11.4f %11.4f %5.4f %5.4f %5.4f\ n',(jieguo)');fprintf(fid,'单位权中误差:%8.4f',(m0)');fclose(fid);====================================================% 单位转换function [S3]=dfm2jd(S1)for i=1:24S3(i,1)=S1(i,1);S3(i,2)=(S1(i,2)+S1(i,3)/60+S1(i,4)/3600);End====================================================% 计算坐标近似值function [X0]=zbjs(S2,S3)% 起始数据X10=[730.024;126.040;855.111;172.232];X0=zeros(1,28);% 预分配内存% 已知边方位角t=180+atand((X10(2)-X10(4))/(X10(1)-X10(3)));% 下方闭合% 起始方位角t1=t;for i=1:1:6% 计算各边方位角if S2(i,5)>0 % i=4t1=t1+S3(S2(i,4),2)+S3(S2(i,5),2)-180;% 边4方位角+角6+角7-180 elset1=t1+S3(S2(i,4),2)-180;endif t1<0t1=t1+360;end% 计算各点近似坐标if i<2X0(1)=X10(1)+S2(1,2)*cosd(t1);X0(2)=X10(2)+S2(1,2)*sind(t1);endif i>=2X0(2*i-1)=X0(2*(i-1)-1)+S2(i,2)*cosd(t1);X0(2*i)=X0(2*(i-1))+S2(i,2)*sind(t1);endend% 上方闭合% 起始方位角t2=t;t2=t2-S3(12,2);if t2<0t2=t2+360;endfor i=8:1:15% 计算个边方位角if i<9 % i=8X0(2*(i-1)-1)=X10(3)+S2(i,2)*cosd(t2);X0(2*(i-1))=X10(4)+S2(i,2)*sind(t2);endif i>8t2=t2+S3(S2(i,4),2)-180;if t2<0t2=t2+360;end% 计算各点近似坐标X0(2*(i-1)-1)=X0(2*(i-2)-1)+S2(i,2)*cosd(t2); X0(2*(i-1))=X0(2*(i-2))+S2(i,2)*sind(t2);endend==================================================== % 计算方位角function [M]=fangweijiao(a,b,X0)X10=[730.024;126.040;855.111;172.232];% 确定边对应两点类型及坐标。
用MATLAB解决-条件平差和间接平差

L1 A
L3 C
9
clc Disp(‘条件平差示例2’) Disp(‘三角形内角观测值’) L1 = [42 12 20] L2 = [78 9 9] L3 = [59 38 40] L = [L1; L2; L3] Disp(‘将角度单位由度分秒转换为弧度’) LL = dms2rad(mat2dms(L))
设误差Δ和参数X的估计值分别为V 和 Xˆ
15
则有
V AXˆ l
为了便于计算,通常给参数估计一个充分接近的近似值 X 0
Xˆ X 0 xˆ 则误差方程表示为
V Axˆ l
其中常数项为
l L (AX 0 d)
16
由最小二乘准则,所求参数的改正数应该满足
V T PV min
目标函数对x求一阶导数,并令其为零
if(sum(LL) == pi) disp(‘检核正确’)
else
V = A'*Ka
disp(‘检核错误’) end
11 例 《误差理论与测量平差基础》P75
在下图中,A、B为已知水准点,其高程为 HA=12.013m, HB = 10.013m, 可视为无误差。为 了确定点C及D点的高程,共观测了四个高差,高差 观测值及相应的水准路线的距离为:
disp(‘系数矩阵B’)
B = [1 0; 0 1; 1 0; 0 1; -1 1; -1 0]
l = [0; 0; 4; 3; 7; 2]
disp(‘C是单位权观测高差的线路公里数,S是线路长度’)
C = l*ones(1,6)
23
h6
E h3
h7 B
S = [1.1, 1.7, 2.3, 2.7, 2.4, 4.0]
用MATLAB解决_条件平差和间接平差(可编辑)

用MATLAB解决_条件平差和间接平差测量程序设计条件平差和间接平差一、条件平差基本原理A LA0函数模型 A VW0r n n 1 r 1r 12 21随机模型D? Q? P0 0TV P Vm i n平差准则条件平差就是在满足r个条件方程式条件下,求使函数V‘PV最小的V值,满足此条件极值问题用拉格朗日乘法可以求出满足条件的V值。
?A LA01、平差值条件方程: 0r n n 1r 1r 1a La L a La01 12 2 n n 0b Lb L b Lb01 12 2 n n 0?r Lr L r Lr01 12 2 n n 0a ,b ,, r i1 , 2 ,, n 条件方程系数i i ia ,b ,, r0 0 0常数项?A LA02、条件方程: 0r n n 1r 1r 1将LLV代入平差值条件方程中,得到A VW0r 1 n 1 r 1 r 1w , w ,, wa b r为条件方程闭合差WA LA闭合差等于观测值减去其应有值。
3、改正数方程:按求函数条件极值的方法引入常数TK k , k ,, ka b rr 1称为联系系数向量,组成新的函数:T T? V P V2 K A VW将Ω对V求一阶导数并令其为零?T T2 V P2 K A0VT1 T TP VA K则: VP A KQ A K4、法方程: 将条件方程 AV+W0代入到改正数方程VQATK 中,则得到:TA Q A KW0N KW0记作: a ar 1 r 1 r 1r rTR N R A Q A R A r由于 a a1 T1K? N W? A Q A A LANaa为满秩方阵,a a 0TLLVVQ A K按条件平差求平差值计算步骤A VW01、列出rn-t个条件方程r 1 n 1 r 1 r 1T1 TN KW0NA Q AA P A2、组成法方程a aa ar 1 r 1 r 1r r1K? N Wa a3、求解联系系数向量4、将 K值代入改正数方程VP-1ATKQATk中,求出V值,并求出平差值LL+V。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验三利用matlab程序设计语言完成某工程导线网平差计算实验数据;某工程项目按城市测量规范(CJJ8-99)不设一个二级导线网作为首级平面控制网,主要技术要求为:平均边长200cm,测角中误差±8,导线全长相对闭合差<1/10000,最弱点的点位中误差不得大于5cm,经过测量得到观测数据,设角度为等精度观测值、测角中误差为m=±8秒,鞭长光电测距、测距中误差为m=±0.8√smm,根据所学的‘误差理论与测量平差基础’提出一个最佳的平差方案,利用matlab完成该网的严密平差级精度评定计算;平差程序设计思路:1采用间接平差方法,12个点的坐标的平差值作为参数.利用matlab进行坐标反算,求出已知坐标方位角;根据已知图形各观测方向方位角;2计算各待定点的近似坐标,然后反算出近似方位角,近似边.计算各边坐标方位角改正数系数;3确定角和边的权,角度权Pj=1;边长权Ps=100/S;4计算角度和边长的误差方程系数和常数项,列出误差方程系数矩阵B,算出Nbb=B’PB,W=B’Pl,参数改正数x=inv(Nbb)*W;角度和边长改正数V=Bx-l;6 建立法方程和解算x,计算坐标平差值, 精度计算;程序代码以及说明:s10=238.619;s20=170.759;s30=217.869;s40=318.173;s50=245.635;s60=215.514;s70=273.829;s80=241.560;s90=224.996;s100=261.826;s110=279.840;s120=346.443;s130=312.109;s140=197.637; %已知点间距离Xa=5256.953;Ya=4520.068;Xb=5163.752;Yb=4281.277;Xc=3659.371;Yc=3621.210;Xd=4119.879;Yd=3891.607;Xe=4581.150;Ye=5345.292;Xf=4851.554;Yf=5316.953; %已知点坐标值a0=atand((Yb-Ya)/(Xb-Xa))+180;d0=atand((Yd-Yc)/(Xd-Xc));f0=atand((Yf-Ye)/(Xf-Xe))+360; %坐标反算方位角a1=a0+(163+45/60+4/3600)-180a2=a1+(64+58/60+37/3600)-180;a3=a2+(250+18/60+11/3600)-180;a4=a3+(103+57/60+34/3600)-180;a5=d0+(83+8/60+5/3600)+180;a6=a5+(258+54/60+18/3600)-180-360;a7=a6+(249+13/60+17/3600)-180;a8=a7+(207+32/60+34/3600)-180;a9=a8+(169+10/60+30/3600)-180;a10=a9+(98+22/60+4/3600)-180;a12=f0+(111+14/60+23/3600)-180;a13=a12+(79+20/60+18/3600)-180;a14=a13+(268+6/60+4/3600)-180;a15=a14+(180+41/60+18/3600)-180; %推算个点方位角aa=[a1 a2 a3 a4 a5 a6 a7 a8 a9 a10 a12 a13 a14 a15]' X20=Xb+s10*cosd(a1);X30=X20+s20*cosd(a2);X40=X30+s30*cosd(a3);X50a=X40+s40*cosd(a4);X60=Xd+s50*cosd(a5);X70=X60+s60*cosd(a6);X80=X70+s70*cosd(a7);X90=X80+s80*cosd(a8);X100=X90+s90*cosd(a9);X50c=X100+s100*cosd(a10);X130=Xf+s110*cosd(a12);X140=X130+s120*cosd(a13);X150=X140+s130*cosd(a14);X50e=X150+s140*cosd(a15); %各点横坐标近似值X0=[X20 X30 X40 X60 X70 X80 X90 X100 X130 X140 X150 X50a X50c X50e]'Y20=Yb+s10*sind(a1);Y30=Y20+s20*sind(a2);Y40=Y30+s30*sind(a3);Y50a=Y40+s40*sind(a4);Y60=Yd+s50*sind(a5);Y70=Y60+s60*sind(a6);Y80=Y70+s70*sind(a7);Y90=Y80+s80*sind(a8);Y100=Y90+s90*sind(a9);Y50c=Y100+s100*sind(a10);Y130=Yf+s110*sind(a12);Y140=Y130+s120*sind(a13);Y150=Y140+s130*sind(a14);Y50e=Y150+s140*sind(a15); %个点从坐标近似值Y0=[Y20 Y30 Y40 Y60 Y70 Y80 Y90 Y100 Y130 Y140 Y150 Y50a Y50c Y50e]'P=[X0 Y0];X50=(X50a+X50c+X50e)/3Y50=(Y50a+Y50c+Y50e)/3s4=sqrt((Y40-Y50)^2+(X40-X50)^2);s1=sqrt((Y100-Y50)^2+(X100-X50)^2);s14=sqrt((Y150-Y50)^2+(X150-X50)^2);A1=[cosd(a1) cosd(a2) cosd(a3) cosd(a4) cos(a5) cosd(a6) cosd(a7) cosd(a8) cosd(a9) cosd(a10) cosd(a12) cosd(a13) cosd(a14) cosd(a15)]';B11=[sind(a1) sind(a2) sind(a3) sind(a4) sin(a5) sind(a6) sind(a7) sind(a8) sind(a9) sind(a10) sind(a12) sind(a13) sind(a14) sind(a15)]';s=blkdiag(s10,s20,s30,s4,s50,s60,s70,s80,s90,s10',s110, s120,s130,s14);a=206.2648026*inv(s)*B11b=-206.2648026*inv(s)*A1ab4=atand((Y50-Y40)/(X50-X40))+180;ab10=atand((Y50-Y100)/(X50-X100));ab14=atand((Y50-Y150)/(X50-X150))+360;m4=ab4-a3+180;m10=ab10-a9+180;m11=ab4-ab10;m15=ab14-a14+180;m16=ab10-ab14+360;m04=103+57/60+34/3600;m010=98+22/60+4/3600;m011=94+53/60+50/3600;m015=180+41/60+18/3600;m016=ab10-ab14+360;l=[0 0 0 m4-103-57/60-34/3600 0 0 0 0 0 m10-98-22/60-4/3600 m11-94-53/60-50/3600 0 0 0 m15-180-41/60-18/3600 m16-103-23/60-8/3600 0 0 0 s40-s4 0 0 0 0 0 s100-s1 0 0 0 s140-s14]';e1=(abs(X20-Xb))/s10;e2=(abs(X30-X20))/s20;e3=(abs(X40-X30))/s30;e4=(abs(X50-X40))/s4;e5=(abs(X60-Xd))/s50;e6= (abs(X70-X60))/s60;e7=(abs(X80-X70))/s70;e8=(abs(X90-X80))/s80;e9=(abs(X100-X90))/s90;e10=(abs(X 50-X100))/s1;e11=(abs(X130-Xf))/s110;e12=(abs(X140-X130 ))/s120;e13=(abs(X150-X140))/s130;e14=(abs(X50-X150))/s 14;e=[e1 e2 e3 e4 e5 e6 e7 e8 e9 e10 e11 e12 e13 e14]'m1=(abs(Y20-Yb))/s10;m2=(abs(Y30-Y20))/s20;m3=(abs(Y40-Y30))/s30;m4=(abs(Y50-Y40))/s4;m5=(abs(Y60-Yd))/s50;m6= (abs(Y70-Y60))/s60;m7=(abs(Y80-Y70))/s70;m8=(abs(Y90-Y80))/s80;m9=(abs(Y100-Y90))/s90;m10=(abs(Y 50-Y100))/s1;m11=(abs(Y130-Yf))/s110;m12=(abs(Y140-Y130 ))/s120;m13=(abs(Y150-Y140))/s130;m14=(abs(Y50-Y150))/s 14;m=[m1 m2 m3 m4 m5 m6 m7 m8 m9 m10 m11 m12 m13 m14]' %以上为求得误差方程系数B=[-0.6851 0.5271 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 00.3872 0.0289 -1.0723 -0.556 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0.9453 1.4942 0.127 -0.9382 -0.9382 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 00 0 0.127 -0.9382 0.4756 1.1776 -0.6026 -0.2394 0 0 0 0 0 00 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0.8256 -0.1536 0 0 0 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0 0 0 -0.6191 -0.7809 -0.2065 0.9345 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 -0.2065 0.9345 0.9518 -1.0435 -0.7453 0.1090 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 -0.7453 0.109 1.5516 0.1722 -0.8063-0.2812 0 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 -0.8063 -0.2812 1.7132 0.4151-0.9069 -0.1339 0 0 0 0 0 00 0 0 0 0 0 -0.2491 0.8277 0 0 0 0 0 0 -0.9069 0.13391.156 -0.6938 0 0 0 0 0 00 0 0 0 0.6026 0.2394 0.8517 -0.5863 0 0 0 0 0 0 0 0-0.2491 0.8277 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.7111-0.194 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0.75880.7875 0.0477 -0.5935 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.0477-0.5935 -0.7078 0.6246 0.6601 -0.03110 0 0 0 0 0 1.0417 -0.0616 0 0 0 0 0 0 0 0 0 00 0 0.6601 -0.0311 -1.7018 0.09270 0 0 0 0 0 -1.2809 0.7661 0 0 0 0 0 0 0 0 0.2491-0.8277 0 0 0 0 1.0417 -0.0666160.6097 0.7926 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0-0.4603 -0.8878 0.4603 0.8878 0 0 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 -0.991 -0.1342 0.991 0.1342 0 0 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 -0.3692 -0.9293 0.3692 0.9293 0 0 0 0 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0.3996 0.9167 0 0 0 0 0 0 0 00 0 0 0 0 00 0 0 0 0 0 0 0 -0.9764 -0.2158 0.9764 0.2158 0 0 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 -0.1447 -0.9895 0.1447 0.9895 0 00 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 -0.3293 -0.9442 0.3293 0.94420 0 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 -0.1461 -0.9893 0.14610.9893 0 0 0 0 0 00 0 0 0 0 0 0.9574 0.2888 0 0 0 0 0 0 0 0 -0.9574-0.2888 0 0 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0.26310.9648 0 0 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 -0.9968-0.0801 0.9968 0.0801 0 00 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0 0-0.047 -0.9989 0.047 0.99890 0 0 0 0 0 0.0594 0.9982 0 0 0 0 0 0 0 0 0 00 0 0 0 -0.0594 -0.9982] %系数矩阵BP=blkdiag(1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,100/s10,100/s 20,100/s30,100/s40,100/s50,100/s60,100/s70,100/s80,100/ s90,100/s100,100/s110,100/s120,100/s130,100/s140); %定义权矩阵Nbb=B'*P*BW=B'*P*l;x=inv(Nbb)*WV=B*x-l;inv(Nbb);Y=V'*P*V;O=sqrt(Y/6)*3600 %精度评定计算结果:平差值坐标X:1.0e+003 *5.414.7794.939666919351774.243722669732694.723766697056704.214495899835014.6064.514.2773.666432027933254.428470738901183.712935194996014.4683.983879165637154.388516421220114.211973756480034.35564105689259 4.434551206907994.9255.9054.579856068353585.5184.59452770624570 4.734Qx1=1.488 Qy1=1.5596 Qx2=2.2058 Qy2=5.1342 ……Qx15=1.1836 Qy15=4.926811 / 11。
