理论力学课后习题第三章解答
清华大学版理论力学课后习题答案大全_____第3章静力学平衡问题习题解
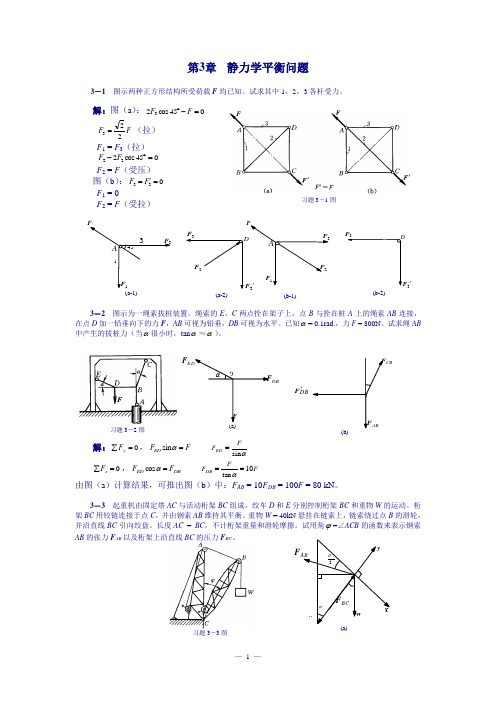
F DBCBDBF '习题3－3图第3章 静力学平衡问题3－1 图示两种正方形结构所受荷载F 均已知。
试求其中1，2，3各杆受力。
解：图（a ）：045cos 23=-︒F FF F 223=（拉） F 1 = F 3（拉） 045cos 232=︒-F F F 2 = F （受压） 图（b ）：033='=F F F 1 = 0F 2 = F （受拉）3－2 图示为一绳索拔桩装置。
绳索的E 、C 两点拴在架子上，点B 与拴在桩A 上的绳索AB 连接，在点D 加一铅垂向下的力F ，AB 可视为铅垂，DB 可视为水平。
已知α= 0.1rad.，力F = 800N 。
试求绳AB 中产生的拔桩力（当α很小时，tan α≈α）。
解：0=∑y F ，F F ED =αsin αs i nFF ED = 0=∑x F ，DB ED F F =αcos F FF DB 10tan ==α由图（a ）计算结果，可推出图（b ）中：F AB = 10F DB = 100F = 80 kN 。
3－3 起重机由固定塔AC 与活动桁架BC 组成，绞车D 和E 分别控制桁架BC 和重物W 的运动。
桁架BC 用铰链连接于点C ，并由钢索AB 维持其平衡。
重物W = 40kN 悬挂在链索上，链索绕过点B 的滑轮，并沿直线BC 引向绞盘。
长度AC = BC ，不计桁架重量和滑轮摩擦。
试用角ϕ=∠ACB 的函数来表示钢索AB 的张力F AB 以及桁架上沿直线BC 的压力F BC 。
(b-1)习题3－1图(a-1)(a-2)'3(b-2)习题3－2图F习题3-5图习题3－4图 解：图（a ）：0=∑x F ，0sin 2cos=-ϕϕW F AB ，2sin2ϕW F AB =0=∑y F ，02sincos =---ϕϕAB BC F W W F即 2s i n 2c o s 2ϕϕW W W F BC ++=W W W W 2)c o s 1(c o s =-++=ϕϕ3－4 杆AB 及其两端滚子的整体重心在G 点，滚子搁置在倾斜的光滑刚性平面上，如图所示。
胡汉才编著《理论力学》课后习题答案第3章习题解答
3-3在图示刚架中，已知kN/m3=mq，26=F kN，mkN10⋅=M，不计刚架自重。
求固定端A处的约束力。
mkN12kN60⋅===AAyAxMFF，，3-4杆AB及其两端滚子的整体重心在G点，滚子搁置在倾斜的光滑刚性平面上，如图所示。
对于给定的θ角，试求平衡时的β角。
Aθ3lGβGθBBFARF32lO解：解法一：AB为三力汇交平衡，如图所示ΔAOG中βsinlAO=，θ-︒=∠90AOG，β-︒=∠90OAG，βθ+=∠AGO由正弦定理：)90sin(3)sin(sinθβθβ-︒=+ll，)cos31)sin(sinθβθβ=+l即βθβθθβsincoscossincossin3+=即θβtantan2=)tan21arctan(θβ=解法二：：=∑x F，0sinR=-θGF A（1）=∑y F，0cosR=-θGF B（2）)(=∑FAM，0sin)sin(3R=++-ββθlFlG B（3）解（1）、（2）、（3）联立，得)tan21arctan(θβ=3-5 由AC 和CD 构成的组合梁通过铰链C 连接。
支承和受力如图所示。
已知均布载荷强度kN/m 10=q ，力偶矩m kN 40⋅=M ，不计梁重。
kN 15kN 5kN 40kN 15===-=D C B A F F F F ；；；解：取CD 段为研究对象，受力如图所示。
0)(=∑F CM，024=--q M F D ；kN 15=D F取图整体为研究对象，受力如图所示。
0)(=∑F AM ，01682=--+q M F F D B；kN 40=B F0=∑yF ，04=+-+D BAyF q F F ；kN 15-=Ay F0=∑x F ，0=AxF3-6如图所示，组合梁由AC 和DC 两段铰接构成，起重机放在梁上。
已知起重机重P1 = 50kN ，重心在铅直线EC 上，起重载荷P2 = 10kN 。
如不计梁重，求支座A 、B 和D 三处的约束反力。
理论力学(胡运康)第三章作业答案
11
3-26 已知：M1=10kN，求FBx 、 FBy 、MB 、FAC 、 FEx 、 FEy 解: 1、整体：
∑M
∑F
MB
FBx FBy
x
B
= 0 ⇒ MB
= 0 ⇒ FBx = 0
= 0 ⇒ FBy
∑F
y
2、AB： FD
A
FEy
E
∑M
FEx
B
E
= 0 ⇒ FD
∑F
∑F
x
= 0 ⇒ FEx
= 0 ⇒ FEy
3-42 已知：q1=4kN/m , q2=2kN/m ，F =2 kN ，M=2 kN.m 。求 A、B处受力；销钉C所受的力。
F1 F2
F B FB FC1y C FC2y
C FC2y 1m
4/3 m
q 解: 1、BC： F1 = 1 ⋅ 2 = 4kN, 2
F2 =
1 q1 ⋅ ⋅ 2 = 2kN 2 2
M1 B
FE
Aቤተ መጻሕፍቲ ባይዱ
∑M
2、DC：
M2
FC
x
A
= 0, ⇒ FE
F'E
D
FE= F'E
C FCy
∑M
C
= 0, ⇒ M 2
8
3-17 求 机构平衡时力偶M1、M2的关系。
FAx FAy
A
FD F'D D
B
M1
FD= F'D
FCx
M2
C FCy
解: 1、AB： ∑ M A = 0, FD ⋅ d − M 1 = 0, ⇒ FD = M 1
2
3-3
几何法
理论力学(哈工第七版) 课后练习答案 第三部分
A
ϕ
O
r ϕ
M
W=
2π
∫ 4ϕ dϕ + (m
0
− mB ) g ⋅ 2π r
A B
A mAg
= 8π 2 + (mA − mB ) g ⋅ 2π r = 8π 2 + 1× 9.8 × 2π × 0.5 = 110 (J)
B
mBg
(a)
(b)
7
12-4 图示坦克的履带质量为 m，两个车轮的质量均为 m1。车轮被看成均质圆盘，半径为 R， 两车轮间的距离为 πR。设坦克前进速度为 v，计算此质点系的动能。 解：系统的动能为履带动能和车轮动能之和。将履带分为四部 分，如图b 所示。履带动能：
O
P2 P aB − 1 a A = FN − P 1−P 2 g g
其中， a A = a ， aB = 解得
A
a 2 1 (2 P 1−P 2 )a 2g
B
(a)
FN = P 1+P 2 −
v FN
O
v P 1
A
v aA
v aB B
v P2
(b)
11-1 质量为 m 的点在平面 Oxy 内运动，其运动方程为
得
G1
320
B C
SB
S A = 170 mm S B = 90 mm
(b)
2
10-12 图示滑轮中，两重物 A 和 B 的重量分别为 P1 和 P2。如物体 A 以加速度 a 下降， 不计滑轮质量，求支座 O 的约束力。 解：对整体进行分析，两重物的加速度和支座 O 的约束力如图b 所示。由 动量定理知：
整体受力和运动分析如图b因为0xf所以x方向系统守恒有21cos0brbmvmvv??解得121cosbrmmvvm1所以该系统动能为设此时三棱柱a沿三棱柱b下滑的距离为s则其重力作的功为1sinwmgs??系统动能22b211221sin12cosmmtmmvm由系统动能定理tw即1sinwmgs??上式对时间求导并注意到rdsdtv整理后得22112121sinsincosbbrmmmmvamgvm?????得2b2a212b2b2r2122b21122
理论力学课外作业加答案解析详解
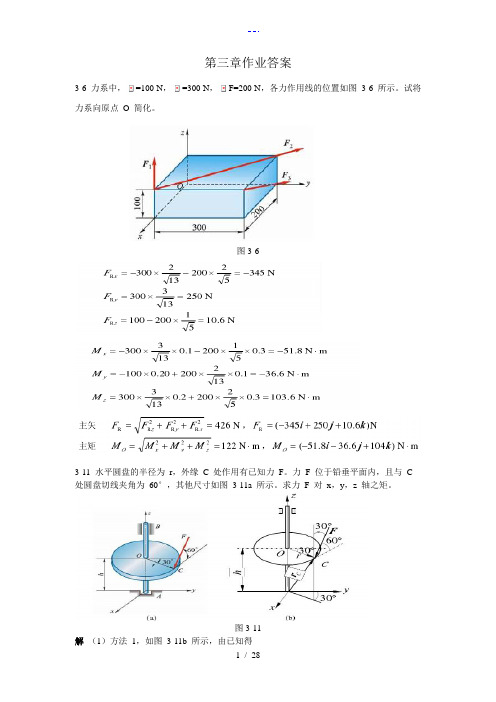
第三章作业答案3-6 力系中，=100 N，=300 N，F=200 N，各力作用线的位置如图3-6 所示。
试将力系向原点O 简化。
图3-63-11 水平圆盘的半径为r，外缘C 处作用有已知力F。
力F 位于铅垂平面内，且与C 处圆盘切线夹角为60°，其他尺寸如图3-11a 所示。
求力F 对x，y，z 轴之矩。
图3-11解（1）方法1，如图3-11b 所示，由已知得（2）方法23-14 图3-14a 所示空间桁架由杆1，2，3，4，5 和6 构成。
在节点A 上作用1 个力F，此力在矩形ABDC 平面内，且与铅直线成45°角。
ΔEAK =ΔFBM。
等腰三角形EAK，FBM和NDB 在顶点A，B 和D 处均为直角，又EC=CK=FD=DM。
若F=10 kN，求各杆的内力。
图3-14解(1) 节点 A 为研究对象，受力及坐标如图3-14b 所示（2）节点B 为研究对象，受力如图3-14b 所示3-19 图3-19a 所示6 杆支撑1 水平板，在板角处受铅直力F 作用。
设板和杆自重不计，求各杆的内力。
图3-19解截开6 根杆，取有板的部分为研究对象，受力如图3-19b 所示。
3-22 杆系由球铰连接，位于正方体的边和对角线上，如图3-22a 所示。
在节点D 沿对角线LD 方向作用力。
在节点C 沿CH 边铅直向下作用F。
如球铰B，L 和H 是固定的，杆重不计，求各杆的内力。
图3-22解（1）节点D 为研究对象，受力如图3-22b 所示（2）节点C 为研究对象，受力如图3-22b 所示3-25 工字钢截面尺寸如图3-25a 所示，求此截面的几何中心。
图3-25解把图形的对称轴作轴x，如图3-25b 所示，图形的形心C 在对称轴x 上，即第五章作业答案5-3 如图5-3 所示，半圆形凸轮以等速= 0.01m/s沿水平方向向左运动，而使活塞杆AB 沿铅直方向运动。
当运动开始时，活塞杆A 端在凸轮的最高点上。
理论力学第三版课后答案第3章
r 由式（1）在 τ 向的坐标式，可得点 B 的速度 r τ ： vB = vO + rω = 2rω
aw .
re vω B r vO
r n
（1）
co
τ
r
m
固定圆弧纯滚动由点 O′ 到点O，有 AD = AD′ ，即 r (φ + θ ) = Rθ ，得 rφ = (R − r )θ ，两边对时
∩
∩
ww w
r 公共基 e 的坐标式为 rA = rB + A1 ρBA ，展开，考虑到图
r x2 r x3
r y3
C
3-2Ca 有
网
θ3
案
0 ⎛ xA ⎞ ⎛ ⎞ ⎛ cos φ1 ⎜ ⎜y ⎟ ⎟=⎜ ⎜ l sin (α − φ )⎟ ⎟+⎜ ⎜ 1 ⎠ ⎝ sin φ1 ⎝ A⎠ ⎝
− sin φ1 ⎞⎛ l cos α ⎞ ⎟⎜ ⎟ ⎜ ⎟ cos φ1 ⎟ ⎠⎝ 0 ⎠
aw .
r y2
B
r r 连体基 e 2 相对于与连体基 e 1 的位形为
r y
co
A
（1）
m
r y1 r x1
φ1 α
r r r r （2）对于连体基 e 1 ，由图 3-2Ca 有 rA = rB + ρ BA 在
.k hd
ρ = (0 − l sin α ) ， θ 3 =
1 C T
π
2
−α
（2）
洪嘉振等《理论力学》第 3 版习题详解
1
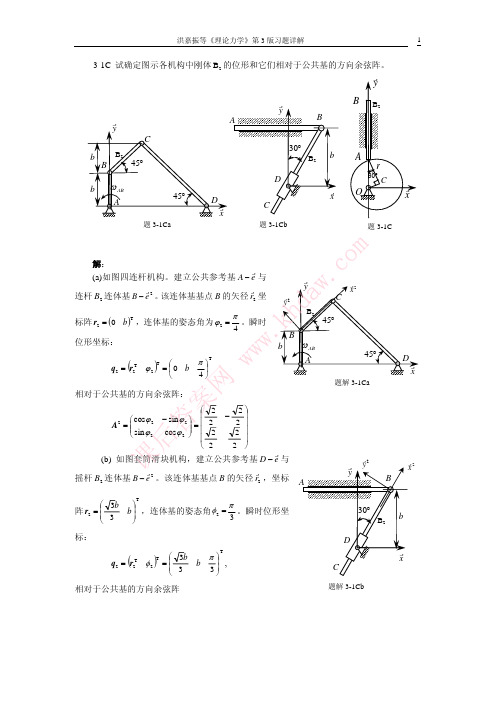
3-1C 试确定图示各机构中刚体 B2 的位形和它们相对于公共基的方向余弦阵。
r y
r y r y
C b
B2
理论力学第三章习题解答
连杆 B2 ：连体基基点 B 的矢径 r2 ，坐标阵 r2 = (0 b ) ，连体基的姿态角为
π ϕ 2 = 。瞬时位形坐标 q 2 = r2T 4
(
ϕ2 )
T
⎛ = ⎜0 b ⎝
π⎞ ⎟ 4⎠
T
-2-
⎛ cos ϕ 2 A2 = ⎜ ⎜ sin ϕ 2 ⎝
⎛ − sin ϕ 2 ⎞ ⎜ ⎟=⎜ cos ϕ 2 ⎟ ⎠ ⎜ ⎜ ⎝
3r 2
π⎞ ⎟ 3⎟ ⎠
T
⎛ cos ϕ 3 A3 = ⎜ ⎜ sin ϕ 3 ⎝
⎛ − sin ϕ 3 ⎞ ⎜ ⎟=⎜ cos ϕ 3 ⎟ ⎠ ⎜ ⎜ ⎝
3⎞ ⎟ 2 ⎟ 1 ⎟ ⎟ 2 ⎠
(3) 凸轮挺杆机构，其中 O 为偏心轮，AB 为挺杆。
-4-
题 3-1 图 题 3-1 答案图(3) 解：建立公共参考基 O − e ，对二个构件进行编号并建立连体基
⎛ cos ϕ 2 A2 = ⎜ ⎜ sin ϕ 2 ⎝
T 2
ϕ2 )
T
⎛ = ⎜0 ⎝
r 2
⎞ 0⎟ ， ⎠
T
− sin ϕ 2 ⎞ ⎛ 1 0 ⎞ ⎟=⎜ ⎟ ⎜ ⎟ cos ϕ 2 ⎟ ⎠ ⎝0 1⎠
-7-
3-2 图示长为 0.2m 的直杆，一端沿水平线运动，方向如图所示，一端沿 铅垂线运动，分别在其端部 A 和杆件中点 C，以及在其端部 A 和 B 分别建立两 个连体基。试求两个连体基位形坐标之间的关系。
理论力学第三章习题解答理论力学习题解答理论力学课后习题答案理论力学习题理论力学习题集理论力学运动学习题理论力学习题详解理论力学习题答案理论力学课后习题理论力学复习题及答案
第三章习题解答
理论力学(机械工业出版社)第三章空间力系习题解答
3-1 在边长为a 的正六面体上作用有三个力，如图 3-26所示，已知：F i =6kN, F 2=2kN, F 3=4kN 。
试求各力在三个坐标轴上的 投影。
图 3-26所示，已知六面体尺寸为 400 mmx 300 mmx300mm 正面有力F i =100N,中间有力F 2=200N,顶面有力偶 M=20N ・m作用。
试求各力及力偶对 z 轴之矩的和。
图 3-274 M z F 1 COS 450.40.3 20 J 34 20^2-240207.125 N m3-3如图3-28所示，水平轮上 A 点作用一力F =1kN,方向与 轮面成a=60°的角，且在过A 点与轮缘相切的铅垂面内，而点 A与轮心0的连线与通过0点平行于y 轴的直线成 b=45°角，图 3-28F COS sin 1000 COS 60 sin 45250^2 N 354 NF COS COS 1000 COS 60 sin 45250 (0 N 354 NF 1x 0F 1yF 2xF 2 COS 45讨仃 4 J 3F iz 72 kNF ,6 kNF 3X F ^y — kNF ayF 2yF COS 45734巧 F^ —— kN 33F 2—33kN3-2 如图 3-27 h =r=1m 。
试求力F 在三个坐标轴上的投影和对三个坐标轴之矩。
F xF z F sin 1000 sin 60 500 866 NM x (F) |F y | h |F z | 1 r cos 354 1866 1 cos 45258 N m M y (F) |F x | h |F z | r sin 354 1 866 1sin 45966 N mM z (F)F cosr1000 cos60 1500 N m主矩。
图 3-30F R xF 1 “2 屁200^5 100(14 821 .4NF R yF 2乐150714 561 .2NF RZF 1亦 F ?L 100V 5 50^14410.7NV 14F RJ ( 821.4)2( 2561.2)2410.71076.3N3-4 曲拐手柄如图3-29所示，已知作用于手柄上的力F =100N, AB=100mm BC=400mrm CC =200mrm a=30°。
理论力学教程(第三版)第三章 周衍柏编
P
∫ yc =
θ0 ρdθR(R cosθ
−θ0
θ0 ρRdθ
− R) = −R + sinθ0
θ0
R
∫−θ0
上式中 ρ 为圆弧的线密度
l = R − sinθ0 R ② θ0
又
[ ] ∫ I =
θ0 ρR (R cosθ − R)2 + (R sinθ )2 dθ
−θ 0
=
c2 ⎜⎜⎝⎛1 −
y2 b2
⎟⎟⎠⎞
故积分
H
S(y)
=
πac⎜⎜⎝⎛1 −
y2 b2
⎟⎟⎠⎞
P∫ ∫ ∫ y2dm =
b −b
y2S(y)
⋅
ρdy
=
b −b
y2πac⎜⎜⎝⎛1 −
y2 b2
⎟⎟⎠⎞ρdy
=
4 πρab3c 15
同理可求
∫ ∫ x2dm = 4 πρa3bc, z2dm = 4 πρabc3
第三章习题解答
3.1 解 如题 3.1.1 图。
y
N1 o
N2 θ
B
θ
x
θθ
G
A
题3.1.1图
S C
I 均质棒受到碗的弹力分别为 N1 ， N2, 棒自身重力为G 。棒与水平方向的夹角为
θ 。设棒的长度为 l 。
S 由于棒处于平衡状态，所以棒沿 x 轴和 y 轴的和外力为零。沿过 A 点且与
z 轴平行的合力矩为 0。即：
I
S O 为正方体中心。Ox 、Oy 、Oz 分别与正方体的边平行。由对称性可知，Ox 、
Oy 、Oz 轴就是正方体的中心惯量主轴。设正方体的边长为 a 。设为平行于轴的 一小方条的体积，则正方体绕轴的转动惯量
理论力学习题答案第三章
第三章思考题解答3.1 答：确定一质点在空间中得位置需要3个独立变量，只要确定了不共线三点的位置刚体的位置也就确定了，故须九个独立变量，但刚体不变形，此三点中人二点的连线长度不变，即有三个约束方程，所以确定刚体的一般运动不需3n 个独立变量，有6个独立变量就够了.若刚体作定点转动，只要定出任一点相对定点的运动刚体的运动就确定了，只需3个独立变量；确定作平面平行运动刚体的代表平面在空间中的方位需一个独立变量，确定任一点在平面上的位置需二个独立变量，共需三个独立变量；知道了定轴转动刚体绕转动轴的转角，刚体的位置也就定了，只需一个独立变量；刚体的平动可用一个点的运动代表其运动，故需三个独立变量。
3.2 答物体上各质点所受重力的合力作用点即为物体的重心。
当物体的大小远小于地球的线度时物体上各质点所在点的重力加速度都相等，且方向彼此平行即重力场为均匀场，此时质心与重心重合。
事实上但物体的线度很大时各质点所在处g 的大小是严格相等，且各质点的重力都指向地心，不是彼此平行的，重心与质心不和。
答 当物体为均质时，几何中心与质心重合；当物体的大小远小于地球的线度时，质心与重心重合；当物体为均质且大小远小于地球的线度时，三者都重合。
3.4 答 主矢F 是力系各力的矢量和，他完全取决于力系中各力的大小和方向，故主矢不随简化中心的位置而改变，故而也称之为力系的主矢；简化中心的位置不同，各力对简化中心的位矢i r 也就不同则各力对简化中心的力矩也就不同，故主矩随简化中心的位置而变，被称之为力系对简化中心的主矩。
分别取O 和O '为简化中心，第i 个力i F 对O 和O '的位矢分别为i r 和i r '，则i r =i r '+O O '，故()()iii ii i O F O O r F r M ⨯'-'=⨯'=∑∑'()∑∑⨯'-⨯'=ii ii i F O O F r ∑⨯'+=ii o F O O M即o o M M ≠'主矢不变，表明刚体的平动效应不变，主矩随简化中心的位置改变，表明力系的作用对刚体上不同点有不同的转动效应，但不改变整个刚体的转动规律或者说不影响刚体绕质心的转动。
理论力学第三章习题解答.ppt
量出FR的长度为161N 和水平方向的夹角为
FR FR2x FR2y 802 1402 161.2N
和水平方向（x轴）的夹角的余弦为
其余弦值为0.496
cos(FR,i ) Fx / FR 80 /161.2=0.496
2－3
解：
因为滑轮的大小忽略不计，且容易看出 AB和BC杆均为二力杆，容易得到B点的 受力如图所示：
Fx 0 FAx 0
FAy FB
Fy 0 FAy FB F 0
MA 0 FB 2a M F 3a 0
解得：
FAx 0
FAy
M Fa 2a
FB
M
3Fa 2a
3－6 （b）解：
AB杆的受力如图所示 显然，AB杆受一平面任意力
FAx
FAy
系作用，有平衡方程
Fx 0 FAx 0
FAx
FAy
系作用，有平衡方程
FB
Fx 0 FAx 0 Fy 0 FAy FB P1 P2 P 0
MA 0 FB (l1 l2) P1(l1 a) P2(l1 b) P(l1 l) 0
代入数值，解得：
FAx 0
FAy 33.23kN
FB 96.77kN
3－7
当成一整体，其受力如图所示
列平衡方程，有
FAx
FAy
Fx 0 FAx FT FBC cos 0
Fy 0 FAy FBC sin W 0
MB 0 FT r W(BD r) FAy (AD DB) 0
又因为 FT W
代入数值，解得
FAx 2400N FAy 1200N FBC 848.53N
A
x F1
FBD
B
60o
理论力学简明教程第三章非惯性参考系课后答案
第三章 非惯性参考系不识庐山真面目，只缘身在此山中。
地球的多姿多彩，宇宙的繁荣，也许在这里可以略见一斑。
春光无限，请君且放千里目，别忘了矢量语言在此将大放益彩。
【要点分析与总结】1 相对运动t r r r '=+t t dr dr dr dr dr r dt dt dt dt dtυω'''==+=++⨯ t r υυω''=++⨯()t dv dv d v r a dt dt dtω''+⨯==+222**22()t d r d r d dr r v r dt dt dt dtωωωω'''''=++⨯+⨯+⨯+⨯()2t a a r r v ωωωω''''=++⨯+⨯⨯+⨯t c a a a '=++〈析〉仅此三式便可以使“第心说”与“日心说”归于一家。
（1） 平动非惯性系 (0ω=)t a a a '=+ 即：()t ma F ma '=+-（2） 旋转非惯性系 (0t t a υ==)()2a a r r ωωωωυ''''=+⨯+⨯⨯+⨯2 地球自转的效应（以地心为参考点）2mr F mg m r ω=--⨯写成分量形式为：2sin 2(sin cos )2cos x y z mx F m y my F m x z mz F mg m y ωλωλλωλ⎧=+⎪=-+⎨⎪=-+⎩ 〈析〉坐标系选取物质在地面上一定点O 为坐标原点，x 轴指向南方，y 轴指向东方，铅直方向为 z 轴方向。
2mr F mg m r ω=--⨯ 为旋转非惯性系 ()2F mg mr m r m r m r ωωωω-=+⨯+⨯⨯+⨯在 ,rR ωω条件下忽略 m r ω⨯与 ()m r ωω⨯⨯所得。
正因如此，地球上的物体运动均受着地球自转而带来的科氏力 2m r ω-⨯的作用，也正是它导致了气旋，反气旋，热带风暴，信风，河岸右侧冲刷严重，自由落体，傅科摆等多姿多彩的自然现象。
理论力学(刘又文 彭献)答案第3章
h
ω α
O
图 3.3
x
对时间 t 求导， 答： 速度计算对， 加速度计算不对， 因只将 ϕ 而没有把 sec 2 ϕ
对 t 求导。正确答案是：
a=
dv + 2tanϕ ⋅ ϕ 2 ) + 2hϕ sec 2 ϕ ⋅ tanϕ ⋅ ϕ = hsec 2ϕ ( ϕ = h sec2 ϕ ⋅ ϕ dt
A
vA
C
vC
dv A = 0； dt
an
aC
ρ
B
vB aB
图 3.2
71
n 法向加速度大小， a A =
v A2
ρ
= 25 m/s 2 。对吗？
答： a τA = 0 不对， 因为 v A = 5 m/s 是瞬时值， 而 aτ = 这个变量对 t 求导，所以只有知道 s=f(t)才能求 aτ 。
n = aA
8．如图 3.7a、b 所示速度矢量图对吗？
A
A
vr
va ve v
vr
M B
ω
O
C
ve
va
(a)
图 3.7
(b)
答：不对。图 a 中 va 方向错误，图 b 中 ve 方向错误。正确答案如图 c、d 所 示。
A
vr
ve vr va O
C
ve
va
(c)
(d)
四、科氏加速度： aC = 2ω × vr 注：全国自然科学名词审定委员会 1993 年公布的《力学名词》中改用“科 氏加速度” 。
dv d 2 s 是对弧坐标 s=f(t) = dt dt 2
v2 A
ρ
n 是对的，因 a A 仅与速度的瞬时值及该点的曲率半径有关。
理论力学 陈立群 第3章 平衡问题 解答
第三章平衡问题：矢量方法习题解答3-1讨论图示各平衡问题是静定的还是静不定的，若是静不定的试确定其静不定的次数。
题3.1图解：（1）以AB杆为对象，A为固定端约束，约束力有3个。
如果DC杆是二力杆，则铰C处有1个约束力，这4个力组成平面一般力系，独立平衡方程有3个，所以是1次静不定；如果DC杆不是二力杆，则铰C和D处各有2个约束力，系统共有7个约束力，AB 杆和DC杆上的约束力各组成平面一般力系，独立平衡方程共有6个，所以，是1次静不定。
（2）AD梁上，固定铰链A处有2个约束力，辊轴铰链B、C和D各有1个约束力，共有5个约束力，这5个约束力组成平面一般力系，可以列出3个独立的平衡方程。
所以，AD梁是2次静不定。
（3）曲梁AB两端都是固定端约束，各有3个共6个约束力组成平面一般力系，而独立的平衡方程只有3个。
所以是3次静不定。
（4）刚架在A、B和C处都是固定端约束，各有3个共9个约束力组成平面一般力系，而独立的平衡方程只有3个。
所以是6次静不定。
（5）平面桁架在A处为固定铰链，B处为辊轴铰链，共有3约束力组成平面一般力系，而独立的平衡方程也有3个，因此，该平面桁架的外力是静定的。
平面桁架由21根杆组成，所以有21个未知轴力，加上3个支座反力，共有24个未知量。
21根杆由10个铰链连接，每个铰链受到平面汇交力系作用。
若以铰链为研究对象，可以列出2×10=20个平衡方程。
所以，此平面桁架的内力是24-20=4次静不定。
（6）整体在A处为固定铰链，B处为辊轴铰链，共有3约束力组成平面一般力系，而独立的平衡方程也有3个，因此，该系统的外力是静定的。
除了3个约束外力外，3根杆的轴力也是未知的，共有6个未知量。
AB梁可以列出3个平衡方程，连接3根杆的铰链可以列出2个平衡方程，共有5个方程，所以，该系统的内力是1次静不定。
3-2炼钢炉的送料机由跑车A与可移动的桥B组成，如图示。
跑车可沿桥上的轨道运动，两轮间距离为2米，跑车与操作架、手臂OC以及料斗相连，料斗每次装载物料重W=15kN，平臂长OC=5m。
《理论力学》课后习题答案赫桐生,高教版)第3章
精品行业资料，仅供参考，需要可下载并修改后使用！第三章习题3-1．求图示平面力系的合成结果，长度单位为m。
解：(1) 取O点为简化中心，求平面力系的主矢：求平面力系对O点的主矩：(2) 合成结果：平面力系的主矢为零，主矩不为零，力系的合成结果是一个合力偶，大小是260Nm，转向是逆时针。
习题3－2．求下列各图中平行分布力的合力和对于A点之矩。
解：(1) 平行力系对A点的矩是：取B点为简化中心，平行力系的主矢是：平行力系对B点的主矩是：向B点简化的结果是一个力R B和一个力偶M B，且：如图所示；将R B向下平移一段距离d，使满足：最后简化为一个力R，大小等于R B。
其几何意义是：R的大小等于载荷分布的矩形面积，作用点通过矩形的形心。
(2) 取A点为简化中心，平行力系的主矢是：平行力系对A点的主矩是：向A点简化的结果是一个力R A和一个力偶M A，且：如图所示；将R A向右平移一段距离d，使满足：最后简化为一个力R，大小等于R A。
其几何意义是：R的大小等于载荷分布的三角形面积，作用点通过三角形的形心。
习题3－3．求下列各梁和刚架的支座反力，长度单位为m。
解：(1) 研究AB杆，受力分析，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(2) 研究AB杆，受力分析，将线性分布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
(3) 研究ABC，受力分析，将均布的载荷简化成一个集中力，画受力图：列平衡方程：解方程组：反力的实际方向如图示。
校核：结果正确。
习题3－4．重物悬挂如图，已知G=1.8kN，其他重量不计；求铰链A的约束反力和杆BC所受的力。
解：(1) 研究整体，受力分析（BC是二力杆），画受力图：列平衡方程：解方程组：反力的实际方向如图示。
习题3－5．图示钻井架，G=177kN，铅垂荷载P=1350kN，风荷载q=1.5kN/m，水平力F=50kN；求支座A的约束反力和撑杆CD所受的力。
理论力学课后答案03
第3章 平面任意力系三、选择题1． D 2.C 3B 4C 5 b 6 D 7 B 8B 9 B 10 A 四、计算题3-1 重物悬挂如图3.27所示，已知G =1.8kN ，其他重量不计。
求铰链A 的约束反力和杆BC 所受的力。
解：选AB 和滑轮D 组成的系统为研究对象，受力分析如图所示。
列平衡方程，有∑=0xF45cos o=--D B Ax F F F∑=0yF45sin o=-+G F F B Ay∑=0)(F AM03.01.06.045sin o =⨯-⨯+⨯G F F D B其中：kN8.1==G F D联立求解，可得：N2400=Ax F ，N1200=AyF ，N5.848=BF3-3求如图3.29(a)、(b)所示平行分布力的合力和对于点A 之矩。
(b)ABq l(a)alAC B q图3.29解：（a ）平行分布力的合力为：qaF R ='( ← )10c GB30cm20c 45°BF A DDF AxFAyF B10c30cm20c 45°CGA D图3.27学 ·24·对于点A 之矩的矩为221qaMA=( )（b ）平行分布力的合力为：qlF R 21'=( ↓ )对于点A 之矩的矩为231qlMA=( )3-4静定多跨梁的荷载及尺寸如图3.30(a)、(b)所示，长度单位为m ，求支座约束反力。
(a)CB36 A 20kN /m30︒(b)B 2 12122.5kN/m5kN ·m5kN C AD40kN ·m图3.30CB620kN /m30︒BxF By FCFCB36A 20kN /m 30︒40kN ·mAxF Ay F CFA M解：(a) 分别选整体和杆BC 为研究对象，受力分析如图所示。
分别列平衡方程，有整体：∑=0xF 030sin o=-C Ax F F∑=0yF62030cos o=⨯-+C Ay F F∑=0)(F AM0662040930cos o =⨯⨯--⨯+C A F M 杆BC ：∑=0)(FB M03620630cos o =⨯⨯-⨯C F联立求解，可得：kN320=Ax F ，N60k F Ay=，mkN 220⋅=AM ，kN 340=C F2 22.5kN/m 5kN ·mCDCx F Cy FDy F 2B21 212.5kN/m 5kN ·m5kN C AD AxF Ay F DyFByF(b) 分别选整体和杆CD 为研究对象，受力分析如图所示。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
理论力学课后习题第三章解答3.1解 如题3.1.1图。
均质棒受到碗的弹力分别为，棒自身重力为。
棒与水平方向的夹角为。
设棒的长度为。
由于棒处于平衡状态，所以棒沿轴和轴的和外力为零。
沿过点且与轴平行的合力矩为0。
即：①②③ 由①②③式得：④ 又由于即⑤ 将⑤代入④得：图题1.3.11N ,2N G θl x y A z 0sin 2cos 21=-=∑θθN N F x0cos 2sin 21=-+=∑G N N Fyθθ0cos 22=-=∑θlG c N M i ()θθ22cos 1cos 22-=c l ,cos 2c r =θrc 2cos =θ3.2解 如题3.2.1图所示，均质棒分别受到光滑墙的弹力，光滑棱角的弹力，及重力。
由于棒处于平衡状态，所以沿方向的合力矩为零。
即①由①②式得：所以()cr c l 2224-=o图题1.3.21N 2N G y 0cos 2=-=∑G N Fyθ0cos 22cos 2=-=∑θθlG d N M z ld=θ3cos 31arccos ⎪⎭⎫ ⎝⎛=l d θ3.3解 如题3.3.1图所示。
棒受到重力。
棒受到的重力。
设均质棒的线密度为。
由题意可知，整个均质棒沿轴方向的合力矩为零。
3.4解 如题3.4.1图。
轴竖直向下，相同的球、、互切，、切于点。
设球的重力大小图题1.3.32AB i G ag ρ=1i G bgρ=2ρz ()BH BF G OD G M z --⋅=∑21sin θ=0sin cos 2sin 2=⎪⎭⎫ ⎝⎛--θθρθρa b gb a ga aba b 2tan 22+=θ图题1.3.4Ox A B C B C D为，半径为，则对、、三个球构成的系统来说，在轴方向的合力应为零。
即：①对于球，它相对于过点与轴平行的轴的合力矩等于零。
即：②由式得：3.5解 如题3.5.1图。
梯子受到地面和墙的弹力分别为，，受地面和墙的摩擦力分别为，。
梯子和人的重力分别为，且。
设梯长为，与地面夹角为。
由于梯子处于平衡，所以①②且梯子沿过点平行于轴的合力矩为零。
即：③ 又因梯子是一个刚体。
当一端滑动时，另一端也滑动，所以当梯与地面的倾角达到最小时，G r A B C x 0cos 23=-=∑αT G F xC D z ()0sin sin =--=∑βαβGr Tr MDαβtan 3tan =1图题1.3.51N 2N 1f 2f 1G 2G 123G G =l θ012=-=∑f N F x02112=--+=∑G G N f FyA z 0sin cos cos 2cos 2212=--+=∑θθθθl N l f lG l G M i④ ⑤ 由①②③④⑤得： 所以3.6解 （a ）取二原子的连线为轴，而轴与轴通过质心。
为质心，则，，轴即为中心惯量主轴。
设、的坐标为，因为为质心（如题3.6.2图）故①且1121N f =2231N f =2441tan =θ⎪⎭⎫⎝⎛=-2441tan 1θx y z O Ox Oy Oz y1m 2m Chax •1m 图题1.3.61m 2m ()()0,0,,0,0,21l lO 02211=+l m l m②由①②得所以中心惯量主轴：（b ）如题3.6.3图所示，该原子由、、三个原子构成。
为三个原子分子的质心。
由对称性可知，图中、、轴即为中心惯量主轴。
设、、三原子的坐标分别为，因为为分子的质心。
所以 =① 又由于② ③由①②③得：l l l =-1221122121,m m lm l m m l m l +=+-=()0221=+=∑i i i z y m I ()22121222l m m m m x z m I i i i +=+=∑()22121223l m m m m y x m I i i i +=+=∑图题3.6.3A B D C Cx Cy Cz A B D ()0,,0A y ⎪⎭⎫⎝⎛⎪⎭⎫ ⎝⎛-0,,2,0,,2D B y a y a C D B A D D B B A A C m m m y m y m y m y ++++=0112112=++++m m m y m y m y m DB A D B y y =h y y B A =-2122112.22m m hm y y m m h m y D B A +-==+=故该分子的中心主转动惯量3.7解 如题3.7.1图所示。
沿轴平行于平切椭球得切面为一椭圆，则该椭圆方程为：可求该切面的面积故积分同理可求故中心主转动惯量：()()D B A i h m m m m z y m I i i i ,,2222121221=+=+=∑()()D B A i a m x z m I i i i ,,221222==+=∑()()D B A i a m h m m m m y x m I i i i ,,2222122121223=++=+=∑y Oxy 11122222222=⎪⎪⎭⎫⎝⎛-+⎪⎪⎭⎫ ⎝⎛-b y c z b y a x ()⎪⎪⎭⎫⎝⎛-=221b y ac S y π()c ab dy b y ac y dy S y dm y bb bb y 3222221541πρρπρ=⎪⎪⎭⎫ ⎝⎛-=⋅=⎰⎰⎰--,15432bc a dm x πρ=⎰32154abc dm z πρ=⎰又由于椭球体积故将代入得：3.8解 设表示距球心为的一薄球壳的质量，则所以该球对球心的转动惯量① 在对称球中，绕直径转动时的转动惯量② 又球的质量③ 又绕直径的回转半径()()22221154c b abc dm z y I +=+=⎰πρ()()22222154c a abc dm z x I +=+=⎰πρ()()22223154b a abc dm y x I +=+=⎰πρ()abc dy b y ac dy S V bb bb y ππ34122=⎪⎪⎭⎫ ⎝⎛-==⎰⎰--abcmV m πρ43==ρ321,,I I I ()22151c b m I +=()22251c a m I +=()22351b a m I +=dm r 202r dr r dm πρρπ==dr R r ⎪⎪⎭⎫⎝⎛-221α3557150220402απραπρ-=⎪⎪⎭⎫ ⎝⎛-==⎰⎰R dr R r r dm r I RRI I 32='153513022020απραπρ-=⎪⎪⎭⎫ ⎝⎛-==⎰⎰R dr R r r dm m RR④ 由①②③④得3.9解 如题3.9.1图所示坐标系。
为正方体中心。
、、分别与正方体的边平行。
由对称性可知，、、轴就是正方体的中心惯量主轴。
设正方体的边长为。
设为平行于轴的一小方条的体积，则正方体绕轴的转动惯量根据对称性得易求正方体的对角线与、、轴的夹角都为。
且故正方体绕对角线的转动惯量① mI k '=R k αα21351014--=Oxyz 图题1.9.3O Ox Oy Oz Ox Oy Oz a ()22222226a m dydz z y a I a a a a xx =+=⎰⎰--ρ26a m I I I xx zz yy ===Ox Oy Oz θ31cos =θ22226cos cos cos a m I I I I zz yy xx ====θθθ又由于②绕对角线的回转半径③ 由①②③得3.10解 如题3.10.1图。
轴过点垂直纸面向外。
均质圆盘的密度为。
设盘沿顺时针转动，则沿的方向有 即① 为转盘绕轴的转动惯量：（为盘的质量）， ②（为盘转动的角频率，负号因为规定顺时针转动）=③ 由①②③得a d 3=mIk =23d k =图题1.3.10z O ρz z zM dtdI =z z M I =ωI z 221ma I =m ωω-=z ω320232a g dr d r g M az ρμπθρμπ==⎰⎰()232a m ma g πρρμ=又因为故所以得3.11解 如题3.11.1图所示，设轴通过点垂直纸面指向外。
则对轴有：设通风机转动的角速度大小为，由于通风机顺时针转动。
所以，将代入上式得： 。
又由于，解得：故当时，㏑。
又由于 （为通风机转动的角度） ag34μω-= (),00ωω=()t agt 340μωω-=(),0=t ωga t μω430=图题1.3.11z O z Z M dtdz=()t ω()t z ωω-=()()t z t k M I z ωω=-=,()()t t k I ωω=- ()()00ωω= ()t Ikt e-=0ωω()2ωω=t kI t =2()()t t θω =θ设，故当㏑时，，时间内通风机转动的转数3.12解 如题3.12.1图，第3.12.1图坐标与薄片固连，则沿轴方向有：且 ①现取如图阴影部分的小区域，该区域受到的阻力对轴的力矩所以②又薄片对轴的转动惯量③()00=θ()t Ikt e -=0ωθ ()()⎪⎪⎭⎫ ⎝⎛-=+=--⎰t I k t Iktt e kI dt e10000ωθωθk It =2()kI t 20ωθ=t ()()kI n t πωπθθ4200=-=Oxyz z Z M dtdz=z I z ω=ady dS =()22y kady kdSv df z ω==df z dy y ka y df dM z z 32ω-=⋅-=2304z az z b a k dM M ω-==⎰()ab m ma bdy y dm y I a a ρρ====⎰⎰2020231由①②③得：当时，3.13解 如题3.13.1图所示，坐标系的原点位于圆弧最顶点。
设圆弧平衡时，质心的坐标为。
如图所示圆弧偏离平衡位置一小角度，则满足微分方程为圆弧相对于轴的转动惯量。
当很小时，，代入上式得：① 圆弧上对应转角为的一小段圆弧的坐标为 质心的纵坐标上式中为圆弧的线密度②()021431ωω+=t m b ka t z ()2ωω=t z 0234ωb ka mt=图题1.3.13Oxyz c ()0,,0l c -θθθθ I mgl =-sin I Oz θθθ≈sin 0=+θθImglθ()0,cos ,sin R R R -θθc ()R R Rd R R R d y csin cos 0θθθρθθρθθθθ+-=-=⎰⎰--ρR R l 0sin θθ-=又③ 其中，将②③代入①得④ 解④式得通解微振动周期3.14解 如题3.14.1图所示坐标系。
由动量定理及动量矩定理得：① ② ③ 其中()()[]θθθρθθd R R R R I ⎰-+-=022sin cos ⎪⎪⎭⎫ ⎝⎛-=002sin 12θθmR 02θρR m =02=+θθRg()⎪⎪⎭⎫⎝⎛+=ϕθt R gA t 2cos g R RgT 2222ππ==Oxyz 题3.14.1图()x c c c R y x m x m =--=θθ 2()mg R x y m y m yc c c -=+-=θθ 2θθsin 2mga mk -= θθcos ,sin a y a x c c -==又根据机械能守恒定律得：④ 由①②③④解得：3.15解 如题3.15.1图所示坐标系。