小学四年级奥数思维训练导引(最新版)
数学思维训练导引(四年级)

第1讲 整数计算综合内容概述熟练运用已学的各种方法解决复杂的整数四则运算问题;学会利用加减抵消、分组计算方法处理各种数列的计算问题。
学会处理“定义新运算”的问题,初步体会用字母表示数。
典型问题兴趣篇1. 计算:(1) 121×32÷8; (2) 4×(250÷8) (3) 25×83×32×1252. 计算:(1) 56×22+56×33+56×44 (2) 222×33+889×66.3. 计算:(1) 37×47+36×53 (2) 123×76-124×75。
4. 计算:100-99+98-97+96-95+…+12-11+10.5. 计算:50+49-48-47+46+45-44-43+…-4-3+2+1.6. 计算:(1+3+5+7+…+199+201) -(2+4+6+8+…+198+200).7. 计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8. 下面是一个叫做“七上八下”的数字游戏。
游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换。
口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大。
例如:给出的数是1995,口令是“8→7,”在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995。
如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?9. 规定运算“∇”为:a ∇b= (a+1) ×(b -1), 请计算:(1)8∇10; (2) 10∇8.10. 规定运算“☺”为:a ☺b=a ×b -(a+b), 请计算:(1) 5☺8; (2) 8☺5; (3) (6☺5)4; (4)6☺ (54)拓展篇1. 计算:(1)72×27×88÷(9×11×12); (2) 31×121-88×125÷(1000÷121).2. 计算:(1) 555×445-556×444; (2) 42×137-80÷15+58×138-70÷15.3. 计算:20092009×2009-20092008×2008-20092008.4. 计算:1+2-3+4+5-6+7+8-9+……+97+98-99.5. 计算:100×99-99×98-98×97-97×96-96×95-95×94+…+4×3-3×2-2×1.6. 在不大于1000的自然数中,A 为所有个位数字为8的数之和,B 为所有个位数字为3的数之和. A 与B的差是多少?7. 求图1-1中所有数的和.8. 已知平方差公式:22()()a b a b a b -=+⨯-,计算: 2222222220191817161521-+-+-++-9. 计算:951×949-52×48.10. 规定运算“Θ”为:a Θb=a+2b -2, 计算:(1) (8Θ7) Θ6;(2) 8Θ(7Θ6)11. 规定运算“”为:a b=(a+1) ×(b -2). 如果6 (5)=91, 那么方格内应该填入什么数?12. 规定:符号“∆”为选择两数中较大的数的运算,“∇”为选择两数中较小的数的运算,例如:3∆5=5,3∇5=3请计算:1∆2∆3∇4∆5∆6∇7∆…∇100.(运算的顺序是从左至右)超越篇1. 观察下面算式的规律:2000+1991-1988-1982+1976+1970-1964-1958+1952+1946-1940-1934+……一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?2. 从1, 2, ……, 9, 10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?3. 计算:1-3+6-10+15-21+28- (4950)4. 已知平方差公式:22()()a b a b a b -=+⨯-, 计算: 222222222222100999897969594934321+--++--+++--5. a Θb 表示从a 开始依次增加的b 个连续自然数的和,例如:4Θ3=4+5+6=15, 5Θ4=5+6+7+8=26, 请计算:(1) 4Θ15 (2) 在算式(Θ7)Θ11=1056中,方框里的数应该是多少?6. 定义两种运算:a Ωb=a -b+1, a ∀b=a ×b+1, 用“Ω”、“∀”和括号填入下面的式子,使得等式成立(不能用别的计算符号):7 3 4 5=27.现定义四种操作的规则如下:①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2. 例如从16可以得到8,从27可以得到14.②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉,例如从5304可以得到50,从408可以得到8. (不含数字3和4的自然数不能进行“丢三落四”操作)③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边。
四年级数学思维训练导引(奥数)第16讲 统筹与对策

四年级数学思维训练导引(奥数)第16讲统筹与对策四年级数学思维训练导引(奥数)第16讲统筹与对策第十六讲总体规划与对策1.妈妈让冬冬给客人烧水沏茶.洗开水壶要用1分钟,烧开水要用15分钟,洗茶壶要用1分钟,洗茶杯要用1分钟,拿茶叶要用2分钟.冬冬估算了一下,完成这些工作要花20分钟,为了尽快给客人沏茶,你认为最合理的安排,最少需要多少分钟?2.理发店同时有三位顾客a、B和C。
剪a的板子需要7分钟,剪秃头需要10分钟,烫C的卷发需要40分钟。
请问:如何安排这三个人的理发顺序,以尽量减少他们花费的总时间?最短的时间是多少?3.西点店里卖的面包都是5个一袋或3个一袋的,不拆开零售.已知5个一袋的售价是8元,3个一袋的售价是5元,要给47位同学每人发1个面包最少要花多少钱?4.如图16-1所示,每个小正方形的边长为1cm。
一条贪婪的蛇从左下角开始沿着网格线爬行。
如果它想吃掉这三个“★“在图中,它至少应该爬多远?请画出路线,5.如图16-2所示,一条环形公路上有a、b、c、d四个仓库.a仓库存盐40吨,b仓库存盐5吨,c仓库存盐35吨,d仓库没有盐.现在要调整存放数量,计划a、b、c、d 每个仓库各存盐20吨,已知每吨盐运1千米需要运费2元.试问:为完成上述调运计划,最少需要多少元运费?(图16-2中公路旁的数字表示相邻仓库间的里程数,单位为千米)6. 2022个小方格从左到右排列成一行。
甲方和乙方轮流在每个空间放置一块。
规定如下:每个空间最多一件;当a放一个棋子时,B必须把它放在棋子旁边的空间;当B把棋子放好时,a必须把棋子放好;任何不能放手的人都将被判失败。
如果乙方在开始时把一个棋子放在左边的第一个方格里,谁会有获胜的策略?7.有9根火柴,甲、乙两人轮流取,规定每次可以取1根或者2根火柴,以取走最后一根火柴的人为胜者.试问:如果甲先取,谁有必胜的策略?有100场比赛。
甲方和乙方轮流工作。
规定每次可进行一场、两场、三场或四场比赛。
四年级数学思维训练导引(奥数)第09讲 多位数与小数

第九讲 多位数与小数1.李老师在黑板上写了四个算式:①7469÷0.7;②7.469÷0.007;③0.7469÷0.07;④746.9÷7.请把它们按照商从小到大的顺序排列起来.2.计算:5795.5795+5.795×579.5.3.计算:13.64×0.25÷1.1.4.计算:24×(0.123+0.127)×0.125×(2.52+1.48).5.计算:(3.74+3.76+3.78+3.8+3.82)×O.04+24×60.6.计算:1.25×3.14+125×0.0257+1250×0.00229.7.计算:3.51×49+35.1×5.1+99×51.8.计算:19+199+1999+…+1091999个 9.求和式3+33+333+…+103333个计算结果的万位数字. 10.计算:10333333 个×9333334个.1.计算:(1)[4.2×5-(1÷0.25+9.1÷0.7)]÷0.004;(2)4.5×4.8÷0.25÷15÷0.24.2.在下面算式的两个方框中填入相同的数,使得等式成立,所填的数应该是多少?22.5-(□×3,2-2.4×□)÷3.2=10×3.计算:(1) 299.9×19.98-199.8×29.971(2) 3.14+64.8×0.537×25+5.37×6.48×75-8×64.8×0.125×53.7.4.计算:27.8×28.7-27.7×28.8.5.计算:24.25×7.19+0,23×281+1.25×0.81.6.计算:0.1+0.3+0.5+0.7+0.9+0.11+0.13+0.15+0.17+0.19+0.21+…+0.99.7.计算:(1) 28+208+2008+…+100020008个;(2) 98+998+9998+…+1099998个. 8.计算:3+33+333+3333+…+503333个. 9.计算:999999×222222+333333×333334.10.计算:1981×198319831983-1982×198119811981.11. 计算:(1)1009999 个×1009999 个+10091999个; (2)203333 个×206666个 12.求算式20009999 个×20008888 个÷20006666个的计算结果的各位数字之和.1.计算:(1+1.2+1.23+1.234)×(1.2+1.23+1.234+1.2345)-(1+1.2+1.23+1.234+1.2345)×(1.2+1.23+1.234).2.一个数去掉小数部分后得到一个整数,这个整数加上原数的4倍,等于27.6.原来这个数是多少?3.计算:404444 个-206666 个+208100888000个个 4.计算:22000888888个-22000111111 个 5.求算式300888888 个×300333333个的计算结果的各位数字之和. 6.计算:3+3.3+3.33+3.333+…+9933.33333个. 7.已知数9949924444622224个个.是某一个小数的平方,请问:这个数是多少的平方?8.计算以下各数的数字和:(1) 99991111111111⨯ 个1个1;(2) 1001001111111111⨯个1个1。
数学思维训练导引 (四年级)

第1讲 整数计算综合内容概述熟练运用已学的各种方法解决复杂的整数四则运算问题;学会利用加减抵消、分组计算方法处理各种数列的计算问题。
学会处理“定义新运算”的问题,初步体会用字母表示数。
典型问题兴趣篇1. 计算:(1) 121×32÷8; (2) 4×(250÷8) (3) 25×83×32×1252. 计算:(1) 56×22+56×33+56×44 (2) 222×33+889×66.3. 计算:(1) 37×47+36×53 (2) 123×76-124×75。
4. 计算:100-99+98-97+96-95+…+12-11+10.5. 计算:50+49-48-47+46+45-44-43+…-4-3+2+1.6. 计算:(1+3+5+7+…+199+201) -(2+4+6+8+…+198+200).7. 计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8. 下面是一个叫做“七上八下”的数字游戏。
游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换。
口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大。
例如:给出的数是1995,口令是“8→7,”在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995。
如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?9. 规定运算“∇”为:a ∇b= (a+1) ×(b -1), 请计算:(1)8∇10; (2) 10∇8.10. 规定运算“☺”为:a ☺b=a ×b -(a+b), 请计算:(1) 5☺8; (2) 8☺5; (3) (6☺5)4; (4)6☺ (54)拓展篇1. 计算:(1)72×27×88÷(9×11×12); (2) 31×121-88×125÷(1000÷121).2. 计算:(1) 555×445-556×444; (2) 42×137-80÷15+58×138-70÷15.3. 计算:20092009×2009-20092008×2008-20092008.4. 计算:1+2-3+4+5-6+7+8-9+……+97+98-99.5. 计算:100×99-99×98-98×97-97×96-96×95-95×94+…+4×3-3×2-2×1.6. 在不大于1000的自然数中,A 为所有个位数字为8的数之和,B 为所有个位数字为3的数之和. A 与B的差是多少?7. 求图1-1中所有数的和.8. 已知平方差公式:22()()a b a b a b -=+⨯-,计算: 2222222220191817161521-+-+-++-9. 计算:951×949-52×48.10. 规定运算“Θ”为:a Θb=a+2b -2, 计算:(1) (8Θ7) Θ6;(2) 8Θ(7Θ6)11. 规定运算“ ”为:a b=(a+1) ×(b -2). 如果6 ( 5)=91, 那么方格内应该填入什么数?12. 规定:符号“∆”为选择两数中较大的数的运算,“∇”为选择两数中较小的数的运算,例如:3∆5=5,3∇5=3请计算:1∆2∆3∇4∆5∆6∇7∆…∇100.(运算的顺序是从左至右)超越篇1. 观察下面算式的规律:2000+1991-1988-1982+1976+1970-1964-1958+1952+1946-1940-1934+……一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?2. 从1, 2, ……, 9, 10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?3. 计算:1-3+6-10+15-21+28- (4950)4. 已知平方差公式:22()()a b a b a b -=+⨯-, 计算: 222222222222100999897969594934321+--++--+++--5. a Θb 表示从a 开始依次增加的b 个连续自然数的和,例如:4Θ3=4+5+6=15, 5Θ4=5+6+7+8=26, 请计算:(1) 4Θ15 (2) 在算式( Θ7)Θ11=1056中,方框里的数应该是多少?6. 定义两种运算:a Ωb=a -b+1, a ∀b=a ×b+1, 用“Ω”、“∀”和括号填入下面的式子,使得等式成立(不能用别的计算符号):7 3 4 5=27.现定义四种操作的规则如下:①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2. 例如从16可以得到8,从27可以得到14.②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉,例如从5304可以得到50,从408可以得到8. (不含数字3和4的自然数不能进行“丢三落四”操作)③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边。
四年级数学思维训练导引(奥数)第01讲 整数计算综合

第一讲整数计算综合1.计算:(1) 121×32+8; (2)4×(250+8); (3)25×83×32×125.2.计算:(1) 56×22+56×33+56×44; (2) 222×33+889×66.3.计算:(1) 37×47+36×53; (2) 123×76-124×75.4.计算:100-99+98-97+96-95+…+12-11+10.5.计算:50+49-48-47+46+45-44-43+…一4-3+2+1.6.计算:(1+3+5+7+…+199+201)-(2+4+6+8+…+198+200).7.计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.8.下面是一个叫做“七上八下”的数字游戏.游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换.口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大.例如:给出的数是1995,口令是“8q”,在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995.如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?9.规定运算“▽”为:a▽b=(a+l)×(b-1),请计算:(1) 8710; (2)1078.10.规定运算“㊣”为:a㊣b=a×b-(a+b),请计算:(1) 5㊣8;(2) 8㊣5;(3) (6㊣5)㊣4;(4) 6㊣(5㊣4).1.计算:(1) 72×27×88+(9×11×12);(2)31×121-88×125+(1000+121).2.计算:(1) 555×445-556×444; (2) 42×137-80+15+58×138-70+15.3.计算:20092009×2009-20092008×2008-20092008.4.计算:1+2-3+4+5-6+7+8-9+…+97+98-99.5.计算:100×99-99×98+98×97-97×96+96×95-95×94+…+4×3-3×2+2×l.6.在不大于1000的自然数中,A为所有个位数字为8的数之和,B为所有个位数字为3的数之和.A与B的差是多少?7.求图1-1中所有数的和.8.已知平方差公式:口2—62=(a+b)×(n-∽,计算: 201—19l+182—172+16z—15z+…+2z—1 2.9.计算:951×949-52×48.10.规定运算“0”为:aOb=a+2b-2,计算:(1) (807)06;(2) 80(706).11.规定运算“o”为:日0 6=(n+1)×(b-2).如果6 0(口0 5)=91,那么方格内应该填人什么数?12.规定:符号“△”为选择两数中较大的数的运算,“V”为选择两数中较小的数的运算,例如:3A5=5,3V5=3.请计算:l&2A3 V4A5A6 V7A...V 100.(运算的顺序是从左至右)1.观察下面算式的规律:2000+1994-1988-1982+1976+1970-1964-1958+1952+1946-1940-1934+…,一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?2.从1,2,…,9,10中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积.把所有这样的乘积全部加起来,总和是多少?3.计算:1-3+6-10+15-21+28一 (4950)4.已知平方差公式:口2一易2=(口+∽×(a-b),计算:1002+992-982-972+962+952-942-932+…+42+32 _22—1 2.5.aOb表示从日开始依次增加的6个连续自然数的和,例如:403 =4+5+6=15,504 =5+6+7+8 =26,请计算:(1) 4015;(2)在算式(口07)011=1056中,方框里的数应该是多少?6.定义两种新运算:aQb=a-b+l,aVb=a×b+l.用“Q”、“V”和括号填人下面的式子,使得等式成立(不能用别的计算符号): 7 3 4 5=2. 7.现定义四种操作的规则如下:①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2.例如从16可以得到8,从27可以得到14.②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉.例如从5304可以得到50,从408可以得到8.(不含数字3和4的自然数不能进行“丢三落四”操作)③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边.例如从98707可以得到77908,从802可以得到28.(不含数字7和8的自然数不能进行“七上八下”操作)④“十全十美”:将一个自然数的个位数字换成0.例如从111可以得到110,从905可以得到900.(个位是0的自然数不能进行“十全十美”操作)(1)请写出对4176依次进行③、①、③、②、④操作后的结果; (2)从655687开始,最少经过几次操作以后可以得到07(3)一个三位数除了“丢三落四”外,其他三个操作各进行一次之后得到的结果是8,求有多少个这样的三位数.8.图1-2是同学们都很熟悉的九九乘法口诀表,表中所有乘积的总和是多少?。
四年级数学思维训练导引(奥数)第10讲 平均数问题

第十讲平均数问题1.阿奇参加射击比赛,他一共打了10枪,每枪都射中靶子,位置如图10-1中的“×”所示.图中数字表示击中靶子各部位能得到的分数,请问:阿奇此次打靶的平均分是多少?2.请求出103,109,105,101,110,102,106,104这8个数的平均数.3.飞碟工厂一周生产的机器台数的统计表破损了,如图10-2所示,表中缺少几个数字,请你根据这张统计表,求出星期三和星期四的产量.4.甲、乙、丙、丁四个小队拾松果,甲、乙、丙三队平均每队拾24千克,乙、丙、丁三队平均每队拾26千克.已知丁队拾28千克,那么甲队拾多少千克?5.阿奇参加了5次天文知识竞赛,平均分是82分,如果不算分数最高的那次,其余4次的平均成绩为80分,阿奇这5次竞赛的最高分是多少?6.张村有25户人家,李村有20户人家,去年张村平均每户收入4.4万元,李村平均每户收入 3.5万元.去年两村平均每户收人多少万元?今年李村有3户人家收入增加,这3户平均每户多收入6000元.请问:今年两村平均每户收入多少万元?7.8个数的平均数为50,若把其中的一个数改为90,平均数就变成60.被改动的数原来是多少?8.小悦参加了若干次考试,在最后一次考试时她发现:如果这次考试得97分,那么她的平均分是90分;如果这次考试得73分,那么她的平均分数是87分,小悦一共参加了多少次考试?9.宇宙汽车厂有甲、乙两个车间生产零件,甲车间有57名工人,每人每天平均生产132个零件,乙车间每人每天平均生产163个零件,两个车间每人每天平均生产144个零件.请问:乙车间有多少名工人?10.甲、乙、丙三个班的人数分别为45、57、54.已知甲班的平均分为91.5分,乙班的平均分为89.5分,三个班的总平均分为92.5分,求丙班的平均分.1.有鸡、鸭、鸽子、麻雀四只小动物,鸽子重0.6千克;鸡的重量比鸽子的2倍少0.2千克;鸭的重量比鸡多0.5千克;麻雀的重量比鸽子少0.4千克.求这四只动物的平均重量.2.求下列20个数的平均数:306,312,306,308,314,304,318,311,313,315, 314, 310, 310, 320, 300, 316, 320, 312, 314, 315.3.小悦在商场买了3斤水果糖、1斤花生糖和2斤奶糖.已知水果糖每斤8元,花生糖每斤7元,奶糖每斤10元.问:小悦买的糖果平均每斤多少钱?4.四年级一班有6名女学生,她们的平均身高是140厘米,如果她们当中有1人离开,剩下5人的平均身高就变成135厘米,请问:离开的那个女生身高是多少厘米?5. 35个数排成5行7列.7列的平均数分别为39、41、40、45、42、39、41,前4行的平均数分别为42、39、44、41.请求出最后一行的平均数.6.汽车配件厂有150名工人,平均每人每天能生产200个零件.后来部分工人的设备被改良了,这些工人每人每天可以多生产30个零件,此时工厂平均每人每天能生产213个零件.请问:有多少名工人的设备被改良了?7.黑板上有7个数,平均数为55.如果把其中一个数改为140,则平均数变为64,求被改动的数是多少.如果再将其余6个数都乘以2,求此时7个数的平均数.8.甲班有33人,乙班有22人.在一次考试中,甲班的平均分是80分,甲班和乙班的总平均分是82分,求乙班的平均分.9.某单位男职工人数是女职工人数的2倍,男职工的平均年龄是31岁,女职工的平均年龄是40岁.请问:该单位全体职工的平均年龄是多少岁?10.甲班有25人,乙班有75人,甲班和乙班的总平均分是90分,如果甲班的平均分比乙班的平均分高5分,那么乙班的平均分是多少?11.功夫小学四年级一班和二班共有学生100名.在一次数学考试中,两班学生的总平均分是"75.4分,其中一班的平均分是73分,二班的平均分是78分,请问:一班和二班的人数之差是多少?12.冬冬期末考试语文、数学、英语、地理、历史五科中的四科成绩如下:语文88分,数学99分,地理94分,历史95分,英语成绩比五科的总平均分低2.4分,冬冬英语的得分是多少?1.小明参加了六次数学测验,这六次测验有一个总平均分,后四次测验的平均分比总平均分多3分,第一次、第二次、第六次这三次测验的平均分要比总平均分少3.6分.请问:前五次测验的平均分与总平均分相比,高还是低?差多少分?2.A、曰、C、D、E这五人在一次满分为100分的考试中,得分互不相同,并且都是大于91的整数,如果A、B、C三人的平均分为95分;B、C、D三人的平均分为94分;A是第一名;E得96分是第三名,请问:D考了多少分?3.老师在黑板上写出了若干个从1开始的连续自然数1,2,3,…,后来擦掉其中的一个数,剩下的数的平均数是10.8.求被擦掉的那个自然数.4.四年级五班有50名同学,在一次数学考试后,王老师把这些学生按成绩排了名次,发现前30名的平均分比后20名的平均分多12分,一位同学对“平均”的概念不清楚,他把前30名的平均分加上后20名的平均分,再除以2,错误地认为这就是全班同学的平均分.这样做全班的平均成绩是提高了,还是降低了?请算出提高或降低了多少分?5.某次数学竞赛原定一等奖10人,二等奖20人.现在将一等奖中最后4人调整为二等奖,那么得二等奖的学生的平均分就提高了1分,得一等奖的学生的平均分就提高了3分.请问:原来一等奖学生的平均分比二等奖学生的平均分多多少?6.小新家有5口人,分别是:爷爷、奶奶、爸爸、妈妈还有小新.今年,爷爷75岁,奶奶比5人的平均年龄大26岁,爸爸34岁,妈妈比5人的平均年龄小13岁,小新又比妈妈小21岁.请你根据以上的信息,求出小新刚出生时爸爸多少岁.7.一次考试,男生的平均分比总平均分高2分,女生的平均分比总平均分低l分.男生的总分数是942分,女生的总分数是1800分.求:男、女生各有多少人?8.少年歌手大奖赛的裁判小组由若干人组成.每名裁判员给歌手的评分最高为10分.第一名歌手演唱后的得分情况是:全体裁判员所给分数的平均分是9.64分;如果只去掉一个最高分,则其余裁判员所给分数的平均分是9.60分;如果只去掉一个最低分,则其余裁判员所给分数的平均分是9.68分,请问:所有裁判员所给分数中的最低分最少可以是多少?这时,大奖赛的裁判员共有多少名?。
四年级数学思维训练导引(奥数)第04讲--数阵图初步
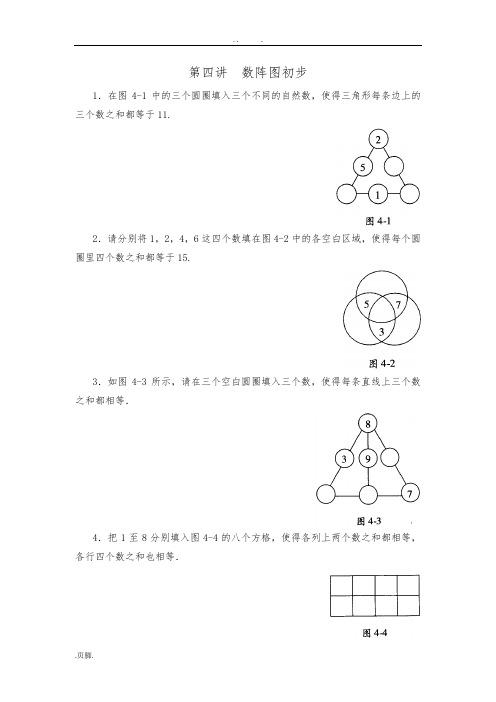
第四讲数阵图初步1.在图4-1中的三个圆圈填入三个不同的自然数,使得三角形每条边上的三个数之和都等于11.2.请分别将1,2,4,6这四个数填在图4-2中的各空白区域,使得每个圆圈里四个数之和都等于15.3.如图4-3所示,请在三个空白圆圈填入三个数,使得每条直线上三个数之和都相等.4.把1至8分别填入图4-4的八个方格,使得各列上两个数之和都相等,各行四个数之和也相等.5.把l至12分别填入图4-5的圆圈,使图中三个小三角形三条边上的六个数之和相等.6.在如图4-6所示的3×3方格表填入1、2、3这三个数字各三次,使得每行每列以及两条对角线上的三个数字之和都相等.7.把1至6分别填入图4-7的六个圆圈,使得每个正方形四个顶点的数之和都为13.8.把1至6分别填入图4-8的六个方格,使得横行三个数之和与竖列四个数之和相等.这个和最大是多少?最小是多少?9.把1至7这七个数分别填入图4-9中各圆圈,使每条直线上三个圆圈所填数之和都相等.如果中心圆填的数相等,那么就视为同一种填法,请写出所有可能的填法.10.在图4-10的6个圆圈分别填入不同的自然数,使得每一个数都是与它相连的上面两个数之和,那么最下面那个数最小是几?1.将1至9分别填入图4-11中的圆圈,可以使得图中所有三角形(共七个)的三个顶点上的数之和都等于15.现在已经填好了其中三个,请你在图中填出剩下的数.2.在图4-12中的八个圆圈分别填入八个不同的自然数,使得正方形每条边上三个数的和相等,现在如果已经填好了五个数,那么每条边上各数之和应该是多少?并将其补充完整.3.图4-13是由四个交叠的长方形组成的,在交点处有八个小圆圈.请你把1、2、3、4、5、6、7、8这八个自然数分别填入这些小圆圈,使得每个长方形上的四个数之和都相等.4.在图4-14中的方格填入三个0、两个2、两个3、两个4,使得每个箭头所指的列中各方格数字之和都是6,并且使得从上到下第二行与第三行的数字之和都是7.5.请在图4-15的每个小圆圈填入1或2,使得每个大圆圈上四个数之和两两不同.那么所填数的总和是多少?6.把1至8分别填入图4-16的八个圆圈,使得任意两个有线段直接相连的圆圈的数字之差都不等于1.7.在图4-17的七个圆圈填入七个连续自然数,使得每两个相邻圆圈所填数之和都等于它们连线上的已知数.请问:标有★的圆圈填的数是多少?8.小悦是8月11日15点整出生的,她想把1,2,3,4,5,6,7这七个数填入图4 -18的七个方框里,每个数只填一次,使三条直线上的三个数之和恰好是8,11,15.问:在圆上的三个数的乘积最大可能是多少?9.把1至6这六个数字填入图4-19六个圆圈,使得三角形每条边上三个数之和都相等,那么这个和最小是多少?最大是多少?10.把1至l 1填入图4-20中“六一”图形的十一个空格,使得每一条直线上的两个或三个数之和都相等.11.请将1至6填入图4-21的六个圆圈,使得四条直线上的数字之和都相等.12.如图4-22,有一座长方形城堡,四周有十个掩体,守城的士兵有十件武器,各种武器的威力数如下表,为了使城堡四条边上的武器威力总数都相同,并且尽量大,应如何在十个掩体中配备武器?1.如图4 -23,四个圆共被分成十二个区域,其中已有六个区域填有数,请将1至12中的另六个数填入其他区域,使得每个圆中四个数之和都是28.2.如图4-24,请在三个圆圈分别填入三个数,使得每条直线上三个数之和都等于大圆上三个数之和.3.把1至8填入图4-25中正方体八个顶点处的圆圈,使得正方体每个面上的四个数之和都相等.4.把1至12分别填入图4-26所示六角星图案的十二个圆圈,使得每条直线上四个数之和都相等,现在已经填好了六个数,那么每条直线上各数之和应该是多少?并把下图补充完整.5.把l至8填入图4 -27的八个圆圈,使得每个三角形三个顶点的数字之和相等,且小正方形顶点的数字之和是大正方形顶点的数字之和的一半.6.图4-28中一共有6条线段,请将九个连续的自然数(其中一个是6)填入其中的九个圆圈,使得每条直线上圆圈的数加起来都等于23.7.如图4 -29,5x5的方格表被分成了五块,请你在每格中填入l、2、3、4、5中的一个(其中两个格子已经分别填入1和2),使得每行、每列、每条对角线的五个数各不相同,且每块上所填数的和都相等.请问:ABCDE是多少?8.图4-30是奥林匹克五环标志,五个圆共分成了九个部分.请在这九个部分中填入1至9这九个数,使得每个圆环的各数之和都相等,请问:这个和最大是多少?最小是多少?。
四年级数学思维训练导引(奥数)第20讲幻方与数阵图拓展
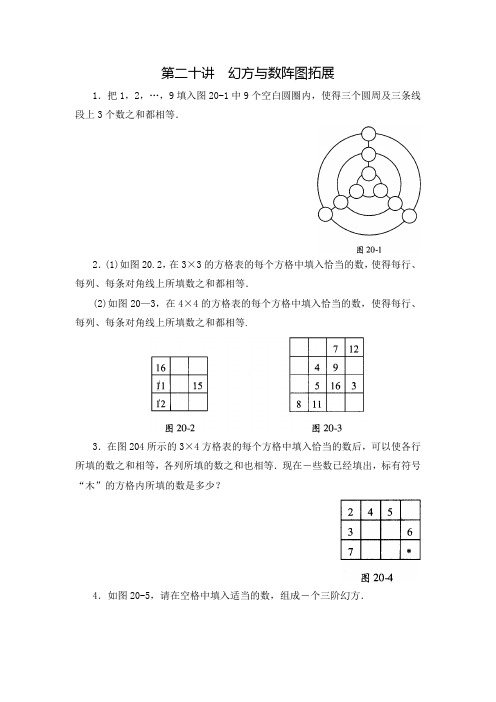
第二十讲幻方与数阵图拓展1.把1,2,…,9填入图20-1中9个空白圆圈内,使得三个圆周及三条线段上3个数之和都相等.2.(1)如图20.2,在3×3的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等.(2)如图20—3,在4×4的方格表的每个方格中填入恰当的数,使得每行、每列、每条对角线上所填数之和都相等.3.在图204所示的3×4方格表的每个方格中填入恰当的数后,可以使各行所填的数之和相等,各列所填的数之和也相等.现在-些数已经填出,标有符号“木”的方格内所填的数是多少?4.如图20-5,请在空格中填入适当的数,组成-个三阶幻方.5.请将图20—6所示的5×5方格表补充完整,使得每个方格内都有-个数字,并且具有如下的性质:方格表中每行,每列和每条对角线的5个方格内所填的5个数中,1、2、3、4、5恰好各出现-次,请问:标有符号“△”,“V”和“O”的方格中所填的数分别是什么?6.请将1至9这9个数填入图20.7中的方框内,使得所有不等号都成立,所有满足要求的填法共有多少种?7.请在图20.8所示的8个小圆圈内,分别填入1至8这8个数字,使得图中用线段连接的两个小圆圈内所填的数的差(大减小)恰好是1、2、3、4、5、6、7.8.将1至5这5个数字填入图20-9中的小圆圈内,使得横线、竖线、大圆周上所填数之和都相等.9.请在图20-10中的六块区域内填入1、2、3、4、5、6,使得对每-个小圆圈来说,与它相邻的区域内的数之和都相等.10.将0至9填入图20-11的10块区域中(阴影区域除外),使得每个圆内的三个数之和都是相等的,请问:这个和最小是多少?最大是多少?1.将1,2,3,…,24,25分别填入图20-12的各个方格中,使得每行、每列及两条对角线上的数的和相等.现在已经填入了-些数,标有符号“术”的方格内所填的数是多少?2.请在图20-13的每个空格内填入-个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.3.(1)在图20-14的每个空格内填入-个数,使得每行、每列及两条对角线上的3个方格中的各数之和都等于19.95.那么,标有“球”的方格内所填的数是多少?(2)请在图20-15的每个空格内填入-个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.4.如图20-16,大正方形的4个角上已填入4个数,4个数之和是264.奇妙的是,把这个图倒过来看,大正方形4个角上的数之和仍然是264.请你在中间的小正方形的4个角的圆圈里,填入另外4个数,使得每条对角线上的4个数正看和倒看时,其和都是264;而且小正方形角上的4个数正看和倒看时,其和也都是264.5.将1、2、3、5、6、7、9、10、1 1填入图20-17中的小圆圈内,使得每条直线上各数之和都相等.6.请将1至10填入图20-18中的10个圆圈中(9已经填好),使得除了第-行外每个圆圈内的数都等于与它相连的上方两个圆圈内的两数之差.7.在图20-19的7个圆圈内各填-个数,要求对于每-条直线上的3个数,居中的数是旁边两个数的平均数.现在已经填好了两个数,请把剩下的圆圈填好.8.请将1个1,2个2,3个3,…,8个8,9个9填入图20-20中,使得相同的数所在的方格都连在-起(相连的两个方格必须有公共边);现在已经给出了其中8个方格中的数,并且知道A、B、C、D、E、F、G各不相同;那么,七位数ABCDEFG是多少?9.将数字1、2、3、4、5、6、7填入图20-21中的小圆圈内,使得每个圆周上的3个数之和与每条直线上的3个数之和都相等.10.将1至9填入图20-22中的9个圆圈内,使4个大圆周上的4个数之和都等于16.11.图20-23中-共有10个方格,现在把2至11这10个自然数填到里面,每个方格各填-个.如果要求图中的3个2x2的正方形中的4个数之和都相等,那么这个和最小可能是多少?请给出-种填法.12.如图20-24,大三角形被分成了9个小三角形,试将1、2、3、4、5、6、7、8、9分别填入这9个小三角形内,每个小三角形内填-个数,要求靠近大三角形三条边的每5个数相加的和相等.这5个数的和最大可能是多少?请给出-种填法,1.请在图20-25的每个空格内填入-个合适的数,使得每行、每列及两条对角线上的3个方格中的各数之和都相等.2.图20-26是有名的“六角幻方”:将1至19这19个自然数填入图中的圆圈中,使得每-条直线上圆圈中的各数之和相等,美国的数学爱好者阿当斯从1910年开始,到1962年,用了52年的时间才找到了解答.我们给大家填入了6个自然数,请你完成这个“六角幻方”.3.在图20-27中有6个正方形,请你将1至9填入图中,使得每个正方形的4个顶点上的数字之和都相等.4.在图20-28的七个圆圈中填入-些自然数,要求所填的自然数中最小的-个数是1,并且相邻两个圆圈内的数字之差(大数减小数)恰好等于这两个圆圈之间标出的数字.5.将1至9分别填入图20-29中的9个圆圈内,使图中每条直线(图中有7条直线)上的圆圈内所填数之和都相等,那么这个和是多少?6.将0,1,2,…,9这10个数分别填入图20-30中的各个圆圈内,使得各阴影三角形的3个顶点上的数之和相等.这个和最大是多少?最小是多少?请分别给出使得和最大、最小的填法.7.在图20-31中有11个空的圆圈,要求把1至13这些数填入各圈内(其中3、4已经填好),使得上面2个圆圈内数的和,等于与它相连的下面的圆圈内的数(例如,虚线框中上面2个圈中的数相加,它们的和应等于相连的下面1个圈中的数),并且最下面空着的4个圆圈中的数之和等于43.8.图20-32中共有10个圆圈,6条直线.请问:(1)能否将1至10填入图中,使得每条直线上各数之和都相等?(2)能否将0至9填入图中,使得每条直线上各数之和都相等?(3)请从1至11中去掉-个数后,将剩下的数填入图中使得每条直线上各数之和都相等.。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第1讲整数计算综合
内容概述
熟练运用已学的各种方法解决复杂的整数四则运算问题;学会利用加减抵消、分组计算方法处理各种数列的计算问题。
学会处理“定义新运算”的问题,初步体会用字母表示数。
典型问题
兴趣篇
1. 计算:(1) 121×32÷8; (2) 4×(250÷8) (3) 25×83×32×125
2. 计算:(1) 56×22+56×33+56×44 (2) 222×33+889×66.
3. 计算:(1) 37×47+36×53 (2) 123×76-124×75。
4. 计算:100-99+98-97+96-95+…+12-11+10.
5. 计算:50+49-48-47+46+45-44-43+…-4-3+2+1.
6. 计算:(1+3+5+7+…+199+201) -(2+4+6+8+…+198+200).
7. 计算:1+2+3+4+…+48+49+50+49+48+…+4+3+2+1.
8. 下面是一个叫做“七上八下”的数字游戏。
游戏规则是:对一个给定的数,按照由若干个7和8组成的口令进行一连串的变换。
口令“7”是指在这个数中插入一个数字,使得新生成的数尽量大;口令“8”是指将这个数中的一个数字去掉,也要使新生成的数尽量大。
例如:给出的数是1995,口令是“8→7,”在第一个口令“8”发出后变成995,在第二个口令“7”发出后变成9995。
如果给出数“6595”以及口令“8→7→8→7→8→8”,问:变换后依次得到的6个数的和是多少?
9. 规定运算“∇”为:a∇b= (a+1) ×(b-1), 请计算:(1)8∇10; (2) 10∇8.
10. 规定运算“☺”为:a☺b=a×b-(a+b), 请计算:
(1) 5☺8; (2) 8☺5; (3) (6☺5)4; (4)6☺ (54)
拓展篇
1. 计算:(1)72×27×88÷(9×11×12); (2) 31×121-88×125÷(1000÷121).
2. 计算:(1) 555×445-556×444; (2) 42×137-80÷15+58×138-70÷15.
3. 计算:20092009×2009-20092008×2008-20092008.
4. 计算:1+2-3+4+5-6+7+8-9+……+97+98-99.
5. 计算:100×99-99×98-98×97-97×96-96×95-95×94+…+4×3-3×2-2×1.
6. 在不大于1000的自然数中,A为所有个位数字为8的数之和,B
为所有个位数字为3的数之和. A与B的差是多少?
7. 求图1-1中所有数的和.
8. 已知平方差公式:22()()
-=+⨯-,计算:
a b a b a b
22222222
20191817161521
-+-+-++-
9. 计算:951×949-52×48.
10. 规定运算“Θ”为:aΘb=a+2b-2, 计算:(1) (8Θ7)Θ6; (2)
8Θ(7Θ6)
11. 规定运算“”为:a b=(a+1) ×(b-2). 如果6(5)=91, 那么
方格内应该填入什么数?
12. 规定:符号“∆”为选择两数中较大的数的运算,“∇”为选择两数中较小的数的运算,例如:3∆5=5,3∇5=3请计算:1∆2∆3∇4∆5∆6∇7∆…∇100.(运算的顺序是从左至右)
超越篇
1. 观察下面算式的规律:
2000+1991-1988-1982+1976+1970-1964-1958+1952+1946-1940-1934+……一直这样写下去,那么最后4个自然数分别是哪4个?符号分别是加还是减?算式最终的结果为多少?
2. 从1, 2, ……, 9, 10 中任意选取一个奇数和一个偶数,并将两数相乘,可以得到一个乘积,把所有这样的乘积全部加起来,总和是多少?
3. 计算:1-3+6-10+15-21+28- (4950)
4. 已知平方差公式:22()()
-=+⨯-, 计算:
a b a b a b
222222222222
+--++--+++--
100999897969594934321
5. aΘb表示从a开始依次增加的b个连续自然数的和,例如:4Θ3=4+5+6=15, 5Θ4=5+6+7+8=26, 请计算:(1) 4Θ15 (2) 在算式(Θ7)Θ11=1056中,方框里的数应该是多少?
6. 定义两种运算:aΩb=a-b+1, a∀b=a×b+1, 用“Ω”、“∀”和括号填入下面的式子,使得等式成立(不能用别的计算符号):7 3 4 5=2
7.现定义四种操作的规则如下:
①“一分为二”:如果一个自然数是偶数,就把它除以2;如果是奇数,就先加上1,然后除以2. 例如从16可以得到8,从27可以得到14.
②“丢三落四”:如果一个自然数中包含数字“3”或“4”,就将其划掉,例如从5304可以得到50,从408可以得到8. (不含数字3和4的自然数不能进行“丢三落四”操作)
③“七上八下”:如果一个自然数中包含数字“7”,就将所有“7”移到最左边;如果一个自然数中包含数字“8”,就将所有“8”移到最右边。
例如从98707可以得到77908,从802可以得到28. (不含数字7和8的自然数不能进行“七上八下”操作)
④“十全十美”:将一个自然数的个位数字换成0. 例如从111可以得到110,从905可以得到900. (个位是0的自然数不能进行“十全十美”
操作)
(1) 请写出对4176依次进行③①③②④操作后的结果:
(2) 从655687开始,最少经过几次操作以后可以得到0?
(3) 一个三位数除了“丢三落四”外,其他三个操作各进行一次之后得到的结果是
8. 求有多少个这样的三位数.
图1-2是同学们都很熟悉的九九乘法口诀表,表中所有乘积的总和是多少?
第2讲和差倍问题三
内容概述
数量关系复杂,需要深入分析的和差倍问题;由于数量大小改变,而产生倍数关系变化的问题;需要利用比较或分组的方法进行分析的问题。
典型问题
兴趣篇
1. 有长、短两根竹竿,长竹竿的长度是短竹竿长度的3倍. 将它们插入水塘中,插入水中的长度都是40厘米,而露出水面部分的总长为160厘米. 请问:短竹竿露在外面的长度是多少厘米?
2. 李师傅某天生产了一批零件,他把它们分成了甲、乙两堆.如果从甲堆中拿出15个放到乙堆中,则两堆零件的个数相等;如果从乙堆中拿出15个放到甲堆中,则甲堆零件的个数是乙堆的3倍. 问:甲堆原来有零件多少个?李师傅这一天共生产零件多少个?
3. 一个六边形广场的边界上插有336面红旗和黄旗. 六边形的每个顶点处都插有红旗,每条边上的红旗数目一样多,并且每两面红旗间插有相同数目的黄旗. 已知每条边上黄旗比红旗的2倍还多12面,那么每两面红旗间插有几面共旗?
4. 爸爸和冬冬一起搬砖,爸爸所搬的砖头数是冬冬的3倍. 冬冬觉得自己搬的砖头太少了,又搬了24块砖头,于是爸爸所搬的砖头数是科科的2倍. 请问:最后爸爸和冬冬各搬了多少块砖?
5. 四年级三班买来单价为5角的练习本若干. 如果将这些练习本只分给女生,平均每人可得15本;如果将这些练习本只分给男生,平均每人可得10本. 请问:将这些练习本平均分给全班同学,每人可以得到多少本?此时每人应付多少钱?
6. 有甲、乙、丙三所小学的同学来参加幼苗杯数学邀请赛,其中甲校参赛人数比乙校多5人,比丙校多7人. 如果乙、丙两校一共有40人参加比赛,那么三所学校各有多少人参加比赛?
7. 有三个箱子,如果两箱两箱地称它们的重量,分别是83千克、85千克和86千克. 问:其中最轻的箱子重多少千克?
8. 小悦和妈妈一起去家具城挑选客厅的桌椅. 她们看中了两款,这两款桌椅都包含一张桌子和若干把椅子.其中桌子的价钱一样,每把椅子
的价钱也一样. 第一款桌椅中有6把椅子,总价为700元;第二款桌椅中有9把椅子,总价为970元. 请问:一张桌子的价钱是多少元?
9. 小白兔与小黑兔一块去森林里采摘了一些胡萝卜,回家后它们就把胡萝卜平分了. 小白兔当天吃了4个胡萝卜,小黑兔则一口气吃了12个胡萝卜. 小白免往后每天都吃4个胡萝卜;小黑兔因为第一天吃得太多,往后每天只吃2个胡萝卜,最后它俩同时把自己的胡萝卜吃完. 小白兔与小黑兔一共采摘了多少个胡萝卜?
10. 一家汔车销售店有若干部福特汽车和丰田汽车等待销售. 福特汽车的数量是丰田汽车的3倍.如果每周销售2辆丰田汽车和4辆福特汽车,丰田汽车销售完时还剩下30辆福特汽车. 请问:原有丰田汽车和福特汽车各多少辆?
拓展篇
1. 李师傅将甲、乙两种零件加工成产品,开始时甲零件的数量乙零件的2倍,每件产品需要5个甲零件和2个乙零件,生产30件产品后,剩下的甲、乙零件数量相等,请问:李师傅还可以生产几件产品?。
