2015数模培训剖析
数学建模竞赛培训的实践与思考

数学建模竞赛培训的实践与思考数学建模竞赛培训的实践与思考马怀远作者简介:马怀远(1963—),男,江苏经贸职业技术学院信息系高级讲师;211168。
摘 要:数学建模竞赛是目前国内大学生最大规模的科技竞赛活动,我院也积极参与了此项竞赛活动,并取得了良好成绩。
这不仅对培养学生的创新精神和实践应用能力起到了积极作用,还促进了教师队伍建设,推动了数学教学改革。
对参赛选手的培训,是参与这项活动的关键。
关键词:大学生数学建模竞赛;培训;创新精神;数学教学改革 数学建模竞赛是目前国内大学生最大规模的科技竞赛活动,仅江苏省今年就有62个高校共851个队参赛。
我院作为一所高职院校,参与此项竞赛并取得了良好的成绩。
大学生数学建模竞赛要求参赛选手(三人为一队),在72小时时间内完成对一道较复杂的应用问题的分析,建立数学模型,用数学软件进行计算得出结论,并完成一篇论文。
竞赛分为两组,理工类本科学生选择A 、B 题中的一题,文科类本科生和专科类学生选择C 、D 题中的一题。
我院作为高职院校,选手参加C 、D 题的竞赛。
作为全国大学生的竞赛,竞赛试题具有较大的难度和灵活性,较高的要求,对于高职院校学生来说,更有难度。
如何搞好参赛前的培训,就显得尤为重要。
我院学生正常教学中只学习过微积分的基本知识,竞赛所必须掌握的线性代数、线性规划、微分方程、运筹学、概率统计等基础知识几乎都未学习过。
而利用数学软件进行计算,也知之甚少。
因此,我们的培训起点是很低的,选手的能力刚开始与竞赛要求差距很大。
不仅如此,师资方面困难也很大,虽然我院参加过几届数学建模竞赛,但由于人员变动等原因,大部分老师都未搞过竞赛培训,软件计算也不在行。
然而,参加数学建模竞赛对参赛学生来说,能够实现追求知识、参与竞争的愿望,能够感受数学的应用价值,能够培养创新思维与解决实际问题的能力,培养计算机应用能力,培养团队合作精神,意义巨大。
虽然我们的条件先天不足,但只要我们精心组织,做好培训工作,一样能使学生有较大的收获,这正是我们参加竞赛的目的意义所在。
2015数模提高班专题3——多元统计分析

从而使得矩阵的每一列均值为0,方差为1 标准化2
标准化的优点:
消除数据量纲的影响;
例如:
杭州市的温度:-10~45℃ 大气压力:105Pa 湿度:0%~100% 怎么分析温度、大气压力和湿度对心情
的影响?
矩阵代数
1.特征向量
向量(3, 2)T表示二维平面中从原点(0, 0)指向点(3,2)
的一个箭头,而矩阵可以认为是转移矩阵; 经转移矩阵变换后还是自身(倍数)的向量称为矩阵的 特征向量; 一般对单位特征向量进行处理。
2.特征值
与特征向量成对出现 协方差矩阵是非负定,存在正交矩阵(由单位正交化 特征向量组成),使其与对角矩阵相似。
PCA的数学原理
假定我们有
观察值; PCA的主要目标是寻找m个变量Xi的线性组 合Fi (m ≤ p),,来解释Xi的方差-协方差结构, 并且Fi 之间不相关。即用少量的p个变量说明 原变量组的大部分变异性。
(3)两个变量的协方差(covariance)
协方差用于衡量数据的协变趋势,公式为:
记为 c( x, y) xy . 若 x
y, c( x, x) v( x)
2
1 T 若X和Y的均值为零,协方差 c( x, y ) x y n
如果X 与Y 是不相关的,二者之间的协方差就是0 matlab命令:cov(x,y)
(2)方差(variance)
方差用于衡量数据的集中或分散程度,公式为:
Matlab命令:var(x) 标准差(standard deviation)是观测值与均值间的平 均距离,公式为:
Matlab命令:std(x)
图1.不同方差数据示意图:变异性越大,说明指标对各种场 景的遍历性越强,提供的信息越充分,信息量越大。
数学建模培训中的教学方法浅析

2 1 年第 1 期 00 1
文化教 育
数学 建模 培训 中的教学 术 学院 素 质教 育部 , 苏 南京 2 0 4 ) 江 10 6
摘 要: 数学建模 可以培养学生的实践精神和创新 能力, 通过对数学建模具体流程及本校数学建模工作情况的分析 , 阐述 了数 学建模培训及竞
赛 中 的教 育 内容 和 教 育 方 法 。
关键词 : 数学建模 ; 创新教育 ; 教学方法 “ 国大学生数学建模竞赛”是由教育部 高教 司 、中国工业 与应用 全 数学学会共 同主办 的 ,面向全 国大学生 的一项 群众性科技活动 ,竞赛 于每年 的 9月进行 , 目的在于激发学生 的学 习积极性 ,提高学生解决 实 际问题 的能力 ,培养 学生的创新精神及协作 意识 ,并借此推动 大学 数学教学改革 。在每年 的比赛 之前 ,很多 院校都 会对参赛学生进行适 当的培训 ,在竞赛培训过 程中如何进行教学 ,是各 高校一直在研究 的 问题 。
次能力测试 ,选出部分优秀的同学进行下一 阶段培训。 2 )第二 阶段主要是数学建模专业知识 的培训 ,在这一 阶段 ,学生 会接触到各种常见 的数学方 法 ,比如线性规划方 法 、微分方程稳定性 方法 、统计分析方法 、层次 分析方法 、灰色 系统 方法等 。这个 阶段 的 授课 主要让学 生边学边练 ,学 生既需要掌握老师上课所 讲内容 ,同时 也需要在课后 能够在计算机上 对相 应程序进行演 练。并 且指导老师在 这一 阶段 也会 布置学生去进行 一定 量的针对性 阅读 ,主要是跟各种方 法相关 的历年赛 题 ,遇到 问题 时可以随时与老师进行讨 论 ,通过这一 阶段 的训 练 ,学生的知识能力 已基本达到 了要求 。这 一阶段为期半个 月 ,通 常 在 暑 假 期 间 进 行 。 3 )第三阶段是实际做题 演练 ,这一 阶段为期半个月 ,同样在暑假 期 间进行 。这 一阶段会让学生 分成 3 人一组 ,然后模 拟比赛情形 ,每 三天完成一道建模 问题 ,与实 际比赛 不同的是 ,指导老 师会 在最后一 天 的下午进行点 评和讲解 ,所 以做题 时间会有所压缩 。通过 这一阶段 的练 习,学生对 建模 的常用方法 和常见题型 已经 比较熟悉 ,同时阅读 面也扩展 了很 多 ,拿 到不熟悉 的问题 也能从容应对 。并且 ,指导老师
大学生数学建模竞赛培训的实践与体会

种 自学能力反过来 又促 进科研 能力 的提升 。通 过竞 赛 , 同学
们锻炼 了写科技论文的能力 。通过参 加美国大学生 数学建模 竞赛 , 同学们锻炼 了英 文写作能力 , 建立 了国际视野 。数 学 也
P a tc n p re c o p tt n ta nn fM a h ma ia o ei g r ciea d Ex e in ei c m e i o r i i go t e t l n i c M dl n
高等数学课程是我 校本科 生必 修的一 门公 共基 础课 , 高
等数学教师在教学过程 中有意识有计划 的把数学建模 的思想 和方法融入到教学 中 , 学生 初步认 识和 理解什 么是数 学建 让 模 以及数学建模 的作用 。例如 : 在讲 授导数 内容 时 , 导数 的概 念及几何意义容 易被学 生理解 , 但对 有 的函数在 某点 处左 导 数 和右导数不相 等理解存 在疑 惑 , 时结合 医学 心 电图 中的 此
数学建模竞赛培 训是 一项成 功的教 学 改革 实践 , 功促 成 进我校数学建模 和数学 实验选 修课 的建设 , 而且培养 了一批
青年教师 。
4 结 语
数学建模竞赛是一 个涉及 多学科 的一 个赛 事 , 是培 养学
生知识、 能力 和素质 的赛事 。例如 2 1 0 0年全 国大学生 的赛题 B是 “0 0年上海世博会 影响 力的定 量评估 ” 需要 参赛 同学 21 ,
要 每组 的学生到黑板上讲解他们 的思路 、 方法 、 用模型 以及 所
利 用模 型得 到的结果 , 同学 们进行 讨论 , 导教 师进行 点评 。 指 通过建模 的模拟训 练 , 选拔优 秀学 生参加 全 国大学 生数学 建 模竞赛 和美 国大 学生数 学建模 竞赛 、 国大学 生交叉 学科 竞 美
数学建模基础课程培训

数学建模基础课程培训江西省南昌市2015-2016学年度第⼀学期期末试卷(江西师⼤附中使⽤)⾼三理科数学分析⼀、整体解读试卷紧扣教材和考试说明,从考⽣熟悉的基础知识⼊⼿,多⾓度、多层次地考查了学⽣的数学理性思维能⼒及对数学本质的理解能⼒,⽴⾜基础,先易后难,难易适中,强调应⽤,不偏不怪,达到了“考基础、考能⼒、考素质”的⽬标。
试卷所涉及的知识内容都在考试⼤纲的范围内,⼏乎覆盖了⾼中所学知识的全部重要内容,体现了“重点知识重点考查”的原则。
1.回归教材,注重基础试卷遵循了考查基础知识为主体的原则,尤其是考试说明中的⼤部分知识点均有涉及,其中应⽤题与抗战胜利70周年为背景,把爱国主义教育渗透到试题当中,使学⽣感受到了数学的育才价值,所有这些题⽬的设计都回归教材和中学教学实际,操作性强。
2.适当设置题⽬难度与区分度选择题第12题和填空题第16题以及解答题的第21题,都是综合性问题,难度较⼤,学⽣不仅要有较强的分析问题和解决问题的能⼒,以及扎实深厚的数学基本功,⽽且还要掌握必须的数学思想与⽅法,否则在有限的时间内,很难完成。
3.布局合理,考查全⾯,着重数学⽅法和数学思想的考察在选择题,填空题,解答题和三选⼀问题中,试卷均对⾼中数学中的重点内容进⾏了反复考查。
包括函数,三⾓函数,数列、⽴体⼏何、概率统计、解析⼏何、导数等⼏⼤版块问题。
这些问题都是以知识为载体,⽴意于能⼒,让数学思想⽅法和数学思维⽅式贯穿于整个试题的解答过程之中。
⼆、亮点试题分析1.【试卷原题】11.已知,,A B C 是单位圆上互不相同的三点,且满⾜AB AC →→=,则A BA C →→的最⼩值为()A .14- B .12-C .34-D .1-【考查⽅向】本题主要考查了平⾯向量的线性运算及向量的数量积等知识,是向量与三⾓的典型综合题。
解法较多,属于较难题,得分率较低。
【易错点】1.不能正确⽤OA ,OB,OC 表⽰其它向量。
2.找不出OB 与OA 的夹⾓和OB与OC 的夹⾓的倍数关系。
大学生数学建模竞赛培训案例模板式教学探析

大学生数学建模竞赛培训案例模板式教学探析大学生数学建模竞赛,由教育部高教司和中国工业与应用数学学会主办,创办于1992年,每年一届,目前已成为全国高校规模最大的基础性学科竞赛,也是世界上规模最大的数学建模竞赛,同时成为高等院校一项重大的课外科技活动。
尤其2014年,来自全国33个省/市/自治区(包括香港和澳门特区)及新加坡、美国的1338所院校、25347个队(其中本科组22233队、专科组3114队)、7万多名大学生报名参加本项竞赛。
每年的9月份举办,三人为一组,比赛时间共三天,最终通过论文的形式来体现,以创新意识、团队精神、重在参与、公平竞争为宗旨,旨在培养大学生的创新意识与团队精神。
一、大学生数学建模竞赛培训的重要性数学建模竞赛作为教育部四大学科竞赛之首,规模最大,影响最大。
因此,数学建模竞赛培训显得尤为重要。
它有利于让学生尽早了解并掌握建模的基础理论知识及相关应用软件;有利于培养学生分析问题和解决实际问题的能力;有利于培养学生的团队合作精神,使队员间尽早磨合,相互了解;有利于培养学生的创新意识和发散思维;有利于训练学生快速获取有用信息和资料的能力;有利于增强学生的写作技能和排版技术等。
通过参加数学建模竞赛,受到了一次科学研究的初步训练,初步具备了科学研究的能力,提高了自身的分析问题和解决问题的能力以及计算机应用能力,培养了刻苦钻研问题的精神以及与他人友好合作的团队精神,培养了敢于战胜困难的坚强意志和创新能力,这些能力和精神为各自今后的学习和工作都带来了巨大的影响。
因为参与数学建模比赛,许多学生收获了知识,取得了荣誉,参赛队员的共同体会是:一次参赛,终生受益。
二、培训中创新方法--案例模板式教学数学建模培训一般是通过给学生讲解数学建模的基本知识与理论,相关的数学软件及软件包,辅以讲座,上机,讨论等方式,让学生对数学建模的基本方法及相关数学软件的使用有一定的了解,对数学建模的基本思想有基本把握。
Petrel2015建模培训2
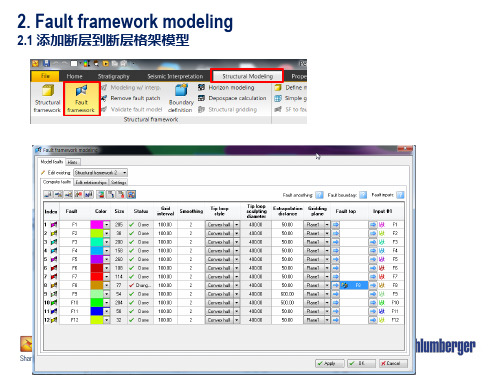
1.基本概念
测井曲线分布概率与粗化平均方法选择
孔隙度:Arithmetic
岩相:Most of
渗透率:Hormonic Geometry
1.基本概念
Biasing to a Discrete Log
Upscaled facies Raw facies Raw porosity Upscaled porosity
Demo & Exercise
4.Structural Gridding
From Structural Framework to a fully populated property model at any grid cell resolution in just a few clicks!
Fully stair-stepped grid matching the Structural Framework faults and horizons
Cells exist along the well path.
Values assigned to cells based on well log values along the well path.
Upscaled logs used to fill in the 3D grid.
NOTE: An upscaled property will have a [U] following its name in the Property folder in the Models pane.
Input
Output
Structural framework grid
Fault Model
Pillar Gridding
Make Horizons
《数学建模》实训的认识与实践-文档资料

《数学建模》实训的认识与实践一、《数学建模》实训的现状与认识数学集抽象、严密、精确于一体,让许多人提起它觉得高不可攀、深不可测。
使得很多学生在一接触到数学的学习时就缺乏信心,没有兴趣。
在学习的过程中不能真切的感受到数学的重要性,更让他们迷茫的是不知道该怎么用、什么时候用。
他们缺乏把理论应用到实际中这样一个平台,不知道学习数学到底究竟有什么用,不会用数学知识来解释遇到的问题和现象,认为数学就是记公式,因而学习过程充满枯燥和乏味,久而久之也就失去信心和兴趣,学不懂也学不进去。
尽管作为传道解惑的专业课的老师们经常强调“理论要联系实际”,但并没有真正做到理论与实际相结合,因而学生才会经常提出“学习数学有什么用啊”等这样的疑问。
那如何在理论和实践的搭建一个很好平台呢?《数学建模》实训的开设就是一个很好的媒介,它将现实问题归结为相应的数学问题,并在此基础上利用数学的概念、方法和理论进行深入的分析和研究,从而从定性或定量的角度来刻画实际问题,并为解决现实问题提供精确的数据或可靠的指导。
让学生在面临众多需要用数学解决的问题时,能应用数学技术和相关的计算机软件解决实际问题,从而激发学生学习数学的兴趣和动力,促使学生把所学的知识与实际应用有机地结合起来,充分发掘学生的潜能,提高学生的综合素质。
此外,《教育部财政部关于实施高等学校本科教学质量与教学改革工程的意见》、以及《教育部关于进一步深化本科教学改革全面提高教学质量的若干意见》明确指出如今高等教育中存在的问题,比如“高等教育质量还不能完全适应经济社会发展的需要,不少高校的专业设置和结构不尽合理,学生的实践能力和创新精神亟待加强”。
从此可以看出,我们目前的教育还不能完全满足我们社会的需要。
我们要想建设创新型国家以及和谐社会主义,我们就要提高高等教育质量,增强学生实践创新能力、就业能力和创业能力。
我们必须着力提高大学生的动手实践能力,以及注重知识传授向更加重视能力和素质培养的转变。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2021/3/2
湖南农业大学数学建模暑期培训
2011年优秀论文讲解 A题
• 附件1列出了采样点的位置、海拔高度及其所属功能区等信息,附件2 列出了8种主要重金属元素在采样点处的浓度,附件3列出了8种主要重 金属元素的背景值。
• 现要求你们通过数学建模来完成以下任务: • (1) 给出8种主要重金属元素在该城区的空间分布,并分析该城区内不
2021/3/2
湖南农业大学数学建模暑期培训
2010年优秀论文讲解 A10年优秀论文讲解 A题
2021/3/2
湖南农业大学数学建模暑期培训
2010年优秀论文讲解 A题
• 命题过程
2021/3/2
湖南农业大学数学建模暑期培训
2010年优秀论文讲解 A题
2021/3/2
湖南农业大学数学建模暑期培训
2010年优秀论文讲解 A题
• 请你们用数学建模方法研究解决储油罐的变位识别与罐容表 标定的问题。
• (1)为了掌握罐体变位后对罐容表的影响,利用如图4的小 椭圆型储油罐(两端平头的椭圆柱体),分别对罐体无变位
和倾斜角为=4.10的纵向变位两种情况做了实验,实验数据
• 现对某城市城区土壤地质环境进行调查。为此,将所考察的城区划分 为间距1公里左右的网格子区域,按照每平方公里1个采样点对表层土 (0~10 厘米深度)进行取样、编号,并用GPS记录采样点的位置。应 用专门仪器测试分析,获得了每个样本所含的多种化学元素的浓度数 据。另一方面,按照2公里的间距在那些远离人群及工业活动的自然 区取样,将其作为该城区表层土壤中元素的背景值。
如附件1所示。请建立数学模型研究罐体变位后对罐容表的影 响,并给出罐体变位后油位高度间隔为1cm的罐容表标定值。
• (2)对于图1所示的实际储油罐,试建立罐体变位后标定罐 容表的数学模型,即罐内储油量与油位高度及变位参数(纵
向倾斜角度和横向偏转角度 )之间的一般关系。请利用罐
体变位后在进/出油过程中的实际检测数据(附件2),根据 你们所建立的数学模型确定变位参数,并给出罐体变位后油 位高度间隔为10cm的罐容表标定值。进一步利用附件2中的实 际检测数据来分析检验你们模型的正确性与方法的可靠性。
2011年优秀论文讲解 A题
问题分析: • 第一问:尽量详细地描述8种重金属的位置关
系,分布情况,包括与坐标、海拔的关系,8 种金属的相关性,与5个区域的关系等。该城 区内不同区域重金属的污染程度要分别针对每 一种重金属评判其污染的等级从而确定其污染 程度。污染的等级是个客观的常数,但可用不 同方法确定,每种方法得到的结果不尽相同。 (如内梅罗指数污染模型)
2021/3/2
湖南农业大学数学建模暑期培训
2011年优秀论文讲解 A题
• 第四问:本问题作为模型的推广,主要是针对 第三问所建模型的缺点进行发散性推广,只需 建模,不需求解。
2021/3/2
湖南农业大学数学建模暑期培训
2011年优秀论文讲解 A题
• 优秀论文1:城市表层土壤重金属污染分析
本文点评:
同区域重金属的污染程度。 • (2) 通过数据分析,说明重金属污染的主要原因。 • (3) 分析重金属污染物的传播特征,由此建立模型,确定污染源的位
置。 • (4) 分析你所建立模型的优缺点,为更好地研究城市地质环境的演变
模式,还应收集什么信息?有了这些信息,如何建立模型解决问题?
2021/3/2
湖南农业大学数学建模暑期培训
2013数学建模培训 优秀论文精讲
• 2011年优秀论文
• 2010年优秀论文
• 2009年优秀论文
• 2008年优秀论文
• 2005年优秀论文
2021/3/2
湖南农业大学数学建模暑期培训
2011优秀论文讲解 A题
城市表层土壤重金属的污染分析
• 随着城市经济的快速发展和城市人口的不断增加,人类活动对城市环 境质量的影响日显突出。对城市土壤地质环境异常的查证,以及如何 应用查证获得的海量数据资料开展城市环境质量评价,研究人类活动 影响下城市地质环境的演变模式,日益成为人们关注的焦点。按照功 能划分,城区一般可分为生活区、工业区、山区、主干道路区及公园 绿地区等,分别记为1类区、2区、……、5类区,不同的区域环境受 人类活动影响的程度不同。
问题分析:
➢ 本文特色
思维细腻,契合实际,考虑全面; 有效利用现有模型进行加工、完善;
➢ 注意事项
污染原因要量化。
2021/3/2
湖南农业大学数学建模暑期培训
2011年优秀论文讲解 A题
• 优秀论文2:城市表层土壤重金属的污染分析
本文点评:
➢ 本文特色
前两问分析详尽,可读性强; 思路简约,程序简单;
2021/3/2
湖南农业大学数学建模暑期培训
2011年优秀论文讲解 A题
• 第二问:分析污染的原因,首先要弄清楚每个 区域污染物的情况,因此应该按照5个区域里 的8种重金属的污染排序,然后再分析每个区 域里排序的原因。(模糊综合评判的方法很多, 如TOPSIS法)
• 第三问:该问题是本论文的重心及难点所在。 分析污染的方向性,不仅仅只是利用附件的数 据进行污染源的“搜索”,而应当结合现有的污 染扩散模型,因为各金属污染是有相互作用的。
• 许多储油罐在使用一段时间后,由于地基变形等原因,使 罐体的位置会发生纵向倾斜和横向偏转等变化(以下称为 变位),从而导致罐容表发生改变。按照有关规定,需要 定期对罐容表进行重新标定。图1是一种典型的储油罐尺寸 及形状示意图,其主体为圆柱体,两端为球冠体。图2是其 罐体纵向倾斜变位的示意图,图3是罐体横向偏转变位的截 面示意图。
➢ 注意事项
寻找污染源应结合现有污染扩散模型 模型智能化需提升 人员分配需更合理
2021/3/2
湖南农业大学数学建模暑期培训
2010年优秀论文讲解 A题
A题 储油罐的变位识别与罐容表标定
• 通常加油站都有若干个储存燃油的地下储油罐,并且一般 都有与之配套的“油位计量管理系统”,采用流量计和油 位计来测量进/出油量与罐内油位高度等数据,通过预先标 定的罐容表(即罐内油位高度与储油量的对应关系)进行 实时计算,以得到罐内油位高度和储油量的变化情况。
