勾股定理最短距离问题蚂蚁爬行的最短路径好
中考复习之——蚂蚁爬行的最短路径问题

蚂蚁爬行的最短路径问题I•专题精讲:当蚂蚁在一个几何体的表面上爬行时,通常情况下都会考虑将其展开成一个平面,运用勾股定理计算其最短路程,也就是运用“化曲为平”或“化折为直”的思想来解决问题n.典型例题剖析:一•两点之间,线段最短与勾股定理相结合台阶问题如图,是一个三级台阶,它的每一级的长、宽和高分别等于5cm, 3cm和1cm, A和B是这个台阶的两个相对的端点,A点上有一只蚂蚁,想到B点去吃可口的食物•请你想一想,这只蚂蚁从的最短距离_____________2. 有一圆形油罐底面圆的周长为24m,高为6m,一只老鼠从距底面1m 的A处爬行到对角B处吃食物,它爬行的最短路线长为_______________ .3. 葛藤是一种刁钻的植物,它的腰杆不硬,为了争夺雨露阳光,常常绕着树干盘旋而上,它还有一手绝招,就是它绕树盘升的路线总是沿最短路线--螺旋前进的,难道植物也懂数学?通过阅读以上信息,解决下列问题:(1 )如果树干的周长(即图中圆柱体的底面周长)为30cm,绕一圈升高(即圆柱的高)40cm, 则它爬行一圈的路程是多少?(2)如果树干的周长为80cm,绕一圈爬行100cm,它爬行10圈到达树顶,则树干高多少?B点, 最短线路是1.有一圆柱体如图,高4cm,底面半径5cm, A处有一蚂蚁,若蚂蚁欲爬行到C处,求蚂蚁爬行A点出发,沿着台阶面爬到A圆柱(锥)问题第1题4.如图,底面半径为1,母线长为4的圆锥,一只小蚂蚁若从A 点出发,绕侧面一周又回到 A点,它爬行的最短路线长是 ______________ .5.如图,圆锥的主视图是等边三角形,圆锥的底面半径为的表面爬行,它要想吃到母线 AC 的中点P 处的食物,那么它爬行的最短路程是6.已知0为圆锥顶点,OA 、OB 为圆锥的母线, 侧面爬行到点A ,另一只小蚂蚁绕着圆锥侧面爬行到点 所示•若沿0A 剪开,则得到的圆锥侧面展开图为2.如图,一只小虫沿边长为 1的正方体的表面从点的路径是最短的,则 AC 的长为 _______________ .3.正方体盒子的棱长为 2 ,BC 的中点为M ,—只蚂蚁从A 点爬行到M 点的最短距离为C 为0B 中点,一只小蚂蚁从点 C 开始沿圆锥 B ,它们所爬行的最短路线的痕迹如右图 ( )(长)方体问题如图,边长为 1. 距离是1的正方体中,一只蚂蚁从顶点 出发沿着正方体的外表面爬到顶点B 的最短2cm ,假若点B 有一蚂蚁只能沿圆锥A 出发,经过3个面爬到点B •如果它运动R第5题A.B.C. D.第2题4.如图,一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点C i处(三条棱长如图所示),问怎样走路线最短?最短路线长为_____________ .5. 如图,长方体的底面边长分别为2cm和4cm,高为5cm.若一只蚂蚁从P点开始经过4个侧面爬行一圈到达Q点,则蚂蚁爬行的最短路径长为_______________ .变式:如图,长方体的底面边长分别为1cm和3cm,高为6cm .如果从点A开始经过4个侧面缠绕n圈到达点B,那么所用细线最短需要 _________ cm .6. (1)如图①,一个无盖的长方体盒子的棱长分别为BC = 3cm、AB = 4cm、AA i = 5cm,盒子的内部顶点C i处有一只昆虫甲,在盒子的内部顶点A处有一只昆虫乙(盒壁的厚度忽略不计)•假设昆虫甲在顶点C i处静止不动,请计算A处的昆虫乙沿盒子内壁爬行到昆虫甲C i处的最短路程•并画出其最短路径,简要说明画法.(2)如果(i)问中的长方体的棱长分别为AB = BC = 6cm, AA i= i4cm,如图②,假设昆虫甲从盒内顶点C i以i厘米/秒的速度在盒子的内部沿棱C i C向下爬行,同时昆虫乙从盒内顶点A以3厘米/秒的速度在盒壁的侧面上爬行,那么昆虫乙至少需要多长时间才能捕捉到昆虫甲?研究课题:蚂蚁怎样爬最近?研究方法:如图1,正方体的棱长为5cm,一只蚂蚁欲从正方体底面上的点A沿着正方体表面爬到点C1处,要求该蚂蚁需要爬行的最短路程的长,可将该正方体右侧面展开,由勾股定理得最短路程的长为A6= .AC2+CC I2= 102+52= 5:...;5cm .这里,我们将空间两点间最短路程问题转化为平面内两点间距离最短问题.研究实践:(1)如图2,正四棱柱的底面边长为5cm,侧棱长为6cm,一只蚂蚁从正四棱柱底面上的点A沿着棱柱表面爬到 6处,蚂蚁需要爬行的最短路程的长为_______________________ .(2)如图3,圆锥的母线长为4cm,圆锥的侧面展开图如图4所示,且/ AOA1=120°, 一只蚂蚁欲从圆锥的底面上的点A出发,沿圆锥侧面爬行一周回到点A.求该蚂蚁需要爬行的最短路程的长.(3)如图5,没有上盖的圆柱盒高为10cm,底面圆的周长为32cm,点A距离下底面3cm.-只位于圆柱盒外表面点A处的蚂蚁想爬到盒内表面对侧中点B处.请求出蚂蚁需要爬行的最短路程的长.。
专题训练蚂蚁爬行的最短路径(附附答案解析)

蚂蚁爬行的最短路径1.一只蚂蚁从原点0出发来回爬行,爬行的各段路程依次为:+5,-3,+10,-8,-9,+12,-10.回答下列问题:(1)蚂蚁最后是否回到出发点0;(2)在爬行过程中,如果每爬一个单位长度奖励2粒芝麻,则蚂蚁一共得到多少粒芝麻. 解:(1)否,0+5-3+10-8-9+12-10=-3,故没有回到0;(2)(|+5|+|-3|+|+10|+|-8|+|-9|+|+12|+|-10|)×2=114粒2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线. AB = 51222=+.3.(2006•茂名)如图,点A 、B 分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A 沿其表面爬到点B 的最短路程是 cm.解:由题意得,从点A 沿其表面爬到点B 的最短路程是两个棱长的长,即2+2=4.4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短第6题路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B解:根据两点之间线段最短可知选A .故选A .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB = ()1012122=++.故选C .6. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为( )解:展开正方体的点M 所在的面,∵BC 的中点为M ,所以MC = 21BC =1, 在直角三角形中AM = = .7.如图,点A 和点B 分别是棱长为20cm 的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A 处向B 处爬行,所走最短路程是 cm 。
解:将盒子展开,如图所示:AB =CD =DF +FC = 21EF + 21GF =21×20+21×20=20cm . 故选C .8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D 1,根据两点之间线段最短,MD =MC +CD =1+2=3,MD 1=132322212=+=+DD MD .9.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB = = cm ;(2)展开底面右面由勾股定理得AB = =5cm ;所以最短路径长为5cm ,用时最少:5÷2=2.5秒.10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
勾股定理应用长方体最短路径

勾股定理的应用之最短距离问题1.如图,是一个棱长为8cm的正方体盒子,在顶点A处有一只蚂蚁,它想沿正方体表面爬行到达顶点C处,则蚂蚁爬行的最短路程是cm.2.如图,一圆柱高8cm,底面圆周长为12cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是cm.3.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为cm(杯壁厚度不计).4.如图,有一棱长为2dm的正方体盒子,现要按图中箭头所指方向从点A到点D拉一条捆绑线绳,使线绳经过ABFE、BCGF、EFGH、CDHG四个面,则所需捆绑线绳的长至少为dm.5.如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是.6.有一个如图所示的凹槽,各部分长度如图中所标.一只蜗牛从A点经过凹槽内壁爬到B点取食,最短的路径长是m.7.如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是.8.如图,已知圆柱的底面直径BC=,高AB=3,小虫在圆柱表面爬行,从点C 爬到点A,然后在沿另一面爬回点C,则小虫爬行的最短路程为.9.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是多少尺?10.如图是一个长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是多少?答案解析1.如图,是一个棱长为8cm的正方体盒子,在顶点A处有一只蚂蚁,它想沿正方体表面爬行到达顶点C处,则蚂蚁爬行的最短路程是8cm.【分析】根据图形是立方体得出最短路径只有一种情况,利用勾股定理求出即可.【解答】解:如图所示:需要爬行的最短距离是AC的长,即AC=.故答案为:8.【点评】此题主要考查了平面展开图最短路径问题以及勾股定理的应用,得出正确的展开图是解决问题的关键.2.如图,一圆柱高8cm,底面圆周长为12cm,一只蚂蚁从点A爬到点B处吃食,要爬行的最短路程是10cm.【分析】先把圆柱的侧面展开,连接AB,利用勾股定理求出AB的长即可.【解答】解:如图所示:连接AB,∵圆柱高8cm,底面圆周长为12cm,∴AC=×12=6cm,在Rt△ABC中,AB==10cm.故答案为:10【点评】本题考查的是平面展开﹣最短路径问题,解答此类问题的关键是画出圆柱的侧面展开图,利用勾股定理进行解答.3.如图,圆柱形玻璃杯高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在杯外壁,离杯上沿3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处到内壁B处的最短距离为20cm(杯壁厚度不计).【分析】将杯子侧面展开,建立A关于EF的对称点A′,根据两点之间线段最短可知A′B的长度即为所求.【解答】解:如图:将杯子侧面展开,作A关于EF的对称点A′,连接A′B,则A′B即为最短距离,A′B===20(cm).故答案为20.【点评】本题考查了平面展开﹣﹣﹣最短路径问题,将图形展开,利用轴对称的性质和勾股定理进行计算是解题的关键.同时也考查了同学们的创造性思维能力.4.如图,有一棱长为2dm的正方体盒子,现要按图中箭头所指方向从点A到点D拉一条捆绑线绳,使线绳经过ABFE、BCGF、EFGH、CDHG四个面,则所需捆绑线绳的长至少为2dm.【分析】把此正方体的一面展开,然后在平面内,利用勾股定理求点A和D点间的线段长,即可得到捆绑线绳的最短距离.在直角三角形中,一条直角边长等于两个棱长,另一条直角边长等于3个棱长,利用勾股定理可求得.【解答】解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB即为最短路线.展开后由勾股定理得:AD2=42+62=2,故AD=2dm.故答案为2.【点评】本题考查了勾股定理的拓展应用.“化曲面为平面”是解决“怎样爬行最近”这类问题的关键.5.如图,一个三级台阶,它的每一级的长宽和高分别为20、3、2,A和B是这个台阶两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,则蚂蚁沿着台阶面爬到B点最短路程是25.【分析】先将图形平面展开,再用勾股定理根据两点之间线段最短进行解答.【解答】解:如图所示,∵三级台阶平面展开图为长方形,长为20,宽为(2+3)×3,∴蚂蚁沿台阶面爬行到B点最短路程是此长方形的对角线长.设蚂蚁沿台阶面爬行到B点最短路程为x,由勾股定理得:x2=202+[(2+3)×3]2=252,解得:x=25.故答案为25.【点评】本题考查了平面展开﹣最短路径问题,用到台阶的平面展开图,只要根据题意判断出长方形的长和宽即可解答.6.有一个如图所示的凹槽,各部分长度如图中所标.一只蜗牛从A点经过凹槽内壁爬到B点取食,最短的路径长是2m.【分析】根据题意作出图形,然后根据勾股定理即可得到结论.【解答】解:如图,∵AC=1+2+1=4m,BC=10m,∴AB==2,∴最短的路径长是2.故答案为:2.【点评】本题考查了平面展开﹣最短路程问题,勾股定理,正确的作出图形是解题的关键.7.如图,一长方体底面宽AN=5cm,长BN=10cm,高BC=16cm.D为BC的中点,一动点P从A点出发,在长方体表面移动到D点的最短距离是cm.【分析】将图形展开,可得到AD较短的展法两种,通过计算,得到较短的即可.【解答】解:(1)如图1,BD=BC=8cm,AB=5+10=15cm,在Rt△ADB中,AD= =cm;(2)如图2,AN=5cm,ND=8+10=18cm,Rt△ADN中,AD===cm.(3)如图3,AD==,综上,动点P从A点出发,在长方体表面移动到D点的最短距离是cm.故答案为:cm.【点评】本题考查了平面展开﹣﹣最短路径问题,熟悉平面展开图是解题的关键.8.如图,已知圆柱的底面直径BC=,高AB=3,小虫在圆柱表面爬行,从点C 爬到点A,然后在沿另一面爬回点C,则小虫爬行的最短路程为6.【分析】要求最短路径,首先要把圆柱的侧面展开,利用两点之间线段最短,然后利用勾股定理即可求解.【解答】解:把圆柱侧面展开,展开图如右图所示,点A、C的最短距离为线段AC的长.在RT△ADC中,∠ADC=90°,CD=AB=3,AD为底面半圆弧长,AD=3,所以AC=3,∴从C点爬到A点,然后再沿另一面爬回C点,则小虫爬行的最短路程为2AC=6,故答案为:6,【点评】本题考查了平面展开﹣最短路径问题,解题的关键是会将圆柱的侧面展开,并利用勾股定理解答.9.我国古代有这样一道数学问题:“枯木一根直立地上,高二丈周三尺,有葛藤自根缠绕而上,五周而达其顶,问葛藤之长几何?,题意是:如图所示,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处.则问题中葛藤的最短长度是多少尺?【分析】根据题意画出图形,再根据勾股定理求解即可.【解答】解:如图所示,在如图所示的直角三角形中,∵BC=20尺,AC=5×3=15尺,∴AB==25(尺).答:葛藤长为25尺.【点评】本题考查的是平面展开﹣最短路径问题,此类问题应先根据题意把立体图形展开成平面图形后,再确定两点之间的最短路径.一般情况是两点之间,线段最短.在平面图形上构造直角三角形解决问题.10.如图是一个长、宽、高分别为12cm,4cm,3cm的木箱,在它里面放入一根细木条(木条的粗细忽略不计),要求木条不能露出木箱,请你算一算,能放入的细木条的最大长度是多少?【分析】直接利用勾股定理得出AC的长,进而得出AD的长.【解答】解:连接AC,AD,在Rt△ABC中,AC2=AB2+BC2,则AC===4,在Rt△ACD中,AD2=AC2+DC2,则AD==13,答:能放入的细木条的最大长度是13cm.【点评】此题主要考查了勾股定理,正确应用勾股定理是解题关键.。
(完整版)勾股定理--最短距离问题
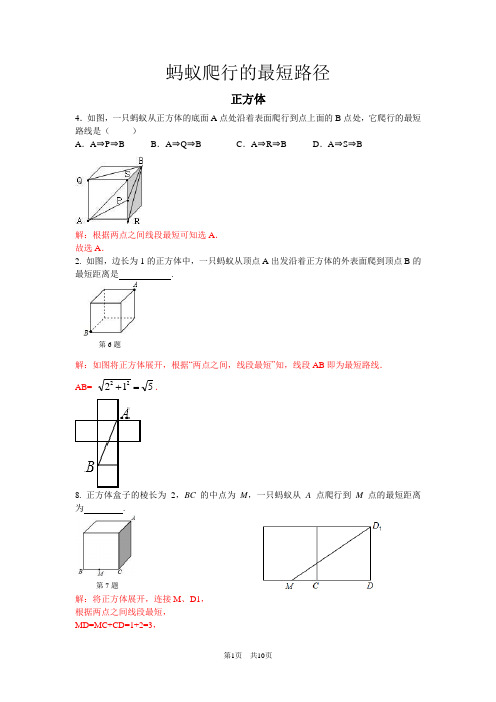
蚂蚁爬行的最短路径正方体4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒ B解:根据两点之间线段最短可知选A . 故选A .2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线. AB=51222=+.8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D1, 根据两点之间线段最短, MD=MC+CD=1+2=3,第6题第7题AB121MD 1=132322212=+=+DD MD .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB= ()1012122=++.故选C .9.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB= = cm ;(2)展开底面右面由勾股定理得AB==5cm ;所以最短路径长为5cm ,用时最少:5÷2=2.5秒.长方体10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
解:将长方体展开,连接A 、B ,根据两点之间线段最短,AB==25.A B A 1B 1D CD 1C 121411. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),问怎样走路线最短?最短路线长为 .解:正面和上面沿A 1B 1展开如图,连接AC 1,△ABC 1是直角三角形, ∴AC 1=()5342142222212=+=++=+BC AB18.(2011•荆州)如图,长方体的底面边长分别为2cm 和4cm ,高为5cm .若一只蚂蚁从P 点开始经过4个侧面爬行一圈到达Q 点,则蚂奴爬行的最短路径长为 cm .解:∵PA=2×(4+2)=12,QA=5 ∴PQ=13.故答案为:13.19.如图,一块长方体砖宽AN=5cm ,长ND=10cm ,CD 上的点B 距地面的高BD=8cm ,地面上A 处的一只蚂蚁到B 处吃食,需要爬行的最短路径是多少?解:如图1,在砖的侧面展开图2上,连接AB , 则AB 的长即为A 处到B 处的最短路程.解:在Rt △ABD 中,因为AD=AN+ND=5+10=15,BD=8, 所以AB 2=AD 2+BD 2=152+82=289=172. 所以AB=17cm .故蚂蚁爬行的最短路径为17cm .49、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?12.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
专题训练-蚂蚁爬行的最短路径(含答案)

蚂蚁爬行的最短路径1.一只蚂蚁从原点0出发来回爬行,爬行的各段路程依次为:+5,-3,+10,-8,-9,+12,-10.答复以下问题:〔1〕蚂蚁最后是否回到出发点0;〔2〕在爬行过程中,如果每爬一个单位长度奖励2粒芝麻,那么蚂蚁一共得到多少粒芝麻.解:〔1〕否,0+5-3+10-8-9+12-10=-3,故没有回到0;〔2〕〔|+5|+|-3|+|+10|+|-8|+|-9|+|+12|+|-10|〕×2=114粒2. 如图,边长为1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外外表爬到顶点B的最短距离是.解:如图将正方体展开,根据“两点之间,线段最短〞知,线段AB即为最短路线.AB= 51222=+.3.〔2006•茂名〕如图,点A、B分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A沿其外表爬到点B的最短路程是cm第6题.解:由题意得,从点A 沿其外表爬到点B 的最短路程是两个棱长的长,即2+2=4.AB4.如图,一只蚂蚁从正方体的底面A 点处沿着外表爬行到点上面的B 点处,它爬行的最短路线是〔 〕A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B解:根据两点之间线段最短可知选A . 应选A .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其外表爬到点B 的最短路程是〔 〕解:如图,AB =()1012122=++.应选C .AB1216.正方体盒子的棱长为2,BC的中点为M,一只蚂蚁从A点爬行到M点的最短距离为〔〕解:展开正方体的点M所在的面,∵BC的中点为M,所以MC=21BC=1,在直角三角形中AM= = .7.如图,点A和点B分别是棱长为20cm的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子外表由A处向B处爬行,所走最短路程是cm。
解:将盒子展开,如下图:AB=CD=DF+FC=21EF+21GF=21×20+21×20=20cm.应选C.8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为.解:将正方体展开,连接M 、D 1, 根据两点之间线段最短, MD =MC +CD =1+2=3, MD 1= 132322212=+=+DD MD .9.如下图一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,那么它从下底面点A 沿外表爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比拟,再从各个路线中确定最短的路线.〔1〕展开前面右面由勾股定理得AB = = cm ;〔2〕展开底面右面由勾股定理得AB ==5cm ;第7题1A BA1B1D CD1C124所以最短路径长为5cm,用时最少:5÷2=2.5秒.10.〔2021•恩施州〕如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5,一只蚂蚁如果要沿着长方体的外表从点A爬到点B,需要爬行的最短距离是。
解决蚂蚁爬行问题的小技巧

解决蚂蚁爬行问题的小技巧关于蚂蚁爬行的最短距离问题,我们通常是通过展开立体图形的表面或侧面,化立体为平面,化曲线或折线为直线,利用“两点之间,线段最短”解决问题。
下面笔者总结了一些解这类题型的小技巧,方便解题。
求一只蚂蚁从顶点A出发,求沿立体图形的表面爬到对角顶点B处的最短距离。
(1)蚂蚁在正方体表面爬行。
设正方体的边长为a,则三种展开方式距离一样,为■=■a.应用:如下图,边长为2的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离是.答案:2■.(2)蚂蚁在长方体表面爬行。
设长方体长、宽、高分别为a、b、c,则最短路线应为下列展开图中的线段l1、l2或者l3。
第一种情况:把我们所看到的前面和右面组成一个长方形l1=■=■.第二种情况:把我们所看到的前面和上面组成一个平面l2=■=■.第三种情况:把我们看到的左面与上面组成一个长方形l3=■=■.所以只需要比较ab、bc、ac的大小,就可以知道哪条线路最短。
应用:如图是一块长,宽,高分别是6cm,4cm和3cm 的长方体木块,一只蚂蚁要从长方体木块的一个顶点A处,沿着长方体的表面到长方体上和A相对的顶点B处吃食物,那么它需要爬行的最短路径的长为。
解:最短距离=■=■.(3)蚂蚁在圆柱表面爬行。
当题目没有强调蚂蚁沿圆柱侧面爬行时,应分两种情况讨论。
在一般情况下,当圆柱的底面周长为C,高为h时,路线1:侧面展开图中的线段AC.如下图所示:距离为l1=AC=■=■,路线2:高线AB+底面直径BC.如下图(1)所示:距离为l2=AB +BC=h+■,分别计算,比较大小即可。
应用:如图,一圆柱体的底面周长为24cm,高BD为4cm,BC是直径,一只蚂蚁从点D出发沿着圆柱的表面爬行到点C的最短路程大约().A.6cmB.12cmC.13cmD.16cm解:将圆柱体展开,连接DC,圆柱体的底面周长为24cm,则BC=12cm,根据两点之间线段最短,CD=■=4■≈13cm.而走B-D-C的距离更短,∵BD=4,BC=■,∴BD+BC≈11.64≈12.故选B.(4)蚂蚁在圆锥的侧面爬行。
勾股定理--最短距离问题蚂蚁爬行的最短路径

1A B A 1B 1DCD 1C 124勾股定理--最短距离问题蚂蚁爬行的最短路径正方体1.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒BD .A ⇒S ⇒B2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .3. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .4.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C 的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
10题 11 12 1311. 如图,一只蚂蚁从实心长方体的顶点A 出发,沿长方体的表面爬到对角顶点C 1处(三条棱长如图所示),蚂蚁到B 处吃食,需要爬行的最短路径是多少?14、如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.(1)在AB 中点C 处有一滴蜜糖,一只小虫从D 处爬到C 处去吃,有无数种走法,则最短路程是多少?(2)此长方体盒子(有盖)能放入木棒的最大长度是多少?15.如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A 点爬到B 点,那么这只蚂蚁爬行的最短路径为 米。
1514 16 17 第2题 第3题 ABCD.1283016.如图,直四棱柱侧棱长为4cm ,底面是长为5cm 宽为3cm 的长方形.一只蚂蚁从顶点A 出发沿棱柱的表面爬到顶点B .求:(1)蚂蚁经过的最短路程;(2)蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程.17.如图,长方体的长、宽、高分别为6cm ,8cm ,4cm .一只蚂蚁沿着长方体的表面从点A 爬到点B .则蚂蚁爬行的最短路径的长是 。
中考数学 蚂蚁爬行的最短路径试题(带解析)
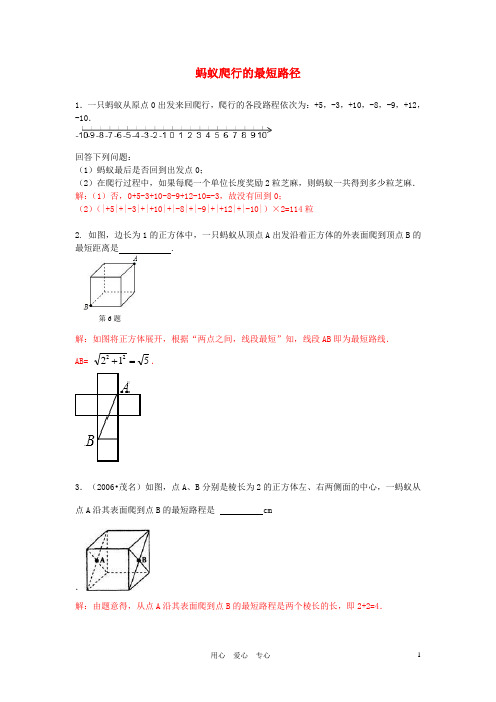
蚂蚁爬行的最短路径1.一只蚂蚁从原点0出发来回爬行,爬行的各段路程依次为:+5,-3,+10,-8,-9,+12,-10.回答下列问题:(1)蚂蚁最后是否回到出发点0;(2)在爬行过程中,如果每爬一个单位长度奖励2粒芝麻,则蚂蚁一共得到多少粒芝麻. 解:(1)否,0+5-3+10-8-9+12-10=-3,故没有回到0; (2)(|+5|+|-3|+|+10|+|-8|+|-9|+|+12|+|-10|)×2=114粒2. 如图,边长为1的正方体中,一只蚂蚁从顶点A 出发沿着正方体的外表面爬到顶点B 的最短距离是 .解:如图将正方体展开,根据“两点之间,线段最短”知,线段AB 即为最短路线. AB= 51222=+.3.(2006•茂名)如图,点A 、B 分别是棱长为2的正方体左、右两侧面的中心,一蚂蚁从点A 沿其表面爬到点B 的最短路程是 cm.解:由题意得,从点A 沿其表面爬到点B 的最短路程是两个棱长的长,即2+2=4.第6题4.如图,一只蚂蚁从正方体的底面A 点处沿着表面爬行到点上面的B 点处,它爬行的最短路线是( )A .A ⇒P ⇒B B .A ⇒Q ⇒BC .A ⇒R ⇒B D.A ⇒S ⇒B解:根据两点之间线段最短可知选A . 故选A .5.如图,点A 的正方体左侧面的中心,点B 是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A 沿其表面爬到点B 的最短路程是( )解:如图,AB=()1012122=++.故选C .6. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为( )解:展开正方体的点M 所在的面,∵BC 的中点为M , 所以MC=21BC=1, 在直角三角形中AM==.7.如图,点A 和点B 分别是棱长为20cm 的正方体盒子上相邻面的两个中心,一只蚂蚁在盒子表面由A 处向B 处爬行,所走最短路程是 cm 。
解:将盒子展开,如图所示: AB=CD=DF+FC= 21EF+ 21GF=21×20+21×20=20cm. 故选C .8. 正方体盒子的棱长为2,BC 的中点为M ,一只蚂蚁从A 点爬行到M 点的最短距离为 .解:将正方体展开,连接M 、D1, 根据两点之间线段最短, MD=MC+CD=1+2=3,MD 1= 132322212=+=+DD MD .第7题A B A 1B 1D CD 1C 12149.如图所示一棱长为3cm 的正方体,把所有的面均分成3×3个小正方形.其边长都为1cm ,假设一只蚂蚁每秒爬行2cm ,则它从下底面点A 沿表面爬行至侧面的B 点,最少要用 2.5秒钟.解:因为爬行路径不唯一,故分情况分别计算,进行大、小比较,再从各个路线中确定最短的路线.(1)展开前面右面由勾股定理得AB= = cm ;(2)展开底面右面由勾股定理得AB==5cm ;所以最短路径长为5cm ,用时最少:5÷2=2.5秒.10.(2009•恩施州)如图,长方体的长为15,宽为10,高为20,点B 离点C的距离为5,一只蚂蚁如果要沿着长方体的表面从点A 爬到点B ,需要爬行的最短距离是 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C. A? R? B
D.
A? S? B
1的正方体中,一只蚂蚁从顶点A出发沿着正方体的外表面爬到顶点B的最短距离
3. 正方体盒子的棱长为2, BC的中点为M,—只蚂蚁从A点爬行到M点的最短距离为 _________________ .
4. 如图,点A的正方体左侧面的中心,点B是正方体的一个顶点,正方体的棱长为2,一蚂蚁从点A沿其
5.如图所示一棱长为3cm 的正方体,把所有的面均分成3X3个小正方形.其边长都为1cm,假设一只蚂蚁
每秒爬行2cm,则它从下底面点A沿表面爬行至侧面的B点,最少要用秒钟.
长方体
10. (2009?恩施州)如图,长方体的长为15,宽为10,高为20,点B离点C的距离为5, 一只蚂蚁如果要
沿着长方体的表面从点
问怎样走路线最短?最短路线长为
12. (2011?荆州)如图,长方体的底面边长分别为2cm和
4cm,高为5cm .若一只蚂蚁从P点开始经过4
个侧面爬行一圈到达Q点,则蚂奴爬行的最短路径长为cm.
13. 如图,一块长方体砖宽AN=5cm,长ND=10cm,CD上的点B距地面的高BD=8cm,地面上A处的一只蚂蚁到
B处吃食,需要爬行的最短路径是多少?
14. 如图,长方体盒子(无盖)的长、宽、高分别12cm ,8cm,30cm.
(1)在AB中点C处有一滴蜜糖,一只小虫从D处爬到C处去吃,有无数种走法,则最短路程是多少?
⑵此长方体盒子(有盖)能放入木棒的最大长度是多少?
15•如图所示:有一个长、宽都是2米,高为3米的长方体纸盒,一只小蚂蚁从A点爬到B点,那么这只蚂
蚁爬行的最短路径为____________ 米。
S
学习好资料欢迎下载
勾股定理--最短距离问题蚂蚁爬行的最短路径
正方体
1如图,一只蚂蚁从正方体的底面A点处沿着表面爬行到点上面的B点处,它爬行的最短路线是__________ A. A? P? B
是 ____________
A? Q? B
第3题
O
A爬到点B,需要爬行的最短距离是
15 16
14 17
16. 如图,直四棱柱侧棱长为 面爬到顶点B .求: (1 )蚂蚁经过的最短路程;
(2 )蚂蚁沿着棱爬行(不能重复爬行同一条棱)的最长路程. 17. 如图,长方体的长、宽、高分别为 6cm , 8cm , 4cm .一只蚂蚁沿着长方体的表面从点 A 爬到点B .则蚂 蚁爬行的最短路径的长是 ___________ 。
18. 圆柱形坡璃容器,高 18cm,底面周长为60cm,在外侧距下底1cm 点S 处有一蜘蛛,与蜘蛛相对的圆柱形 容器的上
口外侧距开口处 1cm 的点F 处有一苍蝇,试求急于捕获苍蝇充饥的蜘蛛所走的最短路线的长度。
第2题
3.有一圆形油罐底面圆的周长为 爬行的最短路线长为
23. 如图,一只蚂蚁沿着图示的路线从圆柱高
AA 1的端点A 到达A 1,若圆柱底面半径为 ,高为5,则蚂 蚁爬行的最短距离为 24. 如图,一圆柱体的底面周长为 24cm ,高AB 为
9cm , BC 是上底面的直径.一只蚂蚁从点
A 出发,沿着
圆柱的侧面爬行到点 C ,则蚂蚁爬行的最短路程是
25. (2006?荆州)有一圆柱体高为 10cm ,底面圆的半径为 4cm , AA 1, BB 1为相对的两条母线.在 AA 1上有 一个蜘蛛Q , QA=3cm ;在BB 1上有一只苍蝇 P , PB 1=2cm ,蜘蛛沿圆柱体侧面爬到 P 点吃苍蝇,最短的路径 是
cm
.(结果用带 n 和根号的式子表示)
学习好资料 欢迎下载 4cm ,底面是长为5cm 宽为3cm 的长方形.一只蚂蚁从顶点 A 出发沿棱柱的表 19
19. 如图是一个三级台阶,它的每一级的长、宽、高分别为 对的端点,点 A 处有一只蚂蚁,想到点 B 处去吃可口的食物, cm
20. 如图,是一
个相对的端点, 面爬到B 点,最短线路是 2.有一圆柱体如图,高 离
20cm 、3cm 、2cm . A 和B 是这个台阶上两个相 则蚂蚁沿着台阶面爬行到点 B 的最短路程为
旦一个三级台阶,它的每一级的长、宽和高分别等于 A 点上有一只蚂蚁,想到 B 点去吃可口的食物 ______ cm 。
圆柱
底面半径5cm , A 处有一蚂蚁, 5cm , 3cm 和1cm , A 和B 是这个台阶的两 •请你想一想,这只蚂蚁从 A 点出发,沿着台阶
4cm ,
若蚂蚁欲爬行到
C 处,求蚂蚁爬行的最短距
24m ,高为6m , —只老鼠从距底面 1m 的A 处爬行到对角 B 处吃食物,它
B
n A
p
B。
