一年级到六年级数学知识点
一至六年级数学知识点

一至六年级数学知识点一至六年级数学知识点概述一、一年级数学知识点1. 数的认识- 认识0-100之间的数字- 了解自然数的基本概念2. 加法与减法- 掌握20以内的加法和减法- 学习加法和减法的基本概念和运算规则3. 简单的几何图形- 认识基本的平面图形,如圆形、正方形、长方形 - 了解图形的基本属性,如边数、角数4. 初步的测量概念- 了解长度、重量和容量的基本概念- 学习使用尺子、天平和量杯进行简单测量5. 数据的收集和整理- 学习简单的数据收集方法- 初步了解数据的分类和整理二、二年级数学知识点1. 进阶的数的认识- 认识100-1000之间的数字- 学习倍数和因数的基本概念2. 乘法与除法- 掌握表内乘法和除法- 理解乘法和除法的意义及其相互关系3. 几何图形的进一步认识- 认识三角形、梯形等基本图形- 学习计算简单图形的面积4. 时间和金钱的认识- 学习读时钟和日历- 了解货币的基本概念和简单的货币计算5. 数据的进一步处理- 学习制作简单的图表,如条形图和饼图 - 理解数据的平均值和中位数的概念三、三年级数学知识点1. 大数的认识和运算- 认识四位数和五位数- 学习简单的大数加减法2. 乘法表的熟练掌握- 熟练掌握1-9的乘法表- 学习简单的乘法分配律3. 分数的初步认识- 了解分数的基本概念- 掌握分数的读法和写法4. 几何图形的性质和分类- 学习图形的对称性- 了解不同图形的分类方法5. 应用题的解答技巧- 学习解决简单的数学应用题- 培养逻辑思维和问题解决能力四、四年级数学知识点1. 多位数的乘除法- 学习多位数乘以一位数和两位数的乘法 - 掌握多位数除以一位数的除法2. 分数的加减法- 学习同分母分数的加减法- 理解分数单位的概念3. 小数的初步认识- 了解小数的读法和写法- 学习小数与整数的相互转换4. 面积和周长的计算- 学习计算矩形、正方形的面积和周长 - 了解面积和周长的概念及其计算公式5. 时间的计算- 学习时间的加减法- 了解时间的计量单位和时间的推算五、五年级数学知识点1. 分数的乘除法- 学习分数乘以整数和分数的乘法- 掌握分数除以整数和分数的除法2. 小数的四则运算- 学习小数的加减乘除- 理解小数点的移动规则3. 比例和百分数- 了解比例的概念和基本性质- 学习百分数的读法、写法和计算4. 几何图形的变换- 学习图形的平移、旋转和翻转- 了解图形变换的基本概念5. 复杂应用题的解答- 学习解决多步骤的数学应用题- 培养综合运用数学知识解决问题的能力六、六年级数学知识点1. 比例和比例关系- 学习比例的计算和应用- 理解比例关系在实际问题中的应用2. 复杂的分数运算- 学习分数的加减乘除混合运算- 掌握分数的化简和比较3. 代数初步- 了解字母表示数的概念- 学习简单的代数式和方程4. 几何图形的面积和体积- 学习计算三角形、梯形等图形的面积- 了解立体图形的体积计算5. 统计和概率- 学习收集、整理和分析数据的方法- 初步了解概率的基本概念以上是一至六年级数学知识点的概述,每个年级的知识点都建立在前一年级的基础上,逐步深入和拓展。
小学数学1-6年级各年级知识点

小学数学1-6年级各年级知识点1.数一数。
2.比一比:“同样多”、“多”、“少”以及“长”、“短”、“高”、“矮”。
3.1~5的认识和加减法:⑴ 1~5的认识(基数、读写、数序、比大小、序数、组成)⑵ 1~5的加减法(加减法含义、计算)⑶ 0的认识(表示起点、没有)和加减法。
4.认识物体和平面图形:长方体、正方体、圆柱和球等立体图形与长方形、正方形、三角形和圆等平面图形。
5.分类:单一标准的分类和不同标准的分类。
6.6~9的认识和加减法:1)6、7的认识和加减法(数数、数序、比大小、序数、写数、组成)。
2)8、9的认识和加减法(出现了“一图两式”和“一图四式”、渗透统计思想、比多比少内容)。
3)10的认识和有关10的加减法(省略了10的序数意义、填未知加数)。
4)连加、连减和加减混合计算。
5)整理和复。
7.11~20各数的认识:数数、读数、数序和大小、序数、写数、个位和十位、10加几和十几加减几(不退位)、十几减十。
8.认识钟表:认识钟面、认识整时、认识半时。
9.20以内的进位加法:9加几(“点数”、“接着数”、“凑十”和“根据具体题目选择特殊方法”);8、7、6加几(“拆小数,凑十数”、“拆大数,凑小数”和“交换加数的位置”);5、4、3、2加几和“用数学”。
一(下)1.位置:用“上、下,前、后,左、右”描述物体的相对位置;根据行、列确定物体的位置。
2.20以内的退位减法:十几减9;十几减几;用数学。
3.图形的拼组:平面图形的特征;立体图形的关系。
4.100以内数的认识:数的认识(包括数数、数的组成、数位的含义、数的顺序)和加减(大小比较、整十数加一位数和相应的减法)。
5.认识人民币:认识人民币的单位元、角、分,知道1元=10角,1角=10分;简单的计算。
6.100以内的加法和减法(一):口算整十数加、减整十数;口算两位数加、减一位和整十数;用加法和减法解决简单的问题。
7.认识时间:认识几时几分(5分5分数、1分1分数)。
小学1—6年级数学知识点归纳

一、小学一年级:
1.数的概念:数的概念,认识0~9的数,会用数字标记简单的概念,认识十位数和个位数;
2.加法:熟练掌握10以内加法的计算,并掌握加法的性质;
3.减法:熟悉十以内减法运算,理解减法的变换性,会用减法合并加
法运算;
4.数的关系:了解数的大小关系,相等关系?
二、小学二年级:
1.掌握20以内的加减法运算;
2.加法中的拆分和整合;
3.减法中的借位和退位;
4.数字比大小;
5.了解方形、正方形、长方形和三角形的名称;
6.熟悉几何物体的属性;
7.多边形的认识。
三、小学三年级:
1.50以内的加减法:熟悉50以内的加减法计算,并能用若干种方式
解决这类问题;
2.认识会和计算时间:根据时钟的分针、时针的位置认识和计算时间;
3.熟悉加减法的性质;
4.圆形、扇形、梯形、正五边形的认识;
5.掌握图形的移动和半径的概念;
7.它们的面积、周长及其计算;
8.列式运算;
9.小数的概念。
四、小学四年级:
1.100以内的加减法:熟练掌握100以内的加减法,掌握若干解题方法;
2.几何图形:掌握几何图形的认识、构。
一至六年级数学知识点

一至六年级数学知识点一年级数学知识点。
一、数与代数。
1. 数字的认识。
- 认识0 - 10这些数字,会读、写。
知道0表示一个也没有,也可以表示起点。
- 能数出物体的个数,会用数字表示物体的个数。
2. 数的大小比较。
- 比较10以内数的大小,例如3<5,7>4等。
- 认识“>”(大于)、“<”(小于)和“=”(等于)符号,会正确使用这些符号比较数的大小。
3. 数的加减法。
- 10以内数的加法:理解加法的意义,如3 + 2就是把3个物体和2个物体合起来,结果是5。
- 10以内数的减法:知道减法是从总数里去掉一部分,求剩下的部分,如5 - 2就是从5个物体里去掉2个,还剩3个。
二、图形与几何。
1. 认识简单图形。
- 认识长方体、正方体、圆柱、球这几种立体图形,能根据它们的特征辨认。
- 认识长方形、正方形、三角形和圆这几种平面图形,能在生活中找出这些图形的实例。
三、分类与整理。
- 能按照给定的标准对物体进行分类,如按颜色、形状分类等。
- 初步认识象形统计图,能根据分类的结果进行简单的统计。
二年级数学知识点。
一、数与代数。
1. 100以内数的认识。
- 认识100以内的数,会数、读、写100以内的数。
- 知道数的组成,如35是由3个十和5个一组成的。
- 100以内数的大小比较,会用“>”“<”“=”比较数的大小。
2. 100以内数的加减法。
- 整十数加、减整十数,如20+30 = 50,50 - 30 = 20。
- 两位数加一位数、整十数(不进位、进位),例如23+4 = 27(不进位),28+9 = 37(进位)。
- 两位数减一位数、整十数(不退位、退位),如35 - 2 = 33(不退位),32 - 5 = 27(退位)。
3. 表内乘法。
- 乘法的初步认识:知道乘法是求几个相同加数和的简便运算,如3 + 3+3+3 = 3×4。
- 2 - 9的乘法口诀:熟练背诵乘法口诀,能根据乘法口诀计算乘法算式。
小学数学一至六年级知识点梳理

一年级:
1、计数:识记数字的读法、数的概念、数量的大小比较,理解几何
简图,简单的加减法运算。
2、比较:比较数量大小、名词、动词、形容词的比较级和最高级。
3、分类:分类、比较、排序、记录。
4、图形:定义形状、识记形状的基本名称、并识记和判断形状的变化。
5、量之间的关系:理解量的变化对应的图形,估算、比较、排序。
6、时间:识记日期、季节、日历、时钟,估算时间的长短。
二年级:
1、数的概念:理解数的理解,估算数量、比较数量大小、排列数量。
2、加减法运算:加减法的计算,理解加减法的运算规则,加减法的混
合运算。
3、数学中的关系:理解数字、图形、量之间的关系,比较量的大小,
探究图形变化规律。
4、图形:识记形状的基本名称、并识记和判断形状的变化、刻画几何
简图的图形、把具体物抽象成简图形。
5、计算:估算、计算和推理,理解计算的程序。
6、时间:估算时间的长短,理解日期、季节、日历、时钟等的概念,了解节日的含义。
三年级:
1、数的概念:理解数的含义,估算数量、比较数量大小、排列数量。
2、四则运算:理解四则运算的规则,运用四则运算解决实际问题,掌握加减乘除的基本概念。
小学1到6年级数学知识点归纳

一、小学一年级数学知识点
1、数的概念:数是用来把不同的东西一一对应的符号,读数时分为个、十、百、千,有数的大小概念。
2、数字:数字是由0、1、2、
3、
4、
5、
6、
7、
8、9等组成的,通过它们可以表示任意大小的数。
3、排序:排序就是把数据进行编号排列,比如从小到大排序,或者从大到小排序。
4、比较:比较就是把两个数据进行对比,判断哪个大哪个小,或者相等与否。
5、加法:加法就是把两个数相加,计算出和的大小。
6、减法:减法就是把两个数相减,计算出差的大小。
7、图形:图形就是用线段构成的多边形,如三角形、正方形、长方形等。
8、数量关系:数量关系就是把两个或者多个数量相互比较,用规律表示关系的数学概念。
9、叠加:叠加就是把两个或者多个数据叠加在一起,来表示各部分之和的大小。
10、拆分:拆分就是把一个数拆分成几个小的数,用来更加准确地表示它的大小。
二、小学二年级数学知识点
1、数的整体性:数的整体性是指把一个数分成几部分,再把几部分
组合成一个整体,用来表示它的大小和数量的概念。
2、数的模式:数的模式是指用不同数字组成的具有一定规律的组合,可以通过此组合来表示数量的变化。
小学数学1—6年级知识点汇总

小学1-6年级数学重点知识、公式汇总+解读一年级知识点和重难点1、数与计算(1)20以内数的认识,加法和减法。
数数。
数的组成、顺序、大小、读法和写法。
加法和减法。
连加、连减和加减混合式题(2)100以内数的认识。
加法和减法。
数数。
个位、十位。
数的顺序、大小、读法和写法。
两位数加、减整十数和两位数加、减一位数的口算。
两步计算的加减式题。
2、量与计量钟面的认识(整时)。
人民币的认识和简单计算。
3、几何初步知识长方体、正方体、圆柱和球的直观认识。
长方形、正方形、三角形和圆的直观认识。
4、应用题比较容易的加法、减法一步计算的应用题。
多和少的应用题(抓有效信息的能力)5、实践活动选择与生活密切联系的内容。
例如根据本班男、女生人数,每组人数分布情况,想到哪些数学问题。
二年级知识点和重难点1、数与计算(1)两位数加、减两位数。
两位数加、减两位数。
加、减法竖式。
两步计算的加减式题。
(2)表内乘法和表内除法。
乘法的初步认识。
乘法口诀。
乘法竖式。
除法的初步认识。
用乘法口诀求商。
除法竖式。
有余数除法。
两步计算的式题。
(3)万以内数的读法和写法。
数数。
百位、千位、万位。
数的读法、写法和大小比较。
(4)加法和减法。
加法,减法。
连加法。
加法验算,用加法验算减法。
(5)混合运算。
先乘除后加减。
两步计算式题。
小括号。
2、量与计量时、分、秒的认识。
米、分米、厘米的认识和简单计算。
千克(公斤)的认识3、几何初步知识直线和线段的初步认识。
角的初步认识。
直角。
4、应用题加法和减法一步计算的应用题。
乘法和除法一步计算的应用题。
比较容易的两步计算的应用题。
5、实践活动与生活密切联系的内容。
例如调查家中本周各项消费的开支情况,想到哪些数学问题。
三年级知识点和重难点1、数与计算(1)一位数的乘、除法。
一个乘数是一位数的乘法(另一个乘数一般不超过三位数)。
0的乘法。
连乘。
除数是一位数的除法。
0除以一个数。
用乘法验算除法。
连除。
(2)两位数的乘、除法。
小学一至六年级数学知识点归纳(大全)
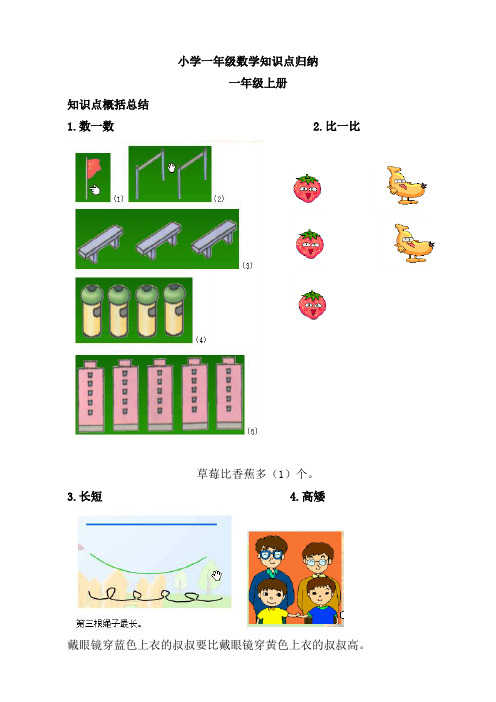
小学一年级数学知识点归纳一年级上册知识点概括总结1.数一数2.比一比草莓比香蕉多(1)个。
3.长短4.高矮戴眼镜穿蓝色上衣的叔叔要比戴眼镜穿黄色上衣的叔叔高。
5.第几6.比大小7.几和几8.加法 9.减法10.认识物体和图形11.分类12.6的认识和加减法13.7的认识和加减法14.8和9的认识15.7、8、9的比较16.9和10的比较17.连加18.连减19.加减混合运算20.认识钟表一年级下册知识点概括总结1.位置:所在或所占的地方,有上下、前后、左右之分。
2.上:位置方位名词,例如:汽车在马路的上面。
3.下:位置方位名词,例如:船在桥的下面。
4.前:位置方位名词。
例如:张三在李四的前排,那么可以说张三在李四的前面。
5.后:位置方位名词。
例如:李四在张三的后排,那么可以说李四在张三的后面。
7.退位减:减法运算中必须向高位借位的减法运算。
8.20以内的退位减法:20以内的数字之间的退位减法。
例如:12-9=3.9.图形的拼组:作风车:10.数一数11.读数24读作“二十四”;169读作“一百六十九”。
12.比较数的大小先比较高数位的数学,再按照数位的高低依次比较。
例如:39和145比较大小,39百位数字为0,145百位数字为1,0小于1,所以39小于145.13.100以内数的认识:100=10个10相加。
14.认识人民币:贰角五角一元五元 10元 20元50元 100元15.整十数:个位数正好为0的两位数,例如:10,20,30等。
16.整十数加:整十数之间的加法,例如:10+20=30等17.整十数减:整十数之间的减法:例如:50-20=30等。
18.两位数加一位数和整十数:两位数加上一个一位数的加法运算,例如:35+3=38等。
19.两位数减一位数和整十数:两位数减去一个一位数的减法运算,例如:35-2=33等。
20.认识时间长针为时针,短针为分针。
上图所示时间为7:00,读作“七点”。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
小学一到六年级数学知识点第一章数和数的运算一概念(一)整数1 整数的意义自然数和0都是整数。
2 自然数我们在数物体的时候,用来表示物体个数的1,2,3……叫做自然数。
一个物体也没有,用0表示。
0也是自然数。
3计数单位一(个)、十、百、千、万、十万、百万、千万、亿……都是计数单位。
每相邻两个计数单位之间的进率都是10。
这样的计数法叫做十进制计数法。
4 数位计数单位按照一定的顺序排列起来,它们所占的位置叫做数位。
5 数的整除整数a除以整数b(b ≠ 0),除得的商是整数而没有余数,我们就说a能被b整除,或者说b能整除a 。
如果数a能被数b(b ≠ 0)整除,a就叫做b的倍数,b就叫做a的约数(或a的因数)。
倍数和约数是相互依存的。
因为35能被7整除,所以35是7的倍数,7是35的约数。
一个数的约数的个数是有限的,其中最小的约数是1,最大的约数是它本身。
例如:10的约数有1、2、5、10,其中最小的约数是1,最大的约数是10。
一个数的倍数的个数是无限的,其中最小的倍数是它本身。
3的倍数有:3、6、9、12……其中最小的倍数是3 ,没有最大的倍数。
个位上是0、2、4、6、8的数,都能被2整除,例如:202、480、304,都能被2整除。
个位上是0或5的数,都能被5整除,例如:5、30、405都能被5整除。
一个数的各位上的数的和能被3整除,这个数就能被3整除,例如:12、108、204都能被3整除。
一个数各位数上的和能被9整除,这个数就能被9整除。
能被3整除的数不一定能被9整除,但是能被9整除的数一定能被3整除。
一个数的末两位数能被4(或25)整除,这个数就能被4(或25)整除。
例如:16、404、1256都能被4整除,50、325、500、1675都能被25整除。
一个数的末三位数能被8(或125)整除,这个数就能被8(或125)整除。
例如:1168、4600、5000、12344都能被8整除,1125、13375、5000都能被125整除。
能被2整除的数叫做偶数。
不能被2整除的数叫做奇数。
0也是偶数。
自然数按能否被2 整除的特征可分为奇数和偶数。
一个数,如果只有1和它本身两个约数,这样的数叫做质数(或素数),100以内的质数有:2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97。
一个数,如果除了1和它本身还有别的约数,这样的数叫做合数,例如 4、6、8、9、12都是合数。
1不是质数也不是合数,自然数除了1外,不是质数就是合数。
如果把自然数按其约数的个数的不同分类,可分为质数、合数和1。
每个合数都可以写成几个质数相乘的形式。
其中每个质数都是这个合数的因数,叫做这个合数的质因数,例如15=3×5,3和5 叫做15的质因数。
把一个合数用质因数相乘的形式表示出来,叫做分解质因数。
例如把28分解质因数几个数公有的约数,叫做这几个数的公约数。
其中最大的一个,叫做这几个数的最大公约数,例如12的约数有1、2、3、4、6、12;18的约数有1、2、3、6、9、18。
其中,1、2、3、6是12和1 8的公约数,6是它们的最大公约数。
公约数只有1的两个数,叫做互质数,成互质关系的两个数,有下列几种情况:1和任何自然数互质。
相邻的两个自然数互质。
两个不同的质数互质。
当合数不是质数的倍数时,这个合数和这个质数互质。
两个合数的公约数只有1时,这两个合数互质,如果几个数中任意两个都互质,就说这几个数两两互质。
如果较小数是较大数的约数,那么较小数就是这两个数的最大公约数。
如果两个数是互质数,它们的最大公约数就是1。
几个数公有的倍数,叫做这几个数的公倍数,其中最小的一个,叫做这几个数的最小公倍数,如2的倍数有2、4、6 、8、10、12、14、16、18 ……3的倍数有3、6、9、12、15、18 …… 其中6、12、18……是2、3的公倍数,6是它们的最小公倍数。
如果较大数是较小数的倍数,那么较大数就是这两个数的最小公倍数。
如果两个数是互质数,那么这两个数的积就是它们的最小公倍数。
几个数的公约数的个数是有限的,而几个数的公倍数的个数是无限的。
(二)小数1 小数的意义把整数1平均分成10份、100份、1000份…… 得到的十分之几、百分之几、千分之几…… 可以用小数表示。
一位小数表示十分之几,两位小数表示百分之几,三位小数表示千分之几……一个小数由整数部分、小数部分和小数点部分组成。
数中的圆点叫做小数点,小数点左边的数叫做整数部分,小数点左边的数叫做整数部分,小数点右边的数叫做小数部分。
在小数里,每相邻两个计数单位之间的进率都是10。
小数部分的最高分数单位“十分之一”和整数部分的最低单位“一”之间的进率也是10。
2小数的分类纯小数:整数部分是零的小数,叫做纯小数。
例如:、都是纯小数。
带小数:整数部分不是零的小数,叫做带小数。
例如:、都是带小数。
有限小数:小数部分的数位是有限的小数,叫做有限小数。
例如:、、都是有限小数。
无限小数:小数部分的数位是无限的小数,叫做无限小数。
例如:…… ……无限不循环小数:一个数的小数部分,数字排列无规律且位数无限,这样的小数叫做无限不循环小数。
例如:∏循环小数:一个数的小数部分,有一个数字或者几个数字依次不断重复出现,这个数叫做循环小数。
例如:…… …… ……?一个循环小数的小数部分,依次不断重复出现的数字叫做这个循环小数的循环节。
例如:……的循环节是“ 9 ” ,……的循环节是“ 54 ” 。
?纯循环小数:循环节从小数部分第一位开始的,叫做纯循环小数。
例如:…… ……?混循环小数:循环节不是从小数部分第一位开始的,叫做混循环小数。
…… ……写循环小数的时候,为了简便,小数的循环部分只需写出一个循环节,并在这个循环节的首、末位数字上各点一个圆点。
如果循环节只有一个数字,就只在它的上面点一个点。
例如:…… 简写作? …… 简写作。
(三)分数1 分数的意义?把单位“1”平均分成若干份,表示这样的一份或者几份的数叫做分数。
?在分数里,中间的横线叫做分数线;分数线下面的数,叫做分母,表示把单位“1”平均分成多少份;分数线下面的数叫做分子,表示有这样的多少份。
?把单位“1”平均分成若干份,表示其中的一份的数,叫做分数单位。
?2 分数的分类?真分数:分子比分母小的分数叫做真分数。
真分数小于1。
?假分数:分子比分母大或者分子和分母相等的分数,叫做假分数。
假分数大于或等于1。
?带分数:假分数可以写成整数与真分数合成的数,通常叫做带分数。
?3 约分和通分?把一个分数化成同它相等但是分子、分母都比较小的分数,叫做约分。
?分子分母是互质数的分数,叫做最简分数。
?把异分母分数分别化成和原来分数相等的同分母分数,叫做通分。
?(四)百分数1 表示一个数是另一个数的百分之几的数叫做百分数,也叫做百分率或百分比。
百分数通常用"%"来表示。
百分号是表示百分数的符号。
?二方法(一)数的读法和写法??1. 整数的读法:从高位到低位,一级一级地读。
读亿级、万级时,先按照个级的读法去读,再在后面加一个“亿”或“万”字。
每一级末尾的0都不读出来,其它数位连续有几个0都只读一个零。
??2. 整数的写法:从高位到低位,一级一级地写,哪一个数位上一个单位也没有,就在那个数位上写0。
?3. 小数的读法:读小数的时候,整数部分按照整数的读法读,小数点读作“点”,小数部分从左向右顺次读出每一位数位上的数字。
?4. 小数的写法:写小数的时候,整数部分按照整数的写法来写,小数点写在个位右下角,小数部分顺次写出每一个数位上的数字。
?5. 分数的读法:读分数时,先读分母再读“分之”然后读分子,分子和分母按照整数的读法来读。
?6. 分数的写法:先写分数线,再写分母,最后写分子,按照整数的写法来写。
?7. 百分数的读法:读百分数时,先读百分之,再读百分号前面的数,读数时按照整数的读法来读。
?8. 百分数的写法:百分数通常不写成分数形式,而在原来的分子后面加上百分号“%”来表示。
?(二)数的改写?一个较大的多位数,为了读写方便,常常把它改写成用“万”或“亿”作单位的数。
有时还可以根据需要,省略这个数某一位后面的数,写成近似数。
?1. 准确数:在实际生活中,为了计数的简便,可以把一个较大的数改写成以万或亿为单位的数。
改写后的数是原数的准确数。
改写成以万做单位的数是 125430 万;改写成以亿做单位的数亿。
?2. 近似数:根据实际需要,我们还可以把一个较大的数,省略某一位后面的尾数,用一个近似数来表示。
4. 大小比较?1. 比较整数大小:比较整数的大小,位数多的那个数就大,如果位数相同,就看最高位,最高位上的数大,那个数就大;最高位上的数相同,就看下一位,哪一位上的数大那个数就大。
?2. 比较小数的大小:先看它们的整数部分,,整数部分大的那个数就大;整数部分相同的,十分位上的数大的那个数就大;十分位上的数也相同的,百分位上的数大的那个数就大……?3. 比较分数的大小:分母相同的分数,分子大的分数比较大;分子相同的数,分母小的分数大。
分数的分母和分子都不相同的,先通分,再比较两个数的大小。
? (三)数的互化?1. 小数化成分数:原来有几位小数,就在1的后面写几个零作分母,把原来的小数去掉小数点作分子,能约分的要约分。
?2. 分数化成小数:用分母去除分子。
能除尽的就化成有限小数,有的不能除尽,不能化成有限小数的,一般保留三位小数。
?3. 一个最简分数,如果分母中除了2和5以外,不含有其他的质因数,这个分数就能化成有限小数;如果分母中含有2和5 以外的质因数,这个分数就不能化成有限小数。
?4. 小数化成百分数:只要把小数点向右移动两位,同时在后面添上百分号。
?5. 百分数化成小数:把百分数化成小数,只要把百分号去掉,同时把小数点向左移动两位。
?6. 分数化成百分数:通常先把分数化成小数(除不尽时,通常保留三位小数),再把小数化成百分数。
7. 百分数化成小数:先把百分数改写成分数,能约分的要约成最简分数。
(四)数的整除1. 把一个合数分解质因数,通常用短除法。
先用能整除这个合数的质数去除,一直除到商是质数为止,再把除数和商写成连乘的形式。
2. 求几个数的最大公约数的方法是:先用这几个数的公约数连续去除,一直除到所得的商只有公约数1为止,然后把所有的除数连乘求积,这个积就是这几个数的的最大公约数。
3. 求几个数的最小公倍数的方法是:先用这几个数(或其中的部分数)的公约数去除,一直除到互质(或两两互质)为止,然后把所有的除数和商连乘求积,这个积就是这几个数的最小公倍数。
4. 成为互质关系的两个数:1和任何自然数互质;相邻的两个自然数互质;当合数不是质数的倍数时,这个合数和这个质数互质;两个合数的公约数只有1时,这两个合数互质。
