(完整word)七年级找规律经典题汇总带答案,推荐文档
初一找规律经典题型(含部分问题详解)

图1 图2 图3初一数学规律题应用知识汇总“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索:一、基本方法——看增幅(一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n 个数可以表示为:a1+(n-1)b ,其中a 为数列的第一位数,b 为增幅,(n-1)b 为第一位数到第n 位的总增幅。
然后再简化代数式a+(n-1)b 。
例:4、10、16、22、28……,求第n 位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,所以,第n 位数是:4+(n-1)6=6n -2例1、已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n = 5时,共向外作出了 个小等边三角形(2)当n = k 时,共向外作出了 个小等边三角形(用含k 的式子表示).例2、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数式表示)。
(二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差n =3 n =4 n =5 ……数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求出,方法就简单的多了。
七年级找规律经典题汇总带答案

七年级找规律经典题汇总带答案431321211⨯+⨯+⨯=)4131()3121()2111(-+-+-=1-41=43 再计算)1(1431321211+++⨯+⨯+⨯n n 的值. 21.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6, 4!=4×3×2×1,…,则100!98!的值为 25.观察下列图形的构成规律,根据此规律,第8个图形中有 个圆.、根据下列5个图形及相应点的个数的变化规律,试猜测第n 个图中有 个点.27、找规律.下列图中有大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n 幅图中共有 个.1、如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子 枚.4、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有个.5、观察下列图形,它们是按一定规律排列的,依照此规律,第16个图形共有 个★.6、如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是 ,第n 个“广”字中的棋子个数是 .9、将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去,结果如下表.则a n = .(用含n 的代数式表示)10、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n 个图案中正三角形的个数为 (用含n 的代数式表示).13、用火柴棒按照如图所示的方式摆图形,则第n个图形中,所需火柴棒的根数是.14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,…,依次规律,拼搭第8个图案需小木棒根.15、一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么8张桌子需配椅子把.16、下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n(n≥2个圆点时,图案的圆点数为Sn .按此规律推断Sn关于n的关系式为:Sn= .17、如图是由火柴棒搭成的几何图案,则第n个图案中有根火柴棒.(用含n的代数式表示)19、观察表一,寻找规律.表二,表三分别是从表一中选取的一部分,则a+b 的值为 . 表一:表二:表三:20、如图所示的图案是由正六边形密铺而成,黑色正六边形周围第一层有六个白色正六边形,则第n 层有 个白色正六边形.21、把边长为3的正三角形各边三等分,分割得到图①,图中含有1个边长是1的正六边形;把边长为4的正三角形各边四等分,分割得到图②,图中含有3个边长是1的正六边形;把边长123 a 1 7为5的正三角形各边五等分,分割得到图③,图中含有6个边长是1的正六边形;…依此规律,把边长为7的正三角形各边七等分,并按同样的方法分割,得到的图形中含有个边长是1的正六边形.22、观察下列图形的排列规律(其中☆,□,●分别表示五角星、正方形、圆)●□☆●●□☆●□☆●●□☆●…若第一个图形是圆,则第2008个图形是(填名称).23、下列图中有大小不同的菱形,第1幅图中有1个菱形,第2幅图中有3个菱形,第3幅图中有5个菱形,按照图示的规律摆下去,则第n幅图中有个菱形.24、如图,观察下列图案,它们都是由边长为1cm的小正方形按一定规律拼接而成的,依此规律,则第16个图案中的小正方形有个.25、用同样大小的黑色棋子按图所示的方式摆图形,按照这样的规律摆下去,则第n个图形需棋子枚.(用含n的代数式表示)27、如图所示是一副“三角形图”,第一行有一个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第七行有个三角形.28、如图,用3根小木棒可以摆出第(1)个正三角形,加上2根木棒可以摆出第(2)个正三角形,再加上2根木棒可以摆出第(3)个正三角形…这样继续摆下去,当摆出第(n)个正三角形时,共用了木棒根.29、观察下列图形,根据变化规律推测第100个与第个图形位置相同.30、如图,用火柴棒按以下方式搭小鱼,搭1条小鱼用8根火柴棒,搭2条小鱼用14根,…,则搭n条小鱼需要根火柴棒.(用含n的代数式表示)参考答案(一):一、1、(1)21004(2)21n )(+ 2、23 30。
初一找规律经典题型(含部分答案)

图1 图2 图3初一数学规律题应用知识汇总“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索: 一、基本方法——看增幅(一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n 个数可以表示为:a1+(n-1)b ,其中a 为数列的第一位数,b 为增幅,(n-1)b 为第一位数到第n 位的总增幅。
然后再简化代数式a+(n-1)b 。
例:4、10、16、22、28……,求第n 位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,所以,第n 位数是:4+(n-1) 6=6n -2例1、已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n = 5时,共向外作出了 个小等边三角形(2)当n = k 时,共向外作出了 个小等边三角形(用含k 的式子表示).例2、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数式表示)。
(二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差n =3n =4n =5……数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求出,方法就简单的多了。
七年级找规律经典题汇总带答案

精心整理一、数字排列规律题1、观察下列各算式:1+3=4=22,1+3+5=9=23,1+3+5+7=16=24…按此规律 (1)试猜想:1+3+5+7+…+2005+2007的值?(2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少? 23410012三、1①1321+2+1=4,1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1=____.3、,,,,已知:24552455154415448338333223222222⨯=+⨯=+⨯=+⨯=+ 规律发现专题训练……1.用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地砖4块;那么第(n )个图案中有白色..地砖块。
2.我国着名数学家华罗庚曾说过:“数形结合百般好,隔裂分家万事非。
”如图,在一个边长为1的正方形纸版上,依次贴上面积为21,41,81,…,n 21的矩形彩色纸片(n 为大于1的整数)。
请你用“数形结合”的思想,依数形变化的规律,计算n 21814121++++ =。
4.将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与上次的折痕保持平行,连续对折三次后,可以得到7条折痕,那么对折四次可以得到_条折痕.如果对折n 次,可以得到条折痕. 5.观察下面一列有规律的数,486,355,244,153,82,31,根据这个规律可知第n 个数是(n 是正整数)8.观察下面一列数:-1,2,-3,4,-5,6,-7,...,将这列数排成下列形式按照上述规律排下去,那么第10行从左边第9个数是. 14.先观察321211⨯+⨯=)3121()2111(-+-=1-31=32 431321211⨯+⨯+⨯=)4131()3121()2111(-+-+-=1-41=43 再计算)1(1431321211+++⨯+⨯+⨯n n 的值. 21.若“!”是一种数学运算符号,并且1!=1,2!=2×1=2,3!=3×2×1=6, 4!=4×3×2×1,…,则100!98!的值为 25.观察下列图形的构成规律,根据此规律,第8个图形中有个圆.、根据下列5个图形及相应点的个数的变化规律,试猜测第n 个图中有 个点.第3题......16-1514-1312-1110-9-76-54-32-1第8题27、找规律.下列图中有大小不同的菱形,第1幅图中有1个,第2幅图中有3个,第3幅图中有5个,则第n 幅图中共有 个.1、如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第100个图案需棋子枚.4、观察图中每一个大三角形中白色三角形的排列规律,则第5个大三角形中白色三角形有个. 5、观察下列图形,它们是按一定规律排列的,依照此规律,第16个图形共有 个★. 6、如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,第5个“广”字中的棋子个数是 ,第n 个“广”字中的棋子个数是 . 9、将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去,结果如下表.则a n = .(用含n 的代数式表示)10、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案多一个正六边形和两个正三角形,则第n 个图案中正三角形的个数为 (用含n 的代数式表示). 13、用火柴棒按照如图所示的方式摆图形,则第n 个图形中,所需火柴棒的根数是 .14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第1个图案需4根小木棒,拼搭第2个图案需10根小木棒,…,依次规律,拼搭第8个图案需小木棒根.15、一张长方形桌子需配6把椅子,按如图方式将桌子拼在一起,那么8张桌子需配椅子 把. 16、下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有n (n ≥2个圆点时,图案的圆点数为S n .按此规律推断S n 关于n 的关系式为:S n = .17、如图是由火柴棒搭成的几何图案,则第n 个图案中有 根火柴棒.(用含n 的代数式表示)次数角形个数19、观察表一,寻找规律.表二,表三分别是从表一中选取的一部分,则a+b 的值为 . 表一:表二:表三:20、如图所示的图案是由正六边21、把边长为422235个菱241625个图形需棋子枚.(用含n 的代数式表示)27、如图所示是一副“三角形图”,第一行有一个三角形,第二行有2个三角形,第三行有4个三角形,第四行有8个三角形,…,你是否发现三角形的排列规律,请写出第七行有 个三角形... .. ..28、如图,用3根小木棒可以摆出第(1)个正三角形,加上2根木棒可以摆出第(2)个正三角形,再加上2根木棒可以摆出第(3)个正三角形…这样继续摆下去,当摆出第(n)个正三角形时,共用了木棒根.29、观察下列图形,根据变化规律推测第100个与第个图形位置相同.30、如图,用火柴棒按以下方式搭小鱼,搭1条小鱼用8根火柴棒,搭2条小鱼用14根,…,则搭n条小鱼需要根火柴棒.(用含n的代数式表示)一、12、343,4,5),3,……二、1三、12、36.457.n+18.909.?10.511.D12.(1)12+2a;12+3a;12+a(n-1)(2)a=2;5413.7;11;n/(n+1)+114.n/(n+1)21.990022.C23.(2)16;26;17824(1)13;16;(2)3n+1;(3)不能,3n+1=20093n=2008因为2008不是3的倍数。
初一找规律经典题型(含部分答案)

精心整理图1 图2 图3初一数学规律题应用知识汇总“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索:n 个n 位的例:4=6n -2例1(1(2例2共有(二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n 位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n 位的增幅;2、求出第1位到第第n 位的总增幅;3、数列的第1位数加上总增幅即是第n 位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求出,方法就简单的多了。
例1.古希腊数学家把数1,3,6,10,15,21,……,叫做三角形数,它有一定的规律性,则第24个三角形数与第22个三角形数的差为。
妙题赏析:规律类的中考试题,无论在素材的选取、文字的表述、题型的设计等方面都别具一格,令人耳目一新,其目的是继续考察学生的创新意识与实践能力,在往年“数字类”、“计算类”、“图形类”的基础上,今年又推陈出新,增加了“设计类”与“动态类”两种新题型,现将历年来中考规律类中考试题分析如下:1、设计类【例1】(2005年大连市中考题)在数学活动中,小明为了求的值(结果用n表示),设计如图a所示的图形。
(1)请你利用这个几何图形求的值为。
(2)请你利用图b,再设计一个能求的值的几何图形。
【例2】(2005年河北省中考题)观察下面的图形(每一个正方形的边长均为1)和相应的等式,探究其中的规律:(1)写出第五个等式,并在下边给出的五个正方形上画出与之对应的图示;(2)猜想并写出与第n个图形相对应的等式。
初一数学“找规律”专项训练Word版
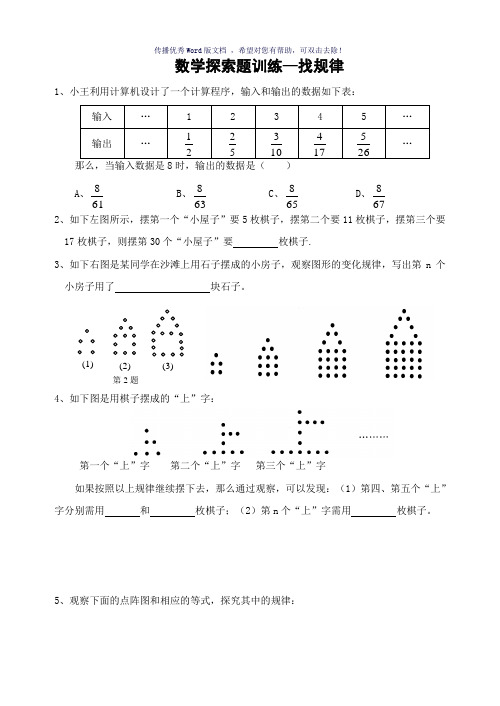
数学探索题训练—找规律1、小王利用计算机设计了一个计算程序,输入和输出的数据如下表:输入 (1)2345… 输出…21 52 103 174 265…那么,当输入数据是8时,输出的数据是( ) A 、618 B 、638 C 、658 D 、6782、如下左图所示,摆第一个“小屋子”要5枚棋子,摆第二个要11枚棋子,摆第三个要17枚棋子,则摆第30个“小屋子”要 枚棋子.3、如下右图是某同学在沙滩上用石子摆成的小房子,观察图形的变化规律,写出第n 个小房子用了 块石子。
4、如下图是用棋子摆成的“上”字:第一个“上”字 第二个“上”字 第三个“上”字如果按照以上规律继续摆下去,那么通过观察,可以发现:(1)第四、第五个“上” 字分别需用 和 枚棋子;(2)第n 个“上”字需用 枚棋子。
5、观察下面的点阵图和相应的等式,探究其中的规律:(1)(2)(3)第2题(1)(2)(3)(4)(1)在④和⑤后面的横线上分别写出相应的等式;(2)通过猜想写出与第n 个点阵相对应的等式_____________________。
6、用边长为1cm 的小正方形搭成如下的塔状图形,则第n 次所搭图形的周长是_______________cm (用含n 的代数式表示)。
7、如图,都是由边长为1的正方体叠成的图形。
例如第(1)个图形的表面积为6个平方单位,第(2)个图形的表面积为18个平方单位,第(3)个图形的表面积是36个平方单位。
依此规律。
则第(5)个图形的表面积 个平方单位。
8、图(1)是一个水平摆放的小正方体木块,图(2)、(3)是由这样的小正方体木块叠放而成,按照这样的规律继续叠放下去,至第七个叠放的图形中,小正方体木块总数应是( )A 25 B 66 C 91 D 1209、如图是由大小相同的小立方体木块叠入而成的几何体,图⑴中有1个立方体,图⑵中有4个立方体,图⑶中有9个立方体,…… 按这样的规律叠放下去,第8个图中小立方体个数是 .…………①1=12; ②1+3=22; ③1+3+5=32④ ;⑤ ;第1次 第2次 第3次 第4次 ······(1)(2)(3)14题10、图1是棱长为a 的小正方体,图2、图3由这样的小正方体摆放而成.按照这样的方法继续摆放,由上而下分别叫第一层、第二层、…、第n 层,第n 层的小正方体的个数为s .解答下列问题:(1)按照要求填表:(2)写出当n =10时,s= .11、如图用火柴摆去系列图案,按这种方式摆下去,当每边摆10根时(即10 n )时,需要的火柴棒总数为 根;12、用火柴棒按如图的方式搭一行三角形,搭一个三角形需3支火柴棒,搭2个三角形需5支火柴棒,搭3个三角形需7支火柴棒,照这样的规律下去,搭n 个三角形需要S 支火柴棒,那么用n 的式子表示S 的式子是 _______ (n 为正整数).13、如图所示,用同样规格的黑、白两色正方形瓷砖铺设矩形地面,请观察下图:则第n 个图形中需用黑色瓷砖 ____ 块.(用含n 的代数式表示)图1 图2 图3第14题图14、如图,用同样规格的黑白两种正方形瓷砖铺设正方形地面,观察图形并猜想填空:当黑色瓷砖为20块时,白色瓷砖为块;当白色瓷砖为120(n为正整数)块时,黑色瓷砖为块.15、观察下列由棱长为1的小立方体摆成的图形,寻找规律:如图1中:共有1 个小立方体,其中1个看得见,0个看不见;如图2中:共有8个小立方体,其中7个看得见,1个看不见;如图3中:共有27个小立方体,其中有19个看得见,8个看不见;……,则第6个图中,看不见的小立方体有个。
初一找规律经典题型(含部分答案)

图1 图2 图3初一数学规律题应用知识汇总“有比较才有鉴别”。
通过比较,可以发现事物的相同点和不同点,更容易找到事物的变化规律。
找规律的题目,通常按照一定的顺序给出一系列量,要求我们根据这些已知的量找出一般规律。
揭示的规律,常常包含着事物的序列号。
所以,把变量和序列号放在一起加以比较,就比较容易发现其中的奥秘。
初中数学考试中,经常出现数列的找规律题,下面就此类题的解题方法进行探索: 一、基本方法——看增幅(一)如增幅相等(实为等差数列):对每个数和它的前一个数进行比较,如增幅相等,则第n 个数可以表示为:a1+(n-1)b ,其中a 为数列的第一位数,b 为增幅,(n-1)b 为第一位数到第n 位的总增幅。
然后再简化代数式a+(n-1)b 。
例:4、10、16、22、28……,求第n 位数。
分析:第二位数起,每位数都比前一位数增加6,增幅都是6,所以,第n 位数是:4+(n-1) 6=6n -2例1、已知一个面积为S 的等边三角形,现将其各边n (n 为大于2的整数)等分,并以相邻等分点为顶点向外作小等边三角形(如上图所示).(1)当n = 5时,共向外作出了 个小等边三角形(2)当n = k 时,共向外作出了 个小等边三角形(用含k 的式子表示).例2、如图,在图1中,互不重叠的三角形共有4个,在图2中,互不重叠的三角形共有7个,在图3中,互不重叠的三角形共有10个,……,则在第n 个图形中,互不重叠的三角形共有 个(用含n 的代数式表示)。
(二)如增幅不相等,但是增幅以同等幅度增加(即增幅的增幅相等,也即增幅为等差n =3n =4n =5……数列)。
如增幅分别为3、5、7、9,说明增幅以同等幅度增加。
此种数列第n位的数也有一种通用求法。
基本思路是:1、求出数列的第n-1位到第n位的增幅;2、求出第1位到第第n位的总增幅;3、数列的第1位数加上总增幅即是第n位数。
此解法虽然较烦,但是此类题的通用解法,当然此题也可用其它技巧,或用分析观察的方法求出,方法就简单的多了。
整理初一数学找规律题及答案

初一数学找规律题及答案整理表姓名:职业工种:申请级别:受理机构:填报日期:A4打印/ 修订/ 内容可编辑初一年级数学竞赛试题一、选择题(每题3分,共30分) 1、与a −b 互为相反数的是( )A a −bB b −aC a+bD −(a +b) 2、使|a +2|=|a |+2成立的条件是( )A a 为任意值B a ≠0C a ≤0D a ≥03、已知数轴上三点,A 、B 、C 分别表示有理数a 、1、-1,那么|a +1|表示( )A A 、B 两点的距离 B A 、C 两点的距离C A 、B 两点到原点的距离之和D A 、C 两点到原点的距离之和 4、若|a |a =1,则a ( )A 是正数或负数B 是正数C 是有理数D 是非负数5、设a 是最小的自然数,b 是最大的负整数,c 是绝对值最小的有理数,则a 、b 、c 三数之和为( )A 1B 0C -1D -2 6、若12≤a ≤3,6≤b ≤63,则ba 的最大值为( )A 21B 2C 12D 1267、如图,已知有理数a 、b 、c 在数轴上的对应位置,则|c −1|+|a +c |+|b −a |的值为( )A b +1B 2a −b −1C 1−2a +b −2cD 1−2c +b8、一台微波炉成本价为a 元,销售价比成本价高22%。
因库存积压,需降价促销,按销售价的80%出售,则每台实际售价为( )A 、 a(1+22%)(1+80%)B 、a(1+22%)×80%C 、a(1+22%)(1-80%)D 、a(1+22%+80%)9、等式ax −3x =3中,若x 是自然数,则整数a 的取值是( )A 6或3B 6或4C 6或4,或0D 不能确定10、一台计算机原来售价100元,先降价15%,再提价15%,这时售价为( ) A 、100元 B 、97.75元 C 、115元 D 、以上答案都不对 二、填空题(每题2分,共28分)11、观察下面一列数,按规律在横线上填一个适当的数−12,16,−112,120,−130,_________。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
5. 观察下面一列有规律的数 1 ,2 3, , 4 , 5 , 6 ,,根据这个规律可知第 n 个数是(n 是正整数) 3 8 15 24 35 48
8.观察下面一列数:-1,2,-3,4,-5,6,-7,..,将这列数排成下列形式
精心整理
精心整理
按照上述规律排下去,那么第 10 行从左边第 9 个数是.
2. 我国着名数学家华罗庚曾说过:“数形结合百般好,隔裂分家
万事非。”如图,在一个边长为 1 的正方形纸版上,依次贴上面积
111
1
为 , , ,…, 的矩形彩色纸片(n 为大于 1 的整数)。
第3题
248
2n
请你用“数形结合”的思想,依数形变化的规律,计算 1 1 1 1 =。
248
2n
4. 将一张长方形的纸对折,如图所示可得到一条折痕(图中虚线).继续对折,对折时每次折痕与 上次的折痕保持平行,连续对折三次后,可以得到 7 条折痕,那么对折四次可以得到_条折痕.如 果对折 n 次,可以得到条折痕.
三、数、式计算规律题
1、已知下列等式:
①13=12;②13+23=32;③13+23+33=62;④13+23+33+43=102;
由此规律知,第⑤个等式是.
精心整理
精心整理
2、观察下面的几个算式:
1+2+1=4,1+2+3+2+1=9, 1+2+3+4+3+2+1=16, 1+2+3+4+5+4+3+2+1=25,…
精心整理
一、数字排列规律题
1、观察下列各算式:1+3=4= 22 ,1+3+5=9= 32 ,1+3+5+7=16= 42 …按此规律 (1)试猜想:1+3+5+7+…+2005+2007 的值? (2)推广:1+3+5+7+9+…+(2n-1)+(2n+1)的和是多少? 2、下面数列后两位应该填上什么数字呢?23581217
3、请填出下面横线上的数字。112358 21
4、有一串数,它的排列规律是 1、2、3、2、3、4、3、4、5、4、5、6、……聪明的你猜猜第 100 个() 二、几何图形变化规律题 1、观察下列球的排列规律(其中●是实心球,○是空心球):●○○●●○○○○○●○○●●○○○○○●○○●●○○ ○○○●……从第 1 个球起到第 2004 个球止,共有实心球个. 2、观察下列图形排列规律(其中△是三角形,□是正方形,○是圆),□○△□□○△□○△□□○△□┅┅,若 第一个图形是正方形,则第2008个图形是(填图形名称).
角形,…如此继续下去,结果如下表.则 an=
.(用含 n 的代数式表示)
精心整理
精心整理
10、用正三角形和正六边形按如图所示的规律拼图案,即从第二个图案开始,每个图案都比上一个图案
多一个正六 正三角形的 表示).
数 形个数
边形和两个正三角形,则第 n 个图案中
个数为
(用含 n 的代数式
13、用火柴棒按照如图所示的方式摆图形,则第 n 个图形中,所需火柴棒的根数是
14.先观察
1
1
=
1 (
1 )
1 (
1 )
=1-
1
=
2
1 2 2 3 1 2 2 3
33
1 1 1 = (1 1) (1 1) (1 1) =1- 1 = 3
1 2 2 3 3 4 1 2 2 3 3 4
44
再计算 1 1 2
1 2
3
1 3
4
1 n(n 1)
的值.
-1 2 -3 4 -5 6 -7 -9 10 -11 12 -13 14 -15 16
. 案是
第一层有六个
精心整理
精心整理
白色正六边形,则第 n 层有
个白色正六边形.
21、把边长为 3 的正三角形各边三等分,分割得到图①,图中含有 1 个边长是 1 的正六边形;把边长为
4 的正三角形各边四等分,分割得到图②,图中含有 3 个边长是 1 的正六边形;把边长为 5 的正三角
.
14、下列图案均是用长度相同的小木棒按一定的规律拼搭而成:拼搭第 1 个图案需 4 根小木棒,拼搭第
2 个图案需 10 根小木棒,…,依次规律,拼搭第 8 个图案需小木棒
根.
15、一张长方形桌子需配 6 把椅子,按如图方式将桌子拼在一起,那么 8 张桌子需配椅子 把.
16、下列每个图是由若干个圆点组成的形如四边形的图案,当每条边(包括顶点)上有 n(n≥2 个圆点
个点.
27、找规律.下列图中有大小不同的菱形,第 1 幅图中有 1 个,第 2 幅图中有 3 个,第 3 幅图中有 5 个,
则第 n 幅图中共有
个.Байду номын сангаас
1、如图,用同样大小的黑色棋子按图所示的方式摆图案,按照这样的规律摆下去,第 100 个图案需棋子 枚.
4、观察图中每一个大三角形中白色三角形的排列规律,则第 5 个大三角形中白色三角形有 个.
5、观察下列图形,它们是按一定规律排列的,依照此规律,第 16 个图形共有
个★.
6、如图①,图②,图③,图④,…,是用围棋棋子按照某种规律摆成的一行“广”字,按照这种规律,
第 5 个“广”字中的棋子个数是
,第 n 个“广”字中的棋子个数是
.
9、将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三
根据你所发现的规律,请你直接写出下面式子的结果:1+2+3+…+99+100+99+…+3+2+1= .
3、已知:2 2 22 2 ,3 3 32 3,4 4 42 4 ,5 5 52 5
3
38
8 15
15 24
24
规律发现专题训练
1. 用黑白两种颜色的正六边形地砖按如下所示的规律拼成若干个图案:第(4)个图案中有黑色地 砖 4 块;那么第( n )个图案中有白色地砖块。
时,图案的圆点数为 Sn.按此规律推断 Sn 关于 n 的关系式为:Sn=
.
17、如图是由火柴棒搭成的几何图案,则第 n 个图案中有
根火柴棒.(用含 n 的代数式表示)
19、观察表一,寻找规律.表二,表三分别是从表一中选取的一部分,则 a+b 的值为 表一:
表二: 表三:
20、如图所示的图 由正六边形密 铺而成,黑色 正六边形周围
...... 第 8 题
21.若“!”是一种数学运算符号,并且 1!=1,2!=2×1=2,3!=3×2×1=6, 4!=4×3×2×1,…,则100! 的值为
98!
25.观察下列图形的构成规律,根据此规律,第 8 个图形中有个圆.
根据下列 5 个图形及相应点的个数的变化规律,试猜测第 n 个图中有
