整数规划例题
第六章 运筹学 整数规划案例
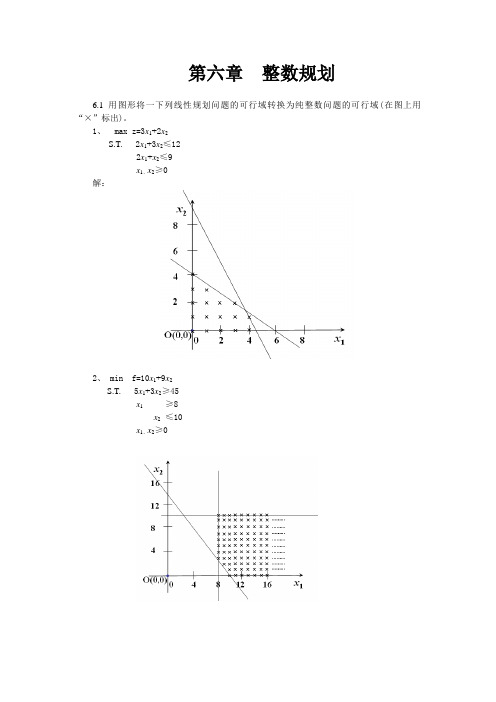
第六章整数规划6.1 用图形将一下列线性规划问题的可行域转换为纯整数问题的可行域(在图上用“×”标出)。
1、 max z=3x1+2x2S.T. 2x1+3x2≤122x1+x2≤9x1、x2≥0解:2、 min f=10x1+9x2S.T. 5x1+3x2≥45x1≥8x2≤10x1、x2≥06.2 求解下列整数规划问题1、 min f=4x1+3x2+2x3S.T. 2x1-5x2+3x3≤44x1+x2+3x3≥3x2+x3≥1x1、x2、x3=0或1解:最优解(0,0,1),最优值:22、 min f=2x1+5x2+3x3+4x3S.T. -4x1+x2+x3+x4≥2-2x1+4x2+2x2+4x2≥4x1+x2-x2+x2≥3x1、x2、x3、x3=0或1解:此模型没有可行解。
3、max Z=2x1+3x2+5x3+6x4S.T. 5x1+3x2+3x3+x4≤302x1+5x2-x2+3x2≤20-x1+3x2+5x2+3x2≤403x1-x2+3x2+5x2≤25x1、x2、x3、x3=正整数解:最优解(0,3,4,3),最优值:474、min z =8x1 +4 x2+3 x3+5 x4+2 x5+3 x6+4 x7+3 x8+4 x9+9 x10+7 x11+5 x12 +10 x13+4 x14+2 x15+175 x16+300 x17+375 x18 +500 x19约束条件x1 + x2+x3≤30x4+ x5+x6-10 x16≤0x7+ x8+x9-20 x17≤0x10+ x11+x12-30 x18≤0x13+ x14+x15-40 x19≤0x1 + x4+ x7+x10+ x13=30x2 + x5+ x8+x11+ x14=20x3 + x6+ x9+x12+ x15=20x i为非负数(i=1,2…..8)x i为非负整数(i=9,10…..15)x i为为0-1变量(i=16,17…..19)解:最优解(30,0,0,0,0,0,0,0,0,0,0,0,0,20,20,0,0,0,1),最优值:8606.3 一餐饮企业准备在全市范围内扩展业务,将从已拟定的14个点中确定8个点建立分店,由于地理位置、环境条件不同,建每个分店所用的费用将有所不同,现拟定的14个店的费用情况如下表:公司办公会决定选择原则如下:(1)B5、B3和B7只能选择一个。
数学建模 -整数规划

松弛问题 L0: max z 30x1 20x 2 2 x1 3 x 2 14.5 s.t 4 x1 x 2 16.5 x1 0, x 2 0
z 2 130 剪枝 ( IP)的最优解:x 3,x 2 1 2
最优值:Z * 130
4x1+x2=16.5
3 L3:xx21 2 z 3 130 关闭
11 L4 x1 4 ,x2 3 28543;3x2=14.5
L5 x1 2,x2 7
剪枝 z 130 5
2
L6 剪枝
无可行解
· · · · · · · · · 1 2 3 4 5 6 7
19:01
分枝定界法
分枝定界法
(1)分枝:通常,把全部可行解空间反复地分割为越 来越小的子集,称为分枝; (2)定界:并且对每个子集内的解集计算一个目标下 界(对于最小值问题),这称为定界。 (3)剪枝:在每次分枝后,凡是界限超出已知可行解 集目标值的那些子集不再进一步分枝,这样,许多子 集可不予考虑,这称剪枝。 求解生产进度问题、旅行推销员问题、工厂选址问题、 背包问题及分配问题。
对( IP) max z 30x1 20x 2 2 x1 3x 2 14.5 4 x1 x 2 16.5 s.t x 0, x 2 0 1 x1 , x 2为整数
父问题
松弛问题 ( L0 ): max z 30x1 20x 2 2 x1 3 x 2 14.5 s.t 4 x1 x 2 16.5 最优解: x1 3.5, x1 0, x 2 0
x 2 2 .5
子问题
( L1 ) max z 30x1 20x 2 ( L ) max z 30x 20x 2 1 2 2 x1 3 x 2 14.5 2 x1 3x2 14.5 4 x1 x 2 16.5 4 x1 x2 16.5 s.t s.t x1 3 x1 4 x1 0, x 2 0 x1 0, x2 0
整数规划例题

〈运筹学〉补充例题例题 1.1 某工厂可以生产产品A和产品B两种产品。
生产单位产品A和B所需要的机时、人工工时的数量以及可利用资源总量由下表给出。
这两种产品在市场上是畅销产品。
该工厂经理要制订季度的生产计划,其目标是使工厂的销售额最大。
产品A 产品B 资源总量机器(时) 6 8 120人工(时) 10 5 100产品售价(元) 800 300MAX 800X1 +300X2ST6X1 +8X2 <= 12010X1 +5X2 <= 100X1, X2 >=0例题 1.2该工厂根据产品A和产品B的销售和竞争对手的策略,调整了两种产品的售价。
产品A和B的价格调整为600元和400元。
假设其它条件不变,请你帮助该工厂经理制订季度的生产计划,其目标仍然是使工厂的销售额最大。
X 600X1 +400X2ST6X1 +8X2 <= 12010X1 +5X2 <= 100X1, X2 >=0例题 1.3由于某些原因,该工厂面临产品原料供应的问题。
因此,工厂要全面考虑各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价等因素。
有关信息在下表中给出。
产品A 产品B 资源总量机器(时) 6 8 120人工(时) 10 5 100原材料(公斤) 11 8 130产品售价(元) 600 400MAX 600X1 +400X2ST6X1 +8X2 <= 12010X1 +5X2 <= 10011X1 +8X2 <= 130X1, X2 >=0例题 1.4随着企业改革的不断深化,该企业的经理的管理思想产生了变化,由原来的追求销售额变为注重销售利润,因此,要考虑资源的成本。
工厂的各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价和各种资源的价格等因素。
有关信息在下表中给出。
产品A 产品B 资源总量资源价格(元/单位)机器(时) 6 8 120 5人工(时) 10 5 100 20原材料(公斤) 11 8 130 1产品售价(元) 600 400设: J为所用机器资源数量(小时);R为所用人力资源数量(小时);L为所用原材料数量(公斤)MAX 600X1 +400X2 -CST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L = 0J <= 120R <= 100L <= 1305J +20R +1L - C = 0x1, x2, J,R,L>=0例题 1.5 学习了管理课程后,该企业的经理明白了产品的成本包括变动成本和固定成本。
整数规划典型问题实例

例1 原料下料问题 生产中通过切割、剪裁、冲压等 手段,将原材料加工成所需大小
按照工艺要求,确定下料方案, 使所用材料最省,或利润最大
(钢管下料) 做100套钢架,用长为2.9m,2.1m,1.5m的元钢各一根,已知原料长 为7.4m,问如何下料,所用最省?
问题分析:每一种下料方式用了多少根钢材,合理的下料方式是剩余料头的
原料钢管总根数上界:13+10+8=31
2 6x1x2x331模式排列顺序可任定
x1 x2 x3
LINGO求解整数非线性规划模型
Local optimal solution found at
iteration: 12211
Objective value:
28.00000
Variable Value Reduced Cost
现有4种需求:4米50根,5米10根,6米20根,8米 15根,用枚举法确定合理切割模式,过于复杂。
对大规模问题,用模型的约束条件界定合理模式 决策变量
xi ~按第i 种模式切割的原料钢管根数(i=1,2,3) r1i, r2i, r3i, r4i ~ 第i 种切割模式下,每根原料钢管 生产4米、5米、6米和8米长的钢管的数量
钢管下料问题2
目标函数(总根数) Mix1 nx2x3
约束 条件 满足需求
模式合理:每根 余料不超过3米
r1x11r1x22r1x33501 6 4 r 1 15 r2 16 r3 18 r4 119
r2x 11r2x 22r2x 33101 6 4 r1 25 r2 26 r3 28 r4 219
模 4米 6米 8米 余 式 根数 根数 根数 料
14
第二章 整数规划+答案

故最优解为:X
0010
1 0
0 1
0 0
0 0
,最优值为 14。
0001
6103 0211 1030 5300
5、在今后三年内有五项工程考虑施工,每项工程的期望收入和年度费用(千元)如表所示。假定 每一项已批准的工程要在三年内完成,目标是要选出使总收入达到最大的那些工程。
工程
第1年
费用(千元) 第2年
2 3 14 s. t. 4 2 18
, 0 且为整数
B:X=(3.25,2.5)z=14.75
x2<=3
x2>=4
B1:X=(3,2.67)z=14.33
B2:X=(4,1)z=14
x2<=2
x2>=3
B11:X=(3,2)z=13
B12:X=(2.5,3)z=13.5
所以,最优解为:X=(4,1),最优值为 14。
人
A
B
C
D
E
甲
25
29
31
42
37
乙
39
38
26
20
33
丙
34
27
28
40
32
丁
24
42
36
23
45
解:(1)由于任务数多于人数,所以需要一名假想的人,设为戊。因为工作 E 必须完成,故设戊完
成 E 的时间为 M,其余的假象为 0,建立如下的效率矩阵。
任务
人
A
B
C
D
E
甲
25
29
31
42
37
乙
39
38
解:变换目标函数 max Z=16‐(2 3 5 6 )
典型的整数线性规划问题

小型 中型 大型
现有量
钢材(吨)
1.5
3
5
600
劳动时间(小时) 280
250
400
60000
利润(万元)
2
3
4
• 制订月生产计划,使工厂的利润最大。
• 如果生产某一类型汽车,则至少要生产80辆,
那么最优的生产计划应作何改变?
汽车厂生产计划
模型建立
设每月生产小、中、大型 汽车的数量分别为x1, x2, x3
模型建立
令xj表示对第j个发展项目的投资数量
n
Max z cj x j j 1 n
s. t. a j xj b j 1
xj 0或1(j=1,2, ,n)
整数 线性 规划 0-1 模型
(IP)
整数线性规划及0-1规划
例1 汽车厂生产计划
汽车厂生产三种类型的汽车,已知各类型每辆车对钢 材、劳动时间的需求,利润及工厂每月的现有量。
方法3:化为非线性规划
x1=0 或 80
x1(x1 80) 0
x2=0 或 80
x2 (x2 80) 0
x3=0 或 80
x3 (x3 80) 0
非线性规划(Non- Linear Programming,简记NLP)
NLP 虽 然 可 用 现 成 的 数 学 软 件 求 解 ( 如 LINGO, MATLAB),但是其结果常依赖于初值的选择。
丙 1’18” 1’07”8 1’24”6 59”4
丁 1’10” 1’14”2 1’09”6 57”2
戊 1’07”4 1’11” 1’23”8 1’02”4
讨论 丁蛙泳c43 =69.675.2,戊自由泳c54=62.4
运筹学整数规划例题

练习4.9 连续投资问题某公司现有资金10万元,拟在今后五年内考虑用于下列项目的投资:项目A:从第一年到第四年每年年初需要投资,并于次年收回本利115%,但要求第一年投资最低金额为4万元,第二.三.四年不限.项目B:第三年初需要投资,到第五年末能收回本利128%,但规定最低投资金额为3万元,最高金额为5万元.项目C:第二年初需要投资,到第五年末能收回本利140%,但规定其投资金额或为2万元,或为4万元,或为6万元,或为8万元.项目D:五年内每年年初都可购买公债,于当年末归还,并获利6%,此项目投资金额不限. 试问该公司应图和确定这些项目的每年投资金额,使到第五年末拥有最大的资金收益.(1) x 为项目各年月初投入向量。
(2) ij x 为 i 种项目j 年的月初的投入。
(3) 向量c 中的元素ijc 为i 年末j 种项目收回本例的百分比。
(4) 矩阵A 中元素ija 为约束条件中每个变量ijx 的系数。
(5) Z 为第5年末能拥有的资金本利最大总额。
因此目标函数为4325max 1.15 1.28 1.40 1.06A B C D Z x x x x =+++束条件应是每年年初的投资额应等于该投资者年初所拥有的资金.第1年年初该投资者拥有10万元资金,故有11100000A D x x +=.第2年年初该投资者手中拥有资金只有()116%D x +,故有22211.06A C D D x x x x ++=.第3年年初该投资者拥有资金为从D 项目收回的本金: 21.06D x ,及从项目A 中第1年投资收回的本金: 11.15A x ,故有333121.15 1.06A B D A D x x x x x ++=+同理第4年、第5年有约束为44231.15 1.06A D A D x x x x +=+,5341.15 1.06DA Dx x x =+max =1.15*x4a+1.28*x3b+1.4*x2c+1.06*x5d; x1a+x1d=100000;-1.06*x1d+x2a+x2c+x2d=0;-1.15*x1a-1.06*x2d+x3a+x3b+x3d=0; -1.15*x2a-1.06*x3d+x4a+x4d=0; -1.15*x3a-1.06*x4d+x5d=0; x2c=40000 ; x2c=60000; x2c=80000; x2c=20000; x3b>=30000; x3b<=50000;x1a>=0;x2a>=0;x3a>=0;x4a>=0;x5a>=0; x1b>=0;x2b>=0;x3b>=0;x4b>=0;x5b>=0; x1c>=0;x2c>=0;x3c>=0;x4c>=0;x5c>=0; x1d>=0;x2d>=0;x3d>=0;x4d>=0;x5d>=0;Variable Value Reduced Cost X4A 22900.00 0.000000 X3B 50000.00 0.000000 X2C 40000.00 0.000000 X5D 0.000000 0.000000 X1A 62264.15 0.000000 X1D 37735.85 0.000000 X2A 0.000000 0.000000 X2D 0.000000 0.3036000E-01 X3A 0.000000 0.000000 X3D 21603.77 0.000000 X4D 0.000000 0.2640000E-01 X5A 0.000000 0.000000 X1B 0.000000 0.000000 X2B 0.000000 0.000000 X4B 0.000000 0.000000 X5B 0.000000 0.000000 X1C 0.000000 0.000000 X3C 0.000000 0.000000 X4C 0.000000 0.000000 X5C 0.000000 0.000000Row Slack or Surplus Dual Price 1 80000.00 1.0000002 0.000000 1.4018503 0.000000 1.3225004 0.000000 1.2190005 0.000000 1.1500006 0.000000 1.0600007 0.000000 -0.8388608E+188 -20000.00 -0.1280000E+109 -40000.00 -0.1280000E+1010 -20000.00 0.1280000E+1011 20000.00 0.00000012 0.000000 0.6100000E-0113 62264.15 0.00000014 0.000000 0.00000015 0.000000 0.00000016 22900.00 0.00000017 0.000000 0.00000018 0.000000 0.00000019 0.000000 0.00000020 50000.00 0.00000021 0.000000 0.00000022 0.000000 0.00000023 0.000000 0.00000024 40000.00 0.00000025 0.000000 0.00000026 0.000000 0.00000027 0.000000 0.00000028 37735.85 0.00000029 0.000000 0.00000030 21603.77 0.00000031 0.000000 0.00000032 0.000000 0.0000004.10某城市的消防总站将全市划分为11个防火区,现有4个消防站,图4-11给出的是该城市各防火区域和防火站的示意图,其中1,2,3,4,表示消防站1,2,…11表示防火区域,根据历史资料证实,各消防站可在事先规定允许的时间内对所负责的区域内的火灾予以扑灭,图中没有虚线连接的就表示不负责,现在总部提出:能否减少消防站的数目,仍能保证负责各地区的防火任务?如果可以的话,应该关闭哪个?练习4.10某城市的消防站总部将全市划分为11个防火区,现有四的。
整数规划案例模型

工厂1、2、3分别生产A、B产品的零件A B 可用时间工厂1 1 0 4工厂2 0 2 12工厂3 3 2 8利润300 500–变化1:增加A、B产品的准备成本,分别为700和1300–变化2:A、B的数量限制在整数范围。
案例1:产量x1、x2,A和B是否生产y1、y2Max z=300x1+500x2-700y1-1300y2X1<=42x2<=123x1+2x2<=18X1<=99y1X2<=99y2X1、x2为非负整数y1、y2为0-1整数包含互斥产品两种产品具有相同的用户,是互相竞争的。
因此,管理层决定不同时生产两种产品,而是只能选择其中的一种。
案例2:A和B是否生产y1、y2;产量x1、x2。
Max z=300x1+500x2X1<=42x2<=123x1+2x2<=18Y1+y2=1X1<=99y1X2<=99y2Y1、y2为0-1整数X1、x2为非负数加入二选一约束公司最近新建了一个与工厂3类似的新厂,因此,新厂也可以生产两种产品。
但是出于管理上的原因,管理层决定只在工厂3、4中选择一个工厂生产,同时要获得最大利润。
案例3:产量x1、x2;工厂3或4是否生产y1、y2 X1<=42x2<=123x1+2x2<=18+99y22x1+4x2<=28+99y1Y1+y2=1Y1、y2为0-1整数X1、x2为非负数如果y1=1,y2=03x1+2x2<=182x1+4x2<=28+99如果y1=0,y2=13x1+2x2<=18+992x1+4x2<=28。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
〈运筹学〉补充例题例题 1.1 某工厂可以生产产品A和产品B两种产品。
生产单位产品A和B所需要的机时、人工工时的数量以及可利用资源总量由下表给出。
这两种产品在市场上是畅销产品。
该工厂经理要制订季度的生产计划,其目标是使工厂的销售额最大。
产品A 产品B 资源总量机器(时) 6 8 120人工(时) 10 5 100产品售价(元) 800 300MAX 800X1 +300X2ST6X1 +8X2 <= 12010X1 +5X2 <= 100X1, X2 >=0例题 1.2该工厂根据产品A和产品B的销售和竞争对手的策略,调整了两种产品的售价。
产品A和B的价格调整为600元和400元。
假设其它条件不变,请你帮助该工厂经理制订季度的生产计划,其目标仍然是使工厂的销售额最大。
X 600X1 +400X2ST6X1 +8X2 <= 12010X1 +5X2 <= 100X1, X2 >=0例题 1.3由于某些原因,该工厂面临产品原料供应的问题。
因此,工厂要全面考虑各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价等因素。
有关信息在下表中给出。
产品A 产品B 资源总量机器(时) 6 8 120人工(时) 10 5 100原材料(公斤) 11 8 130产品售价(元) 600 400MAX 600X1 +400X2ST6X1 +8X2 <= 12010X1 +5X2 <= 10011X1 +8X2 <= 130X1, X2 >=0例题 1.4随着企业改革的不断深化,该企业的经理的管理思想产生了变化,由原来的追求销售额变为注重销售利润,因此,要考虑资源的成本。
工厂的各种产品所需要的机时、人工工时、原材料的资源数量及可用资源的总量、产品的售价和各种资源的价格等因素。
有关信息在下表中给出。
产品A 产品B 资源总量资源价格(元/单位)机器(时) 6 8 120 5人工(时) 10 5 100 20原材料(公斤) 11 8 130 1产品售价(元) 600 400设: J为所用机器资源数量(小时);R为所用人力资源数量(小时);L为所用原材料数量(公斤)MAX 600X1 +400X2 -CST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L = 0J <= 120R <= 100L <= 1305J +20R +1L - C = 0x1, x2, J,R,L>=0例题 1.5 学习了管理课程后,该企业的经理明白了产品的成本包括变动成本和固定成本。
如果生产产品A,工厂要花费1000元的固定成本,如果生产产品B,工厂要花费800元的固定成本。
假设其它情况不变,请你为该工厂设计一个使利润最大化的生产方案。
!在例1_4的基础上改进.!设:Y1,Y2是0,1变量。
若Y1=1,表示生产A,若Y1=0,表示不生产A;! 若Y2=1,表示生产B,若Y2=0,表示不生产B.!分析:如果X1>0,应该让Y1=1。
为此,选一个充分大的数(此处选1000),! 加约束 X1<=1000Y1。
! 如果X1=2,Y1必须为1,不能为零。
! 若X1=0,Y1既可以为零,又可以等于1;由于目标函数越大越好,! Y1的系数为负数,所以Y1选择等于零。
!约束 X1<=1000Y1, 变形为 1000Y1-X1>=0;同理,有1000Y2-X2>=0。
MAX 600X1 +400X2 -C -1000Y1 -800Y2ST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L = 0J <= 120R <= 100L <= 1305J +20R +1L - C = 01000Y1-X1>=01000Y2-X2>=0ENDINT Y1INT Y2见LINDO《IP例1_5.LTX》例题 1.6 通过求解例1.4和1.5中的线性规划模型,从结果分析可知原材料已经用尽,是稀缺资源。
假设,该原材料在总量100公斤以内,按正常价1元/公斤供应;若超过100公斤,超过部分按1.2元/公斤供应。
假设其它情况不变,请你为该工厂设计一个使利润最大化的生产方案。
!在例1_5的基础上改进.!将使用的原材料分为两部分L1和L2。
L1表示100公斤以内使用的原材料数量,L2表示超过100公斤使用的原材料数量。
MAX 600X1 +400X2 -C -1000Y1 -800Y2ST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L1 -L2 = 0J <= 120R <= 100L1 <= 1005J +20R +1L1 +1.2L2- C = 01000Y1-X1>=01000Y2-X2>=0ENDINT Y1INT Y2见LINDO《IP例1_6.LTX》例题 1.7 假设,该原材料在市场上容易买到,是买方市场。
原料生产厂家实行如下的销售策略:如果购买100公斤以下,按正常价1元/公斤供应;若超过100公斤,超过部分按0.8元/公斤供应。
假设其它情况不变,请你为该工厂设计一个使利润最大化的生产方案。
!此题看似与例1.6相同,但是,如果将例1_6中的1.2改为0.8,! 求解后会出现出乎意料的结果:L1=0, L2=120,! 即不使用100公斤以内的,专使用超过100公斤的原材料。
!为了解决此问题,增加一个0-1变量Y.! Y=0,L1没有达到100公斤(L1 <= 100);Y=1, L1已经达到100公斤。
!若L1<100, 必须有Y=0。
添约束:L1>=100Y,! 只有L1=100时Y才可以等于1。
! (变换后为:100Y-L1<=0)!若Y=1, L2可以取正数,添约束:L2<=10000Y,! 其中10000是考虑到其它资源,L2不可能超过的数。
! (变换后为:L2-10000Y<=0)MAX 600X1 +400X2 -C -1000Y1 -800Y2ST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L1 -L2 = 0J <= 120R <= 100L1 <= 1005J +20R +L1 +0.8L2- C = 01000Y1-X1>=01000Y2-X2>=0100Y-L1<=0L2-10000Y<=0ENDINT Y1INT Y2INT Y见LINDO《IP例1_7.LTX》是否可以直接写 L1>=100?例题 1.8 假设,该原材料是买方市场。
原料生产厂家实行如下的销售策略:如果购买100公斤以下,按正常价1元/公斤供应;若超过100公斤,则全部按0.8元/公斤供应。
假设其它情况不变,请你为该工厂设计一个使利润最大化的生产方案。
!在例1.7的基础上解此题。
考虑0-1变量Y. Y=0,L1没有达到100公斤;Y=1, L1已经达到100公斤。
! 若L1达到了100公斤(Y=1),L1应该退回100公斤的差价,共计20元;若没有达到100公斤(Y=0),不退。
MAX 600X1 +400X2 -C -1000Y1 -800Y2 +20YST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L1 -L2 = 0J <= 120R <= 100L1 <= 1005J +20R +L1 +0.8L2- C = 01000Y1-X1>=01000Y2-X2>=0100Y-L1<=0L2-10000Y<=0ENDINT Y1INT Y2INT Y见LINDO《IP例1_8.LTX》!在例1.7的基础上解此题。
考虑0-1变量Y. Y=0,L1没有达到100公斤;Y=1, L1已经达到100公斤。
!改变IP例1_8.ltx中的模型,只用原始数据,不用人工计算退回的钱。
!设C1是机器、人工的费用,C2是100公斤以内的材料费用,100公斤以上的材料费是0.8L2,在目标函数中。
!问题的难点是计算C2。
!用相互排斥的约束:! 约束1: 1L1 <= C2 +MY! 约束2: 0.8L1 <= C2 +M(1-Y)! 若Y=1,买够了前100公斤,约束1自然满足,从约束2看,C2至少是 0.8L1 !若Y=0,没有买够了前100公斤,约束2自然满足,从约束1看,C2至少是 1L1 !达到了约束的目的,又用原始数据。
变换后得下列模型。
求解后与原来得解相同。
MAX 600X1 +400X2 -C1 -C2 -0.8L2-1000Y1 -800Y2ST6X1 +8X2 - J = 010X1 +5X2 - R = 011X1 +8X2 - L1 -L2 = 0J <= 120R <= 100L1 <= 1005J +20R - C1 = 0L1 - C2 -10000Y<= 00.8L1 - C2 +10000Y<= 100001000Y1-X1>=01000Y2-X2>=0100Y-L1<=0L2-10000Y<=0ENDINT Y1INT Y2INT Y见LINDO《IP例1_8B.LTX》例题 4:生产布局问题某公司考虑在北京、上海、广州、武汉四个城市中选择1-2个城市建设销售集散库房,负责向华北、华中、华南三个地区供货。
每个库房每月可以处理货物1500件。
有关的发货费用、建库成本和需求量见下表:! 在满足需求的前提下,请设计一个成本(发货成本+仓库成本)最省的建库方案。
!!设Y1,Y2,Y3,Y4 = 0 或 1,分别表示是否在北京、上海、广州、武汉建立库房。
!设X12是从北京给华北的发货量,......,X44是武汉给东北的供货量。
MIN 45000Y1+50000Y2+70000Y3+40000Y4+CST!供货费用200X11+400X12+500X13+300X14+300X21+250X22+400X23+500X24+600X31+350X32+300X33+750X34+350X41+150X42+350X43+650X44-C=0!满足需求的约束X11+X21+X31+X41>=500X12+X22+X32+X42>=800X13+X23+X33+X43>=750X14+X24+X34+X44>=400!供给的约束!对北京有 X11+X12+X13+X14<=1500Y1,变形为X11+X12+X13+X14-1500Y1 <= 0X21+X22+X23+X24-1500Y2 <= 0X31+X32+X33+X34-1500Y3 <= 0X41+X42+X43+X44-1500Y4 <= 0! 在北京、上海、广州、武汉四个城市中选择1-2个城市Y1+Y2+Y3+y4<=2ENDINT Y1INT Y2INT Y3INT Y4例题 5:相互排斥的约束(在前面例题4的基础上,增加新的选择)某公司考虑在北京、上海、广州、武汉四个城市中选择1-2个城市建设销售集散库房,负责向华北、华中、华南三个地区供货。
