一元二次方程应用(动点问题)

合集下载

一元二次方程的应用——动点问题

分析：点P的运动方向是由A
点Q的运动方向是由B 运动速度都是1cm⁄s C C
运动时间未定
运动距离
点P的运动距离即 AP的长度点Q的运动距离即 BQ的长度
例：在Rt△ABC中，∠C=90°， AC=8,BC=6.点P由A点出发沿AC方向向点C 匀速移动，点Q由B点出发沿BC方向向点C匀速移动，它们的速度都是1cm⁄s，几秒后 △PCQ的面积为△ABC面积的一半？
设时间为x，, 则可表示出CP=2x，BQ=x，QC=25-x
等量关系：P、Q两点相距25cm
解：设x秒后P、Q两点相距25cm.
在Rt△QCP中 QC2+PC2=PQ2
（25-x）2+（2x）2=252
5x2-50x=0
x1=0 （舍），x2=10 答：10秒后PQ相距25cm。
答：2秒后△PCQ的面积为Rt△ABC面积的一半.
例2：在Rt△ABC中，∠C=90°，AC=30cm， BC=25cm，动点P沿CA方向运动，速度是 2cm⁄s；动点Q从B点出发，沿BC方向运动，速度是1cm⁄s，几秒后P、Q两点相距25cm？
分析
运动点P的运动方向是由C 方向
A问题需要注意几个问题： 1、有几个动点？
2、怎样运动？即向哪儿运动？
3、运动的速度、时间、距离分别是多少？
例1：在Rt△ABC中，∠C=90°，AC=8，BC=6. 点P由A点出发沿AC方向向点C匀速移动，点Q 由B点出发沿BC方向向点C匀速移动，它们的速度都是1cm⁄s，几秒后△PCQ的面积为 △ABC面积的一半？
若设时间为x，则可表示出AP=x，BQ=x 所以PC=8-x， QC=6-x
等量关系：△PCQ的面积为△ABC面积的一半

(完整版)一元二次方程动点问题讲解

1)设⊿ ABC位于直线L左侧部分的面积为S,写出S与x之间的函数关系式; 2)当x为何值时,直线L平分⊿ ABC的面积?
(1)解：∠ BAC=45°,AP=x,
∴当L位于CD的右侧时,与
BC交于点Q
L
AP=X,PB=3-X
C
Q
CD=2,PQ=?
p
由小学学习的比例计算PQ 即：CD:DB=PQ:BQ
∴450=½×(2X-50)×3X
Q
X²-25X-30=0
C
解得：X₁=-5(舍去）;X₂=30
解得：综合以上情况在10S,15S,30S时，△OPQ的面积为450
例2 在矩形ABCD中,AB=6cm,BC=12cm,点P从点A开始以1cm/s的速度沿AB边向点B移动,点Q从点B开始以 2cm/s的速度沿BC边向点C移动,如果P、Q分别从A、B 同时出发，几秒后⊿ PBQ的面积等于8cm2？
C
通过观察，有两种情况：（1）蚂蚁未爬完OA这段距离
（2）蚂蚁爬完OA这段距离后，再由O点向B爬行
例1 如图OA=OB=50cm,OC是一条射线，OC⊥AB,一
只蚂蚁由点A以2cm/s的速度向B处爬行，同时另一只蚂
蚁由O点以3cm/s的速度沿oc方向爬行，则是否存在这样
的时刻，使两只蚂蚁所在位置与O点组成的三角形的面积
·ALeabharlann RP∴S◇=S△ABC-S△BPQ-S△APQ
∴16=32-½(8-X)²-½×(X)²
整理：x²-8x+16=0
整理：x₁=x₂=4
CQ
B
∴当AP=4cm时，平行四边形PQCR的面积等于16cm2
例4：⊿ABC中,AB=3, ∠ BAC=45°,CD⊥ AB,垂足为D,CD=2,P 是AB上的一动点(不与A,B重合),且AP=x,过点P作直线L与AB垂直.

一元二次方程的应用动点问题(共8张PPT)

（2）点P，Q出发几秒后，可使△PCQ 的面积为9 cm2 ? △PCQ的面积能为10cm2?
（3）当点P、Q出发几秒后，
PQ的长度为 4 2 cm？
有关“动点”的运动问题”
1)关键—— 以静代动把动的点进行转换,
2)方法—— 时间变路程
变为线段的长度,
2、在直角三角形ABC中,AB=BC=12cm，点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E.
Ｅ
Ａ
Ｄ
Ｂ
一个长为10m的梯子斜靠在墙上，梯子的顶端距地面的垂直距离为8m，如果梯子的顶端下滑1m，梯子的底端滑动xm，可列方程为:__________
：如图，△ABC是边长3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、 BC方向匀速移动，点P的速度为1cm/s,点Q的速度为2cm/s，当点Q到达点C时，P、Q两点停顿运动，设点P的运动时间为t〔s〕，解答以下问题：〔1〕当t为何值时，△PBQ是直角三角形？ (2)△PBQ能否为等边三角形？假设能，请求出t 的值，假设不能，说明理由.
点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平一元二次方程的应用动点问题
2、在直角三角形ABC中,AB=BC=12cm，点D从点A开始以2cm/s的速度沿AB边向点B移动,过点D做DE平行于BC,DF平行于AC,点E. 点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s的速度移动；有关“动点”的运动问题”
一元二次方程的应用动点问题
3）常找的数量关系——面积，勾股定理等；（3）当点P、Q出发几秒后，
F分别在AC,BC上,问：点D出发几秒后四边形DFCE的面积为20cm2？点 P 沿 AC 边从点 A 向终点 C 以 1 cm/s的速度移动；

一元二次方程——动点问题

2
整理，得 x26x80
解这个方程，得 x1 2,x2 4
Q
0x6 所以2秒或4秒后⊿ PBQ的面
积等于8cm2
A
B
P
例2：等腰直角⊿ ABC中,AB=BC=8cm,动点P从A 点出发,沿AB向B移动,通过点P引平行于BC,AC的直线及AC,BC分别交于R、Q.当AP等于多少厘米时,平行四边形PQCR的面积等于16cm2?
A
D
P
（2）P、Q两点从出发开始到几秒时，
点P和点Q的距离是10cm？
Q
B

C
4.如图，在矩形ABCD中，AB=12cm， BC=6cm.点P沿AB边从点A开始向点B以 2cm/s的速度移动，点Q沿DA边从点D开始向点A以1cm/s的速度移动.如果P、Q同时出发，用t（s）表示移动的时间（0≤t≤6）. 那么当t为何值时，ΔQAP的面积等于8cm2？
一元二次方程——动点问题
（2）经过多少时间后，S△PCQ的面积为15cm2？
（3）请用配方法说明，何时△PCQ的面积最大，最大面积是多少？
2．如图，用一块长为50cm、宽为30cm的长方形铁片制作一个无盖的盒子，若在铁片的四个角截去四个相同的小正方形，设小正方形的边长为xcm．（1）底面的长AB=_______cm，宽BC=__________cm （用含x的代数式表示）（2）当做成盒子的底面积为300cm2时，求该盒子的容积．
解：设AP=x，则PR=x，PB=8-x
根据题意得：x8-x 16
整理得：x2 8x 16 0 解这个方程得：x1 x2 4 答：当AP 4cm时，四边形面积为16cm2
CQ
A
R
P
B

一元二次方程应用题(动点问题)

一元二次方程的概述
一元二次方程是指含有一个未知数的二次方程，表达式形式为ax²+bx+c=0。它是数学中常见的方程类型，具有重要的应用价值。
寻找问题的关键变量和已知条件
在解决动点问题时，我们需要仔细分析问题，确定关键变量和已知条件。这样可以帮助我们建立一元二次方程，进而求解问题。
如何列出动点问题的一元二次方程
一元二次方程应用题(动点问题)
在这个演示我们将介绍问题的定义和一元二次方程的基本概念，以及如何寻找关键变量并列出方程。通过实际案例分析，帮助您掌握解决这类问题的技巧。
动点问题的介绍与定义
动点问题是指根据物体的运动轨迹及已知条件，找出该物体的位置或状态。它常常涉及时间、距离、速度等变量。
在列出方程时，我们通常需要根据关键变量和已知条件进行代入。通过代入求解，我们可以得到方程的解，从而解决动点问题。
解方程并求出问题的答案
解一元二次方程通常会涉及到配方法、因式分解、求根公式等解法。通过运用这些方法，我们可以计算出问题的答案，并得出具体的结论。
实际应用案例分析
通过实际应用案例的分析，我们将展示动点问题在现实生活中的应用场景。这些案例将帮助您更好地理解和掌握一元二次方程在动点问题中的应用。
总结和应用技巧
在这个部分，我们将对整个演示进行总结，并提供一些应用技巧，帮助您在解决动点问题时更加高效和准确。

一元二次方程应用(动点问题)

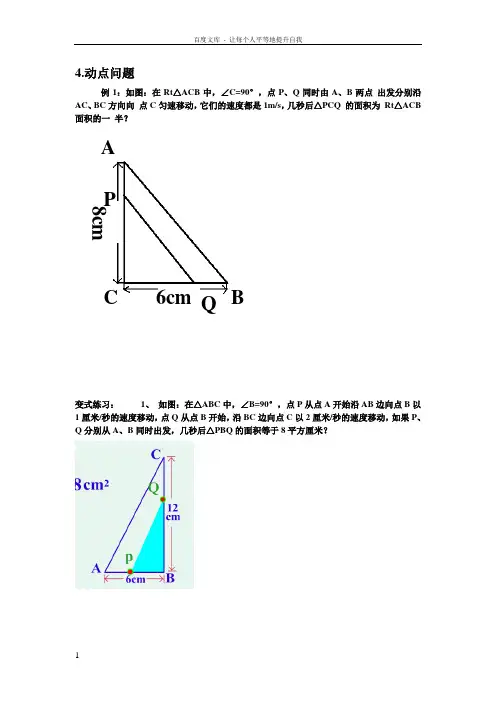
4.动点问题例1：如图：在Rt △ACB 中，∠C=90°，点P 、Q 同时由A 、B 两点出发分别沿AC 、BC 方向向点C 匀速移动，它们的速度都是1m/s ，几秒后△PCQ 的面积为 Rt △ACB 面积的一半？变式练习： 1、如图：在△ABC 中，∠B=90°，点P 从点A 开始沿AB 边向点B 以1厘米/秒的速度移动，点Q 从点B 开始，沿BC 边向点C 以2厘米/秒的速度移动，如果P 、Q 分别从A 、B 同时出发，几秒后△PBQ 的面积等于8平方厘米？AB C P Q 6cm 8cm2、如图，在△ABC 中，AB=6cm ，AC=12cm 动点D 从A 点出发到B 点为止，运动的速度为1cm/秒；同时动点E 从C 点出发到A 点为止，点E 运动的速度为2cm/秒那么当点A 、D 、E 为顶点的三角形与△ABC 相似时，运动的时间是（）3.如图，在矩形ABCD 中，AB=3，BC=4，点P 以每秒2个单位长度的速度从点C 出发，沿CA 向点A 运动；点Q 同时以每秒1个单位长度的速度从点A 出发，沿AB 向点B 运动,设P 、Q 两点移动t 秒（1）求△APQ 与△ABC 相似时t 的值（2）求四边形BCPQ 面积S 与时间t 的关系式（3）求△APQ 为等腰三角形时t 的值BCE D A例2：一艘轮船以20海里/时的速度由西向东航行，途中接到台风警报，台风中心正以40海里/时的速度由南向北移动，距台风中心20 海里的圆形区域(包括边界)都属台10风区.当轮船到A处时，测得台风中心移到位于点A正南方向B处，且AB=100海里.若这艘轮船自A处按原速度继续航行，在途中会不会遇到台风?若会，试求轮船最初遇到台风的时间；若不会，请说明理由.变式练习：某军舰以20节的速度由西向东航行，一艘电子侦察船以30节的速度由南向北航行，它能侦察出周围50海里（包括50海里）范围内的目标。

一元二次方程——动点问题

Day5：一元二次方程之动点问题一元二次方程解决问题1．动点问题几何图形应用题，关键是将点的运动关系表示出来，找出未知量与已知量的内在联系，根据面积或体积公式列出方程.常见题型：选择题、解答题，求最值问题.易错点：找准动点的关系.中考回顾：常考，求最值或三角形为直角三角形等等.例1如图，点O 在线段AB 上，AO=1，OB=2，OC 为射线，且∠BOC=120°，动点P 以每秒2个单位长度的速度从点O 出发，沿射线OC 作匀速直线运动．设运动时间为t 秒，当△ABP 为直角三角形时，t 的值为（）A．t=1B．t=1或8﹣C．t=8D．t=1或8例2如图，已知△ABC中，∠B=90°，AB=5cm，BC=7cm，点P从点A开始沿AB边向点B以1cm/s 的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，当其中一点停止运动时，另一点也随之停止，其中P、Q不与A、B重合.（1）如果P、Q分别从A、B同时出发，那么几秒后，△PBQ的面积等于4cm2？（2）如果P、Q分别从A、B同时出发，那么几秒后，PQ的长度等于5cm？（3）在（1）中，△PBQ的面积能否等于7cm2？请说明理由.例3如图，在平面直角坐标系中，过原点O及点A（0,2）、C（6,0）作矩形OABC，∠AOC的平分线交AB于点D.点P从点O出发，以每秒2个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动.设移动时间为t秒，则当t为何值时，△PBQ为直角三角形？参考答案1.【答案】B【考点】本题考查了动点问题，结合三角形，注意画出图形，帮助理解．【解析】如图1，当∠PAB=90°时，∵∠BOC=120°，∴∠AOP=60°，∴∠APO=30°，∴OP=2OA=2，∵OP=2t，∴t=1；如图2，当∠APB=90°，过P 作PD⊥AB，∵∠OPD=120°﹣90°=30°，∴OD=12∴AD=AO﹣OD=1﹣t，在Rt△ABP 中，根据勾股定理得：AP 2+BP 2=AB 2，即（2+t）222+（1﹣t）2=32，解得：t=8﹣（负值舍去）；当∠ABP=90°时，此情况不存在；综上，当t=1或t=8﹣时，△ABP 是直角三角形．2.【答案】（1）1秒（2）2秒（3）不能【考点】一元二次方程在三角形中动点问题的应用.【解析】（1）设x 秒后，△PBQ 的面积等于4cm².此时，AP=x cm，PB=（5-x）cm，BQ=2x cm，由S △PBQ =4BQ PB 21=∙得()42-521=∙x x ，整理得0452=+-x x ，解得x 1=1，x 2=4.当x=4时，2x=8>7，不合要求.所以1秒后，△PBQ 的面积等于4cm².（2）设x 秒后，PQ 的长度等于5cm.由PB 2+BQ 2=5²得（5-x）²+（2x）²=5²整理得x²-2x=0，解得x 1=0（舍去），x 2=2.经检验，x=2符合要求，所以2秒后，PQ 的长度等于5cm.（3）不能.理由：设x 秒后，△PBQ 的面积等于7cm²，由题意得()72-521=∙x x ，整理得x²-5x+7=0，03-28-25<==∆，此方程无解，所以△PBQ 的面积不可能等于7cm².3.【答案】t=2或55+=t 或5-5=t 【考点】该题考查的是一元二次方程与直角坐标系结合的动点应用题型.【解析】过点P 作PG⊥OC，垂足为G.在Rt△POG 中，∵∠POG=45°，∴∠OPG=45°，∵OP=t 2，∴OG=PG=t，∴点P（t，t），又∵Q（2t，0），B（6,2），根据勾股定理可得PB²=（6-t）²+（2-t）²，QB²=（6-2t）²+2²，PQ²=（2t-t）²+t²=2t².在P、Q 移动过程中，PQ 始终与OD 垂直，容易得知∠BPQ 不可能等于90°.①若∠PQB=90°，则有PQ²+QB²=PB²，即2t²+[（6-2t）²+2²]=（6-t）²+（2-t）²，整理得4t²-8t=0，解得t 1=0（舍去），t 2=2，∴t=2.②若∠PBQ=90°，则有PB²+QB²=PQ²，∴[（6-t）²+（2-t）²]+[（6-2t）²+2²]=2t²，整理得t²-10t+20=0，解得t=5±5.∴当t=2或55+=t 或5-5=t 时，△PQB 为直角三角形.。

一元二次方程的应用(动点问题)

二次函数
一元二次方程的图像是抛物线，其性质和特征对于
顶点和轴对称
抛物线的顶点是二次函数的最值点，而抛物线关于
什么是动点问题
动点问题涉及物体、车辆、人员等在空间或时间中的运动，通过建立一元二次方程描绘其变化规律。
1 运动轨迹
描述物体或人员在空间中的路径或轨迹，了解运动方式和特点。
2 运动速度
计算物体或人员在不同时间点的速度，以推断其行进过程。
例一：物体自由落体问题
考虑一个物体自由落体的场景，建立一元二次方程解决高度、时间和速度等相关问题。
下落距离
计算物体自由落体所经历的高度以及特定时间点的下落距离。
速度计算
根据物体自由落体的加速度和时间，计算物体的速度。
达到特定时间
通过一元二次方程，求解物体自由落体到达特定时
抛物线轨迹
分析抛物线运动的特点，找出物体的最高点和最远
物体自由落体问题
计算自由落体物体的高度、速度等参数，并确定其运动轨迹。
两车相遇问题
研究两辆车从不同地点同时出发，相向而行的问题，求出两车相遇的时间和位置。
跳伞问题
求解跳伞过程中的空中时间、速度、高度等数据，为安全跳伞提供参考。
炮弹射击问题
通过炮弹的射程、发射角度等参数，计算击中目标所需的条件与策略。
一元二次方程的应用(动点问题)
一元二次方程的应用(动点问题) PPT大纲
一元二次方程的定义和基本形式
介绍一元二次方程的定义、基本形式和一些基础概念，帮助理解和解决动点问题。
方程的定义
一元二次方程是形如ax²+bx+c=0的方程，其中a、b、 c都是实数，a≠0。
基本形式
一元二次方程的一般形式为ax²+bx+c=0，其中a、b、 c是已知实数，且a≠0。

九年级数学一元二次方程的应用-动点问题

一元二次方程的应用-动点问题1．如图，在△ABC中，∠ABC＝90°，AB＝8cm，BC＝6cm．动点P，Q分别从点A，B同时开始移动，点P的速度为1cm/秒，点Q的速度为2cm/秒，点Q移动到点C后停止，点P也随之停止运动．下列时间瞬间中，能使△PBQ的面积为15cm2的是（）A．2秒钟B．3秒钟C．4秒钟D．5秒钟2．如图，A、B、C、D为矩形的四个顶点，AB＝16cm，AD＝6cm，动点P、Q分别从点A、C同时出发，点P以3cm/s的速度向点B移动，一直到达B为止，点Q以2cm/s的速度向D移动．（1）P、Q两点从出发开始到几秒时，四边形PBCQ的面积为33cm2；（2）P、Q两点从出发开始到几秒时，点P和点Q的距离是10cm．3．等腰△ABC的直角边AB＝BC＝10cm，点P、Q分别从A、C两点同时出发，均以1cm/秒的相同速度做直线运动，已知P沿射线AB运动，Q沿边BC的延长线运动，PQ与直线AC相交于点D．设P点运动时间为t，△PCQ 的面积为S．（1）求出S关于t的函数关系式；＝S△ABC？（2）当点P运动几秒时，S△PCQ（3）作PE⊥AC于点E，当点P、Q运动时，线段DE的长度是否改变？证明你的结论．4．如图所示，△ABC中，∠B＝90°，AB＝6cm，BC＝8cm．（1）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，经过几秒，使△PBQ的面积等于8cm2？（2）点P从点A开始沿AB边向B以1cm/s的速度移动，点Q从B点开始沿BC边向点C以2cm/s的速度移动．如果P，Q分别从A，B同时出发，线段PQ能否将△ABC分成面积相等的两部分？若能，求出运动时间；若不能说明理由．（3）若P点沿射线AB方向从A点出发以1cm/s的速度移动，点Q沿射线CB方向从C点出发以2cm/s的速度移动，P，Q同时出发，问几秒后，△PBQ的面积为1cm2？5．已知：如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动．（1）如果P，Q分别从A，B同时出发，那么几秒后，△PBQ的面积等于6cm2？（2）如果P，Q分别从A，B同时出发，那么几秒后，PQ的长度等于5cm？（3）在（1）中，△PQB的面积能否等于8cm2？说明理由．6．如图所示，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向C点以2cm/s的速度移动．（1）如果点P，Q分别从A，B同时出发，经过几秒钟后，△PBQ的面积等于8cm2；（2）如果点P，Q分别从A，B同时出发，并且点P到B点后又继续在BC边上前进，点Q到点C后又继续在CA边上前进，则经过几秒钟后，△PCQ的面积等于12.6cm2．7．如图，在边长为12cm的等边三角形ABC中，点P从点A开始沿AB边向点B以每秒钟1cm的速度移动，点Q 从点B开始沿BC边向点C以每秒钟2cm的速度移动．若P、Q分别从A、B同时出发，其中任意一点到达目的地后，两点同时停止运动，求：（1）经过6秒后，BP＝cm，BQ＝cm；（2）经过几秒后，△BPQ是直角三角形？（3）经过几秒△BPQ的面积等于cm2？8．如图，长方形ABCD（长方形的对边相等，每个角都是90°），AB＝6cm，AD＝2cm，动点P、Q分别从点A、C同时出发，点P以2厘米/秒的速度向终点B移动，点Q以1厘米/秒的速度向D移动，当有一点到达终点时，另一点也停止运动．设运动的时间为t，问：（1）当t＝1秒时，四边形BCQP面积是多少？（2）当t为何值时，点P和点Q距离是3cm？（3）当t＝以点P、Q、D为顶点的三角形是等腰三角形．（直接写出答案）9．已知：如图，在△ABC中，∠B＝90°，AB＝5cm，BC＝7cm．点P从点A开始沿AB边向点B以1cm/s的速度移动，同时点Q从点B开始沿BC边向点C以2cm/s的速度移动．当一个点到达终点时另一点也随之停止运动，设运动时间为x秒，（1）求几秒后，△PBQ的面积等于6cm2？（2）求几秒后，PQ的长度等于5cm？（3）运动过程中，△PQB的面积能否等于8cm2？说明理由．10．如图，菱形ABCD中，AC，BD交于O，AC＝8m，BD＝6m，动点M从A出发沿AC方向以2m/s匀速直线运动到C，动点N从B出发沿BD方向以1m/s匀速直线运动到D，若M，N同时出发，问出发后几秒钟时，△MON的面积为？11．如图，在△ABC中，∠B＝90°，AB＝6cm，BC＝8cm，若P点沿AB向B以1cm/s的速度移动，点Q从B沿BC向C以2cm/s的速度移动，问几秒后，△PBQ的面积为8cm2？12．如图，在△ABC中，AB＝6cm，BC＝7cm，∠ABC＝30°，点P从A点出发，以1cm/s的速度向B点移动，点Q从B点出发，以2cm/s的速度向C点移动．如果P、Q两点同时出发，经过几秒后△PBQ的面积等于4cm2？同时点Q从点B开始沿BC这向点C以2cm/s的速度移动．当一个点到达终点时另一点也随之停止运动，运动时间为x秒（x＞0）（1）求几秒后，PQ的长度等于5cm；（2）运动过程中，△PQB的面积能否等于8cm2？说明理由．14．已知：如图，△ABC是边长为3cm的等边三角形，动点P、Q同时从A、B两点出发，分别沿AB、BC方向匀速移动，它们的速度都是1cm/s，当点P到达点B时，P、Q两点停止运动，设点P的运动时间t（s），解答下列各问题：（1）经过秒时，求△PBQ的面积；（2）当t为何值时，△PBQ是直角三角形？（3）是否存在某一时刻t，使四边形APQC的面积是△ABC面积的三分之二？如果存在，求出t的值；不存在请说明理由．点Q从点B开始沿BC边向点C以2cm/s的速度移动．（1）如果P，Q分别从A，B同时出发那么几秒后，PQ的长度等于cm？（2）在（1）中，△PQB的面积能否等于7cm2？请说明理由．16．在长方形ABCD中，AB＝5cm，BC＝6cm，点P从点A开始沿边AB向终点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向终点C以2cm/s的速度移动．如果P、Q分别从A、B同时出发，当点Q运动到点C 时，两点停止运动．设运动时间为t秒．（1）填空：BQ＝，PB＝（用含t的代数式表示）；（2）当t为何值时，PQ的长度等于5cm？（3）是否存在t的值，使得五边形APQCD的面积等于26cm2？若存在，请求出此时t的值；若不存在，请说明理由．17．如图，A、B、C、D为矩形的4个顶点，AB＝16cm，BC＝6cm，动点P、Q分别以3cm/s、2cm/s的速度从点A、C同时出发，点Q从点C向点D移动．（1）若点P从点A移动到点B停止，点P、Q分别从点A、C同时出发，问经过2s时P、Q两点之间的距离是多少cm？（2）若点P从点A移动到点B停止，点Q随点P的停止而停止移动，点P、Q分别从点A、C同时出发，问经过多长时间P、Q两点之间的距离是10cm？（3）若点P沿着AB→BC→CD移动，点P、Q分别从点A、C同时出发，点Q从点C移动到点D停止时，点P 随点Q的停止而停止移动，试探求经过多长时间△PBQ的面积为12cm2？18．如图，在△ABC中，∠C＝90°，AB＝10cm，BC＝8cm，点P从点A开始沿射线AC向点C以2cm/s的速度移动，与此同时，点Q从点C开始沿边CB向点B以1cm/s的速度移动．如果P、Q分别从A、C同时出发，运动的时间为ts，当点Q运动到点B时，两点停止运动．（1）当点P在线段AC上运动时，P、C两点之间的距离cm．（用含t的代数式表示）（2）在运动的过程中，是否存在某一时刻，使得△PQC的面积是△ABC面积的．若存在，求t的值；若不存在，说明理由．19．如图，在矩形ABCD中，AB＝10cm，AD＝8cm，点P从点A出发沿AB以2cm/s的速度向点终点B运动，同时点Q从点B出发沿BC以1cm/s的速度向点终点C运动，它们到达终点后停止运动．（1）几秒后，点P、D的距离是点P、Q的距离的2倍；（2）几秒后，△DPQ的面积是24cm2．20．如图所示，A、B、C、D是矩形的四个顶点，AB＝16cm，AD＝6cm，动点P，Q分别从点A，C同时出发，点P以3cm/s的速度向点B移动，一直到达点B为止，点Q以2cm/s的速度向点D移动（1）P，Q两点从出发开始到几秒时，四边形PBCQ的面积为33cm2？（2）P，Q两点从出发开始到几秒时，点P和点Q的距离第一次是10cm？。

一元二次方程的应用题(动点问题)

解：设第一个正方形的边长X 米，
x²+ (14-x)²=100 x²+ (14-x)²=196 x²+ (14-x)²=200
二课本79页第14题
解:设水渠应挖X米宽
92m 60m
水渠的面积=耕地的民面积-6个矩形的面积
92x+60x+60x=92╳60-6╳885
92m
60-2x 60m
92-2x
. 90-30X
50
东
解得 X1= 56 (不符合题意)
. X2=226
B 答:最早2时能侦察到
把长为36厘米的铁丝剪成相等的两段,用一段弯成一个矩形,另一段弯成一个有一.个有一条边为5厘米的等腰三角形,如果举矩形面积与等腰三角形面积相等,求矩形的边长 .
5
5
3
6.5
6.5
6
44 设:长方形的长X为厘米,则宽为(9-X)厘米. 5
用一元二次方程的数学模型解具体问题
解应用题的步骤: 1弄清题意,设适当的未知数,
注意写上单位. 2寻找已知量,未知量的相等关系,
列出所需要的代数式. 3列出方程,解方程. 4检验方程的根是否符合题意.
是否满足方程.
例1课本65页随堂练习第1题
3 7
X
解:设相遇时甲走X步
10
因为乙速是甲速的七分之三.
.Q 向点C以2cm/s的移动,点 Q从点B出发向点C以 1cm/s的速度移动.若P、 Q分别同时从A、B出发，几秒后四边形APQB是 C ΔABC面积的三分之二？
B
设X秒后四边形APQB是
1x
10
Q ΔABC面积的三分之二.
则AP=2X ,BQ=1X

列一元二次方程解应用题的四种类型(利润、增长率、面积、动点问题)

列一元二次方程解应用题的四种类型（利润、增长率、面积、动点问题）一、商品销售问题售价—进价=利润单价×销售量=销售额一件商品的利润×销售量=总利润某商场销售一批名牌衬衫，平均每天可售出20件，每件盈利40元．为了扩大销售，增加盈利，商场决定采取适当的降价措施．经调查发现，如果每件衬衫每降价1元，商场平均每天可多售出2件．如果商场每天要盈利1200元，每件衬衫应降价多少元？分析：设每件衬衫应该降价x元，则每件衬衫的盈利元；商场每天可以多销售件，则商场降价后每天售出的数量为件。

根据：利润=单件的利润╳数量，我们可以列出方程：解这个方程得：答：；例1. 某花圃用花盆培育某种花苗，经过实验发现每盆的盈利与每盆的株数构成一定的关系.每盆植入3株时，平均单株盈利3圆；以同样的栽培条件，若每盆每增加1株，平均单株盈利就减少0.5元.要使每盆的盈利达到10元，每盆应该植多少株？练习：1、某种服装，平均每天可以销售20件，每件盈利44元，在每件降价幅度不超过10元的情况下，若每件降价1元，则每天可多售出5件，如果每天要盈利1600元，每件应降价多少元？2、某化工材料经售公司购进了一种化工原料,进货价格为每千克30元.物价部门规定其销售单价不得高于每千克70元,也不得低于30元.市场调查发现：单价每千克70元时日均销售60kg；单价每千克降低一元,日均多售2kg。

在销售过程中,每天还要支出其他费用500元（天数不足一天时,按一天计算）.如果日均获利1950元,求销售单价3、某商店购进一种商品，进价30元．试销中发现这种商品每天的销售量P(件)与每件的销售价X(元)满足关系：P=100-2X销售量P，若商店每天销售这种商品要获得200元的利润，那么每件商品的售价应定为多少元？每天要售出这种商品多少件？4、某玩具厂计划生产一种玩具熊猫，每日最高产量为４０只，且每日产出的产品全部售出，已知生产ⅹ只熊猫的成本为Ｒ（元），售价每只为Ｐ（元），且ＲＰ与x的关系式分别为R=500+30X，P=170—2X。

专题八：一元二次方程应用类型中的动点问题(有答案)

专题八：一元二次方程应用类型中的动点问题（有答案）➢知识指引所谓“动点型问题”是指题设图形中存在一个或多个动点，它们在线段、射线或弧线上运动的一类问题．解决这类问题的关键是动中求静，灵活运用有关数学知识解决问题．解题时要注意动点的起始位置和终止位置、运动方向，有时还要关注动点的运动速度，注意在运动过程中寻找等量关系．动点问题思路剖析问题1：动点问题的处理框架是什么？答：读题标注，整合信息（即明确所研究的背景图形）问题2：分析运动过程需要关注四要素是什么？答：①起点、终点、速度：标注到图形中，以示说明②时间范围根据路程、时间和速度的公式s=vt，已知动点的速度，结合基本图形中线段长的研究，可以确定动点的运动时间③状态转折状态转折即点的运协发生变化的时刻，常体现在动点的运动方向，运动速度发生了改变④目标或结论导向根据题意作出图形，有序操作（分段作图并求解）问题3：在分析几何特征，表达时，常见表达线段长的方式有哪些？答：①路程即线段长，可根据s=vt直接进行表达已走路程或未走路程②根据研究几何特征的需求进行表达，即要利用动点的运动情况，又要结合背景图形信息➢知识点睛由点的运动产生的几何问题称为动点问题．动点问题的解决方法：1.研究背景图形并标注；；2.分析运动过程，并适时分段；3.表达线段长，建等式和方程．➢典型例题【例1】如图，在△ABC中，∠B=90°，AB=9，BC=12，点P从点A开始沿边AB向点B以1cm/s的速度移动，与此同时，点Q从点B开始沿边BC向点C以2cm/s的速度移动．如果P．Q分别从A．B同时出发，当点Q运动到点C时，两点停止运动，问：（1）填空：BQ= ，PB= （用含t的代数式表示）（2）经过几秒，PQ的长为6√2cm？（3）经过几秒，△PBQ的面积等于8cm2？【解答】（1）根据题意得：BQ=2t，PB=9-t．故答案为：2t；9-t．（2）根据题意得：（9-t）2+（2t）2=72，，t2=3，解得：t1=35秒或3秒，PQ的长为6√2cm．∴经过35×（9-t）×2t=8，（3）根据题意得：12解得：t1=8，t2=1．∵0≤t≤6，∴t=1．答：经过1秒，△PBQ的面积等于8cm2．【例2】如图，在四边形ABCD中，AD∥BC ，∠C=90°， BC=16，DC=12 ，AD=21 ，动点P从点D出发，沿线段 DA的方向以每秒2个单位长的速度运动；动点Q从点 C出发，在线段 CB 上以每秒1个单位长的速度向点B运动；点P，Q 分别从点D，C同时出发，当点P运动到点 A 时，点Q随之停止运动，设运动的时间为t秒）.（1）当t=2时，求△BPQ的面积；（2）若四边形ABQP为平行四边形，求运动时间t.（3）当t为何值时，以 B，P，Q为顶点的三角形是等腰三角形？备用图【解答】（1）如图，过点P 作PM ⊥BC 于M ，则四边形PDCM 为矩形，∴PM=DC=12．∵QB=16－t ，当t=2时，则BQ=14，则S=12QB ⋅PM =12×14×12=84；（2）当四边形ABQP 是平行四边形时，AP=BQ,即21－2t=16－t ．解得t=5． ∴当t=5时，四边形ABQP 是平行四边形.（3）由图可知，CM=PD=2t ，CQ=t ，若以B 、P 、Q 为顶点的三角形是等腰三角形，可以分为以下三种情况：①若PQ=BQ ，在Rt △PMQ 中，PQ 2=t 2+122，由PQ 2= BQ 2，得t 2+ 122= (16-t)2 解得t=72；②若BP=BQ ，在Rt △PMB 中，PB 2=(16-2t)2+122，由PB 2= BQ 2得(16-2t)2+ 122= (16-t)2，即3t 2+-32t+144= 0．此时，Δ= (-32)2 －4×3×144= －704＜0, 所以此方程无解，所以PB ≠BQ ；③若PB=PA ，由PB 2= PQ 2,得t 2+ 122= (16-2t)2 + 122 , 解得t 1=163,t 2=16，（不合题意，舍去）；综上所述，当t=72或163时，以B ，P ，Q 为顶点的三角形是等腰三角形.➢ 跟踪训练1．如图，在△ABC 中，AC=50cm ，BC=40 cm ，∠C =90°，点P 从点A 开始沿AC 边向点C 以每秒2 cm 的速度匀速移动，同时另一点Q 由C 点开始以每秒3 cm 的速度沿着射线CB 匀速移动，当△PCQ 的面积等于300 cm 2运动时间为（）．A. 5秒B. 20秒C. 5秒或20秒D. 不确定【解答】由题意，得AP=2t ，CQ=3t ，∴PC=50-2t ，∴12•PC•CQ=300，∴12•（50-2t ）•3t=300，解得t=20或5，∴t=20s 或5s 时，△PCQ 的面积为300m 2．故选：C ．2．如图，在△ABC 中，∠B=90°，AB=6cm ，BC=8cm ．点P 从点A 开始沿AB 边向点B 以1cm/s 的速度移动，点Q 从点B 开始沿BC 边向点C 以2cm/s 的速度移动．若P 、Q 两点同时出发，当点P 运动到点B 时，P ，Q 两点同时停止运动，当三角形PQB 的面积是三角形ABC 的面积的三分之一时，所需时间为（）A ．4 sB ．2 sC ．2或4sD ．3或4s【解答】设经过x 秒，三角形PQB 的面积是三角形ABC 的面积的三分之一．∵P 、Q 移动t 秒时，AP=t ，BQ=2t ，则PB=AB-AP=6-t ，∴S △P B Q =13，由S △A B C =12AB•BC=12×6×8=24，当S △P B Q =13S △A B C 时，则12•2t（6-t ）=13×24，整理，得t 2-6t+8=0，解得t 1=2，t 2=4，即当t=2或4时，△PBQ 的面积等于△ABC 的面积的三分之一．故选：C ．3．如图，在Rt △ABC 中，∠B ＝90°，AB ＝BC ＝12 cm ，点D 从点A 开始沿边AB 以2 cm/s 的速度向点B 移动，移动过程中始终保持四边形DFCE (点E ，F 分别在AC ，BC 上)为平行四边形，则出发________s 时，四边形DFCE 的面积为20 cm 2.【解答】设点D从点A出发x s时，四边形DFCE的面积为20 cm2.由题意，得12×12×12−4x22−(12−2x)22＝20，解得x1＝1，x2＝5，故答案为：1或5.4.某校为培育青少年科技创新能力，举办了动漫制作活动，小明设计了点做圆周运动的一个雏形，如图所示，甲、乙两点分别从直径的两端点A、B，以顺时针、逆时针的方向同时沿圆周运动，甲运动的路程l（cm）与时间t（s）满足关系l=t2+3t（t≥0），乙以8cm/s的速度匀速运动，半圆的长度为42cm．（1）甲运动4s后的路程是多少？（2）甲、乙从开始运动到第一次相遇时，它们运动了多少时间？（3）甲、乙从开始运动到第二次相遇时，它们运动了多少时间？【解答】（1）当t=4s 时，l=t2+3t=16+12=28（cm）．答：甲运动4s后的路程是28cm．（2）由图可知，甲乙第一次相遇时走过的路程为半圆21cm，甲走过的路程为t2+3t，乙走过的路程为4t，则t2+3t+8t=42，解得：t1=3，t2=-14（不合题意，舍去）．答：甲、乙从开始运动到第一次相遇时，它们运动了3s．（3）由图可知，甲乙第一次相遇时走过的路程为三个半圆3×42=126cm，则t2+3t+8t=126，解得：t=7或t=-18（不合题意，舍去）．答：甲、乙从开始运动到第二次相遇时，它们运动了7s ．5.如图，在矩形ABCD 中，AB=6cm ，BC=12cm ，点P 从点A 开始以1cm/s 的速度沿AB 边向B 移动，点Q 从点B 开始以2cm/s 的速度沿BC 边向点C 移动．如果P 、Q 分别从A 、B 同时出发，当点Q 运动到点C 时，P 、Q 两点同时停止运动．（1）是否存在某一时刻使得△PQD 的面积等于8cm 2？若存在，求出运动的时间；若不存在，说明理由．（2）几秒后，△PQD 是以DP 为斜边的直角三角形．【解答】（1）不存在，理由如下：设出发秒x 时△DPQ 的面积等于8cm 2． ∵S 矩形A B C D -S △A P D -S △B P Q -S △C D Q =S △D P Q ，∴6×12-12×12×x -12×（6-x ）•2x -12（12-2x ）×6=8，∴x 2-6x+28=0，∵∆=b 2-4ac=36-4×28=-76＜0，∴原方程无实数根，即不存在某一时刻使得△PQD 的面积等于8cm 2．（2）∵∠A=∠B=∠C=90°，∴PD 2=t 2+122，PQ 2=（6-t ）2+（2t ）2，QD 2=（12-2t ）2+62， ∵△PQD 是以DP 为斜边的直角三角形，∴PD 2=PQ 2+QD 2，即t 2+122=（6-t ）2+（2t ）2+（12-2t ）2+62，整理得2t 2-15t+18=0，解之得t 1=6，t 2=32，即当t 为32秒或6秒时，△PQD 是以PD 为斜边的直角三角形．6.如图，在矩形ABCD 中，AB=6cm ，BC=12cm ，点P 从点B 出发沿线段BC 、CD 以2cm/s 的速度向终点D 运动；同时，点Q 从点C 出发沿线段CD 、DA 以1cm/s 的速度向终点A 运动（P 、Q 两点中，只要有一点到达终点，则另一点运动立即停止）．（1）运动停止后，哪一点先到终点？另一点离终点还有多远？（2）在运动过程中，△APQ 的面积能否等于22cm 2？若能，需运动多长时间？若不能，请说明理由【解答】（1）点P 从开始到运动停止用的时间为：（12+6）÷2=9s，点Q 从开始到运动停止用的时间为：（6+12）÷1=18s， ∵9＜18，只要有一点到达终点，则另一点运动立即停止，∴点P 先到终点，此时点Q 离终点的距离是：（6+12）-1×9=9cm，答：点P 先到终点，此时点Q 离终点的距离是9cm ；（2）在运动过程中，△APQ 的面积能等于22cm 2，当P 从点B 运动到点C 的过程中，设点P 运动时间为as ，∵△APQ 的面积能否等于22cm 2， ∴12×6-2a×62−(12−2a)×a2−(6−a)×122=22，解得，此方程无解；当点P 从C 到D 的过程中，设点P 运动的时间为（b+6）s ，∵△APQ 的面积能否等于22cm 2， ∴12×6-(6+2b)×122−b(6−2b)2=22，解得，b 1=1，b 2=14（舍去），即需运动6+1=7s ，△APQ 的面积能等于22cm 2．7．如图，在矩形ABCD 中，AB=5cm ，BC=6cm ，点P 从点A 开始沿边AB 向终点B 以1cm/s 的速度移动，与此同时，点Q 从点B 开始沿边BC 向终点C 以2cm/s 的速度移动．如果P ，Q 分别从A ，B 同时出发，当点Q 运动到点C 时，两点停止运动，设运动时间为t 秒．（1）填空：BQ=__________，PB=_________；（用含t 的代数式表示）（2）当t 为何值时，PQ 的长度等于5cm ？（3）是否存在t 的值，使得五边形APQCD 的面积等于26cm 2？若存在，请求出此时t 的值；若不存在，请说明理由．【解答】（1）∵P从点A开始沿边AB向终点B以1cm/s的速度移动，∴AP=tcm．∵AB=5cm，∴PB=（5-t）cm．∵点Q从点B开始沿边BC向终点C以2cm/s的速度移动，∴BQ=2tcm；（2）由题意，得(5-t)2+(2t)2=52．解得t1=0（不合题意，舍去），t2=2．所以当t=2秒时，PQ的长度等于5cm．（3）存在，t=1秒时，能够使得五边形APQCD的面积等于26cm2．由矩形ABCD的面积是5×6=30cm2，若五边形APQCD的面积等于26cm2，则△PBG的面积为30－26=4 cm2，=4．解得t1=4（不合题意，舍去），t2=1．即（5－t）×2t×12即当t=1秒时，五边形APQCD的面积等于26cm2．8. 如图，在Rt△ABC中，∠ACB＝90°，AC＝BC=6，动点P从点A出发，在线段AC上以每秒1个单位长度的速度向点C作匀速运动，到达点C停止运动．点Q在射线PC上，且PQ ＝2AP，以线段PQ为边向上作正方形PQNM．在运动过程中，设运动时间为t秒，(1)当N点落在BC上时，t= 秒;(2)若设正方形PQNM与△ABC重叠部分的面积为8，求t的值．备用图【解答】(1)当N 落在BC 上时，Q 点在C 处，此时CP+AP=2t+t=6,∴t=2,.故填：2（2）∵AP ＝t ，PQ ＝2AP ，∴PQ ＝2t ，①如图1，当0≤t ≤2时，S ＝（2t ）2﹣12t 2＝72t 2＝8，解得：t 1＝47√7，t 2＝﹣47√7（不合题意，舍去），②如图2，当2≤t ≤3时，S ＝12×6×6﹣12t 2﹣12（6﹣2t ）2＝12t ﹣25t 2＝8，解得：t 1＝4（不合题意，舍去），t 2＝45（不合题意，舍去）， ③如图3，当3≤t ≤6时，S ＝12×6×6﹣12t 2＝8，解得：t 1＝2√5，t 2＝﹣2√5（不合题意，舍去），综上，t 的值为47√7或2√5时，重叠面积为8．9.等腰△ABC 的直角边AB=BC=10cm ，点P 、Q 分别从A 、C 两点同时出发，均以1cm/秒的相同速度作直线运动，已知P 沿射线AB 运动，Q 沿边BC 的延长线运动，PQ 与直线AC 相交于点D ．设P 点运动时间为t ，△PCQ 的面积为S ．（1）当点P 运动几秒时，S △PCQ =S △ABC ？（2）作PE ⊥AC 于点E ，当点P 、Q 运动时，线段DE 的长度是否改变？证明你的结论．【解答】（1）由S △ABC =12AB •BC ＝12×10×10=50.当t ＜10秒时，P 在线段AB 上，此时CQ=t ，PB=10-t. ∴S △PCQ ＝12×t×(10−t)＝12 (10t −t 2) ＝50.整理得t 2-10t+100=0无解.当t ＞10秒时，P 在线段AB 得延长线上，此时CQ=t ，PB=t-10. ∴S △PCQ ＝12×t×(t −10)＝12(t 2−10t) ＝50.整理得t 2-10t-100=0解得t=5±5√5（舍去负值）. ∴当点P 运动5+5√5秒时，S △PCQ =S △ABC .（2）当点P,Q 运动时，线段DE 的长度不会改变．证明：过Q 作QM ⊥AC ，交直线AC 于点M 易证△APE ≌△QCM ，∴AE=PE=CM=QM=√22t ，∴四边形PEQM 是平行四边形，且DE 是对角线EM 的一半．又∵EM=AC=10√2，∴DE=5√2.∴当点P 、Q 运动时，线段DE 的长度不会改变．同理，当点P 在点B 右侧时，DE=5√2。

一元二次方程与动点问题

一元二次方程与动点问题某些动点问题,常可以建立以时间为未知数的一元二次方程模型.通过求解模型,往往会得到两个实数解,这时要根据实际问题作出取舍.既然是动点问题,结果就有多种可能,因此,有时方程模型的两个实数解都是符合题意的,这一点要注意.解决动点问题,我们必须先弄清楚动点是谁?是单动点还是双动点?运动的路径怎样?方向和速度怎样?运动停止的时间怎样?设运动时间为t ,会用t 表示出各个相关的量,找到等量关系并列出关于t 的方程模型.一般情况下,运动路径由几段构成,就需要分几种情况进行讨论,最后做出总结.例1. 如图,在Rt △ABC 中,︒=∠90ACB ,10=AB cm,8=BC cm,点P 从点A 开始沿射线AC 向点C 以2 cm/s 的速度移动,点Q 从点C 开始沿边CB 向点B 以1 cm/s 的速度移动.如果点P 、Q 分别从点A 、C 同时出发,运动的时间为t s,当点Q 运动到点B 时,两点停止运动.（1）当点P 在线段AC 上运动时,P 、C 两点之间的距离为_________cm;（用含t 的代数式表示）（2）在运动的过程中,是否存在某一时刻,使得△PQC 的面积是△ABC 的面积的61若存在,求出t 的值;若不存在,说明理由.分析:（1）由题意可知,t AP 2=cm ,t CQ =cm .由勾股定理求出6=AC cm .所以()t PC 26-=cm ,即P 、C 两点之间的距离为()t 26-cm ;（2）用含t 的代数式表示△PQC 的面积,由ABC PQC S S ∆∆=61建立关于t 的一元二次方程,由方程是否有实数根说明t 的存在性.由于点P 沿射线AC 运动,且运动停止时间为8s,所以需要分两种情况进行讨论:点P 在线段AC 上运动（t <0≤3）和点P 在线段AC 的延长线上运动（t <3≤8）.解:（1）()t 26-;（2）由题意可知:t CQ =cm.当t <0≤3时,()t PC 26-=cm.∴()t t t t PC CQ S PQC 32621212+-=-=⋅=∆（cm 2）由486216161=⨯⨯⨯==∆∆ABC PQC S S 可得: 432=+-t t 即0432=+-t t∵()074432<-=⨯--=∆ ∴该方程无实数根;当t <3≤8时,()t PC 26-=cm.∴()46221=-t t ,即0432=--t t 解之得:1,421-==t t （不符合题意,舍去）综上所述,当4=t 时,△PQC 的面积是△ABC 的面积的61. 例2. 如图,在矩形ABCD 中,5=AB cm,6=BC cm,点P 从点A 开始沿AB 向终点B 以1 cm/s 的速度移动,与此同时,点Q 从点B 开始沿BC 向终点C 以2 cm/s 的速度移动,如果点P 、Q 分别从点A 、B 同时出发,当点Q 运动到点C 时,两点停止运动.设运动的时间为t s.（1）填空:=BQ _________,=PB _________;（用含t 的代数式表示）（2）当t 为何值时,PQ 的长度等于102cm? （3）是否存在t 的值,使得五边形APQCD 的面积等于26 cm 2若存在,请求出此时t 的值;若不存在,请说明理由.解:（1）t 2cm,()t -5cm;（2）在Rt △BPQ 中,由勾股定理得:222PQ PB BQ =+∴()()()22210252=-+t t 解之得:3=t∴当3=t 时,102=PQ cm;（3）3065=⨯=⋅=BC AB S ABCD 矩形 cm 2若五边形APQCD 的面积等于26 cm 2,则4=∆BPQ S cm 2 ∴()45221=-⨯t t ∴4,121==t t （不符合题意,舍去）∴存在1=t ,使得五边形APQCD 的面积等于26 cm 2.例3. 如图,在△ABC 中,︒=∠90B ,6=AB cm,12=BC cm,点P 从点A 开始沿AB 边向点B 以1 cm/s 的速度移动,点Q 从点B 开始沿BC 边向点C 以2 cm/s 的速度移动.（1）如果P 、Q 分别从A 、B 同时出发,几秒钟后△PBQ 的面积等于8 cm 2（2）在（1）中,△PBQ 的面积能否等于10 cm 2说明理由. CA BQP解:（1）设x 秒后△PBQ 的面积等于8 cm 2.由题意可知:x AP =cm,x BQ 2=cm∴()x BP -=6cm∵()86221=-⨯=∆x x S PBQ ∴0862=+-x x解之得:4,221==x x∴2s 或4s 后△PBQ 的面积等于8 cm 2;（2）由题意可得:()106221=-⨯x x ∴01062=+-x x∵()0410462<-=⨯--=∆∴该方程无实数根∴△PBQ 的面积不能等于10 cm 2.。