南昌大学2015_2016第二学期高等数学期末考试试卷A
南昌大学 2008~2009学年第二学期期末考试试卷A

Sin0 t
三、 是非题(每题 1 分,共 10 分)
得分 评阅人
1、信息的载体就是信号。
(
)
2、周期信号可用傅里叶级数展开成正弦和余弦分量两部分,也可能只有正弦或余弦 分量。 ( )
3、当输入信号 x(t ) 一定时,系统的输出 y(t ) 将完全取决于传递函数 H ( s ) ,而与系统 的物理模型无关。 ( ) ) ) ) ) ) ) )
,理想滤波器的 =
。 的关系,
的关系。 的傅氏变换,它反映信号的 的平方。 域
第 1 页 共 6页
二、 选择题(每题 2 分,共 20 分)
得分 评阅人
1、若给时间常数为 的一阶装置输入频率 1/ 的正弦信号,则输出与输入相位差 为 A.-45 度。 B.-90 C.-180 。 A 有波形相位失真 A、B 都没有波形相位失真 D.90
引起电阻的变化。 C. 弹性模量的变化 D. 泊松比的变化
接法的灵敏度最高。 B. 半桥双臂 C. 全桥 而成的。
6、在一定条件下,RC 带通滤波器实际上是低通滤波器与高通滤波器 A. 串联 B. 并联 C. 串并联 D. 叠加
7、如果一信号的自相关函数 Rx( ) 呈一定的周期性不衰减,则说明该信号 A. 均值不为零 B. 含周期分量 C. 是各态历经的 。
第 6 页 共 6页
和 ,后者具有
两类,其频谱不同之处 。
。
、 、
和
表征。 之大小。
4、信号频域描述反映信号的频率组成及其 5、常用的应变片有 灵敏度比后一种 6、滤波器因数定义为 = 7、在相关分析中,自相关可以分析 互相关可以分析 8、自功率谱 S x ( f ) 是 结构,它反映的是 与 。
江西省南昌二中2015-2016学年高一下学期期末数学试卷 含解析

2015—2016学年江西省南昌二中高一(下)期末数学试卷一、选择题1.对于任意实数a、b、c、d,下列命题中,真命题为()①若a>b,c≠0,则ac>bc;②若a>b,则ac2>bc2;③若ac2>bc2,则a>b;④若a>b,则<.A.①B.②C.③D.④2.从编号为001,002,…,500的500个产品中用系统抽样的方法抽取一个样本,已知样本中编号最小的两个编号分别为007,032,则样本中最大的编号应该为()A.480 B.481 C.482 D.4833.根据下列条件解三角形:①∠B=30°,a=14,b=7;②∠B=60°,a=10,b=9.那么,下面判断正确的是()A.①只有一解,②也只有一解 B.①有两解,②也有两解C.①有两解,②只有一解D.①只有一解,②有两解4.直线xsinα+y+2=0的倾斜角的取值范围是()A.[0,π) B.[0,]∪[,π)C.[0,]D.[0,]∪(,π)5.数列的前n项和为()A. B. C. D.6.如图所示,程序框图的输出结果是s=,那么判断框中应填入的关于n的判断条件是()A.n≤8? B.n<8?C.n≤10?D.n<10?7.现安排甲、乙、丙、丁、戊5名同学参加上海世博会志愿者服务活动,每人从事翻译、导游、礼仪、司机四项工作之一,每项工作至少有一人参加.甲、乙不会开车但能从事其他三项工作,丙丁戊都能胜任四项工作,则不同安排方案的种数是()A.152 B.126 C.90 D.548.关于x的不等式x2+ax﹣2<0在区间[1,4]上有解,则实数a的取值范围为()A.(﹣∞,1) B.(﹣∞,1]C.(1,+∞)D.[1,+∞)9.样本(x1,x2,…,x n)的平均数为,样本(y1,y2,…,y m)的平均数为(≠).若样本(x1,x2,…,x n,y1,y2,…,y m)的平均数=a+b,并且>m2+m恒成立,则实数m的取值范围是()A.(﹣∞,﹣2)∪[4,+∞) B.(﹣∞,﹣4]∪[2,+∞) C.(﹣2,4)D.(﹣4,2)10.已知A、B两地之间有6条网线并联,这6条网线能通过的信息量分别为1,1,2,2,3,3.现从中任取3条网线,设可通过的信息量为X,当X≥6时,可保证线路信息畅通(通过的信息量X为三条网线上信息量之和),则线路信息畅通的概率为()A.B.C.D.11.已知x,y满足约束条件,若z=ax+y的最大值为a+1,则a的取值范围为()A.(﹣1,1)B.[﹣1,1] C.[﹣1,1) D.(﹣1,1]12.从集合{1,2,3,4,5,6,7,8,9,10}中任取三个不同的元素作为直线l:ax+by+c=0中a,b,c的值.若直线l的倾斜角小于135°,且l在x轴上的截距小于﹣1,那么不同的直线l有()A.109条B.110条C.111条D.120条二、填空题13.已知a,b均为正数,且直线ax+by﹣6=0与直线2x+(b﹣3)y+5=0互相平行,则2a+3b的最小值是.14.已知f(x)=﹣sinxcosx﹣sin2x,则f(x)在[﹣,]上的最大值为.15.设正实数x,y,z满足x2﹣xy+4y2﹣z=0.则当取得最小值时,x+4y﹣z的最大值为.16.已知数列{a n}满足a n=n•k n(n∈N*,0<k<1),给出下列命题:①当k=时,数列{a n}为递减数列②当<k<1时,数列{a n}不一定有最大项③当0<k<时,数列{a n}为递减数列④当为正整数时,数列{a n}必有两项相等的最大项请写出正确的命题的序号.三、解答题17.已知a、b、c是△ABC三边长,关于x的方程的两根之差的平方等于4,△ABC的面积.(I)求∠C;(II)求a、b的值.18.已知直线l:kx﹣y+1+2k=0(k∈R).(1)若直线l不经过第四象限,求k的取值范围;(2)若直线l交x轴负半轴于点A,交y轴正半轴于点B,O为坐标原点,设△AOB的面积为S,求S的最小值及此时直线l的方程.19.某工厂有工人500名,记35岁以上(含35岁)的为A类工人,不足35岁的为B类工人,为调查该厂工人的个人文化素质状况,现用分层抽样的方法从A、B两类工人中分别抽取了40人、60人进行测试.(I)求该工厂A、B两类工人各有多少人?(Ⅱ)经过测试,得到以下三个数据图表:(茎、叶分别是十位和个位上的数字)(如图)表:100名参加测试工人成绩频率分布表组号分组频数频率1 [55,60) 5 0.052 [60,65)20 0.203 [65,70)4 [70,75)35 0。
高等数学下期末试题(七套附答案)

x1 y 2 z3
x2
1、 求过直线 L1 : 1
0
1 且平行于直线 L 2 : 2
z
z
2、 已知 z f ( xy2 , x2 y) ,求 x , y
D
3、 设
{( x, y) x2
y2
4} ,利用极坐标求
x2dxdy
D
C. (ax b) cex
y1 z 1 1 的平面方程
1 / 22
4、 求函数 f (x, y) e2x ( x y2 2 y) 的极值
1 1x
x0
1 1 ex 1
2
x0
f (x
求0
x 2 及 y2 x 所围图形的面积;
1)dx (6 )
( 2)求所围图形绕 x 轴旋转一周所得的体积。 (6 )
高等数学(下)模拟试卷四
一. 填空题 (每空 3 分,共 15 分)
1 y
1 x2
1、 函数
x
的定义域为
.
e axdx, a 0
2、 0=Fra bibliotek.z
3 .已知 z
e xy ,则
(1,0 )
x
。
4 .设 L 为 x2
y 2 1 上点 1,0 到
1,0 的上半弧段,则
2ds
L
。
e
ln x
dx f ( x, y)dy
5 .交换积分顺序 1
0
。
( 1) n
6 . 级数 n 1 n 是绝对收敛还是条件收敛?
。
7 .微分方程 y sin x 的通解为
。
二.选择题 (每空 3 分,共 15 分)
x
2
d 2y
1、已知 y 1 t ,求 dx2
南昌大学期末考试试题二
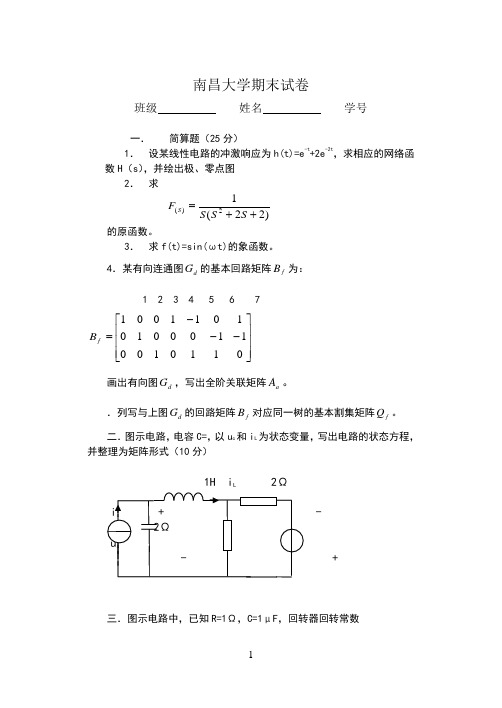
南昌大学期末试卷班级 姓名 学号一. 简算题(25分)1. 设某线性电路的冲激响应为h(t)=e -t +2e -2t,求相应的网络函数H (s ),并绘出极、零点图2. 求的原函数。
3. 求f(t)=sin(ωt)的象函数。
4.某有向连通图d G 的基本回路矩阵f B 为: 1 2 3 4 5 6 7⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡---=011010011000101011001f B画出有向图d G ,写出全阶关联矩阵a A 。
.列写与上图d G 的回路矩阵f B 对应同一树的基本割集矩阵f Q 。
二.图示电路,电容C=,以u c 和i L 为状态变量,写出电路的状态方程,并整理为矩阵形式(10分)1H i L 2Ω三.图示电路中,已知R=1Ω,C=1μF ,回转器回转常数)22(12)(++=S S S F Sr=1000Ω,求1—1端等效元件参数。
(10分)四.图示电路中,直流电压源U s =5V ,R=2Ω,非线性电阻的伏安关系为:现已知当0)(=t u s 时,回路中的电流为1A 。
如果电压源u s (t)=cos(ωt )(V),用小信号分析法求电流i(t)。
(10分)R 五.电路如图所示,已知ω=1000rad/s, C=1μF, R=1Ω, L 1=1H ,H L 312=, 求:(1) u s( t)的有效值;(2) 电阻电压)(t u R ;(3) 电源发出的平均功率(15分)1- u R (t) +32i i u +=V)t 2cos(216)t cos(21512u )t (s ω+ω+=六.图示电路,已知L=, C=1F, R=Ω,电源电压U S1=1V ,U S2=5V ,设开关S 在位置1时电路已达稳态,t=0时将开关S 合到位置2。
(1)做出运算电路;(2)用运算法求电容电压U C (S )。
(15分)七.求图示二端口网络的Y 参数,并做出π形等效电路。
(15分)+1U22I。
高等数学(A)下期末试卷及答案

南京邮电大学2010/2011学年第二学期《高等数学A 》(下)期末试卷A 答案及评分标准 一、选择题(本大题分5小题,每题3分,共15分)1、交换二次积分⎰⎰x e dy y x f dx ln 01),(的积分次序为(c )(A ) ⎰⎰x e dx y x f dy ln 01),( (B )⎰⎰1),(dx y x f dy e ey(C )⎰⎰e e ydx y x f dy ),(10(D )⎰⎰ex dx y x f dy 1ln 0),(2、锥面22y x z +=在柱面x y x 222≤+内的那部分面积为 (D )(A )⎰⎰-θππρρθcos 2022d d (B )⎰⎰-θππρρθcos 20222d d(C )⎰⎰-θππρρθcos 202222d d (D )⎰⎰-θππρρθcos 20222d d3、若级数∑∞=-1)2(n nn x a 在2-=x 处收敛,则级数∑∞=--11)2(n n n x na 在5=x (B ) (A ) 条件收敛 (B ) 绝对收敛 (C ) 发散(D ) 收敛性不确定 4、下列级数中收敛的级数为 (A )(A ) ∑∞=-1)13(n nn n (B )∑∞=+121n n n (C ) ∑∞=+111sin n n (D )∑∞=13!n n n 5、若函数)()2()(2222x axy y i xy y x z f -+++-=在复平面上处处解析,则实常数a 的值 为 (c )(A ) 0 (B ) 1 (C ) 2 (D ) -2二、填空题(本大题分5小题,每题4分,共20分)1、曲面122-+=y x z 在点)4,1,2(处的切平面方程为624=-+z y x2、已知)0(:222>=+a a y x L ,则=-+⎰Lds xy y x )]sin([22 32 a π 3、Ω是由曲面22y x z +=及平面)0(>=R R z 所围成的闭区域,在柱面坐标下化三重积分⎰⎰⎰+Ωdxdydz y x f )(22为三次积分为⎰⎰⎰RR dz f d d ρπρρρθ)(20204、函数x x f =)()0(π≤≤x 展开成以2π为周期的正弦级数为nx nx n n sin )1(211+∞=-=∑,收敛区间为π<≤x 05、=+-)1(i Ln2,1,0),243(2ln ±±=++k k i ππ=-]0,[Re 2zz e s z1-三、(本题8分)设),()(22xy y xg y x f z ++=,其中函数)(t f 二阶可导,),(v u g 具有二阶连续偏导数,求y x z x z ∂∂∂∂∂2,解:2112yg g y f x x z ++'=∂∂ … 3分=∂∂∂yx z2f xy ''4113122221g y x g y xyg g --++ 5分四、(本题8分)在已知的椭球面134222=++z y x 内一切内接的长方体(各边分别平行坐标轴)中,求最大的内接长方体体积。
2015-2016-2大学数学A2期末试题--标准答案

-----4分
注意到 的方程为 ,取下侧,其中 为单位圆面,因此有从而 --- Nhomakorabea---9分
5. 解:对函数 偶延拓,因此
-------2分
----6分
由此得到函数 的余弦级数为
-----9分
四、计算题 (本题满分 12分)
解:考虑幂级数
,所以幂级数在 收敛---------3分
令和函数为 ,即
两边积分 --------6分
3. 解:记 , ,只要 ,便有
,
在区域 内 ,
所以 在区域 内是某个二元函数 的全微分。-----4分
在区域 内取定点 和动点 ,由 知曲线积分 在 内与路径无关,该积分只依赖于点 ,取从 到 再到 的折线作为积分路径,得
----------9分
4. 解:记平面 被 所截得的圆面的下侧为 ,则 构成一个外法线方向的闭曲面,另记 所包围的立体为 ,由Gauss公式得
本科课程考试试题参考答案及评分标准
开课单位:数学学院 学生所在学院: (2015 ~2016年第2学期)
课程编号
0910411012
学分/总学时
6/96
课程名称
高等数学A2
课程类别
█公共课 □专业课
专业/年级
专业 2015 年级
修读方式
█必修 □选修
出题教师
大学数学部
是否主干基础课
是
考试方式
█闭卷 □开卷
一、填空题
(1)2
(2)
(3)
(4)
(6)D
(5)
二、选择题
(1)C
(2)B
(3)C
(4)A
南昌大学20152016学年第2学期期末考试安排表

#大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2) #大学英语(2)
日期
时间
2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50 2016-06-22 上午07:50-09:50
学院
资环 资环;艺术
经管 经管 信工 经管 信工 生命 化学 生命 食品 食品 人文 信工 信工 新闻 信工 新闻 资环
班级
15C26 15C27 15C13 15A22 15C20 15B21 15B36 15A31 15A9 15A30 15A32 15A33 15B25 15A42 15B37 15A36 15C23 15B32 15A45
高等数学期末考试试题及解答

高等数学(下)期末试题(2)二、填空题(每题3分,总计15分)。
1、函数22(,)22f x y x ax xy y =+++在点(1,1)-处取得极值,则常数a =______。
2、若曲面2222321x y z ++=的切平面平行于平面46250x y z -++=,则切点坐标为______________________。
3、二重积分3110x ydyye dx -蝌的值为______________。
5、微分方程2yy x y ¢=+的通解为_____________________。
三、计算题(每题7分,总计35分)。
2、设(,)z f x y xy =-具有连续的二阶偏导数,求2z x y¶抖。
3、将函数23()2f x x x=--展开成x 的幂级数,并指出收敛域。
4、设)(x y y 满足方程322x y y y e ⅱ?-+=,且其图形在点)1,0(与曲线21y x x =-+相切,求函数)(x y 。
5、计算222Ldsx y z++ò,其中L 是螺旋线8cos ,8sin ,x t y t z t ===对应02t p#的弧段。
四、计算题(每题7分,总计35分)。
1、设0a >,计算极限23123lim ()n n na a a a??++++的值。
2、计算z dv W蝌?,其中W 由不等式z ?22214x y z ?+?所确定。
4、将函数()(11)f x x x =-#展开成以2为周期的傅立叶级数。
5、设函数)(x f 具有连续导数并且满足(1)3f =,计算曲线积分22(())(())Ly f x x dx x f x y dy +++ò的值,假定此积分在右半平面内与路径无关,曲线L 是由)2,1(到)1,2(的任一条逐段光滑曲线。
五、本题5分。
对0p >,讨论级数11(1)nn n n p¥+=-å的敛散性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
违者按舞弊处理;不得自备草稿纸。
考 生
承 诺
本人知道考试违纪、作弊的严重性,将严格遵守考场纪律,如若违反则愿意接受学校按有关规定处分!
考生签名:
一、填空题:(每空3分,共15分)
得 分
评阅人
1、函数 的定义域是________________________________。
评阅人
1、已知 ,求 , 。
2、求二重积分 ,其中积分区域 是 。
3、求微分方程 的通解;
四、计算题:(每小题8分,共16分)
得 分
评阅人
1、计算曲线积分 ,其中有向曲线L是从点A(2,0)沿上半圆周 到点O(0,0)。
2、求幂级数 的收敛半径、收敛域以及和函数。
五、计算题:(每小题8分,共16分)
得 分
评阅人
1、求曲面 在点(1,2,0)处的切平面方程和法线方程。
2、求函数 在区域 上的最大值和最小值。
六、计算题:(8分)
得 分
评阅人
用高斯公式计算曲面积分 ,其中∑为曲面 和 , 所围立体的外侧曲面。
七、证明题:(6分)
得 分
评阅人
设 在点 的某一邻域具有二阶连续导数,且 ,证明级数
绝对收敛。
( )。
(A) ; (B) ;
(C) ; (D)
2、幂级数 在 条件收敛,则幂级数 的收敛半径是( )。
(A)2 ; (B)3; (C)4; (D)5
3、已知函数 是微分方程 的解,则 的表达式为( )。
(A) ; (B) ; (C) ; (D)
4、设∑是取外侧的曲面 ,则曲面积分 =
( )。
(A) ; (B)2 ; (C)3 ; (D)4
—南 昌 大 学 考 试 试 卷—
【适用时间:2015~2016学年第二学期试卷类型:[A]卷】
教
师
填
写
栏
课程编号:
J5510N2001
试卷编号:
课程名称:
高等数学序号:
开课学院:
理学院
考试形式:
闭卷
适用班级:
2015年级
考试时间:
120分钟
试卷说明:
1、本试卷共7页。
2、考试结束后,考生不得将试卷、答题纸和草稿纸带出考场。
2、设 ,则 =___________。
3、球面 在(1,2,2)处的切平面方程为___________________。
4、级数 的和为_____。
5、微分方程 的通解为______________。
二、单项选择题ቤተ መጻሕፍቲ ባይዱ(每小题3分,共15分)
得 分
评阅人
1、曲面 上对应于点 处与Z轴正向成锐角的法向量 可取为
5、设 在平面有界闭区域 上具有二阶连续偏导数,且满足 以及
,则下列结论正确的是( )。
(A)最大值点和最小值点必定都在 的部;
(B)最大值点和最小值点必定都在 的边界上;
(C)最大值点在 的部,最小值点在 的边界上;
(D)最小值点在 的部,最大值点在 的边界上
三、计算题:(每小题8分,共24分)
得 分
题号
一
二
三
四
五
六
七
八
九
十
总分
累分人
签 名
题分
15
15
24
16
16
8
6
100
得分
考
生
填
写
栏
考生:
考生学号:
所属学院:
所属班级:
所属专业:
考试日期:
2016年6月23日
考 生
须 知
1、请考生务必查看试卷中是否有缺页或破损。如有立即举手报告以便更换。
2、严禁代考,违者双方均开除学籍;严禁舞弊,违者取消学位授予资格;
