高等数学(上)期末测试卷A答案

合集下载

大一高等数学期末考试试卷及答案详解

⼤⼀⾼等数学期末考试试卷及答案详解⼤⼀⾼等数学期末考试试卷（⼀）⼀、选择题（共12分） 1. （3分）若2,0,(),0x e x f x a x x ?<=?+>?为连续函数,则a 的值为( ). (A)1 (B)2 (C)3 (D)-1 2. （3分）已知(3)2,f '=则0(3)(3)lim2h f h f h →--的值为（）. (A)1 (B)3 (C)-1 (D)123. （3分）定积分22ππ-?的值为（）.(A)0 (B)-2 (C)1 (D)24. （3分）若()f x 在0x x =处不连续,则()f x 在该点处( ). (A)必不可导 (B)⼀定可导(C)可能可导 (D)必⽆极限⼆、填空题（共12分）1．（3分）平⾯上过点(0,1)，且在任意⼀点(,)x y 处的切线斜率为23x 的曲线⽅程为 .2. （3分） 1241(sin )x x x dx -+=? . 3. （3分） 201lim sin x x x→= . 4. （3分） 3223y x x =-的极⼤值为 .三、计算题（共42分） 1. （6分）求20ln(15)lim.sin 3x x x x →+2. （6分）设2,1y x =+求.y '3. （6分）求不定积分2ln(1).x x dx +?(1),f x dx -?其中,1,()1cos 1, 1.x xx f x xe x ?≤?=+??+>?5. （6分）设函数()y f x =由⽅程0cos 0yxte dt tdt +=??所确定,求.dy6. （6分）设2()sin ,f x dx x C =+?求(23).f x dx +?7. （6分）求极限3lim 1.2nn n →∞+四、解答题（共28分）1. （7分）设(ln )1,f x x '=+且(0)1,f =求().f x2. （7分）求由曲线cos 22y x x ππ??=-≤≤与x 轴所围成图形绕着x 轴旋转⼀周所得旋转体的体积.3. （7分）求曲线3232419y x x x =-+-在拐点处的切线⽅程.4. （7分）求函数y x =+[5,1]-上的最⼩值和最⼤值.五、证明题(6分)设()f x ''在区间[,]a b 上连续,证明1()[()()]()()().22bbab a f x dx f a f b x a x b f x dx -''=++--?（⼆）⼀、填空题（每⼩题3分，共18分） 1．设函数()23122+--=x x x x f ，则1=x 是()x f 的第类间断点.2．函数()21ln x y +=，则='y.3． =?+∞→xx x x 21lim.4．曲线xy 1=在点2,21处的切线⽅程为 . 5．函数2332x x y -=在[]4,1-上的最⼤值，最⼩值 . 6．=+?dx xx21arctan . ⼆、单项选择题（每⼩题4分，共20分） 1．数列{}n x 有界是它收敛的（） . () A 必要但⾮充分条件； () B 充分但⾮必要条件； () C 充分必要条件； () D ⽆关条件. 2．下列各式正确的是（） .() A C e dx e x x +=--?； () B C xxdx +=?1ln ； () C ()C x dx x +-=-?21ln 2211； () D C x dx xx +=?ln ln ln 1. 3．设()x f 在[]b a ,上，()0>'x f 且()0>''x f ，则曲线()x f y =在[]b a ,上.() A 沿x 轴正向上升且为凹的； () B 沿x 轴正向下降且为凹的；() C 沿x 轴正向上升且为凸的； () D 沿x 轴正向下降且为凸的.4．设()x x x f ln =，则()x f 在0=x 处的导数（）.() A 等于1； () B 等于1-； () C 等于0； () D 不存在.5．已知()2lim 1=+→x f x ，以下结论正确的是（）.() A 函数在1=x 处有定义且()21=f ； () B 函数在1=x 处的某去⼼邻域内有定义；() C 函数在1=x 处的左侧某邻域内有定义；() D 函数在1=x 处的右侧某邻域内有定义.三、计算（每⼩题6分，共36分） 1．求极限：xx x 1sin lim 20→. 2. 已知()21ln x y +=，求y '. 3. 求函数x x y sin =()0>x 的导数.4. ?+dx xx 221. 5. ?xdx x cos .6.⽅程yxx y 11=确定函数()x f y =，求y '.四、（10分）已知2x e 为()x f 的⼀个原函数，求()?dx x f x 2.五、（6分）求曲线x xe y -=的拐点及凹凸区间. 六、（10分）设()()C e x dx x f x++='?1，求()x f .（三）⼀、填空题(本题共5⼩题，每⼩题4分，共20分).（1） 21(cos lim x x x → e1.（2）曲线x x y ln =上与直线01=+-y x 平⾏的切线⽅程为1-=x y . （3）已知xxxeef -=')(，且0)1(=f , 则=)(x f =)(x f 2)(ln 21x .（4）曲线132+=x x y 的斜渐近线⽅程为 .9131-=x y（5）微分⽅程522(1)1'-=++y y x x 的通解为.)1()1(32227+++=x C x y⼆、选择题 (本题共5⼩题，每⼩题4分，共20分). （1）下列积分结果正确的是（ D ）(A) 0111=?-dx x (B) 21112-=?-dx x(C) +∞=?∞+141dx x (D) +∞=?∞+11dx x（2）函数)(x f 在],[b a 内有定义，其导数)('x f 的图形如图1-1所⽰，则（ D ）.(A)21,x x 都是极值点. (B) ()())(,,)(,2211x f x x f x 都是拐点.(C) 1x 是极值点.，())(,22x f x(D) ())(,11x f x 是拐点，2x 是极值点图1-1（3）函数212e e e x x xy y y x '''--=（B ）23e .xy y y '''--= （C ）23e .x y y y x '''+-= （D ）23e .xy y y '''+-=（4）设)(x f 在0x 处可导，则()()000limh f x f x h h →--为（ A ）. (A) ()0f x '. (B) ()0f x '-. (C) 0. (D)不存在 .（5）下列等式中正确的结果是（ A ）.(A) (())().f x dx f x '=? (B) ()().=?df x f x (C) [()]().d f x dx f x =(D) ()().fx dx f x '=?三、计算题（本题共4⼩题，每⼩题6分，共24分）. 1．求极限) ln 11(lim 1x x x x --→.解 )ln 11(lim 1x x x x --→=x x x x x x ln )1(1ln lim 1-+-→ 1分=x x x xx ln 1ln lim1+-→ 2分= xx x x x x ln 1ln lim1+-→ 1分分2.⽅程??+==t t t y t x sin cos sin ln 确定y 为x 的函数，求dx dy 与2 2dx y d .解 ,sin )()(t t t x t y dx dy =''= （3分） .sin tan sin )()sin (22t t t t t x t t dx y d +=''= （6分）3. 4. 计算不定积分.222(1) =2arctan 2 =2d x C =----------+------+---------??分分（分4.计算定积分?++3011dx xx.解 ??-+-=++3030)11(11dx x x x dx x x ?+--=30)11(dx x （3分）35)1(3（或令t x =+1）四、解答题（本题共4⼩题，共29分）.1．（本题6分）解微分⽅程256xy y y xe '''-+=.2122312*20101*223212-56012,31.1()111.21(1)121(1).12x x x x x x x r r r r e C e y x b x b e b b y x x e y e C e x x e +=----------==----------+-------=+-----------=-=-=-------------=+-+----解：特征⽅程分特征解.分次⽅程的通解Y =C 分令分代⼊解得，所以分所以所求通解C 分2．（本题7分）⼀个横放着的圆柱形⽔桶（如图4-1），桶内盛有半桶⽔，设桶的底半径为R ，⽔的⽐重为γ，计算桶的⼀端⾯上所受的压⼒．解：建⽴坐标系如图22022220322203*********RRRP gx R x dx g R x d R x g R x g R ρρρρ=----------=---------=--------=----------------??分（）分[（）]分分3. （本题8分）设()f x 在[,]a b 上有连续的导数，()()0f a f b ==，且2()1baf x dx =?，试求()()b a222()()()()21 ()221 =[()]()2211=0222b b aab a b b a a xf x f x dx xf x df x xdf x xf x f x dx '=-----=---------=----------解：分分分分4. （本题8分）过坐标原点作曲线x y ln =的切线，该切线与曲线x y ln =及x 轴围成平⾯图形D. (1) (3) 求D 的⾯积A;(2) (4) 求D 绕直线e x =旋转⼀周所得旋转体的体积V.解：(1) 设切点的横坐标为0x ，则曲线x y ln =在点)ln ,(00x x 处的切线⽅程是).(1ln 000x x x x y -+=1分yxyO1e 1D由该切线过原点知 01ln 0=-x ，从⽽.0e x =所以该切线的⽅程为.1x e y =平⾯图形D 的⾯积 ?-=-=10.121)(e dy ey e A y 2分（2）切线xe y 1=与x 轴及直线e x =所围成的三⾓形绕直线e x =旋转所得的圆锥体积为 .3121e V π= 2分曲线x y ln =与x 轴及直线e x =所围成的图形绕直线e x =旋转所得的旋转体体积为dye e V y 2102)(?-=π， 1分因此所求旋转体的体积为).3125(6)(312102221+-=--=-=?e e dy e e e V V V y πππ 1分五、证明题（本题共1⼩题，共7分）.1.证明对于任意的实数x ，1x e x ≥+.解法⼀：2112xe e x x xξ=++≥+解法⼆：设() 1.x f x e x =--则(0)0.f = 1分因为() 1.xf x e '=- 1分当0x ≥时，()0.f x '≥()f x 单调增加，()(0)0.f x f ≥= 2分当0x ≤时，()0.f x '≤()f x 单调增加，()(0)0.f x f ≥= 2分所以对于任意的实数x ，()0.f x ≥即1x e x ≥+。

高等数学a上期末考试试题和答案

高等数学a上期末考试试题和答案高等数学A上期末考试试题一、选择题（每题3分，共30分）1. 极限的定义是（）。

A. 函数在某点的值B. 函数在某点的增量C. 函数在某点的导数D. 函数在某点的无穷小答案：D2. 函数f(x)=x^2在x=0处的导数是（）。

A. 0B. 1C. 2D. 3答案：C3. 定积分∫₀¹x²dx的值是（）。

A. 1/3B. 1/2C. 1D. 2答案：C4. 函数f(x)=sinx在x=π/2处的值是（）。

A. 0B. 1C. -1D. π/2答案：B5. 函数f(x)=e^x的原函数是（）。

A. e^xB. e^(-x)C. ln(x)D. x答案：A6. 函数f(x)=x^3-3x^2+2的极值点是（）。

A. 0B. 1C. 2D. 3答案：B7. 函数f(x)=x^2+2x+1的最小值是（）。

A. 0B. 1C. 2D. 3答案：B8. 函数f(x)=ln(x)的定义域是（）。

A. (-∞, 0)B. (0, +∞)C. (-∞, +∞)D. [0, +∞)答案：B9. 函数f(x)=x^3-6x^2+11x-6的拐点是（）。

A. 1B. 2C. 3D. 4答案：B10. 函数f(x)=x^4-4x^3+6x^2-4x+1的零点是（）。

A. 0B. 1C. 2D. 3答案：B二、填空题（每题3分，共30分）11. 函数f(x)=x^3-3x^2+2的导数是______。

答案：3x^2-6x12. 函数f(x)=e^x的二阶导数是______。

答案：e^x13. 函数f(x)=ln(x)的不定积分是______。

答案：xln(x)-x+C14. 函数f(x)=x^2-4x+4的顶点坐标是______。

答案：(2, 0)15. 函数f(x)=sinx+cosx的周期是______。

答案：2π16. 函数f(x)=x^3-3x^2+2的单调增区间是______。

工程大学2023-2023学年第1学期《高等数学(上)》期末考试试卷(A卷)及标准答案

工程大学2023-2024学年第1学期《高等数学（上）》期末考试试卷（A卷）及标准答案试卷题目：高等数学（上）期末考试试卷（A卷）科目：高等数学（上）时间：2024年1月一、选择题（共30题，每题2分，共60分）1.在直角坐标系中，抛物线y = x^2 - 2x 的顶点坐标是（）A. (1, -1)B. (1, 2)C. (2, 1)D. (-1, 1)2.设函数f(x) = sin(2x + π/3)，则函数 f(x) 的一个周期是（）A. π/3B. π/2C. πD. 2π3.函数 y = 3ln(2x + 1) 的图像在 x 轴上的截距是（）A. -1/2B. 1/2C. 0D. -14.设函数 f(x) = x^3 + 4x^2 + 5x，则 f(x) 的极值点是（）A. (-1, -1)B. (0, 0)C. (0, 5)D. (-5, 0)5.已知曲线 C 的参数方程为 x = t^2 - 4, y = t - 1，则曲线 C 属于（）A. 抛物线B. 椭圆C. 双曲线D. 直线…二、填空题（共10题，每题3分，共30分）1.函数 f(x) = sin(2x) 的最小正周期是 _______。

2.函数 y = x^3 + 4x^2 的导函数是 _______。

…三、解答题（共4题，每题20分，共80分）1.求方程组 x^2 + y^2 = 4, x - y = 1 的解。

2.计算不定积分∫(cos^2x + 2sinx)dx。

…四、大题（共2题，每题20分，共40分）1.设 y = ax^2 + bx + c，其中 a, b, c 均为常数，且a ≠ 0。

若曲线 y = ax^2 + bx + c 的顶点坐标为 (1, -1)，且该曲线与直线 y = x + 1 相切于点 (2, 3)，求曲线方程。

2.设函数 f(x) = e^x / (1 + e^x)，求f’(x) 和f’’(x)。

同济大学《高等数学》(上)期末试卷A及答案

高等数学(上)期末考试试卷试题一、填空、选择题1．函数)(x f 在],[b a 上可积是)(x f 在],[b a 上连续的条件，函数)(x f 在],[b a 上可导是)(x f 在],[b a 上连续的条件．2．曲线(ln y x =在点(),ln(1处的切线方程是．3．函数()(1)cos sin f x x x x =−−在区间0,2π⎡⎤⎢⎥⎣⎦上的最大值是．4．曲线()x x y x −=2e 上有个拐点．5．设可导函数()g x 满足(0)0g =，()00≠′g ，设())(sin 2x g x G =，则当0x →时，．（A ）()G x 与()g x 是等价无穷小．（B ）()G x 与()g x 是同阶的无穷小．（C ）()G x 是比()g x 高阶的无穷小．（D ）()G x 是比()g x 低阶的无穷小．6．极限nnn nnn 333lim 21+++∞→"= ．7．如果一物体沿直线运动，物体的运动速度的变化曲线如图3所示（单位省略），则物体在这段位移过程中的平均速度为．8．微分方程x x y x y sind d =+的通解为．二、1．设函数ln sec y x =，,22x ππ⎛⎞∈−⎜⎟⎝⎠．(1)讨论函数的单调区间与该函数的图形的凹凸性； (2)该曲线在哪点处的曲率半径为2？2．设()⎪⎩⎪⎨⎧=≠=∫,0,,0,d e 22x a x x t x x xt ϕ 求a 的值，使得()x ϕ在0=x 处连续，并用导数定义求(0)ϕ′．三、1．求定积分I =∫−π22d sin 1x x x ．2．若()()⎪⎪⎩⎪⎪⎨⎧>+≤+=,0,11,0,112x x x x xx f 对于(,)x ∈−∞+∞，求()()∫∞−=xt t f x F d ．四、1．设曲边梯形由曲线1y x x=+（0x >）与直线0y =，x a =，1x a =+所围成（其中0a >），问：当a 为何值时，曲边梯形的面积为最小，最小面积是多少？2．设一平板浸没在水中且垂直于水面(水的密度为1000kg/m 3)，平板的形状为双曲四边形，即图形由双曲线2244x y −=，直线1y =与1y =−所围成(如图4所示，单位：m)．(1)如果平板的上边缘与水面相齐，那么平板一侧所受到的水的总压力是多少？(2)如果水位下降，在时刻t ，水面位于y =()h t 处，且水面匀速下降，速率为0.01（m/s ），问：当水面下降至平板的中位线(即x 轴)时，平板一侧所受到的水压力的下降速率是多少？五、设函数()f x 满足方程x x f u u f x u x 2cos )(d )()(0+=−∫，求()f x ．参考答案一、1．必要，充分．2．|1x y ′，因此所求切线是ln(1y x =．3．()(1)sin f x x x ′=−−，在区间(0,)2π内有唯一驻点1x =且为极大值点，因此所求最大值是(1)sin1f =−．4．()x x y x 3e 2+=′′有2个零点3x =−与0x =，且y ′′在这2个零点的左、右两侧邻近异号，因此该曲线上有2个拐点．5．2222000(sin )(0)()(sin )sin (0)sin lim lim lim 00()(0)()()(0)x x x g x g G x g x x g x g x g g x g x x g x→→→−′==⋅=⋅=−′，因此当0x →时，()G x 是比()g x 高阶的无穷小，故选（C ）．6．利用定积分的定义，得3ln 2d 3333lim1021==+++∫∞→x n x nn n n n "． 7．1011()d 101v v t t =−∫，根据定积分的几何意义，其中的定积分101()d v t t ∫是图中的图形面积，即10111118()d [4(61)4(86)(24)(108)]1019223v v t t ==⋅⋅−+⋅−++⋅−=−∫． 8．通解为()11d d sin 1cose e d sin d x x x x x x Cy x C x x C x xx−⎛⎞−+∫∫=+=+=⎜⎟⎝⎠∫∫．二、1．(1)tan y x ′=，在,02π⎛⎞−⎜⎟⎝⎠内，0y ′<；在0,2π⎛⎞⎜⎟⎝⎠内，0y ′>．故,02π⎛⎤−⎜⎥⎝⎦是单调减少区间，0,2π⎡⎞⎟⎢⎣⎠是单调增加区间；而由2sec 0(,)22y x x ππ⎛⎞′′=>∈−⎜⎟⎝⎠得，该函数的图形是凹的． (2)322|||cos |(1)y K x y ′′==′+．由12K =，得3x π=±，故曲率半径为2的点是(,ln 2)3π±．2．11e e 2lim d e lim2224020=−=→→∫xx x xxt x xt ，因此1=a 时，()x ϕ在0=x 处连续． 22020d e lim1d e lim)0()(lim)0(22x x t xx t xx x xt x x xt x x −=−=−=′∫∫→→→ϕϕϕ02e 2e 16lim 21e e 2lim 22224040=−=−−=→→xx x x x x x x x ．三、 1．I =∫∫∫−=ππππ222022d cos d cos d |cos |x x x x x x x x x[][]πππ22202sin 2cos 2sin sin 2cos 2sin xx x x xxx x x x −+−−+=4222−+=ππ．2．当0x <时，()2arctan d 112π+=+=∫∞−x t t x F x ；当0x ≥时，()2arctan 2]arctan 2[2d )1(1d 11002ππ+=+=+++=∫∫∞−x t t t t t t x F xx ．因此()⎪⎪⎩⎪⎪⎨⎧≥+<+=.0,2arctan 2,0,2arctan x x x x x F ππ 四、1．曲边梯形的面积1111()()d ln2a a a A a x x a x a ++=+=++∫， 11()11A a a a ′=+−+．令()0A a ′=，解得在0a >范围内的唯一驻点12a −=，易知该点为极小值点，因此必为最小值点．而其最小面积min 1)ln 22A A −==+ 2．(1)水压力111000(1)2000F g y y g y −=−=∫∫10120002ln(10004ln 2g y g +⎤=++=+⎥⎦．(2)在时刻t ，水面位于()y h t =，平板一侧所受到的水压力为()(()1111000[()]1000()1000h t h t h t F g h t y y gh t y g y −−−=−=−∫∫∫，上式两边对t 求导，得(1d d 1000d d h t F hg y t t−=∫，由于d 0.01d ht=−，因此，当水面下降至平板的中位线(即x 轴)时，平板一侧所受到的水压力的下降速率为01d 10102ln(d F g y g y t −−⎤=−=−++⎥⎦∫154ln 2g =−+．五、原方程为x x f u u f x u u f u xx 2cos )(d )(d )(0+=−∫∫，代入0x =，得(0)1f =−．上式两端对x 求导，得x x f u u f x2sin 2)(d )(0−′=−∫，代入0x =，得(0)0f ′=．上式两端再对x 求导，得x x f x f 2cos 4)()(−′′=−．故()y f x =满足初值问题⎩⎨⎧=′−==+′′==.0|,1|,2cos 400x x y y x y y 解得124cos sin cos 23y C x C x x =+−，代入初始条件解得113C =，20C =．故14()cos cos 233f x x x =−．。

高等数学期末考试试题及答案(大一考试)

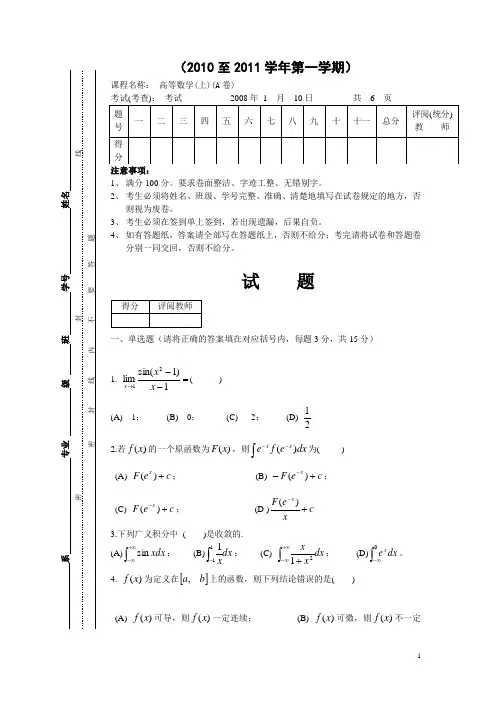
（2010至2011学年第一学期）课程名称：高等数学(上)(A 卷)考试(考查)：考试 2008年 1 月 10日共 6 页注意事项：1、满分100分。

要求卷面整洁、字迹工整、无错别字。

2、考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方，否则视为废卷。

3、考生必须在签到单上签到，若出现遗漏，后果自负。

4、如有答题纸，答案请全部写在答题纸上，否则不给分；考完请将试卷和答题卷分别一同交回，否则不给分。

试题一、单选题（请将正确的答案填在对应括号内，每题3分，共15分）1. =--→1)1sin(lim21x x x ( ) (A) 1； (B) 0； (C) 2； (D)212.若)(x f 的一个原函数为)(x F ，则dx e f e xx )(⎰--为( )(A) c e F x +)(； (B) c eF x+--)(；(C) c e F x+-)(； (D )c xe F x +-)( 3.下列广义积分中 ( )是收敛的. (A)⎰+∞∞-xdx sin ； (B)dx x⎰-111； (C) dx x x ⎰+∞∞-+21； (D)⎰∞-0dx e x。

4. )(x f 为定义在[]b a ,上的函数，则下列结论错误的是( )(A) )(x f 可导，则)(x f 一定连续； (B) )(x f 可微，则)(x f 不一定可导；(C) )(x f 可积（常义），则)(x f 一定有界； (D) 函数)(x f 连续，则⎰xadt t f )(在[]b a ,上一定可导。

5. 设函数=)(x f nn x x211lim++∞→ ，则下列结论正确的为( )(A) 不存在间断点； (B) 存在间断点1=x ； (C) 存在间断点0=x ； (D) 存在间断点1-=x二、填空题（请将正确的结果填在横线上.每题3分，共18分）1. 极限=-+→xx x 11lim 20 _____.2. 曲线⎩⎨⎧=+=321ty t x 在2=t 处的切线方程为______. 3. 已知方程xxe y y y 265=+'-''的一个特解为x e x x 22)2(21+-，则该方程的通解为 .4. 设)(x f 在2=x 处连续，且22)(lim2=-→x x f x ，则_____)2(='f5．由实验知道，弹簧在拉伸过程中需要的力F （牛顿）与伸长量s 成正比，即ks F =（k 为比例系数），当把弹簧由原长拉伸6cm 时，所作的功为_________焦耳。

大一上学期高数期末考试试题(五套)详解答案

2010级高等数学(上)A 解答一、填空题：(每题3分，共18分)(请将正确答案填入下表，否则不给分)1．已知极限01lim 2=⎪⎪⎭⎫⎝⎛--+∞→b ax x x x ，则常数b a ,的值分别是(空1)。

解：0x b a 1x x lim b ax 1x x x 1lim x 2x =⎪⎭⎫ ⎝⎛--+=⎪⎪⎭⎫ ⎝⎛--+∞→∞→ ⇒1-a=0⇒a=1⎪⎪⎭⎫⎝⎛-+=⎪⎪⎭⎫ ⎝⎛-+=∞→∞→x 1x x lim ax 1x x lim b 2x 2x 1x111lim 1x x lim 1x x x x lim x x 22x -=+-=+-=⎪⎪⎭⎫ ⎝⎛+--=∞→∞→∞→ 或：01x b x )b a (x )a 1(lim b ax 1x x lim 2x 2x =⎪⎪⎭⎫⎝⎛+-+--=⎪⎪⎭⎫ ⎝⎛--+∞→∞→ 所以1-a=0,a+b=0⇒a=1,b=-1。

或：⎪⎪⎭⎫⎝⎛++--+-=⎪⎪⎭⎫ ⎝⎛--+∞→∞→1x 1b ax 1x 1x lim b ax 1x x lim 2x 2x 01x 1)b 1(x )a 1(lim 1x 1b ax 1x lim x x =⎪⎭⎫ ⎝⎛+++--=⎪⎭⎫ ⎝⎛++---=∞→∞→ 所以1-a=0,1+b=0⇒a=1,b=-1。

2．函数xx x x x f 323)(23---=的第一类间断点是(空2)。

解：f(x)在x=3,0,-1处无定义，是间断点。

121)3x )(1x (x 3x lim x 3x 2x 3x lim)x (f lim 3x 233x 3x =-+-=---=→→→，x=3是第一类间断点。

∞=---=-→-→x3x 2x 3x lim)x (f lim 231x 1xx=-1是第二类间断点。

∞=---=→→x3x 2x 3x lim)x (f lim 230x 0xx=0是第二类间断点。

3．设函数)(x f 可导，)(1)(2x f x g +=，则)('x g ＝(空3)。

高数(大一上)期末试题及答案

高数(大一上)期末试题及答案第一学期期末考试试卷（1）课程名称：高等数学（上）考试方式：闭卷完成时限：120分钟班级：学号：姓名：得分：一、填空（每小题3分，满分15分）1.lim (3x^2+5)/ (5x+3x^2) = 02.设 f''(-1) = A，则 lim (f'(-1+h) - f'(-1))/h = A3.曲线 y = 2e^(2t) - t 在 t = 0 处切线方程的斜率为 44.已知 f(x) 连续可导，且 f(x)。

0，f(0) = 1，f(1) = e，f(2) = e，∫f(2x)dx = 1/2ex，则 f'(0) = 1/25.已知 f(x) = (1+x^2)/(1+x)，则 f'(0) = 1二、单项选择（每小题3分，满分15分）1.函数 f(x) = x*sinx，则 B 选项为正确答案，即当x → ±∞ 时有极限。

2.已知 f(x) = { e^x。

x < 1.ln x。

x ≥ 1 }，则 f(x) 在 x = 1 处的导数不存在，答案为 D。

3.曲线 y = xe^(-x^2) 的拐点是 (1/e。

1/(2e))，答案为 C。

4.下列广义积分中发散的是 A 选项，即∫dx/(x^2+x+1)在区间 (-∞。

+∞) 内发散。

5.若 f(x) 与 g(x) 在 (-∞。

+∞) 内可导，且 f(x) < g(x)，则必有 B 选项成立，即 f'(x) < g'(x)。

三、计算题（每小题7分，共56分）1.lim x^2(e^(2x)-e^(-x))/((1-cosx)sinx)lim x^2(e^(2x)-e^(-x))/((1-cosx)/x)*x*cosxlim x(e^(2x)-e^(-x))/(sinx/x)*cosxlim (2e^(2x)+e^(-x))/(cosx/x)应用洛必达法则)2.lim {arcsin(x+1) + arcsin(x-1) - 2arcsin(x)}/xlim {arcsin[(x+1)/√(1+(x+1)^2)] + arcsin[(x-1)/√(1+(x-1)^2)] - 2arcsin(x)/√(1+x^2)}lim {arcsin[(x+1)/√(1+(x+1)^2)] - arcsin(x/√(1+x^2)) + arcsin[(x-1)/√(1+(x-1)^2)] - arcsin(x/√(1+x^2))}lim {arcsin[(x+1)/√(1+(x+1)^2)] - arcsin(x/√(1+(x+1)^2)) + arcsin[(x-1)/√(1+(x-1)^2)] - arcsin(x/√(1+(x-1)^2))}lim {arcsin[(x+1)/√(1+(x+1)^2)] - arcsin[(x-1)/√(1+(x-1)^2)]} π/2 (应用洛必达法则)3.y = y(x) 由 x + y - 3 = 0 确定，即 y = 3 - x，因此 dy/dx = -1.4.f(x) = arctan(2x-9) - arctan(x-3) 的导数为 f'(x) = 1/[(2x-9)^2+1] - 1/[(x-3)^2+1]，因此 f'(x)。

高等数学期末考试试题及答案(大一考试)

高等数学期末考试试题及答案(大一考试)姓名：__________ 班级：__________ 学号：__________课程名称：高等数学(上)(A卷) 考试日期：2008年1月10日注意事项：1.本试卷满分100分，要求卷面整洁、字迹工整、无错别字。

2.考生必须将姓名、班级、学号完整、准确、清楚地填写在试卷规定的地方，否则视为废卷。

3.考生必须在签到单上签到，若出现遗漏，后果自负。

4.如有答题纸，请将答案全部写在答题纸上，否则不给分。

考完请将试卷和答题卷分别一同交回，否则不给分。

一、单选题（每题3分，共15分）1.lim(sin(x^2-1)/(x-1))，x趋近于1，等于()A)1；(B)0；(C)2；(D)不存在。

2.若f(x)的一个原函数为F(x)，则∫e^(-x)f(e^x)dx等于()A)F(e^x)+c；(B)-F(e^-x)+c；(C)F(e^-x)+c；(D)F(e^-x^2/2)+c。

3.下列广义积分中()是收敛的。

A)∫sinxdx，从负无穷到正无穷；(B)∫1/|x|dx，从-1到1；(C)∫x/(1+x^2)dx，从负无穷到正无穷；(D)∫e^x dx，从负无穷到0.4.f(x)为定义在[a,b]上的函数，则下列结论错误的是()A)f(x)可导，则f(x)一定连续；(B)f(x)可微，则f(x)不一定可导；(C)f(x)可积（常义），则f(x)一定有界；(D)函数f(x)连续，则∫f(x)dx在[a,b]上一定有定义。

5.设函数f(x)=lim(n→∞)(1+x^2n)^2，则下列结论正确的是()A)不存在间断点；(B)存在间断点x=1；(C)存在间断点x=0；(D)存在间断点x=-1.二、填空题（每题3分，共18分）1.极限lim(x→∞)(x^2+1-1)/x=______。

2.曲线y=3t在t=2处的切线方程为y=______。

3.已知方程y''-5y'+6y=xe^(2x)的一个特解为-1/2(x+2x)e^(2x)，则该方程的通解为______。

《高等数学》期末考试A卷(附答案)

《高等数学》期末考试A卷（附答案）【编号】ZSWD2023B0089一、填空题（每小题2分，共20分）1．设是正整数，为非零实数，若20001lim ()x x x x，则 _________________，______________________。

【答案】120012001,2．设)(x f 的定义域是]1,0[，且102a ，则()()f x a f x a 的定义域是____________________________ .【答案】1[,]a a3．2211sin()lim x x x x ______________________。

【答案】04．设1111010,(),x x x x e e x f x e e x，0 x 是)(x f 的___________间断点. 【答案】跳跃5．设24cos y x ，则dy ________________________. 【答案】3448sin cos x x x dx6．203sin limxx t dt x _________________________________.【答案】137．函数2412()()x f x x的渐近线有______________________________.【答案】20,x y8．函数()x f x x e 的单调递增区间为____________________________.【答案】(,0)9．若 C x dx xx f sin )(ln '，则 )(x f .【答案】C e x )sin( 10.[()()]aaf x f x dx ______________________________________.【答案】0二、单项选择题（每小题2分，共10分） 1．若下列极限存在，则成立的是( ) .A. 0()()lim '()x f a x f a f a x B. 0000()()lim '() x f x f x x f x xC. 0(12)(1)lim '(1)t f t f f tD. 4(8)(4)lim '(4)4x f x f f x【答案】B2．当0 x 时，与x 等价的无穷小量是( )A. x x 1sinsin B. xx sin C. x x 22 D. )1ln(x【答案】D3．当0x x 时，0'()f x ，当0x x 时，0'()f x ，则0x 必定是函数()f x 的（）A. 驻点B. 最大值点C.极小值点D. 以上都不对【答案】D4．设'()f x 存在且连续，则()'df x （）A. ()f xB. '()f xC. '()f x cD. ()f x c 【答案】B 5．设4()2xx f t dt，则40 f dx （）A. 16B. 8C. 4D. 2【答案】A三、计算下列各题（每小题5分，共35分）1. 求极限)sin 11(cot lim 0xx x x解: )sin 11(cot lim 0x x x x xx x xx x tan sin sin lim 030sin lim x xx x （0 x 时x sin ～x ，x tan ～x ）2031cos lim x x x 616sin lim 0 x x x2. 设3sin 2,0()9arctan 2(1),0xx ae x f x x b x x ，确定,a b 的值，使函数在0 x 处可导。

《高等数学(一)》期末复习题(答案)

《高等数学（一）》期末复习题一、选择题1. 极限)x x →∞的结果是（ C ）.（A ）0 （B ） ∞ （C ） 12（D ）不存在 2. 设()xxx f +-=11ln，则)(x f 是 ( A ). （A ）奇函数（B) 偶函数（C ）非奇非偶函数（D ）既奇又偶函数 3. 极限21lim sinx x x→= ( A ) . （A ）0 （B) 1 （C ）+∞ （D ）-∞ 4. 方程3310x x -+=在区间(0,1)内（ B ）.（A ）无实根（B ）有唯一实根（C ）有两个实根（D ）有三个实根 5. 设()()ln 1f x x =+，g (x )=x ，则当0x →时，()f x 是()g x 的( A ).（A ）等价无穷小（B) 低阶无穷小（C ）高阶无穷小（D) 同阶但非等价无穷小 6. 下列变量中，是无穷小量的为（ A ）.（A ）)1(ln →x x （B ）)0(1ln +→x x （C ）cos (0)x x → （D ）)2(422→--x x x 7. 极限011lim(sinsin )x x x x x→- 的结果是（ C ）.（A ）0 （B ） 1 （C ） 1- （D ）不存在8. 下列函数中满足罗尔定理条件的是( D ).（A ）()2,[0,1]f x x x =-∈ （B) 3(),[0,1]f x x x =∈ （C ）(),[1,1]f x x x =∈- （D)4(),[1,1]f x x x =∈-9. 函数1cos sin ++=x x y 是（ C ）.（A ）奇函数（B ）偶函数（C ）非奇非偶函数（D ）既是奇函数又是偶函数 10. 当0→x 时，下列是无穷小量的是（ B ）.（A ）1+x e (B) )1ln(+x (C) )1sin(+x (D) 1+x11. 当x →∞时，下列函数中有极限的是（ A ）.（A ）211x x +- (B) cos x (C) 1xe(D)arctan x 12. 方程310(0)x px p ++=>的实根个数是（ B ）.（A ）零个（B ）一个（C ）二个（D ）三个 13.21()1dx x '=+⎰（ B ）.（A ）211x + （B ）211C x++ （C ） arctan x （D ） arctan x c + 14. 定积分()f x dx ⎰是（ A ）.（A ）一个函数族（B ）()f x 的的一个原函数（C ）一个常数（D ）一个非负常数15.函数(ln y x =+是（ A ）.（A ）奇函数（B ）偶函数（C ）非奇非偶函数（D ）既是奇函数又是偶函数 16. 设函数在区间上连续，在开区间内可导，且，则( B ).(A) (B) (C) (D) 17. 设曲线221x y e-=-，则下列选项成立的是（ C ）. (A) 没有渐近线 (B) 仅有铅直渐近线 (C) 既有水平渐近线又有铅直渐近线 (D) 仅有水平渐近线 18. 设是的一个原函数，则等式（ D ）成立.（A ）（B) （C ）（D)19. 设⎰+=C x dx x xf arcsin )(，则⎰=dx x f )(1（ B ）. （A ）C x +--32)1(43 （B ）C x +--32)1(31 （C ）C x +-322)1(43 （D ）C x +-322)1(32()f x []0,1()0,1()0f x '>()00f <()()10f f >()10f >()()10f f <F x ()f x ()dd d x f x x F x (())()⎰='=+⎰F x x f x c()()d '=⎰F x x F x ()()d dd d xf x x f x (())()⎰=20. 数列})1({nn n-+的极限为（ A ）.（A ）1(B) 1-(C) 0(D) 不存在21. 下列命题中正确的是（ B ）.（A ）有界量和无穷大量的乘积仍为无穷大量（B ）有界量和无穷小量的乘积仍为无穷小量（C ）两无穷大量的和仍为无穷大量（D ）两无穷大量的差为零 22. 若()()f x g x ''=，则下列式子一定成立的有（ C ）.(A)()()f x g x = (B)()()df x dg x =⎰⎰(C)(())(())df x dg x ''=⎰⎰(D)()()1f x g x =+ 23. 下列曲线有斜渐近线的是 ( C ).(A)sin y x x =+ (B)2sin y x x =+ (C)1siny x x =+ (D)21sin y x x=+ 24. 函数)1,0(11)(≠>+-=a a a a x x f x x （ B ）.（A ）是奇函数（B ）是偶函数（C ）既奇函数又是偶函数（D ）是非奇非偶函数 25. 下列函数中满足罗尔定理条件的是( D ).（A ）]1,0[,1)(∈-=x x x f （B)]1,0[,)(2∈=x x x f （C ）()sin ,[1,1]f x x x =∈- （D)]1,1[,)(2-∈=x x x f26. 若函数221)1(xx x x f +=+，则=)(x f （ B ）. （A ）2x （B ）22-x （C ）2)1(-x （D ）12-x 27. 设函数,ln )(x x x f =则下面关于)(x f 的说法正确的是( A ).（A ）在（0，e 1）内单调递减（B)在（+∞,1e）内单调递减（C ）在（0，+∞）内单调递减（D)（0，+∞）在内单调递增28. 设1)(+=x x f ，则)1)((+x f f =（ D ）．（A ）x （B ）x + 1 （C ）x + 2 （D ）x + 329. 已知0)1(lim 2=--+∞→b ax x x x ，其中a ,b 是常数，则（ C ）.（A ）1,1==b a , （B ）1,1=-=b a （C ）1,1-==b a （D ）1,1-=-=b a 30. 下列函数在指定的变化过程中，（ B ）是无穷小量.（A ）（B ）（C ）（D ）31. 设函数(),2x xe ef x -+=则下面关于)(x f 的说法正确的是( B ) .（A ）在(0,)+∞内单调递减（B)在(,0)-∞内单调递减（C ）在(,0)-∞内单调递增（D)在(,)-∞+∞内单调递增32. 下列函数中，在给定趋势下是无界变量且为无穷大的函数是（ C ）.（A ）)(1sin∞→=x xx y （B ）())(1∞→=-n n y n （C ）)0(ln +→=x x y （D ）)0(1cos 1→=x xx y33. 设⎪⎩⎪⎨⎧≤>=0,0,1sin )(x x x xx x f ，则)(x f 在0=x 处（ B ）. （A ）连续且可导（B ）连续但不可导（C ）不连续但可导（D ）既不连续又不可导34. 在下列等式中，正确的是( C ).（A ）()()f x dx f x '=⎰ （B) ()()df x f x =⎰（C ）()()df x dx f x dx=⎰ （D)[()]()d f x dx f x =⎰ 35. 曲线x x y -=3在点（1，0）处的切线是（ A ）．（A ）22-=x y（B ）22+-=x ye 1xx ,()→∞sin ,()xxx →∞ln(),()11+→x x x xx +-→110,()（C ）22+=x y（D ）22--=x y36. 已知441x y =，则y ''=（ B ）．（A ） 3x （B ）23x （C ）x 6 （D ） 6 37. 若x xf =)1(，则=')(x f （ D ）.（A ）x 1 （B ）21x （C ）x 1- （D ）21x-38. 下列各组函数中，是相同的函数的是（ B ）.（A ）()()2ln 2ln f x x g x x == 和（B ）()||f x x = 和 ()g x =（C ）()f x x = 和 ()2g x =（D ）()||x f x x=和 ()g x =1 39. 函数()()20ln 10x f x x a x ≠=+⎨⎪=⎩ 在0x =处连续，则a =（ B ）.（A ）0 （B ）14（C ）1 （D ）240. 曲线ln y x x =的平行于直线10x y -+=的切线方程为（ A ）.（A ）1y x =- （B ）(1)y x =-+ （C ）()()ln 11y x x =-- （D ）y x = 41. 设函数()||f x x =，则函数在点0x =处（ C ）.（A ）连续且可导（B ）连续且可微（C ）连续不可导（D ）不连续不可微 42. 设()f x 可微，则0()(2)limh f x f x h h→--=（ D ）.(A ）()f x '- （B)1()2f x ' （C ）2()f x '- （D)2()f x '43. 点0x =是函数4y x =的（ D ）.（A ）驻点但非极值点（B ）拐点（C ）驻点且是拐点（D ）驻点且是极值点 44. 曲线1||y x =的渐近线情况是（ C ）. （A ）只有水平渐近线（B ）只有垂直渐近线（C ）既有水平渐近线又有垂直渐近线（D ）既无水平渐近线又无垂直渐近线45.211f dx x x⎛⎫' ⎪⎝⎭⎰的结果是（ D ）. （A ）1f C x ⎛⎫-+ ⎪⎝⎭（B ）1f C x ⎛⎫--+ ⎪⎝⎭（C ）1f C x ⎛⎫+ ⎪⎝⎭（D ）1f C x ⎛⎫-+ ⎪⎝⎭46.x x dxe e -+⎰的结果是（ A ）.（A ）arctan x e C + （B ）arctan x e C -+ （C ）x x e e C --+ （D ）ln()x x e e C -++47. 下列各组函数中,是相同函数的是( C ).(A) ()f x x =和()g x =()211x f x x -=-和1y x =+(C) ()f x x =和()22(sin cos )g x x x x =+ (D) ()2ln f x x =和()2ln g x x =48. 设函数()()2sin 21112111x x x f x x x x -⎧<⎪-⎪⎪==⎨⎪->⎪⎪⎩，则()1lim x f x →=（ D ）.(A) 0 (B) 1 (C) 2 (D)不存在49. 设函数22456x y x x -=-+，则2x =是函数的( A ).(A) 可去间断点 (B) 跳跃间断点（C) 无穷间断点（D) 振荡间断点 50. 设函数()y f x =在点0x 处可导，且()f x '>0, 曲线则()y f x =在点()()00,x f x 处的切线的倾斜角为（ C ）. (A) 0 (B)2π(C)锐角 (D)钝角 51. 曲线ln y x =上某点的切线平行于直线23y x =-,则该点坐标是( D ).(A) 12,ln2⎛⎫ ⎪⎝⎭ (B) 12,ln 2⎛⎫- ⎪⎝⎭ (C) 1,ln 22⎛⎫ ⎪⎝⎭ (D) 1,ln 22⎛⎫- ⎪⎝⎭52. 函数2x y x e -=及图象在()1,2内是( B ).(A)单调减少且是凸的 (B)单调增加且是凸的 (C)单调减少且是凹的 (D)单调增加且是凹的 53. 以下结论正确的是( C ).(A) 若0x 为函数()y f x =的驻点,则0x 必为函数()y f x =的极值点. (B) 函数()y f x =导数不存在的点,一定不是函数()y f x =的极值点. (C) 若函数()y f x =在0x 处取得极值,且()0f x '存在,则必有()0f x '=0. (D) 若函数()y f x =在0x 处连续,则()0f x '一定存在.54. 设函数22132x y x x -=-+，则1x =是函数的( A ).（A ）可去间断点（B) 跳跃间断点（C) 无穷间断点（D) 振荡间断点 55. 设函数()y f x =的一个原函数为12x x e ,则()f x =( A ).(A) ()121x x e - (B)12xx e - (C) ()121x x e + (D) 12xxe56. 若()()f x dx F x c =+⎰,则()sin cos xf x dx =⎰( D ).(A) ()sin F x c + (B) ()sin F x c -+ (C) ()cos F x c + (D) ()cos F x c -+57. 函数21,0e ,0xx x y x ⎧+<=⎨≥⎩在点0x =处( D ).（A ）连续且可导（B) 不连续且不可导（C) 不连续但可导（D) 连续但不可导 58. 函数 2)1ln(++-=x x y 的定义域是（ C ）.（A ） []1,2- （B ） [)1,2- （C ）(]1,2- （D ）()1,2- 59. 极限x x e ∞→lim 的值是（ D ）.（A ）∞+ （B ） 0 （C ）∞- （D ）不存在 60. =--→211)1sin(limx x x （ C ）.（A ）1 （B ） 0 （C ）21-（D ）2161. 曲线 23-+=x x y 在点)0,1(处的切线方程是（ B ）.（A ） )1(2-=x y （B ）)1(4-=x y （C ）14-=x y （D ）)1(3-=x y62. 函数, 0,0xx x y e x <⎧=⎨≥⎩在点0x =处( B ). （A ）连续且可导（B) 不连续且不可导（C) 不连续但可导（D) 连续但不可导 63. 下列各微分式正确的是（ C ）.（A ）)(2x d xdx = （B ）)2(sin 2cos x d xdx = （C ）)5(x d dx --= （D ）22)()(dx x d = 64. 设⎰+=C xdx x f 2cos 2)( ，则 =)(x f （ B ）. （A ）2sin x （B ） 2sin x - （C ）C x +2sin （D ）2sin 2x-65. 设()f x 可微，则0(2)()limh f x h f x h→+-=（ D ）.（A ）()f x '- （B)1()2f x ' （C)2()f x '- （D)2()f x ' 66.⎰=+dx x xln 2（ B ）.（A ）Cx x ++-22ln 212 （B ）C x ++2)ln 2(21（C ）C x ++ln 2ln （D ）C xx++-2ln 1 67. 函数)1lg(12+++=x x y 的定义域是（ B ）.（A ）()()+∞--,01,2 （B ）()),0(0,1+∞- （C ）),0()0,1(+∞- （D ）),1(+∞-68. 设0tan 4()lim6sin x x f x x →+=，则0()lim x f x x→=（ B ） .（A ）1 （B ）2 （C ）6 （D ）24 69. 下列各式中，极限存在的是（ A ）.（A ） x x cos lim 0→ （B ）x x arctan lim ∞→ （C ）x x sin lim ∞→ （D ）x x 2lim +∞→70. =+∞→xx xx )1(lim （ D ）. （A ）e （B ）2e （C ）1 （D ）e1 71. 设0sin 4()lim5sin x x f x x →+=，则0()lim x f x x→=（ B ） .（A ）0 （B ）1 （C ）5 （D ）2572. 曲线x x y ln =的平行于直线01=+-y x 的切线方程是（ C ）.（A ）x y = （B ）)1)(1(ln --=x x y （C ）1-=x y （D ）)1(+-=x y73. 已知x x y 3sin = ，则=dy （ B ）.（A ）dx x x )3sin 33cos (+- （B ）dx x x x )3cos 33(sin + （C ）dx x x )3sin 3(cos + （D ）dx x x x )3cos 3(sin + 74. 下列等式成立的是（ C ）.（A ）⎰++=-C x dx x 111ααα （B ）⎰+=C x a dx a x x ln （C ）⎰+=C x xdx sin cos （D ）⎰++=C xxdx 211tan 75. 极限01lim sinx x x→= ( A ) . （A ） 0 （B) 1 （C ）+∞ （D) -∞ 76. 设()1cos f x x =-，()2g x x =，则当0x →时，()f x 是()g x 的( D ).（A ）等价无穷小（B) 低阶无穷小（C ）高阶无穷小（D) 同阶但非等价无穷小 77. 计算⎰xdx x e x cos sin sin 的结果中正确的是（ D ）.（A ）C e x +sin （B ）C x e x +cos sin （C ）C x e x +sin sin （D ）C x e x +-)1(sin sin78. 5lg 1)(-=x x f 的定义域是（ D ）.（A ）()),5(5,+∞∞- （B ）()),6(6,+∞∞-（C ）()),4(4,+∞∞- （D ）())5,4(4, ∞- ()),6(6,5+∞79. 如果函数f (x )的定义域为[1，2]，则函数f (x )+f (x 2)的定义域是（ B ）.（A ）[1，2] （B ）[1，2] （C ）]2,2[- （D ）]2,1[]1,2[ --80. 函数)1lg()1lg(22x x x x y -++++=( D ).（A ）是奇函数，非偶函数（B ）是偶函数，非奇函数（C ）既非奇函数，又非偶函数（D ）既是奇函数，又是偶函数 81. 设()sin f x x x =，则)(x f 是( C ).（A ）非奇非偶函数（B) 奇函数（C)偶函数（D) 既奇又偶函数 82. 函数)10(1)(2≤≤--=x x x f 的反函数=-)(1x f（ C ）.（A ）21x - （B ）21x --（C ）)01(12≤≤--x x （D ）)01(12≤≤---x x 83. 下列数列收敛的是（ C ）.（A ）1)1()(1+-=+n n n f n （B ）⎪⎩⎪⎨⎧-+=为偶数为奇数n nn n n f ,11,11)(（C ）⎪⎩⎪⎨⎧+=为偶数为奇数n n n n n f ,11,1)( （D ）⎪⎪⎩⎪⎪⎨⎧-+=为偶数为奇数n n n f nn n n ,221,221)(84. 设1111.0个n n y =，则当∞→n 时，该数列（ C ）.（A ）收敛于0.1 （B ）收敛于0.2 （C ）收敛于91（D ）发散 85. 下列极限存在的是（ A ）.（A ）2)1(lim x x x x +∞→ （B ）121lim -∞→x x （C ）x x e 10lim → （D ）x x x 1lim 2++∞→ 86. xx xx x x sin 2sin 2lim 22+-+∞→=（ A ）.（A ）21（B ）2 （C ）0 （D ）不存在 87. =--→1)1sin(lim 21x x x （ B ）.（A ）1 （B ）2 （C ）21（D ）0 88. 下列极限中结果等于e 的是（ B ）.（A ）xx x x x sin 0)sin 1(lim +→ （B ）x xx x x sin )sin 1(lim +∞→ （C ）xxx xxsin )sin 1(lim -∞→- （D ）xxx xxsin 0)sin 1(lim +→89. 函数||ln 1x y =的间断点有（ C ）个. （A ）1 （B ）2 （C ）3 （D ）4 90. 下列结论错误的是（ A ）.（A ）如果函数f (x )在点x =x 0处连续，则f (x )在点x =x 0处可导；（B ）如果函数f (x )在点x =x 0处不连续，则f (x )在点x =x 0处不可导；（C ）如果函数f (x )在点x =x 0处可导，则f (x )在点x =x 0处连续；（D ）如果函数f (x )在点x =x 0处不可导，则f (x )在点x =x 0处也可能连续。

安徽财经大学大学《高等数学A》2023-2024学年第一学期期末试卷

一、选择题：（每小题3分，共18分安徽财经大学试卷安徽财经大学2０23-2０24学年度第1学期试卷《高等数学A 》（上）试题(A 卷)参考答案和评分标准）1、已知,2)3('=f 则h f h f h 2)3()3(lim 0--→=（D ）1-)(1)(2/3-)(2/3A D C B ）（2、当0→x 时，下列无穷小中与2x 为同阶无穷小的是（C ）11)()3arcsin()()1ln()(1A 423-+--x D x C x B e x ）（3、如果)(x f 的导数为x cos ，则)(x f 的一个原函数为（D ）x D x C x B x cos 1)(cos 1)(sin 1)(sin 1A -+-+）（4、设函数⎪⎪⎩⎪⎪⎨⎧>+=<---=0,1sin 0,0,1cos 1)(x b x x x a x x e x x f x 在0=x 处连续，则常数b a,的值为（A ）1,0)(0,1)(1,0)(1,1A -========b a D b a C b a B b a ）（5、曲线32122---=x x x y 有（A ）铅直渐近线没有水平渐进线，两条铅直渐近线两条水平渐进线，一条铅直渐近线一条水平渐进线，两条条铅直渐近线）一条水平渐进线，一（)()()(A D C B 6、设)(x f 在0=x 点附近有二阶连续导数，且1cos 1)(''lim 0=-→x x xf x ，则（C ）专业班级姓名学号----------------------密------------------------------封-----------------------线-----------------------------的极小值。

是且的拐点。

）是曲线，且（的极小值。

是且的拐点。

）是曲线，但（）（)()0(,0)0('')()()0(0,0)0('')()()0(,0)0('')()()0(0,0)0(''A x f f f D x f f f C x f f f B x f y f f ≠===≠二、填空题（每小题3分，共18分）在以下各小题中画有_______处填上答案。

人教A版高一数学上学期期末测试卷(带答案)

高一数学本卷共三大题，时量120分钟，满分120分，试卷总页4页一.选择题：（本大题共10个小题，每小题4分，共40分，每小题都有四个不同的答案，其中只有一个是正确的，请把正确的答案选出来） 1.函数f(x)=x x ln 1+-的定义域为（）A.]1,(-∞B.(0,+∞)C.(0,1]D.(0,1)),1(+∞⋃2.下列函数中，既是奇函数，又是增函数的是（）A . y=-2xB . x y 2= C. x y lg = D . 3x y = 3. 已知空间直角坐标系中一点A(-3,1,-4)，则点A 关于x 轴对称点的坐标为（）A ．（-3，－1，4） B.（-3，-1，-4） C.（3，1，4） D.（3，-1，-4） 4．函数()3log 82f x x x =-+的零点一定位于区间（） A. ()5,6 B. ()3,4 C. ()2,3 D. ()1,2 5．下列几何体中，正视图、侧视图、俯视图都相同的几何体的序号是（）A.(1)(2)B.（2）（3）C.(3)(4)D.(1)(4)6．半径为R 的球的内接正方体的表面积是（）A.234R B.22R C.24R D.28R7.已知,αβ,γ是三个不同的平面， m,n 是两条不同的直线，下列命题中正确．．的是（） A.若m//α，n//α，则m//n B. 若m//α，m//β，则α//β C.若γα⊥，γβ⊥则α//βD .若α⊥β，m ⊥β，m ⊄α,则m ∥α8、若0,0ac bc <<，则直线0ax by c ++=不经过（） A ．第一象限 B.第二象限 C.第三象限 D.第四象限 9、若直线L ：ax+by=1与圆C ：122=+y x 相切，则点P （a,b)与圆C 的位置关系是（）A.在圆上B.在圆外C.在圆内D.以上皆有可能 10、如图，在长方体ABCD -A 1B 1C 1D 1中，AB =BC =2,AA 1=1,则BC 1与平面BB 1D 1D 所成角的正弦值为（）A.3B.5C.5D.5二．填空题（本大题共5个小题，每小题4分，共20分） 11．圆心在（2，-1）且与y 轴相切的圆的标准方程为。

高等数学(上学期)期末考试试卷及答案

考试试卷答案课程名称：高等数学（A ）课程所在学院：理学院一、填空题（每空2分，共20分）1. 设221)1(x x x x f +=+，则)(x f = 2()2f x x =- ．2. 1lim sin x x x→∞= 0 ． 3. 已知函数1(1),0(),0x x x f x a x ⎧⎪-≠=⎨⎪=⎩在0=x 处连续，则=a 1/e ．4. 当0x →时，232x x +-与x 是同阶（填同阶或等价）无穷小.5. 函数()x f x xe =的带皮亚诺余项的n 阶麦克劳林公式为342()2!3!(1)!n n x x x x x x n ο++++++-. 6. d 212x e C +2.x e dx =7. 曲线42y ax x =-拐点的横坐标为1x =，则常数a =16． 8. 35425cos 32x xdx x x -=++⎰ 0 . 9. 若22()x f x dx x e C =+⎰，则()f x =222()x e x x +. 10. 方程2dyxy dx= 的通解是 2x yCe =.二、解答题（每题5分，共60分）1.求极限 0x → 00sin cos 1cos sin lim lim 21212x x x x x x x →→-++===解：原式2. 已知21lim ()01x x ax b x →∞⎡⎤+-+=⎢⎥+⎣⎦，求常数,a b ．解: 221(1)()1()11x a x a b x bax b x x +--++--+=++ 由21lim ()01x x ax b x →∞⎡⎤+-+=⎢⎥+⎣⎦可得 10,0a a b -=+=,故1,1a b ==- 3. 设1ln 2arctan 1xy x x +=+-，求xy d d 及22d y dx . 解：241124[ln(1)ln(1)2arctan ]1111dy x x x dx x x x x'=+--+=++=+-+- 22d y dx =()()334224444(4)16111x x x x x'⋅-⎛⎫=-= ⎪-⎝⎭-- 4. 设063sin 33=+-+y x y x ，求.0=x dxdy解：把方程两边分别对x 求导，得,063cos 33322=+-+dxdy x dx dy y x （*）故 .23cos 22+-=y x x dx dy 由原方程可得，0=x 时，0=y ，将0,0==y x 代入上式，即得 .210==x dxdy 5. 求极限1ln 0lim(cot )xx x +→解 1ln 011limln(cot )ln(cot )ln ln 0lim(cot )lim xx x x x xx x x e e+→++→→==201(csc )cot lim 11x x xxee +→--==．6. 设220()()x F x tf x t dt =-⎰，其中()f x 在0x =的某邻域内可导，且(0)0,(0)1f f '==，求4()limx F x x →. 解：2220222044300011()(()2)()22lim lim lim 4xu x t x x x x f u du f x x tf x t dt x x x=-→→→---⋅-===⎰⎰原式 2201()11lim (0)444x f x f x →'===7. 求不定积分dx ⎰ 解：332221==2x x C +原式8. 求不定积分解：655332666==6ln(1)1)()1x t dx t t dt dt t C C t t t t ====++=+++⎰⎰原式 9. 求定积分1arctan x xdx ⎰解：22211110000arctan arctan arctan arctan 222x x x x xdx xd x d x ==-⎰⎰⎰ 2110201111(arctan )24218242x dx x x x πππ=-=--=-+⎰ 10. 求反常积分2032dx x x +∞++⎰解：20001132(1)(2)12dx dx dx x x x x x x +∞+∞+∞==-++++++⎰⎰⎰ 01ln(1)ln(2)lnln 22x x x x +∞+∞+=+-+==+11. 求曲线()y f x =，使其切线在纵轴上的截距等于切点的横坐标.解：切线方程为()()Y y f x X x '-=-；当0X =，()()Y xf x f x '=-+由题意可得：()()x xf x f x '=-+；即11y y x'-=- 通解是 (ln )(ln )y x x C or y x x C =-+=+.12. 求初值问题()(0)1,(0)1x f e f x f f ''⎧=-⎨'==⎩.解：由题意，特征方程为210r +=，特征根为12,r i r i ==-，故对应齐次方程通解为12cos sin y C x C x =+；1λ=不是特征方程的根，故可设原方程有特解()x f x Ae *=，解得()12x f x e *=，故原方程的通解为()121cos sin 2x f x C x C x e =++；由(0)1,(0)1f f '==得本题解为()111cos sin 222x f x x x e =++.三、设)(x f 在区间[,]a b 上连续，且()0f x >，()(),[,]()x xabdtF x f t dt x a b f t =+∈⎰⎰. 证明：（1）()2F x '≥; （2）方程()0F x =在区间(,)a b 内有且仅有一个根.（5分）. 证明：（1）1()()2()F x f x f x '=+≥；（2）()()()()a ab aba dtdt F a f t dt f t f t =+=-⎰⎰⎰；()()()()b b b a b a dt F b f t dt f t dt f t =+=⎰⎰⎰ 又()0f x >，所以()()0F a F b <，从而方程()0F x =在区间(,)a b 内有一个根. 又()20F x '≥>，是单调递增的，从而方程()0F x =在区间(,)a b 内仅有一个根. 四、设()f x 在[0,1]上连续，在(0,1)内可导，且(1)0f =，证明在(0,1)内存在一点ξ，使 ()()f f ξξξ'=-．（5分）证明：令()()F x xf x =，则()F x 在[0,1]上连续，在(0,1)内可导，且因(1)0f =，则(0)0(1)F F == 即()F x 在[0,1]上满足罗尔定理的条件，则至少存在(0,1)ξ∈使()0F ξ'= 又()()()F x f x xf x ''=+，即()()0f f ξξξ'+=，即 ()()f f ξξξ'=-．五、设抛物线2y ax bx c =++通过点(0,0)，且当[0,1]x ∈时，0y ≥.试确定,,a b c 的值，使得该抛物线与直线1,0x y ==所围图形的面积为4/9，且使该图形绕x 轴旋转而成的旋转体的体积最小. (10分)解：由于设抛物线2y ax bx c =++通过点(0,0)，故0c =.且11222004;()9ax bxdx V ax bx dx π+==+⎰⎰；即有2241;()329523a b a b V ab π+==++；于是221444[2()()]5293393a a a V a π=+-+-且令1()053a V π'=+=.得唯一驻点53a =-，进而2b =. 所以，5,2,03a b c =-==.。

高数(大一上)期末试题及答案

第一学期期末考试试卷（1）课程名称：高等数学(上) 考试方式：闭卷完成时限：120分钟班级：学号：姓名：得分： . 一、填空(每小题3分，满分15分)1、xx x x 2sin 3553lim 2++∞→ 2、设A f =-'')1(，则=--'--'→hh f f h )12()1(lim 0 3、曲线⎩⎨⎧==-t tey e x 2在0=t 处切线方程的斜率为4、已知)(x f 连续可导，且2)2(,)1(,1)0(,0)(e f e f f x f ===>，='⎰10)2()2(dx x f x f5、已知21)(xe xf x+=，则='')0(f 二、单项选择(每小题3分，满分15分)1、函数x x x f sin )(=，则 ( )A 、当∞→x 时为无穷大B 、当∞→x 时有极限C 、在),(+∞-∞内无界D 、在),(+∞-∞内有界2、已知⎩⎨⎧≥<=1,ln 1,)(x x x e x f x ，则)(x f 在1=x 处的导数( )A 、等于0B 、等于1C 、等于eD 、不存在3、曲线xxe y -=的拐点是( )A 、1=xB 、2=xC 、),1(1-eD 、)2,2(2-e 4、下列广义积分中发散的是( )A 、⎰10sin x dxB 、⎰-101xdx C 、⎰+∞+02/31x dx D 、⎰+∞22ln xx dx5、若)(x f 与)(x g 在),(+∞-∞内可导，)()(x g x f <，则必有( ) A 、)()(x g x f -<- B 、)()(x g x f '<'C 、)(lim )(lim 0x g x f xx xx →→< D 、⎰⎰<0000)()(x x dx x g dx x f三、计算题（每小题7分，共56分）答题要求：写出详细计算过程1、求xx e e x x x x sin )cos 1()(lim 220---→2、求)arcsin(lim 2x x x x -++∞→3、设)(x y y =由03=-+xyy x 确定，求0|=x dy 。

大一高数a1期末试题及答案

大一高数a1期末试题及答案一、选择题（每题4分，共20分）1. 已知函数f(x)=x^2-4x+4，求f(2)的值。

A. 0B. 4C. 8D. 12答案：A2. 计算极限lim(x→0) (sin x / x)。

A. 0B. 1C. 2D. ∞答案：B3. 求不定积分∫(3x^2-2x+1)dx。

A. x^3 - x^2 + x + CB. x^3 + x^2 - x + CC. x^3 - x^2 + x - CD. x^3 + x^2 + x - C答案：A4. 判断以下级数是否收敛：∑(n=1 to ∞) (1/n^2)A. 收敛B. 发散答案：A5. 求函数y=ln(x)的导数。

A. 1/xB. xC. ln(x)D. x^2答案：A二、填空题（每题5分，共20分）1. 已知等差数列的首项为2，公差为3，求第5项的值：______。

答案：172. 计算定积分∫(0 to 1) x^2 dx的值：______。

答案：1/33. 求函数f(x)=x^3-6x^2+11x-6的极值点。

答案：x=1, x=24. 判断函数f(x)=x^3-3x+1的单调性。

答案：在区间(-∞, 1)上单调递增，在区间(1, +∞)上单调递减。

三、解答题（共60分）1. 求函数f(x)=x^3-6x^2+11x-6的极值点，并说明极值类型。

（15分）答案：函数f(x)的导数为f'(x)=3x^2-12x+11，令f'(x)=0，解得x=1, x=2。

通过二阶导数测试，f''(x)=6x-12，f''(1)=-6<0，f''(2)=6>0，所以x=1处为极大值点，x=2处为极小值点。

2. 计算定积分∫(0 to 2) (x^2-2x+1) dx，并求出原函数。

（15分）答案：原函数为F(x)=1/3x^3-x^2+x，定积分值为F(2)-F(0)=8/3-4+2=2/3。

浙江师范大学高等数学(上) 期末试题 A卷答案(理科1)

浙江师范大学《高等数学（上）》 A 卷答案（理科1）一、选择题（每小题2分，共12分）1、C2、C3、D4、D5、B6、A二、填空题（每小题2分，共16分）①e -3 ② 0 ③[1,1]- ④ln cos sin 2x x x C --++⑤ 5ln 6⑥ 2 ⑦ ⑻ x xy 224+'=() 三、问答题（5分） 221()x f x x x x-=-指出sin 的间断点，并判别其类型．解 (1)(1)()01()(1)x x x f x x x f x x x +-===-sin ，与是的间断点 00(1)lim ()lim 2x x x x f x x →→+==sin 因，11(1)sin lim ()lim 2sin1x x x x f x x→→+==， 1()f x 所以0和都是的可去间断点。

四、计算题（每小题7分，共49分）1、1lim xx x →+∞求极限 11ln lim ln lim lim 0.1xx x x x x y x y x →+∞→+∞→+∞====解设,则 01e ==原式2、44411ln ,d 4(1)41x y y x x=+++设　求．解d ()d y y x x '=33324442141441d d 4(1)41(1)x x x x x x x x x x ⎡⎤⎛⎫-=+-=⎢⎥ ⎪+++⎝⎭⎣⎦ 3、.d )1(3x e e x x ⎰+求解x e e x x ⎰+d )1(3)1d()1(3++=⎰x x e e 41(1).4x e C =++ 4、.)1)(1(d 2⎰++x x x 求 22d 111:()d (1)(1)211x x x x x x x -=-++++⎰⎰解2221d 1d(1)1d 214121x x x x x x +=-++++⎰⎰⎰ 2111l n 1l n 1a r c t a n .242x x x C =+-+++（） 1200d ()d ln(1)d d y t y y x xy e t t t x -=+⎰⎰5、设是由方程所确定的隐函数，求．解 y xy e y y +'-'=0，'=-y y e xy6、求232sec ,d sec tan d sec tan d 1d cos d sin cos sec tan sec 22x t x t t tt t t t t t t t t C t t t ==⋅⋅====++⋅⎰⎰⎰解令原式11arccos .2C x = 7、求微分方程d 1d e yy x x =+的通解。

高等数学上期末试卷(含答案)

一．选择题：（每小题3分，共15分）1. 若当0x →时，arctan x x -与nax 是等价无穷小，则a = ( ) B A. 3 B.13 C. 3- D. 13- 2. 下列函数在[1,1]-上满足罗尔定理条件的是 ( )C A. ()f x x = B. 3()f x x =C. ()e e xxf x -=+ D. 1,10()0,01x f x x -≤≤⎧=⎨<≤⎩3. 如果()e ,xf x -=则(ln )d f x x x'=⎰ ( )B A. 1C x -+ B. 1C x+ C. ln x C -+ D. ln x C + 4.曲线y x=渐近线的条数是( ) C A. 1 B. 2 C. 3 D. 45. 设函数()f x 与()g x 在[,]a a -上均具有二阶连续导数，且()f x 为奇函数，()g x 为偶函数，则[()()]d aa f x g x x -''''+=⎰( ) DA. ()()f a g a ''+B. ()()f a g a ''-C. 2()f a 'D. 2()g a '二．填空题：（每小题3分，共15分）1. 要使函数2232()4x x f x x -+=-在点2x =连续，则应补充定义(2)f = .142. 曲线2e x y -=在区间上是凸的.(,22-序号3．设函数322(21)e ,x y x x x =+++则(7)(0)y =______________.77!2+4. 曲线231x t y t⎧=+⎨=⎩在2t =点处的切线方程是 . 37.y x =- 5.定积分11(cos x x x -+=⎰ .π2三．解下列各题：（每小题10分，共40分）1．求下列极限（1）22011lim .ln(1)x x x →⎡⎤-⎢⎥+⎣⎦. 解：原式=2240ln(1)lim x x x x→-+ …………..2分 2302211lim.42x xx x x →-+== ………….3分（2）()22220e d lim e d xt xx t t t t-→⎰⎰.解：原式= ()222202e d e limext x x x t x --→⋅⎰………….3分 22000e d e =2lim2lim 2.1x t xx x t x--→→==⎰ …………..2分2. 求曲线0πtan d (0)4x y t t x =≤≤⎰的弧长.解：s x x == …………..5分ππ440sec d ln sec tan |ln(1x x x x ==+=+⎰ ………..5分 3. 设()f x 满足e ()d ln(1e ),x x f x x C =-++⎰求()d .f x x ⎰解：1(),1e xf x -=+ …………..4分 1e ()d d d 1e 1e xx xf x x x x ---=-=++⎰⎰⎰ …………..3分 ln(1e ).x C -=++ …………..3分4. 已知2lim e d ,xc x x x c x x x c -∞→+∞+⎛⎫= ⎪-⎝⎭⎰求常数.c 解：2lim e ,xc x x c x c →+∞+⎛⎫= ⎪-⎝⎭………….4分 221e d (24cxc c x x -∞=-⎰ …………. 4分 5.2c = …………. 2分四．解下列各题：（每小题10分，共30分）1. 设()f x 在[,]a b 上连续，且()0,f x >且1()()d d ,()xba xF x f t t t f t =-⎰⎰求证：（1）[,],()2;x a b F x '∀∈≥（2）()F x 在(,)a b 内恰有一个零点.证明：（1）1()()2,()F x f x f x '=+≥= ……3分（2）()F x 在[,]a b 上连续 ……1分11()()d d d 0,()()a bb aaa F a f t t t t f t f t =-=-<⎰⎰⎰ ……2分1()()d d ()d 0,()b bb aba Fb f t t t f t t f t =-=>⎰⎰⎰ ……2分由零点定理，()F x 在(,)a b 内至少有一个零点. ……1分又()F x 在[,]a b 上严格单调增，从而()F x 在(,)a b 内恰有一个零点.……1分2. 设直线(01)y ax a =<<与抛物线2y x =所围成图形的面积为1,S 它们与直线1x =围成图形的面积为2.S（1）确定a 的值，使12S S S =+取得最小值，并求此最小值; （2）求该平面图形绕x 轴旋转一周所得的旋转体的体积.解：22(0,0),(,)y ax a a y x=⎧⇒⎨=⎩ ……..2分 1220()d ()d a aS ax x x x ax x =-+-⎰⎰31,323a a =-+21()0,22S a a a '=-=⇒=唯一驻点()20,S a a ''=>最小值2(.26S = ……..4分1222222π[()()]d π[()()]d 22x V x x x x x x =-+-1π.30+=……..4分 3. 设()f x 在[0,1]上二次可微，且(0)(1)0,f f ==证明：存在(0,1),ξ∈使得()()0.f f ξξξ'''+=证明：令()(),F x xf x '=则()F x 在[0,1]上可微， ……..3分(0)(1)0,f f ==()f x 在[0,1]上可微，由罗尔定理存在(0,1),η∈使()=0f η'……..3分(0)()0,F F η==由罗尔定理存在(0,)(0,1),ξη∈⊂使()=0F ξ' ()()()，F x f x xf x ''''=+(0,1),()()=0.f f ξξξξ'''∴∈+ ……..4分。

高数a上册期末试题及答案

高数a上册期末试题及答案一、选择题（每题5分，共20题）1. 设函数 $f(x) = \sqrt{3x-2}$，则其定义域为A. $(-\infty, \frac{2}{3}]$B. $\left[ \frac{2}{3}, \infty \right)$C. $[\frac{2}{3}, \infty)$D. $(-\infty, \frac{2}{3}) \cup [\frac{2}{3}, \infty)$答案：C2. 函数 $y = \sin^2 x + \cos^2 x$ 的值域为A. $(-\infty, 1]$B. $[0, 1]$C. $[1, \infty)$D. $[\frac{1}{2}, 1]$答案：B3. 设函数 $f(x) = e^x \ln x$，则 $f'(x) = $A. $e^x \ln x$B. $e^x \left( \frac{1}{x} + \ln x \right)$C. $e^x \left( \ln x - \frac{1}{x} \right)$D. $e^x \left( \frac{1}{x} - \ln x \right)$答案：B4. 若直线 $y = 3x + b$ 与抛物线 $y = ax^2 + bx + 1$ 相切，则 $a + b = $A. 2B. 3C. 4D. 5答案：D5. 函数 $f(x) = \frac{x-1}{\sqrt{x^2 + 1}}$ 的渐近线为A. $y = x - 1$B. $y = x + 1$C. $y = -x + 1$D. $y = -x - 1$答案：A6. 函数 $f(x) = \ln(1 + e^{2x})$ 的反函数为A. $f^{-1}(x) = \ln(x) - \ln(1 - x^2)$B. $f^{-1}(x) = \ln(x^2 - 1)$C. $f^{-1}(x) = \frac{e^x - 1}{2}$D. $f^{-1}(x) = \frac{1}{2} \ln(x) + \ln(1 - x)$答案：D7. 设函数 $f(x) = \arcsin (\sin x)$，则当 $x = \frac{5\pi}{6}$ 时，$f(x) =$A. $\frac{5\pi}{6}$B. $\frac{\pi}{6}$C. $\frac{\pi}{3}$D. $\frac{2\pi}{3}$答案：C8. 函数 $f(x) = \frac{\sin x}{\cos^2 x}$ 的最大值为A. 1B. $\sqrt{3}$C. 2D. $2\sqrt{3}$答案：D9. 函数 $f(x) = x^2 + 2x + 1$ 在区间 $[-1, 1]$ 上的最大值为A. 0B. 1C. 2答案：D10. 函数 $f(x) = \frac{x^2 - 1}{x^2 + 1}$ 的图像关于直线 $x = a$ 对称，则 $a = $A. 1B. 0C. -1D. 2答案：B11. 设 $\sin \alpha = \frac{1}{4}$，$\cos \beta = \frac{4}{5}$，且$\alpha$ 和 $\beta$ 都是第二象限角，则下列四个式子中成立的是A. $\sin (\alpha - \beta) = -\frac{3}{4}$B. $\sin (\alpha + \beta) = \frac{3}{8}$C. $\cos (\alpha - \beta) = \frac{1}{5}$D. $\cos (\alpha + \beta) = \frac{2}{5}$答案：C12. 如果点 $A(1, 2)$ 在抛物线 $y = -x^2 + 3x + k$ 上，那么 $k = $A. -3B. -5D. -9答案：B13. 设函数 $f(x) = x^3 - 3x^2 - 4x + 12$，则 $f'(x)$ 的零点有A. -2, 2B. -1, 3C. -4, 3D. -1, 4答案：A14. 设点 $P(x, y)$ 满足 $y^2 = px$，其中 $p > 0$ 是常数，则焦点所在的直线方程为A. $y = -\frac{p}{2}$B. $x = -\frac{p}{2}$C. $y = \frac{p}{2}$D. $x = \frac{p}{2}$答案：B15. 函数 $f(x) = x^3 - 3x + 1$ 在区间 $[0, 2\pi]$ 上的最小值为A. -1B. 0D. 2答案：A16. 设直线 $y = 2x + 1$ 与曲线 $y = x^2 + bx + c$ 相切，则 $b + c = $A. 0B. $\frac{1}{2}$C. 1D. 2答案：C17. 设函数 $f(x) = (1 - x^2) \cos x$，则 $f''(x)$ 的一个零点在A. $(0, \frac{\pi}{2})$B. $(0, \pi)$C. $(\pi, 2\pi)$D. $(\pi, 3\pi)$答案：B18. 设函数 $f(x) = \sin^2 x - \sqrt{3} \sin x \cos x + \cos^2 x$，则$f(x)$ 的最大值为A. 2B. $2\sqrt{2}$C. 3D. $2 + \sqrt{3}$答案：C19. 设函数 $f(x) = e^x$，$g(x) = x^2$，则 $f(x) \cdot g(x) = $A. $e^{x^2}$B. $x^2 e^x$C. $x^2 e^{x^2}$D. $x^2 + e^x$答案：B20. 设 $a > 0$，则 $\lim\limits_{x \to +\infty} \frac{x^a}{e^x}$ 的值为A. 0B. $\frac{1}{e}$C. 1D. $+\infty$答案：A二、计算题（每题10分，共4题）1. 求函数 $f(x) = \frac{2x^2 - 3x + 1}{x - 1}$ 的极限 $\lim\limits_{x\to 1} f(x)$.解：使用“分子分母可约”的性质，可将函数 $f(x)$ 化简为 $f(x) = 2x - 1$，则 $\lim\limits_{x \to 1} f(x) = \lim\limits_{x \to 1} (2x - 1) = 2(1) - 1 = 1$.答案：12. 求曲线 $y = e^x$ 与直线 $y = kx$ 相交的两个点的坐标，其中 $k > 0$ 是常数.解：将曲线 $y = e^x$ 和直线 $y = kx$ 代入方程中，得到 $e^x = kx$，然后可以使用迭代法或图像法求得相交点的坐标.答案：相交点的坐标为 $(x_1, e^{x_1})$ 和 $(x_2, e^{x_2})$，其中$x_1$ 和 $x_2$ 是满足方程 $e^x = kx$ 的两个解.3. 求曲线 $y = \sin x$ 与直线 $y = x$ 相交的点的个数，并说明理由.解：将曲线 $y = \sin x$ 和直线 $y = x$ 代入方程中，得到 $\sin x = x$，然后可以通过分析函数的周期性和图像来确定相交点的个数.答案：方程 $\sin x = x$ 的解存在无穷个，但相交点的个数取决于给定的区间. 在区间 $[0, \pi]$ 上，方程有一个解；在区间 $[2\pi, 3\pi]$ 上，方程又有一个解. 因此，相交点的个数是不确定的.4. 求函数 $y = x^2 + x$ 在区间 $[-2, 2]$ 上的最大值和最小值，并求出取得最大值和最小值的点.解：首先求导数 $y' = 2x + 1$，然后令 $y' = 0$，解得 $x = -\frac{1}{2}$，将 $x = -2, -\frac{1}{2}, 2$ 代入函数 $y = x^2 + x$，得到对应的 $y$ 值. 最大值为 $y = y_{\text{max}}$ 对应的点为 $(-\frac{1}{2},y_{\text{max}})$，最小值为 $y = y_{\text{min}}$ 对应的点为 $(-2,y_{\text{min}})$ 和 $(2, y_{\text{min}})$.答案：最大值为 $y_{\text{max}} = \frac{5}{4}$，取得最大值的点为 $(-\frac{1}{2}, \frac{5}{4})$；最小值为 $y_{\text{min}} = -2$，取得最小值的点为 $(-2, -2)$ 和 $(2, -2)$.三、证明题（每题20分，共2题）1. 证明函数 $f(x) = \frac{x^3}{3} - x^2 + 2x$ 的导数 $f'(x)$ 恒大于零.证明：求导数 $f'(x) = x^2 - 2x + 2$，我们可以通过判别式来判断 $f'(x)$ 的正负性.判别式为 $\Delta = (-2)^2 - 4(1)(2) = 4 - 8 = -4$，由于 $\Delta < 0$，所以判别式小于零，即 $f'(x)$ 的二次项系数小于零，说明二次项的系数是正的，从而导数 $f'(x)$ 恒大于零.证毕.2. 证明函数 $f(x) = x^3 - 3x^2 + 3$ 的图像关于直线 $x = 1$ 对称.证明：要证明函数的图像关于直线 $x = 1$ 对称，需证明对于任意$x$ 值，函数 $f(x)$ 和 $f(2 - x)$ 的函数值相等.将 $f(x) = x^3 - 3x^2 + 3$ 代入 $f(2 - x)$，得到 $f(2 - x) = (2 - x)^3 -3(2 - x)^2 + 3$，对其进行展开和化简得到 $f(2 - x) = (2 - x)^3 - 3(2 -x)^2 + 3 = x^3 - 3x^2 + 3 = f(x)$，即 $f(x) = f(2 - x)$，证明了函数的图像关于直线 $x = 1$ 对称.证毕.四、应用题（每题50分，共1题）1. 求函数 $f(x) = x^3 + x^2 - 3x$ 的驻点及其对应的极值.解：求导函数 $f'(x) = 3x^2 + 2x - 3$，令 $f'(x) = 0$，求得驻点的 $x$ 坐标，然后将其代入原函数求得对应的 $y$ 坐标.求导的一阶导数方程为 $f'(x) = 3x^2 + 2x - 3 = 0$，通过求根公式求得 $x = -1$ 和 $x = \frac{1}{3}$，将其代入原函数 $f(x)$ 得到对应的$y$ 坐标.将 $x = -1$ 代入 $f(x)$，得到 $f(-1) = (-1)^3 + (-1)^2 - 3(-1) = -1 + 1+ 3 = 3$，将 $x = \frac{1}{3}$ 代入 $f(x)$，得到 $f(\frac{1}{3}) =(\frac{1}{3})^3 + (\frac{1}{3})^2 - 3(\frac{1}{3}) = \frac{1}{27} +\frac{1}{9} - 1 = 0$.因此，函数 $f(x) = x^3 + x^2 - 3x$ 的驻点及其对应的极值为 $(-1, 3)$ 和 $(\frac{1}{3}, 0)$.答案：驻点为 $(-1, 3)$ 和 $(\frac{1}{3}, 0)$，分别对应极大值和极小值.。

(完整版),期末高等数学(上)试题及答案,推荐文档

1、(本小题 3 分)
解: 原式
lim
x2
3x 6x2
2 12 18x
12
6x lim x 2 12 x 18
2
2、(本小题 3 分)
(1
x x2)2
dx
1 d(1 x2 ) 2 (1 x 2) 2
11 2 1 x2 c.
3、(本小题 3 分)
因为 arctan x
而 lim arcsin 1 0
lim
x
x
x
x
1
1
(10 )(11 )
x
x
10 11 21
(10 1 ) 2 x
6 10 11 7
2
16、( 本小题 10 分 )
解:
cos2x dx
1 sin x cosx
d( 1 sin 2x 1) 2
1 1 sin 2x 2
1 ln 1 sin 2x c
2
二、解答下列各题 (本大题共 2 小题，总计 13 分 ) 1、(本小题 5 分)
且
F ( 1) 1 0 ， F (1) 1 0 .
22
由零点定理知存在
x1
1 [
,1]
，使
F ( x1 )
0.
2
由 F ( 0) 0 ，在 [ 0, x1] 上应用罗尔定理知，至少存在一点
(0, x1) ( 0,1) ，使 F ( ) f ( ) 1 0 ，即 f ( ) 1 …
第 7 页，共 7 页
9、(本小题 5 分)
3
求 x 1 x dx． 0
10、( 本小题 5 分 )
求函数 y 4 2 x
11、( 本小题 5 分 )

高等数学(上)期末测试卷A答案

大一高等数学期末考试试卷及答案详解

高等数学a上期末考试试题和答案

工程大学2023-2023学年第1学期《高等数学(上)》期末考试试卷(A卷)及标准答案

同济大学《高等数学》(上)期末试卷A及答案

高等数学期末考试试题及答案(大一考试)

大一上学期高数期末考试试题(五套)详解答案

高数(大一上)期末试题及答案

高等数学期末考试试题及答案(大一考试)

《高等数学》期末考试A卷(附答案)

《高等数学(一)》期末复习题(答案)

安徽财经大学大学《高等数学A》2023-2024学年第一学期期末试卷

人教A版高一数学上学期期末测试卷(带答案)

高等数学(上学期)期末考试试卷及答案

高数(大一上)期末试题及答案

大一高数a1期末试题及答案

浙江师范大学 高等数学(上) 期末试题 A卷答案(理科1)

高等数学上期末试卷(含答案)

高数a上册期末试题及答案

(完整版),期末高等数学(上)试题及答案,推荐文档

浙江师范大学高等数学(上) 期末试题 A卷答案(理科1)