等效转动惯量的计算专题培训课件
合集下载
最全的转动惯量的计算ppt课件
有
l
J0
r 2dm l 2 x2dx l3
l 2
12
将 l m 代入上式，得：
J0
1 12
ml 2
2
（2）当转轴通过棒的一端A并与棒垂直时
A
xO
dx l
J0
r2dm l x2dx 1 ml 2
ቤተ መጻሕፍቲ ባይዱ
0
3
3
例题2）半径为R的质量均匀分布的细圆环，质 量均为m，试分别求出对通过质心并与环面垂 直的转轴的转动惯量。
x
9
常见刚体的转动惯量
J mr 2 J mr2 / 2 J mr2 / 2 J m(r12 r22) / 2
J ml 2 /12
J mr2 / 2
J 2mr 2 / 5 J 2mr 2 / 3
10
例题1 一长为l,质量为m的匀质细杆竖直放置, 其下端与一固定铰链o相连,并可绕其转动.当其 受到微小扰动时,细杆将在重力的作用下由静止
开始绕铰链o转动.试计算细杆转到与铅直线呈
角时的角加速度和角速度.
解:受力分析
取任一状态,由转动定律
M外
1 2
mgl sin
J
P o
J 1 ml2 3
3g sin
2l
11
d d d 3g sin d t d d t 2l
d 3g sind
16
例一静止刚体受到一等于M0（N.m)的不变力矩的 作用,同时又引起一阻力矩M1， M1与刚体转动的 角速度成正比,即| M1 |= a(Nm),(a为常数)。又
已知刚体对转轴的转动惯量为J,试求刚体角速度
最全的转动惯量的计算 ppt课件
aCX C
mg
N
NY
求N，N就Y得求maCg
maCY
，即C点的
NX
C 加速度，现在C点作圆周运动， mg 可分为切向加速度和法向加速
度但对一点来说，只有一个加
速度。故这时：
aCX ….实际上正是质心的转动的切向加速度 aCY ….实际上正是质心ppt课的件 转动的法向加速度23
N
XO N
aCX
YZ
当 l > R 2时，f < 0，静摩擦力向前。
ppt课件
16
例一静止刚体受到一等于M0（N.m)的不变力矩的 作用,同时又引起一阻力矩M1， M1与刚体转动的 角速度成正比,即| M1 |= a(Nm),(a为常数)。又
已知刚体对转轴的转动惯量为J,试求刚体角速度
变化的规律。
已知：M0 J M1= –a |t=0=
N YZ
L
已知：m，L
XO
求：，，N 解：1）以杆为研究对
象
mg
受力：mg，N（不产生 对轴的力矩）
建立OXYZ坐标系
ppt课件
19
建立OXYZ坐标系（并以Z轴为转动量的正方向）
N
Y
M
Z
L
XO
r
M mg L sin
r故取JF正值沿。13Z轴m正2L2向，(1)
mg 0则 0
/ 2则 3g / 2L
N
YZ
XO
r
d /2 3g cosd
0
0 2L
1 2
2
3g 2L
sin
0
/
2
3g 2L
mg
3g L
3）求N=？ 轴对杆的力，不影响到杆的转动，但影响质 心的运动，故考虑用p质pt课件心运动定理来解。 22
等效转动惯量的折算ppt课件
• (1) 系统等效转动惯量 的计算
• 系统运动部件动能的总和J d为x
E
1 2
m i 1
Mi
Vi 2
1 2
n
Jj
j 1
2 j
；.
1
二、伺服系统稳态设计
• 设等效到执行元件输出轴上的总动能为
Edx
1 2
J dx
2 d
• 根据动能不变的原则，有 Edx ，E 系统等效转动惯
量为
J dx
m i 1
d
d，t 则
• 由矩于为Wd W，所以执行元件输出轴所承受的负载转
Td
m i 1
FiV i
d
n Tj j j1 d
；.
3
M
i
Vi
d
2
n
J
j 1
j
j d
2
• 式中 d为执行元件输出轴的转速(rad／s)
；.
2
二、伺服系统稳态设计
• (2) 等效负载转矩的计算
• 设上述系统在时间内克服负载所作的功的总和
为
m
n
W FiVit Tj jt
i 1
j 1
•
执行元件输出轴在时间内的转角为
执行元件所作的功为 Wd Td d t
系统等效转动惯量的计算系统运动部件动能的总和为二伺服系统稳态设计湖南农业大学dx根据动能不变的原则有系统等效转动惯为执行元件输出轴的转速rads二伺服系统稳态设计dxdx由于所以执行元件输出轴所承受的负载转
二、伺服系统稳态设计（湖南农业大学）
• 如图所示系统中，由m个移动部件和n个转动 部件组成。mi、Vi和Fi分别为移动部件的质量(kg)、 运动速度(m／s)和所承受的负载力(N)；Jj、nj和 Tj分别为转动部件的转动惯量(kg﹒m2)、转速(r ／min或rad／s)和所承受负载力矩(Nm)。
• 系统运动部件动能的总和J d为x
E
1 2
m i 1
Mi
Vi 2
1 2
n
Jj
j 1
2 j
；.
1
二、伺服系统稳态设计
• 设等效到执行元件输出轴上的总动能为
Edx
1 2
J dx
2 d
• 根据动能不变的原则，有 Edx ，E 系统等效转动惯
量为
J dx
m i 1
d
d，t 则
• 由矩于为Wd W，所以执行元件输出轴所承受的负载转
Td
m i 1
FiV i
d
n Tj j j1 d
；.
3
M
i
Vi
d
2
n
J
j 1
j
j d
2
• 式中 d为执行元件输出轴的转速(rad／s)
；.
2
二、伺服系统稳态设计
• (2) 等效负载转矩的计算
• 设上述系统在时间内克服负载所作的功的总和
为
m
n
W FiVit Tj jt
i 1
j 1
•
执行元件输出轴在时间内的转角为
执行元件所作的功为 Wd Td d t
系统等效转动惯量的计算系统运动部件动能的总和为二伺服系统稳态设计湖南农业大学dx根据动能不变的原则有系统等效转动惯为执行元件输出轴的转速rads二伺服系统稳态设计dxdx由于所以执行元件输出轴所承受的负载转
二、伺服系统稳态设计（湖南农业大学）
• 如图所示系统中，由m个移动部件和n个转动 部件组成。mi、Vi和Fi分别为移动部件的质量(kg)、 运动速度(m／s)和所承受的负载力(N)；Jj、nj和 Tj分别为转动部件的转动惯量(kg﹒m2)、转速(r ／min或rad／s)和所承受负载力矩(Nm)。
转动实验I转动惯量ppt课件
轉動實驗(II)：角動量
• 溜滑梯（純滾＋水平拋射）
線動量與角動量
轉動實驗(III)：角動量守恆
• 角動量守恆
角動量人體實驗(影片)
實驗C2：角動量守恆定律。做實驗順便運動，看看今年的擂臺冠軍是誰？ 實驗C3：角動量守恆定律。看看怎樣可以讓你的旋轉椅說轉就轉，說停就停。
mri?角加速度的測量?轉動慣量的測量?轉動慣量的計算平行軸定理然後和實驗值比較然後和理論值比較itotal轉動實驗ii
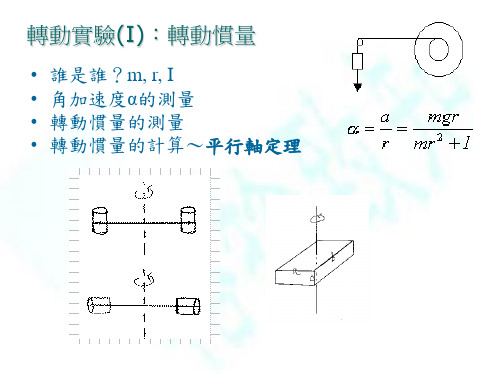
轉動實驗(I)：轉動慣量
• 誰是誰？m, r, I • 角加速度α的測量 • 轉動慣量的測量 • 轉動慣量的計算～平行軸定理～然後和實驗值比較 ～然後理論值比較Itotal
理论力学-转动惯量PPT课件
O
z
rz
y
x
x y
图1
在国际单位制中，转动惯量的常用单位是kg·m2 。
转动惯量
§1 转动惯量的概念
2.回转半径
刚体对于某轴z的转动惯量与其质量m之比值的平方根为一 个当量长度，称为刚体对于该轴的回转半径。因此，有关系式
z
Jz , m
Jz mz2
可见，如果假想地把刚体的全部质量集中于一点，而不改变 这刚体对于该轴的转动惯量，则这个点到该轴的距离应等于回转 半径。
式中
Jx m (y2z2)
Jy m (z2x2)
(1)
Jz m (x2y2)
分别是刚体对轴 x，y 和 z 的转动惯量。
转动惯量
§4 刚体对任意轴的转动惯量·惯性积和惯性主轴
J m L 2 r m ( y 2 z 2 ) c2 o s m (z2x2)co 2 s
m(x2y2)co2s2 m yczo cso s
转动惯量
§1 转动惯量的概念
1.转动惯量的概念
刚体对轴z的转动惯量，是刚体内所有各点的质量与其对该轴
的转动半径的平方的乘积的总和（如图1）。
z
可以表示为
Jz mz2r
可见，转动惯量永远是正值。
rz A
对于质量连续分布刚体： Jz srz2dm
影响转动惯量大小的因素。
● 整个刚体质量的大小。 ● 刚体各部分的质量分布。
解： 由图可见，矩形板在y方向的尺寸a不影响Jy，故可利用上例的结果。
Jy
1 mb2 12
y
dx
类似地可得
Jx
1 ma2 12
利用
Jz Jx Jy
a
C
x
等效转动惯量的计算PPT20页
60、人民的幸福是至高无个的法。— —西塞 罗
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
等效转动惯量的计算
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益， 而是为 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物
谢谢你的阅读
❖ 知识就是财富 ❖ 丰富你的人生
71、既然我已经踏上这条道路，那么，任何东西都不应妨碍我沿着这条路走下去。——康德 72、家庭成为快乐的种子在外也不致成为障碍物但在旅行之际却是夜间的伴侣。——西塞罗 73、坚持意志伟大的事业需要始终不渝的精神。——伏尔泰 74、路漫漫其修道远，吾将上下而求索。——屈原 75、内外相应，言行相称。——韩非
等效转动惯量的计算
56、极端的法规，就是极端的不公。 ——西 塞罗 57、法律一旦成为人们的需要，人们 就不再 配享受 自由了 。—— 毕达哥 拉斯 58、法律规定的惩罚不是为了私人的 利益， 而是为 了公共 的利益 ；一部 分靠有 害的强 制，一 部分靠 榜样的 效力。 ——格 老秀斯 59、假如没有法律他们会更快乐的话 ，那么 法律作 为一件 无用之 物
《转动惯量的计算》课件
刚体的转动惯量可以通过对每个质点的转动惯量求和 得到。
常见形状的转动惯量公式
涵盖了圆盘、长棒、球体等常见形状的刚体转动惯量
转动惯量的实验测定
1
二次转动法
通过测量刚体在不同轴上的旋转惯量，判断转Βιβλιοθήκη 惯量的大小。2转动摆法
利用转动摆的运动进行转动惯量的实验测定。
3
牛顿第二定理法
根据牛顿第二定理，实验测定刚体的转动惯量。
总结
1 转动惯量的重要性
转动惯量是研究物体旋转运动的关键参数，对于理解物体的稳定性和运动规律至关重要。
2 转动惯量计算方法的应用
掌握转动惯量计算方法可以帮助我们解决各种旋转运动的问题，推导出物体的运动方程。
3 研究转动惯量的意义和作用
研究转动惯量可以帮助我们深入理解物体的旋转运动规律，拓展我们的物理知识。
质点的转动惯量
定义
质点绕某一轴旋转时的转动惯 量是指质点对该轴的抵抗程度。
计算公式
质点的转动惯量等于质量与离 轴距离之积的总和。
常见形状的转动惯量公式
涵盖了球体、长方体、圆柱体 等常见形状的转动惯量计算公 式。
刚体的转动惯量
定义
刚体的转动惯量是指刚体绕某一轴旋转时，对该轴的 整体抵抗程度。
计算公式
参考文献
本课件参考了相关物理学教材和科研论文。
转轴的平移对转动惯量的影响
平行轴定理
平行轴定理说明了转轴平移时，转动惯量的计算公 式的变化规律。
垂直轴定理
垂直轴定理说明了转轴垂直平移时，转动惯量的计 算公式的变化规律。
应用实例
圆环的转动惯量计算
通过应用公式计算圆环绕垂直直径轴的转动惯量。
圆柱的转动惯量计算
通过应用公式计算圆柱绕其轴线的转动惯量。
常见形状的转动惯量公式
涵盖了圆盘、长棒、球体等常见形状的刚体转动惯量
转动惯量的实验测定
1
二次转动法
通过测量刚体在不同轴上的旋转惯量，判断转Βιβλιοθήκη 惯量的大小。2转动摆法
利用转动摆的运动进行转动惯量的实验测定。
3
牛顿第二定理法
根据牛顿第二定理，实验测定刚体的转动惯量。
总结
1 转动惯量的重要性
转动惯量是研究物体旋转运动的关键参数，对于理解物体的稳定性和运动规律至关重要。
2 转动惯量计算方法的应用
掌握转动惯量计算方法可以帮助我们解决各种旋转运动的问题，推导出物体的运动方程。
3 研究转动惯量的意义和作用
研究转动惯量可以帮助我们深入理解物体的旋转运动规律，拓展我们的物理知识。
质点的转动惯量
定义
质点绕某一轴旋转时的转动惯 量是指质点对该轴的抵抗程度。
计算公式
质点的转动惯量等于质量与离 轴距离之积的总和。
常见形状的转动惯量公式
涵盖了球体、长方体、圆柱体 等常见形状的转动惯量计算公 式。
刚体的转动惯量
定义
刚体的转动惯量是指刚体绕某一轴旋转时，对该轴的 整体抵抗程度。
计算公式
参考文献
本课件参考了相关物理学教材和科研论文。
转轴的平移对转动惯量的影响
平行轴定理
平行轴定理说明了转轴平移时，转动惯量的计算公 式的变化规律。
垂直轴定理
垂直轴定理说明了转轴垂直平移时，转动惯量的计 算公式的变化规律。
应用实例
圆环的转动惯量计算
通过应用公式计算圆环绕垂直直径轴的转动惯量。
圆柱的转动惯量计算
通过应用公式计算圆柱绕其轴线的转动惯量。
二、等效质量和等效转动惯量
第十一章机器的运转及其速度波动的调节（一）教学要求1、掌握等效力（力矩），等效质量（转动惯量）的计算，理解机器运动微分方程2、理解速度波动调节的原理，掌握飞轮设计方法（二）教学的重点与难点1、等效力（力矩），等效质量（转动惯量）2、速度波动的原因，盈亏功、飞轮设计（三）教学内容§11-1 研究机器运转及其速度波动调节的目的一、研究机器运转的目的确定原动件真实运动规律→确定其它运动构件的运动规律，参数。
二、调节机器速度波动的目的1、周期性速度波动危害：①引起动压力，η↓和可靠性。
②可能在机器中引起振动，影响寿命、强度。
③影响工艺，↓产品质量。
2、非周期性速度波动危害：机器因速度过高而毁坏，或被迫停车。
§11-2 机器等效动力学模型研究机器运动和外力的关系时，必须研究所有运动构件的动能变化和所有外力所作的功。
这样不方便。
单自由度的机械系统：某一构件的运动确定了→整个系统的运动确定了。
∴整个机器的运动问题化为某一构件的运动问题。
为此，引出等效力、等效力矩、等效质量、等效转动惯量概念一、等效力和等效力矩研究机器在已知力作用下的运动时，作用在机器某一构件上的假想F或M代替作用在机器上所有已知外力和力矩。
代替条件：机器的运动不变，即：假想力F或力矩M所作的功或所产生的功率等于所有被代替的力和力矩所作的功或所产生的功率之和。
假想力F——等效力假想力矩M——等效力矩等效力或等效力矩作用的构件——等效构件等效力作用的点——等效点通常，选择根据其位置便于进行机器运动分析的构件为等效构件。
等效力或等效力矩所产生的功率B FV P =或P =MW设F i ，M i ——作用在机器第i 个构件上的已知力和力矩V i ——力F i 作用点的速度W i ——构件i 的角速度i θ——F i 和V i 夹角作用在机器所有构件上的已知力和力矩所产生的功率：∑∑∑===±+=k i i ik i i i i k i i W M V F P 111cos θi M 和i W 同向取“+”，否则“-”∴∑∑==±+=k i i ik i i i i B W M V F FV 11cos θ 或∑∑==±+=ki i i k i i i i W M V F MW 11cos θ ∴∑∑==±+=k i B i i k i B i i i V W M V V F F 11cos θ （1） 或∑∑==±+=k i i i ki i i i W W M W V F M 11cos θ （2） 公式讨论：①等效力F 和等效力矩M 只与各速度比有关，∴F 和M 是机构位置的函数。
转动惯量课件 PPT
i
a (b c) b(a c) c(a b)
mi[ωri2 ri (ω ri )]
i
ri xiex yiey ziez
(1)
静止系或活
(2)
动系都可以
ω xex yey zez
(3)
(2)(3)代入(1)可得 J J xex J yey J zez
3、5、1 刚体得动量矩
做定点转动的刚体
则点集{Q1,Q2,…,Qn,…}在空间密布成一个椭球 面,此椭球称为此刚体得惯量椭球。
3、5、4 惯量张量与惯量椭球
惯量椭球得概念
求证：定点转动刚体上满足 OQ 1 所有点Q
构成一个椭球面。
I
证明: 在刚体上建立活动系O-xyz, 并设瞬轴l的方
向余弦为 , , 。
令 OQ 1 R
y
ω l 解:如图建立主轴坐
标系。
b
O
a
薄板对对角线l的转 x 动惯量，在主轴坐标
系下的计算式为
Il I1 2 I2 2 I3 2 (1)
其中I1,I2,I3分别是薄板对三个坐标轴的转动惯量， 是对角,线, l的三个方向余弦。
3、5 转动惯量
例题
对角线l得三个方向余弦分别为
y
ωl
cos a
(
I
xx
2 x
I
yy
2 y
I
zz
2 z
2I xyx y
2I yz yz
2I zxzx )
3、5、3 转动惯量得概念
由转动动能引入转动惯量
T 1
2
i
mivi vi
1 2
i
mi (ω ri ) (ω ri )
ez ω
转动惯量 ppt课件
可见，转动惯量与厚度 l 无关。所以，实心圆柱对
其轴的转动惯量与圆盘的相同。
（3） 球体绕其直径的转动
将均质球体分割成一系
列彼此平行且都与对称轴垂
直得圆盘，则有
J O
1 dm r2 2
1 2
r 2 d z r 2
R 1 ( R 2 z 2 ) 2 d z
R 2
8 R 2 2 m R 2
节始终保持不动，整个刚体绕着这根直线转动，该直
线称作转轴。 Z
只有一个转动自由度。
各质元的线速度、加速
度一般不同，但角量（角 位移、角速度、角加速度） 都相同。
P X
Q
X
描述刚体整体的运动用角量最方便。
2、定轴转动的角量描述
z
角坐标 ：确定刚体的位置
运动学方程： t
角速度 ：描述转动的快慢
• “不怕太阳晒，也不怕那风雨狂，只怕先生骂我 笨，没有学问无颜见爹娘 ……”
• “太阳当空照，花儿对我笑，小鸟说早早早……”
5 . 刚体运动概述：
0 • 刚体——一种特殊质点系 节
质点
刚体
质点系
刚体：在任何情况下形状和大小都不变的物体。即任 意两质点之间的距离保持不变的质点系（理想模型）。
• 刚体 —— ?个自由度
本章将介绍一种特殊的质点 系—刚体—所遵从的力学规律。 它实际上就是质点系的基本原 理在刚体上的应用。重点是定 轴转动，重要的概念是转动惯 量。
精品资料
• 你怎么称呼老师？
• 如果老师最后没有总结一节课的重点的难点，你 是否会认为老师的教学方法需要改进？
• 你所经历的课堂，是讲座式还是讨论式？ • 教师的教鞭
正交轴Ox和Oy的转动惯量之和。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
J
I cq
m i 1
mi
vi
k
2 Leabharlann n j 1Jj
j k
2
vi vi，/ 60
n2/60
m i 1
mi
n
vi，/ 60
I 2/60
2
n j 1
J
j
n n
j I
2/60 2/60
E
EI
1 2
m
m
i
v
2 i
i 1
1 2
n
J
j
2 j
j 1
1 2
J
I eq
2 I
等效惯量：
J
I cq
m i 1
mi
vi I
2
n j 1
J
j
j I
2
3等效转动惯量的推导
等效转动惯量的计算
根据工程上常用的转速 为 n (r / min) ，将时间用分钟表示， 转角由弧度转换成转， 则公式化为：
目
掌握转动惯量及其等效 的分析和计算方法
标 转动惯量的计算公式
转动惯量的等效原则
等效转动惯量的计算 公式及计算分析
说课 等效转动惯量的计算
教 学 内 容 重教点学 与 难内点容 目 标
转动惯量等效的意义 转动惯量的等效原则 转动惯量的计算公式
等效转动惯量的计算公式及计算分析
说课 等效转动惯量的计算
动)相等
拓展 视野
通过对比剖析理论力学和机电一体化中对公式的不同 要求
在工程背景上进行拓展训练
1问题的引出
等效转动惯量的计算
例：由直流伺服电动机驱动的全闭
环系统，如图1所示，检测传感器安装
在移动工作台导轨上。这种方式常用
于不能采用大变速比的直流伺服电动
机或CNC机床的连续切削控制等的驱
动系统中。已知： 电机 :转数 :nI 120r/0min;
★机电一体化系统设计：机电一体化系统稳态设计与
分析
maxn
KJeIq ——主谐振频率。 JI Jeq
★机电一体化系统设计：机电一体化系统负载分析
（执行元件的选择与校核） P 电机 TeIqJ9 eI.5 q15 nmax
3等效转动惯量的推导
等效转动惯量的计算
等效原则 无论是直线运动还是回转运动，应用等效前后总动能不
理论力学和机械
原理中学习过，
学 情
保留旧有的
分
思维习惯
析
缺乏工程认识和 实践
大学工科学生
说课 等效转动惯量的计算
教学 方法
案例式教学 采取对比、反问、提问、归纳等方法
教 学 设 计
构建 框架
提炼知识点结构主线： 动能守恒定理——系统中所有零部件动能(包
括平移和转动)总和与等效后的动能(一般为转
情 容 分 与 析 目
（满足机电系统响应快 要求）
标
理论力学：
圆柱体转动
惯量计算
关键词 等效 转动惯量
机械原理： 建立机械系 统等效动力
学模型
说课 等效转动惯量的计算
教学目标
素质目标：
教
理解机电一体化系统中
学
能力目标：
转动惯量等效的意义
内
形成正确的机电一体化
容 知识目标 与 (掌握):
系统稳态设计的思维方 初步理解课程结构框架 法
等效转动惯量的计 算
机电一体化系统设计
第六章
机电一体化系统——机电有机结合分析与设计
6.1 机电一体化系统的稳态与动态设计内容和考虑的方法 6.2 机电有机结合之一——机电一体化系统的稳态设计考 虑方法
6.2.1典型负载分析 一、典型负载 二、负载的等效换算 1、等效转动惯量的计算 2、负载转矩的等效换算 6.2.2 执行元件的匹配选择
min;
问题：
工作台: 移动部件总重: W 2000N, 水平工作载荷: FL水平 800N 垂直工作载荷: FL垂直 800N 最大进给速度为：xmax 4.8m/ min, 导轨摩擦系数：f 0.05;
1、该机械传动系 谐统 振的 频主 n率 ？
2、由轴向刚度和 动齿 间轮 隙传 引起的位 量移 △ x？ 失动
2 等效转动惯量计算的意义
等效转动惯量的计算
★机械系统设计：建立机械系统等效动力学模型
d(1 2Je I(q1)12)/d tT eI(q1, 1,t)1
★机电一体化系统机械传动系统设计：传动系统各级
传动比的最佳分配原则—等效转动惯量最小原则，满足
机电系统响应快速的要求 J e I q m J e I( i q 1 ,i n 2 ,i 3 , i n )
变的原理，进行等效转动惯量公式的推导。
设系统中有 m个移动部件、 n个转动部件，则系统中 总动能为：
E
1 2
m
m
i
v
2 i
i 1
1 2
n
J
j
2 j
j 1
设等效到电机转子所在
轴 I轴的转动惯量为
J
I eq
，则进行转动
惯量等效后系统的动能
为： E I
1 2
J
I eq
2 I
根据能量守恒定理，系 统在转动惯量等效前后 的动能相等，则：
图1 直流伺服电动机驱动全闭环控制系统
转子转动Jm惯 1量 104： kg2m
齿轮箱 :高速减速:比 滚珠丝杠: 直径: d 60mm,
i 3,z1 17,z2 51, m0.002m,B0.015m;
长度：l 2.16m, 导程：l0 0.012m, 丝杠转速：ns 400r /
◎电机是机电一体化系统的执行元件，执行元件在机电一体化系统中为
强 机度和电的有机结合点，它的选取至关重要，等效转动惯量的计算就是 为问题后续执行元件的选择和校核做好准备；
◎根据理论力学的知识：对于旋转体零件转动惯量J=ρπd4L/32。
式中： ρ—材料密度，ρ钢=7.8×103kg/m3；d—直径(m)； L—长度(m) 。
………………………………
6.3 机电有机结合之二——机电一体化系统的动态设计考 虑方法
6.4 机电一体化系统的可靠性设计
说课 等效转动惯量的计算
机电一体化机械系统设
教
计：传动系统各级传动
机电一体化系统设计：第六 章 机电一体化系统稳态设
学 学 内
比的最佳分配原则—等 效转动惯量最小原则
计与分析——负载分析（执 行元件选择与校核）
2
1
4 2
m i 1
mi
vi， 2 n I
n i 1
J
j
nj nI
2
注： vi，的单位为 m / min
4 等效梁转的动强惯度量条的计件算 等效转动惯量的计算公式的相关问题
注问题1：
意
问题2：
为什么将转动惯量常等效到电机输出轴而不等效到其他轴？ 公式中的零件转动惯量J又如何得来？