水文地质学基础之地下水运动基本规律
合集下载
地下水运动的基本规律
地下水运动的基本规律
因为流速V=Q/A，故达西定律也可以用式（56）来表达。 V=Ki（5-6） 式中，V为渗透流速（m/d或cm/s）。
由式（5-6）可知，K是水力坡度为1时的 渗透流速，称为渗透系数。渗透系数可以用来 比较不同岩石的透水性，是水文地质学中一个 非常重要的水文地质参数。
地下水运动的基本规律
地下水运动的基本规律
在满足生产要求和方便研究的前提下，可以不将含 水层概括为均质各向同性、均质各向异性、非均质各向 同性和非均质各向异性的含水层。所谓均质各向同性就 是指渗透系数在含水层的任何空间位置上、任何渗透方 向上均为一个常数；如不为常数则属非均质各向异性， 其余可类推。
对于渗透系数的测定，一般采用室内土柱试验（达 西试验）和野外抽水试验两种方法。一些松散岩石的渗 透系数参考值见表5-4，表见下页。
应该明确，渗透系数不仅取决于 岩石的空隙性质及水在空隙中的存在 形式，而且与地下水的一些物理性质 ，如黏滞性等有关。在具有同样空隙 的岩石中，当水力坡度相等时，黏滞 性大的水（或液体）渗透系数小。
一般情况下，当地下水的黏 滞性相近时可以不予考虑，但在 研究卤水时，不可忽视。因此， 除个别特殊情况外，可以把渗透 系数看作衡量岩石透水性能的参 数。岩石的透水性能在不同空间 位置和渗透方向上是不一致的， 即渗透系数是不相等的。
地下水运动的基本规律
工程地质Βιβλιοθήκη 工程地质地下水运动的基本规律
地下水在岩石空隙（孔隙、裂隙及溶穴） 中的运动称为渗流（渗透），地下水运动的 场所称为渗流场。渗流是在与介质发生密切 联系的条件下进行的，由于受到介质的阻滞， 地下水的运动远较地表水缓慢。
在岩层空隙中渗流时，水的质点有秩序 地、互不混杂地流动，称为层流运动。水的 质点无秩序地、互相混杂地流动，称为紊流 运动。一般认为渗流属于层流。
水文地质-地下水的运动
第三节 地下水向井的稳定运动
四、裘布依公式的讨论
（2）抽水井流量与井径的关系
但实际情况远非如此,井径 对流量的影响比Dupuit公 式反映的关系要大得多。
第三节 地下水向井的稳定运动
四、裘布依公式的讨论
（3）水跃对裘布依公式计算结果的影响
在潜水的出口处一般都存 在渗出面。当潜水流入井 中时也存在渗出面,也称水 跃，即井壁水位hs高于井 中水位hw(图4一10)，而潜 水井的Dupuit公式并没有 考虑渗出面的存在。
H Z p
图4-5 流网示意图
在渗流场中，把水头值相等的点连成线或面就构成了等水 头线或等水头面。
流网是由等水头线和流线所组成的正交网格。流网直观地 描述了渗流场（或流速场）的特征。它可以是正方形、长 方形或曲边方形。
第二节 地下水运动规律
水流类型
一维流任意点的水力坡度均相等（
图4-6a）；
s1=1.00 m s2=1.75 m s3=2.50 m 求K？
Q1=4500 m3/d； Q2=7850 m3/d； Q3=11250 m3/d；
第三节 地下水向井的稳定运动
五、地下水流向非完整井和直线边界附近的完整井
1、承压水非完整井 当α=1时，A=0，就变成 完整井公式，当α很小， A值很大，则公式变为：
第三节 地下水向井的稳定运动
五、地下水流向非完整井和直线边界附近的完整井
2、潜水非完整井 潜水非完整井可以看做上段 是潜水完整井，下段是承压 水非完整井。这样可以近似 的看做总流量Q等于两段Q1 和Q2的和。
第三节 地下水向井的稳定运动
裘布衣假设：
天然水力坡度为0，井附近水力坡度<1/4； 含水层是均质各向同性的，含水层的底板
5地下水运动的基本规律
第五章地下水运动的基本规律5. 1 港流基本概念渗流一地卞水在岩石空隙中的运动称为渗流（渗透，地下径流）。
渗流场一发生渗流的区域。
层流运动——水的质点作有秩序的、互不混杂的流动。
紊流运动——水的质点无秩序的、互相混杂的流动。
稳定流一各个运动要素（水位、流速、流向等）不随时间改变的水流运动。
非稳定流——运动要素随时间变化的水流运动。
地卜•水总是从能量校高处流向能量较低处。
能态差异是地卜水运动的驱动力。
地下水的机械能包括动能和势能，水力学中用总水头（hydiaulic head）H表示，水总是从总水头高的地方流向总水头低的地方。
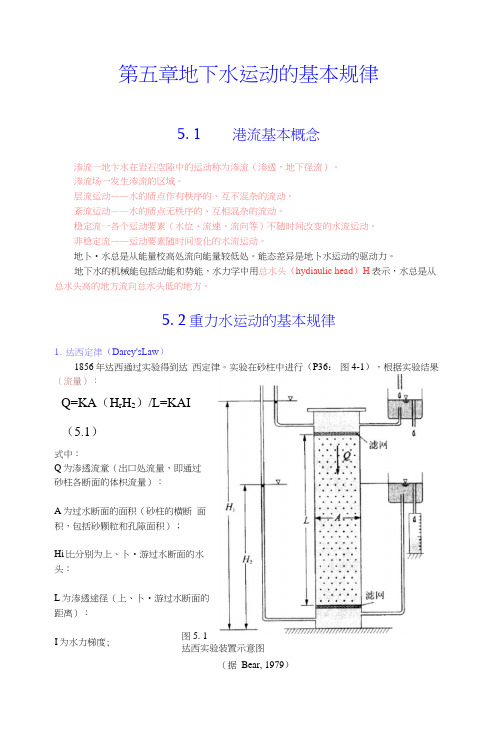
5. 2重力水运动的基本规律1.达西定律（Darcy'sLaw）1856年达西通过实验得到达西定律。
实验在砂柱中进行（P36：图4-1），根据实验结果（流量）：Q=KA（H r H2）/L=KAI（5.1）式中：Q为渗透流童（出口处流量，即通过砂柱各断面的体枳流量）：A为过水断面的面积（砂柱的横断面积，包括砂颗粒和孔隙面积）；Hi比分别为上、卜•游过水断面的水头：L为渗透途径（上、卜•游过水断面的距离）：图5. 1I为水力梯度;达西实验装置示意图（据Bear, 1979）K 为渗透系数。
由水力学：Q=vA达西定律也可以另一种形式表达（流速）: 由公式（5.1）及Q=\A 得：v=KI式中：£ ---- 渗透流速，m/d, cm/s ；K ----- 渗透系数，nVd, cm/s ：I —水力梯度，无量纲（比值）。
具体到实际问题：计算流最:H _ HQ =川F ----------- (单位一•般为：m 3/d, L/s)L微分形式:式中：负号表示水流方向与水力梯度方向相反，水流方向（坐标方向）：由水位高一 低: 而水力梯度方向：由等水位线低一高。
在三维空间中（向量形式）:■\v = -K x ^-i-K v ^- j-K,-51k = -KgradH dy dz或V = -KVH ,式中：K 一为渗透系数张量:gradH =更 i +更* 更 Amdy dz若用标量表示，V 的三个分最分别为:得到 v=Q/A（对地下水也适用）(5.2) (5.3)v=-KdH £Vy= ~K - dy—呻**■ dz2. 渗透流速（V ） （seepage velocity, Daicy velocity ）与实际流速（u ）渗透流速一水流通过整个过水断面（包括砂砾和孔隙）的流速。
地下水运动的基本规律
断面的水头，水头差为h；两断面相距L； (5)下端出口测定流量为Q。
0
0
图4-1 达西实验装置图
5.4.1.2 实验成果
Q KA h KAI L
Q AV
V KI
5.4.2 达西公式中各项的物理意义
5.4.2.1 渗透流速(V) >>在达西定律表达公式中，渗透流速是一个宏观概念，并且
它很容易测量。 >>因此，必须把它与单个水质点在砂粒中寻路而曲折前进的
地下水迹线示意图
5.1.2.3 二者区别
流线和迹线都是流场中的一簇曲线，都与流 体的运动有关，但各自代表了不同的概念：
>>流线反映的是某时刻流体的流速向量，迹线 是反映流体中某一质点不同时间走过的轨迹；
>>因此流线可看作水质点运动的摄影，迹线则 可看作对水质点运动所拍摄的电影。
5.1.3 过水断面与流量
5.4 地下水运动的基本规律
5.4.1 达西定律
达西定律是法国水利学家H.Darcy通过大量的实验，得到的线 性渗透定律。
5断面面积A；
(2)上游置一个稳定的溢水装置→保持稳定
水头；
(3)实验上端进水，下端出水→示意流线；
(4)圆筒中上、下断安装测压管→测定两个
>>稳定流条件下，流体的流线与迹线重合！
>>严格说来，自然界中的地下水都属于非稳定流，但是， 但为了便于分析和运算，也可以将某些运动要素变化微小的 渗流，近似地看作稳定流。
5.1.7 均匀流与非均匀流
>>均匀流——在实际水流中，如果流线是彼此平行的直线， 而且在同一流线上的点，其实际流速相等，即沿水流方向实 际流速的大小和方向皆不变。显然，在均匀流中，质点的时 变加速度和位变加速度都等于零。亦即流体在运动过程中， 其运动要素不随坐标位置而改变！
水文地质学基础之地下水运动基本规律
h ——水头损失（m）；L ——渗流途径； K——与试样有关的比例常数。
由水力学中水动力学基本原理：
定 反 正义比比（： ， 。2单 与）Lh位 过时 水I间 断内面J通wQ，过=上K砂水I、力 的ω下梯 流度 测量压与管h渗yd的透ra水长uli头c度g差lr成a成dient
10
第2节 重力水运动基本规律
27
第3节 流 网
28
等水头线 、流线与各类边界的关系
已知边界 a—湿周 b—隔水边界 c\d—水位线
Company Logo
第3节 流 网
均质各向同性介质中的流网及其绘制
在均质各相同性介质中，地下水必定沿着水头 变化最大的方向，即垂直于等水头线的方向运动， 因此，流线与等水头线构成正交网格。 稳定流网的绘制步骤：
21
第2节 重力水运动基本规律
含水层介质特征
均质(homogeneous medium)：K在岩层中处处相等， 不随空间变化。
非均质(inhomogeneous medium)：K在岩层中随空间 位置变化而改变。
各向同性介质(isotropic medium)：K不随渗流方向改 变。
各向异性介质(anisotropic medium)：K随水流方向改 变。
渗透流速
根据水力学流速与流量的关系对上式转化：
Q
U
Q = ω ·V
A
与（2）式比较
V = K·I -----
（3）
称为渗透流速（seepage velocity \Darcy velocity \specific discharge）
上式为单位面积上的流量----称比流量
达西定律中由此看出：
I H1 H 2 ΔH h
水文地质学第4章 地下水运动的基本规律改.ppt
u =Q/w′
渗透流速：假想水流通过单位过水断面的流量称
为渗透流速。
V=Q/ w
松散岩石孔隙中的水示意图
渗流必须满足下列条件：
1）通过任一断面的渗透流量等于通过该断 面的实际流量；
2）作用于任一面积的渗透压力或水头等于 作用于该面积的实际压力或水头；
3）渗透通过任一体积所受的阻力等于实际 水流通过该体积所受到的阻力。
2、达西定律的讨论与适用范围 1)达西定律的讨论
公式：V=K × I 反映通过任一断面一维流的
渗流速度与其水力坡度之间的关系式，这种关系的
微分表达式：V=－K×dh/dL，对于二维流和三维
流同样适用。
达西定律是在稳定运动条件下得到的，当地下 水为非稳定运动时，渗流中任一点处瞬时流速与水 力坡度之间的关系仍可用上面关系表征，只是渗透 流速和水力坡度随时间在变化。
（1）渗透流速： 根据水力学流速与流量的关系，上式可转化：
与（2）式比较
Q = W ·V
V = K·I
（3）
称为渗透流速（seepage velocity \Darcy velocity \specific discharge）
上式为单位面积上的流量——称比流量。 由此看出，达西定律中： 渗透流速与水力梯度的一次方成正比，故达西定律又称为线性渗透定律
水力梯度：渗流通过A点单位渗流途径长度
上的水头损失称为水力坡度。
I = dH/dL 或 I =（H1－H2）/ L
水 力 梯 度 示 意 图
3、流线、迹线、等水头线和流网： 流线：同一时间内不同液流质点的连线，这 根连线上的各液流质点速度矢量都与这根连 线相切。 迹线：某一液流质点在某一时间段内的运动 轨迹。 等水头线：水头值相等点的连线。
水文地质学 地下水运动的基本规律
（3）稳定流与非稳定流 水在渗流场内运动，各个运动要素(水位、流速、流向 等)不随时间改变时，称作稳定流。 运动要素随时间变化的水流运动，称作非稳定流。严 格地讲，自然界中地下水都属于非稳定流。
7.1
重力水运动的基本规律
7.1.1达西定律 1856年，法国水力学家达 西(H．Darcy) 通过大量的实 验，得到线性渗透定律。 实验是在装有砂的圆筒中 进行的(图7—1)。
对于图7—5(c)的V-I曲线，可从直线部分引一切线交于 I轴，截距I。称为起始水力梯度。V—I曲线的直线部分 可表达为： V ＝ K(1-Io) (7—9)
当地下水流线通过具有不同渗透系数的两层边界时，必 然像光线通过一种介质进入另一种一样，发生折射，服从 以下规律： K1/ K2 = tanθ 1/tanθ 2 (7—8) 式中θ 1是流线在K1层中与层界法线间的夹角；θ 2是流线 在K2层中与层界法线间的夹角。
为了保持流量相等 (Q1 = Q2) ，流线进 入 渗 透 性 好 的 K2 层 后将更加密集，等 水头线的间隔加大 (dl2>dl1) 。 也 就 是 说，流线趋向于在 强透水层中走最长 的途径，而在弱透 水层中走最短的途 径。使强透水层中 流线接近于水平， 而在弱透水层中流 线接近于垂直层面 (囱7—7)。
从水力学已知，通过某一断面的流量 Q 等于流速 V 与过水 断面面积的乘积，即： Q＝WV ( V＝Q／w ) 据此及公式 (7一1)，达西定律也可以另一种形式表达之： V ＝ KI V—渗透流速。
练习
例1
某向斜盆地在d点有线状泉水出露，平均单宽流量为 120m3／d。根据勘探工作获得a、b、c、d点的水头和水 文地质剖面图，如图1-23所示。已知：M1=10 m， L11=100m，L12=50m，M2=20 m，L21=2000 m， L22=1500m，cd含水层平均渗透系数Kl=20m／d，ab含 水层平均渗透系数K2=30m／d，断层为导水断层。试求 ab含水层在断层带B点和cd含水层在断层带A点相应的 水头值。
水文地质学基础 第四章 地下水运动的基本规律.
第四章 地下水运动的基本规律
1.渗透与渗流
渗透： 地下水在岩石空隙中的运动
渗流是一种假想水流。
假想水流应满足下列条件： （1）性质（如密度、粘滞
性等）和真实地下水相同； （2）充满含水层的整个空
间； （3）运动时，在任意岩石
体积内所受的阻力与真实水流 相同；
（4）通过任一断面的流量 及任一点的压力或水头均和实 际水流相同。 渗流区或渗流场：假想水流所 占据的空间。
• 流线：是渗流场中某一瞬时的一条线，线上各水 质点在此瞬时的流向均与此线相切。
• 迹线：则是对水质点运动所拍的电影。在稳定流 条件下，流线与迹线重合。
一、均质各向同，流线与等水头线构成 正交网格。 • 分析均质各向同性介质中的稳定流网。 • 徒手绘制定性流网
地下水的运动绝大多数服从Darcy定律。
二、非线性渗透定律—哲才（Chezy）定律
地下水在较大的空隙中运动且流速较大时，呈紊 流运动，此时的渗流服从哲才定律。有：
1
Q KI 2
1
V KI 2
即此时渗透流速V与水力梯度I的1/2次方成正比.
4.2 流 网
• 流网：在渗流场的某一典型剖面或切面上，由一 系列等水头线与流线组成的网格.
2.层流和紊流
层流运动：水质点作有秩序的、互不混杂的流动. 紊流运动：水质点无秩序的、互相混杂的流动.
地下水在岩石空隙中的运动速度一般较慢，大多为层流 运动。只有在大裂隙、溶洞中地下水流速大，才可能出现紊 流运动。此外，在抽水井附近小范围内，当降深很大时，流 速增大，也可出现紊流现象。
3. 稳定流和非稳定流
实际流速，ω有：
Q Kw h KwI Vw L
Q＝ ω／·u＝ ω·ne·u＝
1.渗透与渗流
渗透： 地下水在岩石空隙中的运动
渗流是一种假想水流。
假想水流应满足下列条件： （1）性质（如密度、粘滞
性等）和真实地下水相同； （2）充满含水层的整个空
间； （3）运动时，在任意岩石
体积内所受的阻力与真实水流 相同；
（4）通过任一断面的流量 及任一点的压力或水头均和实 际水流相同。 渗流区或渗流场：假想水流所 占据的空间。
• 流线：是渗流场中某一瞬时的一条线，线上各水 质点在此瞬时的流向均与此线相切。
• 迹线：则是对水质点运动所拍的电影。在稳定流 条件下，流线与迹线重合。
一、均质各向同，流线与等水头线构成 正交网格。 • 分析均质各向同性介质中的稳定流网。 • 徒手绘制定性流网
地下水的运动绝大多数服从Darcy定律。
二、非线性渗透定律—哲才（Chezy）定律
地下水在较大的空隙中运动且流速较大时，呈紊 流运动，此时的渗流服从哲才定律。有：
1
Q KI 2
1
V KI 2
即此时渗透流速V与水力梯度I的1/2次方成正比.
4.2 流 网
• 流网：在渗流场的某一典型剖面或切面上，由一 系列等水头线与流线组成的网格.
2.层流和紊流
层流运动：水质点作有秩序的、互不混杂的流动. 紊流运动：水质点无秩序的、互相混杂的流动.
地下水在岩石空隙中的运动速度一般较慢，大多为层流 运动。只有在大裂隙、溶洞中地下水流速大，才可能出现紊 流运动。此外，在抽水井附近小范围内，当降深很大时，流 速增大，也可出现紊流现象。
3. 稳定流和非稳定流
实际流速，ω有：
Q Kw h KwI Vw L
Q＝ ω／·u＝ ω·ne·u＝
4.水文地质学基础-地下水的基本运动规律
4.1 重力水运动的基本规律
渗透系数（K）的影响因素：
d0 —— 孔隙直径；γ——水的重率；μ——动力粘滞系数
K与岩石空隙性质、水的某些物理性质有关。
（1）孔隙直径大则渗透性强，取决于最小孔隙直径。 （2）圆管通道：形状弯曲而变化时，渗透性较差。 （3）颗粒分选性：比对孔隙度的影响要大。 （4）水的物理性质：粘滞性大的液体K<粘滞性小的液体
4.1 重力水运动的基本规律
4.1.4渗透系数 渗透系数（K）是水力梯度等于1时的渗透流速,单位：m/d,cm/s. 关系： V = K I 1）I为定值时，K大，V大；K小，V小（V＝KI）； 2）V为定值时，K大，I小等水位线疏；K小，I大等水位线密。 渗透系数可定量说明岩石的渗透性：K大→渗透性强；K小→渗 透性弱。
Q K ω I K M 1 I H H H H b a b K a 2 L K 2 2 Ha H b 2L
4.2 流 网
流线（flow line, stream line）是渗流场中某一瞬时的一条 线，线上各个水质点在此时刻的流向均与此线相切。 迹线（path line）是渗流场中某一时间段内某一水质点的运动 轨迹。
h1 0
K
M
h2
0’ L
dh dx 单宽流量为： v K dh dh q v K M 1 KM dx dx
qdx KMdh
L
0
qdx KMdh
h1 L h2 0 h1
h2
分离变量并积分：
q dx KM dh h1 h2 q KM KMI L
0 h1 L h2
h1 h2 h1 h2 qK KM I 2 L
第四章 地下水运动的基本规律.
第四章地下水运动的基本规律第一节重力水运动的基本规律（1）达西定律达西定律是由法国水力学家H.Darcy于1856年通过大量的室内实验得出的。
达西实验装置与条件：等径圆筒装入均匀砂样，圆筒断面为ω；上下各置一个稳定的溢水装置——保持实验过程水流的稳定；水流实验时，上端进水，下端出水——参见图4-1，示意流线（图中兰色线）；砂筒中，安装了2个测压管；下端出水口，测定出水量Q。
实验过程：（1）通过改变水头，稳定测量出水量；（2）改变试样筒内的砂样（粒径变化），重复实验。
实验结果：出水端的流量Q与砂柱断面为ω、测压管水头之间的关系为：图4—1 达西试验示意图（4—1）式中：——渗透流量（出口处流量，即为通过砂柱各断面的流量）；——过水断面（在实验中相当于砂柱横断面积）；——水头损失（，即上下游过水断面的水头差）；——渗透途径（上下游过水断面的距离）；——渗透系数（与砂柱样品有关的系数）。
（4—1）为达西定律表达方法之一。
达西公式的变化形式：由水力学中水动力学基本原理：（4—2）——水力梯度，相当于/，即水头差除以渗透途径。
（4—2）代入（4—1）有：（4—3）（4—1）与（4—3）为达西定律的不同表达方法。
由（4—3）达西公式表明：渗透流量（Q）与渗透系数（K）、过水断面（ω）及水力梯度（I）成正比。
从水力学已知，通过某一断面的流量等于流速与过水断面的乘积，即：（4—4）即。
比照公式（4—4）与（4—1），达西定律又可以表达为：（4—5）式中：称作渗透流速，即单位面积上的流量——也称为比流量。
由（4—5）式表明：渗透流速与水力梯度一次方成正比关系，故达西定律又称为线性渗透定律。
下面探讨达西公式（4—5）式中各项的物理涵义。
（2）渗透流速（V）过水断面ω：砂柱的横切面积，是指水流通过的包括岩石骨架与空隙在内的整个断面。
实际过水断面：扣除结合水所占据范围以外的空隙面积，也就是重力水所占据的空隙面积。
实际过水断面ω′与过水断面ω的关系，可以表示为：（参见图4-2，插图4-1）图4—2 过水断面（斜阴线部分）与实际过水断面（直阴线部分）颗粒边缘涂黑部分（最好改为红色）为夸大表示的结合水A 过水断面（水流可以穿越颗粒）B 实际过水断面（水流只沿孔隙运动）插图4-1 过水断面与实际过水断面动画有效孔隙度：重力水流动的空隙体积（不包括结合水占据的空间）与岩石体积之比。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
不去追踪实际水质点的运移轨迹 ——简化的研究
13
第2节 重力水运动基本规律
过水断面ω与实际过水断面ω'
过水断面（ω ）
实际过断面（ω ' ）
14
第2节 重力水运动基本规律
水力梯度（ I）（hydraulic gradient ）
? 水力学中 水力坡度 （J ）:单位距离上的水头损失
? 是沿渗流途径上的水头损失与 相应的渗流长度 之比
? h ——水头损失（ m）；L ——渗流途径； ? K——与试样有关的比例常数。
?由水力学中水动力学基本原理：
定反义比：，单与Lh位 过?时 水I间 断?内 面J通w?过，?砂上水的、流下力量测与压梯渗管hyd透的ra度长u水lic度头g差rla成成die
正比（。2）
Q=KIω
10
第2节 重力水运动基本规律
? 在达西实验中：
H1 ? Z1 ?
p1 ?
?
u12 2g
其原因是 u2/2g 很小而忽略
?在地下水渗流研究中常：
H1 ? Z1 ?
? 总水头 ? 测压水头 (这是习惯用法)
p1
?
我们仍然用 △H = H 1-H2 代表该程 L 1—2 上的总水头损失， I — 则为总能量损失率
?渗流过程中总机械能的损耗原因（与水力学相近）
4
第1节 地下水运动的基本特点
?非稳定流
?水的各个运动要素（水位、流速、流向等）随时间变化
关系分为稳定流和非稳定流。 ?渗流场中任意点的水位（或流速、流向）与时间无关时， 称作稳定流。 ?渗流场中任意点的水位（或流速、流向）随时间变化时 为非稳定流。 ?自然界的地下水流一般均为非稳定流，原因有三：
I ? H 1 ? H 2 ? ΔH ? h
L1? 2
LL
? 物理涵义 上来看 I：代表着渗流过程中，机械能的损失
率，由水力学中水头的概念加以分析：
? 在地下水渗流研究中 任意点的水头表达式
p
v2
H ?Z? ?
? 2g
总水头 机械能
测压水头 速度水头
势能
动 能 15
第2节 重力水运动基本规律
水力梯度（ I）
? 渗透流速
? 根据水力学流速与流量的关系对上式转化：
Q
U?
Q = ω ·V
A
? 与（2）式比较
V = K·I -----
（3）
称为渗透流速（seepage velocity \Darcy velocity \specific discharge ）
上式为单位面积上的流量 ----称比流量
? 达西定律中由此看出：
Q
实际孔隙断面 ——ω n 孔隙度 过水断面比较 U ?
实际水流断面 ——ω n 有效孔隙度
A
Q/ ω = V 比照水力学，实际流速 Q/ω'= u
关系：地下水渗透流速 V= u ne
渗透流速 V：是假设水流通过整个岩层断面（骨架 + 空隙）时
所具有的虚拟的平均流速。
意义 ：研究水量时，只考虑水流通过的总量与平均流速，而
水文地质学基础
General Hydrogeology
--主讲：李明辉
1
第四章 地下水运动基本规律
第1节 地下水运动的基本特点 第2节 重力水运动基本规律 第3节 流 网 第4节 包气带水水分运动规律
2
第1节 地下水运动的基本特点
?曲折复杂的水流通道
? 用假象水流代替真实水流，假设：
?假象水流的性质（密度、粘滞性等）与真实水流相同，且 充满了含水层空隙和颗粒所占据的空间； ?假象水流任意断面的流量、水头或压力和实际水流相同； ?假象水流运动时在任意的岩石体积内所受的阻力和真实水 流所受的阻力相同。 ?这时的假象地下水在岩石空隙中的运动称为渗流(seepage flow)。发生渗流的区域称为渗流场。 ?假象水流发生渗流的区域称为渗流场。 ?渗流场由固体骨架和岩石空隙中的水两部分组成。渗流只 发生在岩石空隙中。
地下水空间运动上的特征主要取决于含水层的几何形状， 含水层的边界条件以及地下水的开采方式。
6
第1节 地下水运动的基本特点
达西定律（Darcy's law）—线性渗透定律（linear law ） H.Darcy —
法国水力学家， 1856 年（以实验为基础研究时期） 通过大量的室内实验得出的
4.1.1 实验条件：装置图—P36，图4-1 1）等径圆筒装入均匀砂样（uniform sand ），断面为ω 2）上（下各）置一个稳定的溢水装置——保持稳定水流 3）实验时上端进水，下端出水——示意流线 4）砂筒中安装了2个测压管 5）下端测出水量（outflow ）—Q
⑴补给水源受水文、气象因素影响大，呈季节性变化； ⑵排泄方式具有不稳定性； ? ⑶径流过程中存在不稳定性。
5
第1节 地下水运动的基本特点
地下水根据运动要素在空间上的变化规律一维流（线 流）、二维流（平流）、三维流（空间流）。
?流场中任意一点的速度变化只与空间坐标的一个方 向有关时称为一维流（线流）。 ?流场中任意一点的速度变化与空间坐标的两个方向 有关时称为二维流（平流）。 ?流场中任意一点的速度变化与空间坐标的两个方向 有关时称为三维流（空间流）。
? 渗透流速与水力梯度是一次方成正比
? 故达西定律又称为线性渗透定律
11
第2节 重力水运动基本规律
V V——I 曲线 1 砂样
2
O
I
V = K ·I ——（3）
12
第2节 重力水运动基本规律
?讨论
渗透流速（V）与过水断面（ω ）
Q=KωI=ωV
过水断面与水力学中的水流过断面是否一致？
否
过水断面 ——ω，假想的断面
7
第1节 地下水运动的基本特点
断面 1 断面 2
h L
H1
H2 Q
O
O'
ω
8
达 西 试 验 装 置_两种
1 —常水头装置
2 —变水头装置
第2节 重力水运动基本规律
? 通过变水头，多次实验得出：出水端的流量 Q与砂柱、
测压管水头之间的关系为：
（1）
Qω——砂柱断面面积；
3
第1节 地下水运动的基本特点
?迟缓的流速
? 一般以m/d计算，而河道或管网中的水流则以m/s计算；
? 根据流速的大小(按运动状态)，渗流分两种流态：
?层流：在岩石层空隙中渗流时，水的质点作有秩序的、 互不混杂的流动。 ?紊流：水的质点无秩序地、互相混杂的流动 。 ?用雷诺数（Re）判别：
? Re＜1~10 层流 ? Re ＞1~10 紊流 ?地下水在岩石空隙中的运动速度一般较小，大多为层流。