6.6 传热过程的计算
化工原理.传热过程的计算ppt课件

饱
和
液
蒸 汽
体 沸
t T t tm
冷
腾
凝
t
T
5
2. 变温传热 2.1 一侧恒温、一侧变温
T1
T
T2
t
t2
t1
一侧热流体被冷却, 另一侧冷流体沸腾。
一侧饱和蒸汽冷凝, 另一侧冷流体被加热。
6
2.2 两侧均有温度的变化:
逆流
并流
错流
冷热流体的四种流向
折流
7
2.2.1 逆流和并流时的tm
20
讨论: (1)当传热面为平面时,dA=dA1=dA2=dAm
1 1 b 1
K 1 2
(2)以外表面为基准(dA=dA1):
1 1 b dA1 1 dA1
K1 1 dAm 2 dA2 1 1 b d1 1 d1
K1 1 dm 2 d2
21
K1——以换热管的外表面为基准的总传热系数;
d1 d2
1
2
d1 d2
式中 R1、R2——传热面两侧的污垢热阻,m2·K/W。
污垢热阻Rd的倒数称为污垢系数(dirty factor)
23
(6)平壁与薄管的总传热系数计算
1 K
1
1
Rd1
b
d1 dm
Rd 2
d1 d2
1
2
d1 d2
当传热壁为平壁或薄壁管时, A1 A2 Am
11
b
17
T
Tw
热 流 体
对流 导 热
冷 流 体
Q tw
t
•热流体
Q1 对流
固体壁面一侧
•固体壁面一侧 热Q传2导另一侧
传热过程计算公式

传热过程计算公式传热啊,就像是一场热的接力赛。
你知道传热过程计算公式吗?那可真是个神奇的东西。
想象一下,热量就像一群调皮的小恶魔,总是到处乱窜。
热传导就像是小恶魔们在固体里一个传一个地挤着走。
傅立叶定律这个计算公式呢,就像是给小恶魔们规定了行走路线的魔法规则。
如果把热量比作水流,那热传导就像是在细细的管道里慢慢流淌的涓涓细流,而这个公式就是控制水流速度和方向的阀门。
再说说对流传热吧。
这就好比是热小恶魔们搭上了风的便车或者水流的小船。
牛顿冷却定律这个计算公式,就像是给小恶魔们的乘车规则。
就像你在大风天里,热量从你身上被风快速带走,那速度就像小偷在夜色中溜走一样快。
对流传热里的热量传递速度,按照这个公式计算起来,有时候就像火箭发射一样迅速,一下子就把热从一个地方带到另一个地方。
辐射传热更是神奇,就像是热小恶魔们变身成了看不见的小超人,直接发射自己的热量能量。
斯蒂芬 - 玻尔兹曼定律这个计算公式,那就是小超人的超能力使用手册。
热辐射的热量传递,感觉就像是来自外太空的神秘力量,在黑暗中默默地传递着能量,而且速度之快,就像闪电在天空中划过一样让人惊叹。
要是把这三种传热方式放到一起,就像一场热的大杂烩派对。
计算总的传热过程的公式就像是派对的组织者,要把每个小恶魔在不同活动(热传导、对流传热、辐射传热)中的表现综合起来。
这个综合的公式看起来复杂,其实就是把热的小恶魔们在各种不同路径传递热量的情况都算个清楚明白。
有时候看着这些传热过程计算公式,就像在看一场魔术表演。
你以为热量的传递是无章可循的,但是这些公式就像魔术师的魔法棒,一挥之下,所有的奥秘都展现在眼前。
它们就像是打开热传递这个神秘大门的钥匙,让我们能够精确地知道热到底是怎么在不同的物体和环境中跑来跑去的。
要是没有这些公式,我们就像是在黑暗中摸索热传递的盲人。
有了它们,我们就能像超级侦探一样,追踪热量的每一个踪迹,不管它是偷偷摸摸地传导,还是大张旗鼓地辐射,都逃不过我们的计算大法。
传热实验数据的计算过程

实验数据的计算过程(光滑管)孔板流量计压力差计算读数 △P=1.10Kpa ,空气进口温度t 1=27.0℃ 出口温度t 2=62.5℃,传热管壁面温度tw=99.1℃ (1)传热管内径di 及流通截面积Fi di=20.00(mm )=0.0200(m )Fi=π·di 2/4=3.14×(0.0200)2/4=0.0003142(m 2) (2)传热管有效长度L 及传热面积Si L=1.00mSi =π·di ·L=3.142×0.02×1.00=0.06284(m 2) (3)空气平均物性常数的确定 先算出空气的定性温度tm ,tm=75.442t t 21=+(℃) 在此温度下空气物性数据如下:平均密度ρm=1.1131(kg/m 3) 平均比热Cpm=1005(J/kg ·k )平均导热系数λm=0.027856(W/m ·K ) 平均粘度μm=1.744510-⨯(Pa ·s ) (4)空气流量过换热器内管时平均体积流量Vm 和平均流速的计算 20℃时对应的孔板流量计体积流量V 20=22.696×△P 0.5=22.696×1.100.5=23.80(m 3/h ) 因为流量计处温度不是20℃,故需校正: V t1= V 2010.24202730.2727380.2320273t1273=++=++(m 3/h )传热管内平均体积流量Vm : Vm= V t1×51.250.2727375.4427310.24t 273t 2731m =++⨯=++(m 3/h )平均流速u m :u m = Vm/(Fi ×3600)=25.51/(0.0003142×3600)=22.55(m/s )(5)壁面和冷流体间的平均温度差△tm=tw-35.545.471.992t t 21=-=+(℃) (6)传热速率()()W C V Q 43.28136005.3510051131.151.253600t t pm m m 12=⨯⨯⨯=-⋅⋅=ρ(7)管内传热系数αi=()40.8206284.035.5443.281t i m =⨯=⨯∆)(S Q (W/m 2·℃)(8)各准数Nu=αi ×di/λ=82.40×0.020/0.027856=59.16Re=2878500001744.01131.155.22020.0m m um di =⨯⨯=⨯μρ629.0027856.010744.11005Pr 5=⨯⨯=⋅=-λμCp(9)求关联式Nu=ARe mPr 0.4中的常数项以4.0r u P N 为纵坐标,Re 为横坐标,在对数坐标系上标绘4.0r uP N ~Re 关系,见图1中直线。
热传递热量计算公式

热传递热量计算公式
热传递是指热量从一个物体传递到另一个物体的过程。
热传递的计算可以通过多种公式来实现,具体取决于热传递的方式。
以下是一些常见的热传递计算公式:
1. 热传导(导热)的计算公式:
热传导是指热量通过物质内部传递的过程。
其计算公式可以用傅立叶定律来表示:
Q = -kAΔT/Δx.
其中,Q表示传导热量,k表示热导率,A表示传热面积,ΔT表示温度差,Δx表示传热距离。
2. 热对流的计算公式:
热对流是指热量通过流体(气体或液体)对流传递的过程。
其计算公式可以用牛顿冷却定律来表示:
Q = hAΔT.
其中,Q表示对流热量,h表示对流换热系数,A表示传热面积,ΔT表示温度差。
3. 热辐射的计算公式:
热辐射是指热量通过辐射传递的过程。
其计算公式可以用斯特藩-玻尔兹曼定律来表示:
Q = εσA(T₁^4 T₂^4)。
其中,Q表示辐射热量,ε表示发射率,σ表示斯特藩-玻尔兹曼常数,A表示辐射面积,T₁和T₂分别表示两个物体的绝对温度。
以上是一些常见的热传递计算公式,它们分别适用于不同的热传递方式。
在实际问题中,需要根据具体情况选择合适的公式进行计算。
传热过程的计算
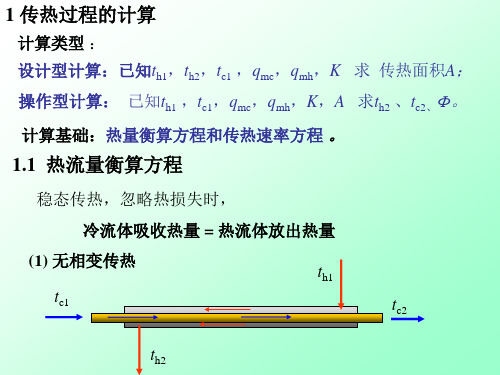
说明:① 换热过程中各流股热流量间关系; ② 各流股间相互制约,热量守恒。
过冷液体
1.2 总传热速率方程
间壁传热过程:
th
热量:热流体对流传热 管内壁
热 流 体
Φ
Φ
热传导 管外壁
对流传热 冷流体
th,w
tc,w
冷 流 体 tc
各部分传热速率方程: 管内侧流体: 管壁导热: 管外侧流体:
t h tc 因此, 1 b 1 hi Ai Am h0 A0
热 流 体
Φ
Φ
t R
th,w
tc,w
冷 流 体 tc
1 1 b 1 令: R KA h A A h A i i m 0 0
用平均传热温差t m 代替(t h tc)
式中,K — 总传热系数,W/m2· K。
t’h t’c
(2) 变温传热 ① 一侧有温度变化
②
tc1
两侧流体均有温度变化
th2 tc2
th1
th1 tc2 th2
tc1
沿管长某截面取微元传热面积dA, 传热速率方程: d KtdA 热量衡算方程:
d qm ,h c p ,h dt h qm ,c c p ,c dtc
d qm ,h c p ,h dt h qm ,c c p ,c dtc
④ 应用 已知R和NTU,可求得ε, 进而求th2 和tc2 ,
可避免试差计算。
为便于工程计算,将ε、NTU、R之间关系绘制成曲线
1.0
R=0 0.25
0.8
0.5 0.75 1.0
ε
0.6
0.4 th1 0.2 K=常数 th2
传热过程的计算

必须着力减少控制步骤的热阻,才更易以达到强化传热的目的。 。
实际计算换热管热流量,可依据管壁内表面积或外表面积写出两个方程 内表面: 外表面: Ql=KlA1 (T-t) Q2=K2A2 (T-t) (6-116)
式中,K1、K2分别为以内、外表面积为基准的传热系数,明显两者是不相等的。 但有 K1A1=K2A2 如圆管的内、外直径分别用d1、d2表示,结合式子: K 可导出: K 1
即
Q KAt m
称为传热过程基本方程式
式中
t m
T t 1 T t 2 T t 1 ln T t 2
称为对数平均温差或对数平均推动力。
对数平均推动力
对数平均推动力恒小于算术平均推动力,特别是当换热器两端推动力相差悬 殊时,对数平均值要比算术平均值小得多。 当换热器一端两流体温差接近于零时,对数平均推动力将急剧减小。 对数平均推动力这一特性,对换热器的操作有着深刻的影响。 例如,当换热器两端温差有一个为零时,对数平均温差必为零。 这意味着传递相应的热流量,需要无限大的传热面。 但是,当两端温差相差不大时,如0.5<(T-t)1/(T-t)2<2时,对数平均推动 力可用算术平均推动力代替。
qm1CP1dT=q1dA1=dQ (热流体在微元体内放出的热量) 同样,对冷流体作类似假定,并以微元体内环隙空 间为控制体作热量衡算,可得到 qm2CP2dt=q2dA2=dQ (冷流体在微元体内吸收的热量)
2、传热速率方程式 热流密度q是反映具体传热过程速率 大小的特征量。从理论上讲,根据前面 导热或对流给热规律,热流密度q已可以 计算。但是,这种做法必须引入壁面温 度;而在实际计算时,壁温往往是未知 的。为实用方便,希望能够避开壁温, 直接根据冷、热流体的温度进行传热速 率的计算。 如图所示的套管换热器中,热量序 贯地由热流体传给管壁内侧、再由管壁 内侧传至外侧,最后由管壁外侧传给冷 流体(参见 P201 图 6-35 )。在定态条 件下,并忽略管壁内外表面积的差异, 则各环节的热流量相等,即
传热过程的计算及换热器2
传热过程的计算及换热器2传热过程的计算及换热器2传热是物体间因温度差而引起的热能传递过程。
在工程实际中,传热过程的计算是非常重要的,尤其是在换热器设计和运行中。
本文将对传热过程的计算方法和换热器进行详细介绍。
一、传热过程的计算方法1.传热方程求解:传热方程主要包括热传导方程、对流传热方程和辐射传热方程。
热传导方程适用于固体传热,对流传热方程适用于流体传热,辐射传热方程适用于热辐射传热。
通过对这些方程进行求解,可以得到传热过程中的温度分布和传热速率。
2.传热电阻法:传热电阻法是根据传热过程中各个物体的热阻来计算传热速率的方法。
传热过程中,一般包括热源(或热池)、传热介质和传热表面。
根据热阻的串/并联关系,可以将传热系统简化为一个等效的传热电路,然后通过电路的电流和电阻来计算传热速率。
3.传热系数法:传热系数法是根据传热过程中的传热系数来计算传热速率的方法。
传热系数是指传热介质和传热表面之间传热的能力,可以通过实验测定或者理论计算来获取。
根据传热系数的定义和传热公式,可以直接计算传热速率。
二、换热器换热器是用来实现热能传递的设备,广泛应用于化工、电力、石油、冶金、轻工等行业,是工业生产中的重要设备之一、换热器的主要功能是将两种介质之间的热量传递给另一种介质,实现冷热介质的热能转化。
换热器按照结构特点可以分为管壳式换热器和板式换热器。
管壳式换热器由壳体、管束和管板等组成,各种不同的构造形式可以满足不同的工艺要求。
板式换热器是利用板状换热元件将冷热介质进行交叉传热,具有紧凑、高效、节能的优点。
换热器的性能主要是通过换热系数和压力损失来评价的。
换热器的换热系数是指单位时间内传递热量与温度差的比值,表示换热器的传热能力,可以通过实验测定和理论计算来获取。
压力损失是指流体通过换热器时产生的阻力损失,与换热器的结构和流体特性密切相关。
换热器的设计和运行中,需要考虑的因素包括传热面积的确定、流体流速的选择、换热介质的性质以及换热器的材料选择等。
第三节传热过程计算讲义
0.53%
(3)α2增大一倍,即α2 =100W/m2·K时的传热系数 K
1 0.0004 0.00058 0.000062 0.000625 0.0125 K
0.0142m2 K /W
K 70.4W / m2 K
K值增加的百分率 K K 100% 70.4 37.5 100% 87.8%
总传热系数K 12~60 800~1800 350左右 280~850 12~35 1400~4700 30~300 60~350 290~870
W/(m2·K)
获取 K 的另外两种途径
(2) 实验测定
➢通过实验测定现有换热器的流体流量和温度,再由传热基
本方程计算 K 值:
K2
Q A2t m
➢实验测定的 K 值较为可靠。实测 K 值的方法不仅是为了在 缺乏工业实验数据时提供设计依据,而且还可以籍助实测的 K 值判断换热器的工作状况,从而寻求强化传热的措施。
(2)α1增大一倍,即α1 =5000W/m2·K时的传热系数K’
1 0.0002 0.00058 0.000062 0.000625 0.025 K
0.0265m2 K /W
K 37.7W / m2 K
K值增加的百分率 K K 100% 37.7 37.5 100%
K
37.5
➢计算得到的 K 值与查取或实测值相差较大,主要原因是给 热系数 α的关联式有一定误差和污垢热阻不易估计准确。
➢使用计算的 K 值时应慎重,最好与另外两种方法作对照, 以确定合理的 K 值。
污垢热阻
➢换热器在运行一段时间后,流体介质中的可沉积物会在换 热表面上生成垢层,有时换热面还会被流体腐蚀而形成垢层
第三节 传热过程计算
传热过程的计算
6.6 传热过程的计算工业上大量存在传热过程(我们指间壁式传热过程),他包括了流体与固体表面间的给热和固体内部的导热。
前面我们已经学过了导热和各种情况下的给热所遵循的规律,本节讨论传热过程的计算问题。
6.6.1 传热过程的数学描述在连续化的工业生产中,换热器内进行的大都是定态传热过程。
(1)热量衡算微分方程式如图为一套管式换热器,内管为传热管,传热管外径1d ,内径2d ,微元传热管外表面积d A 1,管外侧1α;内表面积d A 2,内侧2α,平均面积d A m ,壁面导热系数λ。
对微元体做热量衡算得 Q A q T c m p s d d d 11==-Q A q T c m p s d d d 22==-以上两式是在以下的假设前提下:① 热流体流量1s m 和比热1p c 沿传热面不变;② 热流体无相变化; ③ 换热器无热损失;④ 控制体两端面的热传导可以忽略。
(2)微元传热速率方程式如图所示套管换热器中,热量由热流体传给管壁内侧,再由管壁内侧传至外侧,最后由管壁外侧传给冷流体。
对上述微元,我们可以得到33211321d d d d d d d A q A q A q Q Q Q Q m =======阻力推动力=++-=-=-=-22m 1122w m w w 11w d 1d d 1d 1d d 1A A b A t T A t t A b t T A T T αλααλα 令 2211d 1d d 1d 1A A b A A K m αλα++= 则 )(d d 1d t T A K A K tT Q -=-=)(d d t T K AQ q -==式中 K ——总传热系数,W/m 2·K 。
因为沿着流体流动方向(套管换热器沿管长)流体的温度是变化的,所以α值也是变化的。
但若取一定性温度,则α与传热面无关,可以认为是一常数,这样K 也为一常数。
对上式进行积分,可以得到m t KA Q ∆= (3)传热系数和热阻 ① K 的计算由前面的分析可知,传热过程的总热阻1/K 由各串联环节的热阻叠加而成,原则上减小任何环节的热阻都可提高传热系数,增大传热过程的速率。
传热过程常用计算方法
传热过程常用计算方法6.2.2.1 换热器热工计算的基本公式换热器热工计算的基本公式为传热方程式和热平衡方程式。
(1)传热方程(6-12)式中,Δt m为换热器的平均温差,是整个换热面上冷热流体温差的平均值,它是考虑冷热两流体沿传热面进行换热时,其温度沿流动方向不断变化,故温度差Δt也是不断变化的。
它不能像计算房屋的墙体的热损失或热管道的热损失等时,都把其Δt作为一个定值来处理。
换热器的平均温差的数值,与冷、热流体的相对流向及换热器的结构型式有关。
(2)热平衡方程式(6-13)式中 G1,G2:热、冷流体的质量流量,kg/s;c1,c2:热、冷流体的比热,J/(kg·℃);t1′、t2′:热、冷流体的进口温度,℃;t1″、t2″:热、冷流体的出口温度,℃;G1c1,G2c2:热、冷流体的热容量,W/℃。
即各项温度的角标意义为:“1”是指热流体,“2”是指冷流体;”′”指进口端温度,”″”指出口端温度。
6.2.2.2 对数平均温差法应用对数平均温差法计算的基本计算公式如式(6-12)所示,式中平均温差对于顺流和逆流换热器,由传热学可得,均为:(6-14)由于温差随换热面变化是指数曲线,顾流与逆流相比,顺流时温差变化较显著,而逆流时温差变化较平缓,故在相同的进出口的温度下,逆流比顾流平均温差大。
此外,顾流时冷流体的出口温度必然低于热流体的出口温度,而逆流则不受此限制。
故工程上换热器一般都尽可能采用逆流布置。
逆流换热器的缺点是高温部分集中在换热器的一端。
除顺流、逆流外,根据流体在换热器中的安排,还有交叉流、混合流等。
对于这些其它流动形式的平均温差,通常都把推导结果整理成温差修正系数图,计算时,先一律按逆流方式计算出对数平均温差,然后按流动方式乘以温差修正系数。
用对数平均温差法计算虽然较精确,但稍显麻烦。
当Δt′/Δt″<1.7时,用算术平均温差代替对数平均温差的误差不超过2.3%,一般当Δt′/Δt″<2时,即可用算术平均温差代替对数平均温差,这时误差小于4%,即Δt m=(Δt′+Δt″)/26.2.2.3 效能-传热单元数法(ε-NTU法)换热器热工计算分为设计和校核计算,它们所依据的都是式(6-12)、(6-13)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
6.6 传热过程的计算工业上大量存在传热过程(我们指间壁式传热过程),他包括了流体与固体表面间的给热和固体内部的导热。
前面我们已经学过了导热和各种情况下的给热所遵循的规律,本节讨论传热过程的计算问题。
6.6.1 传热过程的数学描述 在连续化的工业生产中,换热器内进行的大都是定态传热过程。
(1)热量衡算微分方程式如图为一套管式换热器,内管为传热管,传热管外径1d ,内径2d ,微元传热管外表面积d A 1,管外侧1α;内表面积d A 2,内侧2α,平均面积d A m ,壁面导热系数λ。
对微元体做热量衡算得 Q A q T c m p s d d d 11==-Q A q T c m p s d d d 22==-以上两式是在以下的假设前提下:① 热流体流量1s m 和比热1p c 沿传热面不变;② 热流体无相变化; ③ 换热器无热损失;④ 控制体两端面的热传导可以忽略。
(2)微元传热速率方程式如图所示套管换热器中,热量由热流体传给管壁内侧,再由管壁内侧传至外侧,最后由管壁外侧传给冷流体。
对上述微元,我们可以得到33211321d d d d d d d A q A q A q Q Q Q Q m =======阻力推动力=++-=-=-=-22m 1122w m w w 11w d 1d d 1d 1d d 1A A b A t T A t t A b t T A T T αλααλα 令 2211d 1d d 1d 1A A b A A K m αλα++= 则 )(d d 1d t T A K A K tT Q -=-=)(d d t T K AQ q -==式中 K ——总传热系数,W/m 2·K 。
因为沿着流体流动方向(套管换热器沿管长)流体的温度是变化的,所以α值也是变化的。
但若取一定性温度,则α与传热面无关,可以认为是一常数,这样K 也为一常数。
对上式进行积分,可以得到m t KA Q ∆=(3)传热系数和热阻 ① K 的计算由前面的分析可知,传热过程的总热阻1/K 由各串联环节的热阻叠加而成,原则上减小任何环节的热阻都可提高传热系数,增大传热过程的速率。
但是,各环节热阻不同时,其对总热阻的影响也不同,由K 的表达式我们可以知道,热阻1/K 的数值将主要由其中最大热阻所决定。
以下讨论K 的计算。
A d 可取d A ≠d A 1≠d A 2≠d A m 中的任何一个,但我国换热器的基准都是取传热管的外表面积,即d A =d A 1,则A212m 111111dA dA dA dA b K αλα++= 对于套管换热器,l d A d d π=,则212m 111111d d d d b K αλα++= 对于平壁,d A =d A 1=d A 2=d A m ,则21111αλα++=b K ② 污垢热阻s R以上的推导过程中,都未涉及传热面污垢的影响。
实践证明,表面污垢会产生相当大的热阻。
换热器使用一段时间后,传热表面有污垢积存,因此污垢层的热阻一般不可忽略。
但是,污垢层的厚度及其导热系数无法测量,故污垢热阻只能是根据经验数据确定。
计及污垢热阻的总热阻为212212111111d d d d R d d b R K s m s αλα++++= 式中 R s1、R s2——分别为传热管外侧、内侧的污垢热阻,m 2·K/W 。
(4)壁温的计算由22wm w w 11w d d d A tt A t T A T T αλα-=-=-可以看出,在传热过程中热阻大的环节其温差也大。
若金属壁的热阻可忽略,即w w t T ≈,则2211w w d 1d 1A AtT T T αα=--,即壁温w T 接近于热阻较小或给热系数较大的一侧流体的温度。
(5)传热基本方程式(设两流体作逆流流动) 由前面分析可知A t K t T A K T c m s d )(d d 1p 1∆=-=-A t K t T A K t c m s d )(d d 2p 2∆=-=-t c m T c m t T A K s s d d )(d 2p 21p 1-=-=-=[]mt T c m c m t T c m t c m T s s s s )d()/(1)/(1)d()/(1d )/(1d 2p 21p 12p 21p 1-=--=-=-式中 )/(1)/(12p 21p 1c m c m m s s -=对于稳定操作,1s m 、2s m 是常数,取流体平均温度下的比热,则1p c 、2p c 也是常数,若将换热面各微元的局部K 值也作为一常数,则上式中只有t T t -=∆沿换热面而变。
分离变量,并在A =0(1t t ∆=∆)至A =A (2t t ∆=∆)间积分,得⎰⎰⎰∆∆∆∆∆∆-=---=2121d )d(d 0t t t t AtttT t T A mK 21ln t tmKA ∆∆=对整个换热面作热量衡算得:)()(122p 2211p 1t t c m T T c m Q s s -=-= 211p 1T T Q c m s -=,122p 2t t Qc m s -=[][]Q t t Q t T t T Q t t T T m /)(/)()(/)()(2112211221∆-∆=---=---=T 1 T 2t 2 t12121ln t t t t KAQ ∆∆∆-∆= 因此可得出逆流时:2121m ln t t t t t ∆∆∆-∆=∆,称为对数平均温度差。
当21t t ∆∆<2是,221m t t t ∆=∆=∆。
同样,我们也可以导出并流时的2121m ln t t t t t ∆∆∆-∆=∆。
(6)对数平均推动力m t ∆在传热过程中,冷热流体的温差是沿加热面连续变化的,但由于此温差与冷、热流体温度成线性关系,故可用换热器两端温差的某种组合(即对数平均温度差)来表示。
对数平均温度差(或推动力)恒小于算术平均温度差,特别是当换热器两端温度差相差悬殊时,对数平均温度差将急剧减小。
在冷、热流体进出口温度相同的情况下,并流操作的两端推动力相差较大,其对数平均值必小于逆流操作。
因此,就增加传热过程推动力而言,逆流操作总是优于并流操作。
问:当一侧为饱和蒸汽冷凝时,并流与逆流的m t ∆的关系又是如何呢?相等,无并流、逆流之分,即2112m ln t T t T tt t s s ---=∆。
在实际操作的换热器内,纯粹的逆流和并流操作是不多见的,经常采用的是错流、折流及其他复杂流动,复杂流动的m t ∆该怎么求呢?可根据逆流流动求出逆m t ∆,然后再乘以温差校正系数ψ得到实际的平均温差m t ∆,即逆m m t t ∆=∆ψψ的取值见教材。
温差校正系数ψ<1,这是由于在列管换热器内增设了折流挡板及采用多管程,使得换热的冷、热流体在换热器内呈折流或错流,导致实际平均传热温差恒低于纯逆流时的平均传热温差。
若一侧为饱和蒸汽冷凝的复杂流动,其逆m m t t ∆=∆。
6.6.3 换热器的设计型计算第一章我们学过,管路计算包括设计型和操作型两类,同样换热器计算也包括设计型和操作型两类。
(1)设计型计算的命题方式设计任务:将一定流量1s m 的热流体自给定温度1T 冷却至指定温度2T ;或将一定流量2s m 的冷流体自给定温度1t 加热至指定温度2t 。
设计条件:可供使用的冷却介质即冷流体的进口温度1t ;或可供使用的加热介质即热流体的进口温度1T 。
计算目的:确定经济上合理的传热面积及换热器其它有关尺寸。
(2)设计型问题的计算方法设计计算的大致步骤如下:① 首先由传热任务用热量衡算式计算换热器的热负荷Q ; ② 作出适当的选择并计算平均推动力m t ∆;③ 计算冷、热流体与管壁的对流传热系数1α、2α及总传热系数K ; ④ 由总传热速率方程计算传热面积A 或管长l 。
(3)设计型计算中参数的选择由总传热速率方程式m t KA Q ∆=可知,为确定所需的传热面积,必须知道平均推动力m t ∆和总传热系数K 。
为计算对数平均温差,设计者首先必须:① 选择流体的流向,即决定采用逆流、并流还是其它复杂流动方式;② 选择冷却介质的出口温度2t 或加热介质的出口温度2T 。
为求得传热系数K ,须计算两侧的给热系数α,故设计者必须决定:① 冷、热流体各走管内还是管外;② 选择适当的流速。
同时,还必须选定适当的污垢热阻。
由上所述,设计型计算必涉及设计参数的选择。
各种选择决定之后,所需的传热面积及管长等换热器其它尺寸是不难确定的。
不同的选择有不同的计算结果,设计者必须作出恰当的选择才能得到经济上合理、技术上可行的设计,或者通过多方案计算,从中选出最优方案。
近年来,利用计算机进行换热器优化设计日益得到广泛的应用。
本节后面的例题仅讨论根据题给条件即可进行设计计算,不涉及设计参数的选择问题。
(4)选择的依据 ① 流向选择对热敏性物料,并流操作可避免出口温度过高而影响产品质量。
在某些高温换热器中,逆流操作因冷却流体的最高温度2t 和1T 集中在一端,会使该处的壁温特别高。
为降低该处的壁温可采用并流,以延长换热器的使用寿命。
② 冷却或加热介质的出口温度的选择。
③ 流速的选择。
(5)设计型计算的例题例 1 有一套管换热器,由5.357⨯φmm 与5.489⨯φmm 的钢管组成。
甲醇在内管流动,流量为5000kg/h ,由60℃冷却到30℃,甲醇侧的对流传热系数15122=αW/( m 2·℃)。
冷却水在环隙中流动,其入口温度为20℃,出口温度拟定为35℃。
忽略热损失、管壁及污垢热阻,且已知甲醇的平均比热为2.6kJ/(kg·℃),在定性温度下水的粘度为0.84cP 、导热系数为0.61 W/( m 2·℃)、比热为4.174 kJ/(kg·℃)。
试求:(1)冷却水的用量;(2)所需套管长度;(3)若将套管换热器的内管改为φ48×3mm 的钢管,其它条件不变,求此时所需的套管长度。
解:(1)冷却水的用量2s m 可由热量衡算式求得,由题给的1P c 与2P c 单位相同,不必换算,1s m 的单位必须由kg/h 换算成kg/s ,故有:73.1)2035(174.4)3060(6.2)36005000()()(122p 211p 12=-⨯-⨯⨯=--=t t c T T c m m s s kg/s(2)题目没有指明用什么面积为基准,在这种情况下均当作是以传热管的外表面积为基准(以后的例题都按这个约定,不另行说明),对套管换热器而言就是以内管外表面积为基准,即A =l d 1π=-=)(211p 1s T T c m Q m 1t l d K ∆π得 ()m1211p 1s m 1t d K T T c m t d K Ql ∆-=∆=ππ (a ) 建议读者分别先求出Q 、K 、m t ∆的值后再代入式(a )求l 不易错。
