粒子群算法
基本粒子群算法

基本粒子群算法粒子群算法(Particle Swarm Optimization,PSO)是一种群体智能算法。
粒子群算法的灵感来源于模拟一群鸟的行为,这些鸟往往会通过互相沟通,得到更好的食物来源。
类比到优化问题中,粒子群算法的每个个体被称为粒子,它们互相传递信息,从而实现全局最优解的搜索。
在粒子群算法中,每个粒子代表了一个解空间内的可行解。
每个粒子的位置被编码成一组向量,这个向量就是这个粒子的位置,每个粒子还有一个速度向量,决定了它在解空间内的运动方向和速度大小。
在每一次迭代中,每个粒子会对自己的位置和速度进行更新,这依赖于当前的个体最优解,和全局最优解。
个体最优解是这个粒子对解空间的局部搜索结果,全局最优解是所有粒子对解空间的全局搜索结果。
粒子群算法通过不断迭代,更新每个粒子的位置和速度,直到达到收敛条件。
收敛条件可以通过迭代次数,目标函数的阈值等来定义。
在应用上,粒子群算法已被广泛应用于优化问题中,包括函数优化,组合优化,路径规划等等。
它的应用在电力系统,通信网络,机器人,图像处理和数据挖掘等领域也被证明是有效的。
在实际应用中,粒子群算法需要注意一些问题。
一是在选择惯性权重时需要遵守准则,即越接近最优解惯性权重应该越小,越远离最优解惯性权重应该越大。
二是需要确定好种群大小,如果种群太小,可能会导致粒子局限于局部最优解,而丢失全局优解的机会。
三是需要合适的约束条件,保证解空间的可行性,尤其是在优化问题中。
综上所述,粒子群算法是一种十分有用的优化算法,它通过模拟鸟群的行为,实现有效的搜索全局最优解。
但是在实际应用中需要注意一些问题,特别是在惯性权重,种群大小和约束条件的确定上,这样才能达到最好的优化效果。
粒子群算法及应用

粒子群算法及应用粒子群算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,源于对鸟群集群行为的观察和模拟。
粒子群算法通过模拟鸟群中个体间的协作与信息传递,以寻找最优解。
在实际应用中,粒子群算法已被广泛应用于函数优化、组合优化、图像处理、各类工程设计等领域。
粒子群算法的基本原理是模拟鸟群中每只鸟(粒子)的行为。
每个粒子表示问题的一个候选解,在解空间中最优解。
算法从一个随机初始解的种子集合出发,通过迭代更新粒子位置和速度,直到满足终止条件。
每个粒子维护自身的历史最优解和全局最优解,通过个体经验和邻域协作来引导过程。
粒子在解空间中自由移动,并通过其中一种适应度函数评价解的质量,并更新自身位置和速度。
整个过程中,粒子会不断地向全局最优解靠拢,从而找出最优解。
粒子群算法广泛应用于函数优化问题。
对于复杂的多峰函数,粒子群算法能够通过群体间的信息共享来克服局部最优解,找到全局最优解。
此外,粒子群算法还可以解决许多实际问题,如资源调度、网络路由、机器学习等。
例如,在图像处理中,可以使用粒子群算法进行图像分割、图像识别和图像增强等任务,通过优化算法自动化地寻找最优解。
除了以上应用,粒子群算法还可以用于各种优化问题的求解。
例如,粒子群算法在组合优化问题中的应用表现得较为出色。
在组合优化问题中,需要从大量的解空间中找到最佳的组合方案。
通过粒子群算法的迭代和全局协作,可以有效地找到最优解。
另外,粒子群算法还可以用于工程设计中的自动优化。
在工程设计过程中,需要考虑多个目标和多个约束条件,粒子群算法可以通过多目标优化或多约束优化来处理复杂的工程设计问题。
总之,粒子群算法作为一种群体智能算法,在函数优化、组合优化、图像处理和工程设计等领域都得到了广泛的应用。
其优势在于全局寻优能力和自适应性,能够找到复杂问题的最优解。
随着对算法的研究和改进,粒子群算法有望在更多领域得到应用和推广。
粒子群算法粒子维度

粒子群算法粒子维度粒子群优化算法(Particle Swarm Optimization,PSO)是一种基于群体智能的优化算法,源自对鸟群行为的模拟。
它通过模拟鸟群在食物等目标时的行为,利用群体协作和信息交流来优化问题的解。
在粒子群算法中,解空间被表示为多维空间,每个解被称为一个粒子,粒子的位置表示解在各个维度上的取值。
每个粒子都有自己的位置和速度,通过更新速度和位置来更优的解。
粒子的移动策略是受到个体历史最优位置和全局最优位置的影响,个体历史最优位置是粒子自身的最优解,全局最优位置是整个群体中历史最优解。
粒子群算法的基本过程如下:(1)初始化群体的位置和速度;(2)根据适应度函数评估每个粒子的适应度;(3)更新每个粒子的速度和位置;(4)更新个体历史最优位置和全局最优位置;(5)重复步骤(2)到(4),直到达到指定的迭代次数或满足停止条件。
更新速度和位置的过程可以通过以下公式实现:速度更新公式:V[i] = w * V[i] + c1 * rand( * (P_best[i] -X[i]) + c2 * rand( * (G_best[i] - X[i])位置更新公式:X[i]=X[i]+V[i]其中,V[i]表示粒子i的速度,X[i]表示粒子i的位置,w是惯性权重,P_best[i]是粒子i的个体历史最优位置,G_best[i]是粒子i周围邻域中最优的全局最优位置,c1和c2是学习因子,rand(是一个随机数。
(1)全局能力强:通过群体的协作和信息交流,可以在解空间中进行全局,避免陷入局部最优解;(2)收敛速度快:通过粒子的速度更新,可以有效地引导过程,加快算法的收敛速度;(3)不依赖问题的具体形式:粒子群算法不需要对问题进行求导或者建立模型,适用于不同类型的问题。
然而,粒子群算法也存在一些不足之处:(1)对参数设置敏感:学习因子和惯性权重的选择对算法的性能有重要影响,需要进行合理的参数设置;(2)易陷入局部最优解:粒子群算法在过程中容易陷入局部最优解,特别是在解空间比较复杂的问题中,需要采取一些措施来增强其全局能力。
粒子群算法

粒子群算法原理及简单案例[ python ]介绍粒子群算法(Particle swarm optimization,PSO)是模拟群体智能所建立起来的一种优化算法,主要用于解决最优化问题(optimization problems)。
1995年由 Eberhart和Kennedy 提出,是基于对鸟群觅食行为的研究和模拟而来的。
假设一群鸟在觅食,在觅食范围内,只在一个地方有食物,所有鸟儿都看不到食物(即不知道食物的具体位置。
当然不知道了,知道了就不用觅食了),但是能闻到食物的味道(即能知道食物距离自己是远是近。
鸟的嗅觉是很灵敏的)。
假设鸟与鸟之间能共享信息(即互相知道每个鸟离食物多远。
这个是人工假定,实际上鸟们肯定不会也不愿意),那么最好的策略就是结合自己离食物最近的位置和鸟群中其他鸟距离食物最近的位置这2个因素综合考虑找到最好的搜索位置。
粒子群算法与《遗传算法》等进化算法有很多相似之处。
也需要初始化种群,计算适应度值,通过进化进行迭代等。
但是与遗传算法不同,它没有交叉,变异等进化操作。
与遗传算法比较,PSO的优势在于很容易编码,需要调整的参数也很少。
一、基本概念与遗传算法类似,PSO也有几个核心概念。
粒子(particle):一只鸟。
类似于遗传算法中的个体。
1.种群(population):一群鸟。
类似于遗传算法中的种群。
2.位置(position):一个粒子(鸟)当前所在的位置。
3.经验(best):一个粒子(鸟)自身曾经离食物最近的位置。
4.速度(velocity ):一个粒子(鸟)飞行的速度。
5.适应度(fitness):一个粒子(鸟)距离食物的远近。
与遗传算法中的适应度类似。
二、粒子群算法的过程可以看出,粒子群算法的过程比遗传算法还要简单。
1)根据问题需要,随机生成粒子,粒子的数量可自行控制。
2)将粒子组成一个种群。
这前2个过程一般合并在一起。
3)计算粒子适应度值。
4)更新种群中每个粒子的位置和速度。
粒子群算法详解

粒子群算法详解粒子群算法(Particle Swarm Optimization,PSO)是一种模拟鸟群觅食行为的优化算法,通过模拟个体之间的协作和信息共享来寻找最优解。
它是一种全局优化算法,可以应用于各种问题的求解。
粒子群算法的基本思想是通过模拟鸟群的行为来寻找最优解。
在算法中,将待优化问题看作一个多维空间中的搜索问题,将问题的解看作空间中的一个点。
每个解被称为一个粒子,粒子的位置代表当前解的状态,速度代表解的更新方向和速度。
粒子之间通过互相交流信息,以共同寻找最优解。
在粒子群算法中,每个粒子都有自己的位置和速度。
每个粒子根据自身的经验和邻域中最优解的经验来更新自己的速度和位置。
速度的更新由三个因素决定:当前速度、个体最优解和全局最优解。
粒子根据这些因素调整速度和位置,以期望找到更优的解。
通过不断迭代更新,粒子群逐渐收敛于最优解。
粒子群算法的核心是更新速度和位置。
速度的更新公式如下:v(t+1) = w * v(t) + c1 * rand() * (pbest - x(t)) + c2 * rand() * (gbest - x(t))其中,v(t+1)为下一时刻的速度,v(t)为当前速度,w为惯性权重,c1和c2为学习因子,rand()为[0,1]之间的随机数,pbest为个体最优解,gbest为全局最优解,x(t)为当前位置。
位置的更新公式如下:x(t+1) = x(t) + v(t+1)通过调整学习因子和惯性权重,可以影响粒子的搜索能力和收敛速度。
较大的学习因子和较小的惯性权重可以增强粒子的探索能力,但可能导致算法陷入局部最优解;较小的学习因子和较大的惯性权重可以加快算法的收敛速度,但可能导致算法过早收敛。
粒子群算法的优点是简单易实现,收敛速度较快,对于大多数问题都能得到较好的结果。
然而,粒子群算法也存在一些缺点。
首先,算法对于问题的初始解和参数设置较为敏感,不同的初始解和参数可能导致不同的结果。
粒子群优化算法-参数寻优
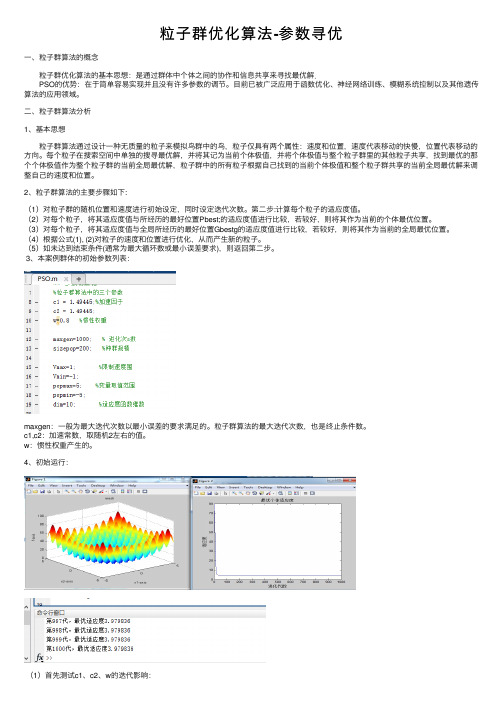
粒⼦群优化算法-参数寻优⼀、粒⼦群算法的概念 粒⼦群优化算法的基本思想:是通过群体中个体之间的协作和信息共享来寻找最优解. PSO的优势:在于简单容易实现并且没有许多参数的调节。
⽬前已被⼴泛应⽤于函数优化、神经⽹络训练、模糊系统控制以及其他遗传算法的应⽤领域。
⼆、粒⼦群算法分析1、基本思想 粒⼦群算法通过设计⼀种⽆质量的粒⼦来模拟鸟群中的鸟,粒⼦仅具有两个属性:速度和位置,速度代表移动的快慢,位置代表移动的⽅向。
每个粒⼦在搜索空间中单独的搜寻最优解,并将其记为当前个体极值,并将个体极值与整个粒⼦群⾥的其他粒⼦共享,找到最优的那个个体极值作为整个粒⼦群的当前全局最优解,粒⼦群中的所有粒⼦根据⾃⼰找到的当前个体极值和整个粒⼦群共享的当前全局最优解来调整⾃⼰的速度和位置。
2、粒⼦群算法的主要步骤如下:(1)对粒⼦群的随机位置和速度进⾏初始设定,同时设定迭代次数。
第⼆步:计算每个粒⼦的适应度值。
(2)对每个粒⼦,将其适应度值与所经历的最好位置Pbest;的适应度值进⾏⽐较,若较好,则将其作为当前的个体最优位置。
(3)对每个粒⼦,将其适应度值与全局所经历的最好位置Gbestg的适应度值进⾏⽐较,若较好,则将其作为当前的全局最优位置。
(4)根据公式(1), (2)对粒⼦的速度和位置进⾏优化,从⽽产⽣新的粒⼦。
(5)如未达到结束条件(通常为最⼤循环数或最⼩误差要求),则返回第⼆步。
3、本案例群体的初始参数列表:maxgen:⼀般为最⼤迭代次数以最⼩误差的要求满⾜的。
粒⼦群算法的最⼤迭代次数,也是终⽌条件数。
c1,c2:加速常数,取随机2左右的值。
w:惯性权重产⽣的。
4、初始运⾏:(1)⾸先测试c1、c2、w的迭代影响:利⽤函数来表⽰各变量:运⾏得:逐渐迭代得:可以看出迭代收敛最早。
随着不断的迭代,最优适应度承不稳定状态。
(2)dim与sizepop的影响:适应度函数维数dim=12:适应度函数维数dim=8:适应度函数维数dim=5:适应度函数维数dim=3:种群规模sizepop=220:种群规模sizepop=200:种群规模sizepop=150:种群规模sizepop=130:将种群规模sizepop调制到<130时,迭代次数⽆法收敛到接近于0,所以判别种群规模sizepop在200最佳。
粒子群算法(基础精讲)课件

神经网络训练
神经网络训练是指通过训练神经网络来使其能够学习和模拟特定的输入输出关系 。粒子群算法可以应用于神经网络的训练过程中,通过优化神经网络的参数来提 高其性能。
例如,在机器视觉、语音识别、自然语言处理等领域中,神经网络被广泛应用于 各种任务。粒子群算法可以用于优化神经网络的结构和参数,从而提高其分类、 预测等任务的准确性。
优势
在许多优化问题中,粒子群算法表现出了良好的全局搜索能 力和鲁棒性,尤其在处理非线性、多峰值等复杂问题时具有 显著优势。
粒子群算法的核心要素
02
粒子个体
01
粒子
在粒子群算法中,每个解被称为一个粒子,代表问题的 一个潜在解。
02
粒子状态
每个粒子的位置和速度决定了其状态,其中位置表示解 的优劣,速度表示粒子改变方向的快慢。
社会认知策略的引入
总结词
引入社会认知策略可以增强粒子的社会性,提高算法的群体协作能力。
详细描述
社会认知策略是一种模拟群体行为的方法,通过引入社会认知策略,可以增强粒子的社会性,提高算 法的群体协作能力。在粒子群算法中引入社会认知策略,可以使粒子更加关注群体最优解,促进粒子 之间的信息交流和协作,从而提高算法的全局搜索能力和鲁棒性。
03 粒子群算法的实现步骤
初始化粒子群
随机初始化粒子群的 位置和速度。
初始化粒子的个体最 佳位置为随机位置, 全局最佳位置为随机 位置。
设置粒子的个体最佳 位置和全局最佳位置 。
更新粒子速度和位置
根据粒子个体和全局最佳位置计 算粒子的速度和位置更新公式。
更新粒子的速度和位置,使其向 全局最佳位置靠近。
每个粒子都有一个记录其历史最 佳位置的变量,用于指导粒子向
粒子群算法基本原理

粒子群算法基本原理粒子群算法(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,模拟了鸟群或鱼群等生物群体在自然界中求解问题的行为。
粒子群算法是一种无约束优化算法,可以用于求解各种优化问题。
粒子群算法的基本原理是通过模拟粒子在解空间中的过程来寻找最优解。
每个粒子表示了一个潜在的解,其位置和速度表示了解的状态和速度。
整个粒子群可以看作是一个多维解空间中的群体,每个粒子都具有一个解向量和速度向量,通过不断调整速度和位置来寻找最优解。
1.初始化粒子群:根据问题的维度和约束条件,随机初始化粒子的位置和速度。
其中位置表示解向量,速度表示方向和速度。
2.计算粒子适应度:根据问题的定义,计算每个粒子的适应度。
适应度函数根据问题的不同而变化,可以是目标函数的取值或其他综合评价指标。
3.更新粒子速度和位置:通过利用粒子当前的位置、速度和历史最优解来更新粒子的速度和位置。
速度的更新过程包括两部分,第一部分是加速度项,其大小与粒子所处位置与个体最优解、群体最优解的距离有关;第二部分是惯性项,保持原有的速度方向并控制的范围。
位置的更新通过当前位置和速度得到新的位置。
4.更新个体最优解和群体最优解:将每个粒子的适应度与其历史最优解进行比较并更新。
个体最优解是粒子自身到的最优解,群体最优解是所有粒子中的最优解。
5.判断停止条件:根据预定的停止条件判断是否终止算法。
停止条件可以是达到最大迭代次数、适应度值达到一定阈值或范围满足一定条件等。
6.返回最优解:将群体最优解或个体最优解作为最终结果返回。
粒子群算法通过不断地更新粒子的速度和位置,通过粒子之间的信息交流和协作来找到最优解。
在算法的早期阶段,粒子的范围较大,有较高的探索性;随着的进行,粒子逐渐聚集在最优解周围,并逐渐减小范围,增强了局部的能力。
这种全局和局部的结合使得粒子群算法能够更好地求解多峰优化问题。
粒子群算法的优点是简单易实现、全局能力强,对于非线性、非凸性、多峰性问题有很好的适应性。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(3)
18
为非负数,称为惯性因子,惯性权重,是控制速度的权重
2013-7-14
(1)线性调整的策略 允许的最大速度vmax实际上作为一个约束,控制PSO能够具有的 最大全局搜索能力。如果vmax较小,那么最大的全局搜索能力将 被限制,不论惯性权重的大小,PSO只支持局部搜索;如果设 置vmax较大,那么PSO通过选择 ,有一个可供很多选择的搜索 能力范围。 由此可以看出,允许的最大速度间接地影响全局搜索能力,而 惯性权重直接影响全局搜索能力,所以希望找到一个非常好的 惯性权重来达到全局搜索和局部搜索之间的平衡。 类似于人的“原动力”,如果原动力比较大,当达到某个目 标的时候,会继续向前实现更高的目标:如果原动力较小,到 达某个目标就停滞。
2013-7-14
13
(4)粒子的最大速度vmax :粒子的速度在空间中的每一维上都有 一个最大速度限制值vdmax ,用来对粒子的速度进行钳制,使速 度控制在范围[-vdmax,+vdmax ]内,这决定问题空间搜索的力 度,该值一般由用户自己设定。 vmax是一个非常重要的参数,如果该值太大,则粒子们也许会 飞过优秀区域;另一方面如果该值太小,则粒子们可能无法对 局部最优区域以外的区域进行充分的探测。实际上,它们可能 会陷入局部最优,而无法移动足够远的距离跳出局部最优达到 空间中更佳的位置。 (5) rand1和rand2是介于[0,1]之间的随机数,增加了粒子飞行 的随机性。 (6)迭代终止条件:一般设为最大迭代次数Tmax、计算精度或最 优解的最大停滞步数△t。
2013-7-14
2
粒子群算法的基本原理
PSO的基本概念源于对鸟群捕食行为的研究:
一群鸟在随机搜寻食物,在这个区域里只有一块食物,所有鸟 都不知道食物在哪里。但是他们知道当前的位置离食物还有多 远。 那么找到食物的最优策略是什么呢?最简单有效的就是搜寻目 前离食物最近的鸟的周围区域。
2013-7-14
3
PSO算法就从这种生物种群行为特性中得到启发并用于求解优化 问题。
在PSO中,把一个优化问题看作是在空中觅食的鸟群,那么“食 物”就是优化问题的最优解,而在空中飞行的每一只觅食的 “鸟”就是PSO算法中在解空间中进行搜索的一个“粒 子”(Particle)。 “群”(Swarm)的概念来自于人工生命,满足人工生命的五个基 本原则。因此PSO算法也可看作是对简化了的社会模型的模拟, 这其中最重要的是社会群体中的信息共享机制,这是推动算法 的主要机制。
——Calculate particle velocity according equation (1) ——Update particle position according equation (2) — End
While maximum iterations or minimum error criteria is not attained
粒子i前一时刻的速度
k vid ;
k k 粒子当前位置与自己历史最好位置之间的距离 ( Pbestid xid ) ;
k k 粒子当前位置与群体最好位置之间的距离 (Gbestd xid ) 。
粒子通过公式(2)计算新位置的坐标。
2013-7-14
10
式(1)的第一部分称为动量部分,表示粒子对当前自身运动状 态的信任,为粒子提供了一个必要动量,使其依据自身速度进 行惯性运动; 第二部分称为个体认知部分,代表了粒子自身的思考行为,鼓 励粒子飞向自身曾经发现的最优位置; 第三部分称为社会认知部分,表示粒子间的信息共享与合作, 它引导粒子飞向粒子群中的最优位置。 公式(1)的第一项对应多样化(diversification)的特点,第二项、 第三项对应于搜索过程的集中化(intensification)特点,这三项之 间的相互平衡和制约决定了算法的主要性能。
2013-7-14 16
PSO的各种改进算法
PSO收敛速度快,特别是在算法的早期,但也存在着精度较低, 易发散等缺点。 若加速系数、最大速度等参数太大,粒子群可能错过最优解, 算法不收敛; 而在收敛的情况下,由于所有的粒子都向最优解的方向飞去, 所以粒子趋向同一化(失去了多样性),使得后期收敛速度 明显变慢,同时算法收敛到一定精度时,无法继续优化,所 能达到的精度也不高。 因此很多学者都致力于提高PSO算法的性能。
2013-7-14 8
i=1,2,3…,M:种群大小。
c1和c2:学习因子,或称加速系数,合适的c1和c2既可加快收 敛又不易陷入局部最优。
rand1和rand2:是介于[0,1]之间的随机数。
k Pbestid 是粒子i在第d维的个体极值点的位置;
Gbest 是整个种群在第d维的全局极值点的位置。
2013-7-14
5
每个粒子使用下列信息改变自己的当前位置: (1)当前位置; (2)当前速度; (3)当前位置与自己最好位置之间的距离; (4)当前位置与群体最好位置之间的距离。
2013-7-14
6
粒子群算法的基本思想
用随机解初始化一群随机粒子,然后通过迭代找到最优解。在 每一次迭代中,粒子通过跟踪两个“极值”来更新自己:
粒子群算法
2013-7-14
1
粒子群算法的研究背景
粒子群算法(Particle Swarm Optimization,简称PSO),是一种基 于群体智能的进化计算方法。PSO由Kennedy和Eberhart博士于 1995年提出。 PSO一经提出,由于算法简单,容易实现,立刻引起了进化 计算领域学者们的广泛关注,形成一个研究热点,目前已广 泛应用于函数优化、神经网络训练、模式分类、模糊控制等 领域,取得了较好的效果。 目前PSO算法已被“国际进化计算会议”(IEEE International Conferences on Evolutionary Computation, CEC)列为一个讨论的 专题。
2013-7-14 14
算法流程
开始 初始化粒子X、V
计算Pbest、Gbest
粒子位置、速度更新
计算适应函数值
更新Pbest、Gbest
达到迭代次数或精 度要求? 是
否
输出所需参数
结束
2013-7-14
15
程序伪代码
For each particle —Initialize particle End Do —For each particle ——Calculate fitness value ——If the fitness value is better than the best fitness value (pbest) in history ——set current value as the new pbest — End —Choose the particle with the best fitness value of all the particles as the gbest —For each particle
2013-7-14
4
粒子在搜索空间中以一定的速度飞行,这个速度根据它本身的 飞行经验和同伴的飞行经验来动态调整。所有的粒子都有一个 被目标函数决定的适应值(fitness value),这个适应值用于评价 粒子的“好坏”程度。 每个粒子知道自己到目前为止发现的最好位置(particle best, 记为pbest)和当前的位置,pbest就是粒子本身找到的最优解, 这个可以看作是粒子自己的飞行经验。 除此之外,每个粒子还知道到目前为止整个群体中所有粒子发 现的最好位置(global best,记为gbest),gbest是在pbest中的最 好值,即是全局最优解,这个可以看作是整个群体的经验。
2013-7-14
11
参数意义
(1)粒子的长度N:问题解空间的维数。 (2)粒子种群大小M:粒子种群大小的选择视具体问题而定,但 是一般设置粒子数为20-50。对于大部分的问题10个粒子已经可 以取得很好的结果,不过对于比较难的问题或者特定类型的问 题,粒子的数量可以取到100或200。另外,粒子数目越多,算 法搜索的空间范围就越大,也就更容易发现全局最优解。当然, 算法运行的时间也较长。 (3)加速常数c1和 c2:分别调节向Pbest和Gbest方向飞行的最大 步长,决定粒子个体经验和群体经验对粒子运行轨迹的影响, 反映粒子群之间的信息交流。 如果c1=0,则粒子只有群体经验,它的收敛速度较快,但容易 陷入局部最优;
2013-7-14 12
如果c2 = 0,则粒子没有群体共享信息,一个规模为M的群体等 价于运行了M个各行其是的粒子,得到解的几率非常小,因此 一般设置c1 = c2 。这样,个体经验和群体经验就有了相同重要 的影响力,使得最后的最优解更精确。 改变这些常数会改变系统的“张力”,较低的c1 和 c2值使得粒 子徘徊在远离目标的区域,较高的c1 和 c2值产生陡峭的运动或 越过目标区域。 Shi和Eberhart建议,为了平衡随机因素的作用,一般情况下设 置c1 = c2,大部分算法都采用这个建议。
一个是粒子本身所找到的最好解,即个体极值(pbest),另一个 极值是整个粒子群中所有粒子在历代搜索过程中所达到的最优 解(gbest)即全局极值。 找到这两个最好解后,接下来是PSO中最重要的“加速”过程, 每个粒子不断地改变其在解空间中的速度,以尽可能地朝pbest 和gbest所指向的区域“飞”去。
2013-7-14
7
粒子群优化算法的一般数学模型
个N维向量 来表示:
第i个粒子的位置可表示为 xi xi1 , xi 2 , xiN
速度为 vi vi1, vi 2 ,viN
T
T
在找到两个最优解后,粒子即可根据下式来更新自己的速度和 位置:
