第三章正弦波振荡器习题剖析
第3章 正弦波振荡器答案
第3章 正弦波振荡器3.1 为什么振荡电路必须满足起振条件、平衡条件和稳定条件？试从振荡的物理过程来说明这三个条件的含义。
答：（1）在刚接通电源时，电路中会存在各种电扰动，这些扰动在接通电源瞬间会引起电路电流的突变（如晶体管b i 或c i 突变），这些突变扰动的电流均具有很宽的频谱，由于集电极LC 并联谐振回路的选频作用，其中只有角频率为谐振角频率o ω的分量才能在谐振回路两端产生较大的电压()o o u j ω。
通过反馈后，加到放大器输入端的反馈电压()f o u j ω与原输入电压()i o u j ω同相，并且有更大的振幅，则经过线性放大和正反馈的不断循环，振荡电压振幅会不断增大。
故要使振荡器在接通电源后振荡幅度能从小到大增长的条件是：()()()()f o o i o i o u j T j u j u j ωωωω=>即： ()1o T j ω> ……起振条件 （2）振荡幅度的增长过程不可能无休止地延续下去。
随着振幅的增大，放大器逐渐由放大区进入饱和区截止区，其增益逐渐下降。
当因放大器增益下降而导致环路增益下降至1时，振幅的增长过程将停止，振荡器达到平衡状态，即进入等幅状态。
振荡器进入平衡状态后，直流电源补充的能量刚好抵消整个环路消耗的能量。
故平衡条件为：()1o T j ω=（3）振荡器在工作过程中，不可避免地要受到各种外界因素变化的影响，如电源电压波动、噪声干扰等。
这些会破坏原来的平衡条件。
如果通过放大和反馈的不断循环，振荡器能产生回到原平衡点的趋势，并且在原平衡点附近建立新的平衡状态，则表明原平衡状态是稳定的。
振荡器在其平衡点须具有阻止振幅变化、相位变化的能力，因此：振幅平衡状态的稳定条件是：()0i iAo iU U T U ω=∂<∂;相位平衡状态的稳定条件是：()0oT o ωωϕωω=∂<∂3.2 图题3.2所示的电容反馈振荡电路中，1100pF C =，2300pF C =，50μH L =。
正弦波振荡器振荡电路分析
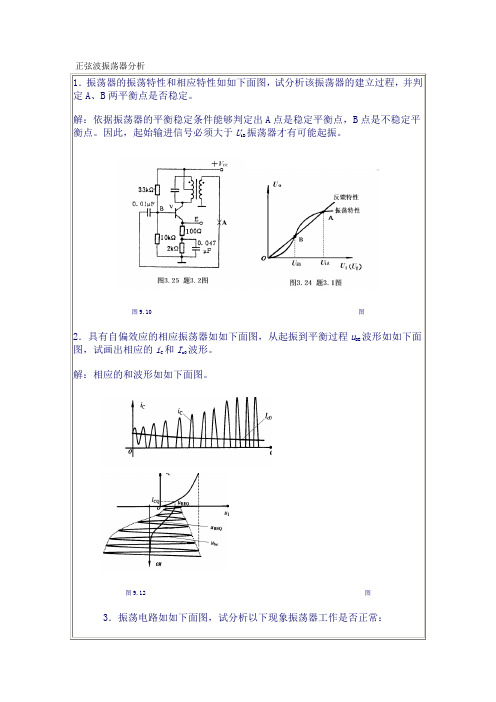
正弦波振荡器分析1．振荡器的振荡特性和相应特性如如下面图，试分析该振荡器的建立过程，并判定A、B两平衡点是否稳定。
解：依据振荡器的平衡稳定条件能够判定出A点是稳定平衡点，B点是不稳定平衡点。
因此，起始输进信号必须大于U iB振荡器才有可能起振。
图9.10 图2．具有自偏效应的相应振荡器如如下面图，从起振到平衡过程u BE波形如如下面图，试画出相应的i C和I c0波形。
解：相应的和波形如如下面图。
图9.12 图3．振荡电路如如下面图，试分析以下现象振荡器工作是否正常：〔1〕图中A点断开，振荡停振，用直流电压表测得V B＝3V，V E＝。
接通A点，振荡器有输出，测得直流电压V B＝，V E＝。
〔2〕振荡器振荡时，用示波器测得B点为余弦波，且E点波形为一余弦脉冲。
解：〔1〕A点断开，图示电路变为小信号谐振放大器，因此，用直流电压表测得V＝3V，V E＝。
当A点接通时，电路振荡，由图所示的振荡器从起振到平衡的过程B中能够瞧出，具有自偏效应的相应振荡器的偏置电压u BEQ，从起振时的大于零，等于零，直到平衡时的小于零〔也能够不小于零，但一定比停振时的u BEQ小〕，因此，测得直流电压V B＝，V E＝是正常的，讲明电路已振荡。
〔2〕是正常的，因为，振荡器振荡时，u be为余弦波，而i c或i e的波形为余弦脉冲，所示E点波形为一余弦脉冲。
4．试咨询仅用一只三用表，如何判定电路是否振荡？解：由上一题分析可知，通过测试三极管的偏置电压u BEQ即可判定电路是否起振。
短路谐振电感，令电路停振，要是三极管的静态偏置电压u BEQ增大，讲明电路差不多振荡，否那么电路未振荡。
5．一相应振荡器，假设将其静态偏置电压移至略小于导通电压处，试指出接通电源后应采取什么措施才能产生正弦波振荡，什么缘故？解：必须在基极加一个起始鼓舞信号，使电路起振，否那么，电路可不能振荡。
6．振荡电路如如下面图，试画出该电路的交流等效电路，标出变压器同名端位置；讲明该电路属于什么类型的振荡电路，有什么优点。
第三章正弦波振荡器3
+ C1 Vo T RE RL +L +C
+ Vo -
e
/ re Cb e
C
Vi
-
2
gm V i
Vf
-
b 共基极等效电路
Zi
+ C1 + T RE RL C2 + Zi L Reo Vo
gi
/ L
g
Z1
1 RE
1 Reo
1 re
Zi
/ 2
1 gi
//
1 jwC
b/e
1 RL
T（wosc）
1
若Vi很小时，|T（jwosc）|＜1，即Vf ＜Vi且同相 无法得到Vo，即停振。 满足起振和 平衡条件时，只能说明电路是 正反馈；不能说明输出的稳定性。 （Vcc、T） （V f 、（ wosc）） T
A
T（wosc） 破坏平衡条件 T（wosc） T（wosc）=1 停振 达到新的平衡点 A B 平衡状态 1 回到原平衡点：稳定
⑵相位稳定条件
①稳定条件
（ T w） w w wo sc
2n 相位平衡条件：（ T wosc） 当温度变化或外界干扰时
相频特性 （ T w）
（ T wosc）＞0 / wosc
w
|
＜ 0 w ＞0
t
在w=wosc处具有 负斜率特性
②不稳定条件
（ // T wosc）＞ 0 V f 超前Vi wosc wos W＞wosc c t 不稳定 （ T wosc）＜ 0 （ w ） ＜ 0 落后 V V T osc f i
/ 1 2
第3章正弦波振荡电路.
.
.
F ()
V
.
f
V0
jM
r jL1
A( )
.
F
( )
1
jMgm 2L1C jrC
rC
Mg m j(1
2 L1C)
00:56
21
.
根据相位平衡条件，A() F() 的模值应该为实数，则可以得到：
1
1 2 L1C 0 振荡角频率o为： o = L1C
9
振荡平衡条件: A( j )F( j ) 1
它是维持振荡的基本条件，通常也称为振荡的平衡条件。
A ( j ) Ae j A
又由于
F
(
j
)
Fe
j F
所以振荡平衡条件的约束方程可以分为两个方程:
AF 1
A F 2n (n 0，1，2)
一、开环法
开环法是先假定将振荡环路在某一点处断开，计算它的开环传递函数
.
A() F()
，然后用巴克豪森准则确定平衡条件，从而确定电路的
振荡频率和起振条件。
00:56
18
开环法步骤
1．画出振荡电路的交流通路，判别其是否能构成正反馈电路，即 是否有可能满足振荡的相位平衡条件。
2．画出微变等效电路，并在某一点（一般取晶体管输入端）开环。
3．计算开环传递函数
.
A() F ()
4．利用相位平衡条件确定振荡角频率0。
5．利用o角频率下的幅度平衡条件，确定维持振荡幅度所需要的gm值gmo。
6．选择晶体管的gm使gm ＞gmo 。此时电路就能够满足起振条件。
00:56
正弦波振荡器习题解答
3-1若反馈振荡器满足起振和平衡条件， 则必然满足稳定条件， 这种说法是否正确为什么解：否。
因为满足起振与平衡条件后， 振荡由小到大并达到平衡。
但当外界因素（T 、V C C ） 变化时，平衡条件受到破坏，若不满足稳定条件，振荡器不能回到平衡状态，导致停振。
3-2 一反馈振荡器，欲减小因温度变化而使平衡条件受到破坏，从而引起振荡振幅和振若满足振幅稳定条件，当外界温度变化引起 V i 增大时，T （osc ）减小，V i 增大减缓，最终 回到新的平衡点。
若在新平衡点上负斜率越大，则到达新平衡点所需 V i 的变化就越小，振荡振幅就越稳定。
最终回到新平衡点。
这时，若负斜率越大，则到达新平衡点所需osc 的变化就越小，振荡频率就越稳定。
3-3并联谐振回路和串联谐振回路在什么激励下 （电压激励还是电流激励）才能产生负斜率的相频特性解：并联谐振回路在电流激励下，回路端电压V 的频率特性才会产生负斜率的相频特性， 如图（a ）所示。
串联谐振回路在电压激励下， 回路电流I 的频率特性才会产生负斜率的相频特 性，如图（b ）所示。
T ~~―rqcIiJ Ap叱荡频率的变化，应增大T （v °sc ）和T（）状态的过程（振幅和相位）。
解：由振荡稳定条件知：振幅稳定条件：T （ osc ）V i l ViA相位稳定条件：T （）为什么试描述如何通过自身调节建立新平衡若满足相位稳定条件，外界因素变化osc T（）osc阻止osc 增大,OSC$-4 在一个山主刚络和反潰网纠缁股的闭合环略中、如图NP3- 4U)J9r 示・F(j 血屋如何确走的？试写岀満足振荡器三条件时 〔叫J 將二网堀之间的去系式m ：在图 M 爭—4(■詁脑示闭合环路中的用处斷开.斷卄点例右侧加屯爪 V ，左删淇放大鹘时做人31抗「如謝Mr? 4(b)所示.分别求出放女签的増总A (i<v)——卞利氐馈网缔陵诚奈数左][js ) = ——^ ..则■「(★”、— A {j f ri ) x v f t j £±j )=由此碍.振站器的起惊条件为T C 仏十)—d (炒”〕此.(w —,〉> 1 *r (曲J -审小蚀卡衡条件为Y < cw ：M ：} -■罔NP3- - 4贬酿抵薪骼拆珂方和•罔3-5试判断下图所示交流通路中，哪些可能产生振荡，哪些不能产生振荡。
正弦波振荡器习题课
正弦波振荡器习题课一、主要内容提要1. 振荡器的振荡的一般条件 起振条件：,1>FA )3,2,1(2⋅⋅⋅⋅⋅⋅==+n n f A πϕϕ 平衡条件： ,1=FA )3,2,1(2⋅⋅⋅⋅⋅⋅==+n n f A πϕϕ2. LC 振荡器⑴变压器反馈式——集电极调谐型（调C ）、基极调谐型（调B ）、发射极调谐型（调E ） （2）三端式（三点式）——①电容三端式：特点——波形好，用在频率高的场合，不易调节频率（改变C 时，同时会改变反馈系数），②改进的电容三端式（考必玆电路）——在电感支路串联一个容量远小于原电路电容量的小电容，特点是：解决了原电容三点式电路，频率调节不便；但存在调节C3时易改变电路增益，所以频率调节范围（覆盖系数）不大。
③西勒电容三端式——在考必玆电路基础上，在电感两端并联一个小容量电容，解决了考必玆电路频率调节范围（覆盖系数）不大的问题。
④电感三端式：特点——波形不好，用在频率不太高的场合，频率调节方便（调节电容量,不会改变反馈系数。
3. 石英晶体振荡器 （1） 特点：频率稳定度高（2） 等效电路：有两个谐振频率——fs 和fp （3） 实际电路——串联型和并联型 4. RC 振荡器是低频的振荡器，分为“桥式”和“相移式”两种。
“桥式”电路的组成——正反馈：RC 串并联网络，负反馈：电压串联负反馈(电阻有一热敏电阻——限幅)，同相放大器 振荡频率: 二、典型例题解析1．画出电容三点式振荡器电路图，说明它的应用特性。
2．画出电感三点式振荡器电路图，并说明它的应用特征。
3．分析下图所示电路的工作原理。
RCf o π21=4．分析下图所示电路的工作原理。
5.在下图所示收音机变频器电路中，那些元件构成振荡器电路？属于那种振荡器类型？CR B2至中放收音机变频器电路三、课后习题解析。
实验三LC正弦波振荡器
实验三 LC正弦波振荡器
C T 1 0 0 p F ,C C 1 0 0 1 2 0 0 改变晶体管IEQ使其分别为表 所标各值，测出振荡频率，并填入表
实验三 LC正弦波振荡器
五、思考题 1、为什么起振后直流工作点电流不同于起振前的静态工作点
电流？对于一个实际的振荡器，用万用电表检查它，能不 能判断它是否起振呢？ 2、为什么静态电流IEQ增大，振幅增强。而IEQ过大反而会使振 荡器输出幅度下降？ 3、为什么反馈系数要选取B＝0.5~0.01 ，过大，过小有什么不好？ 4、在电容Ce上建立平均电压的条件是什么？ 5、为什么提高回路的Q值，可以提高振荡频率的稳定度？
（1）改变CT电容，当分别接C9、C10、C11时，记录相应的频率值， 并填入表。
（2）改变CT电容，当分别接C9、C10、C11时，用示波器测量振荡 电压的峰峰值VP－P，并填入表
（3）比较起振前后工作点的变化，其中起振前 VBEQ＝VBQ－VEQ 起振后为VBE0＝VB0－VE0
实验三 LC正弦波振荡器
实验三 LC正弦波振荡器
二、实验原理
➢ 正弦波振荡器是指振荡波形接近理想正弦波的振荡器， 这 是应用十分广泛的一类电路。
➢ 产生正弦信号的振荡电路形式很多，但归结起来，不外 是 RC、LC和晶体振荡器三种电路形式。在本实验中，我们 研究的主要是LC三端式振荡器及晶体振荡器。LC三端式 振荡器的基本电路如图3-1所示。根据相位平衡条件，图
中 电构抗成，振X3荡必电须X路为3＝ 的异三性－ 个质（ 电的抗X 电1中抗＋ 间，X，且2） X它1们、之X2间必应须满为足同下性列质关的
系式：
实验三 LC正弦波振荡 器
图3-1 三端式振荡器的交流等效电路
(完整版)高频电子线路杨霓清答案第三章-正弦波振荡器
思考题与习题3.3 若反馈振荡器满足起振和平衡条件，则必然满足稳定条件，这种说法是否正确？为什么？ 解：不正确。
因为满足起振条件和平衡条件后，振荡由小到大并达到平衡。
但当外界因素（温度、电源电压等）变化时，平衡条件受到破坏。
若不满足稳定条件，振荡起就不会回到平衡状态，最终导致停振。
3.4 分析图3.2.1(a)电路振荡频率不稳定的具体原因？解：电路振荡频率不稳定的具体原因是晶体管的极间电容与输入、输出阻抗的影响，电路的工作状态以及负载的变化，再加上互感耦合元件分布电容的存在，以及选频回路接在基极回路中，不利于及时滤除晶体管集电极输出的谐波电流成分，使电路的电磁干扰大，造成频率不稳定。
3.7 什么是振荡器的起振条件、平衡条件和稳定条件？各有什么物理意义？振荡器输出信号的振幅和频率分别是由什么条件决定的？ 解：（1） 起振条件： 振幅起振条件 01A F >相位起振条件 2A F n ϕϕπ+=（n=0,1,…）(2)平衡条件：振幅平衡条件AF=1相位平衡条件 2A F n ϕϕπ+=（n=0,1,…）（3） 平衡的稳定条件：振幅平衡的稳定条件0AU ∂<∂ 相位平衡的稳定条件0Zϕω∂<∂振幅起振条件01A F >是表明振荡是增幅振荡，振幅由小增大，振荡能够建立起来。
振幅平衡条件AF=1是表明振荡是等幅振荡，振幅保持不变，处于平衡状态。
相位起振条件和相位平衡条件都是2A F n ϕϕπ+=（n=0,1,…），它表明反馈是正反馈，是构成反馈型振荡器的必要条件。
振幅平衡的稳定条件A ∂/0U ∂<0表示放大器的电压增益随振幅增大而减小，它能保证电路参数发生变化引起A 、F 变化时，电路能在新的条件下建立新的平衡，即振幅产生变化来保证AF=1。
相位平衡的稳定条件Z ϕ∂/ω∂<0表示振荡回路的相移Z ϕ随频率增大而减小是负斜率。
它能保证在振荡电路的参数发生变化时，能自动通过频率的变化来调整A F ϕϕ+=YF Z ϕϕ+=0，保证振荡电路处于正反馈。
第3章正弦波振荡器练习
第3章正弦波振荡器练习1．反馈型振荡器是由（主网络放大器/放大网络）和（反馈网络/选频网络）组成的一个闭合环路,构成能量补偿部分和选频线性网络。
2．电容三点式振荡电路输出的谐波成分比电感三点式的大，因此波形较差。
(╳)3．正弦波谐振电路1）LC三点式振荡器属于正反馈放大器（√）2）克拉泼电路是电感三点式的一种改进形式（╳）3）在串联型晶体振荡器中，石英晶体相当于一个特殊的高Q电感元件。
（╳）4）LC三点式振荡器的幅度稳定条件是由并联谐振回路的幅频特性决定的（╳）4．晶体管LC正弦波振荡器采用的偏置电路大都是：（C）A、固定偏置B、自给偏置C、固定与自给的混合偏置D、不需要偏置5．要产生频率较高的正弦波信号应采用（A）振荡器，要产生频率较低的正弦波信号应采用（B）振荡器，要产生频率稳定度高的正弦波信号应采用（C）振荡器。
A）LC振荡器B）RC振荡器C）晶体振荡器6．正弦波自激振荡器振荡建立过程，晶体管的工作状态是（D）。
A）甲类B）甲乙类C）丙类D）甲类－>甲乙类－>丙类7．克拉泼振荡电路比考毕兹振荡电路的频率稳定度高，是因为克拉泼电路的振荡回路中接入一个电容C3，从而能减小晶体管输入、输出电容对振荡回路的影响。
(√)8．写出反馈振荡器的平衡条件、起振条件表达式。
答：平衡条件：振幅平衡条件：T(oc)1相位平衡条件：T(oc)2n起振条件：振幅起振条件：T(oc)1相位起振条件：T(oc)2nVf9．振荡器的环路增益为T(j)T()ejT()，振荡频率为oc，试写出振幅稳定条件：Vi[T(OSC)0]ViViAVf10.振荡器的环路增益为T(j)T()ejT()，振荡频率为oc，试写出相位稳定条件：Vi[T()oc0]11.有一个LC并联谐振电路，其电感损耗电阻为r，则谐振频率fp=12LC1112Q2LC(Q0Lr1，00rC1LC)，当f〈fp时，回路阻抗呈感性，当f〉fp时，回路阻抗呈容性12.三点式振荡器的基本组成原则是晶体管的e到c和b间要接同性电抗，而b-c间接异性电抗。
通信电子线路第3章_正弦波振荡器
第3章 正弦波振荡器
3.2 LC正弦波振荡器
3.2.1 LC正弦波振荡器电路构成的原则 凡采用LC谐振回路作为选频网络的反馈式振荡器
称为LC正弦波振荡器。LC振荡电路的形式很多，按 反馈网络的形式来分，有变压器耦合反馈式及电感或 电容反馈式振荡电路两种。
第3章 正弦波振荡器
c
Uce
b
x3
I2
I1
x1
Uf e
x2
c
b
L
I2
I1
则相位稳定平衡就可实现。以n=0为例，这一过程可用
如下流程关系表示：
第3章 正弦波振荡器
由此可得相位稳定条件为
P
( Y
P
F
P
Z
P) 0
在窄带情况下，均可认为 F 0, Y 0
则相位稳定条件为
Z
P 0
(3.1―12) (3.1―13)
图3.1示出的是一个反馈式放大器的框图。它由基本
放复大振器幅A，和U反i 是馈基网本络放F大组器成输，入图电中 压，U复o 是振放幅大，器U输f 出是电反压馈 网络输出的反馈电压复振幅， Ui' 是反馈放大器输入电
压复振幅，其中基本放大器增益
A
Uo
Ae jA
Ui
(3.1―1)
第3章 正弦波振荡器
如果振幅稳定是由放大器的非线性工作实现的， 称这种振幅稳定方式叫内稳幅方式。
2. 当A=常数时，振幅稳定条件为
F Ui p 0
正弦波振荡器练习题及答案
正弦波振荡器练习题及答案一、选择题1、振荡器的振荡频率取决于。
（）A ．供电电源B ．选频网络C ．晶体管的参数D ．外界环境2、为提高振荡频率的稳定度，高频正弦波振荡器一般选用。
（）A ．LC 正弦波振荡器B ．晶体振荡器C ．RC 正弦波振荡器3、设计一个振荡频率可调的高频高稳定度的振荡器，可采用（）A ．RC 振荡器B ．石英晶体振荡器C ．互感耦合振荡器D ．并联改进型电容三点式振荡器4、串联型晶体振荡器中，晶体在电路中的作用等效于。
( )A ．电容元件B ．电感元件C ．大电阻元件D ．短路线5、振荡器是根据反馈原理来实现的，反馈振荡电路的波形相对较好。
（）A 、正、电感B 、正、电容C 、负、电感D 、负、电容6、振荡器的频率稳定度高。
（）A ．互感反馈B ．克拉泼电路C ．西勒电路D ．石英晶体7、石英晶体振荡器的频率稳定度很高是因为（）A ．低的Q 值B ．高的Q 值C ．小的接入系数D. 大的电阻8、正弦波振荡器中正反馈网络的作用是（）A ．保证产生自激振荡的相位条件B ．提高放大器的放大倍数，使输出信号足够大C ．产生单一频率的正弦波D ．以上说法都不对9、在讨论振荡器的相位稳定条件时，并联谐振回路的Q 值越高，值ω???越大，其相位稳定性（）A 、越好B 、越差C 、不变D 、无法确定10、并联型晶体振荡器中，晶体在电路中的作用等效于( )A ．电容元件B ．电感元件C ．电阻元件D ．短路线11、克拉拨振荡器属于振荡器。
( )A . RC振荡器B .电感三点式振荡器C .互感耦合振荡器D .电容三点式振荡器12、振荡器与放大器的区别是（）A．振荡器比放大器电源电压高B．振荡器比放大器失真小C．振荡器无需外加激励信号，放大器需要外加激励信号D．振荡器需要外加激励信号，放大器无需外加激励信号13、如图所示电路，以下说法正确的是（）A．该电路由于放大器不能正常工作，不能产生正弦波振荡B．该电路由于无选频网络，不能产生正弦波振荡C．该电路由于不满足相位平衡条件，不能产生正弦波振荡D．该电路满足相位平衡条件，可能产生正弦波振荡14、改进型电容三点式振荡器的主要优点是（）A．容易起振B．振幅稳定C．频率稳定度较高D．减小谐波分量15、在自激振荡电路中，下列哪种说法是正确的（）A．LC振荡器、RC振荡器一定产生正弦波B．石英晶体振荡器不能产生正弦波C．电感三点式振荡器产生的正弦波失真较大D．电容三点式振荡器的振荡频率做不高16、利用石英晶体的电抗频率特性构成的振荡器是（）A．f＝fs时，石英晶体呈感性，可构成串联型晶体振荡器B．f＝fs时，石英晶体呈阻性，可构成串联型晶体振荡器C．fs<f<fp时，石英晶体呈阻性，可构成串联型晶体振荡器< p="">D．fs<f<fp时，石英晶体呈感性，可构成串联型晶体振荡器< p="">17、如图所示是一个正弦波振荡器的原理图，它属于振荡器。
第3章 正弦波振荡器
)
AF = 1 = n = 0,1,2, L ϕ A + ϕ F = 2 nπ
分别称为振幅平衡条件和相位平衡条件。
1. 振幅平衡条件
Uo
U0 U f U f AF = . = =1 Ui U0 Ui U f = Ui
Uf
0
Uo
θ＞90° θ＜90°
放大特性
A B
Ui
① ②
F 0 Uo
0
C Ui＝Uf
ω02 < ω g < ω01
图3.9 多回路三点式振荡器组成
ωg < M min (ω01 , ω02 )
实际上电抗元件总有电阻损耗；管子各极间存在极间 阻抗，这些都影响振荡器的工作状态。工程中，振荡器工 作频率ωg近似等于回路谐振角频率ω0。
例3.1 在右图所示振 荡器交流等效电路中, 三 个ＬＣ并联回路的谐振频 率分别是f01, f02, f03， 试问 ｆ01、 ｆ02、ｆ03满足什么 条件时该振荡器能正常工 作？ 解: 只要满足三点式组成 法则, 该振荡器就能正常 工作。
（6）利用自偏置保证振荡器能自行起振，并使放大器由甲 类工作状态转换成丙类工作状态。 根据振荡条件，振荡器应包括放大器、选频网络、反馈 网络。 放大器采用有源器件，如晶体三极管、场效应管、差分 放大器、运算放大器等。 选频网络可用LC并联谐振回路、RC选频网络、晶体滤波 LC RC 器等。 反馈网络可以是RC移相网络、电容分压网络、电感分压 网络、变压器耦合反馈网络或电阻分压网络等。
V X1 C2 X3 L (a) X2 C1 L2 X1 X3
V L1 X2 C (b)
反馈网络是由电容元件完成的, 称为电容反馈振荡器, 也称 为考必兹(Colpitts)振荡器。图(b)称为电感反馈振荡器，也 称哈特莱(Hartley)振荡器。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
第三章 正弦波振荡器习题解3-5(a) 不振。
不满足正反馈；(b)能振。
变压器耦合反馈振荡器；(c)不振。
不满足三点式振荡电路的组成法则；(d)能振。
当ω1<ωosc <ω2(ω1、ω2分别L 1C 1、L 2C 2谐振频率)，即L 2C 2回路呈感性，L 1C 1回路呈容性，组成电感三点式振荡电路；(e)能振。
计入结电容e 'b C ，组成电容三点式振荡电路；(f)能振。
(b) 当ω1、ω2<ωosc (ω1、ω2分别L 1C 1并联谐振回路、L 2C 2串联谐振回路谐振频率)时，L 1C 1回路呈容性，L 2C 2回路呈感性，组成电容三点式振荡电路。
3-6交流通路如图3-6所示。
(a)、(c)、(f)不振；不满足三点式振荡电路的组成法则；(b)、(d)、(e)、(g)能振。
(b)、(d)为电容三点式振荡电路，其中(d)的管子发射结电容e 'b C 成为回路电容之一，(e)为电感三点式振荡电路，(g)LC1o osc =ω≈ω,电路同时存在两种反馈。
由于LC 串联谐振回路在其谐振频率o ω上呈现最小的阻抗，正反馈最强，因而在o ω上产生振荡。
L图3-7CL 2L 1 T C R CL 1 L 2MTR ELC 2C 1TC L 1 L 2R DTR E1R E3C LR C1R C2RT 1T 2C 2C 1LT(a)(b)(c)(d)(e)(f)(g)3-7按并联谐振回路相频特性可知：在电感三点式振荡电路中ωo3<ωosc <ωo1、ωo2,在电容三点式振荡电路中ωo1、ωo2<ωosc <ωo3。
振荡电路如图3-7所示，图中1C C 、2C C 、B C 、E C 对交流呈短路。
设1B R 、2B R 阻抗较大，对回路影响不大。
3-8改正后的电路如图3-8所示。
说明，图(c)中可在2B R 两端并联旁路电容B C 。
3-9图(a)满足正反馈条件，LC 并联回路保证了相——频特性负斜率，因而满足相位稳定条件，电路可振。
图(b)不满足正反馈条件，将1T 基极开路，反馈电压f V 比1i V 滞后一个小于 90的相位。
图(c)不满足正反馈条件，不振。
3-10用万用表测量发射极偏置电阻E R 上的直流电压：先使振荡器停振（例如回路线(a)BCCR B1R B2ECC CCCR B1R B2(b)(c)(e)(f)(g)R f圈短路）测得EQ V ，得E EQ EQ R /V I =，然后使振荡器工作，测得EO V ，得E EO EO R /V I =。
若EQ EO I I ≠，则说明电路产生振荡。
3-11C)L L (121o osc +=ω≈ω，∵ 12o 22osc 22osc o osc 2osc 2osc of L L V C L 1C L V Cj 1L j L j V V -=ω-ω-=ω+ωω=， i D m o V R g V -=， ∴1L /L R g )(T 12D m osc >=ω即D21m R L L g >。
3-12LC 2o osc =ω≈ω， ∵1C1L C 1V V k osc osc osc o ffv-=ω-ωω-==，D m V R g A -=， ∴1R g k A D m fv v >=或ms 1R 1g Dm =>。
∵)V V (W C g )th (GS GS OX n m -μ=∴V 5.0121V WC g V )th (GS OX n m min GS =-=+μ=3-13在发射极处E L 拆环后，混合∏型等效电路如图3-13 所示。
根据振幅起振条件得式(3-2-8a)i 'L m ng g n1g +>，V i (j ω)+V f (j ω)-图3-13∵015.033205151C C C n '211=+=+=，ms 30g r 1g m ei ===∴v 10443.0g 3'L -⨯<。
∵L'Leo R 1g 1R -=∴Ω=⨯-⨯>--k 115.410210443.01R 43eo ，80105.010115.4LQ R 63o eo ⨯⨯⨯>=ω-- sec /rad 109.1026⨯=能起振。
相应pF 189105.09.1021L 1C 622=⨯⨯<ω=， ∵pF 77.1383371332051189C C C C C C 21213=⨯-<+-=，当pF 12C min 3=时相应∑=ωLC 1max sec /rad 102.17910)33205133205112(105.016126⨯=⨯+⨯+⨯⨯=--。
因而sec /rad 10)2.1799.102(6max min ⨯-=ω-ω，振荡频率MHz 52.288.163f f max min -=-。
3-15图3-15所示为ω-ϕ特性曲线，其中(a)图e e Q Q >'。
首先，当o oω>ω'时引起ω∆osc(1-2)变化，然后f f ϕ>ϕ'又引起ω∆osc(2-3)变化，因而o ω、f ϕ变化引起ω∆osc(1-3)变化，最后e e Q Q >'又引起ω∆osc(3-4)变化，使总频率变化为ω∆osc(1-4)<ω∆osc(1-3)。
图3-15图(b) e e Q Q <'。
通过类似分析得总频率变化为ω∆osc(1-4)>ω∆osc(1-3)。
3-16混合∏型等效电路如图3-16所示。
sec,/rad 1052.8410701021LC 161263osc ⨯=⨯⨯⨯=≈ω--Ω===Ω=⨯⨯⨯⨯=ω=-k 95.79.16//15R //R R ,k 9.161001021052.84LQ R eo L 'L 66o osc eo ,pF 4.800501040101000C C C )C C (C C C C C Ce b 21e b 21'21'21'21''=⨯=+++=+=- ,88.50R n R ,08.04.8007070C C C n 'L 22''L '21332Ω=≈=+=+=- ,26I 5001r 1R 1g ,2.0401010001000C C C n EQ e E i'211+=+==+=+=mA 21.3I ),26I 5001(2.088.5012.0126I ,ng g n 1g EQ EQ EQ i ''L m >++⨯>+>3-17起振时应满足i 'L m ng g n1g +>，其中，m ee E i g r 1r 1R 1g ≈≈+=，所以上式可改写为 ">-L m g n1)n 1(g ，由上题得0.2n =，192.31mS g m =， O 3OSC O OSC eo Q C 1LQ R ω≈ω=，eo L L R //R R ='，图3-16'⎪⎪⎭⎫⎝⎛+="="-L 22133L L R C C C g 1R ，当pF 60C 3=时， Ω=⨯⨯⨯⨯=-k 7.1910010601052.841R 126eo ，Ω='k 5.8R L ，Ω="k 041.0R L ，mS 154)2.01(31.192)n 1(g m =-⨯=-，mS 12210041.02.01g n 13L =⨯⨯="，可振。
当pF 40C 3=时，Ω=k 58.29R eo ，Ω='k 95.9R L ，Ω="k 023.0R L ，mS 4.217g n1L ="，不振。
3-18改正后的交流通路如图3-18所示。
图3-18(a)、(d)并联型晶体振荡器，晶体呈电感，器件的gd C 为振荡电路的部分电容，(b) 、(c) 、(e)串联型晶体振荡器，晶体呈短路元件。
3-19电路如图3-19所示。
图(a)中 1OSC OSC C 1L ω<ω，1LC 回路呈感性，而在图(b)中，1OSC OSC C 1L ω>ω，1LC 回路呈容性。
图3-193-20交流通路如图3-20所示。
由图可知，若晶体呈感性，11C L 并联谐振回路、22C L 串联谐振回路呈容性，则形成皮尔斯振荡电路，1OSC 2ω>ω>ω。
图3-203-21晶体呈感性，为使振荡器起振，要求-+>V V ，O f 11OV 31R R R V V =+=-，,R R R V V eo eo O+=+31R R R eo eo >+，Ω=<+k 240R 3R R eo eo ，Ω=<k 160R 2R eo 。
3-22图(a)不能振荡。
同相放大器加180°相移，电路构成负反馈，不满足相位条件。
图(b)可以振荡。
T 2发射极的输出电压V O 与T 1输入电压反相，三节RC 移相网络可移相180°，因此满足相位条件，能够起振。
图(c)不能振荡。
差分对管组成同相放大器，三节RC 导前移相网络最大相移不超过270°，所以不能满足相位条件，不能振荡。
图(d)不能振荡。
由于T 1 、T 2组成反相放大器，RC 串并联选频电路的相移为零，所以整个电路为负反馈，不满足相位条件，不振。
图(a)(c)(d)改正后的电路如图3-22所示。
图3-223-23图3-23所示为电桥形式电路。
图(a)中灯泡是非线性器件，它的阻值随温度高而增加，即是正温度系数的非线性器件，它的正向阻值随信号增加反而少，这样，振荡器起振时D1、D2截止，负反馈弱，随着振荡加强，二极管正向阻值减小，负反馈增大，从而使振幅达到平衡。
图3-23 3-24∵串并联选频电路网络2211221//11//C j R C j R C j R VV k OSC OSC OSC bfvf ωωω'++'==31)()1()1(122212112=='-+++=OSC vf OSC OSC k C R C R j R R C C ωωω ，式中32L R //R R ='，0C R 1C R 12OSC 21OSC ='ω-ω，2121OSC C C R R 1'=ω。
(1),S /rad 1041005.01051C R 1,C C ,R k 5R //R R 36311OSC 211322⨯=⨯⨯⨯==ω==Ω=='- 3R R C C 12112='++∴要求二反相放大器增益 ;k 32.17R 3R ,3R R V V ,3V V 3min f 23minf i 0i 0Ω===⎪⎪⎭⎫ ⎝⎛=≥ (2),S /rad 1047.4101.001.0105101,k 5R 31234OSC 2⨯=⨯⨯⨯⨯⨯=ωΩ='-.k 06.361013R 13R ,13V V 1351001.01.01R R C C 13min f io 2112Ω=⨯==≥∴=++=++3-25(1)三节RC 移相网络或变压器耦合电路如图3-25(a) 、(b)所示；(2)LC 串联谐振电路、RC 串并联选频网络、晶体、变压器耦合电路，如图(c) 、(d) 、(e) 、(f)所示；(3)反馈支路同(2)，但T 1、T 2组成振荡器，T 3组成放大器。