出栈入栈演示的超详细过程(汉诺塔)
汉诺塔系统栈求解过程

汉诺塔系统栈求解过程一、什么是汉诺塔问题汉诺塔问题是一个经典的数学问题,源自印度的一个传说。
问题的设定是有三根柱子,其中一根柱子上从下往上按照大小顺序摆放着若干个圆盘,大盘在下,小盘在上。
现在的目标是将所有的圆盘从起始柱子上移动到目标柱子上,期间可以借助另一根柱子作为中转。
但是有一个限制条件,即在移动过程中,任意时刻都不能出现大盘在小盘上面的情况。
二、汉诺塔问题的递归求解汉诺塔问题可以使用递归的方式进行求解。
递归的思想是将大问题分解为小问题,然后通过解决小问题来解决大问题。
对于汉诺塔问题来说,如果我们能解决将n-1个盘子从起始柱子移动到中转柱子上的问题,那么将剩下的最大盘子从起始柱子移动到目标柱子上的问题就相对简单了。
因此,我们可以将问题分解为以下三个步骤:1.将n-1个盘子从起始柱子移动到中转柱子上;2.将最大的盘子从起始柱子移动到目标柱子上;3.将n-1个盘子从中转柱子移动到目标柱子上。
这个过程可以通过递归的方式来实现。
下面是汉诺塔问题的递归求解代码示例:def hanoi(n, start, target, temp):if n == 1:print("Move disk 1 from {} to {}".format(start, target))else:hanoi(n-1, start, temp, target)print("Move disk {} from {} to {}".format(n, start, target))hanoi(n-1, temp, target, start)# 调用函数求解汉诺塔问题hanoi(3, "A", "C", "B")三、汉诺塔问题的系统栈求解过程除了使用递归求解汉诺塔问题外,我们还可以使用系统栈来模拟整个求解过程。
系统栈是计算机系统中用于保存函数调用信息的一种数据结构,每当一个函数被调用时,系统会将该函数的相关信息存入栈中,当函数执行完毕后,系统会将该函数的信息出栈,回到上一层函数的执行。
大学数据结构课件--第3章 栈和队列

栈满 top-base=stacksize
top
F
E
D C B
top top top top top top base
入栈PUSH(s,x):s[top++]=x; top 出栈 POP(s,x):x=s[--top]; top
base
4
A
3.1 栈
例1:一个栈的输入序列为1,2,3,若在入栈的过程中 允许出栈,则可能得到的出栈序列是什么? 答: 可以通过穷举所有可能性来求解:
3.2 栈的应用举例
二、表达式求值
“算符优先法”
一个表达式由操作数、运算符和界限符组成。 # 例如:3*(7-2*3) (1)要正确求值,首先了解算术四则运算的规则 a.从左算到右 b.先乘除后加减 c.先括号内,后括号外 所以,3*(7-2*3)=3*(7-6)=3*1=3
9
3.2 栈的应用举例
InitStack(S); while (!QueueEmpty(Q))
{DeQueue(Q,d);push(S,d);}
while (!StackEmpty(S)) {pop(S,d);EnQueue(Q,d);} }
第3章 栈和队列
教学要求:
1、掌握栈和队列的定义、特性,并能正确应用它们解决实 际问题;
用一组地址连续的存储单元依次存放从队头到队尾的元素, 设指针front和rear分别指示队头元素和队尾元素的位置。
Q.rear 5 4 Q.rear 3 2 3 2 5 4 Q.rear 3 3 5 4 5 4
F E D C
C B A
Q.front
2 1 0
C B
Q.front 2 1 0
深入浅出学算法021-汉诺塔问题

深入浅出学算法021-汉诺塔问题汉诺塔问题是一个传统的数学问题,也是一个经典的递归问题。
它是基于以下几个规则:1. 有三根柱子,分别是A、B、C,开始时A柱上有n个从小到大叠放的圆盘。
2. 每次只能移动一个圆盘。
3. 大圆盘不能放在小圆盘上面。
目标是将A柱上的圆盘全部移动到C柱上,可以利用B柱作为辅助。
解决这个问题的一种方法是使用递归。
下面是求解汉诺塔问题的算法步骤:1. 如果只有一个圆盘,直接从A柱移动到C柱。
2. 如果有n个圆盘,可以将问题分解为三个步骤:- 将n-1个圆盘从A柱移动到B柱,可以借助C柱作为辅助。
- 将最大的圆盘从A柱移动到C柱。
- 将n-1个圆盘从B柱移动到C柱,可以借助A柱作为辅助。
递归地应用这个步骤,就可以解决任意数量的圆盘移动问题。
下面是用Python实现汉诺塔问题的代码:```pythondef hanoi(n, A, B, C):if n == 1:print("Move disk", n, "from", A, "to", C)else:hanoi(n-1, A, C, B)print("Move disk", n, "from", A, "to", C)hanoi(n-1, B, A, C)n = int(input("Enter the number of disks: "))hanoi(n, 'A', 'B', 'C')```以上代码中,`hanoi`函数接受四个参数:n表示圆盘的数量,A、B、C分别表示三根柱子的名称。
函数根据递归算法进行移动,并输出每一步的操作。
运行程序,输入圆盘的数量,即可看到详细的移动步骤。
汉诺塔实现步骤
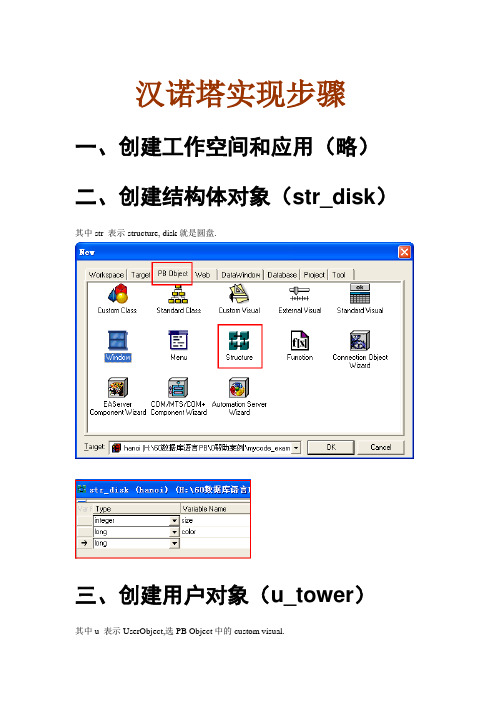
汉诺塔实现步骤一、创建工作空间和应用(略)二、创建结构体对象(str_disk)其中str_表示structure, disk就是圆盘.三、创建用户对象(u_tower)其中u_表示UserObject,选PB Object中的custom visual.(1)操作界面(2)设计控件(3)控件名称(4)部分控件不可见(5)声明实例变量其中roundrectangle irr_disk[14]定义栈空间(空栈)int ii_count栈顶指针(栈内盘子数)(6)编写constructor事件代码作用:在空栈中放置栈元素(盘子)//将14个圆角矩形控件对象加到数组中//即初始化栈//其结果数组元素irr_disk[1]-- irr_disk[14] 分别对应存放的是对象rr_1--rr_14。
int li_indexint li_array_limitint li_control_indexint li_control_limitstring rr_namedrawobject ldo_templi_array_limit = upperbound (irr_disk[])//返回数组维界li_control_limit = upperbound (control[])//返回控件数组维界//将控件数组里的隐藏矩形,放置在定义的实例对象数组中。
For li_control_index = 1 to li_control_limit //对控件数组的每个元素ldo_temp = control[li_control_index]rr_name= ldo_temp.classname()li_index=dec(right(rr_name,len(rr_name)-3)) If li_index>=1 and li_index<= li_array_limit Thenirr_disk[li_index] = ldo_tempEnd IfNext思考:要将irr_disk[1]中放置rr_1对象,能不能这样处理irr_disk[1]=rr_1?为什么?(7)编写函数的操作方法(8)编写adddisk函数(压栈)//注意形式参数的引用方式public subroutine adddisk (str_disk astr_disk);//局部变量int li_x//盘子的x坐标int li_y//盘子的y坐标//针上盘子数加1(栈顶指针加1)ii_count++//u_tower成员//only 14 rectangles were predefined.If ii_count > 14 ThenMessagebox("Peg Error","Error only 14 disk are allowed")ii_count --ReturnEnd If//(图)计算盘子位置//(式)计算盘子位置li_y = r_base.y - ((irr_disk[ii_count].height+ 5)*ii_count) li_x = rr_pole.x + (rr_pole.width / 2) - (astr_disk.size / 2)//盘子宽度和颜色由实参提供irr_disk[ii_count].width = astr_disk.sizeirr_disk[ii_count].fillcolor = astr_disk.colorirr_disk[ii_count].visible = trueirr_disk[ii_count].x = li_x//(图)产生向下的效果//(代码)产生向下的效果irr_disk[ii_count].y = rr_pole.y + irr_disk[ii_count].heightdo while irr_disk[ii_count].y < li_yIf irr_disk[ii_count].y + irr_disk[ii_count].height> li_y Then irr_disk[ii_count].y = li_yElseirr_disk[ii_count].y = irr_disk[ii_count].y&+ irr_disk[ii_count].heightirr_disk[ii_count].visible = trueirr_disk[ii_count].show()yield()End Ifloop(9)编写removedisk函数(弹栈)//注意形式参数的引用方式public subroutine removedisk (ref str_disk as_disk);//确保针上没有盘子时不做该操作If ii_count <= 0 Then return//产生向上的效果do while irr_disk[ii_count].y > rr_pole.y + irr_disk[ii_count].heightIf irr_disk[ii_count].y &- (irr_disk[ii_count].height) <&rr_pole.y &+ irr_disk[ii_count].height Thenirr_disk[ii_count].y = rr_pole.y&+ irr_disk[ii_count].heightElseirr_disk[ii_count].y = irr_disk[ii_count].y&- (irr_disk[ii_count].height)irr_disk[ii_count].visible = trueirr_disk[ii_count].show()yield()//放在循环中,发现信息消息会立即响应,否则等该程序执行完了,才会响应消息队列中的事件。
入栈和出栈的基本操作

入栈和出栈的基本操作栈是一种常见的数据结构,它具有后进先出(LIFO)的特点,即最后进入的元素最先被取出。
在计算机科学中,栈被广泛应用于程序的运行、内存管理等方面。
本文将介绍栈的基本操作——入栈和出栈。
一、入栈入栈是指将一个元素放入栈中的操作。
在栈中,新元素总是被放在栈顶,而原有的元素则依次向下移动。
入栈操作可以用以下伪代码表示:```push(Stack, element)Stack[top] = elementtop = top + 1```其中,Stack表示栈,element表示要入栈的元素,top表示栈顶指针。
入栈操作的实现过程是将元素放入栈顶,然后将栈顶指针向上移动一位。
二、出栈出栈是指将栈顶元素取出的操作。
在栈中,只有栈顶元素可以被取出,而其他元素则不能被访问。
出栈操作可以用以下伪代码表示:```pop(Stack)top = top - 1element = Stack[top]return element```其中,Stack表示栈,top表示栈顶指针,element表示要取出的元素。
出栈操作的实现过程是将栈顶指针向下移动一位,然后将栈顶元素取出并返回。
三、应用栈的入栈和出栈操作在计算机科学中有着广泛的应用。
以下是一些常见的应用场景:1. 程序调用栈在程序运行时,每个函数都会被压入一个调用栈中。
当函数执行完毕后,它会从栈中弹出,控制权会返回到调用该函数的位置。
程序调用栈的实现依赖于栈的入栈和出栈操作。
2. 表达式求值在表达式求值中,栈可以用来存储操作数和运算符。
当遇到运算符时,可以将它入栈,当遇到操作数时,可以将它出栈并进行计算。
表达式求值的实现依赖于栈的入栈和出栈操作。
3. 内存管理在内存管理中,栈可以用来存储函数的局部变量和参数。
当函数被调用时,它的局部变量和参数会被压入栈中,当函数执行完毕后,它们会从栈中弹出。
内存管理的实现依赖于栈的入栈和出栈操作。
四、总结栈是一种常见的数据结构,它具有后进先出的特点。
数据结构编程-汉诺塔

数据结构课程Project 3汉诺塔Type:IndividualProgrammer:Tester:Report Writer:Date of completion:2010/11/10第一章: 绪论问题背景描述汉诺塔游戏是这样的:有三个桩(桩1,桩2和桩3)和N个半径不同的盘子。
初始所有的盘子按半径从小到大堆叠在桩1上,半径最小的盘子在最上面。
规则:每次只可以移动一个桩上最顶端的盘子到另一个桩上,而且不可以把大盘子堆在小盘子上。
问题是要把所有盘子移动到桩3上。
每次用两个整数a (1 <= a <= 3) 和b (1 <= b <= 3)表示一次移动,表示移动桩a最顶端的盘子到桩b上。
如果桩a上至少有一个盘子,而且桩a顶端的盘子可以在不违反规则的情况下移动到桩b上,那么这次移动才是一个有效的移动。
基本要求:输入:每次输入包含几个测试样例。
输入的第一行包含一个整数T (1 <= T <= 55),表示测试样例的个数。
后面紧跟T个测试样例。
每个测试样例第一行有两个整数,n (1 <= n <= 10) 和 m (1 <= m <= 12000),表示有n个盘子,m次移动。
后面m行表示具体的移动步骤。
输出:对每个测试样例,输出一行表示该测试样例最后的移动结果。
(1)如果所有的盘子移动到桩3之前,第p次(从1开始记)移动是无效的移动,输出-p,忽略后面的移动步骤。
(2)如果经过p次移动后,所有的盘子都已经移动到桩3,则输出p,并忽略后面的移动步骤。
(3)其他情况输出0int main(void)主函数,打开输入输出文件,将各测试样例送入func( )执行void func(int n,int m)操作函数,处理一个测试样例构造一个三元堆栈数组表示三个桩将n个盘子从大到小放入桩1依次进行m次移动,被移栈弹出的盘子压入目的栈有效或无效移动判断,输出结果销毁堆栈void destroy()关闭输入输出文件第二章: 算法详述FILE *fp_in 输入文件指针FILE *fp_out 输出文件指针定义堆栈typedef struct {int *base; 栈底指针int *top; 栈顶指针int stacksize; 栈所占的存储空间大小}stack;stack stake[3]; 一个三元栈顶数组,表示三个桩int T 测试样例的个数int n 每个测试样例的盘子数int m 每个测试样例移动的次数int from 被移桩号int to 目的桩号int plate 被移盘子号(从小到大依次为1到n)int topplate 目的桩原来的顶层盘号int law 移动合法性判断int main(void){for i:=1 to T dobegin{输入m,n送入func( )执行}}void func(int n,int m){为三个桩构造三个空栈for j:=n to 1 dobegin{stake[0]=push(stake[0],j);}for k:=1 to m dobegin{fscanf(fp_in, "%d%d",&from,&to)plate:=getplate(stake[from-1]) 得到移出的盘子号if(被移桩无盘子) thenfprintf(fp_out, "-%d\n",k)跳出循环,忽略以后步骤stake[from-1]:=pop(stake[from-1]) 该桩弹出顶端的盘子topplate:=getplate(stake[to-1]) 得到目的桩原来的顶层盘子号stake[to-1]=:push(stake[to-1],plate) 将盘子移入该桩if(被移动盘子比原来桩顶盘子大) thenfprintf(fp_out, "-%d\n",k)跳出循环,忽略以后步骤else if(桩3的盘子数为n) thenfprintf(fp_out, "%d\n",k)跳出循环,忽略以后步骤}if(k<=m) thenfor(i=k+1;i<=m;i++){fscanf(fp_in, "%d%d",&from,&to);}以免影响后面的读入else if(桩3的盘子数不为n且每次移动合法) thenfprintf(fp_out, "%d\n",0)销毁三个堆栈}第三章: 测试结果补充说明:1.in_1使用老师所给的参考输入,初步测试程序是否正确。
简述栈的工作原理(一)

简述栈的工作原理(一)栈的工作原理简述什么是栈栈(Stack)是一种常见的数据结构,它遵循“先进后出”(LIFO, Last In First Out)的原则。
栈可以看作是一种容器,数据只能从栈顶进行插入或者删除操作。
栈的基本操作栈的基本操作包括入栈和出栈。
入栈(Push)将一个新的元素插入到栈的顶部,栈的深度增加一。
出栈(Pop)从栈的顶部删除一个元素,栈的深度减少一。
栈的实现方式栈可以使用数组或链表来实现。
数组实现栈在数组实现的栈中,我们使用一个固定大小的数组来存储栈中的元素,同时使用一个变量来追踪栈的顶部元素的位置。
•入栈:将元素插入到数组的尾部,并更新栈顶指针。
•出栈:删除数组尾部的元素,并更新栈顶指针。
链表实现栈在链表实现的栈中,我们使用一个链表来存储栈中的元素,同时使用一个指针来追踪栈的顶部元素。
•入栈:在链表的头部插入元素,并更新栈顶指针。
•出栈:删除链表头部的元素,并更新栈顶指针。
栈的应用场景栈在计算机科学和软件开发中有着广泛的应用。
调用栈在编程中,函数的调用过程通常由栈来管理。
每当一个函数被调用时,它的相关信息(如参数、返回地址等)会被保存到调用栈中,当函数执行完毕后,这些信息会被弹出。
表达式求值栈常用于表达式求值过程中,可以用于处理括号匹配、中缀表达式转后缀表达式等问题。
后退按钮浏览器的后退按钮实际上就是一个使用栈来记录访问历史的功能。
每当用户访问一个新页面时,页面的URL会被压入栈中,点击后退按钮时,栈顶的URL会被弹出,从而返回上一个页面。
总结栈是一种常用的数据结构,通过入栈和出栈操作实现数据的后进先出。
栈可以使用数组或链表来实现,并被广泛应用于函数调用、表达式求值以及浏览器后退等场景中。
栈是计算机科学中必不可少的工具,了解栈的工作原理对于深入理解其他数据结构和算法也非常有帮助。
栈的应用举例1. 模拟函数调用栈栈在编程中经常被用来模拟函数调用栈。
例如,在递归算法中,函数会反复地调用自身,每次调用都会将相关信息(如参数、局部变量等)压入栈中,当算法逐渐返回时,栈中的信息会被依次弹出,直到返回到最初的调用点。
汉诺塔递归算法范文

汉诺塔递归算法范文汉诺塔是一种经典的数学问题,它涉及到递归算法的应用。
汉诺塔问题的描述是:有三个柱子A、B、C,其中A柱上有n个从小到大放置的圆盘,现在要将这n个圆盘按照从小到大的顺序移动到C柱上,并且每次只能移动一个圆盘,且在移动过程中,必须保证大圆盘在小圆盘上面。
那么如何用递归算法解决汉诺塔问题呢?为了更好地理解汉诺塔问题,我们可以将问题简化为只有三个圆盘的情况。
设三个柱子分别为A、B、C,初始时将三个圆盘都放在A柱上,目标是将这三个圆盘从A柱移动到C柱上。
我们可以给每个圆盘编号,编号越小表示圆盘越小。
问题解决的步骤如下:1.将编号为1的圆盘从A柱移动到C柱上;2.将编号为2的圆盘从A柱移动到B柱上;3.将编号为1的圆盘从C柱移动到B柱上;4.将编号为3的圆盘从A柱移动到C柱上;5.将编号为1的圆盘从B柱移动到A柱上;6.将编号为2的圆盘从B柱移动到C柱上;7.将编号为1的圆盘从A柱移动到C柱上。
以上步骤可以总结为以下规律:1)当只有一个圆盘时,直接将它从起始柱移动到目标柱;2)当有两个以上的圆盘时,可以将它们看作两个部分:最底下的圆盘和上面的所有圆盘。
首先将上面的所有圆盘从起始柱移动到中间柱(借助目标柱),然后将最底下的圆盘从起始柱移动到目标柱,最后将上面的所有圆盘从中间柱(借助起始柱)移动到目标柱。
基于以上规律,我们可以得到如下的递归算法实现汉诺塔问题。
```pythondef hanoi(n, start, end, middle):if n == 1:print('Move disk', n, 'from', start, 'to', end)else:hanoi(n-1, start, middle, end)print('Move disk', n, 'from', start, 'to', end)hanoi(n-1, middle, end, start)#测试hanoi(3, 'A', 'C', 'B')```在上述代码中,hanoi函数代表了汉诺塔问题的递归解决方案。
