冷却塔阻力计算
冷却塔热力性能计算书及计算方法

冷却塔热力性能计算书及计算方法工艺设计计算书1.热力性能计算1.1热力性能计算方法工艺设计采用CTI颁布的权威软件“CTIToolkit”进行设计,并按GB7190.2―1997《大型玻璃纤维增强塑料冷却塔》进行校核,用焓差法计算,积分计算采用辛普逊20段近似积分计算公式。
计算公式逆流冷却塔热力计算基本方程式:NCwdt(1)t2iit1式中:t1、t2―进、出塔水温℃i―冷却塔淋水装置中对应于某点温度的空气比焓kJ/kgi″―与i对应的饱和空气焓kJ/kgK―蒸发水量带走的热量系数K1t2(2)5850.56(t220)20段近似积分计算公式:NCwt111111114()2()60i0i20i1i3i19i2i4i18(3)式中:Cw―水的比热4.1868kJ/(kg·℃)Δt―进出水温差℃Δt=t1-t2Δi0,Δi1,Δi2,······Δi19,Δi20―分别表示对应于t2,t2+Δt/20,t2+2Δt/20······t2+19Δt/20,t1时的焓差,即i″-ikJ/kg空气的焓按下式计算:“PiCg0.622(r0Cq)(4)“P0P式中:Cg―干空气的比热1.005kJ/kgCq―水蒸气的比热1.842kJ/kgr0―温度为0度时水的汽化热2500.8kJ/kgθ―空气干球温度℃Φ―相对湿度P0―进塔空气大气压kPaP“θ―空气温度为t时的饱和水蒸气分压力kPa如取Φ=1,可将(4)改写为温度t时的饱和湿空气焓计算式:\tP“t(5)iCgt0.622(r0Cqt)P0P“t饱和水蒸气分压力及相对湿度按下式计算:E0.01419663142.305(11373.16)8.2lg()0.0024804(373.16T)T373.16 TPt\98.066510E(6)式中:T―绝对温度KT=273.16+tP\0.0006P62)0((7)\P式中:τ―空气湿球温度,由机械通风干湿表测得℃P“τ―空气温度为τ时的饱和水蒸气分压力kPa将进塔空气干球温度θ1、湿球温度τ1及大气压P0代入以上各式,即可求得进塔空气的相对湿度Φ和焓值i1。
10章—5冷却塔的设计与计算

10章—5冷却塔的设计1与计2算
10
Gp——由空气重量流量换算成的风量m3/s H——实际工作压力(Pa)
η1——风机机械效率; η2——与叶片安装角相应的风机效率,可由特性 曲线查得。
B——电机安全系数B:1.15~1.20
2、风筒式自然通风冷却塔: (1)原理: (2)计算: 抽力Z=阻力H
He——塔风筒有效高,填料中点到塔顶。
He
vm2 2g
m 1 2
ξ——总阻力系数。
2
4D 2H.050 120章—05.冷3却2D 塔的0 设计与FF计m T算 p
12
10章—5冷却塔的设计与计算
13
H0——进风口高度,(m) D0——进风口直径, (m) Fm——淋水填料面积,(㎡) FT——风筒出风口面积,(㎡) ξp——填料阻力系数,(实验定) D——填料1/2高处直径, (m)
10章—5冷却塔的设计与计算
5
5、效率(η)——冷却后达到极限τ的程度。
t1 t2 t1
1
1
t2
t
6、冷却后水温的保证率:用百分数表示,应该
用可靠度的概念。 不同的行业据冷却水在工业
中的重要程度,可有不同的保证率,在近期连
续5~10年以上的观测气象资料中,取夏季三个
月中,超过平均每年最热的10天(或5天)的日
Pe=K·△t K——系数(L/℃)与环境有关。(见下表) △ t——进出塔水温差℃
10章—5冷却塔的设计与计算
16
G——进塔风量。
G3.8D 42
He12m3 m S
10章—5冷却塔的设计与计算
14
(三)水力计算: 1、目的:确定配水管渠尺寸;
喷嘴数及布置; 水的阻力; 选定循环水泵。 2、系统分类:(1)管式配水系统
冷却塔设计计算举例

冷却塔设计计算举例冷却塔符号说明(名称及单位)这⾥列出的符号是按习惯形成和长期延⽤的统⼀符号。
实际上符号是⼈为定的,不同的名称可⽤各种符号来代替,但为便于识别和运⽤,尽可能予以统⼀。
常⽤的有关冷却塔设计计算的符号与名称⼤致如下:t 1——进冷却塔⽔温(℃);t 2——出冷却塔⽔温(℃);Δt——进、出冷却塔⽔温差(℃),即Δt =t 1 -t 2 ;t m——平均⽔温(℃),t m =(t 1 -t 2 )/2 ;T——绝对温度(城),T =273 +ti ;θ——空⽓⼲球温度(℃);τ——空⽓湿球温度(℃);t 2 –τ——冷幅⾼(℃),此值越⼩,冷却效率越⾼;θ1 ——进冷却塔空⽓的⼲球温度(℃);θ2 ——出冷却塔空⽓的⼲球温度(℃);τ1 ——进冷却塔空⽓的湿球温度(℃);τ2 ——出冷却塔空⽓的湿球温度(℃);P a——⼤⽓压⼒(m m H g ),P a =P g +P q ;P g——空⽓中⼲空⽓的分压⼒(kg/cm2 ,或m m H g );P q——空⽓中⽔蒸⽓的分压⼒(kg/cm2 ,或m m H g );P ″τ1——进冷却塔空⽓温度为湿球温度τ1 时饱和空⽓中⽔蒸⽓分压⼒(kg/cm2 ,或m m H g );P ″θ1——进冷却塔空⽓温度为⼲球温度θ1 时饱和空⽓中⽔蒸⽓分压⼒(kg/cm2 ,或m m H g ); P ″——饱和空⽓中⽔蒸⽓分压⼒(kg/cm2 ,或m m H g );P ″t1——空⽓为进冷却塔⽔温t 1 时饱和⽔蒸⽓分压⼒(kg/cm2 ,或m m H g );P ″t2——空⽓为出冷却塔⽔温t 2 时饱和⽔蒸⽓分压⼒(kg/cm2 ,或m m H g );P ″tm——平均⽔温时饱和⽔蒸⽓压⼒(kg/cm2 ,或m m H g );Q——冷却塔冷却⽔量(m3/h 或kg/h );q——冷却塔淋⽔密度(m3/(m2· h ));G ——进冷却塔的空⽓量,即风量(m3/h 或kg/h );g ——进冷却塔空⽓重量速度(kg/(m2·h )或kg/(m2 ·s ));有时表⽰重⼒加速度(m/s2 );V——外界风速风向(m/s);i 1 ——进塔空⽓的焓(kcal/kg );i 2 ——出塔空⽓的焓(kcal/kg );i m ——平均温度时空⽓的焓(kcal/kg );i″1 ——空⽓温度为进塔⽔温t 1 时的饱和空⽓焓(kcal/kg );i″2 ——空⽓温度为出塔⽔温t 2 时的饱和空⽓焓(kcal/kg );i″m ——空⽓温度为进、出塔⽔温的平均温度t m 时的饱和空⽓焓(kcal/kg );γg——空⽓的密度(⽐重)(kg/m3 );γ——⽔的汽化热(kcal/kg );λ——⽓、⽔⽐(⽆量纲);K——蒸发⽔量带⾛的热量系数(⽆量纲);βxv ——以焓差为基准的容积散质系数(kg/(m 3·h ));V m——塔内平均风速(m/s);Z ——淋⽔填料装置⾼度(m );Z g ——淋⽔填料装置尾部⾼度(m );F——冷却塔内断⾯积(m2 );V——淋⽔填料装置有效容积(m3 ):(注:有时表⽰⽔流或⽓流速度,m/s);N (或Ω)——以温度进⾏积分的交换数(⽆量纲);Σhi——空⽓总阻⼒(mmH2O);hi ——进塔空⽓各部分的阻⼒(mmH2O);D N——⽔管⼦内径(m m );L——管⼦长度(m );n——有时表⽰转速(r/min );有时表⽰根数;有时表⽰孔眼数;ηi——表⽰电机、风机、传动装置等效率(%);ξi——流体(⽔或空⽓)有关阻⼒系数。
冷却塔的热力计算

冷却塔的热力计算冷却塔的任务是将一定水量Q ,从水温t 1冷却到t 2,或者冷却△t =t 1-t 2。
因此,要设计出规格合适的冷却塔,或核算已有冷却塔的冷却能力,我们必须做冷却塔的热力计算。
为了便于计算,我们对冷却塔中的热力过程作如下简化假设:(1)散热系数α,散质系数v β,以及湿空气的比热c ,在整个冷却过程被看作是常量,不随空气温度及水温变化。
(2) 在冷却塔内由于水蒸气的分压力很小,对塔内压力变化影响也很小,所以计算中压力取平均大气压力值。
(3)认为水膜或水滴的表面温度与内部温度一致,也就是不考虑水侧的热阻。
(4) 在热平衡计算中,由于蒸发水量不大,也可以将蒸发水量忽略不计。
(5) 在水温变化不大的范围内,可将饱和水蒸汽分压力及饱和空气与水温的关系假定为线性关系。
冷却塔的热力计算方法有焓差法、湿差法和压差法等,其中最常用的是麦克尔提出的焓差法,以下简要介绍冷却塔的焓差法热力计算。
麦克尔提出的焓差法把过去由温度差和浓度差为动力的传热公式,统一为一个以焓差为动力的传热公式。
在方程式中,麦克尔引进入刘易斯关系式,导出了以焓差为动力的散热方程式。
()dV h h dH t xv q 0"-=β (1) 式中:q dH —— 水散出热量;xv β —— 以含湿差为基准的容积散质系数()[]kg kg s m kg //3⋅⋅ ;"t h —— 温度为水温t 时饱和空气比焓 (kg kJ /); 0h —— 空气比焓 (kg kJ /)。
将式(1)代入冷却塔内热平衡方程:n w w q tdQ c Qdt c dH += (2)式中:q dH —— 水散出热量;w c —— 水的比热()[]C /J o ⋅kg k ;Q —— 冷却水量 (s /g k );u Q —— 蒸发水量 (s /g k )t —— 水温度 (℃) 并引入系数K :式中 m r ——塔内平均汽化热(kg kJ /)经整理,并积分后,可得冷却塔热力计算的基本方程式:⎰-=120"t t t w xv h h dt c Q v K β (3) 上式的左端表示在一定淋水填料及格型下冷却塔所具有的冷却能力,它与淋水填料的特性、构造、几何尺寸、冷却水量有关,称冷却塔的特性数,以符号愿'Ω表示,即:(3)式的右端表示冷却任务的大小,与气象条件有关,而与冷却塔的构造无关,称为冷却数(或交换数),以符号'Ω表示,也即:由于水温不是空气焓的直接函数,直接积分有困难,所以,在求解冷却数的时候,一般均采用近似积分方法。
冷却塔计算

冷却塔设计计算参考方法本文简述了冷却塔、冷却塔的选型,校核计算,模拟计算方法等,供大家参考。
一、简述如上图,冷却塔放于层间,运行时冷却塔进/排风大致可分为6个区间(图中箭头表示风向,其长度表示风量大小);它们分别是:a 区——冷却塔在A轴方向的主要进风面,该处装有1250mm高百叶3层。
b1/b2——冷却塔入风回流区,在这两个区很可能出现负压;回流在b2区会较多出现。
c 区——冷却塔高速排风区。
d 区——冷却塔在1/A轴方向通风区,该区为负压区,风速较a区高,且以乱流出现居多。
e 区——热风扩散区;冷却塔排风经过一段距离(冷却塔排风口到建筑顶部百叶约4000mm)后,动压明显下降,静压上升,该区属正压区,其间大部分热风经建筑顶部百叶排入大气,少部分弥散后排风受阻会滞留一段时间,但,由于上下(e 区~b区)空间随机存在着压差,使得部分e区弥散的热风回流。
二、冷却塔的选型1、设计条件温度:38℃进水,32℃出水,27.9℃湿球;水量:1430M³/H;水质:自来水;耗电比:≤60Kw/台,≤0.04Kw/M³·h,场地:23750mm×5750mm;通风状况:一般。
2、冷却塔选型符合以上条件的冷却塔为:LRCM-H-200SC8×1台。
(冷却塔[设计基准]37-32-28℃,此条件下冷却塔处理水量为名义处理水量)其中,LRC表示良机方形低噪声冷却塔,M表示大陆性气候适用,H表示加高型,200表示冷却塔单元名义处理水量200M³/H,S表示该机型区别于一般冷却塔,C8表示该塔共由8个单元并联组合而成,即名义处理总水量为1600M³/H。
冷却塔的外观尺寸为:22630×3980×4130。
冷却塔配电功率:7.5Kw×8=60Kw,耗电比为60÷1600=0.0375Kw/M³·h。
逆流开式冷却塔热力阻力计算书

计算依据:计算程序:冷却塔型号:数据输大气压P92.3Kpa风筒底径 6.66m单塔长度10m干球温度θ31.2℃风筒顶径 6.48m喷淋高度0.5m湿球温度τ20℃风筒中径 6.06m气室高度 1.7m处理水量Q1300m3/h m风筒高度2m进水温度t131℃m总高10.45m出水温度t224℃平台高8.45m风机直径D6m风机数量1台喷头个数144个轮毂直径d1m填料高度 1.25m单个流量9.027778m3/h 淋水面积F80m2喷嘴压力0.03Mpa 进风口高度5m293.16K饱和水蒸汽压的计算公式:lgP"=2.0057173-3142.305/T+3142.305/373.16-0.0024804*373.16+0.0024804*T+8.2lg(373.10.36863湿球时饱和水蒸汽压P"τ=Kpa304.36K0.65732干球时饱和水蒸汽压P"θ=Kpa空气相对湿度φ=[P"τ-0.000662P(θ-τ)]/P"θ=0.36376进塔干空气密度ρ1=(P-φP"θ)*103/[287.1 4(273+θ)]=kg/m3设计参数热力计算冷却塔热力阻力计算书1.037774548湿球绝对温度:Tτ=273.16+τ=湿球温度时的饱和水蒸汽压对数:lgP"τ=2.336830359干球绝对温度:Tθ=273.06+θ=干球温度时的饱和水蒸汽压对数:lgP"θ=4.542782523选用气水比λ0.7170.7670.8170.8670.917风量G898172960806102344010860741148708m 3/h进塔湿空气比焓:h 1=1.005θ+0.622(2500.8+1.846θ)*φ*P"θ/(P-φ*P"θ)=60.365KJ/kg(DA)蒸发带走热量系数:K=1-t 2/[586-0.56(t 2-20)]=0.958887不同气水比出塔湿空气比焓:h 2=h 1+4.1868(t 1-t 2)/(K λ)=102.9933100.21497.7756595.618293.69601KJ/kg(DA )进水绝对温度:T(t1)=273.16+t 1=304.16K0.65238进水时饱和水蒸汽压P"t1= 4.49136Kpa 出塔饱和空气比焓:h"2=112.538KJ/kg(DA )温差分段数:n=8温差等分值:δt=0.875℃δh=(h 2-h 1)/n= 5.328483 4.981124.676282 4.40664.166327t 1-δt=30.125℃t 1-2δt=29.25℃t 1-3δt=28.375℃t 1-4δt=27.5℃t 1-5δt=26.625℃t 1-6δt=25.75℃t 1-7δt=24.875℃一般水温差<15℃常取n=2就可以保证精度了进水温度时的饱和水蒸汽压对数:lgP"t1=T 1=273.16+t 1-δt=303.285℃T 2=273.16+t 1-2δt=302.41℃T 3=273.16+t 1-3δt=301.535℃T 4=273.16+t 1-4δt=300.66℃T 5=273.16+t 1-5δt=299.785℃T 6=273.16+t 1-6δt=298.91℃T 7=273.16+t 1-7δt=298.035℃T (t2)=273.16+t 2=297.16℃0.630794.27358Kpa107.472KJ/kg(DA )0.608934.0638Kpa102.583KJ/kg(DA )0.586933.86303Kpa97.886KJ/kg(DA )0.564783.67095Kpa93.373KJ/kg(DA )0.542483.48725Kpa89.0354KJ/kg(DA )0.520043.3116Kpa84.8651KJ/kg(DA )0.497443.14372Kpa80.8546KJ/kg(DA )0.47472.98332Kpa76.9965KJ/kg(DA )T 7温度时饱和空气焓:h"T7=T 6温度时的饱和水蒸汽压对数:lgP"6=T 6温度时的饱和水蒸汽压:P"6=T 6温度时饱和空气焓:h"T6=T 7温度时的饱和水蒸汽压对数:lgP"7=T 4温度时饱和空气焓:h"T4=T 5温度时的饱和水蒸汽压对数:lgP"5=T 2温度时的饱和水蒸汽压:P"2=T 1温度时饱和空气焓:h"T1=T 1温度时的饱和水蒸汽压对数:lgP"1=T 1温度时的饱和水蒸汽压:P"1=T 2温度时的饱和水蒸汽压对数:lgP"2=T (t2)温度时的饱和水蒸汽压:P"(t2)=T 2温度时饱和空气焓:h"T2=T 3温度时的饱和水蒸汽压对数:lgP"3=T 5温度时饱和空气焓:h"T5=T 3温度时的饱和水蒸汽压:P"3=T 3温度时饱和空气焓:h"T3=T 4温度时的饱和水蒸汽压对数:lgP"4=T 5温度时的饱和水蒸汽压:P"5=T 7温度时的饱和水蒸汽压:P"7=T 4温度时的饱和水蒸汽压:P"4=T (t2)温度时饱和空气焓:h"1=T (t2)温度时的饱和水蒸汽压对数:lgP"(t2)=理论冷却数:N=4.1868(t1-t2)/(3n)*[1/(h"1-h2)+4/(h"T1-(h2-δh))+2/(h"T2-(h2-2δh))+4/(h"T3-(h2-3δh))+2/(h"T4-(h2-4δh))+4/(h"T5-(h2-5δh))+2/(h"T6-(h2-6δh))+4/(h"T7-(h2-7δh))+1/(h"2-h1)]不同气水比时N2.25441 1.980671.796947 1.66275 1.558852 S波填料设计,填料特性数Ω=2.12λ0.61填料特性数Ω1.730623 1.803271.874094 1.943242.010857 由上图曲线可知,当气水0.817时,Ω>N满足设计容积散质系数βxv =NQ/(KV)=24884.85kg/m 3.h填料容积散质系数β"xv=3710g 0.584q0.355其中空气重量风速g=G*γ/3600/F= 3.687847kg/m 2.s 淋水密度q=Q/F=16.25m 3/m 2.h 填料容积散质系数β"xv=21390.6kg/m 3.h填料容积散质系数β"xv>设计容积散质系数βxv 不满足结论:该逆流冷却塔的热力性能达不到设计要求。
冷却塔的通风阻力计算
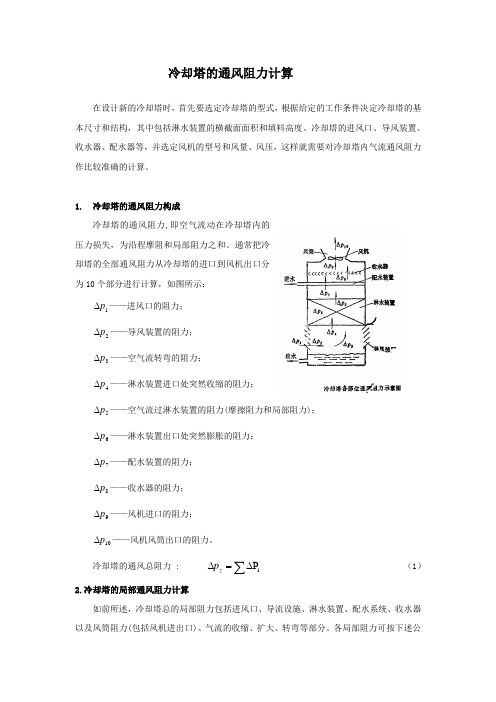
冷却塔的通风阻力计算在设计新的冷却塔时,首先要选定冷却塔的型式,根据给定的工作条件决定冷却塔的基 本尺寸和结构,其中包括淋水装置的横截面面积和填料高度、冷却塔的进风口、导风装置、 收水器、配水器等,并选定风机的型号和风量、风压,这样就需要对冷却塔内气流通风阻力作比较准确的计算。
1. 冷却塔的通风阻力构成冷却塔的通风阻力,即空气流动在冷却塔内的压力损失,为沿程摩阻和局部阻力之和。
通常把冷却塔的全部通风阻力从冷却塔的进口到风机出口分为10个部分进行计算,如图所示: 1p ∆——进风口的阻力; 2p ∆——导风装置的阻力; 3p ∆——空气流转弯的阻力;4p ∆——淋水装置进口处突然收缩的阻力;5p ∆——空气流过淋水装置的阻力(摩擦阻力和局部阻力); 6p ∆——淋水装置出口处突然膨胀的阻力; 7p ∆——配水装置的阻力; 8p ∆——收水器的阻力; 9p ∆——风机进口的阻力; 10p ∆——风机风筒出口的阻力。
冷却塔的通风总阻力 : ∑∆P =∆iz p (1)2.冷却塔的局部通风阻力计算如前所述,冷却塔总的局部阻力包括进风口、导流设施、淋水装置、配水系统、收水器以及风筒阻力(包括风机进出口)、气流的收缩、扩大、转弯等部分。
各局部阻力可按下述公式来计算:gv P i i i22i ⋅=∆γξ(毫米水柱) (2)式中: i ξ ——各局部阻力系数;i v ——相应部位的空气流速(米/秒); i γ——相应部位的空气比重(公斤/米3);g ——重力加速度。
而冷却塔的总局部阻力可写成:gv P h i i i22i ⋅∑=∑∆=γξ(毫米水柱)由于气流密度在冷却塔内变化很小,所以在球求解时,各处的密度值均取冷却塔进、出口的几何平均值。
气流通过冷却塔各种部件处的速度,可先根据风机特性曲线及热力计算时确定的气水比选择风量G(公斤/时)后,由下式确定:10...3,2,110...3,2,13600F Gv =冷却塔各部件处局部阻力系数 3,2,1ξ值的确定: (1)进风口 55.01=ξ(2)导风装置式中:()L q 25.01.02+=ξq ——淋水密度(米3/米2·小时);L ——导风装置长度(米)。
冷却塔阻力计算

冷却塔的通风阻力计算在设计新的冷却塔时,首先要选定冷却塔的型式,根据给定的工作条件决定冷却塔的基 本尺寸和结构,其中包括淋水装置的横截面面积和填料高度、冷却塔的进风口、导风装置、 收水器、配水器等,并选定风机的型号和风量、风压,这样就需要对冷却塔内气流通风阻力作比较准确的计算。
1. 冷却塔的通风阻力构成冷却塔的通风阻力,即空气流动在冷却塔内的压力损失,为沿程摩阻和局部阻力之和。
通常把冷却塔的全部通风阻力从冷却塔的进口到风机出口分为10个部分进行计算,如图所示: 1p ∆——进风口的阻力; 2p ∆——导风装置的阻力; 3p ∆——空气流转弯的阻力;4p ∆——淋水装置进口处突然收缩的阻力;5p ∆——空气流过淋水装置的阻力(摩擦阻力和局部阻力); 6p ∆——淋水装置出口处突然膨胀的阻力; 7p ∆——配水装置的阻力; 8p ∆——收水器的阻力; 9p ∆——风机进口的阻力; 10p ∆——风机风筒出口的阻力。
冷却塔的通风总阻力 : ∑∆P =∆iz p (1)2.冷却塔的局部通风阻力计算如前所述,冷却塔总的局部阻力包括进风口、导流设施、淋水装置、配水系统、收水器以及风筒阻力(包括风机进出口)、气流的收缩、扩大、转弯等部分。
各局部阻力可按下述公式来计算:gv P i i i22i ⋅=∆γξ(毫米水柱) (2)式中: i ξ ——各局部阻力系数;i v ——相应部位的空气流速(米/秒); i γ——相应部位的空气比重(公斤/米3);g ——重力加速度。
而冷却塔的总局部阻力可写成:gv P h i i i22i ⋅∑=∑∆=γξ(毫米水柱)由于气流密度在冷却塔内变化很小,所以在球求解时,各处的密度值均取冷却塔进、出口的几何平均值。
气流通过冷却塔各种部件处的速度,可先根据风机特性曲线及热力计算时确定的气水比选择风量G(公斤/时)后,由下式确定:10...3,2,110...3,2,13600F Gv =冷却塔各部件处局部阻力系数 3,2,1ξ值的确定: (1)进风口 55.01=ξ(2)导风装置式中:()L q 25.01.02+=ξq ——淋水密度(米3/米2·小时);L ——导风装置长度(米)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
冷却塔的通风阻力计算在设计新的冷却塔时,首先要选定冷却塔的型式,根据给定的工作条件决定冷却塔的基 本尺寸和结构,其中包括淋水装置的横截面面积和填料高度、冷却塔的进风口、导风装置、 收水器、配水器等,并选定风机的型号和风量、风压,这样就需要对冷却塔内气流通风阻力作比较准确的计算。
1. 冷却塔的通风阻力构成冷却塔的通风阻力,即空气流动在冷却塔内的压力损失,为沿程摩阻和局部阻力之和。
通常把冷却塔的全部通风阻力从冷却塔的进口到风机出口分为10个部分进行计算,如图所示: 1p ∆——进风口的阻力; 2p ∆——导风装置的阻力; 3p ∆——空气流转弯的阻力;4p ∆——淋水装置进口处突然收缩的阻力;5p ∆——空气流过淋水装置的阻力(摩擦阻力和局部阻力); 6p ∆——淋水装置出口处突然膨胀的阻力; 7p ∆——配水装置的阻力; 8p ∆——收水器的阻力; 9p ∆——风机进口的阻力; 10p ∆——风机风筒出口的阻力。
冷却塔的通风总阻力 : ∑∆P =∆iz p (1)2.冷却塔的局部通风阻力计算如前所述,冷却塔总的局部阻力包括进风口、导流设施、淋水装置、配水系统、收水器以及风筒阻力(包括风机进出口)、气流的收缩、扩大、转弯等部分。
各局部阻力可按下述公式来计算:gv P i i i22i ⋅=∆γξ(毫米水柱) (2)式中: i ξ ——各局部阻力系数;i v ——相应部位的空气流速(米/秒); i γ——相应部位的空气比重(公斤/米3);g ——重力加速度。
而冷却塔的总局部阻力可写成:gv P h i i i22i ⋅∑=∑∆=γξ(毫米水柱)由于气流密度在冷却塔内变化很小,所以在球求解时,各处的密度值均取冷却塔进、出口的几何平均值。
气流通过冷却塔各种部件处的速度,可先根据风机特性曲线及热力计算时确定的气水比选择风量G(公斤/时)后,由下式确定:10...3,2,110...3,2,13600F Gv =冷却塔各部件处局部阻力系数 3,2,1ξ值的确定: (1)进风口 55.01=ξ(2)导风装置式中:()L q 25.01.02+=ξq ——淋水密度(米3/米2·小时);L ——导风装置长度(米)。
(3)进入淋水装置处气流转弯:5.03=ξ(4)淋水装置进口处突然收缩: ⎪⎪⎭⎫ ⎝⎛-=ξcp F F 0415.0 cp F ——淋水装置的截面(m 2)。
(5)淋水装置 ()Z Kq e +ξ=ξ15式中:e ξ——单位高度淋水装置的阻力系数; K ——系数;Z——淋水装置高度(m )。
淋水装置的阻力亦可以从试验资料直接查得,若需改变形水装置的尺度时,其阻力降的近似值计算可参阅资料。
(6)淋水装置出口突然膨胀2061⎪⎪⎭⎫ ⎝⎛-=ξcp F F(7)配水装置⎪⎪⎭⎫ ⎝⎛⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+=ξ323713.15.0F F F F cp cp 式中:3F ——配水装置中气流通过的有效截面积(米2)cp F ——塔壁内的横截面积(米2)。
(8)收水器式中:22228125.0⎪⎪⎭⎫ ⎝⎛⋅⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-+=ξF F F F cpcp 式中:2F ——收水器中气流通过的有效截面积(米2);cp F ——塔壁内的横截面积(米2)。
(9)风机进口9ξ可根据下式确定:ξξξ+⎪⎪⎭⎫ ⎝⎛-=cp F F 4091 0ξ——根据0D l 查表取值;4F ——收缩后的截面积(㎡); cp F ——收缩前的截面积(㎡);2sin8124α⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛-λ=ξcp F F式中:λ—摩擦系数;可采用0.03。
(10)风机凤筒出口(扩散筒) ()p ξδ+=ξ110式中:δ —-风筒速度分布不均匀而影响修正系数,根据0/l D ; p ξ——根据0D l 查表取值。
由上述计算,我们得到冷却塔的总通风阻力,然后再确认它是否与风机的额定风量下所能提供的风压相适应。
如果相适应且又能满足热力性能要求,则该冷却塔的设计计算完成。
若不适应就要选用另外的风机或改变冷却塔部件的结构尺寸,重新计算空气的流动阻力,经过多次反复直到既满足风机的风压要求又满足热力性能时为止。
空调用封闭式冷却塔空气动力特性的实验研究作者:李永安李继志尚丰伟阅读:1183次上传时间:2005-08-09推荐人:source00 (已传论文360套)简介:本课题在理论研究的基础上,建立了由锅炉、换热器、孔板流量计、水泵、微压计、温度计等仪器设备组成的封闭式冷却塔实验台。
在该实验台上,详细测试了在封闭式冷却塔内空气与水逆向流动条件下,空气流经冷却盘管的阻力,探讨了封闭式冷却塔内空气的流动规律,分析了空气流过正三角排列管束的特性。
关键字:封闭式冷却塔空气动力特性准则方程相关站中站:空调水泵选型设计锅炉及锅炉房专题如何选择冷却塔?冷却塔最新技术资料大全1 引言我国水资源非常紧张,城市缺水现象比较严重。
据统计,我国人均水资源量约2304m3/人,1984年在世界排名为88位,1996年降为第109位[1]。
我国666座城市中,有333座城市缺水,有108座城市严重缺水。
因此,我国人均水资源占有量呈下降趋势,农业缺水量大,城市供水不足,地下水位严重下降。
进入21世纪,随着我国经济建设的飞速发展和人口增加,水资源供需矛盾将进一步加剧,据预测,2010年全国供水缺口近1000亿立方米。
国际上有“19世纪争煤,20世纪争石油,21世纪可能争水” 和21世纪国际投资与经济发展,一看人,二看水的说法。
因此,水可能成为我国可持续发展的重要制约因素。
在城市用水中,冷却水量占较大的比例,这些冷却水直接排放不仅造成热污染,还会造成较大的经济和资源浪费,所以,需要将这些冷却水循环重复利用,以提高水的有效利用率,缓解当前水资源短缺的状况。
封闭式冷却塔是一种既能降低冷却水的温度,又能保持水质纯净的新型冷却设备,同时还具有功能多、用途广、对环境的适应能力强、可冷却高温水、安全防火等特点,因此,封闭式冷却塔在空调领域有着广阔的应用前景,在水环热泵系统、冷却塔直接供冷系统中更显示了其独特的优势。
空调用封闭式冷却塔空气动力特性实验研究的主要目的是寻求塔内进风口、冷却盘管、淋水装置、挡水板、风机进口、风筒出口等各部件阻力的计算方法;分析对比冷却塔内总阻力与风机压头之间的关系,使风机始终运行在最佳工况点;进一步揭示冷却塔内气流流动的规律,优化塔体形状,降低空气阻力,提高冷却效率。
2 空气的流动特性空调用封闭式冷却塔主要由冷却盘管、风机、管通泵、喷淋排管、淋水喷头(喷咀)、挡水板、底池、百叶进风口、塔体等几部分组成[2] 。
空调用封闭式冷却塔的工作原理是,从冷凝器、吸收器或工艺设备等出来的温度较高的水,由冷却水循环泵加压输送到封闭式冷却塔的冷却盘管中。
另一方面,利用管道泵将冷却塔底池中的水抽吸到喷淋排管中,然后,喷淋在冷却盘管的外表面上,蒸发吸取冷却水的热量,从而使冷却水的温度得以降低。
与此同时,靠安装在挡水板上面风机的抽吸作用,使空气自下而上流经冷却盘管,这样不仅可以强化冷却盘管外表面的放热,而且还可以及时带走蒸发所形成的水蒸汽,以加速水分的蒸发,提高冷却效果。
具体说来,就是冷却盘管内温度较高的水以对流的形式将热量传给冷却盘管内表面,这部分热量再由冷却盘管的内表面传到冷却盘管的外表面。
由于冷却盘管外表面喷淋循环水,循环水落到冷却盘管的外表面,靠对流和蒸发将这部分热量散到空气中去。
图1是封闭式冷却塔中冷却盘管的一种排列形式即正三角形排列,纵向管间距与横向管间距相等,均等于两倍管径。
封闭式冷却塔中除冷却盘管外,其余部件的空气阻力,均可用下式计算[3]:(Pa)(1)式中,ρ为冷却塔内空气密度,kg/m3;v为冷却塔内空气流速,m/s ;ζ为各部件的局部阻力系数。
如图1所示,在空调用封闭式冷却塔中,空气在管束间交替收缩和扩张的弯曲通道中流动。
空气在管束中流动,除第一排管子保持了外掠单管的特征外,另一个重要特点是从第二排管子起流动被前面几排管子引起的涡旋所干扰,因此,管束中流动的状态比较复杂。
影响空气流动阻力的主要因素是流速和管束本身所引起的紊流度。
因此,管束的几何条件,即管径、管间距、管排数、管子的排列方式等与空气流动阻力密切相关。
空气的流动阻力表现为流经冷却盘管后的压力降低,可表示成欧拉数E u和雷诺数Re之间的关系[4]。
(2)式中,E u 为欧拉数,; Re为雷诺数,Re=V·do/;ΔP为空气阻力,Pa;ρ为空气密度,kg/m3;V为空气流速,m/s;d0为定性长度,m ;为空气的运动粘滞系数(运动粘度),m2/s。
从式(2)可见,在做冷却盘管外侧空气阻力实验时,需要测定空气流经冷却盘管所产生的压力降、空气的流速、空气的温度,然后,根据空气的温度查物性参数表,求得空气的密度ρ和运动粘滞系数,就可以计算出对应的Re数、E u数。
在封闭式冷却塔中,由于温度的变化,会导致空气物理性质的改变,这就涉及到确定空气物性参数的温度如何选定,也就是如何确定定性温度值。
有人主张用动力粘度的比值μf /μw来考虑物性变化的影响[5]。
对于空气、水这类流体,粘性比较小,流体随着温度变化的物性主要是粘性,所以,P rf / P rw≈μf /μw。
但是,热交换的基础是所形成的温度场,是用普朗特准则表征的,所以,应用比值P rf / P rw是比较好的,其结果也是令人满意的。
因此,在本课题的研究中,按空气的平均温度确定空气的物性参数,同时,在准则方程中增加一项补充参数考虑物性变化的影响,即(P rf / P rw)0.25。
封闭式冷却塔进口空气的温度t i可用玻璃管温度计测出,出口空气的温度t0可由出口空气的焓值i0求出,因为,出冷却塔的空气状态可以近似地认为是饱和湿空气[3],所以,由i0查饱和水蒸汽表可求出t0,其平均温度t m=(t i+ t0)/2。
冷却盘管的几何特性如管束的排列方式、管间距、管径、管子的排数、管子的几何形状等因素都对空气流动阻力有重要影响[6]。
经分析,在式(2)中定型尺寸为管外径d0。
在式(2)中流速V采用流通截面最窄处的空气速度,结合图1可见,最窄处的流通面积可用式(3)计算。
(3)式中,B1为封闭式冷却塔的宽,m; L1为封闭式冷却塔的长,m;n1为每排管子的根数。
式(2)中的Δp可由测点分设于冷却盘管上下的微压计测出[7]。
3 实验数据的整理表1 是用拉制光滑铜管作冷却盘管,管子外径为20 mm,壁厚 1 mm, 管排数为10排,每排32根管(奇数排)、31根管(偶数排),正三角形排列条件下,所测得的值。
表1 空气阻力测试记录表号平均温度(℃)空气密度(kg/m3)运动粘度(10-6m2/s)流速(m/s)空气阻力(Pa)Re数lg(Re)E u数lg(E u)23 1.1815.977.159.58.89×1033.952.07.3124 1.18 167.578.73 1.90.06 0 .8 2×103.94 4 .2925 1.1716.167.260.78.92×1033.952.03.3126 1.1716.256.42.17.38×1033.871.39.1427 1.1616.346.244.67.59×1033.881.47.1728 1.1616.436.143.27.43×1033.871.41.1529 1.1516.525.433.56.54×1033.821.09.1430 1.1516.615.534.86.62×1033.821.12.0531 1.1516.715.332.36.34×1033.801.03.010 32 1.1416.814.826.35.72×1033.768.36×10-1-0.081 33 1.1416.914.523.15.32×1033.737.23×10-1-0.142 34 1.1317.014.725.05.53×1033.747.82×10-1-0.11根据上面的分析及式(2),可得下列准则方程:(4)为了求出上式中的系数C及指数n,对式(4)作如下处理。
