基于MATLAB的时间序列建模与预测
如何在MATLAB中进行序列模型预测

如何在MATLAB中进行序列模型预测序列模型预测是一种在机器学习和统计学中被广泛应用的技术。
MATLAB作为一种功能强大的编程语言和环境,为序列模型预测提供了许多有用的工具和函数。
在本文中,我们将探讨如何使用MATLAB进行序列模型预测,并介绍一些常用的方法和技巧。
一、序列模型预测的基本概念序列模型预测是指根据已有的序列数据,利用统计学和机器学习的方法,预测未来的序列值。
序列数据通常具有时间序列的性质,因此在进行预测时需要考虑时间的因素。
序列模型预测的目标是找到最佳的模型,使得预测值与真实值之间的误差最小化。
二、数据准备与探索在进行序列模型预测之前,需要对数据进行准备和探索。
首先,需要加载数据并进行预处理。
MATLAB提供了丰富的数据导入和处理函数,可以帮助我们对数据进行清洗和转换。
其次,需要对数据进行探索性分析,了解数据的分布、趋势和季节性等特征。
MATLAB提供了多种可视化工具和统计函数,可以帮助我们进行数据探索。
三、模型选择与训练在进行序列模型预测之前,需要选择适合的模型和算法。
MATLAB提供了许多常用的序列模型和算法,如ARIMA、LSTM等。
根据数据的特征和需求,可以选择合适的模型进行训练。
在模型训练过程中,可以使用交叉验证和网格搜索等技术选择最佳的参数和超参数。
MATLAB提供了优化和调参的函数,可以帮助我们进行模型选择和训练。
四、模型评估与优化在进行序列模型预测之后,需要对模型进行评估和优化。
评估模型的性能是很重要的,可以使用各种指标如均方根误差(RMSE)、平均绝对百分比误差(MAPE)等来评估模型预测的准确度。
MATLAB提供了许多评估指标的函数,可以帮助我们进行模型评估。
如果模型表现不佳,可以考虑改进模型或调整参数,以提高预测的准确性。
五、实例应用与案例分析为了更好地理解和应用序列模型预测,我们可以结合实际案例进行分析。
以股票价格预测为例,我们可以使用MATLAB进行序列模型预测,并评估模型的准确性。
利用Matlab进行数据预测和建模

利用Matlab进行数据预测和建模引言:在当今信息时代,数据的达成速度越来越快,数据的确保来自于不同的途径。
但是对于用户来说,如何将这些数据转变为有价值的信息是一个巨大的挑战。
数据预测和建模是一种有效的方式来解决这个问题。
本文将介绍如何利用Matlab进行数据预测和建模的方法和技巧。
一、数据预处理在进行数据预测和建模之前,首先需要进行数据预处理。
数据预处理是一个重要的步骤,它包括数据清洗、缺失值处理、异常值处理等。
在Matlab中,有许多工具可以帮助我们完成这些任务。
例如,Wiener滤波器可以用来降噪,空值可以使用插值法来填充,异常值可以通过统计方法进行识别和修复。
二、数据可视化在进行数据预测和建模之前,我们需要对数据进行可视化分析,以了解数据的特征和趋势。
Matlab提供了丰富的绘图函数,可以方便地绘制各种图表。
例如,绘制折线图可以显示数据的变化趋势,绘制散点图可以显示数据之间的关系。
此外,Matlab还提供了交互式绘图工具,可以通过交互操作来进一步分析数据。
三、数据预测数据预测是根据已有的数据,来预测未来的走势。
利用Matlab进行数据预测主要有两种方法:基于统计模型的预测和基于机器学习的预测。
1. 基于统计模型的预测在Matlab中,我们可以使用统计工具箱中的函数来构建各种统计模型,如线性回归模型、ARMA模型、时间序列模型等。
这些模型可以通过最小二乘法、极大似然估计等方法来求解,从而得到模型的参数。
利用这些参数,我们可以对未来的走势进行预测。
2. 基于机器学习的预测Matlab提供了强大的机器学习工具箱,可以用来构建各种机器学习模型。
例如,我们可以使用神经网络模型来进行预测,也可以使用支持向量机模型来进行分类。
这些模型可以通过训练数据进行学习,然后利用学习得到的模型对未知数据进行预测。
四、数据建模数据建模是根据已有的数据,来构建一个模型,从而描述数据的特征和规律。
利用Matlab进行数据建模主要有两种方法:基于物理模型的建模和基于统计模型的建模。
基于matlab的arima算法

一、介绍ARIMA算法自回归积分滑动平均模型(ARIMA)是一种常用于时间序列分析和预测的方法。
它通过对时间序列数据进行自回归、差分和滑动平均操作来建立模型,从而对未来的数据进行预测。
二、ARIMA算法原理1. 自回归(AR):ARIMA模型中的自回归部分是指利用过去的观测值来预测未来的值。
这一部分通过使用时间序列数据的滞后值来建立模型,从而预测未来的观测值。
2. 积分(I):ARIMA模型中的积分部分是指对时间序列数据进行差分操作,以消除非平稳性。
通过对时间序列数据进行一阶或多阶的差分操作,可以将非平稳时间序列转化为平稳时间序列。
3. 滑动平均(MA):ARIMA模型中的滑动平均部分是指使用过去的预测误差来预测未来的观测值。
这一部分通过使用滞后的预测误差来建立模型,从而进一步提高预测的准确性。
三、ARIMA算法在MATLAB中的应用1. 数据准备:在使用MATLAB进行ARIMA算法的建模前,需要先准备好时间序列数据,并对其进行必要的预处理,包括检查数据的平稳性、趋势性和季节性等。
2. ARIMA模型构建:在MATLAB中,可以使用arima函数来构建ARIMA模型。
通过指定模型的阶数和参数,可以建立符合实际数据特征的ARIMA模型。
3. 模型诊断:建立ARIMA模型后,需要对模型进行诊断,以确保其符合统计假设。
在MATLAB中,可以使用模型诊断函数来进行检验,包括残差的自相关性和偏自相关性等。
4. 模型预测:利用建立好的ARIMA模型对未来的数据进行预测。
在MATLAB中,可以使用forecast函数来实现对未来数据的预测,并得到相应的置信区间。
四、ARIMA算法的特点和优势1. 灵活性:ARIMA算法可以适用于各种类型的时间序列数据,包括具有趋势和季节性的数据。
通过调整模型的阶数和参数,可以灵活地适应不同的数据特征。
2. 准确性:ARIMA算法在时间序列预测方面具有较高的准确性,尤其适用于对短期未来数据的预测。
平稳时间序列的分析,建模以及预测
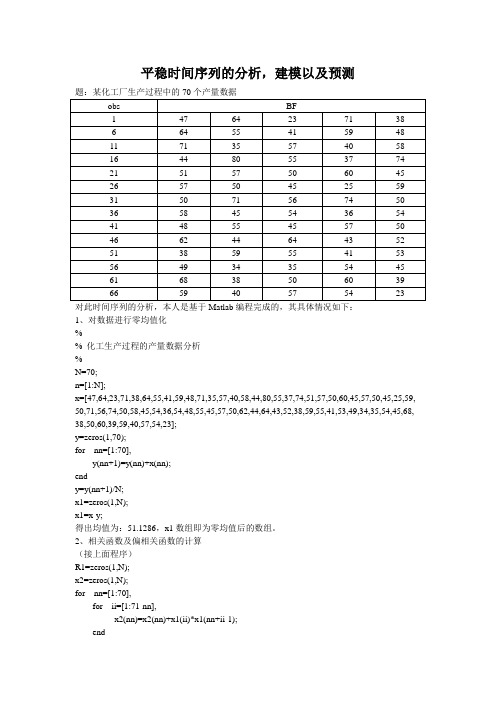
平稳时间序列的分析,建模以及预测对此时间序列的分析,本人是基于Matlab编程完成的,其具体情况如下:1、对数据进行零均值化%% 化工生产过程的产量数据分析%N=70;n=[1:N];x=[47,64,23,71,38,64,55,41,59,48,71,35,57,40,58,44,80,55,37,74,51,57,50,60,45,57,50,45,25,59, 50,71,56,74,50,58,45,54,36,54,48,55,45,57,50,62,44,64,43,52,38,59,55,41,53,49,34,35,54,45,68, 38,50,60,39,59,40,57,54,23];y=zeros(1,70);for nn=[1:70],y(nn+1)=y(nn)+x(nn);endy=y(nn+1)/N;x1=zeros(1,N);x1=x-y;得出均值为:51.1286,x1数组即为零均值后的数组。
2、相关函数及偏相关函数的计算(接上面程序)R1=zeros(1,N);x2=zeros(1,N);for nn=[1:70],for ii=[1:71-nn],x2(nn)=x2(nn)+x1(ii)*x1(nn+ii-1);endendfor jj=[1:70],R1(jj)=x2(jj)/N;endR2=R1;R3=zeros(1,16);for jj=[1:16]R3(jj)=R2(jj)/139.7978;endh=zeros(1,15);g=zeros(1,15);A=zeros(15);for k=[1:14],for j=[1:k],A(1,1)=R3(2);h(k)=h(k)+R3(k+2-j)*A(k,j);g(k)=g(k)+R3(j+1)*A(k,j);A(k+1,k+1)=(R3(k+2)-h(k))/(1-g(k));A(k+1,j)=A(k,j)-A(k+1,k+1)*A(k,k+1-j);endendB=A;figure(1)set(1,'Position',[10,35,350,650])ii=[1:16];plot(ii,R3,'b');gridfigure(2)jj=[1:16];m=zeros(1,16);m(1)=1;for j=[2:16],m(j)=A(j-1,j-1);endplot(jj,m,'b');grid运行程序后得出的自相关函数偏相关函数数据如下表:0ˆr=139.7978, 0ˆρ=1题中:=0.2390 运行程序后得出的散点图如下:自相关散点图(R (n )为图中的R (n+1))偏相关散点图(R (n )为图中的R (n+1))分析中横轴应为0-15,在该图中,横轴为1-16,所以散点图应视为往左移一位。
利用Matlab进行时间序列分析的方法

利用Matlab进行时间序列分析的方法时间序列分析是一种重要的统计分析方法,用于研究随时间变化的数据。
利用时间序列分析方法,我们可以对数据的趋势和周期性进行探索,从而预测未来的发展。
Matlab是一种功能强大的数值计算软件,广泛应用于科学计算、数据分析等领域。
在时间序列分析方面,Matlab也提供了丰富的函数和工具,使得我们能够更加方便地进行分析和建模。
下面,我们将介绍一些常用的利用Matlab进行时间序列分析的方法,希望对大家的研究和实践有所帮助。
1. 数据准备首先,我们需要将要分析的时间序列数据导入Matlab,可以选择将数据存储在一个矩阵或一个向量中。
确保数据的格式正确,并进行必要的预处理,例如去除缺失值、平滑处理等。
2. 数据可视化在进行时间序列分析之前,我们可以先对数据进行可视化,以了解数据的基本特征和趋势。
Matlab提供了丰富的绘图函数,如plot、histogram等,可以帮助我们对数据进行直观的展示。
3. 平稳性检验时间序列分析的前提是数据的平稳性,即数据的均值、方差和自协方差在时间上不发生明显的变化。
为了检验数据的平稳性,我们可以使用一些常见的统计检验方法,如单位根检验(ADF检验)、Ljung-Box检验等。
Matlab提供了相应的函数,如adftest、lbqtest等,可以方便地进行平稳性检验。
4. 自相关和偏自相关分析自相关和偏自相关函数(ACF和PACF)可以帮助我们了解时间序列数据中的相关关系。
ACF表示序列与其自身滞后版本之间的相关性,而PACF则表示序列与其滞后版本之间的部分相关性。
利用Matlab中的autocorr和parcorr函数,我们可以计算序列的ACF和PACF,并绘制相关的图表。
5. 模型识别与拟合根据自相关和偏自相关分析的结果,我们可以初步判断应该采用哪种时间序列模型进行建模。
常见的时间序列模型包括AR模型(自回归模型)、MA模型(移动平均模型)和ARMA模型(自回归移动平均模型)等。
如何使用Matlab进行时间序列分析和预测模型构建

如何使用Matlab进行时间序列分析和预测模型构建引言时间序列分析和预测在许多领域都具有重要的应用价值,如金融、经济、气象等。
而Matlab作为一种功能强大的数学软件,提供了丰富的工具和函数用于时间序列分析和预测模型的构建。
本文将介绍如何使用Matlab进行时间序列分析和预测模型构建,帮助读者快速掌握这一有用的技能。
一、数据预处理在进行时间序列分析和预测之前,首先需要对数据进行预处理。
常见的预处理方法包括数据清洗、缺失值处理、异常值检测等。
1. 数据清洗数据清洗是指对数据进行筛选和剔除,以保证数据的质量和准确性。
在Matlab 中,可以使用各种函数进行数据清洗,如isnan、isinf等。
例如,可以通过isnan函数判断数据是否含有缺失值,并使用isnan函数将缺失值替换为NaN。
2. 缺失值处理缺失值是指数据中的某些观测值缺失或无法获取。
在时间序列分析中,缺失值会对模型的预测产生较大影响。
因此,对于缺失值的处理是非常重要的。
在Matlab中,可以使用一些统计函数,如mean、median等,来对缺失值进行插补或填充。
例如,可以使用mean函数将缺失值替换为数据的均值。
3. 异常值检测异常值是指与其他观测值相比,具有异常数值的观测值。
异常值可能由于测量误差、数据录入错误或其他原因造成。
在时间序列分析中,异常值会对模型的精度和可靠性产生较大影响。
因此,需要对异常值进行检测并进行相应的处理。
在Matlab中,可以使用箱线图、离群点检测等方法来检测异常值,并使用插补或删除等方法进行处理。
二、时间序列分析时间序列分析是指对一系列时间上连续观测值的统计分析与建模。
时间序列分析常用于探索数据的内在规律和结构,并建立相应的数学模型。
1. 数据可视化数据可视化是进行时间序列分析的重要步骤,可以帮助我们直观地了解数据的特征和趋势。
在Matlab中,可以使用plot、scatter等函数进行数据可视化。
例如,可以使用plot函数绘制时间序列的折线图,以展示数据的趋势和变化。
Matlab时间序列预测与趋势分析方法

Matlab时间序列预测与趋势分析方法近年来,随着大数据技术的发展,时间序列数据的应用越来越广泛。
无论是金融领域的股票价格预测,还是气象领域的天气预报,时间序列分析都发挥着重要的作用。
在这个背景下,Matlab成为了一个广泛使用的工具,用于帮助研究人员进行时间序列的预测与趋势分析。
时间序列预测是指根据已有的时间序列数据,通过建立合适的模型来预测未来一段时间内的值。
预测的准确性对于决策者和分析师来说至关重要。
以股票价格预测为例,如果能准确地预测到某只股票未来的涨跌情况,将有助于投资者制定更明智的投资策略。
Matlab提供了丰富的工具箱,可以辅助进行时间序列的预测和趋势分析。
其中最常用的工具箱是Econometrics Toolbox和Time Series Toolbox。
在进行时间序列预测时,首先需要对时间序列数据进行可视化和观察。
Matlab提供了多种绘图函数,例如plot和scatter,可以轻松地绘制时间序列的折线图和散点图。
这有助于我们对时间序列的整体趋势有一个直观的认识。
接下来,我们可以使用Matlab的自回归(AR)模型进行预测。
AR模型是一种最为简单和常用的时间序列预测模型。
它假设未来的值与过去的值有一定的线性关系。
Matlab提供了arima函数,可以方便地对时间序列数据建立AR模型。
然后,我们可以使用该模型对未来的值进行预测。
除了AR模型,Matlab还提供了ARMA模型和ARIMA模型。
这些模型在AR模型的基础上进一步进行了改进,对时间序列的趋势和季节性进行了更好的控制。
使用这些模型,我们可以更精确地进行时间序列预测。
除了时间序列预测,趋势分析也是时间序列分析的重要内容之一。
趋势分析旨在揭示时间序列中的长期趋势和周期性变化。
通过了解时间序列的趋势,我们可以更好地预测未来的值。
Matlab提供了一些常用的趋势分析方法,例如移动平均法和指数平滑法。
移动平均法基于滑动窗口计算指定时间段内的平均值,从而得到时间序列的趋势。
利用Matlab进行时序数据分析和时间序列预测

利用Matlab进行时序数据分析和时间序列预测时序数据是指按时间顺序排列的一系列观测值,通过对时序数据的分析和预测可以帮助我们了解现象的变化趋势以及发展规律。
在现代社会中,人们对于时序数据的分析和预测需求日益增加,例如股票价格走势的预测、天气变化的预测、货物销售量的预测等。
Matlab作为一种功能强大且易于使用的科学计算软件,其提供的一系列工具和函数可以帮助我们进行时序数据的分析和时间序列的预测。
首先,我们将介绍Matlab提供的用于时序数据分析的一些基本函数。
Matlab提供了丰富的时间和日期处理函数,可以帮助我们对不同粒度的时间数据进行操作和分析。
例如,使用"datenum"函数可以将字符串类型的日期转换为Matlab中的日期格式,而"datestr"函数则可以将Matlab日期格式转换为字符串类型。
此外,Matlab还提供了诸如"weeknum"、"year"、"quarter"等用于计算日期所属的周数、年份、季度等函数,这些函数可以将时间数据按照不同的粒度进行分组和统计。
其次,我们将介绍Matlab用于实现时间序列预测的一些常用工具和方法。
Matlab提供了自动回归移动平均模型(ARMA)和自动回归积分移动平均模型(ARIMA)等经典时间序列预测模型的实现函数。
通过利用这些函数,我们可以根据已有的时序数据进行模型拟合,并使用模型来预测未来的数据值。
此外,Matlab还提供了支持向量回归(SVR)和人工神经网络(ANN)等机器学习方法的实现函数,这些方法在一些复杂的时序数据预测问题中往往能够取得更好的效果。
然后,我们将介绍Matlab用于展示时序数据和预测结果的可视化工具。
Matlab 提供了丰富的绘图函数和工具箱,可以帮助我们将时序数据和预测结果以直观的方式展示出来。
例如,使用"plot"函数可以将时序数据按照时间顺序绘制成折线图,这样可以清晰地显示出数据的变化趋势。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
th = armax ( z, nn, ’thace’) 2) resid和 p redict函数对模型进行验证和预测 p redict函数的功能为 :根据历史输入输出数据计算辨识 模型的预测输出 ; resid函数 的功能为 :计算模型预测误差并进行相关分析 p redict函数格式 : yp = p redict( z, th)
析 。相关性分析的任务是计算序列 { X t}的样本自相关函数
和样本偏相关函数 ,并由他们的截尾性和拖尾性来进行模型
类别的判断 。可根据表 1进行模型结构的初选 。
— 105 —
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
表 1 ARM A( p, q)模型的序列特征表
AR (p)
自相关函数
拖尾
偏自相关函数 截尾 k = p处
MA ( q) 截尾 k = p处
拖尾
ARMA ( p , q) 拖尾 拖尾
ARMA (p, q)中 p, q参数的确定 : p, q并不能直接确定 ,而是需要先假定一组值 ,一般是从 (1, 1)开始 ,建立模型 ,然后逐步升高 p, q的值 ,求出一系列 模型 ,并根据 loss function, A IC等准则 ,找出一个最优模型 。 这里介绍一种粗略的判断方法 : P的选择是看平稳序列的偏自相关图 。选择有三 :落入 随机区间外的偏自相关个数 ;有效偏自相关的时滞 ;自相关 函数的震荡周期 。
=
xt - k , B k at = at - k , B k c≡c, c为常数
并令
< (B ) = 1 - <1B - <2B 2 - … - <pB p
θ(B )
=
1
-
θ 1
B
-
θ 2
B
2
-
… - θpB q
则可简记为 :
< (B ) xt =θ(B ) at
这一模型就称作 p阶自回归 - q阶滑动平均混合模型 ,
应数学模型的分析研究 ,能更本质的认识这些动态数据内在
结构和复杂性 ,从而达到在最小方差意义下的最佳预测 。
2. 1 ARM A模型的定义
ARMA 模型的一般形式为 :
xt
-
φ 1
xt
-
1
-
…
-
φ p
xt -
p
= at
-
θ 1
at
-
1
-
…
-
θ q
at
-
q用
B k 表示
k步线性推移算子 ,即
B k xt
1 引言
时间序列是随时间改变而随机地变化的序列 。时间序 列分析的目的是找出它的变化规律 ,即线性模型 ,主要有三 种 : AR模型 (自回归模型 ) 、MA 模型 (滑动平均模型 )和 AR2 MA模型 (自回归滑动平均模型或混合模型 ) 。时间序列在 工程中常用于做预报 ,如气象预报 、地震预报 、水文预报 、电 力负荷预报等 。例如某地区根据已有的电力负荷数据 ,预报 下一小时的电力负荷 ,以便控制下一小时发电机的发电量 。 目前在以上三种模型的实现算法上已有多种方法 ,但是往往 需要工程人员自己编程实现 ,在选择一个最优模型时 ,比较 繁杂 。本文介绍了 MATLAB 系统辨识工具箱在时间序列建 模及预测方面的应用 ,给广大工程技术人员提供了一种快捷 方便的实现途径 。
M odeling and Pred iction of T im e Ser ies Ba sed on M a tlab
HAN Lu - yue, DU X ing - jian
(Xi’an J iaotong University, Xi’an Shanxi 710049, China)
ABSTRACT: In this paper the app lication of System Identification Toolbox of M atlab in time series was introduced. Firstly, the method for analyzing and dealing w ith the dynam ic data, the p rocess of rank - determ ining and model constructing of time series were discussed. Then, the method and step s of data p retreatment, correlation analyzing, parameter estimation of ARMA model and forecasting of time series w ith System Identification Toolbox ofM atlab were disp layed. A t last the daily water p roviding of a water p lant was p redicted w ith this method. The result show s that it is very useful in p ractice. KEYW O RD S: Time series; Model; System identification
© 1994-2010 China Academic Journal Electronic Publishing House. All rights reserved.
测 ,画出一步预测曲线 ,取 N /10 ( 124 /10 )为上限 ,根据 Loss Function、A IC、FPE等准则来定阶 。计算误差的自相关函数 和误差与输入的互相关函数 ,并检验误差是否为白噪声 。
Z0 , Z1 …, Zk …Zk + l …,其中 k≥1, l≥1。若以观测到 Z1 …, Zk
的数值 ,要估计
Zk
+
的
l
数
值
,
称
为
在
k时刻作
l步预报 , Zk + l
∧
地估计值记为
Zk
+
。预
l
ห้องสมุดไป่ตู้
报通
常
都
采用
最
小方
差
线
性
估
计
的
原则 。
2. 5 模型拟合残量的自相关检验
对序列通过了平稳性检验 ,并建立了相应的 ARMA模型 之后 ,为考核所建模性的优劣 ,一般还需对 ARMA 模型残量 a1 , a2 , …aN 检验是不是白噪声 。也就是说 ,如果经检验确是 白噪声序列 ,则可认为模型是合理的 ,否则 ,就应当进一步改 进模型 。
记为 ARMA ( p, q)模型 , 特殊地 , 若 p = 0, 称作纯滑动平均模
型 ,记为 MA ( q) ; 若 q = 0,称作纯自回归模型 , 记为 AR ( p) .
若 p = q = 0,模型退化为 xt = at ,即 { xt }为白噪声列 。 2. 2 模型阶次的确定
对时间序列的 X t ( t = 1, 2, …N ) , 首先要进行相关性分
4 应用实例
本文的原始数据是某市自来水公司 5个月的日给水量 , 预测的方法是根据前 4 个月的数据来预测第 5 个月的日用 水量 。主要步骤为 :
1)输入原始数据 2)对建模用的原始数据进行零均值化 ,平稳化处理 ,然 后进行分析 。本文用 ff = dtrend ( f)函数将建模用的原始数据 实现去趋势处理 ,即零均值化 ,平稳化处理 ; 3)用 [ acf, lags1, bounds1 ] = autocorr ( ff) 计算置信度为 95%的 acf(自相关函数 ) ,并画出其自相关函数的曲线 ; 4)用 [ pacf, lags1, bounds1 ] = parcorr ( ff) 计算置信度为 95%的 pacf (偏自相关函数 ) ,并画出其偏自相关函数的曲 线; 5)由 acf(自相关函数 )和 pacf(偏自相关函数 )的拖尾性 可初步判断为 ARMA 模型 ; 6)用 system identification toolbox中的 ident GU I或者直 接使用 resid和 p redict函数建立一系列模型并实现一步预
第 22卷 第 4期 文章编号 : 1006 - 9348 ( 2005) 04 - 0105 - 03
计 算 机 仿 真
2005年 4月
基于 M ATLAB的时间序列建模与预测
韩路跃 ,杜行检
(西安交通大学电子与信息工程学院 ,陕西 西安 710049)
摘要 :该文介绍了 MATLAB 系统辨识工具箱在时间序列方面的应用 。首先叙述了动态数据的分析与处理方法 ,时间序列模 型阶次的判定及建模过程 ,然后给出了利用 Matlab系统辨识工具箱对时间序列进行数据预处理 ,相关分析 , ARMA 模型参数 估计 ,以及预报的方法和步骤 ,最后使用该方法对某水厂日供水量进行预测 ,结果说明该方法具有极强的实践意义 。 关键词 :时间序列 ;模型 ;系统辨识 中图分类号 : TP391. 4 文献标识码 : A
2 ARM A 模型辨识和预测
ARMA 方法是一种精 确度较高的 短 期 时 间 序 列 预 测 方 法 。他将预测对象随时间变化形成的序列 ,看作是一个随机 序列 。ARMA法的基本思想是 :一串随时间变化而又相互关 联的数字序列 ,可以用相应的模型加以近似描述 。通过对相
