苏州大学2018届高考考前指导卷2(含答案)
苏州大学高考数学考前指导卷
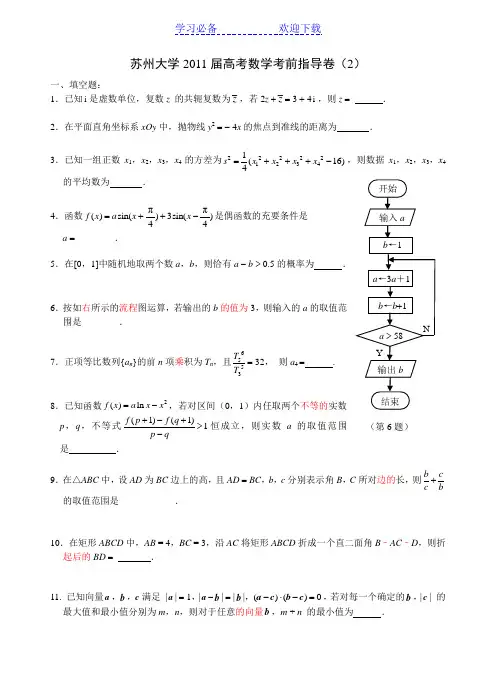
苏州大学2011届高考数学考前指导卷(2)一、填空题:1.已知i 是虚数单位,复数z 的共轭复数为z -,若2z +z -= 3 + 4i ,则z = .2.在平面直角坐标系xOy 中,抛物线y 2 = - 4x 的焦点到准线的距离为 .3.已知一组正数x 1,x 2,x 3,x 4的方差为2222212341(16)4s x x x x =+++-,则数据x 1,x 2,x 3,x 4的平均数为 .4.函数ππ()sin()3sin()44f x a x x =++-是偶函数的充要条件是 a = ________.5.在[0,1]中随机地取两个数a ,b ,则恰有a - b > 0.5的概率为 .6.按如右所示的流程图运算,若输出的b 的值为3,则输入的a 的取值范围是________.7.正项等比数列{a n }的前n 项乘积为T n ,且6553T T = 32, 则a 4 = .8.已知函数2()ln f x a x x =-,若对区间(0,1)内任取两个不等的实数p ,q ,不等式(1)(1)1f p f q p q+-+>-恒成立,则实数a 的取值范围是 .9.在△ABC 中,设AD 为BC 边上的高,且AD = BC ,b ,c 分别表示角B ,C 所对边的长,则b cc b+的取值范围是____________.10.在矩形ABCD 中,AB = 4,BC = 3,沿AC 将矩形ABCD 折成一个直二面角B –AC –D ,则折起后的BD = .11. 已知向量a ,b ,c 满足 |a | = 1,|a -b | = |b |,()()0-⋅-=a c b c ,若对每一个确定的b ,|c | 的最大值和最小值分别为m ,n ,则对于任意的向量b ,m + n 的最小值为 .(第6题)12.已知实数a ,b ,c 成等差数列,点P ( - 1,0)在动直线0ax by c ++=上的射影为M ,点N (2,1),则线段MN 长的取值范围是____________.13.设222(,)()()2x F x y x y y=-++,对于一切x ,y ∈R ,y ≠0,(),F x y 的最小值为________.14.已知等差数列{a n }的公差d 不为0,等比数列{b n }的公比q 为小于1的正有理数.若a 1 = d ,b 1 = d 2,且222123123a a ab b b ++++是正整数,则q 等于________.二、解答题15.设△ABC 的内角A ,B ,C 所对边的长分别为a ,b ,c,且(2)cos cos b A C =. (1)求角A 的大小; (2)若角6B π=,BC 边上的中线AMABC ∆的面积.16.如图,在三棱锥P - ABC 中,∠CAB = 90︒,P A = PB ,D 为AB 中点,PD ⊥平面ABC ,PD = AB = 2,AC = 1.(1)求证:平面P AB ⊥平面P AC ;(2)点M 是棱PB 上的一个动点,求△MAC 周长的最小值.CA B P D M17.某地发生地质灾害,使当地的自来水受到了污染,某部门对水质检测后,决定往水中投放一种药剂来净化水质.已知每投放质量为m 的药剂后,经过x 天该药剂在水中释放的浓度y (毫克/升) 满足()y m f x =,其中()22,04,1614, 4,22x x f x x x x ⎧+<≤⎪⎪=⎨+⎪>⎪-⎩当药剂在水中释放的浓度不低于4(毫克/升) 时称为有效净化;当药剂在水中释放的浓度不低于4 (毫克/升) 且不高于10(毫克/升)时称为最佳净化.(1)如果投放的药剂质量4m =,试问自来水达到有效净化一共可持续几天?(2)如果投放的药剂质量为m ,为了使在7天(从投放药剂算起包括7天)之内的自来水达到最佳净化,试确定应该投放的药剂质量m 的最小值.18.已知椭圆C 的中心在坐标原点O ,焦点在x 轴上,F 1,F 2分别是椭圆C 的左、右焦点,M 是椭圆短轴的一个端点,过F 1的直线l 与椭圆交于A ,B 两点,12MF F V 的面积为4,2ABF ∆的周长为(1)求椭圆C 的方程;(2)设点Q 的坐标为(1,0),是否存在椭圆上的点P 及以Q 为圆心的一个圆,使得该圆与直线PF 1,PF 2都相切,若存在,求出点P 的坐标及圆的方程;若不存在,请说明理由.19.已知数列{}n a 是各项均不为0的等差数列,公差为d ,n S 为其前n 项和,且满足221n n a S -=,n *N ∈.数列{}n b 满足11n n n b a a +=,n T 为数列{}n b 的前n 项和. (1)求1a ,d 和n T ;(2)若对任意的n *N ∈,不等式8(1)nn T n λ<+⋅-恒成立,求实数λ的取值范围;(3)是否存在正整数,m n (1)m n <<,使得1,,m n T T T 成等比数列?若存在,求出所有,m n 的值;若不存在,请说明理由.20.在区间D 上,如果函数()f x 为增函数,而函数1()f x x为减函数,则称函数()f x 为“弱增函数”. 已知函数()f x = 1.(1)判断函数()f x 在区间(0,1]上是否为“弱增函数”;(2)设1x ,2x ∈[0,)+∞,且1x ≠2x ,证明:21()()f x f x -<121||2x x -;(3)当x ∈[0,1]时,不等式1 - ax1 - bx 恒成立,求实数a ,b 的取值范围.苏州大学2011届高考数学考前指导卷(2)参考答案1.1 + 4i 2.2 3.2 4.-3 5.186.(6,19] 78.[10,)+∞ 9.[2]. 10.11.32 12. 13.165 14.12 15.(1)∵(2)cos cos b A C =,∴(2sin )cos cos B C A A C =.即2sin cos cos cos B A A C C A =.∴2sin cos )B A A C =+.则2sin cos B A B =,∴cos A =6A π=. (2)由(1)知π6A B ==,所以AC BC =,23C π=,设AC x =,则12MC x =,又AM =在AMC ∆中由余弦定理得2222cos ,AC MC AC MC C AM +-⋅=即222()2cos120,22x x x x +-⋅⋅=o 解得2,x =故212sin 23ABC S x π∆==16.(1)∵PD ⊥平面ABC ,AC ⊂平面ABC ,∴PD ⊥AC .又AB ⊥AC ,AB ∩PD = D , ∴AC ⊥平面P AB . ∵AC ⊂平面P AC ,∴平面P AB ⊥平面P AC . (2)当AM ⊥PB 时,AM 取得最小值.∵AC ⊥平面P AB ,∴AC ⊥PB .则PB ⊥平面MAC .即CM ⊥PB .∴CM 也取得最小值,则△MAC 周长取得最小值.∵PD = AB = 2,∴AB PD AM PB ⋅=. 而CA ⊥AM,∴CM ==∴△MAC周长的最小值为11+=+17.解:(1)由题意,当药剂质量为4m =,所以()()2804,162284.1x x y x x x ⎧+<≤⎪⎪=⎨+⎪>⎪-⎩当04x <≤时28416x +≥显然符合题意.4x >228x +≥416x <≤016x <≤所以自来水达到有效净化一共可持续16天.(2)由()y m f x =⋅=()()220416(14)422mx m x m x x x ⎧+<≤⎪⎪⎨+⎪>⎪-⎩,得在区间(]0,4上单调递增,即23m y m <≤;在区间(]4,7上单调递减,即734m y m ≤<,综上734my m ≤≤, 为使410y ≤≤恒成立,只要744m ≥且310m ≤即可,即161073m ≤≤.所以应该投放的药剂质量m 的最小值为167.18.(1) 由题意知:124,4,2c b bc ⨯⨯==4a a == 解得 2b c ==.∴ 椭圆的方程为22184x y +=.(2)假设存在椭圆上的一点00(,)P x y ,使得直线12,PF PF 与以Q 为圆心的圆相切,则Q 到直线12,PF PF 的距离相等,12(2,0),(2,0)F F -, 1PF :000(2)20x y y x y +--=,2PF :000(2)20x y y x y --+=,=。
2020年6月苏州大学2020届高三高考考前指导卷(二)数学试题(含附加题)及答案

绝密★启用前江苏省苏州大学2020届高三高考考前指导卷(二)数学试题2020年6月数学Ⅰ试题一、填空题:不需要写出解答过程,请把答案直接填在答题卡相应位置上. 1.已知集合{}1A x x =>,{}1,2,3B =,则A B =________.2.已知复数2i z =+(其中i 为虚数单位),若()i ,iza b a b =+∈R ,则ab 的值为________. 3.已知一组数据4,a ,7,5,8的平均数为6,则该组数据的标准差是________.4.在平面直角坐标系xOy 中,若双曲线1C :()2210x y m m-=>的一条准线与抛物线2C :22x y=的准线重合,则正数的值是________.5.运行如图的程序框图,则输出的结果是________.6.《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化阴阳术数之源.河图的排列结构如图所示,一与六共宗居下,二与七为朋居上,三与八同道居左,四与九为友居右,五与十相守居中,其中白圈为阳数,黑点为阴数,若从阳数和阴数中各取一数,则其差的绝对值为5的概率为________.7.已知{}n a 为等差数列,n S 为其前n 项和,若2552a a +=,则15S 的值是________.8.圆柱形容器的内壁底面半径是10cm,有一个实心铁球浸没于容器的水中,若取出这个铁球,测得容器的水面下降了5cm 3,则这个铁球的表面积为________2cm .9.若直线1y kx =+与曲线y x =相切,则实数k 的值为________. 10()tan1234cos 122sin12︒-=︒-︒________. 11.已知向量a ,b ,满足3b =,a b a ⋅=,则a b -的最小值为________.12.在平面直角坐标系xOy 中,已知A ,B 为圆C :()()2224x m y -+-=上两个动点,且23AB =若直线l :2y x =-上存在点P ,使得OC PA PB =+,则实数m 的取值范围为________. 13.已知函数()31111,1,3442111,0,362x x x f x x x ⎧-+<⎪⎪=⎨⎪-+⎪⎩≤≤≤()()e 2x g x ax a =+-∈R ,若存在1x ,[]20,1x ∈,使得()()12f x g x =成立,则实数a 的取值范围是________.14.已知在锐角三角形ABC 中,AH BC ⊥于点H ,且()229449BA CA AH CA BA -=⋅-,若2BC =,则sin sin sin B CA的取值范围是________.二、解答题:请在答题卡指定区域内作答,解答时应写出文字说明、证明过程或演算步骤. 15.在ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,且3B π=. (1)若23b =2a =,求c 的值; (2)若13cos A =,求cos C 的值. 16.已知直三棱柱111ABC A B C -,E ,F 分别是BC ,1AA 的中点,1CB CC =,AC BC ⊥.。
江苏省2018年普通高等学校招生全国统一考试-试题、参考答案(含语数英、政史地、物化生)

2018年普通高等学校招生全国统一考试试题、参考答案目 录 语文Ⅰ试题1 ……………………………………………………………语文Ⅰ试题参考答案4 …………………………………………………语文Ⅱ(附加题)5 ……………………………………………………语文Ⅱ(附加题)参考答案6 …………………………………………英语试题6 ………………………………………………………………英语试题参考答案14 …………………………………………………数学Ⅰ试题15 …………………………………………………………数学Ⅰ试题参考答案17 ………………………………………………数学Ⅱ(附加题)20 ……………………………………………………数学Ⅱ(附加题)参考答案21 …………………………………………政治试题23 ……………………………………………………………政治试题参考答案28 …………………………………………………历史试题29 ……………………………………………………………历史试题参考答案33 …………………………………………………地理试题34 ……………………………………………………………地理试题参考答案41 …………………………………………………物理试题42 ……………………………………………………………物理试题参考答案47 …………………………………………………化学试题48 ……………………………………………………………化学试题参考答案54 …………………………………………………生物试题55 ……………………………………………………………生物试题参考答案62 …………………………………………………江苏省教育考试院二〇一八年六月语文Ⅰ试题一㊁语言文字运用(15分)1.在下面一段话的空缺处依次填入词语,最恰当的一组是(3分) 中国古代的儒家经典,莫不是古圣人深思熟虑㊁ ▲ 的结晶㊂如果把经典仅仅当作一场 ▲ 的说教,那你永远进不了圣学大门㊂必得躬亲实践,才能切实 ▲ 圣人的心得,如此我们的修为才能日有所进㊂A.特立独行 耳提面命 顿悟B.特立独行 耳濡目染 领悟C.身体力行 耳提面命 领悟D.身体力行 耳濡目染 顿悟2.在下面一段文字横线处填入语句,衔接最恰当的一项是(3分) 理性经济人”,把利己看作人的天性,只追求个人利益的最大化,这是西方经济学的基本假设之一㊂ ▲ , ▲ ㊂ ▲ , ▲ , ▲ , ▲ ,更倾向于暂时获得产品或服务,或与他人分享产品或服务㊂使用但不占有,是分享经济最简洁的表述㊂①反而更多地采取一种合作分享的思维方式②不再注重购买㊁拥有产品或服务③但在分享经济这一催化剂的作用下④人们不再把所有权看作获得产品的最佳方式⑤在新兴的互联网平台上⑥这个利己主义的假设发生了变化A.③⑥⑤①④②B.③⑥⑤④②①C.⑤⑥③①④②D.⑤⑥③④②①3.下列诗句与所描绘的古代体育活动,对应全部正确的一项是(3分)①乐手无踪洞箫吹,精灵盘丝任翻飞㊂②雾縠云绡妙剪裁,好风相送上瑶台㊂③浪设机关何所益,仅存边角未为雄㊂④来疑神女从云下,去似姮娥到月边㊂A.①下围棋 ②荡秋千 ③抖空竹 ④放风筝B.①抖空竹 ②荡秋千 ③下围棋 ④放风筝C.①下围棋 ②放风筝 ③抖空竹 ④荡秋千D.①抖空竹 ②放风筝 ③下围棋 ④荡秋千4.对下面一段文字主要意思的提炼,最准确的一项是(3分) 偏见可以说是思想的放假㊂它是没有思想的人的家常日用,是有思想的人的星期天娱乐㊂假如我们不能怀挟偏见,随时随地必须得客观公正㊁正经严肃,那就像造屋只有客厅,没有卧室,又好比在浴室里照镜子还得做出摄影机前的姿态㊂A.没有思想的人往往更容易产生偏见㊂B.即使有思想的人也常常会怀挟偏见㊂C.人无法做到随时随地保持客观公正㊂D.对思想而言偏见自有其存在的价值㊂5.下列选项中,对右图漫画寓意的理解最贴切的一项是(3分)A.过程特别艰难,可能预示着这一次收获很大㊂B.在我们不注意的地方往往隐藏着巨大的困难㊂C.对努力挣得的东西,人们会牢牢地抱住不放㊂D.懂得知足常乐,会使生活中的困难更少一些㊂二㊁文言文阅读(18分)阅读下面的文言文,完成6~9题㊂ 重到沭阳图记 袁枚 古之人往往于旧治之所三致意焉㊂盖贤者视民如家,居官而不能忘其地者,其地之人,亦不能忘之也㊂余宰∙沭阳二年,乙丑,量移白下㊂今戊申矣,感吕峄亭观察三札见招,十月五日渡黄河,宿钱君接三家㊂钱故当时东道主,其父鸣和癯而髯,接三貌似之,与谈乃父事,转不甚晓㊂余离沭时,渠裁断乳故也㊂夜阑置酒,闻车声啍啍,则峄亭遣使来迎㊂迟明行六十里,峄亭延候于十字桥,彼此喜跃,骈辚同驱㊂食倾,望见百雉遮迣,知沭城新筑㊂衣冠数十辈争来扶车㊂大概昔时骑竹马者,俱龙钟杖藜矣㊂越翌日,入县署游观,到先人秩膳处,姊妹斗草处,昔会宾客治文卷处,缓步婆娑,凄然雪涕,虽一庖湢㊁一井匽,对之情生,亦不自解其何故㊂有张㊁沈两吏来,年俱八旬㊂说当时决∙某狱,入帘荐某卷,余全不省记㊂憬然重提,如理儿时旧书,如失物重得㊂邑中朱广文工诗,吴中翰精鉴赏,解㊁陈二生善画与棋,主人喜论史鉴,每漏尽,口犹澜翻㊂余或饮,或吟,或弈,或写小影,或评书画,或上下古今,或招人来,或呼车往,无须臾闲㊂遂忘作客,兼忘其身之老且衰也㊂居半月,冰霰渐飞,岁将终矣,不得已苦辞主人㊂主人仍送至前所迎处,代为治∙筐箧,束缰靷毕,握手问曰: 何时再见先生?”余不能答,非不答也,不忍答也㊂嗟乎!余今年七十有三矣,忍欺君而云再来乎?忍伤君而云不来乎?然以五十年前之令尹,朅来旧邦,世之如余者少矣;四品尊官,奉∙母闲居,犹能念及五十年前之旧令尹,世之如吕君者更少矣㊂离而合,合而离,离可以复合,而老不能再少㊂此一别也,余不能学太上之忘情,故写两图,一以付吕,一以自存,传示子孙,俾知官可重来,其官可想,迎故官如新官,其主人亦可想㊂孟子曰:闻伯夷㊁柳下惠之风者,奋乎百世之下,而况于亲炙之者乎?提笔记之,可以风世①,又不徒为区区友朋聚散之感也㊂ [注]①风世:劝勉世人㊂(选自‘小仓山房诗文集“,有删节) 6.对下列加点词的解释,不正确∙∙∙的一项是(3分)A.余宰∙沭阳二年 宰:治理B.说当时决∙某狱 决:打开C.代为治∙筐箧 治:备办D.奉∙母闲居 奉:侍奉7.下列对原文有关内容的概括和分析,不正确∙∙∙的一项是(3分)A.四品官员吕峄亭在家闲居期间,连续写信邀请老县令旧地重游,袁枚因此再到沭阳㊂B.当年袁枚离开沭阳时,钱接三才断奶,因此谈及其父钱鸣和的往事,接三不太清楚㊂C.八十多岁的张㊁沈两吏是袁枚的老同事,还能依稀记得些许往事,多数事已忘记了㊂D.吕峄亭在寒冬时节送客至十字桥,宾主作别时,袁枚觉得自己有生之年很难再来了㊂8.把文中画线的句子翻译成现代汉语㊂(8分)(1)迟明行六十里,峄亭延候于十字桥,彼此喜跃,骈辚同驱㊂(2)闻伯夷㊁柳下惠之风者,奋乎百世之下,而况于亲炙之者乎?9.文中 可以风世”的内容有哪些?请简要概括㊂(4分)三㊁古诗词鉴赏(11分) 阅读下面这首唐诗,完成10~11题㊂寄和州刘使君①张籍别离已久犹为郡,闲向春风倒酒瓶㊂送客特过沙口堰,看花多上水心亭㊂晓来江气连城白,雨后山光满郭青㊂到此诗情应更远,醉中高咏有谁听? [注]①刘使君,指唐代诗人刘禹锡,时任和州刺史㊂诗中沙口堰㊁水心亭,均在和州㊂10.根据前两联,概括刘禹锡 闲”的表现,并分析他如此表现的原因㊂(5分)11.尾联表达了作者什么样的情感?(6分)四㊁名句名篇默写(8分)12.补写出下列名句名篇中的空缺部分㊂(1)既见复关, ▲ ㊂(‘诗经㊃卫风㊃氓“)(2)故不积跬步, ▲ ㊂(‘荀子㊃劝学“)(3)今年欢笑复明年, ▲ ㊂(白居易‘琵琶行“)(4) ▲ ,不知东西㊂(杜牧‘阿房宫赋“)(5)沙鸥翔集, ▲ ㊂(范仲淹‘岳阳楼记“)(6)八百里分麾下炙, ▲ ㊂(辛弃疾‘破阵子“)(7)浴乎沂, ▲ ,咏而归㊂(‘论语㊃先进“)(8) ▲ ,辣手著文章㊂(杨继盛名联)五㊁现代文阅读(一)(20分)阅读下面的作品,完成13~16题㊂小哥儿俩凌叔华清明那天,不但大乖二乖上的小学校放一天假,连城外七叔叔教的大学堂也不用上课了㊂这一天早上的太阳也像特别同小孩子们表同情,不等闹钟催过,它就跳进房里来,暖和和地爬在靠窗挂的小棉袍上㊂前院子一片小孩子的尖脆的嚷声笑声,七叔叔带来了一只能说话的八哥㊂笼子放在一张八仙方桌子上,两个孩子跪在椅上张大着嘴望着那里头的鸟,欢喜得爬在桌上乱摇身子笑,他们的眼,一息间都不曾离开鸟笼子㊂二乖的嘴总没有闭上,他的小腮显得更加饱满,不用圆规,描不出那圆度了㊂吃饭的时候,大乖的眼总是望着窗外,他最爱吃的春卷也忘了怎样放馅,怎样卷起来吃㊂二乖因为还小,都是妈妈替他卷好的,不过他到底不耐烦坐在背着鸟笼子的地方,一吃了两包,他就跑开不吃了㊂饭后爸爸同叔叔要去听戏,因为昨天已经答应带孩子们一块去的,于是就雇了三辆人力车上戏园去了㊂两个孩子坐在车上还不断地谈起八哥㊂到了戏园,他们虽然零零碎碎地想起八哥的事来,但台上的锣鼓同花花袍子的戏子把他们的精神占住了㊂ 快天黑的时候散了戏,随着爸爸叔叔回到家里,大乖二乖正是很高兴地跳着跑,忽然想到心爱的八哥,赶紧跑到廊下挂鸟笼的地方,一望,只有个空笼子掷在地上,八哥不见了㊂ 妈 八哥呢?”两个孩子一同高声急叫起来㊂给野猫吃了!”妈的声非常沉重迟缓㊂给什么野猫吃的呀?”大乖圆睁了眼,气呼呼的却有些不相信㊂二乖愣眼望着哥哥㊂大乖哭出声来,二乖跟着哭得很伤心㊂他们也不听妈的话,也不听七叔叔的劝慰,爸爸早躲进书房去了㊂忽然大乖收了声,跳起来四面找棍子,口里嚷道: 打死那野猫,我要打死那野猫!”二乖爬在妈的膝头上,呜呜地抽咽㊂大乖忽然找到一根拦门的长棍子,提在手里,拉起二乖就跑㊂妈叫住他,他嚷道: 报仇去,不报仇不算好汉!”二乖也学着哥哥喊道: 不报仇不算好看!”妈听了二乖的话倒有些好笑了㊂王厨子此时正走过,他说: 少爷们,那野猫黑夜不出来的,明儿早上它来了,我替你们狠狠地打它一顿吧㊂”那野猫好像有了身子,不要太打狠了,吓吓它就算了㊂”妈低声吩咐厨子㊂大乖听见了妈的话,还是气呼呼地说: 谁叫它吃了我们的八哥,打死它,要它偿命㊂” 打死它才 ”二乖想照哥哥的话亦喊一下,无奈不清楚底下说什么了㊂他也挽起袖子,露出肥短的胳臂,圆睁着泪还未干的小眼㊂第二天太阳还没出,大乖就醒了,想起了打猫的事,就喊弟弟: 快起,快起,二乖,起来打猫去㊂”二乖给哥哥着急声调惊醒,急忙坐起来,拿手揉开眼㊂然后两个人都提了毛掸子,拉了袍子,嘴里喊着报仇,跳着出去㊂这是刚刚天亮了不久,后院地上的草还带着露珠儿,沾湿了这小英雄的鞋袜了㊂树枝上小麻雀三三五五地吵闹着飞上飞下地玩,近窗户的一棵丁香满满开了花,香得透鼻子,温和的日光铺在西边的白粉墙上㊂二乖跷高脚摘了一枝丁香花,插在右耳朵上,看见地上的小麻雀吱喳叫唤,跳跃着走,很是好玩的样子,他就学它们,嘴里也哼哼着歌唱,毛掸子也掷掉了㊂二乖一会儿就忘掉为什么事来后院的了㊂他蹓达到有太阳的墙边,忽然看见装碎纸的破木箱里,有两个白色的小脑袋一高一低动着,接着咪噢咪噢地娇声叫唤,他就赶紧跑近前看去㊂原来箱里藏着一堆小猫儿,小得同过年时候妈妈捏的面老鼠一样,小脑袋也是面团一样滚圆得可爱,小红鼻子同叫唤时一张一闭的小扁嘴,太好玩了㊂二乖高兴得要叫起来㊂ 哥哥,你快来看看,这小东西多好玩!”二乖忽然想起来叫道,一回头哥哥正跑进后院来了㊂哥哥赶紧过去同弟弟在木箱子前面看,同二乖一样用手摸那小猫,学它们叫唤,看大猫喂小猫奶吃,眼睛转也不转一下㊂它们多么可怜,连褥子都没有,躺在破纸的上面,一定很冷吧㊂”大乖说,接着出主意道, 我们一会儿跟妈妈要些棉花同它们垫一个窝儿,把饭厅的盛酒箱子弄出来,同它做两间房子,让大猫住一间,小猫在一间,像妈妈同我们一样㊂”哥哥,你瞧它跟它妈一个样子㊂这小脑袋多好玩!”弟弟说着,又伸出方才收了的手抱起那只小黑猫㊂(有删改)13.小哥儿俩是在什么样的家庭环境中成长的?请简要分析㊂(6分)14.分析小说画线部分的景物描写对情节发展的作用㊂(4分)15.二乖的天真可爱表现在哪些方面?请简要概括㊂(4分)16.小说叙述了小哥儿俩的日常故事,请探究作者在其中所寄寓的情感态度㊂(6分)六㊁现代文阅读(二)(18分)阅读下面的作品,完成17~19题㊂中国建筑的希望梁思成建筑之始,本无所谓一定形式,更无所谓派别㊂所谓某系或某派建筑,其先盖完全由于当时彼地的人情风俗㊁政治情况之情形,气候及物产材料之供给,和匠人对于力学知识㊁技术巧拙之了解等复杂情况总影响所产生㊂一系建筑之个性,犹如一个人格,莫不是同时受父母先天的遗传和朋友师长的教益而形成的㊂中国的建筑,在中国整个环境总影响之下,虽各个时代各有其特征,其基本的方法及原则,却始终一贯㊂数千年来的匠师们,在他们自己的潮流内顺流而下,如同欧洲中世纪的匠师们一样,对于他们自己及他们的作品都没有一种自觉㊂19世纪末叶及20世纪初年,中国文化屡次屈辱于西方坚船利炮之下以后,中国却忽然到了 凡是西方的都是好的”的段落,又因其先已有帝王骄奢好奇的游戏,如郎世宁辈在圆明园建造西洋楼等事为先驱,于是 洋式楼房” 洋式门面”,如雨后春笋,酝酿出光宣以来建筑界的大混乱㊂正在这个时期,有少数真正或略受过建筑训练的外国建筑家,在香港㊁上海㊁天津 乃至许多内地都邑里,将他们的希腊罗马哥特等式样,似是而非地移植过来,同时还有早期的留学生,敬佩西洋城市间的高楼霄汉,帮助他们移植这种艺术㊂这可说是中国建筑术由匠人手中升到 士大夫”手中之始;但是这几位先辈留学建筑师,多数却对于中国式建筑根本鄙视㊂近来虽然有人对于中国建筑有相当兴趣,但也不过取一种神秘态度,或含糊地骄傲地用些抽象字句来对外人颂扬它;至于其结构上的美德及真正的艺术上的成功,则仍非常缺乏了解㊂现在中国各处 洋化”过的旧房子,竟有许多将洋式的短处,来替代中国式的长处,成了兼二者之短的 低能儿”,这些亦正可表示出他们对于中国建筑的不了解态度了㊂欧洲大战以后,艺潮汹涌,近来风行欧美的 国际式”新建筑,承认机械及新材料在我们生活中已占据了主要地位㊂这些 国际式”建筑,名目虽然笼统,其精神观念,却是极诚实的㊂这种建筑现在已传至中国各通商口岸,许多建筑师又全在抄袭或模仿那种形式㊂但是对于新建筑有真正认识的人,都应知道现代最新的构架法,与中国固有建筑的构架法,所用材料不同,基本原则却一样 都是先立骨架,次加墙壁的㊂这并不是他们故意抄袭我们的形式,乃因结构使然㊂我们若是回顾到我们古代遗物,它们的每个部分莫不是内部结构坦率的表现,正合乎今日建筑设计人所崇尚的途径㊂这样两种不同时代不同文化的艺术,竟融洽相类似,在文化史中确是有趣的现象㊂我们这个时期,正该是中国建筑因新科学㊁材料㊁结构而又强旺更生的时期,也是中国新建筑师产生的时期㊂他们自己在文化上的地位是他们自己所知道的;他们对于他们的工作是依其意向而设计的;他们并不像古代的匠师,盲目地在海中漂泊,他们自己把定了舵,向着一定的目标走㊂我认为,他们是最有希望的㊂(有删改)17.分析文中 兼二者之短的 低能儿’”出现的原因㊂(6分)18.文中 国际式’新建筑”的内涵是什么?(6分)19.中国建筑的希望体现在哪些方面?请联系全文,简要概述㊂(6分)七㊁作文(70分)20.根据以下材料,选取角度,自拟题目,写一篇不少于800字的文章;文体不限,诗歌除外㊂花解语,鸟自鸣,生活中处处有语言㊂不同的语言打开不同的世界,音乐㊁雕塑㊁程序㊁基因 莫不如此㊂语言丰富生活,语言演绎生命,语言传承文明㊂语文Ⅰ试题参考答案一㊁语言文字运用(15分)1.C2.B3.D4.D5.A二㊁文言文阅读(18分)6.B7.C8.(1)天快亮的时候,行驶了六十里,吕峄亭在十字桥迎接,两人(见面)十分欣喜,便驱车一同前往㊂(2)伯夷㊁柳下惠那样的高风,百代之后的人听到,也能奋发,更何况亲受熏陶的人呢?9.为官当勤政爱民,百姓会怀念他;为人当感恩重义,后代会仿效他㊂三㊁古诗词鉴赏(11分)10.表现:把酒当春,绕道送客,常去赏花㊂原因:长期得不到升迁,怀才不遇;喜欢自然山水㊂11.对刘禹锡诗歌艺术的钦佩之情;对刘禹锡目前境况的同情之感;对自己能感知对方心意的知音之许㊂四㊁名句名篇默写(8分)12.(1)载笑载言 (2)无以至千里 (3)秋月春风等闲度 (4)高低冥迷(5)锦鳞游泳 (6)五十弦翻塞外声(7)风乎舞雩 (8)铁肩担道义五㊁现代文阅读(一)(20分)13.经济状况良好:家有厨子和花园等;文化氛围浓厚:家有书房,经常看戏,注重教育等;人际关系和谐:尊重孩子,兄弟友爱,主仆融洽等㊂14.鸟语花香与温暖的阳光,营造了充满生机的氛围,为人物的兴趣转移和情绪变化作铺垫; 日光” 西边的白粉墙”等描写,为二乖在墙边发现小猫埋下伏笔㊂15.外貌憨态可掬;言行稚拙,爱模仿;情感表达率真;注意力易转移;喜爱小动物,好奇心强㊂16.对童真童趣的欣赏;对儿童成长的关注;对母爱的颂扬;对和谐家庭氛围的赞许;对善良人性的礼赞㊂六㊁现代文阅读(二)(18分)17.社会上有崇洋媚外的风气;一部分建筑师对中国建筑存在鄙视;一部分建筑师虽对中国建筑感兴趣,但缺乏真正的了解㊂18.承认机械及新材料的主要地位;有极诚实的精神观念;其构架法的基本原则是先立骨架㊁次加墙壁㊂19.数千年来中国建筑取得了真正的艺术成就,有其一贯的基本方法及原则;中国建筑因新科学㊁材料㊁结构正赶上强旺更生的时期;拥有文化自信和自觉艺术追求的新建筑师群体正在产生㊂七㊁作文(70分)20.略语文Ⅱ(附加题)一㊁阅读材料,完成21~23题㊂(10分)书‘汤海秋诗集“后龚自珍人以诗名,诗尤以人名㊂唐大家若李㊁杜㊁韩及昌谷㊁玉溪;及宋㊁元,眉山㊁涪陵㊁遗山,当代吴娄东,皆诗与人为一㊂人外无诗,诗外无人,其面目也完㊂益阳汤鹏,海秋其字,有诗三千余篇,芟而存之二千余篇,评者无虑数十家,最后属龚巩祚作一言,巩祚亦一言而已,曰:完㊂何以谓之完也?海秋心迹尽在是所欲言者在是所不欲言而卒不能不言在是所不欲言而竟不言于所不言求其言亦在是㊂要不肯挦撦①他人之言以为己言,任举一篇,无论识与不识,曰:此汤益阳之诗㊂ [注]①挦撦:摘取㊂21.用斜线 /”给上面文言文中的画线部分断句㊂(限∙4∙处∙)(4分)22.文中昌谷㊁玉溪的本名分别是 ▲ ㊁ ▲ ㊂(2分)23.根据材料,用自己的话概括汤鹏诗作的特点㊂(4分)二㊁名著阅读题(15分)24.下列对有关名著的说明,不正确的两项∙∙∙∙∙∙是(5分)(选择两项且全答对得5分,选择两项只答对一项得2分,其余情况得0分)A.‘三国演义“中,曹操攻陷徐州后,派遣张辽劝降陷入困境中的关羽,关羽提出了 卸甲”的三个条件,这一情节突出了关羽的忠义形象㊂B.‘茶馆“中,秦仲义说: 只有那么办,国家才能富强!”他说的 那么办”是指通过收回房子㊁卖掉土地等途径,筹集资金来开办工厂㊂C.‘风波“中,七斤曾经在喝醉后骂有些遗老臭味的赵七爷是 贱胎”,并在革命后很快剪掉了辫子,这体现了他是一个具有新思想的农民㊂D.‘老人与海“中,老渔夫圣地亚哥奋力捕到的大马林鱼被鲨鱼给毁了,回到港口后,男孩遗憾地对他说,以后他们俩不能一起捕鱼了㊂E.‘欧也妮㊃葛朗台“中,葛朗台太太的性情极好,从不向丈夫要钱,她有着天使般的温柔,她的善良和忍让反衬了葛朗台的冷漠和贪婪㊂25.简答题(10分)(1)‘红楼梦“ 散余资贾母明大义,复世职政老沐天恩”一回中,贾母得知府中库藏已空㊁入不敷出的实情后,将自己多年的积蓄拿出来,以渡难关㊂请结合这一情节,分析贾母的形象特点㊂(6分)(2)巴金的‘家“中,梅表姐因躲避炮火再次来到高家,她在花园里看见觉新站在树下,她嘴唇微微动一下,像要说话”,最终还是 转过身默默地走了”㊂请说明梅表姐为什么会有这样的举动㊂(4分)三㊁材料概括分析题(15分) 阅读材料,完成26~28题㊂ 1982年,一位美国教授在校园BBS上建议用字符 :-)”来表示笑话,这个由ASCII(美国标准信息交换代码)元素组成的笑脸大大激发了人们的想象力和生产力,此后各种各样的表情符号被源源不断地创造出来,因此它被称为 改变历史的一张笑脸”㊂颜文字是它的升级版,其显著特点是用键盘符㊁标点或者两者的结合体模拟出人的面部和某种身体姿态,用来方便快捷地表达和传递情绪㊂以QQ表情中的基础默认表情 小黄脸”为代表的表情符号,被称作绘文字,呲牙 ”㊁偷笑 ”㊁笑哭 ”等惟妙惟肖的符号简洁而又形象,极大丰富了聊天时的选择和乐趣㊂以90后㊁00后为代表的年轻群体成为网络主力军后,一些真人表情在网络上竞相出彩,GIF动画表情的传播也如火如荼,标志着网络表情符号进入自定义创作发展阶段㊂在网络社交中,网络表情符号比文字有着先天的优势㊂从接受者方面说,解读文字容易对信息发送者的语气㊁态度产生理解偏差,而图文搭配的表情图像,会让信息的准确度和可接受度更加凸显,使传播效果事半功倍㊂表情符号还使人们在交流时打破了时间和空间上的限制,建立欢快轻松的 在场”语境,可以加强交流的互动性㊂其实人的社会互动也是一场关于 自我呈现”的表演㊂长期处于表情符号丰富的交流语境中,通过独特的表情符号进行自我表达,展现个性,会不知不觉地将 我”塑造为社交所需要的形象㊂(节选自胡远珍‘网络社交中表情符号的表达与象征意义分析“,有删改)26.网络表情符号经历了哪几个发展阶段?(4分)27.请简要概括网络表情符号的特点㊂(5分)28.根据材料,概括网络表情符号流行的原因㊂(6分)语文Ⅱ(附加题)参考答案一㊁阅读材料,完成21~23题㊂(10分)21.海秋心迹尽在是/所欲言者在是/所不欲言而卒不能不言在是/所不欲言而竟不言/于所不言求其言亦在是㊂22.李贺㊁李商隐23.言为心声,诗如其人;不沿袭他人之言㊂二㊁名著阅读题(15分)24.CD25.(1)处变不惊,性格坚强;处置果断,能力出众;分配得当,处事公平;轻财重义,顾全大局㊂(2)心中仍有旧情,想跟心上人说话;婚姻现状和礼教束缚,不便单独与觉新见面㊂三㊁材料概括分析题(15分)26.ASCII元素组成的表情符号;颜文字;绘文字;自定义表情符号㊂27.直观形象;方便快捷;简洁;时尚;娱乐性强㊂28.信息传播具有更高的准确度和可接受度;建立 在场”语境,加强交流的互动性;有助于个体的自我表达㊂英 语 试 题第一部分 听力(共两节,满分20分) 做题时,先将答案标在试卷上㊂录音内容结束后,你将有两分钟的时间将试卷上的答案转涂到答题卡上㊂第一节 (共5小题;每小题1分,满分5分) 听下面5段对话㊂每段对话后有一个小题,从题中所给的A㊁B㊁C三个选项中选出最佳选项㊂听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题㊂每段对话仅读一遍㊂例:How much is the shirt?A.£19.15.B.£9.18.C.£9.15.答案是C㊂1.What will James do tomorrow?A.Watch a TV program.B.Give a talk.C.Write a report.2.What can we say about the woman?A.She’s generous.B.She’s curious.C.She’s helpful.3.When does the train leave?A.At6∶30.B.At8∶30.C.At10∶30.4.How does the woman go to work?A.By car.B.On foot.C.By bike.5.What is the probable relationship between the speakers?A.Classmates.B.Teacher and student.C.Doctor and patient.第二节 (共15小题;每小题1分,满分15分) 听下面5段对话或独白㊂每段对话或独白后有几个小题,从题中所给的A㊁B㊁C三个选项中选出最佳选项㊂听每段对话或独白前,你将有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间㊂每段对话或独白读两遍㊂听第6段材料,回答第6㊁7题㊂。
苏州大学2018届高考考前指导卷2(终稿)

(2)①若
,求
的最大值;
②在 x轴上是否存在一点 P,使得
为定值,若存在,求出点 P;若不存在,请说明理由.
y
B
OQ
x
A
(第 18题图)
3
19.(本小题满分 16分) 已知数列{an},{bn}满足:bn=an+1-an(n∈N*).
(1)若 a1=1,bn=n,求数列{an}的通项公式;
(2)若 bn+1bn-1=bn(n≥2),且 b1=1,b2=2.
(1)若点 M 是线段 BC的中点,
,求 b的值;
(2)若
,求△ ABC的面积.
,
.
2
17.(本小题满分 14分) 某校在圆心角为直角,半径为
的扇形区域内进行野外生存训练.如图所示,在相距
的 A,B
两个位置分别有 300,100名学生,在道路 OB上设置集合地点 D,要求所有学生沿最短路径到 D点集
S← 2I+1 I← I+2 End While Print S (第 5题图)
为▲.
8.设 Sn是等比数列{an}的前 n项和,若满足 a4+3a11=0,则
▲.
9.已知
,函数
和
存在相同的极值点,则
▲.
10.在平面直角坐标系 xOy中,已知圆 C:x2+(y-1)2=4,若等边△PAB的一边 AB为圆 C的一条弦,
所以
平面 CDE.
(2)在△ABD中,因为∠ABD=60º,BD=2AB,
所以
,即
,
因为
,所以
又
,所以
平面 ACD,
又
面 ABC,所以平面 ABC⊥平面 ACD.
16.解(1)因为点 M 是线段 来自C的中点,,设,则
最新-2018苏州高三物理二模试题 精品

2018年苏州市高三教学情况调查物理本试卷分第1卷(选择题)和第Ⅱ卷(非选择题)两部分,共150分.考试时间120分钟.第1卷(选择题共40分)选择题部分共10小题,每小题4分,共40分.在每小题给出的四个选项中,有的小题只有一个选项正确,有的小题有多个选项正确.全部选对的得4分,选不全的得2分,有选错的或不答的得O分.1.1964年至1967年6月我国第一颗原子弹和第一颗氢弹相继试验成功.1999年9月18日,中共中央、国务院、中央军委隆重表彰为研制“两弹一星”作出杰出贡献的科学家.下列核反应方程中属于“两弹”的基本反应方程式是2.如图所示,半圆形玻璃砖abc,o为圆心.c为圆弧顶点.一束很细的平行白光束沿co方向射人玻璃砖.现保持光的方向不变.使玻璃砖绕o点沿顺时针方向转动,则首先在界面ab上发生全反射的应是白光中的A.红光部分,因为玻璃对红光折射率大B.红光部分,因为玻璃对红光折射率小C.紫光部分,因为玻璃对紫光折射率大D.紫光部分,因为玻璃对紫光折射率小3.历史上,为了说明光的性质,牛顿提出了光的微粒说,惠更斯提出了光的波动说,如今人们对光的性质有了更进一步的认识.在下面四幅示意图中所表示的实验,能说明光的性质的是4.微波炉是一种利用微波的电磁能加热食物的新型炊具.微波的电磁作用使食物内的分子高频地运动而产生热,并能最大限度地保存食物中的维生素.下列说法中正确的是ABCD.实验中,微波比光波更容易产生明显的衍射现象5.在用油膜法估测分子的大小的实验中,若已知油的摩尔质量为M,密度为ρ,油滴N.以上各量质量为m,油滴在液面上扩散后的最大面积为S,阿伏加德罗常数为A 均为国际单位,那么6.对于一定质量的理想气体,下列说法中正确的是A. 如果体积减小,气体分子在单位时间内作用于器壁单位面积的冲量一定增大B.如果压强增大,气体分子在单位时间内作用于器壁单位面积的冲量一定增大C.如果密度不变,气体分子在单位时间内作用于器壁单位面积的冲量一定不变D.如果温度不变,气体分子在单位时间内作用于器壁单位面积的冲量一定不变7.当氢原子的核外电子从高能级b向低能级a跃迁时,电子动能8.两列简谐横波在空间叠加,其中简谐横波a(图中虚线所示)沿x轴的正方向传播,简谐横波b(图中实线所示)沿x轴的负方向传播,波速都是20m/s.当t=O时,这两列波的波动图像如图所示,那么位于x=45m处的质点P第一次到达波峰的时间和第一次处于平衡位置的时间分别是9.图示为一理想变压器的电路图,图中S为单刀双掷开关,P为滑动变阻器R的滑动头,U1为加在原线圈两端的电压,I1为原线圈中的电流,则下列说法中正确的是A.若保持U1及P的位置不变,S由a合到b时,I1将增大B.若保持U1及P的位置不变,S由b合到a时,R消耗的功率将增大C.若保持U1不变,S接在a处,使P向上滑时,I1将增大D.若保持P的位置不变,S接在a处,使U1增大时,I1将增大10.地面附近空间中存在着水平方向的匀强电场和匀强磁场,已知磁场方向垂直纸面向里,一个带电油滴能沿一条与竖直方向成α角的直线MN运动,如图所示.则以下判断中正确的是A.如果油滴带正电,它是从M点运动到N点B.如果油滴带正电,它是从N点运动到M点C.如果电场方向水平向左,油滴是从M点运动到N点D.如果电场方向水平向右,油滴是从M点运动到N点2018年苏州市高三教学情况调查物 理第Ⅱ卷(非选择题 共110分)非选择题部分共8小题,共110分.把答案填在题中的横线上或按题目要求作答.解答题应写出必要的文字说明、方程式和重要的演算步骤.只写出最后答案的不能得分.有数值计算的题,答案中必须明确写出数值和单位.11.(8分)如图是多用电表的示意图,现用它测量一个约为20~30Ω定值电阻的阻值,具体测量步骤如下:12.(10分) 如图所示,A 为放置在气垫导轨上的滑块,B 为砝码.某同学用它来探究物体运动的加速度a 与所受外力F的关系时,保持滑块的质量M 不变,通过增减砝码数改变细绳对滑块拉力F 的大小.再由打点计时器对与滑块相连的纸带打点,从而出计算滑块的加速度,并将有关实验数据记入下表.该同学在比较表中的数据时发现:前3组数据,砝码的重力G 跟滑块的加速度a 基AB本成正比关系;而后3组数据,砝码的重力G 跟滑块的加速度a 则明显不成正比关系.试通过列式分析,说明造成这一情况的原因.13.(14分)有些人,如电梯修理员、牵引专家等,常需要知道绳(或金属线)中的张力T ,可又不便到绳(或线)的自由端去测量.现某家公司制造了一种夹在绳上的仪表(图中B 、C 为该夹子的横截面).测量时,只要如图示那样用一硬杆竖直向上作用在绳上的某点A ,使绳产生一个微小偏移量a ,借助仪表很容易测出这时绳对硬杆的压力F .现测得该微小偏移量为a =12mm ,BC 间的距离为2L =250mm ,绳对横杆的压力为F =300N ,试求绳中的张力T .排版注意:图中英文字母均改为斜体→→14. (14分) 电磁炮的基本原理如图所示,把待发射的炮弹(导体)放置在强磁场中的两条平行导轨(导轨与水平方向成α角)上,磁场和导轨平面垂直.若给导轨以很大的电流I ,使炮弹作为一个载流导体在磁场的作用下,沿导轨作加速运动,以某一速度发射出去.已知匀强磁场的磁感强度为B ,两导轨间的距离为L ,磁场中导轨的长度为s ,炮弹的质量为m ,炮弹和导轨间摩擦不计.试问:在导轨与水平方向夹角一定时,要想提高炮弹的发射时的速度0v ,从设计角度看可以怎么办(通过列式分析,加以说明)?排版注意:图中→→2L①磁感线的方向改画为垂直于导轨; ②导轨与水平面间加画一α角。
江苏省苏州2018届高考数学考前指导卷Word版含解斩

江苏省苏州2018届高考数学考前指导卷一、填空题:(本大题共14小题,每小题5分,共70分)1. 已知集合{}{}21,0,2,2,A B a =-=,若B A ⊆,则实数a 的值为 .2. 已知()()2210,i m i i -+=是虚数单位,则实数m 的值为 .3.一个总体分为A,B 两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B 层中每个个体抽到的概率都为112,则总体中的个数为 .4.已知双曲线()22210y x b b -=>则b = . 5.右图是一个算法的流程图,则输出k 的值是 .6.若{},0,1,2a b ∈,则函数()22f x ax x b =++有零点的概率为 .7.设实数,x y 满足约束条件236y x x y y x ≤⎧⎪+≥⎨⎪≥-⎩,则目标函数2z x y =+的最小值为 .8.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺133寸,容纳谷2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛 1.62≈立方尺,3π≈),则圆柱底面周长约为 丈.9.等比数列{}n a 的前n 项和为n S ,公比1q ≠,若3232S S =,则q 的值为 . 10.已知圆()()22:116C x y a -+-=,若直线20ax y +-=与圆C 相交于A,B 两点,且CA CB ⊥,则实数a 的值为 . 11.设点()1,2A ,非零向量(),a m n =,若对于直线340x y +-=上任意一点P ,AP a ⋅恒为定值,则m n= . 12.已知0,0a b >>,且11121a b b +=++,则2a b +的最小值为 . 13.已知函数()2,0,0x x x e f x x x e ⎧+<⎪⎪=⎨⎪≥⎪⎩,若()()()()123123f x f x f x x x x ==<<,则()21f x x 的取值范围为 .14.在ABC ∆中,已知3sin 2sin C B =,点M,N 分别是边AC,AB 的中点,则BM CN的取值范围为 . 二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.(本题满分14分)已知函数()()21cos .f x x x =(1)求函数()f x 的定义域和最小正周期;(2)当0,2x π⎛⎫∈ ⎪⎝⎭时,求函数()f x 的值域.16.(本题满分14分)如图,在四棱锥S ABCD -中,四边形ABCD 为矩形,E 为SA 的中点,2,3,SB BC SC ==(1)求证://SC 平面BDE ;(2)求证:平面ABCD ⊥平面SAB .17.(本题满分14分)在平面直角坐标系xoy 中,已知点()2,1P 在椭圆()2222:10x y C a b a b +=>>上且离心率为2(1)求椭圆C 的方程;(2)不经过坐标原点O 的直线l 与椭圆C 交于A,B 两点(不与点P 重合),且线段AB 的中为D ,直线OD 的斜率为1,记直线PA ,PB 的斜率分别为12,k k ,求证:12k k ⋅为定值.18.(本题满分16分)如图,某地区有一块长方形植物园,8ABCD AB =(百米),4BC =(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG 满足下列要求:E 在CD 的延长线上,H 在BA 的延长线上,0.5DE =(百米),4AH =(百米),N 为AH 的中点,,FN AH EF ⊥为曲线段,它上面的任意一点到AD 与AH 的距离乘积为定值,,FG GH 均为线段,,0.5GH HA GH ⊥=(百米).(1)求四边形FGHN 的面积;(2)已知音乐广场M 在AB 上,2AM =(百米),若计划在EFG 的某一处P 开一个植物园大门,在原植物园ABCD 内选一点Q ,为中心建一个休息区,使得QM PM =,且90QMP ∠=,问点P 在何处,AQ 最小.19.(本题满分16分)已知函数()212ln x f x x +=,且方程()0f x m -=有两个相异实数根()1212,.x x x x >. (1)求函数()f x 的单调递增区间;(2)求实数m 的取值范围;(3)证明:2212122x x x x +>.20.(本题满分16分)已知数列{}n c 的前n 项和为n S ,满足()22.n n S n c =+(1)求1c 的值,并证明数列{}n c 是等差数列;(2)若2n n n c a =,且数列{}n a 的最大项为54. ①求数列{}n a 的通项公式;②若存在正整数x ,使,,m n k a a xa 成等差数列(),,,m n k m n k N *<<∈,则当()m n k T x a a xa =++取得最大值时,求x 的最小值.江苏省苏州2018届高考数学考前指导卷答案。
江苏省苏州大学高三数学考前指导试题(含解析)
2017年江苏省苏州大学高考数学考前指导试卷一、填空题:(本大题共14小题,每小题5分,共70分)1.已知集合A={﹣1,0,2},B={2,a2},若B⊆A,则实数a的值为.2.已知(2﹣i)(m+2i)=10,i是虚数单位,则实数m的值为.3.一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中每个个体被抽到的概率都为,则总体中的个体数为.4.已知双曲线的离心率为,则b= .5.如图是一个算法流程图,则输出的k值是6.若a,b∈{0,1,2},则函数f(x)=ax2+2x+b有零点的概率为.7.设变量x,y满足约束条件,则目标函数z=2x+y的最小值为.8.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺寸,容纳谷2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底面周长约为丈.9.等比数列{a n}的前n项和为S n,公比q≠1,若,则q的值为.10.已知圆C:(x﹣1)2+(y﹣a)2=16,若直线ax+y﹣2=0与圆C相交于AB两点,且CA⊥CB,则实数a的值是.11.设点A(1,2),非零向量,若对于直线3x+y﹣4=0上任意一点P,恒为定值,则= .12.若a>0,b>0,且,则a+2b的最小值为.13.已知函数,若f(x1)=f(x2)=f(x3)(x1<x2<x3),则的取值范围为.14.在△ABC中,若3sinC=2sinB,点E,F分别是AC,AB的中点,则的取值范围为.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.已知函数f(x)=(1+tanx)cos2x.(Ⅰ)求函数f(x)的定义域和最小正周期;(Ⅱ)当x∈(0,)时,求函数f(x)的值域.16.如图,在四棱锥S﹣ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,.(Ⅰ)求证:SC∥平面BDE;(Ⅱ)求证:平面ABCD⊥平面SAB.17.在平面直角坐标系xoy中,已知点P(2,1)在椭圆C:上且离心率为.(1)求椭圆C的方程;(2)不经过坐标原点O的直线l与椭圆C交于A,B两点(不与点P重合),且线段AB的中为D,直线OD的斜率为1,记直线PA,PB的斜率分别为k1,k2,求证:k1•k2为定值.18.如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).(1)求四边形FGHN的面积;(2)已知音乐广场M在AB上,AM=2(百米),若计划在EFG的某一处P开一个植物园大门,在原植物园ABCD内选一点Q,为中心建一个休息区,使得QM=PM,且∠QMP=90°,问点P在何处,AQ最小.19.已知函数f(x)=,且方程f(x)﹣m=0有两个相异实数根x1,x2(x1>x2).(1)求函数f(x)的单调递增区间;(2)求实数m的取值范围;(3)证明:x12x2+x1x22>2.20.已知数列{c n}的前n项和为S n,满足2S n=n(c n+2).(1)求c1的值,并证明数列{c n}是等差数列;(2)若,且数列{a n}的最大项为.①求数列{a n}的通项公式;②若存在正整数x,使a m,a n,xa k成等差数列(m<n<k,m,n,k∈N*),则当T(x)=a m+a n+xa k 取得最大值时,求x的最小值.2017年江苏省苏州大学高考数学考前指导试卷参考答案与试题解析一、填空题:(本大题共14小题,每小题5分,共70分)1.已知集合A={﹣1,0,2},B={2,a2},若B⊆A,则实数a的值为0 .【考点】18:集合的包含关系判断及应用.【分析】由B⊆A,可得a2=0,解得a.【解答】解:∵B⊆A,∴a2=0,解得a=0.故答案为:0.2.已知(2﹣i)(m+2i)=10,i是虚数单位,则实数m的值为 4 .【考点】A5:复数代数形式的乘除运算.【分析】利用复数的运算法则、复数相等即可得出.【解答】解:(2﹣i)(m+2i)=10,化为:2m﹣8+(4﹣m)i=0,∴2m﹣8=4﹣m=0,解得m=4.故答案为:4.3.一个总体分为A,B两层,用分层抽样方法从总体中抽取一个容量为10的样本.已知B层中每个个体被抽到的概率都为,则总体中的个体数为120 .【考点】B3:分层抽样方法;C7:等可能事件的概率.【分析】本题考查分层抽样,抽样过程中每个个体被抽到的可能性相同,这是解决一部分抽样问题的依据,样本容量、总体个数、每个个体被抽到的概率,这三者可以知二求一.【解答】解:∵B层中每个个体被抽到的概率都为,∴总体中每个个体被抽到的概率是,∴由分层抽样是等概率抽样得总体中的个体数为10÷=120故答案为:120.4.已知双曲线的离心率为,则b= .【考点】KC:双曲线的简单性质.【分析】利用双曲线的离心率列出关系式求解即可.【解答】解:双曲线,可得a=1,e=,可得c=,则b==.故答案为:.5.如图是一个算法流程图,则输出的k值是11【考点】EF:程序框图.【分析】先判断程序框图的结构为直到型循环结构,然后按照程序框图进行循环,直到满足条件时输出k的值即可.【解答】解:根据程序框图分析,本框图为直到型循环结构第1次循环:k=2 S=4﹣5=﹣1 k=﹣1第2次循环:S=1﹣5=﹣4 k=﹣4第3次循环:S=16﹣5=11 k=11第3次循环:S=121﹣5=106 满足条件S>100,跳出循环输出k的值为11.故答案为:11.6.若a,b∈{0,1,2},则函数f(x)=ax2+2x+b有零点的概率为.【考点】CB:古典概型及其概率计算公式.【分析】当函数f(x)=ax2+2x+b没有零点时,a≠0,且△=4﹣4ab<0,即ab>1,由此利用对立事件概率计算公式能求出函数f(x)=ax2+2x+b有零点的概率.【解答】解:a,b∈{0,1,2},当函数f(x)=ax2+2x+b没有零点时,a≠0,且△=4﹣4ab<0,即ab>1,∴(a,b)有三种情况:(1,2),(2,1),(2,2),基本事件总数n=3×3=9,∴函数f(x)=ax2+2x+b有零点的概率为p=1﹣.故答案为:.7.设变量x,y满足约束条件,则目标函数z=2x+y的最小值为 3 .【考点】7C:简单线性规划.【分析】先根据条件画出可行域,设z=2x+y,再利用几何意义求最值,将最小值转化为y轴上的截距,只需求出直线z=2x+y,过可行域内的点B(1,1)时的最小值,从而得到z最小值即可.【解答】解:设变量x、y满足约束条件,在坐标系中画出可行域△ABC,A(2,0),B(1,1),C(3,3),则目标函数z=2x+y的最小值为3.故答案为:3.8.《九章算术》商功章有题:一圆柱形谷仓,高1丈3尺寸,容纳谷2000斛(1丈=10尺,1尺=10寸,斛为容积单位,1斛≈1.62立方尺,π≈3),则圆柱底面周长约为 5.4 丈.【考点】L2:棱柱的结构特征.【分析】根据圆柱的体积和高计算出圆柱的底面半径,从而求出圆周的底面周长.【解答】解:由题意得,圆柱形谷仓底面半径为r尺,谷仓高h=尺.于是谷仓的体积V==2000×1.62.解得r≈9.∴圆柱圆的周面周长为2πr≈54尺.故答案为:5.4.9.等比数列{a n}的前n项和为S n,公比q≠1,若,则q的值为﹣.【考点】89:等比数列的前n项和.【分析】根据等比数列的前n项和公式,列方程求解即可.【解答】解:等比数列{a n}中,其前n项和为S n,公比q≠1,由得=,整理得2q2﹣q﹣1=0,即(q﹣1)(2q+1)=0,解得q=﹣或q=1(不合题意,舍去),所以q的值为﹣.故答案为:﹣.10.已知圆C:(x﹣1)2+(y﹣a)2=16,若直线ax+y﹣2=0与圆C相交于AB两点,且CA⊥CB,则实数a的值是﹣1 .【考点】J9:直线与圆的位置关系.【分析】求出圆C的圆心C(1,a),半径r=4,由直线ax+y﹣2=0与圆C相交于AB两点,且CA⊥CB,得到AB=4,由此利用圆心C(1,a)到直线AB的距离d==,能求出a.【解答】解:圆C:(x﹣1)2+(y﹣a)2=16的圆心C(1,a),半径r=4,∵直线ax+y﹣2=0与圆C相交于AB两点,且CA⊥CB,∴AB==4,∴圆心C(1,a)到直线AB的距离:d==,解得a=﹣1.故答案为:﹣1.11.设点A(1,2),非零向量,若对于直线3x+y﹣4=0上任意一点P,恒为定值,则= 3 .【考点】9R:平面向量数量积的运算.【分析】设点P(x,y),由点P为直线上的任意一点,表示出向量,由•恒为定值,求出m、n的关系,再计算.【解答】解:设点P(x,y),∵点P为直线3x+y﹣4=0上的任意一点,∴y=4﹣3x,∴=(x﹣1,2﹣3x);又非零向量=(m,n),∴•=m(x﹣1)+n(2﹣3x)=(m﹣3n)x+(2n﹣m),且恒为定值,∴m﹣3n=0,即m=3n;∴==3.故答案为:3.12.若a >0,b >0,且,则a+2b 的最小值为.【考点】7F :基本不等式.【分析】把a+2b 变形为a+2b=,再利用已知可得a+2b=,利用基本不等式即可得出.【解答】解:∵a >0,b >0,且,∴a+2b===﹣==.当且仅当,a >0,b >0,且,即,a=时取等号.∴a+2b 的最小值为.故答案为.13.已知函数,若f (x 1)=f (x 2)=f (x 3)(x 1<x 2<x 3),则的取值范围为 (﹣1,0) .【考点】5B:分段函数的应用.【分析】利用导数法,分析函数的单调性及极值,可得f(x1)=f(x2)=f(x3)∈(0,),即有﹣<x1<﹣,可得==1+,计算即可得到所求范围.【解答】解:函数,∴函数f′(x)=,故当x<0时,函数为增函数,且f(x)<,当0≤x<1时,函数为增函数,且0≤f(x)<,当x≥1时,函数为减函数,且0<f(x)≤,若f(x1)=f(x2)=f(x3)(x1<x2<x3),则f(x1)=f(x2)=f(x3)∈(0,),即﹣<x1<﹣,故==1+∈(﹣1,0),故答案为:(﹣1,0).14.在△ABC中,若3sinC=2sinB,点E,F分别是AC,AB的中点,则的取值范围为.【考点】HP:正弦定理.【分析】由已知及正弦定理得AC=AB,AE=AC,AF=,由余弦定理可求BE2=AB2﹣AB2cosA,CF2=AB2﹣AB2cosA,从而化简可得=,结合范围cosA ∈(﹣1,1),可求的取值范围.【解答】解:∵3sinC=2sinB ,可得:3AB=2AC ,即:AC=AB ,又∵点E ,F 分别是AC ,AB 的中点,∴AE=AC ,AF=,∴在△ABE 中,由余弦定理可得:BE 2=AB 2+AE 2﹣2AB•AEcosA=AB 2+(AB )2﹣2AB•AB•cosA=AB 2﹣AB 2cosA ,在△ACF 中,由余弦定理可得:CF 2=AF 2+AC 2﹣2AF•ACcosA=(AB )2+(AB )2﹣2•AB•AB•cosA=AB 2﹣AB 2cosA ,∴==,∵A ∈(0,π),∴cosA ∈(﹣1,1),可得:∈(,),∴可得: =∈.故答案为:.二、解答题:本大题共6小题,共90分.解答应写出必要的文字说明或推理、验算过程.15.已知函数f (x )=(1+tanx )cos 2x .(Ⅰ)求函数f (x )的定义域和最小正周期;(Ⅱ)当x∈(0,)时,求函数f(x)的值域.【考点】GL:三角函数中的恒等变换应用;H1:三角函数的周期性及其求法.【分析】(1)由二倍角公式和两角和的正弦公式对函数化简,利用周期公式求得函数的最小正周期.(2)根据x的范围确定2x+的范围,进而利用正弦函数的性质求得函数的值域.【解答】解:(Ⅰ)函数f(x)的定义域为{x|x≠+kπ,k∈Z},∵f(x)=(1+tanx)cos2x=cos2x+sinxcosx,=cos2x+sin2x+=sin(2x+)+,∴f(x)的最小正周期为T=π.(Ⅱ)∵x∈(0,),∴<2x+<,∴sin(2x+)∈(﹣,1],∴f(x)∈(0,],即当x∈(0,)时,求函数f(x)的值域为(0,].16.如图,在四棱锥S﹣ABCD中,四边形ABCD为矩形,E为SA的中点,SB=2,BC=3,.(Ⅰ)求证:SC∥平面BDE;(Ⅱ)求证:平面ABCD⊥平面SAB.【考点】LY:平面与平面垂直的判定;LS:直线与平面平行的判定.【分析】(Ⅰ)连接AC交BD于F,则F为AC中点,连接EF,可得EF∥SC,即SC∥平面BDE.(Ⅱ)由SB2+BC2=SC2,得BC⊥SB,又四边形ABCD为矩形,即BC⊥平面SAB,可证平面ABCD ⊥平面SAB.【解答】证明:(Ⅰ)连接AC交BD于F,则F为AC中点,连接EF,∵E为SA的中点,F为AC中点,∴EF∥SC,又EF⊂面BDE,SC⊄面BDE,∴SC∥平面BDE.(Ⅱ)∵SB=2,BC=3,,∴SB2+BC2=SC2,∴BC⊥SB,又四边形ABCD为矩形,∴BC⊥AB,又AB、SB在平面SAB内且相交,∴BC⊥平面SAB,又BC⊂平面ABCD,∴平面ABCD⊥平面SAB.17.在平面直角坐标系xoy中,已知点P(2,1)在椭圆C:上且离心率为.(1)求椭圆C的方程;(2)不经过坐标原点O的直线l与椭圆C交于A,B两点(不与点P重合),且线段AB的中为D,直线OD的斜率为1,记直线PA,PB的斜率分别为k1,k2,求证:k1•k2为定值.【考点】KH:直线与圆锥曲线的综合问题;K4:椭圆的简单性质;KL:直线与椭圆的位置关系.【分析】(1)根据椭圆的离心率公式,将P代入椭圆方程,即可求得a和b的值,求得椭圆方程;(2)根据中点坐标公式及直线斜率公式,求得x1+x2=y1+y2,利用点差法求得直线l的斜率,将直线方程代入椭圆方程,利用韦达定理及直线的斜率公式,即可求得k1•k2为定值.【解答】解:(1)由椭圆的离心率e===,则a2=2b2,由P(2,1)在椭圆上,则,解得:b2=3,则a2=6,∴椭圆的标准方程:;(2)证明:设A(x1,y1),B(x2,y2),则D(,),由直线的斜率为1,则x1+x2=y1+y2,由点A,B在椭圆上,则,,两式相减整理得:,x1﹣x2+2(y1﹣y2)=0,则=﹣,设直线l的方程y=﹣x+t,,整理得:3x2﹣4tx+4t2﹣12=0,则x1+x2=,x1x2=,则k1•k2==,===,∴k1•k2为定值.18.如图,某地区有一块长方形植物园ABCD,AB=8(百米),BC=4(百米),植物园西侧有一块荒地,现计划利用该荒地扩大植物园面积,使得新的植物园为HBCEFG满足下列要求:E在CD的延长线上,H在BA的延长线上,DE=0.5(百米),AH=4(百米),N为AH的中点,FN⊥AH,EF为曲线段,它上面的任意一点到AD与AH的距离乘积为定值,FG,GH均为线段,GH⊥HA,GH=0.5(百米).(1)求四边形FGHN的面积;(2)已知音乐广场M在AB上,AM=2(百米),若计划在EFG的某一处P开一个植物园大门,在原植物园ABCD内选一点Q,为中心建一个休息区,使得QM=PM,且∠QMP=90°,问点P在何处,AQ最小.【考点】5C:根据实际问题选择函数类型.【分析】(1)建立坐标系,根据E点坐标得出曲线EF的方程,从而得出F点坐标,代入梯形的面积公式即可;(2)设P(x,y),用x,y表示出,,根据Q点位置求出x的范围得出P在曲线EF上,利用距离公式和基本不等式的性质得出AQ最小时的x的值即可得出P点位置.【解答】解:(1)以A为原点,以AB,AD所在直线为坐标轴建立平面直角坐标系xOy,如图所示:则E(﹣,4),∴曲线EF的方程为y=﹣,∴F(﹣2,1),N(﹣2,0),H(﹣4,0),G(﹣4,),∴FN=1,GH=,HN=2,∴四边形FGHN的面积为S==(平方百米).(2)设P(x,y),则=(x﹣2,y),=(y,2﹣x),=(2+y,2﹣x),∴,解得﹣2≤x≤2,∴P点在曲线EF上,﹣2≤x≤﹣,∴y=﹣,∴|AQ|=====﹣x﹣+2≥2+2,当且仅当﹣x=即x=﹣时取等号.∴当P为(﹣,﹣)时,|AQ|最小.19.已知函数f(x)=,且方程f(x)﹣m=0有两个相异实数根x1,x2(x1>x2).(1)求函数f(x)的单调递增区间;(2)求实数m的取值范围;(3)证明:x12x2+x1x22>2.【考点】6B:利用导数研究函数的单调性;6K:导数在最大值、最小值问题中的应用.【分析】(1)求出函数的导数,解关于导函数的不等式,求出函数的递增区间即可;(2)根据函数的单调性求出f(x)的最大值,通过讨论m的范围,结合函数的单调性判断出方程f(x)﹣m=0有两个相异实数根的m的范围即可;(3)由f(x1)=f(x2),得=,令x1=x2t,∵x1>x2,∴t>1,问题转化为证明lnt﹣1>0,即证lnt﹣>0,(*),令g(t)=lnt﹣,根据函数的单调性证明即可.【解答】解:(1)函数f(x)的定义域是(0,+∞),f′(x)=,令f′(x)>0,解得:0<x<1,故f(x)在(0,1)递增;(2)由(1),令f′(x)<0,解得:x>1,故f(x)在(0,1)递增,在(1,+∞)递减,故f(x)max=f(1)=1,①m>1时,f(x)=m无解,②m=1时,f(x)=1有1个解,③m≤0,x∈(1,+∞)时,f(x)>0,f(x)=m无解,x∈(0,1)时,f(x)递增,f(x)=m至多1个解,故x∈(0,+∞)时,f(x)=m至多1个解,④0<m<1时,x∈(0,1)时,f(x)递增,f()=0,f(1)=1,f(x)的图象不间断,f()<m<f(1),f(x)=m在(,1)内有1个解,即在(0,1)内有1个解,x∈(1,+∞)时,f(x)是减函数,先证明lnx≤x,令g(x)=lnx﹣x,则g′(x)=,令g′(x)>0,解得:0<x<e,令g′(x)<0,解得:x>e,故g(x)在(0,e)递增,在(e,+∞)递减,故g(x)max=g(e)=0,故lnx≤x,x∈(1,+∞)时,f(x)=≤<<=,令=m,即x=时,f()<m,又m<f(1),f(x)在(1,+∞)递减,故f(x)=m在(1,)内有1解,即在(1,+∞)内有1解,综上,当且仅当0<m<1时,f(x)=m在(0,+∞)内有2解,实数m的范围是(0,1);(3)由f(x1)=f(x2),得=,令x1=x2t,∵x1>x2,∴t>1,=1+2lnx2,则lnx2=lnt﹣,下面证明x1x2>1,∵lnx1+lnx2=2lnx2+lnt=lnt﹣1,故只需证明lnt﹣1>0,即证lnt﹣>0,(*),令g(t)=lnt﹣,∵g′(t)=>0,∴g(t)在(1,+∞)递增,g(t)在(0,+∞)上的图象不间断,则g(t)>g(1)=0,(*)成立,故x1x2>1,由基本不等式得x1+x2>2>2,故x12x2+x1x22>2.20.已知数列{c n}的前n项和为S n,满足2S n=n(c n+2).(1)求c1的值,并证明数列{c n}是等差数列;(2)若,且数列{a n}的最大项为.①求数列{a n}的通项公式;②若存在正整数x,使a m,a n,xa k成等差数列(m<n<k,m,n,k∈N*),则当T(x)=a m+a n+xa k 取得最大值时,求x的最小值.【考点】8H:数列递推式;8E:数列的求和.【分析】(1)2S n=n(c n+2),2S1=2c1=c1+2,解得c1=2,n≥2时,2c n=2S n﹣2S n﹣1.化为:(n﹣2)c n﹣(n﹣1)c n﹣1+2=0.可得(n﹣1)c n+1﹣nc n+2=0,相减可得:2c n=c n+1+c n﹣1.即可证明.(2)①设数列{c n}的公差为d,则a n=.对d分类讨论,d≤0时舍去,d>0,a n+1﹣a n=<0,在n≥2时恒成立,可得a2为最大值.由a2==,解得d.可得a n.②存在正整数x,使a m,a n,xa k成等差数列(m<n<k,m,n,k∈N*),可得2a n=a m+xa k,T(x)=a m+a n+xa k=3a n,由①可知:a2最大,首先考察a2.此时xa k=2a2﹣a1.即=,解得x=(k≥3).利用其单调性即可得出.【解答】解:(1)∵2S n=n(c n+2),∴2S1=2c1=c1+2,解得c1=2,n≥2时,2c n=2S n﹣2S n﹣1=n(c n+2)﹣(n﹣1)(c n﹣1+2).化为:(n﹣2)c n﹣(n﹣1)c n﹣1+2=0.∴(n﹣1)c n+1﹣nc n+2=0,相减可得:2c n=c n+1+c n﹣1.∴数列{c n}是等差数列,首项为2.(2)①设数列{c n}的公差为d,则a n=.若d≤0,则a n=≤a1=1,与已知数列{a n}的最大项为矛盾.若d>0,a n+1﹣a n=﹣=<0,在n≥2时恒成立,可得a2为最大值.由a2==,解得d=3.∴a n=.②∵存在正整数x,使a m,a n,xa k成等差数列(m<n<k,m,n,k∈N*),∴2a n=a m+xa k,T(x)=a m+a n+xa k=3a n,由①可知:a2最大,首先考察a2.此时xa k=2a2﹣a1=﹣1=.即=,解得x=(k≥3).考察3k﹣1=8,11,14,17,….当k=11时,x取得最小值,x==96∈N*.∴当T(x)=a m+a n+xa k取得最大值时,x的最小值为96.- 21 -。
苏州大学2017届高考考前指导卷2(终稿)PDF
2
17. (本小题满分 14 分)
某油库的容量为 31 万吨,年初储油量为 10 万吨,从年初起计划每月初先购进石油 m 万吨, 然后再调出一部分石油来满足区域内和区域外的需求.若区域内每月用石油 1 万吨,区域外 前 x 个月的需求量 y (万吨)与 x 的函数关系为 y 5 前 4 个月区域外的需求量为 15 万吨.
4 3 . 3
x2 y 2 3 2 1 a b 0 的离心率是 ,右准线的方程 2 2 a b
1 (2)已知点 P ,2 ,过 x 轴上的一个定点 M 作直线 l 与椭圆 C 交于 A,B 两点,若三条直 2
线 PA,PM,PB 的斜率成等差数列,求点 M 的坐标.
10. 在△ABC 中, ∠ABC = 120, AB = 2, BC = 3, D, E 分别是边 AC 上的两个三等分点, 则 BD BE
a8 2, S 4 4 ,则 S8 a4
▲ .
数 ,则实数的最小值是 ▲ . 的值为 ▲ .
11.已知直线 l : x 3 y 1 0 ,圆 C: x y 2ax 2ay 1 2a (a 0) ,过原点的直线 l1 与
a 3b≤t 恒成立,则 t 的 c 在区间 (0,1) 内取极大值, 在区 间 (1,2) 内取极小值,若 3 2
2a b 的最大值为 ▲ . a b a b2
2
▲ .
▲ .
1
二、解答题:本大题共 6 小题,共计 90 分.请在答题卡指定区域内 作答,解答时应写出必要的 ........ 文字说明、证明过程或演算步骤. 15. (本小题满分 14 分) 已知函数 f ( x ) 2sin( x
2018全国著名重点中学领航高考冲刺试卷(江苏卷二)(每题均有详细解答)
全国著名重点中学领航高考冲刺试卷数 学(江苏卷)2命题:王建宏【命题报告】 本套试卷在命题前,通过学习了实施新课标高考的四个省区的高考试题,对新课标高考的热点、难点和重点进行了认真细致的研究.命题时,注重对数学基础知识的全面考查的同时又兼顾考查学生的思维能力.在试题的设计上,结合新课标高考的特点进行了一些创新尝试,注重设置情景比较新颖的题目,并对江苏新课标高考作出了大胆的预测.比如第5题是将平面几何的性质与几何概型相结合的题,第5题是一道将集合与椭圆知识相结合的问题.命题时还在知识点的交汇点处设计试题,强调知识的整合,比如第4题是向量与三角函数相结合,注重开放性、探究性的考查,如20题,21题,总之本套试卷很好地代表了高考的命题趋势和方向.本试卷分为第I 卷(选择题)和第II 卷(非选择题)两部分.满分160分.考试时间120分钟.第I 卷(选择题 共40分)一、选择题:本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的. 1.集合{}||1|2M x x =-<,{}2|0N x ax x c =-+≥,且MN =∅,M N R =,则有a c -=( )A .-2B .2C . 1D .-12.函数()f x =的定义域为( )A . (1,2) B. (2,3] C . (1,2] D. (2,3)3.已知{}n a 是等差数列,1356a a a ++=,其前9项和927S =,则其公差d =( ). A .12 B. 1 C. 2 D. 324.已知非零向量AB 与AC 满足()0||||AB AC BC AB AC +=,且12||||AB AC AB AC =-, 则△ABC 为A . 等腰非等边三角形B . 等边三角形C . 三边均不相等的三角形D . 直角三角形 5.若集合{}2|60,A m m m m Z =--<∈,则使得椭圆2213x y m+=的焦点恰在x 轴的m 值的个数是( )A .1B .2C .3D .4 6.下面是一个算法的程序框图,当输入的 值x 为14时,则其输出的结果是( ) A .118 B .121C .14 D .217.如图,设M 是半径为R 的圆周上一个定点,在圆周上等可能地 任取一点N ,连结MN ,则弦MN的概率为( )A .15 B .14 C .13 D .128.已知p :21()ln 222xf x e x x tx =++++在 [1,+∞)内单调递增,:q 5t ≥-,则p 是q 的( )A .充分不必要条件B .必要不充分条件C .充分必要条件D .既不充分也不必要条件第Ⅱ卷(非选择题 共120分)二、填空题:本大题共8小题,每小题5分,共40分.将答案填在题中的横线上.9.i 是虚数单位21ii=+ . 10.如右图所示是一批水果产品中抽样得到数 据的频率分布直方图中,由图上可以看出数据 中频率最大的范围是 .11.设变量x y ,满足约束条件000 1.y x y x y -≥⎧⎪+≥⎨⎪≤≤⎩,, 则目标函数2z x y =+的最大值为 .12.已知7sin cos 5θθ-=,且324θππ≤≤, 则cos2θ的值是 .13.如图,在正三棱柱ABC —A 1B 1C 1中,已知AB =1, D 在BB 1上,且BD =1,若AD 与侧面AA 1CC 1所成的 角为α,则sin α= .14.已知a 、b 、c 是△ABC 中A 、B 、C 的对边, 关于x 的方程b (x 2 + 1 ) + c (x 2– 1 ) –2ax = 0 有两个相等的实根, 且sinCcosA – cosCsinA=0, 则△ABC 的形状为 .15.若不过原点的直线l 与抛物线22(0)y px p =>相交于不同的两点,P Q ,与x 轴,y 轴相交于点,A B ,当,AP PB AQ QB λμ==时,则11λμ+= .16.设M 是具有以下性质的函数()f x 的全体:对于任意s >0,t >0,都有()()f s f t +()f s t <+.给出函数.12)(,log )(221-==xx f x x f 则1()f x M , 2()f x M . (填∈或∉)样本数据三、解答题:本大题共6小题,共80分.解答应写出文字说明、证明过程或演算步骤. 17.(本小题满分12分)已知函数()()3sin f x x πωφ=+,0ω>,1cos 2φ=,0φπ<<,且3,,πωφ依次成等比数列,1sin 1(cos 22)2t ωφω⎛⎫⎛⎫=+-=- ⎪ ⎪⎝⎭⎝⎭+t ,,,a b ,t R ∈,且函数y =a b ,求函数y 的最值.18.(本小题满分12分)某县直学校有2位优秀女教师和3位优秀男教师,某县教育局拟从该学校5位优秀教师中选拔3位作为第三批支教教师.(I) 求选拔的3位教师中恰有1位女教师的概率;(II)求选拔的3位教师中至少有1位女教师的概率.19.(本小题满分14分)若点12,F F 为椭圆22214x y b +=的左右两个焦点,椭圆的左准线为3x =-.(Ⅰ)求椭圆方程;(Ⅱ)过定点(0,3)M 且倾斜角为60︒的直线l 与椭圆交于不同的两点,A B ,求 ||AB 的值.20.(本小题满分14分)已知函数31()43f x x ax =-+与函数3()(0)g x x bx c c =-+>在同一点处取得极小值,1(1)3f =, (Ⅰ)求,a b 的值;(Ⅱ) 记函数()()()F x g x f x =-,求()F x 的单调区间与极值; (Ⅲ)求函数()F x 在点(1,(1))F 处的切线与坐标轴所围成三角形的面积.21.(本小题满分14分)在如图所示的几何体中,BA BC ⊥,AF ⊥平面ABC ,BE ⊥平面ABC ,CD ⊥平面ABC ,112BA BC BE AF CD =====,M 是AC 的中点.(Ⅰ)求证:BM DM ⊥(Ⅱ)求平面DEF 与平面CBA 所成二面角的大小;(Ⅲ)求几何体的体积.22.(本小题满分14分)已知二次函数()f x 的图象的对称轴为1x =-,最小值为1-,且3(0)4f =-,对于正数数列{}n a ,其前n 项和()n n S f a =.(I )求证数列{}n a 为等差数列,并求出它的通项公式; (II )记11()n n n b n N a a ++=∈⋅,求数列{}n b 的前n 项和n S '.(Ⅲ))是否存在等比数列{}n c ,使得211122222n n n n a c a c a c n ++++⋅⋅⋅+=-+对一切正整数n 都成立,并证明你的结论.MABCDEF答案及详细解析:【复习指南】正确处理好必修与选修内容的关系,以必修内容为重点,对于有些选修内容是必修内容的进一步加深,即使是文科的同学也要注意,这也往往是高考解答题命题的重点,如圆锥曲线、导数及应用等. 复习中要加强必修与选修的联系,尽量地把知识系统化.通过认真研读教材及各地模拟试卷,就能体会到高考命题的原则“在知识网络的交汇处设计试题”,备考应加强知识的横向、纵向联系,如函数与不等式、函数与数列、向量与三角、数与形、实际问题与数学模型等,使知识形成网络,不仅加强了对知识的理解和识记,而且有利于解题时进行观察、联想、类比,提高分析、解决问题的能力.比如高考中的压轴题一般是几个重点和热点的有机组合,并设计陷阱,这需要系统掌握知识,综合运用知识,只有在大脑中形成知识网络和体系,才能从不同角度审视问题,将复杂问题分解成简单问题,有利于难题的解决. 1.解题探究:由MN =∅,M N R =可知集合M 与N 是互补关系,先由|1|2x -<得到13x -<<,再利用韦达定理即可求得a c -的值解析:B {}||1|2(1,3)M x x =-<=-,由题意得集合M 与N 是互补关系,所以{}|13M N x x x ==≤-≥或ð,所以13-与是方程20ax x c -+=的两根,所以113a=-+, (1)3c a =-⨯,得12a =,32c =-,故 2.a c -=故应选B . 2.解题探究:本题的入口宽,可以考虑两种方法加以解答.解答本题的关键是熟练掌握函数的及定义域的求法,即根式中的被开方式要为非负数,对数的真数部分要大于零,分母不能不为零. 解法1:A 直接法:由题意可得10x ->,11x -≠,且420x-≥,解得12x <<,选A.解法2:A 代入法:由420x-≥得2x ≤,排除B 、D;当2x =时,lg(1)lg10x -==,无意义,选A. 评析:本题考查函数的解析式,定义域.3.解题探究:由1356a a a ++=与927S =联立即可解得公差d 的值.解析:A 由1359627a a a S ++=⎧⎨=⎩可得11366989272a d a d +=⎧⎪⎨⨯+=⎪⎩,解得12d =,选A . 4.解题探究:本题是向量与三角形结合的题目,向量主要涉及到几何意义、垂直和夹角,根据边角关系来判断三角形的形状.解析:A AB →|AB →| 、AC →|AC →| 分别是、方向的单位向量,向量(AB →|AB →| +AC→|AC →| )在∠BAC 的平分线上,由(AB →|AB →| +AC →|AC →| )·BC →=0知,AB=AC ,由AB →|AB →| ·AC →|AC →| 12=-,可得∠CAB=1200,∴△ABC 为等腰非等边三角形,故选A.5.解题探究:解答本题要熟练掌握一元二次不等式的解法及椭圆的基本概念解析: B 由260m m --<可得23m -<<,又m Z ∈,得1,0,1,2m =-,由椭圆2213x y m+=的焦点恰在x轴上,则有03m <<,所以1,2m =,选B.6.解题探究:本题是算法与指数函数、对数函数的定义域、值域整合问题. 解析: D 输入的值x 为14时,得121log 2,4=则12log 21,=- 112,2y -==选D. 7.解题探究:本题考查几何概率的求法,关键是弄清楚事件的基本结果构成的是长度、面积还是体积。
推荐-苏大附中2018年高考模拟试卷 精品
苏大附中2018年高考模拟试卷数 学本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分。
共150分,考试时间120分钟。
第Ⅰ卷(选择题 共60分)一、选择题:本大题共12小题,每小题5分,共60分。
在每小题给出的四个选项中,有且只有一项是符合题目要求的.请把所选项前的字母填在题后括号内. 1.已知集合A ={1,2},B ={x ︱ax+1=0},若A B =B ,则实数a 的值组成的集合是 ( )A .{1-,2}B .{1,21-}C .{0,—1,21-}D .{1-,21-}2.已知31)4sin(=-πα,)4cos(απ+的值等于 ( )A .322B .322-C .31- D .313. 有50件产品,编号为0,1,2,…,49,现从中抽取5件进行检验,用系统抽样法所抽样本的编号可以是 ( ) A .5,10,15,20,25 B .5,13,21,29,37 C .8,22,23,1,20 D . 0,10,20,30,404. 方程04)1(22=-+-+y x y x 表示的曲线是 ( )A .一直线与一圆B .一直线与一半圆C .两射线与一圆D .两射线与一半圆5. 已知()43+=x x f ,则()11+-x f 的表达式为 ( )A .34+xB .37-xC .131-xD .34-x6.设︱a x -︱<ε,︱a y -︱<ε,则下列不等式中必成立的是 ( ) A .︱y x +︱<ε B .︱y x -︱<ε C .︱y x -︱>2ε D .︱y x -︱<2ε 7.已知a ,b 为两条不同的直线,α,β为两个不同的平面,且a ⊥α,b ⊥β,则下列命题中的假命题是 A .若a ∥b ,则α∥β B .若α⊥β,则a ⊥b ( )C .若a 、b 相交,则α、β相交D .若α、β相交,则a 、b 相交8.某厂产值第二年比第一年增长p %,第三年比第二年增长q %,又这两年的平均增长率为s %,则s 与2qp +的大小关系是 ( )A .s >2qp + B .s =2qp + C .s ≥2qp + D .s ≤2qp + 9.设(1+x )3+(1+x )4+…+(1+x )50=a 0+a 1x+a 2x 2+…+a 50x 50,则a 3等于 ( )A .351CB .451CC .350CD .450C10.将五列车停在五条不同的轨道上,其中a 列车不停在第一轨道上,b 列车不停在第二轨道上,那么不同的停放方法有 ( ) A .120种 B .96种 C .78种 D .72种 11.已知向量=(2,0),向量OC =(2,2),向量CA =()ααsin 2,cos 2,则向量OA 与OB 的夹角的取值范围为 ( )A .⎥⎦⎤⎢⎣⎡4,0π B .⎥⎦⎤⎢⎣⎡125,4ππ C .⎥⎦⎤⎢⎣⎡2,125ππ D .⎥⎦⎤⎢⎣⎡125,12ππ12.设函数()xx x f ++=11,a ,b *R ∈,且a ≠b ,则下列关系式成立的是( )A .⎪⎭⎫⎝⎛+2b a f >()ab f>⎪⎭⎫ ⎝⎛+b a ab f 2B .⎪⎭⎫⎝⎛+2b a f >⎪⎭⎫ ⎝⎛+b a ab f 2>()ab fC . ()ab f>⎪⎭⎫ ⎝⎛+b a ab f 2>⎪⎭⎫ ⎝⎛+2b a f D .⎪⎭⎫ ⎝⎛+b a ab f 2>()ab f >⎪⎭⎫ ⎝⎛+2b a f第Ⅱ卷(非选择题 共90分)二、填空题:本大题共有4小题,每小题4分,共16分.把答案填在题中横线上.13.设p :x <2-或x >1,则使┐p 成立的一个必要不充分条件是 (只需写出一个条件即可) 14.设x 、y 、z 满足x+y+z =1及0≤x ≤1,0≤y ≤2,3y+z ≥2,则2x+6y+4z 的最大值为 . 15.若把一个函数f (x )的图像按=⎪⎭⎫ ⎝⎛--2,3π平移后得到函数y =cosx 的图像,则f (x )的解析式为 .16. 已知α,β是实数,给出四个论断:①︱α+β︱=︱α︱+︱β︱;②︱α—β︱≤︱α+β︱;③︱α︱>22,︱β︱>22;④︱α+β︱>5。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏州大学2018届高考考前指导卷2一、填空题:本大题共14小题,每小题5分,共计70分.不需要写出解答过程,请把答案直接填在答题卡相应位......置上... 1.设全集{|2,}U x x x =∈N ≥,集合2{|5,}A x x x =∈N ≥,则U A =ð ▲ . 2.已知i 是虚数单位,复数(12i)(i)a -+是纯虚数,则实数a 的值为 ▲ . 3.利用计算机随机产生0~1之间的数a ,则事件“310a ->”发生的概率为 ▲ . 4.某地区连续5天的最低气温(单位:C ︒)依次为8,4,1,0,2--,则该组数据的方差为▲ .5.执行如图所示的伪代码,则输出的结果为 ▲ .6.若抛物线24x y =的弦AB 过焦点F ,且AB 的长为6,则弦AB 的中点M 的纵坐标为▲ .7.已知一个正方体的外接球体积为1V ,其内切球体积为2V ,则21V V 的值 为 ▲ .8.设S n 是等比数列{a n }的前n 项和,若满足a 4 + 3a 11= 0,则2114S S = ▲ . 9.已知0a >,函数2()()f x x x a =-和2()(1)g x x a x a =-+-+存在相同的极值点,则a = ▲ .10. 在平面直角坐标系xOy 中,已知圆C :x 2+(y -1)2=4,若等边△PAB 的一边AB 为圆C 的一条弦,则PC 的最大值为 ▲ .11. 若cos 2cos()4ααπ=+,则tan()8απ+= ▲ .12. 已知0,0a b >>,则222a ba b b a+++的最大值为 ▲ . 13. 在ABC △中,90C =∠°,24AB BC ==,,M N 是边AB 上的两个动点,且1MN =,则CM CN ⋅的取值范围为 ▲ .14. 设函数()33,2,,x x x a f x x x a ⎧-<=⎨-⎩,≥若关于x 的不等式()4f x a >在实数集R 上有解,则实数a 的取值范围是▲ .二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内........作答,解答时应写出必要的文字说明、证明过程或演算步骤.15.(本小题满分14分)如图,在多面体ABCDE 中,∠ABD =60º,BD =2AB ,AB ∥CE ,AB ⊥CD , (1)求证://AB 平面CDE ; (2)求证:平面ABC ⊥平面ACD . 16.(本小题满分14分)在△ ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,已知60B =︒,8c =. (1)若点M 是线段BC 的中点,AMBM=b 的值; (2)若12b =,求△ ABC 的面积.C ABDE(第15题图)17.(本小题满分14分)某校在圆心角为直角,半径为1km 的扇形区域内进行野外生存训练.如图所示,在相距1km 的A ,B 两个位置分别有300,100名学生,在道路OB 上设置集合地点D ,要求所有学生沿最短路径到D 点集合,记所有学生行进的总路程为S (km ).(1)设ADO θ∠=,写出S 关于θ的函数表达式; (2)当S 最小时,集合地点D 离点A 多远?18.(本小题满分16分)在平面直角坐标系xOy 中,椭圆2222:1(0)x y C a b a b+=>>的离心率为2,右准线方程为4x =,(,0)Q n 是椭圆C 的长轴上一点(Q 异于长轴端点),过点Q 的直线l 交椭圆于A ,B 两点. (1)求椭圆C 的标准方程;(2)①若2n =,求OA OB ⋅的最大值;②在x 轴上是否存在一点P ,使得PA PB ⋅为定值,若存在,求出点P ;若不存在,请说明理由.19.(本小题满分16分)(第17题图)(第18题图)已知数列{a n },{b n }满足:b n =a n +1-a n (n ∈N *). (1)若a 1=1,b n =n ,求数列{a n }的通项公式; (2)若b n +1b n -1=b n (n ≥2),且b 1=1,b 2=2.①记c n =a 6n -1(n ≥1),求证:数列{c n }为等差数列;②若数列{an n}中任意一项的值均未在该数列中重复出现无数次,求首项a 1应满足的条件.20.(本小题满分16分)已知函数()ln f x x =,1()g x x x=-. (1)①若直线1y kx =+与()ln f x x =的图像相切, 求实数k 的值;②令函数()()()h x f x g x =-,求函数()h x 在区间[,1]a a +上的最大值. (2)已知不等式2()()f x kg x <对任意的(1,)x ??恒成立,求实数k 的范围.苏州大学2018届高考考前指导卷(2)参考答案一、填空题1.{2} 2.2- 3.234.16 5.11 6.2 7. 8.76 9.3 10.4 11.1312.23- 13. 11[,9]4 14. 1(,)(7,)2-∞+∞ 填空题参考解答或提示1. {}{|2}2U A x x x =<∈=N ≤ð.2. (12i)(i)(2)(12)i a a a -+=++-是纯虚数,所以实数a 的值为2-.3.本题为几何概型,因为13103a a ->⇒>,所以所求概率112313P -==. 4. 8(4)(1)0215x +-+-++==,所以该组数据的方差为52211()165i i s x x ==-=∑.5.第1次,33S I ==,;第2次,75S I ==,;第三次,117S I ==,. 6.设1122(,),(,)A x y B x y ,则126AB y y p =++=,所以1262222M y y y +-===. 7.设正方体棱长为a,则333311132224π214π2V R R V R R a ⎛⎫⎪⎛⎫ ⎪===== ⎪⎪⎝⎭ ⎪⎝⎭8.由题意得74430a a q +⋅=,又40a ≠,所以713q =-,321211421411()1731161()3S q S q ---===---. 9. 2322()()2+f x x x a x ax a x =-=-,所以22()34+(3)()f x x ax a x a x a '=-=--;由题意得132a a -=或12a a -=,又0,a >所以3a =. 10.由题意知,在PAC △中,由正弦定理可得,sin sin PC ACPAC APC=∠∠, 所以2sin 4sin sin30PC PAC PAC =∠=∠︒,所以当90PAC ∠=︒时,PC 的最大值为4. 11. cos 2cos(),cos()2cos()48888ααααπππππ=++-=++,所以3sin()sin cos()cos 8888ααππππ+=+所以11tan()833tan8απ+===π.12.设20,20m a b n b a =+>=+>,则22,33m n n ma b --==,所以原式242233222333m n n mn m m n m n --=+=---=-≤, 当且仅当233n mm n=即n,也即b =时等号成立. 13.设MN 的中点为D ,则2221=()()4C M C N CD D M C D D N C D D M C D ⋅+⋅+=-=-, 故只需考虑||CD 的最大、最小值.如图,点D 在D 1及D 2处(1212AD CD AB =⊥,)分别取得最大、最小值.由222137,34CD CD ==,所以CM CN ⋅的取值范围为11[,9]4. 14.由题意知,max ()4f x a >①当0a <时,因为(0)0f =, max ()4f x a >显然成立;②当0a =时,()33,02,0,x x x f x x x ⎧-<=⎨-⎩,≥ m a x ()(1)204f x f a =-=>=, 满足题意;③当0a >时,令332,x x -=解得121,2x x =-=,所以 i )当02a <<时,max max ()(1)24,f x f a =-=>解得102a <<; ii )当2a >时,3()3f x a a <-,由题意334a a a ->,解得7a >; 综上所述,实数a 的取值范围是1(,)(7,)2-∞+∞.二、解答题15. 证明(1)由题意AB ∥CE ,CE ⊂面CDE ,AB ⊄平面CDE ,所以//AB 平面CDE.(2)在△ABD 中,因为∠ABD =60º,BD =2AB ,所以︒⋅⋅-+=60cos 2222BD AB BD AB AD ,即223AB AD =, 因为222BD AD AB =+,所以AB AD ⊥, 又AB CD AD CD D ⊥=,,所以⊥AB 平面ACD , 又⊂AB 面ABC ,所以平面ABC ⊥平面ACD.16. 解(1)因为点M 是线段BC的中点,AMBM=BMx =,则AM =, 又60B =︒,8c =,在△ABM 中,由余弦定理得2236428cos60x x x =+-⨯︒, 解得4x =(负值舍去),则4BM =,8BC =. 所以△ABC 中为正三角形,则8b =.(2)在△ ABC 中,由正弦定理sin sin b c B C =,得8sin 2sin 12c BC b==又b c >,所以B C >,则C为锐角,所以cos C =则()1sin sin sin cos cos sin 2A B C B C B C =+=+=+=, 所以△ ABC的面积1sin 4826S bc A ==⨯=17. 解(1)因为在△OAD 中,θ=∠ADO ,1OA =,所以由正弦定理可知1ππsin sin sin 33AD ODθθ==⎛⎫+ ⎪⎝⎭, 解得πsin 3sin AD OD θθ⎛⎫+ ⎪⎝⎭==,且π2π(,)33θ∈,故πsin 33001001001sin S AD BD θθ⎤⎛⎫+ ⎪⎥⎝⎭⎥=+=-⎢⎥⎢⎥⎣⎦3cos 50sin θθ-=+,π2π(,)33θ∈, (2) 令3cos sin y θθ-=,则有23cos 1sin y θθ-+'= ,当1cos 3θ>时,0y '<; 当1cos 3θ<时,0y '>;可知,当且仅当1cos 3θ=时,y 有最小值22,当AD =时,此时总路程S有最小值50km .答:当集合点D 离出发点A时,总路程最短,其最短总路程为50km .18. 解(1)由c e a ==24a x c==,所以,a =2b =,即椭圆22:184x y C +=.(2)①由已知,(2,0)Q ,当直线AB 垂直于x 轴时,A,(2,B , 2O A O B ⋅=.当直线AB 不垂直于x 轴时,设直线AB :(2)y k x =-,代入22184x y +=得2222(12)8880k x k x k +-+-=,设11(,)A x y ,22(,)B x y ,212121212(2)(2)OA OB x x y y x x k x x ⋅=+=+--2221212(1)2()4k x x k x x k =+-++2222222(1)(88)8241212k k k k k k k +-=-⋅+++224812k k -=+210212k =-+<2. 所以,当直线AB 垂直于x 轴时,OA OB ⋅取到最大值2. ②设点(,0)P t ,11(,)PA x t y =-,22(,)PB x t y =-, 当直线AB 不垂直于y 轴时,设AB :x my n =+,代入22184x y +=得222(2)280m y mny n +++-=,12121212()()()()PA PB x t x t y y my n t my n t y y ⋅=--+=+-+-+221212(1)()()()m y y m n t y y n t =++-++-22222(8)(1)2()()2n m m n n t n t m -+--=+-+ 22222[82()]8()2m n n n t n n t m ---+-=+-+, 令2282()812n n n t n ----=得2384n t n+=, 当2384n t n+=时,2222222883894()()522416n n n PA PB n t n n n n --+⋅=+-=+-=+-.当直线AB 垂直于y 轴时,(2A n ,(,2B n ,238(,0)4n P n + 2222238894()54216n n PA PB n n n n+-⋅=-+=+-.所以,在x 轴上存在点238(,0)4n P n +,使得PA PB ⋅为定值2294516n n+-.方法二 先利用直线l 垂直于x 轴和垂直于y 轴两种情况下PA PB ⋅的值不变,猜想点238(,0)4n P n+,然后再证明此时PA PB ⋅为定值2294516n n+-. 19. 解(1)当n ≥2时,有a n =a 1+(a 2-a 1)+(a 3-a 2)+…+(a n -a n -1)=a 1+b 1+b 2+…+b n -1=n 22-n2+1.又a 1=1也满足上式,所以数列{a n }的通项公式是a n =n 22-n2+1.(2)①因为对任意的n ∈N *,有b n +6=b n +5b n +4=1b n +3=b n +1b n +2=b n , 所以c n +1-c n =a 6n +5-a 6n -1=b 6n -1+b 6n +b 6n +1+b 6n +2+b 6n +3+b 6n +4=1+2+2+1+12+12=7.所以数列{c n }为等差数列.②设c n =a 6(n -1)+i (n ∈N *)(其中i 为常数且i ∈{1,2,3,4,5,6},所以c n +1-c n =a 6(n -1)+6+i -a 6(n -1)+i =b 6(n -1)+i +b 6(n -1)+i +1+b 6(n -1)+i +2+b 6(n -1)+i +3+b 6(n -1)+i +4+b 6(n -1)+i +5=7,即数列{a 6(n -1)+i }均为以7为公差的等差数列.设f k =a 6k +i 6k +i =a i +7k i +6k =76(i +6k )+a i -76i i +6k =76+a i -76ii +6k (其中n =6k +i ,k ≥0,i 为{1,2,3,4,5,6}中一个常数)当a i =76i 时,对任意的n =6k +i ,有a n n =76;当a i ≠76i 时,f k +1-f k =a i -76i i +6(k +1)-a i -76ii +6k =(a i -76i )-6[i +6(k +1)](i +6k ),①若a i >76i ,则对任意的k ∈N 有f k +1<f k ,所以数列{a 6k +i 6k +i }为递减数列;②若a i <76i ,则对任意的k ∈N 有f k +1>f k ,所以数列{a 6k +i 6k +i }为递增数列.综上所述,集合B ={76}∪{43}∪{12}∪{-13}∪{-16}={76,43,12,-13,-16}.当a 1∈B 时,数列{an n}中必有某数重复出现无数次;当a 1 B 时,数列{a 6k +i 6k +i }(i =1,2,3,4,5,6)均为单调数列,任意一个数在这6个数列中最多出现一次,所以数列{an n }任意一项的值均未在该数列中重复出现无数次.20. 解(1)设切点00(,)x y ,1()f x x¢=. 所以000001ln 1x y x y kx k ,,,ìï=ïïï=+íïï=ïïî所以20x e =,21k e =. (2)因为1()g x x x=-在(0,)+?上单调递增,且(1)0g =. 所以1ln ,01,1()()|()|ln ||1ln , 1.x x x xh x f x g x x x x x x x x ìïï+-<<ïïï=-=--=íïï-+?ïïïî当01x <<时,1()ln h x x x x =+-,211()10h x x x¢=++>, 当1x ≥时,1()ln h x x x x=-+,222111()10x x h x x x x -+-¢=--=<, 所以()h x 在(0,1)上单调递增,在(1,)+?上单调递减,且max ()(1)0h x h ==. 当01a <<时,max ()(1)0h x h ==; 当1a ≥时,max 1()()ln h x h a a a a==-+.(3)令1()2ln ()F x x k x x=--,(1,)x ??. 所以222212()(1)kx x kF x k x x x-+-¢=-+=. 设2()2x kx x k j =-+-,①当0k £时,()0F x ¢>,所以()F x 在(1,)+?上单调递增,又(1)0F =,所以不成立; ②当0k >时,对称轴01x k=, 当11k≤时,即1k ≥,(1)220k j =-≤,所以在(1,)+?上,()0x j <,所以()0F x ¢<, 又(1)0F =,所以()0F x <恒成立;当11k>时,即01k <<,(1)220k j =->,所以在(1,)+?上,由()0x j =,0x x =, 所以0(1,)x x Î,()0x j >,即()0F x ¢>;0(,)x x ??,()0x j <,即()0F x ¢<, 所以max 0()()(1)0F x F x F =>=,所以不满足()0F x <恒成立. 综上可知:1k ≥.。
