苏教版数学必修五调研试题
苏教版高中数学必修五模块综合检测卷

高中数学学习资料金戈铁骑整理制作模块综合检测卷(测试时间: 120 分钟评论分值:150分)一、选择题 (每题共 10 个小题,每题共 5 分,共 50 分,在每题给出的四个选项中,只有一项切合题目要求 )1.已知 {a n}为等比数列, a4+a7= 2,a5a6=- 8,则 a1+a10= (D) A.7 B.5 C.- 5D.- 7分析:∵{a n}为等比数列,∴ a4a7=a5a6=- 8.又a4+a7= 2,∴a4=4,a4=- 2,或a7= 4.a7=- 2当 a4=4,a7=- 2 时, a1=- 8, a10=1,∴ a1+a10=- 7;当 a4=- 2,a7= 4 时, a10=- 8,a1=1,∴ a1+a10=- 7.综上, a1+a10=- 7.2.某人投资 10 000 万元,假如年利润利率是5% ,按复利计算,5 年后能回收本利和为 (B)A .10 000×(1+5×5%)B . 10 000× (1+5%)5C .10 000××( 1-4)D .10 000××( 1-5)1-1-分析:注意与每年投入 10 000 万元差别开来.533.在△ ABC 中,已知 cosA =13,sin B =5,则 cosC 的值为 (A)1656A.65B.6516 56 16C.65或65D .- 65512 3分析: ∵cosA =13>0,∴ sin A =13>sin B =5.∴B 为锐角,故 cosB =4进而 =- + =-5.cosC cos(A B) cos Acos16B + sin Asin B = 65.4.若 a<b<0,d>c>0,则不等式① ad>bc ;②a c >cb ;③ a 2>b 2;④ a-d<b -c 中正确的个数是 (C)A .1 个B .2 个C .3 个D .4 个分析:①错,②③④正确. 将 a<b<0 转变为- a>-b>0,可得 (-1 1ad)>(-bc),即 ad<bc ,故知 ①错;由 a<b<0? a >b ,c>0,故 ②正确;由于函数 y =x 2 在(-∞,0)上单一递减,故 ③正确;由 d>c>0,得-d<-c<0,故知 a -d<b -c ,故 ④正确.+5.设 x ,y ∈R ,且 xy -(x +y)=1,以下结论中正确的选项是 (A)C.x+y≤( 2+1)2D.xy≥2 2+2分析:∵1+x+y=xy≤x+y 2,∴ (x+ y)2-4(x+ y)-4≥0.即 x 2+y≥2(1+2)(当 x=y=1+ 2等号建立 ),x+ y 的最小 2(1+2).nπ6.数列 {a n}的通公式a n=ncos 2,其前n和S n,S2 015等于 (D)A.1 006 B.1 008C.- 1 006 D.- 1 008nπ分析:由 a n= ncos 2 可得S2 015=1×0-2×1+3×0+ 4×1+⋯-2 014×1+2 015×0=-2+4-6+⋯-2 010+2 012-2 014=2×503-2 014=- 1 008.7.已知方程 x2+(m+2)x+m+5=0 有两个正根,数m 的取范是 (D)A.(-∞,- 2) B.(-∞,- 4]C.(-5,+∞ ) D.(-5,- 4]分析:方程两根正,Δ≥0,-( m+2)>0,?-5<m≤-4.m+5>08.已知- 1<a+b<3 且 2<a-b<4, 2a+3b 的取范是(D)A. -13,17B. -7,11 2222C. -7,13D. -9,132222分析:用待定系数法可得512a+3b=2(a+b)-2(a-b),-1<a+b< 3,-5<5(a+b)<15,2 22由<-<?12 a b 4-2<-2(a- b)<- 1.913两式相加即得-2<2a+3b<2 .9.已知锐角三角形的边长分别是2,3,x,则 x 的取值范围是(B)A.(1,3) B.( 5,13) C.(0, 5) D.( 13,5)分析:由三角形的三个角为锐角,联合余弦定理的推论可知,22+32- x2>0,22+x2- 32>0,解得 5< x2<13,即 5<x<13.32+x2- 22>0,10.已知函数 f(x)=ax2+2ax+ 4(a>0),若 x1<x2,x1+x2= 0,则(A)A.f(x1)<f(x2) B.f(x1)=f(x2)C.f(x1)>f(x2) D.f(x1)与 f(x2)的大小不可以确立分析:函数 f(x)=ax2+2ax+4(a>0),二次函数的图象张口向上,对称轴为 x=- 1,a>0,又∵ x1+ x2=0,x1与 x2的中点为 0,x1<x2,∴x2到称的距离大于 x1到称的距离.∴ f(x1)<f(x2),故 A. 二、填空(本大共 4 小,每小 5 分,共 20 分,把答案填在中横上 )11.(2013 ·新全国卷Ⅰ)已知角△ ABC 的内角 A,B,C 的2分 a,b,c,23cosA+cos 2A=0,a=7,c=6, b=________.分析:先求出角 A 的余弦,再利用余弦定理求解.2+=得2+2-=,由 23cosA cos 2A 023cosA2cosA 101解得 cosA=±.51∵A 是角,∴ cosA=5.又 a2=b2+c2-2bccosA,∴49=b2+36- 2×b×6×1 5.13∴b=5 或 b=-5 .又∵b> 0,∴ b=5.答案:512. (2013 · 西卷 )察以下等式: 12= 1,12-22=- 3,12-22+32= 6,12-22+32- 42=- 10,⋯,照此律,第n 个等式可____________.分析:当 n 偶数, (12-22)+(32-42+⋯+-2-n2]=)[(n1)-n(n+1);2当 n 奇数, (12-22)+(32-42)+⋯+[(n-2)2-(n-1)2]+n2(n -1)n2n (+ )=-n1.2+n =2答案: 12-22+ 32-42+⋯+ (-1)n +1n 2=(-1)n +1n ( n +1)2y ≤1,.若 量 x , y 足 束条件x +y ≥0,= - 2y 的最13z xx -y -2≤0,大 ________.分析:作出可行域 (如 ),由 z =x - 2y 得 y =12x -2z, 当目函数 C(1,- 1)z 获得最大 ,所以z max =1-2×(-1)=3.答案:314.若b a b +m a + na >b >0,m >0,n >0, a ,b ,a +m ,b + n 由大到小的 序是.分析:用特别 法或作差比 法都很简单得出答案.a a +nb +m b答案: b>b +n>a +m>a三、解答 (本 共 6 小 ,共 80 分.解答 写出文字 明、证明过程或推演步骤 )15.(本小题满分 12 分)等差数列{a n}不是常数列, a5= 10,且 a5,a7,a10是某一等比数列{b n}的第 1,3, 5 项.(1)求数列{a n}的第 20 项;(2)求数列{b n}的通项公式.分析:(1)设数列{a n}的公差为 d,则 a5=10,a7=10+2d,a10=10+5d.由于等比数列 {b n}的第1、3、5项成等比数列,所以 a72= a5a10,即 (10+2d)2=10(10+5d).解得 d=,d= 0(舍去 ).所以 a20=47.5.(2)由 (1)知{a n}为各项非负的数列,所以2b3a73q=b1=a5=2.∴q=±3.又 b1=a5= 10,2-3 n-1∴b n=b1q n 1=±10·2,n∈ N* .216.(本小题满分12 分)(2013 北·京卷 )在△ ABC 中,a=3,b=26,∠B=2∠A.(1)求 cosA 的值;(2)求 c 的值.分析: (1)由正弦定理得:3266sin A =sin 2A,解得cosA=3.(2)由=6? sin A =3,又 ∠B =2∠ A ,cosA33212 2∴cosB =2cosA - 1=3.∴ sin B = 3 ,sin C =sin(A +B)=sin Acos B +cos Asin B = 3 1 6 2 23 ×3+3 × 3=59 3.asin C∴c = sin A =5.17.(本小题满分 14 分)已知对于 x 的不等式 ax 2+2x +c >0 的解集为 -31,12 ,求- cx 2+2x -a >0 的解集.21 11 1分析:由 ax +2x +c > 0 的解集为 -3,2 知 a <0,-3和2是方21 1 21 1 c程 ax +2x +c =0 的两个根,由韦达定理- 3+2=-a ,- 3×2=a ,解得 a =- 12,c =2,∴- cx 2+2x -a >0,即- 2x 2+2x +12>0 亦即x 2-x -6<0.其解集为 (-2,3).18. (本小题满分 14 分 )某营养师要为某个小孩预定午饭和晚餐.已知一个单位的午饭含12 个单位的碳水化合物、 6 个单位的蛋白质和 6 个单位的维生素 C ;一个单位的晚饭含 8 个单位的碳水化合物、 6 个单位的蛋白质和 10 个单位的维生素 C.此外,该小孩这两餐需要的营养中起码含64 个单位的碳水化合物、42 个单位的蛋白质和54 个单位的维生素C.假如一个单位的午饭、晚饭的花费分别是元和 4 元,那么要知足上述的营养要求,而且花销最少,应该为该小孩分别预定多少个单位的午饭和晚饭?分析:方法一设需要预定知足要求的午饭和晚饭分别为 x 个单位和y 个单位,所花的花费为 z 元,则依题意得: z=+4y,且 x,y知足x≥0,y≥0,x≥ 0,y≥0,12x+8y≥64,3x+2y≥16,即6x+6y≥42,x+y≥7,6x+10y≥54,3x+5y≥27.z在可行域的四个极点 A(9, 0),B(4, 3),C(2,5),D(0,8)处的值分别是z A=×9+4×0=,z B=×4+4×3=22,z C=×2+4×5=25,z D=×0+ 4×8=32.比较之, z B最小,所以,应该为该小孩预定 4 个单位的午饭和3个单位的晚饭,便可知足要求.方法二设需要预定知足要求的午饭和晚饭分别为x 个单位和 y 个单位,所花的花费为 z 元,则依题意得 z=+4y,且 x,y 知足x≥0,y≥0,x≥ 0,y≥0,12x+8y≥64,3x+2y≥16,即6x+6y≥42,x+y≥7,6x+10y≥54,3x+5y≥27.作出平行域以以下图所示.让目标函数表示的直线+4y=z 在可行域上平移,由此可知z=+4y 在 B(4,3)处获得最小值.所以,应该为该小孩预定 4 个单位的午饭和 3 个单位的晚饭,就可知足要求.19.(本小题满分 14 分)如右图,某观察站 C 在城 A 南偏西 20°的方向上,由 A 城出发有一条公路,走向是南偏东40°,在C 处测得距 C 为31 千米的公路上 B 处有一人正沿公路向 A 城走去,走了20 千米后,抵达 D 处,此时 C、D 间距离为 21 千米,问这人还需走多少千米抵达 A 城?分析:依据题意,可得以下图,此中 BC = 31 千米, BD = 20 千米, CD =21 千米,∠CAD =60 ° .设∠ACD =α,∠ CDB =β.在△CDB 中,由余弦定理得:cos β= CD 2+BD 2-BC 2 212+202-312 12CD · = × × =- 7,BD 2 21 202 4 3sin β= 1-cos β= 7 .sin α=sin(180°- ∠CAD -∠CDA)=sin(180°- 60°- 180°+ β)= s in(β-60°)=sin βcos 60°- cos βsin 60°4 3 1 1 3= 7 ×2+7×25 3= 14 .在△ACD 中,由正弦定理得:CD 215 3AD =sin A ·sin α= °× 14 = 15.sin 60这人得走 15 千米抵达 A 城.20.(本小分 14 分)数列 {a n}中, a1=8,a4=2 且足 a n+2=2a n+1-a n, n∈N *.(1)求数列 {a n}的通公式;(2)S n =|a1+ 2 +⋯+n,求S n;||a ||a |(3)b n =1∈ *,T n=b1+b2+⋯+ b n∈*,是n(12-a n)(n N )(n N )否存在最大的整数m,使得随意 n∈N*,均有 T n>m建立?若存32在,求出 m 的;若不存在,明原因.分析:(1)由 a n+2=2a n+1-a n? a n+2- a n+1=a n+1-a n,a4-a1可知 {a n}成等差数列, d==-2,∴a n=8+ (n-1) ·(-2)= 10- 2n(n∈N).(2)由 a n=10-2n≥0 得 n≤5,∴当 n≤5 , S n=- n2+9n.当 n>5 ,S n=|a1|+ |a2|+⋯+|a n|=a1+a2+⋯+a5-a6-a7-⋯-a n=2(a1+a2+⋯+a5)-(a1+a2+⋯+ a n)=n2-9n+40.-n2+9n,1≤n≤5,故 S n=n2- 9n+40,n≥5.11 1 11(3)b n=n(12-a n)=n(2n+2)=2 n-n+1.∴T n=b1+ b2+⋯+b n1 1 1 1 1 1=2 1-2 + 2-3 + 3- 4 +⋯+1 1 1 1- -n + n - + 1 n 1n 1 1=2 1-n +1n )> n -1 = ( + 2n =T n -1>T n - 2>⋯T 1. 2 n 1∴要使 m T n >32 建立,需 m 1 32< T 1=4恒建立,即 m < 8(m ∈ Z).故合适条件的 m 的最大。
苏教版高中数学必修五末调研考试高一

2007~2008学年末调研考试高一数学试题(满分160分,考试时间120分钟)一、填空题:本大题共14小题,每小题5分,共70分. 不需写出解答过程.请把答案直接填写在答题卡相应位置上......... 1.在空间直角坐标系中,线段A B 的端点坐标为A (1,0,2),B (1,-4,4),则线段AB 的中点坐标为 ▲ .2.与直线270x y ++=垂直的一条直线的斜率k = ▲ .3.如图,一个空间几何体的主视图和左视图都是边长为1的正方形, 俯视图是一个圆,那么这个几何体的侧面积为 ▲ .4.直线x -y -5=0被圆x 2+y 2-4x +4y +6=0所截得的弦的长为 ▲ .5. 对于相异三条直线l 、m 、n 和相异两个平面α、β,给出下列四个命题: ①若m ∥l ,n ∥l ,则m ∥n ;②若m ⊥α ,m ∥β, 则α ⊥β;③若m ∥α ,n ∥α ,则m ∥n ; ④若m ⊥β ,α ⊥β ,则m ∥α. 其中真命题的序号是 ▲ .6. 在数列{a n }中,若对n ∈N*,总有a 1+a 2+…+a n =2n -1,则a 12+a 22+…+a n 2= ▲ . 7. 设M 为平面内以A (4,1),B (-1,-6),C (-2,2)三点为顶点的三角形及其内部,当点(x , y )在区域M 上运动时,4x -y 的最小值是 ▲ .8. 设△ABC 的内角A 、B 的对边分别为a 、b ,且a =4,b=A =30o ,则B = ▲ . 9. 设等差数列{}n a 中,a 8=2000,a 2000=8,则a 2008= ▲ .10.设m ≠0,则圆2222220x y mx my m +-+-=与圆22286160x y mx my m +--+=的位置关系是ABCDA 1B 1C 1D 1▲ .(请填写“内含”、“内切”、“相交”、“外切”、“外离”之一) 11.设0x ≥,则当x = ▲ 时,函数(2)(3)1x x y x ++=+取得最小值.12.若△ABC 的三个内角A ,B ,C 成等比数列,则B 的取值范围是 ▲ .13.在△ABC 中,如果sin :sin :sin :(1):(2)A B C n n n =++,其中n *∈N ,那么cos C 的最小值等于▲ .14.一只蚂蚁从棱长为1cm 的正方体的表面上某一点P 处出发,走遍正方体的每个面的中心的最短距离d =f (P ), 那么d 的最大值是 ▲ .二、解答题:本大题共6小题,共90分.请在答题卡指定区域.......内作答,解答时应写出文字说明、证明过程或演算步骤. 15.(本小题满分14分)在直四棱柱ABCD -A 1B 1C 1D 1中,底面ABCD 是菱形. 求证: (1)平面B 1AC //平面DC 1A 1; (2)平面B 1AC ⊥平面B 1BDD 1.16.(本小题满分14分)如图,在四边形ABCD 中,BC =20,DC =40, 105,60,150ABC BCD ADC ︒︒︒∠=∠=∠=.求: (1)AB ;(2)四边形ABCD 的面积.17.(本小题满分15分)ABCD已知无穷等差数列{a n }的前三项依次为11,14,17. (1)该数列有多少项在区间[100, 200]上?并求这些项的和; (2)设832n a n b -=,S n 为{b n }的前n 项和,试比较S n 与1的大小.18.(本小题满分15分)过点Q (2,-作圆C :x 2+y 2=r 2(0r >)的切线,切点为D ,且QD =4.(1)求r 的值;(2)设P 是圆C 上位于第一象限内的任意一点,过点P 作圆C 的切线l ,且l 交x 轴于点A ,交y轴于点B ,设OM OA OB =+u u u u r u u u r u u u r ,求OM u u u u r的最小值(O 为坐标原点).19.(本小题满分16分)设函数f (x )的定义域和值域均为[)0,+∞,且对任意x ∈[)0,+∞数列.又正项数列1{},3,n a a =中 其前n 项和S n 满足*1()().n n S f S n +=∈N (1)求数列{}n a 的通项公式;(2)133,n na a +的等比中项,求数列{b n }前n 项的和T n .20.(本小题满分16分)已知梯形ABCD , AB ∥CD , AB =a , CD =b , a >b .现给出端点在两腰上、且与两底边平行的三条线ADBC段PQ 、RS 、MN :①线段PQ 是梯形的中位线;②线段RS 将梯形的面积等分;③线段MN 将梯 形分成相似的两个梯形.(1)在图中大致作出三条线段PQ 、RS 、MN ,并由此得出三条线段的大小关系是 ▲ ; (2)证明你的结论;(3)另有一条端点在两腰上、且与两底边平行的线段, 其 长度为1112a b ,请你给出该线段的特征,并证明它与(1)中的三条线段比较,长度最小.高一数学参考答案及评分标准200807一、填空题1.(1,-2,3) 2. 2 3. π 45. ①②6. 413n - 7. -10 8. 60o 或120o9. 0 10. 外切 111 12. (π0,3⎤⎥⎦13. 14- 14. 5+二、解答题15.(1)因为ABCD -A 1B 1C 1D 1是直四棱柱,所以,A 1C 1//AC ,而A 1C 1⊄平面B 1AC ,AC ⊂平面B 1AC ,所以A 1C 1//平面B 1AC . …………3分 同理,A 1D //平面B 1AC . …………5分 因为 A 1C 1、A 1D ⊂平面DC 1A 1,A 1C 1I A 1D =A 1,所以平面B 1AC //平面DC 1A 1. …………7分(2) 因为ABCD -A 1B 1C 1D 1是直四棱柱,所以B 1B ⊥平面ABCD , …………9分 而AC ⊂平面ABCD ,所以AC ⊥B 1B . 因为底面ABCD 是菱形,所以AC ⊥BD .因为B 1B 、BD ⊂平面B 1BDD 1,B 1B I BD =B ,所以AC ⊥平面B 1BDD 1. …………12分 因为AC ⊂平面B 1AC ,故有平面B 1AC ⊥平面B 1BDD 1. …………14分16.(1) 连结BD ,因为105,60,150ABC C ADC ︒︒︒∠=∠=∠=,所以3601056015045A ︒∠=---=o o o o , …………2分 在BCD ∆中,2222cos BD BC CD BC CD C =+-⋅ 22120402204012002=+-⨯⨯⨯=,于是BD =…………5分 因为222BD BC CD +=,所以90CBD ︒∠=,从而1059015,1804515120ABD BDA ∠=-=∠=--=o o o o o o o . …………7分 在ABD ∆中, sin sin AB BDADB A=∠∠所以sin sin BD ADB AB A ∠===∠ …………10分 (2)因为sin15sin(4530)=-=o o o 所以四边形ABCD 的面积S ABCD =S △DBC + S △DBA=112022⨯⨯⨯…………14分17. 已知等差数列11,14,17,…的通项公式为()113138n a n n =+-=+. …………3分(1)由10038200n ≤+≤,得3164n ≤≤,又n ∈N *, 所以该数列在[100,200]上有34项. (6)分其和()31643417(101200)51172n a a S +==+=. …………9分(2)因为38n a n =+,所以()8312.2n a nn b -== …………11分对任意的正整数n ,112n n b b +=,且112b =, 于是{}n b 是首项和公比均为12的等比数列. (13)分所以()()1112211 1.1212nnn S ⎡⎤-⎢⎥⎣⎦==-<- …………15分18.(1) 圆C :x 2+y 2=r 2(0r >)的圆心为O (0,0),于是()222225,QO =-+=由题设知,QDO ∆是以D 为直角顶点的直角三角形,故有 3.r OD === …………5分 (2) 设P (x 0,y 0)(000,0x y >>),则22009x y +=,且直线l 的方程为009x x y y +=. (7)分令y =0,得x =09x ,即09,0A x ⎛⎫⎪⎝⎭,令x =0,得y =09y ,即090,B y ⎛⎫⎪⎝⎭.于是OM OA OB =+u u u u r u u u r u u u r 00009999,00,,x y x y ⎛⎫⎛⎫⎛⎫=+= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭. (10)分因为000,0x y >>, 且22009x y +=,所以2200009.22x y x y +≤= (12)分所以0027276,92OM x y ====≥=u u u u r …………14分 当且仅当00x y =时取“=”号.故当P ⎝⎭时,OM u u u u r 取得最小值6. …………15分19.(1)0)x ≥2于是2().f x = …………2分 因为*1()(),n n S f S n =∈N +所以21()n n S f S +==,ED C FOAMDCNP Q RS= 故…………6分因为113,(S a n ==-=,所以2*3().n S n n =∈N …………8分 所以*13,(1),3,(1),63(),(2,)63,(2,)n n n n n a n n S S n n n n n -==⎧⎧===-∈⎨⎨-≥∈-≥∈⎩⎩N N N . …………10分(2)133,n n aa +的等比中项,所以2133,n n a a +=⋅ …………12分于是()191111.(21)(21)22121n n n b a a n n n n +===-+⨯--+ …………14分故()()()121111111.2335212121n n n T b b b n n n ⎡⎤⎢⎥⎣⎦=+++=-+-++-=-++L L …………16分20.(1)如图(只要求三条线段的顺序关系正确). …………2分三条线段的大小关系是 MN <PQ <RS ; …………4分 (2)中位线PQ =2a b +. …………5分由于梯形ABNM 与梯形MNCD 相似,所以DCMN MN AB =,即MN = …………7分设RS =x ,梯形ABCD 的高=h ,则梯形RSCD 的高=x b h a b --,则1()()2x b x b h a b h a b -+=+-,解之,RS …………9分<2a b +;又()2222()0224a b a b a b -++-=>,所以2a b +故MN <PQ <RS . …………12分(3)设梯形ABCD 的对角线AC 与BD 相交于点O , 则端点在两腰上、且与两底边平行并过点O 的线段长为1112a b +.如图,设EF 为上述线段,由三角形相似可得 EO DO DO b AB DB DO OB b a ===++,于是ab EO a b=+. 同理可得ab OF a b =+,从而2ab EF a b==+1112a b +. …………14分因为112a b +,所以EF=1112a b <=+MN , 而MN <PQ <RS ,故该线段与(1)中的三条线段比较,长度最小. (16)分。
苏教版高中数学必修五第一学期期中调研考试.doc

高中数学学习材料马鸣风萧萧*整理制作江苏省前黄中学2007-2008学年第一学期期中调研考试高二数学试卷命题人 张雷 2007年11月18日 一、选择题(每小题5分,共20分)1.在等比数列{}n a 中,已知245,10a a ==,则公比q 的值为 ( )A .2±B .2C .-2D .22±2.“命题P :1x >”是“命题q :0x >”的 ( ) A. 充分不必要条件 B. 必要不充分条件 C . 充要条件 D. 既不充分又不必要条件3.椭圆短轴长是2,长轴长是短轴长的2倍,则椭圆的中心到其准线的距离为 ( )A .558B .554C .338D .3344.对于“x x N x >+∈∃21,”的理解不正确...的是 ( )A .有些N x ∈ ,使得x x >+21成立 B. 至少有一个N x ∈ ,使得x x >+21成立 C. 有无数个N x ∈ ,使得x x >+21成立 D. 存在N x ∈,使得x x >+21成立 二、填空题(每小题5分,共60分)5.命题“所有乌鸭都是黑色的”的否定是 ▲ ;6.椭圆22146x y +=的焦点坐标是 ▲ ; 7.焦点在y 轴上的椭圆22213x y m +=(0)m >的离心率为21,则=m ▲ ; 8. 若椭圆形状越来越扁,则这个椭圆的离心率越来越 ▲ (填“大”或“小”);9. 已知n S 是数列{}n a 的前n 项和,且*21()n S n n N =-∈,则56a a += ▲ ;10.不等式21a x >-对于[1,2)x ∈恒成立,则实数a 的取值范围是 ▲ ; 11.若数列{n a }的前n 项和为323-=n n a S ,那么数列{n a }的通项公式为 ▲ ; 12.不等式11||2ax x ->的解集为M ,且2M ∉,则a 的取值范围是 ▲ ; 13.已知12=+y x ,则yx 42+的最小值为 ▲ ;14.定义在*N 上的函数()f x ,(1)1f =,(1)f n +=⎪⎩⎪⎨⎧.),(,),(21为奇数 为偶数n n f n n f ,则(10)f = ▲ ; 15.在数列{}n a 中,如果存在非零常数T ,使得n T n a a +=对于任意的非零自然数n 均成立,那么就称数列{}n a 为周期数列,其中T 叫做数列{}n a 的周期。
苏教版高中数学必修五春学期高一年级调研测试(一).docx

高中数学学习材料马鸣风萧萧*整理制作2015年春学期高一年级调研测试(一)高 一 数 学(满分160分,120分钟)2015.3.29一、填空题:(本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案填写在答题..纸.的相应位置上.) 1.直线l :330x y -+=的倾斜角为 . 2.已知数列{n a }的通项公式为22n a n n=+,那么110是它的第_ __项.3.在等比数列{n a }中,若274=a ,3-=q ,则=7a .4.已知直线l 过点()0,0,斜率为2,则直线l 的方程是 。
5.等差数列{}n a 中,10120S =,那么29a a += . 6.数列{}n a 满足)(511,311++∈=-=N n a a a nn 则=n a . 7.不等式201xx -≤+的解集是 . 8.若等比数列{}n a 满足2412a a =,则2135a a a = .9.已知等比数列{}n a 中,公比0>q ,且14239,8a a a a +==,则2012201320102011a a a a +=+ .10.已知关于x 的不等式ax ﹣b <0的解集是(3,+∞),则关于x 的不等式>0的解集是 _________ .11.若{}n a 是等差数列,首项01>a ,20132014201320140,0a a a a +>⋅<,则使前n 项和0n S >成立的最大自然数n 是 .12.若数列{}n a 满足:112a =,112n n n a a n++=(*n N ∈),则{}n a 的通项公式为n a = .13.已知等差数列{}n a 中,10a <且前n 项和满足2040s s =,下列结论正确的序号是_________①30s 是n s 中的最大值;②30s 是n s 中的最小值;③300s =;④600s = 14.已知等比数列{}n a 满足11a =,102q <<,且对任意正整数k ,12()k k k a a a ++-+仍是该数列中的某一项,则公比q 为____________.二、解答题(本大题共6小题,共90分.解答题应写出文字说明,证明过程或演算步骤。
苏教版高中数学必修5试卷必修5综合检测
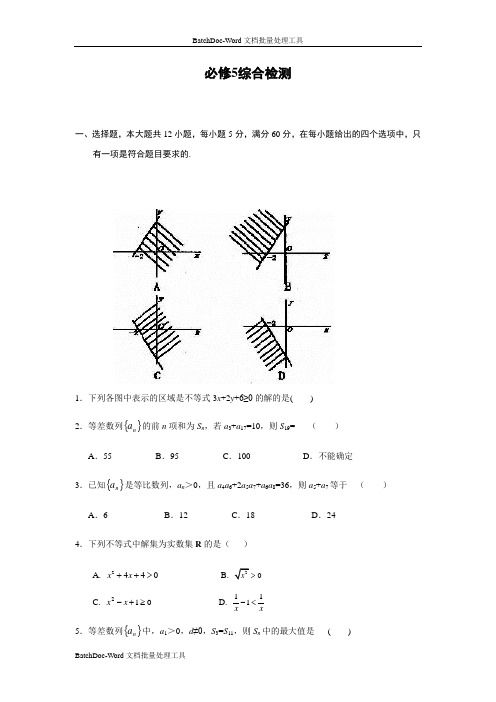
必修5综合检测一、选择题,本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.下列各图中表示的区域是不等式3x +2y +6≥0的解的是( )2.等差数列{}n a 的前n 项和为S n ,若a 3+a 17=10,则S 19= ( )A .55B .95C .100D .不能确定3.已知{}n a 是等比数列,a n >0,且a 4a 6+2a 5a 7+a 6a 8=36,则a 5+a 7等于() A .6 B .12 C .18 D .244.下列不等式中解集为实数集R 的是( )A. 2440x x ++>B. 0C. 012≥+-x xD. x x 111<-5.等差数列{}n a 中,a 1>0,d ≠0,S 3=S 11,则S n 中的最大值是 ( )A .S 7B .S 7或S 8C .S 14D .S 86. 不等式0)1)(1(>-+x x 的解集是( )A .{}10<≤x x B. {}1,0-≠<x x x C. {}11<<-x x D. {}1,1-≠<x x x7. 已知12=+y x ,则y x 42+的最小值为( )A .8B .6C .22D .238.设{}n a 是正数等差数列,{}n b 是正数等比数列,且a 1=b 1,a 2n +1=b 2n +1,则 ( )A .a n +1=b n +1B .a n +1>b n +1C .a n +1<b n +1D .a n +1≥b n +19. 不等式2(2)2(2)40a x a x -+--<对一切x ∈R 恒成立,则实数a 的取值范围是A. )2,(-∞B. []2,2-C. ]2,2(-D.)2,(--∞10.已知A 、B 、C 是△ABC 的三个内角,且sin 2cos sin A B C =,则------------------( )(A) B =C (B) B >C (C) B <C (D) B ,C 的大小与A 的值有关11.在△ABC 中,如果sin :sin :sin 2:3:4A B C =,那么cos C 等于 ( )2A.3 2B.-3 1C .-3 1D.-412.给出下列三个命题(1)若tan A tan B >1,则△ABC 一定是钝角三角形;(2)若sin 2A +sin 2B =sin 2C ,则△ABC 一定是直角三角形;(3)若cos(A -B )cos(B -C )cos(C -A )=1,则△ABC 一定是等边三角形以上正确命题的个数有 ( )A .0个B .1个C .2个D .3个二、填空题,本大题共6小题,每小题4分,满分24分,把正确的答案写在题中横线上.13.在等差数列{a n }中,已知公差d =21,且a 1+a 3+a 5+…+a 99=60,则a 1+a 2+a 3+…+a 99+a 100=______________14.已知平面平域D 由下列约束条件确定:2x -3y +5≥0,x +2y -8≤0,x -5y +6≥0,当点(x ,y )在D 上时,(1) 若y =3x -4y,则y 的最大值是______________,最小值是_______________(2) 当y =x 2+y 2时,则y 的最大值是_____________,最小值是_________________ 15.设等比数列{a n }共有3n 项,它的前2n 项的和为100,后2n 项之和为200,则该等比数列中间n 项的和等于___________________16. 设1≥x ,则函数1)3)(2(+++=x x x y 的最小值是 .17.在△ABC 2sin b A =,则B 等于_____________18.等差数列{a n }中,S n 是它的前n 项之和,且S 6<S 7,S 7>S 8,则①比数列的公差d <0 ②S 9一定小于S 6③a 7是各项中最大的一项 ④S 7一定是S n 中的最大值其中正确的是_______________________(填入你认为正确的所有序号)三、解答题, 本大题共5小题,共66分,解答应写出必要的文字说明、证明过程和演算步骤.19.(本题满分12分)若不等式0252>-+x ax 的解集是⎭⎬⎫⎩⎨⎧<<221x x ,求不等式01522>-+-a x ax 的解集.已知f (x +1)=x 2-4,等差数列{a n }中,a 1=f (x -1),a 2=-23,a 3=f (x ) (1)求x 的值;(2)求通项a n ;(3)求a 2+a 5+a 8+…+a 26的值.△ABC 的三个内角A 、B 、C 对边分别是a , b , c ,且t a n t a n 3t a n t a n A B A B +=-72c =,又△ABC 的面积为ABC S ∆=. 求(1)角C ;(2)a +b 的值.某工厂要制造A种电子装置45台,B种电子装置55台,需用薄钢板给每台装置配一个外壳,已知薄钢板的面积有两种规格:甲种薄钢板每张面积2㎡,可做A、B的外壳分别为3个和5个,乙种薄钢板每张面积3㎡,可做A、B的外壳分别为5个和6个,求两种薄钢板各用多少张,才能使总的用料面积最小?试判断,能否构造一个等比数列{a n},使其满足下列三个条件:①a1+a6=11 ②a3a4=329③至少存在一个自然数m,使23a m-1、a m2、a m+1+49依次组成等差数列,若能,写出这个数列的通项公式;若不能,请说明理由.。
苏教版高中数学必修五春学期高一年级调研测试(一)

2015年春学期高一年级调研测试(一)高一数学(满分160分,120分钟)2015.3.29一、填空题:(本大题共14小题,每小题5分,共70分.不需写出解答过程,请把答案填写在答题纸...的相应位置上.)1.直线l :30x -+=的倾斜角为 . 2.已知数列{n a }的通项公式为22n a n n=+,那么110是它的第_ __项. 3.在等比数列{n a }中,若274=a ,3-=q ,则=7a . 4.已知直线l 过点()0,0,斜率为2,则直线l 的方程是 。
5.等差数列{}n a 中,10120S =,那么29a a += . 6.数列{}n a 满足)(511,311++∈=-=N n a a a nn 则=n a . 7.不等式201xx -≤+的解集是 .8.若等比数列{}n a 满足2412a a =,则2135a a a = . 9.已知等比数列{}n a 中,公比0>q ,且14239,8a a a a +==,则2012201320102011a a a a +=+ .10.已知关于x 的不等式ax ﹣b <0的解集是(3,+∞),则关于x 的不等式>0的解集是 _________ .11.若{}n a 是等差数列,首项01>a ,20132014201320140,0a a a a +>⋅<,则使前n 项和0n S >成立的最大自然数n 是 . 12.若数列{}n a 满足:112a =,112n n n a a n++=(*n N ∈),则{}n a 的通项公式为n a = .13.已知等差数列{}n a 中,10a <且前n 项和满足2040s s =,下列结论正确的序号是_________①30s 是n s 中的最大值;②30s 是n s 中的最小值;③300s =;④600s = 14.已知等比数列{}n a 满足11a =,102q <<,且对任意正整数k ,12()k k k a a a ++-+仍是该数列中的某一项,则公比q 为____________.二、解答题(本大题共6小题,共90分.解答题应写出文字说明,证明过程或演算步骤。
苏教版高中数学必修5试卷参考答案【试题试卷】.docx

参考答案专题一《正弦定理、余弦定理及其应用》综合检测一、选择题二、填空题11. 45°12. —13.40°14. 30^23三、解答题15.a= *+ 耳 A = 105°, C=30°16.略17. 60°18.不能2专题一《正弦定理、余弦定理及其应用》模拟试卷二、填空题13. 45°14. 5^2 15. (V2,V3)16. 9 17. (V5,而)18. V5 :3三、解答题19.468m 20 .等腰三角形或直角三角形21・tz=6, Z?=5, c~~422.-9 23. (l)sin<9-V3 cos^ + —V34(2)2+-^34【选做题】方法1正确.专题二《等差数列、等比数列》综合检测、选择题二、填空题17. (1)第2年养鸡场的个数为26个,全县出产鸡的总只数是31.2万只18. 3n -n-1专题二《等差数列、等比数列》模拟试卷二、填空题13.芝314. 2n15.曜416. ±16n(n +1) 117. D ——+1- —2 2"18. 1三、解答题19. 60 20.略21. q =]或 a n32 12 = - n5 522. 299623.冬 1-0aq(l-q n ^(F【选做题】(1)4022031(2)3 (3)5928专题三《不等关系、一元二次不等式》综合检测一、选择题二、填空题11. (—8, 8) 12.(-, +oo| 13. -2A /2 14. 1812.713. 1 =h 也…如"(n < 17,n e N*)三、解答题15.⑴ a.=6 2n -'n(ji +1)(x = 1),16. (1) a n = In(2) S n =\2x(l-r) 2"z. v I(5、(l-x)1-.X⑵到第6年这个县的养鸡业比第1年缩小了(3)第2年的规模最大三、解答题15. 当。
2022-2021学年高二数学苏教版必修5 综合检测卷

综合检测卷(时间:120分钟 满分:160分)一、填空题(本大题共14小题,每小题5分,共70分)1.已知集合A ={x |x 2-16<0},B ={x |x 2-4x +3>0},则A ∪B =________. 答案 R解析 A ={x |-4<x <4},B ={x |x <1,或x >3},所以A ∪B =R .2.△ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若a 、b 、c 成等比数列,且c =2a ,则cos B =________.答案 34解析 由题意,得b 2=ac , 又c =2a ,由余弦定理,得cos B =a 2+c 2-b 22ac =a 2+4a 2-a ×2a 2a ×2a=34.3.若S n 是等差数列{a n }的前n 项和,a 2+a 10=4,则S 11的值为________. 答案 22解析 S 11=(a 1+a 11)×112=11×(a 2+a 10)2=22.4.当x >1时,不等式x +1x -1≥a 恒成立,则实数a 的取值范围是________.答案 (-∞,3]解析 ∵x >1,∴x +1x -1=(x -1)+1x -1+1≥2(x -1)·1x -1+1=3.∴a ≤3.5.等差数列{a n }满足a 24+a 27+2a 4a 7=9,则其前10项之和为________.答案 ±15解析 a 24+a 27+2a 4a 7=(a 4+a 7)2=9,∴a 4+a 7=±3,∴a 1+a 10=±3, ∴S 10=10(a 1+a 10)2=±15.6.在△ABC 中,BC =2,B =π3,当△ABC 的面积等于32时,sin C =________.答案 12解析 由三角形的面积公式,得S =12AB ·BC sin π3=32,易求得AB =1,由余弦定理,得AC 2=AB 2+BC 2-2AB ·BC ·cos π3,得AC =3,再由三角形的面积公式,得S =12AC ·BC sin C =32,即可得出sin C =12.7.函数y = x 2+mx +m2对一切x ∈R 恒成立,则实数m 的取值范围是________.答案 0≤m ≤2解析 Δ=m 2-4×m2=m 2-2m ≤0,∴0≤m ≤2.8.已知数列{a n }的通项公式为a n =2×3n -1,则由此数列的偶数项所组成的新数列的前n 项的和为________.答案 34(9n -1)解析 新数列是首项为a 2=6,公比为q =9的等比数列,所以S n =6(9n -1)9-1=34(9n -1).9.若变量x ,y 满足⎩⎪⎨⎪⎧2x +y ≤40,x +2y ≤50,x ≥0,y ≥0.则z =3x +2y 的最大值是________.答案 70解析 作出可行域如图所示.由于2x +y =40、x +2y =50的斜率分别为-2、-12,而3x +2y =0的斜率为-32,故线性目标函数的倾斜角大于2x +y =40的倾斜角而小于x +2y =50的倾斜角,由图知,3x +2y =z 经过点A (10,20)时,z 有最大值,z 的最大值为70.10.国家为了加强对烟酒生产的宏观管理,实行征收附加税政策.现知某种酒每瓶70元,不加附加税时,每年大约产销100万瓶,若政府征收附加税,每销售100元要征税k 元(叫做税率k %),则每年的产销量将削减10k 万瓶.要使每年在此项经营中所收取附加税金不少于112万元,则k 的取值范围为________.答案 [2,8]解析 设产销量为每年x 万瓶,则销售收入每年70x 万元,从中征收的税金为70x ·k %万元,其中x =100-10k .由题意,得70(100-10k )k %≥112,整理得k 2-10k +16≤0,解得2≤k ≤8.因此,当2≤k ≤8(单位:元)时,每年在此项经营中所收附加税金不少于112万元. 11.设正实数x ,y ,z 满足x 2-3xy +4y 2-z =0.则当zxy 取得最小值时,x +2y -z 的最大值为________.答案 2解析 由题意知:z =x 2-3xy +4y 2,则z xy =x 2-3xy +4y 2xy =x y +4y x-3≥1,当且仅当x =2y 时取等号,此时z =xy =2y 2. 所以x +2y -z =2y +2y -2y 2=-2y 2+4y =-2(y -1)2+2≤2. 12.观看下列等式 12=1 12-22=-312-22+32=6 12-22+32-42=-10 ……照此规律,第n 个等式可为12-22+32-…+(-1)n +1n 2=________.答案 (-1)n +1·n (n +1)2解析 观看等式左边的式子,每次增加一项,故第n 个等式左边有n 项,指数都是2,且正、负相间,所以等式左边的通项为(-1)n +1n 2.等式右边的值的符号也是正、负相间,其确定值分别为1,3,6,10,15,21,….设此数列为{a n },则a 2-a 1=2,a 3-a 2=3,a 4-a 3=4,a 5-a 4=5,…,a n -a n -1=n ,各式相加得a n -a 1=2+3+4+…+n ,即a n =1+2+3+…+n =n (n +1)2.所以第n 个等式为12-22+32-42+…+(-1)n +1n 2=(-1)n +1n (n +1)2. 13.如图,在坡度为15°的观礼台上,某一列座位所在直线AB 与旗杆所在直线MN 共面,在该列的第一个座位A 和最终一个座位B 测得旗杆顶端N 的仰角分别为60°和30°,且座位A 、B 的距离为106米,则旗杆的高度为____米.答案 30解析 由题意,可知∠BAN =105°,∠BNA =30°, 由正弦定理,得AN sin 45°=106sin 30°,解得AN =203米,在Rt △AMN 中,MN =203sin 60°=30米. 故旗杆的高度为30米.14.设z =kx +y ,其中实数x ,y 满足⎩⎪⎨⎪⎧x +y -2≥0,x -2y +4≥0,2x -y -4≤0.若z 的最大值为12,则实数k =________.答案 2解析 作出可行域如图阴影部分所示:由图可知当0≤-k <12时,直线y =-kx +z 经过点A (4,4)时z 最大,所以4k +4=12,解得k =2(舍去);当-k ≥12时,直线y =-kx +z 经过点B (0,2)时z 最大,此时z 的最大值为2,不合题意;当-k <0时,直线y =-kx +z 经过点A (4,4)时z 最大,所以4k +4=12,解得k =2,符合题意. 综上可知,k =2.二、解答题(本大题共6小题,共90分)15.(14分)设S n 是等差数列{a n }的前n 项和,已知13S 3,14S 4的等比中项为15S 5;13S 3,14S 4的等差中项为1,求数列{a n }的通项公式.解 设等差数列{a n }的首项a 1=a ,公差为d ,则S n =na +n (n -1)2d ,依题意,有⎩⎨⎧13⎝⎛⎭⎫3a +3×22d ×14⎝⎛⎭⎫4a +4×32d =125⎝⎛⎭⎫5a +5×42d 2,13⎝⎛⎭⎫3a +3×22d +14⎝⎛⎭⎫4a +4×32d =1×2.整理得⎩⎪⎨⎪⎧3ad +5d 2=0,2a +52d =2.∴a =1,d =0或a =4,d =-125.∴a n =1或a n =325-125n ,经检验,a n =1和a n =325-125n 均合题意.∴所求等差数列的通项公式为a n =1或a n =325-125n .16.(14分)已知a ,b ,c 分别为△ABC 三个内角A ,B ,C 的对边,a cos C +3a sin C -b -c =0. (1)求A ;(2)若a =2,△ABC 的面积为3,求b ,c .解 (1)由a cos C +3a sin C -b -c =0及正弦定理得sin A cos C +3sin A sin C -sin B -sin C =0. 由于B =π-A -C ,所以3sin A sin C -cos A sin C -sin C =0.由于sin C ≠0,所以sin ⎝⎛⎭⎫A -π6=12. 又0<A <π,故A =π3.(2)△ABC 的面积S =12bc sin A =3,故bc =4.而a 2=b 2+c 2-2bc cos A ,故b 2+c 2=8. 解得b =c =2.17.(14分)某渔业公司今年年初用98万元购进一艘渔船用于捕捞,第一年需要各种费用12万元.从其次年起包括修理费在内每年所需费用比上一年增加4万元.该船每年捕捞总收入50万元. (1)问捕捞几年后总盈利最大,最大是多少? (2)问捕捞几年后的平均利润最大,最大是多少? 解 (1)设该船捕捞n 年后的总盈利y 万元.则 y =50n -98-[12×n +n (n -1)2×4]=-2n 2+40n -98 =-2(n -10)2+102∴当捕捞10年后总盈利最大,最大是102万元.(2)年平均利润为y n =-2(n +49n -20)≤-2(2 n ·49n -20)=12,当且仅当n =49n ,即n =7时上式取等号.所以,当捕捞7年后年平均利润最大,最大是12万元. 18.(16分)已知函数f (x )=x 2-2x -8,g (x )=2x 2-4x -16,(1)求不等式g (x )<0的解集;(2)若对一切x >2,均有f (x )≥(m +2)x -m -15成立,求实数m 的取值范围. 解 (1)g (x )=2x 2-4x -16<0, ∴(2x +4)(x -4)<0,∴-2<x <4, ∴不等式g (x )<0的解集为{x |-2<x <4}. (2)∵f (x )=x 2-2x -8.当x >2时,f (x )≥(m +2)x -m -15恒成立, ∴x 2-2x -8≥(m +2)x -m -15, 即x 2-4x +7≥m (x -1). ∴对一切x >2,均有不等式x 2-4x +7x -1≥m 成立.而x 2-4x +7x -1=(x -1)+4x -1-2≥2(x -1)×4x -1-2=2(当x =3时等号成立).∴实数m 的取值范围是(-∞,2].19.(16分)如图,某校有一块形如直角三角形ABC 的空地,其中∠B 为直角,AB 长为40米,BC 长为50米,现欲在此空地上建筑一间健身房,其占地外形为矩形,且B 为矩形的一个顶点,求该健身房的最大占地面积.解 如图,设矩形为EBFP ,FP 长为x 米,其中0<x <40,健身房占地面积为y 平方米. 由于△CFP ∽△CBA ,所以FP BA =CF CB ,x 40=50-BF 50,求得BF =50-54x ,从而y =BF ·FP =(50-54x )x =-54x 2+50x=-54(x -20)2+500≤500,当且仅当x =20时,等号成立.答 该健身房的最大占地面积为500平方米.20.(16分)已知数列{a n }的前n 项和为S n ,a 1=1,a n +1=2S n +1(n ∈N *),等差数列{b n }中,b n >0(n ∈N *),且b 1+b 2+b 3=15,又a 1+b 1、a 2+b 2、a 3+b 3成等比数列. (1)求数列{a n }、{b n }的通项公式; (2)求数列{a n ·b n }的前n 项和T n , 解 (1)∵a 1=1,a n +1=2S n +1(n ∈N *), ∴a n =2S n -1+1(n ∈N *,n >1), ∴a n +1-a n =2(S n -S n -1),即a n +1-a n =2a n ,∴a n +1=3a n (n ∈N *,n >1). 而a 2=2a 1+1=3,∴a 2=3a 1.∴数列{a n }是以1为首项,3为公比的等比数列, ∴a n =3n -1(n ∈N *).∴a 1=1,a 2=3,a 3=9, 在等差数列{b n }中,∵b 1+b 2+b 3=15,∴b 2=5.又∵a 1+b 1、a 2+b 2、a 3+b 3成等比数列,设等差数列{b n }的公差为d ,则有(a 1+b 1)(a 3+b 3)=(a 2+b 2)2. ∴(1+5-d )(9+5+d )=64,解得d =-10或d =2, ∵b n >0(n ∈N *),∴舍去d =-10,取d =2,∴b 1=3,∴b n =2n +1(n ∈N *).(2)由(1)知T n =3×1+5×3+7×32+…+(2n -1)·3n -2+(2n +1)3n -1,① ∴3T n =3×3+5×32+7×33+…+(2n -1)3n -1+(2n +1)3n ,② ∴①-②得-2T n =3×1+2×3+2×32+2×33+…+2×3n -1-(2n +1)3n =3+2(3+32+33+…+3n -1)-(2n +1)3n =3+2×3-3n1-3-(2n +1)3n=3n -(2n +1)3n =-2n ·3n . ∴T n =n ·3n .。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
苏教版数学必修五调研试题一、填空题:本大题共14小题,每小题5分,共70分.1. 若点P (a ,3)在不等式2x +y <3表示的区域内,则实数a 的取值范围是 .2. 在△ABC 中,sin 2A=sin 2B+sin 2C ,则△ABC 的形状为3. 数列{a n }的通项公式为a n =2n -49,S n 达到最小时,n 等于_______________.4. 2x 2-3x -2≥0的解集是 .5. △ABC 的内角A 、B 、C 的对边分别为a 、b 、c .若a 、b 、c 成等比数列,且c =2a ,则cosB= .6. 等差数列{a n }中,已知a 1=13,a 2+a 5=4,a n =33,则n 为 .7. 已知x >0,则xx 432++的最小值等于________8. 数列{}n a 为等比数列,n S 为其前n 项和.已知11a =,3q =,364k S =,则k a = . 9. 三角形两条边长分别为3 cm,5 cm ,其夹角的余弦值是方程5x 2-7x -6=0的根,则此三角形的面积是____________________.10. 在△ABC 中,三顶点坐标为(2,4),(1,2),(1,0)A B C -,点(,)P x y 在ABC 内部及边界上运动,则z x y =-的最大是 ;最小值是 . 11. 已知数列{}n a 中,131+=+n n n a a a ,919=a ,则a 2009 .12. 在R 上定义运算:(1)x y x y ⊗⊗=-,若不等式()()1x a x a -⊗+< 对任意实数x 成立,则实数a 的取值范围是 .13. 一船以每小时15km 的速度向东航行,船在A 处看到一个灯塔B 在北偏东060,行驶4h 后,船到达C 处,看到这个灯塔在北偏东015,这时船与灯塔的距离为 .14. 设)(x f y =是一次函数,,1)0(=f 且)13(),4(),1(f f f 成等比数列,则++)4()2(f f …=+)2(n f .二、解答题:本大题共6小题,共90分.解答应写出文字说明、证明过程或演算步骤. 15. (本小题满分14分) 在ABC △中,5cos 13A =-,3cos 5B =.(Ⅰ)求sin C 的值; (Ⅱ)设5BC =,求ABC △的面积.16. (本小题满分14 分)已知不等式2230x x --<的解集为A ,不等式260x x +-<的解集为B.(1)求A∩B ;(2)若不等式20x ax b ++<的解集为A∩B ,求不等式20ax x b ++<的解集.17. (本小题满分14分)数列{}n a 中,12a =,1n n a a cn +=+(c 是常数,123n = ,,,),且123a a a ,,是公比不为1的等比数列. (I )求c 的值; (II )求{}n a 的通项公式.18. (本小题满分16分)在ABC ∆中,,,a b c 分别为角,,A B C 的对边,且满足274coscos 2()22A B C -+=(1)求角A 大小;(2)若3b c +=,当a 取最小值时,判断ABC ∆的形状.19. (本小题满分16分)经过长期观察得到:在交通繁忙的时段内,某公路段汽车的流量y (千辆∕时)与汽车的平均速度v (千米∕时)之间的函数关系为)0(160039202>++=v v v v y ,(1)在该时段内,当汽车的平均速度v 为多少时,车流量最大?最大车流量是多少?(精确到0.1千辆∕时)(2)若要求在该时段内车流量超过10千辆∕时,则汽车的平均速度应在什么范围内?20.(本小题满分16 分)设{a n }是正数组成的数列,其前n 项和为S n ,并且对于所有的n N +,都有2)2(8+=n n a S .(1)写出数列{a n }的前3项;(2)求数列{a n }的通项公式(写出推证过程); (3)设14+⋅=n n n a a b ,n T 是数列{b n }的前n 项和,求使得20m T n <对所有nN +都成立的最小正整数m 的值.参考答案一、填空题:1. (-∞,0)2. 直角三角形3. 244. {x |x ≥2或x ≤-12} 5. 436. 507. 2+438. 2439. 6 cm 2 10. 1,-3 11.6009112. 21(-,)2313.km 14. )32(+n n二、解答题:15.解:(Ⅰ)ABC ∆中,由5cos 13A =-,得12sin 13A =由3cos 5B =,得4sin 5B =.………………………………………………………4分所以16sin sin()sin cos cos sin 65C A B A B A B =+=+=………………………7分(Ⅱ)由正弦定理得45sin 13512sin 313BC B AC A ⨯⨯=== …………………………10分所以ABC △的面积1sin 2S BC AC C =⨯⨯⨯1131652365=⨯⨯⨯83=.…………14分16. 解:(1)由2230x x --<得13x -<<,所以A=(-1,3)…………3分 由260x x +-<得32x -<<,所以B=(-3,2),…………6分 ∴A∩B=(-1,2)………………………………8分 (2)由不等式20x ax b ++<的解集为(-1,2), 所以10420a b a b -+=⎧⎨++=⎩,………………………………10分解得12a b =-⎧⎨=-⎩………………………………12分∴220x x -+-<,解得解集为R. ………………………………14分 17. 解:(I )12a =,22a c =+,323a c =+,………………2分因为1a ,2a ,3a 成等比数列,所以2(2)2(23)c c +=+,………………4分 解得0c =或2c =.……………………………………6分当0c =时,123a a a ==,不符合题意舍去,故2c =.……………………7分(II )当2n ≥时,由于21a a c -=,322a a c -=, ,1(1)n n a a n c --=-, 所以1(1)[12(1)]2n n n a a n c c --=+++-=.………………………………10分又12a =,2c =,故22(1)2(23)n a n n n n n =+-=-+= ,,.……………12分 当1n =时,上式也成立,…………13分所以22(12)n a n n n =-+= ,,.…………14分 18.解:(1)A B C π++= ,…………1分2274coscos 2()2(1cos )cos 22cos 2cos 322A B C A A A A ∴-+=+-=-++=,………… 4分212cos 2cos 02A A ∴-+=. 1c o s 2A ∴=,…………6分0A π<< , 60oA ∴=.…………8分(2)由余弦定理222cos 2b c aA bc+-=,得 222bc b c a =+-.…………10分2229()39393()24b c a b c bc bc +∴=+-=-≥-=, 32a ∴≥.…………13分所以a 的最小值为32,当且仅当32b c ==时取等号.此时ABC ∆为正三角形.…………16分19、解:(1)依题意,83920160023920)1600(3920=+≤++=vv y …………6分当且仅当,1600v v =即v=40时,上式等号成立,…………8分所以,1.1183920m ax ≈=y (千辆∕时)…………9分(2)由条件得: 10160039202>++v v v ,…………12分整理得v 2-89v +1600<0,解得25<v <64…………15分答:(1)当汽车的平均速度v 为40千米∕时时,车流量最大,最大车流量约为11.1千辆∕时。
(2)如果要求在该时段内车流量超过10千辆∕时,则汽车的平均速度应大于25千米∕时且小于64千米∕时。
…………16分20. 解:(1) n=1时 2118(2)a a =+ ∴12a =n=2时 21228()(2)a a a +=+ ∴26a =n=3时 212338()(2)a a a a ++=+ ∴310a = ………………………3分 (2)∵28(2)n n S a =+ ∴2118(2)(1)n n S a n --=+> 两式相减得: 2218(2)(2)n n n a a a -=+-+即2211440n n n n a a a a -----=………………………5分 也即11()(4)0n n n n a a a a --+--=∵0n a > ∴14n n a a --= ………………………8分 即{}n a 是首项为2,公差为4的等差数列∴2(1)442n a n n =+-⋅=- ………………………10分 (3)1441111()(42)(42)(21)(21)2(21)(21)n n n b a a n n n n n n +====-⋅-+-+-+………………………12分 ∴12111111[(1)()()]2335(21)(21)n n T b b b n n =+++=-+-++--+11111(1)2212422n n =-=-<++………………………14分∵20n mT <对所有n N +∈都成立 ∴1202m ≥即10m ≥故m 的最小值是10. ………………………16分。
