第四版运筹学部分课后习题解答(内容参考)
《管理运筹学》第四版课后习题答案

《管理运筹学》第四版课后习题答案-标准化文件发布号:(9556-EUATWK-MWUB-WUNN-INNUL-DDQTY-KII《管理运筹学》第四版课后习题解析(上)第2章线性规划的图解法1.解:(1)可行域为OABC。
(2)等值线为图中虚线部分。
(3)由图2-1可知,最优解为B点,最优解x =12 ,x157 7图2-1;最优目标函数值69 。
72.解:(1)如图2-2所示,由图解法可知有唯一解x0.2,函数值为3.6。
x图2-2(2)无可行解。
(3)无界解。
(4)无可行解。
2(5)无穷多解。
x (6)有唯一解203 ,函数值为 92 。
83 x 33.解: (1)标准形式max f 3x 2x 0s 0s 0s9x 2x s 303x 2x s 132x 2x s 9x , x , s , s , s ≥ 0(2)标准形式min f = 4x + 6x + 0s + 0s3x - x - s = 6x + 2x + s = 107x - 6x = 4x , x , s , s ≥ 0(3)标准形式min f = x ' - 2x ' + 2x '' + 0s + 0s-3x + 5x ' - 5x '' + s = 702x ' - 5x ' + 5x '' = 503x ' + 2x ' - 2x '' - s = 30x ', x ' , x '', s , s ≥ 04.解:标准形式max z = 10x + 5x + 0s + 0s3x + 4x + s = 95x + 2x + s = 8x , x , s , s ≥ 0≤ 松弛变量(0,0)最优解为 x =1,x 2=3/2。
5.解:标准形式min f = 11x + 8x + 0s + 0s + 0s10x + 2x - s = 203x + 3x - s = 184x + 9x - s = 36x , x , s , s , s ≥ 0剩余变量(0, 0, 13)最优解为 x 1=1,x 2=5。
《管理运筹学》第4版课后习题解析(韩伯棠)
《管理运筹学》第四版课后习题解析
韩伯棠
(2)模型变为 max z 5 xA 4 xB
50 xA 100 xB ≤ 1 200 000 100 xB ≥ 300 000 xA , xB ≥ 0
推导出 x1 18 000 , x2 3 000 ,故基金 A 投资 90 万元,基金 B 投资 30 万元。
第 2 章 线性规划的图解法
1.解: (1)可行域为 OABC。 (2)等值线为图中虚线部分。 (3)由图 2-1 可知,最优解为 B 点,最优解 x1 =
12 15 69 , x2 ;最优目标函数值 。 7 7 7
图 2-1 2.解: (1)如图 2-2 所示,由图解法可知有唯一解
8
《管理运筹学》第四版课后习题解析
韩伯棠
第 3 章 线性规划问题的计算机求解
1.解: ⑴甲、乙两种柜的日产量是分别是 4 和 8,这时最大利润是 2720 ⑵每多生产一件乙柜,可以使总利润提高 13.333 元 ⑶常数项的上下限是指常数项在指定的范围内变化时, 与其对应的约束条件的对偶价格不变。 比如油漆时间变为 100,因为 100 在 40 和 160 之间,所以其对偶价格不变仍为 13.333 ⑷不变,因为还在 120 和 480 之间。 2.解: ⑴不是,因为上面得到的最优解不为整数解,而本题需要的是整数解 ⑵最优解为 (4,8) 3 .解: ⑴农用车有 12 辆剩余 ⑵大于 300 ⑶每增加一辆大卡车,总运费降低 192 元 4.解: 计算机得出的解不为整数解,平移取点得整数最优解为(10,8) 5.解: 圆桌和衣柜的生产件数分别是 350 和 100 件,这时最大利润是 3100 元 相差值为 0 代表,不需要对相应的目标系数进行改进就可以生产该产品。 最优解不变,因为 C1 允许增加量 20-6=14;C2 允许减少量为 10-3=7,所有允许增加百分比 和允许减少百分比之和(7.5-6)/14+(10-9)/7〈100%,所以最优解不变。 6.解: (1) x1 150 , x2 70 ;目标函数最优值 103 000。 (2)1、3 车间的加工工时数已使用完;2、4 车间的加工工时数没用完;没用完的加工工时 数为 2 车间 330 小时,4 车间 15 小时。 (3)50,0,200,0。 含义:1 车间每增加 1 工时,总利润增加 50 元;3 车间每增加 1 工时,总利润增加 200 元; 2 车间与 4 车间每增加一个工时,总利润不增加。 (4)3 车间,因为增加的利润最大。 (5)在 400 到正无穷的范围内变化,最优产品的组合不变。 (6)不变,因为在 0,500 的范围内。 (7)所谓的上限和下限值指当约束条件的右边值在给定范围内变化时,约束条件 1 的右边 值在 200,440 变化,对偶价格仍为 50(同理解释其他约束条件) 。 (8)总利润增加了 100×50=5 000,最优产品组合不变。 (9)不能,因为对偶价格发生变化。
运筹学基础及应用第四版胡运权主编课后练习答案

运筹学基础及应用习题解答z 3。
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
(a)约束方程组的系数矩阵12 3 6 3 0A 8 1 4 0 23 0 0 0 0基基解是否基可行解目标函数值X1 X2 X3 X4 X5 X6P1 P2 P3163 7-60 0 0否P1 P2 P4 0 10 0 7 0 0 是10P1 P2 P50 3 0 0 72是 3习题一P46x i1-的所有X i,X2,此时目标函数值o(b)约束方程组的系数矩阵A 12 3 4A2 2 12⑻(1)图解法基 基解 是否基可行解 目标函数值X 1X 2X 3X 4P 1P 24 11否"2P 1P 3 2 0 110 是435 ~5~5P 1P 4111否—36P 2P 312是52P 2P 41否22P 3P 40 0 1 1是5最优解xT2 11 5吋omax z 10x 1 5x 2 0x 3 0x 4 3x i 4X 2 X 3st. 5x 1 2x 2 x 48 9 8 12。
min—,— — 5 3 5C j 105 0 0 C B基b X 1X 2X 3X 421143 0 X 3— 1—"5"5582110X 11C j 105 0 0 C B 基bX 1 X 2 X 3 X 4 0 X 3 9 341 0 0X 48[5] 20 1 C j Z j105令 X iX 20,0,9,8,由此列出初始单纯形表最优解即为3x1 4x2 9的解x5x 1 2x 2 81,-,最大值z 竺 2 2(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式则P 3,P 4组成一个基。
得基可行解xC j Z j0 1221 8320,min14 22新的单纯形表为C j 105 0 0 C B基b X 1X 2X 3X 435 3 5X 2— 01— —2141410X 11121—7525c jZ j14 143*35x i 1, x 2 - , X 3 0, X 4 0。
[运筹学第四版课后答案]课后答案
![[运筹学第四版课后答案]课后答案](https://img.taocdn.com/s3/m/24ea5b5d814d2b160b4e767f5acfa1c7aa008294.png)
[运筹学第四版课后答案]课后答案课后答案一:《蜀道难》课后题答案《蜀道难》课后题答案一、这是一首乐府诗,以七言为主,却有不少杂言句,节奏多变化,与散文句法相似。
试给下面的诗句划分节奏,朗读几遍,说说它们对本诗的风格起什么作用。
1.噫吁戏,危乎高哉!蜀道之难,难于上青天!2.上有六龙回日之高标,下有冲波逆折之回川。
3.其险也如此,嗟尔远道之人胡为乎来哉!4.剑阁峥嵘而崔嵬,一夫当关,万夫莫开。
解题指导这首诗较长,且内容有一定难度所以先设计此题,目的是使你初步适应这首诗节奏的变化。
在完成本题时你一定要朗读几遍,读出一点韵味来。
但要注意:不要把这些句子读成散文,这对领会诗人炽烈奔放的感情和飘逸的风格极为必要。
这是一首杂言体诗,但跟其他诗人的这类体裁作品和李白的另一些这类体裁作品(如《将进酒》《梁甫吟》《庐山谣寄卢待御虚舟》等)相比,都有显著的不同。
这不同就在于:其中的某些句子,如练习中所列举的,如果孤立地看,确属散文句。
但我们不这样称它们,因为它们毕竟是诗的整体中的一部分,只能说它们是散文化的诗句,或句法与散文近似。
这当然不能随意而为,没有李白那样的气概,那样的英才,是驾驭不了的。
参考答案这些诗句都仿佛是诗人在炽烈感情的驱动下,不能自已,脱口而出,生动地表现了诗人奔放豪迈的风格。
二、“蜀道之难,难于上青天”这句诗有什么含义它重复出现三次,有什么作用解题指导这道题是为鉴赏诗的内容设计的。
重点是前一问,后一问是对前一问的补充,意思是可以从形式入手鉴赏诗的内容。
因此在完成本题时,你可以先思考后一问,然后分析“蜀道之难”一句的含义。
此题有一定的难度,你最好先理清课文的结构层次并了解诗的大意,在此基础上完成本题。
李白善于从民歌中吸取养料。
这首诗中“一咏三叹”的写法,明显地是对《诗经》中复沓形式的继承,同时又有很大的发展。
这一特点同你已学过的《君子于役》《无衣》等相同。
参考答案诗人创造性地继承了古代民歌中常见的复沓形式(又称反复),主旨句凡三见:开头、中间、结尾各出现一次。
《管理运筹学》第四版课后习题解析[下]
![《管理运筹学》第四版课后习题解析[下]](https://img.taocdn.com/s3/m/97cbd28969dc5022aaea006f.png)
给 标号 ,同理 标号 。得到最短路线为 ,最短时间为1.35小时。
4.解:
以 为起始点, 标号为 ;
,
边集为 =
且有
所以, 标号(4,1)。
则 ,
边集为
且有
所以, 标号(5,1)。
则 ,
边集为
且有
所以, 标号(7,2)。
则 ,
边集为
且有
所以, 、 标号(8,2)。
则 ,
边集为
且有
所以, 标号(9,4)。
则 ,
边集为
且有
所以, 标号(11.5,6)。
则 ,
边集为
且有
所以, 标号(12,7)。
, 为空集。
所以,最短路径为
5.解:
(1)从 出发,令 ={ },其余点为 ,给 标号 。 的所有边为 ,
累计距离最小为 ,给 标号为 ,令 。
(2) 的所有边为 ,累计距离最小为 ,令 。
(2)
图解法求解如图9-1所示,目标1,2可以达到,目标3达不到,所以有满意解为A点(150,120)。
6、解:
假设甲乙两种产品量为x1,x2,建立数学规划模型如下。
用管理运筹学软件求解得:
所以,甲乙两种产品量分别为8.333吨,3.333吨,该计划内的总利润为250元。
7、解:
设该汽车装配厂为达到目标要求生产产品A 件,生产产品B 件。
图解法略,求解得 。
(2)目标规划模型如下。
图解法略,求解得 。
由此可见,所得结果与(1)中的解是不相同的。
(3)加权目标规划模型如下,
求解得 。
9、解:
假设甲乙两种洗衣机的装配量分别是x1,x2,建立数学规划模型如下。
《管理运筹学》第四版课后习题答案
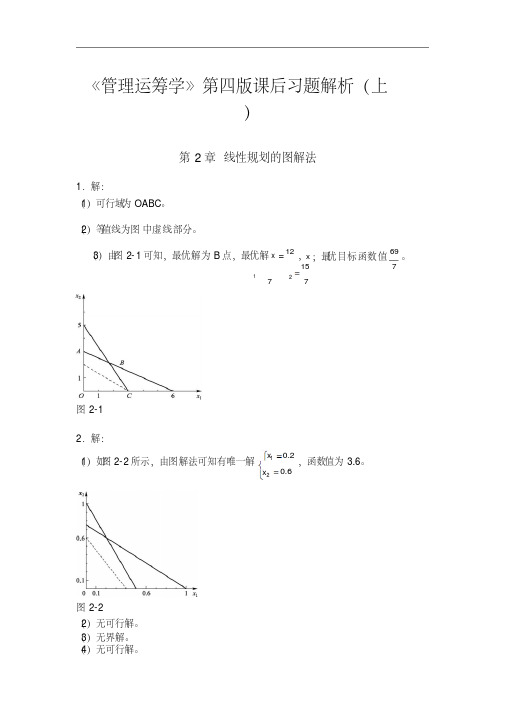
(4)3 车间 ,因为增加的利 润最大。
(5)在400 到正无 穷的范 围内 变化,最优产 品的 组合不 变。
(6)不变,因为在 0,500 的范 围内。
(7)所谓的上限和下限 值指当 约束条件的右 边值 在 给定范 围 内变化 时,约束条件 1 的右 边值 在 200,440 变化,对 偶价格仍 为 50(同理解释 其他 约 束条件)。
当 c1 不变时 ,c2 在 负无穷 到 6.4 的范 围内变 化,最优 解不 变。 (5)约 束条件 1 的右 边值 在 780 000,1500 000 变化,对偶价格仍 为 0.057(其他同理) 。 (6)不能,因为允 许减少的百分比与允 许 增加的百分比之和 4 2 100% ,理由
4.25 3.6
11.解: 设圆 桌和衣柜的生 产件数分 别为 x、y,所获 利润为 z,则 z=6x+10y.
0.18x 0.08x
x0 y0
0.09 y 0.28 y
72 2x y 800
56 2x 7 y 即 x0
1400 作出可行域.平移 6x+ 10y=0 ,如图
y0
2x y 800
x 350
得
即 C(350,100) .当直线 6x+ 10y=0 即 3x+ 5y=0 平移
x1
0.2
,函数值为 3.6。
x2 0.6
图 2-2
(2)无可行解。 (3)无界解。 (4)无可行解。
(5)无穷多解。
x1
(6)有唯一解
x2
20
3 ,函数值为 92 。
8
3
3
3.解: (1)标 准形式
max f 3x1 2x2 0s1 0s2 0s3
第四版运筹学部分课后习题解答

第四版运筹学部分课后习题解答篇一:运筹学基础及应用第四版胡运权主编课后练习答案运筹学基础及应用习题解答习题一P461.1(a)41的所有?x1,x2?,此时目标函数值2该问题有无穷多最优解,即满足4x1?6x2?6且0?x2?z?3。
(b)用图解法找不到满足所有约束条件的公共范围,所以该问题无可行解。
1.2(a)约束方程组的系数矩阵?1236300A??81?4020??30000?1最优解x??0,10,0,7,0,0?T。
(b) 约束方程组的系数矩阵?1234?A2212?????211?最优解x??,0,,0?。
5??5T1.3(a)(1) 图解法最优解即为??3x1?4x2?935?3?的解x??1,?,最大值z?5x?2x?822??2?1(2)单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式max z?10x1?5x2?0x3?0x4?3x?4x2?x3?9s.t. ?1?5x1?2x2?x4?8则P3,P4组成一个基。
令x1?x2?0得基可行解x??0,0,9,8?,由此列出初始单纯形表?1??2。
??min?,89??53?8 5?2?0,??min??218?3,??142?2?335?1,?2?0,表明已找到问题最优解x1?1, x2?,x3?0 ,x4?0。
最大值z*?22(b)(1) 图解法6x1?2x2x1?x2?最优解即为??6x1?2x2?2417?73?的解x??,?,最大值z?2?22??x1?x2?5(2) 单纯形法首先在各约束条件上添加松弛变量,将问题转化为标准形式max z?2x1?x2?0x3?0x4?0x5?5x2?x3?15?s.t. ?6x1?2x2?x4?24?x?x?x?5?125则P3,P4,P5组成一个基。
令x1?x2?0得基可行解x??0,0,15,24,5?,由此列出初始单纯形表?1??2。
??min??,??245?,??461?3?3?15,24,??2?2?5?2?0,??min?新的单纯形表为篇二:运筹学习题及答案运筹学习题答案第一章(39页)1.1用图解法求解下列线性规划问题,并指出问题是具有唯一最优解、无穷多最优解、无界解还是无可行解。
清华大学胡运权运筹学
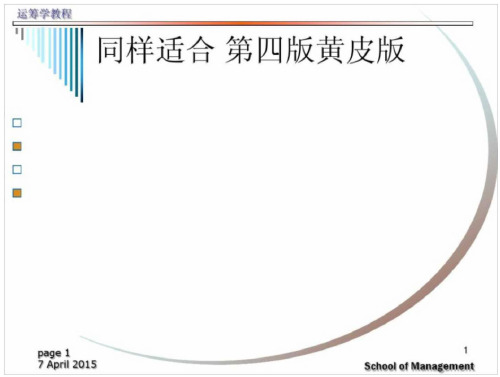
cx°-cx* >0;
V是maxZ = C*X的S优解, 故 /
C*X*-C'X°>0;
Jr
(C*-C)(X*-X°)
= C(X°-X*) + C*(X*-X°)>0
page 25 7 April 2015
25
School of Management
第一章习题解答
1.11考虑线性规划问题
□
minZ =叫 +2JC2 + — 4X4
□
行域的每个顶点依次使目标函数达到最优。 鲤. 锒剎曷錄里姉取妾加下.
c广
cd
0
0
基b Xi x2
x3
d
x2 3/ 0 1
5/14
2
X4 j
-3/4
c
page 14
7 April 2 ns
Xi 1 1 0
Qi—'0
0
-2/14 ^W35
-
3/14d- i
第一章习题解答
□ □
当c/d在3/10到5/2之间时最优解为图中 的A 点;当c/d大于5/2且c大于等于0时最优解 为图中 的B点;当c/d小于3/10且d大于0时最优 解为图中
Bi. ■
规划问题的 maxZ = C1 X (AX =b
□
最优解, 证明[在x >0这两点连线
■
上的所有点也是 对于任何0 < a < 1, 两点连线」:的点¥满足:
X =aX⑴+(l-a)JT2)也是可行解, 且
CTX = CTaXG) +Cf\l-a)X(2y
=CTaXay -aCrX(2} +CrX
School of Management
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学部分课后习题解答P47 1.1 用图解法求解线性规划问题
a)
12
12
12
12
min z=23
466 ..424
,0
x x
x x
s t x x
x x
+
+≥
⎧
⎪
+≥
⎨
⎪≥
⎩
解:由图1可知,该问题的可行域为凸集MABCN,且可知线段BA上的点都为
最优解,即该问题有无穷多最优解,这时的最优值为
min 3
z=2303
2
⨯+⨯=
P47 1.3 用图解法和单纯形法求解线性规划问题
a)
12
12
12
12
max z=10x5x
349 ..528
,0
x x
s t x x
x x
+
+≤
⎧
⎪
+≤
⎨
⎪≥
⎩
解:由图1可知,该问题的可行域为凸集OABCO,且可知B点为最优值点,
即
1
12
122
1
349
3
528
2
x
x x
x x x
=
⎧
+=
⎧⎪
⇒
⎨⎨
+==
⎩⎪
⎩
,即最优解为*
3
1,
2
T
x
⎛⎫
= ⎪
⎝⎭
这时的最优值为
max
335
z=1015
22
⨯+⨯=
单纯形法: 原问题化成标准型为
121231241234
max z=10x 5x 349
..528,,,0x x x s t x x x x x x x +++=⎧⎪
++=⎨⎪≥⎩ j c →
10
5
B C
B X b 1x
2x
3x
4x
0 3x 9 3 4 1 0 0
4x
8
[5] 2 0 1 j j C Z -
10
5 0 0 0 3x 21/5 0 [14/5] 1 -3/5 10
1x
8/5
1 2/5 0 1/5 j j C Z -
1 0 -
2 5 2x 3/2 0 1 5/14 -3/14 10
1x
1
1 0 -1/7
2/7
j j C Z -
-5/14 -25/14
所以有*max 33351,,1015222T
x z ⎛⎫
==⨯+⨯= ⎪⎝⎭
P78 2.4 已知线性规划问题:
1234
12
4122341231234max
24382669,,,0
z x x x x x x x x x x x x x x x x x x x =+++++≤⎧⎪+≤⎪⎪
++≤⎨
⎪++≤⎪≥⎪⎩
求: (1) 写出其对偶问题;(2)已知原问题最优解为)0,4,2,2(*=X ,试根据对偶理论,直接求出对偶问题的最优解。
解:(1)该线性规划问题的对偶问题为:
1234
12
4123434131234min
86692234
11,,,0
w y y y y y y y y y y y y y y y y y y y =+++++≥⎧⎪+++≥⎪⎪
+≥⎨
⎪+≥⎪≥⎪⎩
(2)由原问题最优解为)0,4,2,2(*=X ,根据互补松弛性得:
12
412343422341y y y y y y y y y ++=⎧⎪
+++=⎨⎪+=⎩
把)0,4,2,2(*=X 代入原线性规划问题的约束中得第四个约束取严格不等号,即4224890y ++=<⇒=
从而有12
123322341y y y y y y +=⎧⎪
++=⎨⎪=⎩
得123443
,,1,055
y y y y ====
所以对偶问题的最优解为*43
(,,1,0)55
T y =,最优值为min 16w =
P79 2.7 考虑如下线性规划问题:
123123123123123min 6040803224342223,,0
z x x x x x x x x x x x x x x x =++++≥⎧⎪++≥⎪⎨
++≥⎪⎪≥⎩
(1)写出其对偶问题;(2)用对偶单纯形法求解原问题; 解:(1)该线性规划问题的对偶问题为:
123123123123123max 2433426022403280,,0w y y y y y y y y y y y y y y y =++++≤⎧⎪++≤⎪⎨
++≤⎪⎪≥⎩
(2)在原问题加入三个松弛变量456,,x x x 把该线性规划问题化为标准型:
12312341235123
6max 60408032243422230,1,,6j z x x x x x x x x x x x x x x x x j =------+=-⎧⎪---+=-⎪⎨
---+=-⎪⎪≥=⎩
j c →
-60
-40
-80
B C
B X b 1x
2x
3x
4x
5x
6x
0 4x -2 -3 -2 -1 1 0 0 0 5x -4 [-4] -1 -3 0 1 0 0
6x
-3
-2 -2 -2 0 0 1 j j C Z -
-60
-40
-80。
