背诵圆柱和圆锥知识点归纳总结
圆柱圆锥知识点总结

圆柱圆锥知识点总结一、圆柱的定义和性质圆柱是由一个矩形绕着一条平行于其中一边的直线移动而得到的几何体。
圆柱的底面是一个圆,上下底面平行且相等,侧面是一个矩形。
通常情况下,我们所说的圆柱指的是直圆柱,即底面和侧面直角相交的圆柱。
圆柱的性质:1. 圆柱的侧面是一个矩形,其面积等于底面周长乘以高度。
2. 圆柱的体积等于底面积乘以高度,即V=πr^2*h。
3. 圆柱的表面积等于两个底面积之和加上侧面积,即S=2πr^2+2πrh。
二、圆锥的定义和性质圆锥是由一个直角三角形绕着它的一个直角边旋转一周而得到的几何体。
圆锥的侧面是一个由母线和母线上一点到底面的连线组成的扇形。
通常情况下,我们所说的圆锥指的是直圆锥,即底面圆和侧面直角相交的圆锥。
圆锥的性质:1. 圆锥的侧面是一个扇形,其面积等于底面周长乘以母线的一半。
2. 圆锥的体积等于1/3底面积乘以高度,即V=1/3πr^2*h。
3. 圆锥的表面积等于底面积加上底面到顶点的母线所绕成的曲面积,即S=πr^2+πrl。
三、圆柱和圆锥的应用1. 圆柱和圆锥在日常生活中有着广泛的应用,比如有些容器的外形就是圆柱或者圆锥;例如筒形创可贴盒,花瓶,饮料瓶等。
2. 圆柱和圆锥的公式和计算方法可以用来解决一些实际问题,比如计算容器的容积和表面积,计算油桶的容量,设计工程建筑结构等。
3. 圆柱和圆锥的几何图形在工程实践中也有着广泛的应用,比如圆柱形的桥墩,圆锥形的喷水池等。
四、圆柱和圆锥知识点的考点在中学数学课本和考试中,圆柱和圆锥作为基础几何图形经常出现,特别是在解题和推导中经常需要用到它们的性质和公式。
掌握好圆柱和圆锥的知识对于初中数学的学习和考试成绩至关重要。
总结通过对圆柱和圆锥的定义、性质、公式和应用等方面的了解,我们可以更好地理解这两种几何图形的特点和作用,进而提高我们的数学运算能力和解决实际问题的能力。
在学习和应用过程中,我们要注重在不断的练习和实践中巩固这些知识,才能更好地应用它们解决实际问题,提高数学素养。
(完整版)圆柱和圆锥知识点总结

长方体里削出最大的圆柱、圆锥:圆柱、圆锥底面直径等于宽(宽﹥高),圆柱、圆锥高等于长方体高。
4.浸物体积问题(排水法测不规则物体的体积):水面上升部分的体积就是浸
入水中物品的体积,等于盛水容器的底面积乘上升的高度。
也就是变化的水的体积。
主要类型:①盛满水,浸物溢水;②浸物水面上升;③取物水面下降。
5.等体积转换问题:圆锥体沙堆铺路;长方体钢材熔铸成圆柱或圆锥;橡皮泥
改变形状;圆柱中的溶液倒入圆锥……都是体积不变的问题。
解决此类问题,最好列出体积相等公式,再代入数据进行计算。
圆柱和圆锥知识点归纳总结

(背诵)圆柱和圆锥知识点归纳总结(总3页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除圆柱和圆锥有关知识点一、圆柱和圆锥各部分的名称以及特征1、圆柱(1)认识圆柱各部分的名称:上下两个圆面叫做底面,圆柱的周围叫侧面,圆柱两个底面之间的距离叫做高。
(2)圆柱的特征:圆柱的上下底面是两个圆,它们是完全相同的;圆柱的侧面是曲面;圆柱的高有无数条,高的长度都相等。
(3)沿高剪开:圆柱的侧面展开后是长方形(当圆柱底面周长与高相等时,展开后是正方形)。
这个长方形的长就是圆柱底面的周长,宽就是圆柱的高。
2. 圆锥(1)认识圆锥各部分的名称:下面一个圆面叫做底面,它周围叫侧面,从圆锥的顶点到底面圆心的距离叫做高。
(2)圆锥的特征圆锥的底面都是一个圆。
圆锥的侧面是曲面。
一个圆锥只有一条高。
(3)圆锥的侧面沿着一条母线展开后是一个扇形,这个扇形的弧长等于圆锥的底面周长,半径等于圆锥的母线长。
(如下图所示)二、基本公式1、圆的知识圆的周长=直径×π=半径×2×πC=πd =2πr逆推公式有:直径=圆的周长÷πd = C÷π半径=圆的周长÷π÷2r = C÷π÷2圆的面积=半径的平方×π=(直径÷2)2×π=(圆的周长÷π÷2)2×πS=πr2=(d÷2)2×π=(C÷π÷2)2×π2、( 1 )圆柱的侧面积:把圆柱侧面沿高展开,得到一个长方形(或正方形),长方形的长是圆柱的底面周长,长方形的宽是圆柱的高。
圆柱的侧面积=底面周长×高=直径×π×高=半径×2×π×高S 侧=C h=πd h=2πr h逆推公式有:圆柱的高=圆柱的侧面积÷底面周长=圆柱的侧面积÷(π×高) =圆柱的侧面积÷(半径×2×π) h=S 侧÷C圆柱的底面周长=圆柱的侧面积÷高C =S 侧÷h(2)圆柱的表面积=圆柱的侧面积+圆柱的底面积×2 S 表=S 侧+2S 底(3) 圆柱的体积=底面积×高V 柱=S h=πr 2 h逆推公式有:圆柱的高=圆柱的体积÷底面积h=V 柱÷S圆柱的底面积=圆柱的体积÷高h=V 柱÷S3 ( 1 )如果圆柱的侧面展开是一个正方形,那么这个圆柱的高和底面周长相等。
(背诵)圆柱和圆锥知识点归纳总结

31 圆柱和圆锥1、圆柱上下两个圆面叫做底面,圆柱的周围叫侧面,圆柱两个底面之间的距离叫做高。
(2)圆柱的特征:圆柱的上下底面是两个圆,它们是完全相同的;圆柱的侧面是曲面; 圆柱的高有无数条,高的长度都相等。
(3)沿高剪开:圆柱的侧面展开后是长方形(当圆柱底面周长与高相等时,展开后是正方形)。
这个长方形的长就是圆柱的底面周长,宽就是圆柱的高。
2. 圆锥下面一个圆面叫做底面,它周围叫侧面,从圆锥的顶点到底面圆心的距离叫做高。
(2)圆锥的特征圆锥的底面都是一个圆。
圆锥的侧面是曲面。
一个圆锥只有一条高。
(3)圆锥的侧面沿着一条母线展开后是一个扇形5、等底等高情况下,圆柱体积是圆锥体积的3倍。
等底等高的情况下,圆锥体积是圆柱体积的316、等体积等高的圆柱和圆锥,圆锥底面积是圆柱底面积的3倍;等体积等底面积的圆柱和圆锥,圆锥的高是圆柱高的3倍。
7、圆柱的横切:切成n 段,需要n-1次,增加2×(n-1)个底面积8、把一个正方体削成一个最大的圆柱(或圆锥),正方体的棱长就是圆柱(或圆锥)的底面直径和高。
4.圆柱表面积=2底面积+侧面积圆柱侧面积=底面周长×高圆柱体积=底面积×高 圆锥体积=底面积×高×3.14×22=12.56 3.14×4=12.56 3.14×9=28.26 3.14×32=28.26 3.14×5=15.7 3.14×12=37.68 3.14×42=50.24 3.14×6=18.843.14×52=78.5 3.14×7=21.983.14×62=113.04 3.14×8=25.12。
小学数学六年级圆柱、圆锥知识点总结复习
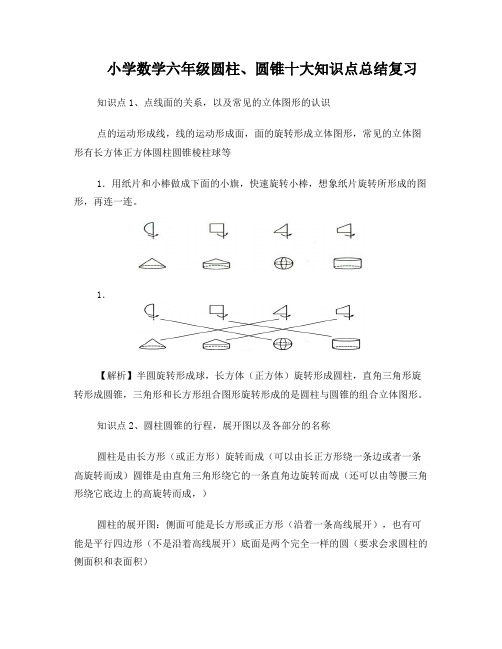
小学数学六年级圆柱、圆锥十大知识点总结复习知识点1、点线面的关系,以及常见的立体图形的认识点的运动形成线,线的运动形成面,面的旋转形成立体图形,常见的立体图形有长方体正方体圆柱圆锥棱柱球等1.用纸片和小棒做成下面的小旗,快速旋转小棒,想象纸片旋转所形成的图形,再连一连。
1.【解析】半圆旋转形成球,长方体(正方体)旋转形成圆柱,直角三角形旋转形成圆锥,三角形和长方形组合图形旋转形成的是圆柱与圆锥的组合立体图形。
知识点2、圆柱圆锥的行程,展开图以及各部分的名称圆柱是由长方形(或正方形)旋转而成(可以由长正方形绕一条边或者一条高旋转而成)圆锥是由直角三角形绕它的一条直角边旋转而成(还可以由等腰三角形绕它底边上的高旋转而成,)圆柱的展开图:侧面可能是长方形或正方形(沿着一条高线展开),也有可能是平行四边形(不是沿着高线展开)底面是两个完全一样的圆(要求会求圆柱的侧面积和表面积)圆锥的展开图:侧面是一个扇形,底面是一个圆(不要求会求圆锥的侧面积和表面积)2.下面()图形是圆柱的展开图。
(单位:cm)2.A【解析】圆柱的展开图,侧面是长方形(或正方形)底面是两个圆,并且底面圆的周长等于长方形的长,高是长方形的宽。
三个选项中底面圆的直径是3,底面周长是3.14×3=9.42,三个选项的高都是2,所以选择A。
3.一个圆柱体的侧面是一个正方形,直径是5dm,正方形面积是_________。
3.246.49平方分米【解析】圆柱体的侧面是一个正方形,说明圆柱的底面圆的周长与圆柱的高相等。
底面圆的周长等于3.14×5=15.7(分米),即正方形的边长是15.7分米,所以面积是15.7×15.7=146.49(平方分米)。
4.用一张长4.5分米, 宽2分米的长方形纸, 围成一个圆柱形纸筒, 它的侧面积是。
4.9平方分米【解析】圆柱形纸筒的侧面积就是长方形的面积:4.5×2=9(平方分米)。
完整版)六年级下册圆柱和圆锥知识点

完整版)六年级下册圆柱和圆锥知识点文章已经没有格式错误和明显有问题的段落了,但可以对每段话进行小幅度改写,如下:第一单元圆柱和圆锥知识点一、圆柱的特征:圆柱有两个底面、一个侧面和无数条高。
其底面为大小相同的圆形。
圆柱的侧面展开后可以得到长方形、正方形或平行四边形,与圆柱有密切关系。
例如,长方形的长等于圆柱的底面周长,长方形的宽等于圆柱的高,长方形的面积等于圆柱的侧面积。
当圆柱的底面周长和高相等时,其侧面展开图为正方形。
二、圆锥的特征:圆锥有一个圆形底面和一个扇形侧面,只有一条高。
圆锥的高是从圆锥顶点到底面圆心的距离。
三、基本公式:在求圆柱表面积、圆柱和圆锥的体积时,需要先复圆的半径计算公式。
已知直径求半径为r=d÷2,已知周长求半径为r=c÷π÷2.圆柱的底面积为πr²,侧面积为底面周长×高,即S侧=Ch=πdh=2πrh,圆柱的表面积为侧面积加上底面积的两倍。
圆柱的体积为底面积乘以高,即V圆柱=Sh=πr²h。
圆锥的体积为底面积乘以高再除以3,即V圆锥=1/3Sh=1/3πr²h。
四、单位换算:在长度单位换算中,相邻两个长度单位之间的进率是10,1千米等于1000米,1米等于10分米,1分米等于10厘米,1厘米等于10毫米。
在面积单位换算中,相邻两个面积单位之间的进率是100,1平方千米等于100公顷,1公顷等于平方米,1平方米等于100平方分米,1平方分米等于100平方厘米,1平方厘米等于100平方毫米。
在体积单位换算中,相邻两个体积单位之间的进率是1000,1立方米等于1000升,1升等于1立方分米,1立方分米等于1000立方厘米,1立方厘米等于1毫升。
在单位换算中,大单位化为小单位使用乘法,小单位化为大单位使用除法。
小学圆柱圆锥知识点总结

小学圆柱圆锥知识点总结
一、圆柱的定义和性质
1. 定义:圆柱是由两个平行并且等圆的底面以及连接这两个底面的侧面组成的几何体。
2. 性质:
- 圆柱的底面是两个相同的圆,其半径为r;
- 圆柱的侧面是一条沿着两个圆周运动的直线;
- 圆柱的高度为h;
- 圆柱的体积为V = πr²h;
- 圆柱的表面积为S = 2πr² + 2πrh。
二、圆锥的定义和性质
1. 定义:圆锥是由一个圆锥面和一个平面底面组成的几何体。
2. 性质:
- 圆锥的底面是一个圆,其半径为r;
- 圆锥的侧面是由底面到顶点的直线组成;
- 圆锥的高度为h;
- 圆锥的体积为V = (1/3)πr²h;
- 圆锥的表面积为S = πr² + πrl。
三、圆柱和圆锥的应用
1. 在日常生活中,圆柱和圆锥经常被用来制作容器和器皿。
例如,铅笔筒、花瓶、圆锥形的帽子等都是圆柱和圆锥的典型应用。
2. 在工程建筑中,圆柱和圆锥也有着广泛的应用。
例如,建筑物中的柱子和锥形的塔尖都是圆柱和圆锥结构。
4. 在数学问题中,圆柱和圆锥的概念也经常被用来解决问题。
例如,通过计算圆柱和圆锥的体积和表面积来求解实际问题。
小学生在学习圆柱和圆锥的过程中,可以通过观察实物和图形来加深对这两种几何体的理解。
老师可以通过示范和练习来帮助学生掌握圆柱和圆锥的相关知识,鼓励他们通过实际的应用来体会几何知识的重要性。
希望本文的介绍对小学生学习圆柱和圆锥有所帮助。
圆柱和圆锥知识点总结

圆柱和圆锥知识点总结一、圆柱的定义和性质1.定义:圆柱是由一个圆沿着一个平行于圆所在平面的直线移动形成的,在移动过程中,圆始终垂直于移动线段。
2.元素:圆柱由两个平行的底面、两个底面之间的侧面和两个底面的圆所组成。
3.特点:(1)底面积相等:圆柱的两个底面积相等。
(2)高度:圆柱的高度是连接两个底面的垂直线段。
(3)侧面积:圆柱的侧面积等于底面周长乘以高度。
(4)体积:圆柱的体积等于底面积乘以高度。
(5)闭曲面:圆柱的底面和侧面构成闭合的曲面。
4.圆柱的投影:圆柱的投影形态为一个矩形。
二、圆锥的定义和性质1.定义:圆锥是由一个圆沿着一个平行于圆所在平面的直线移动形成的,在移动过程中,圆始终垂直于移动线段。
2.元素:圆锥由一个底面、一个尖顶和底面与尖顶之间的侧面组成。
3.特点:(1)底面:圆锥的底面是一个圆。
(2)高度:圆锥的高度是连接底面和尖顶的垂直线段。
(3)侧面:圆锥的侧面是由底面上任意一点到尖顶的直线构成。
(4)侧面积:圆锥的侧面积等于圆周长乘以半斜高。
(5)体积:圆锥的体积等于底面面积乘以高度再除以3(6)闭曲面:圆锥的底面和侧面构成闭合的曲面。
4.圆锥的投影:圆锥的投影形态为一个三角形。
三、圆柱和圆锥的应用1.圆柱的应用:圆柱广泛应用于各个领域,如:(1)建筑:柱子、立柱、柱圈等结构都是圆柱体的应用。
(2)机械:轴、销、滚筒等都是圆柱体的应用。
(3)制造:瓶子、罐子、圆筒形容器等都是圆柱体的应用。
(4)数学:柱体的几何性质是数学中的重要内容,如计算底面积、侧面积、体积等。
(5)其他:圆柱的轴对称性质也常用于解决几何问题。
2.圆锥的应用:圆锥也有广泛的应用,如:(1)建筑:塔、锥形屋顶、圆锥形尖塔等都是圆锥体的应用。
(2)环境工程:漏斗、喷泉、喷水池等都是圆锥体的应用。
(3)制造:圆锥形工件的制造是机械加工中常见的任务。
(4)数学:圆锥的几何性质也是数学中的重要内容,如计算底面积、侧面积、体积等。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
背诵圆柱和圆锥知识点
归纳总结
公司内部档案编码:[OPPTR-OPPT28-OPPTL98-OPPNN08]
圆柱和圆锥有关知识点
一、圆柱和圆锥各部分的名称以及特征
1、圆柱
(1)认识圆柱各部分的名称:
上下两个圆面叫做底面,
圆柱的周围叫侧面,
圆柱两个底面之间的距离叫做高。
(2)圆柱的特征:
圆柱的上下底面是两个圆,它们是完全相同的;圆柱的侧面是曲面;圆柱的高有无数条,高的长度都相等。
(3)沿高剪开:圆柱的侧面展开后是长方形(当圆柱底面周长与高相等时,展开后是正方形)。
这个长方形的长就是圆柱底面的周长,宽就是圆柱的高。
2. 圆锥
(1)认识圆锥各部分的名称:下面一个圆面叫做底面,它周围叫侧面,从圆锥的顶点到底面圆心的距离叫做高。
(2)圆锥的特征
圆锥的底面都是一个圆。
圆锥的侧面是曲面。
一个圆锥只有一条高。
(3)圆锥的侧面沿着一条母线展开后是一个扇
形,这个扇形的弧长等于圆锥的底面周长,半径等于圆锥的母线长。
(如下图所示)
二、基本公式
1、圆的知识
圆的周长=直径×π=半径×2×π
C=πd =2πr
逆推公式有:
直径=圆的周长÷π
d = C÷π
半径=圆的周长÷π÷2
r = C÷π÷2
圆的面积=半径的平方×π
=(直径÷2)2×π
=(圆的周长÷π÷2)2×π S=πr2
=(d÷2)2×π
=(C÷π÷2)2×π
2、( 1 )圆柱的侧面积:把圆柱侧面沿高展开,得到一个长方形(或正方形),长方形的长是圆柱的底面周长,长方形的宽是圆柱的高。
圆柱的侧面积=底面周长×高
=直径×π×高
=半径×2×π×高
S 侧=C h=πd h=2πr h
逆推公式有:
圆柱的高=圆柱的侧面积÷底面周长
=圆柱的侧面积÷(π×高)
=圆柱的侧面积÷(半径×2×π)
h=S 侧÷C
圆柱的底面周长=圆柱的侧面积÷高
C =S 侧÷h
(2)圆柱的表面积
=圆柱的侧面积+圆柱的底面积×2
S表=S 侧+2S底
(3) 圆柱的体积=底面积×高
V柱=S h=πr2 h
逆推公式有:
圆柱的高=圆柱的体积÷底面积
h=V柱÷S
圆柱的底面积=圆柱的体积÷高
h=V柱÷S
3 ( 1 )如果圆柱的侧面展开是一个正方形,
那么这个圆柱的高和底面周长相等。
( 2 )半个圆柱的表面积
= 侧面积÷2 +一个底面积+直径×高
(3)
1
4
圆柱的表面积
=侧面积÷4+半个底面积+直径×高
4、圆锥的体积=底面积×高×
1
3
V锥=
3
1
Sh
逆推公式有:
圆锥的高=圆锥的体积×3÷底面积
h=V锥×3÷S
圆锥的底面积=圆锥的体积×3÷高
S= V锥×3 ÷h
5、等底等高情况下,圆柱体积是圆锥体积的3倍。
等底等高的情况下,圆锥体积是圆柱体积
的
3
1
等底等高的情况下,圆锥体积比圆柱体积少
3
2
等底等高的情况下,圆柱体积比圆锥体积多2倍
6、等体积等高的圆柱和圆锥,圆锥底面积是圆柱底面积的3倍;
等体积等底面积的圆柱
和圆锥,圆锥的高是圆柱
高的3倍。
7、圆柱的横切:切成n段,需要n-1次,增加2×(n-1)个底面积
8、圆柱的纵切:切1次,增加2个长方形,长方形的长是底面的直径,宽是圆柱的高
9、圆锥的纵切:切1次,增加2个三角形,三角形的底是圆锥的直径,
三角形的高是圆锥的高
10、把一个正方体削成一个最大的圆柱(或圆锥),正方体的棱长就是圆柱(或圆锥)的底面直径和高。
11、①熔铸(或铸成),体积不变。
②注水问题:上升的(或下降)的水的体积等于放入的的物体的体积。
(完全浸没)
12.一个圆柱的侧面展开图是一个正方形,说明底面周长和高的比是1∶1,
半径和高的比是1∶2π,
直径和高的比是1∶π13、当侧面积一定时,越是细、长的圆柱体积越小,越是粗、矮的圆柱体积越大。
