安徽艺术学院2019-2020学年

合集下载

2019-2020学年安徽省黄山市“八校联盟”高二上学期期中数学试题(解析版)

，，由勾股定理可得，同理可知，
，为等边三角形，
设的外接圆圆心为点，连接，则，且，
由中位线的性质可知点为的中点，为圆的一条直径，
所以，，由圆的内接四边形的性质可知，，
，由正弦定理可得，
，因此，球的表面积为，故答案为： .
【点睛】
本题考查多面体的外接球表面积的计算，解题时要充分分析多边形的形状，找出球心的位置，考查推理能力与计算能力，属于中等题.
【答案】或5
【解析】由点到直线的距离公式进行解答，即可求出实数a的值．
【详解】
点（1，a）到直线x﹣y+1＝0的距离是，
∴ ；
即|a﹣2|＝3，
解得a＝﹣1，或a＝5，
∴实数a的值为﹣1或5．
故答案为：﹣1或5．
【点睛】
本题考查了点到直线的距离公式的应用问题，解题时应熟记点到直线的距离公式，是基础题．
【点睛】
本题考查的知识点是斜二侧画法，三角形形状的判断，解答的关键是斜二侧画法还原在直角坐标系的图形．
6．圆台的两个底面面积之比为，母线与底面的夹角是，轴截面的面积为，则圆台的母线长 ()
A． B． C． D．12
【答案】D
【解析】设圆台的上底面半径为，根据面积比可知下底面半径为；利用圆台的轴截面面积构造关于的方程，求得后，利用即可得到结果.
【详解】
对于A，由正方体的特征可得平面即平面，因为平面，所以平面平面，故A正确；
对于B，由正方体特征可得平面，，所以，由可得平面，则，故B正确；
对于C，由且平面，平面，所以平面，所以点到平面的距离为定值，由为定值可得为定值，故C正确；

2020年安徽艺术学院专升本招生章程

安徽艺术学院2020年普通高校专升本招生章程一、学校全称：安徽艺术学院二、办学层次：本科三、办学类型：公办普通高等学校四、办学地址：合肥市新站区前岭路与淮海大道交口东北五、招生专业及计划：六、报名（一）招生对象：安徽省省属普通高校（以及经过批准举办普通高等职业教育的成人高等院校）的应届全日制普通高职（专科）毕业生及安徽省高校毕业的具有普通高职（专科）学历的退役士兵。

（二）报名条件（参照普通高等学校高等职业教育（专科）专业目录（2015年）)：1、音乐表演：“文化艺术大类”中的“表演艺术类”的表演艺术、歌舞表演、音乐剧表演、现代流行音乐、作曲技术、音乐制作、钢琴伴奏、钢琴调律、音乐表演专业和“民族文化类”的民族表演艺术专业；“教育与体育大类”中的“教育类”的早期教育、学前教育、小学教育、音乐教育、艺术教育、现代教育技术专业；“交通运输大类”中的“航空运输类”的空中乘务专业；“新闻传播大类”中的“广播影视类”的音像技术、录音技术与艺术专业。

2、表演：戏曲与影视表演方向：高职（专科）各大类专业。

舞美方向：高职（专科）各大类专业。

综合艺术方向：“文化艺术大类”中的“表演艺术类”的戏曲表演、表演艺术、音乐表演、戏剧影视表演、音乐剧表演、舞蹈表演、国际标准舞专业；“新闻传播大类”中的“广播影视类”的影视编导、播音与主持、摄影摄像技术专业；“交通运输大类”中的“航空运输类”的空中乘务专业和“水上运输类”的国际邮轮乘务管理专业和“铁道运输类”的高速铁路客运乘务专业；“教育与体育大类”中的“教育类”的学前教育、音乐教育、小学教育、舞蹈教育专业。

3、播音与主持艺术：“新闻传播大类”中的“新闻出版类”的网络新闻与传播专业和“广播影视类”所含专业；“文化艺术大类”中的“表演艺术类”所含专业；“教育与体育大类”中的“文秘类”的文秘专业和“语言类”的商务英语、旅游英语、应用英语专业；“交通运输大类”中的“航空运输类”的空中乘务专业；“旅游大类”中的“旅游类”的导游专业。

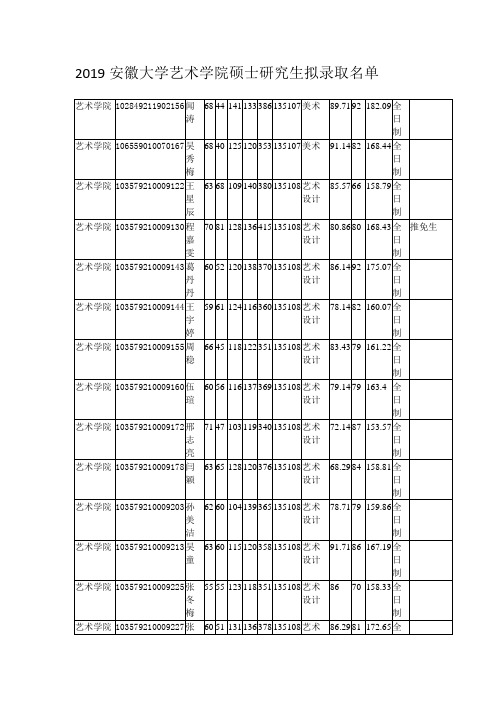
2019安徽大学艺术学院硕士研究生拟录取名单

154.76
全日制
推免生
艺术学院
103579210009276
孙文怡
66
41
113
121
341
135108
艺术设计
82.86
90
164.43
全日制
艺术学院
103579210009311
和玉玉
65
62
119
117
363
135108
艺术设计
79
72
154.17
全日制
推免生
艺术学院
103579210009314
103579103570065
王进庆
0
0
0
0
0
135108
艺术设计
0
0
0
全日制
艺术学院
103579106360066
王楠楠
0
0
0
0
0
135108
艺术设计
0
0
0
全日制
艺术学院
103579103700069
兰婷婷
0
0
0
0
0
135108
艺术设计
0
0
0
全日制
艺术学院
103579103700070
程轩楠
0
0
0
专业码
拟录取专业
复试
面试
复试
笔试
总得分
学习方式
村官，初试加15分
艺术学院
105339410618054
黄亚茹
66
48
135
134
383
135107
美术
84

2019-2020学年安徽大学附属学校高三英语上学期期中考试试题及答案解析

2019-2020学年安徽大学附属学校高三英语上学期期中考试试题及答案解析第一部分阅读（共两节，满分40分）第一节（共15小题；每小题2分，满分30分）阅读下列短文，从每题所给的A、B、C、D四个选项中选出最佳选项AIt looks like 2017 is shaping up to be a record-breaking year in movie History. Here is a list of some of the year’s biggest blockbusters so far.Kong: Skull IslandA reboot (重启) of King Kong would normally get laughed at in this day and age, but it looks like this modem version of the story will be worth watching. With US actress Brie Larson and UK actor Tom Hiddleston in the mix, this film is set to be this year’s biggest monster tale.Release Date:3/10/17Beauty and the BeastDirector Bill Condon is bringing back a part of our childhood in live action, complete with the songs we all remember and love. With British stars Emma Watson and Dan Stevens leading thecast, the classic Walt Disney story already sounds like it’ll be a delight for both children and adults.Release Date:3/17/17The Fate of the FuriousThere was doubt that we’d even get a Fast 8, especially after the fitting ending US actor Paul Walker’s character was given at the end of Furious 7. Fans thought they’d never see Dom and the rest of the crew back in action, but thankfully, US star Vin Diesel himself confirmed that The Fate of the Furious is fueling up for another go.Release Date:4/14/17Spider-Man: HomecomingSpider Man is heading home to Marvel Studios for the first time. The movie will show us Peter Parker’s high school days, and will continue the threads we saw formed during his initial appearance in Captain America: Civil War. We know that Michael Keaton is playing The Vulture in this story, and that both Happy Hogan and Tony Stark, played by US actors Jon Favreau and Robert Downey Jr., are along for the ride.Release Date:7/7/171.Which of the following movies can’t you see on May Day?A.Kong: Skull Island.B.Beauty and the Beast.C.The Fate of the Furious.D.Spider-Man: Homecoming.2.What can we know about Beauty and the Beast?A.It is fueling up for another go.B.It is produced by Marvel StudiosC.It’ll show us Peter Parker’s school days.D.It’ll be enjoyable for both children and adults.3.What does the underlined word “cast” probably mean?A.Characters.B.Actors.C.Directors.D.Teachers.BI’ve long believedthat positive living isn’t about being optimistic every minute of every day. That kind of permanently happy state can’t be the goal, because it’s impossible to achieve.It turns out that psychological research finds true happiness comes from authentic positivity, and authentic positivity comes from emotional flexibility.Being flexible emotionally means being open to the full range of emotional experiences, including the challenging ones like anger, disappointment and sadness. Emotional flexibility means being able to shift behaviors and mindsets to meet different situational needs, and adapting when circumstances change.However, emotionally flexible people are not chameleons (变色龙) whose outlook changes based on which way the wind is blowing. Instead, emotional flexibility is a skill that helps people judge the complexities of daily life, and stick to their deeply held values.I’ve learned a new word that I’d like to share with you: Eudaimonia (幸福感). Eudaimonia is the opposite of hedonism (享乐主义), the idea that happiness comes from the constant pursuit of pleasure and avoidance of pain. Eudaimonia, by contrast, encourages us to pursue meaning and authenticity, growth and honest joy. Both are philosophical approaches to happiness, and recent psychological thought is leaning toward eudaimonia as a more sustainable, satisfying model.Eudaimonia was first mentioned by Aristotle, who got the term from the Greek word “daimon,” which means “true nature.” Tome, walking a positive path means accepting that we each have positive true nature and permanent goodness. What we learn from the concept of eudaimonia is that we are best equipped to realize thisnature when we are emotionally honest and flexible.4. What is the author’s belief?A. People should live alone.B. People can’t always be happy.C. People can’t always achieve their goals.D. People should pursue true achievements.5. What do enmotionally flexible people commit themselves to?A. Their strongly believed values.B. Their different needs.C. Permanent happiness.D. The pursuit of hedonism.6. How can people gain eudaimonia according to the author?A. By being honest to others.B. By changing true nature.C. By keeping realstically optimistic.D. By pursuing pleasure constantly.7. Which of the following is a suitable title for the text?A. What is the meaning of eudaimonia?B. What should we do to keep positive?C. How can we keep happy forever?D. Why can’t people be happy all the time?CNew Yorkis among the slowest cities during rush hour in the world, according to a report published in January. Crossing midtown by car is soul-destroying. The average speed is 4.7 miles per hour, not much quicker than a quick walk. But relief is in sight. On April 1st, state lawmakers agreed to introduce road charges, makingNew Yorkthe first big American city to do so. By next year vehicles will have to pay to enterManhattansouth of60th Street.The details of the new rule, including how much drivers will have to pay, how they will pay and how often they will pay, haveyet to be decided. A “traffic mobility review board" will be set up to work all this out. New Yorkers living in the fee zone who make less than $60,000 a year will be exempt (获豁免) . Other drivers, including motorcyclists, the city' s civil servants, disabled drivers and the trucking industry, all want discounts or exemptions, which might not be a good sign.If done right, road pricing could be expanded beyondManhattan.New Yorkcan learn from other cities.Singapore, for instance, which has had pricing for decades, adjusts prices regularly. It can also learn from mistakes.London, which rolled out its pricing in 2003, is only starting to charge on-demand car hires like Uber.Stockholm exempted too many vehicles, which caused a drop in revenues (收入) .Other cities considering road charges, includingLos Angeles, Philadelphia Portland,San FranciscoandSeattle, are watchingNew York. "We really have t1o make a good example," says Nicole Gelinas of the Manhattan Institute, aNew Yorkthink tank.8. What does the report find?A.New Yorkhas terrible road traffic.B.New Yorkoften introduces new laws.C. New Yorkers prefer walking to driving.D. New Yorkers face an increased cost of living.9. What can be inferred about the new rule from paragraph 2?A. It faces some potential problems.B. It has clear and detailed fee standards.C. It favors New Yorkers living in the fee zone.D. It fails to win a traffic mobility review board s approval.10. What doLondonandStockholmhave in common?A. They learn a lot fromSingapore.B. They have greatly increased revenues.C. They charge on-demand car hires heavily.D. They are bad examples of placing road charges.11. What is the best title for the text?A. How much does it cost to drive intoManhattan?B.New Yorkapproves road pricing forManhattanC. Drivers fear crossingManhattansouth of60th StreetD. Who will be exempt from road charges inManhattan?DLight pollution is a significant but overlooked driver of the rapid decline of insect populations, according to the most comprehensive review of the scientific evidence to date.Artificial light at night can affect every aspect of insects' lives, the researchers said. "We strongly believe artificial light at night — in combination with habitat loss, chemical pollution.invasive (入侵的) species, and climate change — is driving insect declines, " the scientists concluded after assessing more than 150 studies.Insect population collapses have been reported around the world, and the first global scientific review published in February,said widespread declines threatened to cause a "catastrophic collapse of nature's ecosystems".There are thought to be millions of insect species, most still unknown to science, and about half are active at night. Those active in the day may also be disturbed by light at night when they are at rest.The most familiar impact of light pollution is moths (飞蛾) flapping around a bulb, mistaking it for the moon. Some insects use the polarisation of light to find the water they need to breed, as light waves line up after reflecting from a smooth surface. But artificial light can scupper (使泡汤) this. Insects areimportant prey (猎物) for many species, but light pollution can tip the balance in favour of the predator if it traps insects around lights. Such increases in predation risk were likely to cause the rapid extinction of affected species, the researchers said.The researchers said most human-caused threats to insects have analogues in nature, such as climate change and invasive species. But light pollution is particularly hard for insects to deal with.However, unlike other drivers of decline, light pollution is ly easy to prevent. Simply turning off lights that are not needed is the most obvious action, he said, while making lights motion-activated also cuts light pollution. Shading lights so only the area needed is lit up is important. It is the same with avoiding blue-white lights, which interfere with daily rhythms. LED lights also offer hope as they can be easily tuned to avoid harmful colours and flicker rates.12. What is discussed in the passage?A. Causes of declining insect populations.B. Consequences of insect population collapses.C. Light pollution: the key bringer of insect declines.D. Insect declines: the driver of the collapsed ecosystem.13. What is the 5th paragraph mainly about?A. How light travels in space.B. How light helps insects find food.C. How the food chain is interrelated.D. How light pollution affects insects.14. What does the underlined word"analogues"in Paragraph 6probably mean?A. Selective things.B. Similar things.C. Variations.D. Limitations.15. What is the purpose of the last paragraph?A. To offer solutions.B. To give examples.C. To make comparisons.D. To present arguments.第二节（共5小题；每小题2分，满分10分）阅读下面短文，从短文后的选项中选出可以填入空白处的最佳选项。

安徽省宣城市2019-2020学年高一上学期期末考试物理试题 - 副本

物理试题考生注意：1．本试卷分1卷（选择題）和Ⅱ卷（非选择題）两部分。

满分100分，考试时间100分钟。

2．考生作答时，请将答案答在答题卡上。

第I卷每小题选出答案后，用2B铅笔把答题卡上对应题目的答标号涂黑；第Ⅱ卷请用直径0.5毫黑色签宇笔在答题卡上各题的答题区域内作答，想出答区城书写的各家无，在要春、稿纸上作答无效。

3．本卷命题范围：必修①。

第I卷（选择题，共48分）一、选择题：本题共12小题，在每小题出的四个选项中，第1～8題只有一个选项正确，第9-12题有多个选项正确，全部选对的得4分，选对但不全的得2分，有选错的得0分。

1．宣城市第二届运动会于2019年10月4日-20日举行，关于此次运动会比赛的论述，下列说法正确的是A．运动员跑完800m比赛，800m指的是路程B．某场球比赛打了加时赛，共需10min，指的是时刻C．运动员铅球成绩为12.50m，指的是铅球路程的大小为12.50mD．足球比赛挑边时，上抛的硬币落回地面猜测正反面，该硬币可以看成质点2．关于伽利路的两个斜面实验，下面说法中正磉的是A．们利略使用图甲斜面进行实验，得出力是改变物体运动状态的原因B．们利略使用图乙斜面进行实验，得出自由落体运动的揽律C．你利略使用图乙斜面进行实验，得出力是维持物体运动的原因D．伽利略使用图甲斜面进行实验，得出自由落体运动的速度随时问变化的规律3．如图为甲、乙丙三个物体相对于同一位置的x-t图象，它们向同一方向开始运动，则在0-t0的时间内，下列说法正确的是A．它们的平均速度相同B．乙的平均速度最小C．甲的位移最大D．图象表示甲、乙、丙三个物体各自的运动轨迹4．北京时间2019年9月28日，中国女排3∶0战胜塞尔维亚女排，提前一轮获得2019年女排世界杯的冠军。

主攻手朱婷扣球跳起可分为下蹲、置地（加速上升）、离地上升、下落四个过程，下列关于她离地上升和下落两个过程的说法正确的是（忽略空气阻力）A．两过程中她都处于超重状态B．两过程中她都处于失重状态C ．前过程为超重，后过程为完全失重D ．前过程为完全失重，后过程为超重5．如图，三段不可伸长的轻质细绳OA 、OB 、OC 共同悬挂一质量为m 的物块，平衡时OB 是水平的，OA 与水平面的夹角为θ，A 、B 端是固定的，AO 的拉力为F 1，BO 的拉力为F 2，则下列判断正确的是A ．OC 绳的拉力就是物块的重力B ．AO 的拉力F 1＝sin mg θ，B0的拉力为F 2＝tan mg θC ．AO 的拉力F 1＝cos mg θ，B0的拉力为F 2＝mgtan θD ．AO 的拉力F 1＝mgsin θ，B0的拉力为F 2＝mgtan θ6．如图，质量均为M 的A 、B 两滑块放在粗糙水平面上，两轻杆等长，杆与滑块、杆与杆间均用光滑铵链连接，在两杆铰合处悬挂一质量为m 的重物C ，整个装置处于静止状态，设杆与水平面间的夹角为θ。

安徽省示范高中培优联盟2019-2020学年高二下学期春季联赛数学(文)试题含解析

安徽省示范高中培优联盟2020年春季联赛(高二)数学(文科) 第Ⅰ卷(选择题共60分)一、选择题(本大题共12小题，每小题5分，共60分．在每小题给出的四个选项中，只有一项是符合题目要求的．)1.已知全集U ＝{x ∈N *|x ≤7}，集合M ＝{1，3，5，7}，集合N ＝{3，4，5，6，7}，则(UM )∩N＝（） A. {1，2，4，6} B. {3，5，7} C. {4，6} D. {2}【答案】C 【解析】【分析】根据集合补集、交集运算的定义计算．【详解】∵{}1,2,3,4,5,6,7U =，{}2,4,6U M =，∴()UM N {}4,6=．故选：C .【点睛】本题考查集合的综合运算，掌握集合运算的定义是解题关键． 2.设复数z ＝12ii-+(其中i 为虚数单位)，则复数z 的共轭复数z 在复平面内对应的点位于（） A. 第一象限 B. 第二象限C. 第三象限D. 第四象限【答案】A 【解析】【分析】首先根据复数代数形式的除法运算求出复数z ，即可得到其共轭复数，再根据复数的几何意义判断可得；【详解】解：因为()()()()1i 2i 1i 13i 2i 2i 2i 5z ----===++-，所以13i 55z =+ 故z 在复平面内对应的点的坐标为13,55⎛⎫ ⎪⎝⎭位于第一象限．故选：A【点睛】本题考查复数代数形式的除法运算及复数的几何意义，属于基础题3.在集合{1，2，3，4，5}中任取两个不同的数x ，y ，则事件x ＋y ≤5的概率等于（） A. 0.3 B. 0.4C.37D. 0.5【答案】B 【解析】【分析】不妨令x y <，列出(),x y 的不同取值，再列出满足5x y +≤额事件数，根据古典概型的概率公式计算可得；【详解】解：不妨令x y <，则(),x y 的不同取值有()1,2，()1,3，()1,4，()1,5，()2,3，()2,4，()2,5，()3,4，()3,5，()4,5共10种，其中满足5x y +≤的有()1,2，()1,3，()1,4，()2,3共4种，，所以事件5x y +≤的概率为.40410=．故选：B【点睛】本题考查列举法求古典概型的概率问题，属于基础题. 4.“a <1”是“方程ax 2＋2x ＋1＝0有两个不同实根”的（） A. 充分不必要条件 B. 必要不充分条件C. 充要条件D. 既不充分也不必要条件【答案】B 【解析】【分析】首先求出使方程有两个不相同实根参数的值，再根据充分条件、必要条件的定义判断即可；【详解】解：方程2210ax x ++=有两个不同实根00a ≠⎧⇔⇔⎨∆>⎩1a <且0a ≠，所以“1a <”是“方程2210ax x ++=有两个不同实根”的必要不充分条件．故选：B【点睛】本题考查充分条件、必要条件的判断，考查了方程实数根的判断，属于基础题.5.比较甲、乙两名学生的数学学科素养的各项能力指标值(满分为5分，分值高者为优)，绘制了如图所示的六维能力雷达图，例如图中甲的数学抽象指标值为4，乙的数学抽象指标值为5，则下面叙述正确的是（）A. 甲的逻辑推理能力指标值优于乙的逻辑推理能力指标值B. 甲的数学建模能力指标值优于乙的直观想象能力指标值C. 甲的六维能力指标值整体水平优于乙的六维能力指标值整体水平D. 甲的数学运算能力指标值优于甲的直观想象能力指标值【答案】A【解析】【分析】利用雷达图对每一个选项的命题逐一分析推理得解.【详解】对于选项A，甲的逻辑推理能力指标值为4，乙的逻辑推理能力指标值为3，所以甲的逻辑推理能力优于乙的逻辑推理能力，故A正确；对于选项B，甲的数学建模能力指标值为3，乙的直观想象能力指标值为5，所以乙的直观想象能力指标值优于甲的数学建模能力指标值，故B错误；对于选项C，甲的六维能力指标值的平均值为123(434534)66+++++=，乙的六维能力指标值的平均值为1(543543)46+++++=，2346<，故C错误；对于选项D，甲的数学运算能力指标值为4，甲的直观想象能力指标值为5，所以甲的数学运算能力指标值不优于甲的直观想象能力指标值，故D错误．故选：A【点睛】本题主要考查雷达图的识别和平均数的计算，意在考查学生对这些知识的理解掌握水平和分析推理能力.6.已知△ABC中，AB＝3，AC＝4，∠BAC＝60°，点D，E分别是边BC和AC的中点，则AB BE⋅＝（）A.294- B. -72C. -2D.72【答案】C 【解析】设AB a =，AC b =，以它们为基底，把,AB BE 都用基底表示后根据数量积的运算律计算．【详解】设AB a =，AC b =，则3a =，4b =，6a b ⋅=，111222AD BE a b b a ⎛⎫⎛⎫⋅=+⋅- ⎪ ⎪⎝⎭⎝⎭22221111113462244244a b a b =-+-⋅=-⨯+⨯-⨯=-．故选：C ．【点睛】本题考查平面向量数量积，解题关键是选取,AB AC 为基底．用基底表示其他向量后再进行数量积的运算．7.圆C 1：x 2＋y 2＝16与圆C 2：(x -3)2＋(y -4)2＝9的公共弦的长为（） A.125B.165C.245D.325【答案】C 【解析】【分析】先用两圆的方程相减求得公共弦方程,再利用垂径定理求解弦长即可.【详解】两圆方程相减得公共弦方程为34160x y +-=,圆心()10,0C ,到公共弦的距离为165d ==,所以所求弦长为245=. 故选：C【点睛】本题主要考查了两圆相交弦的求解以及垂径定理求弦长的问题.属于基础题.8.关于函数()21cos cos 2f x x x x =+-有下述三个结论： ①()f x 在区间,42ππ⎡⎤⎢⎥⎣⎦上是减函数；②()f x 的图象关于直线3x π=-对称；③()f x 在区间,4ππ⎡⎤⎢⎥⎣⎦上的值域为1,2⎡-⎢⎣⎦其中正确结论的个数是（） A. 0B. 1C. 2D. 3【解析】【分析】根据题意，先将函数化简为()sin 26f x x π⎛⎫+⎝=⎪⎭，再利用正弦函数的性质即可.【详解】由题意，()21cos cos sin 226f x x x x x π⎛⎫=-=+ ⎪⎝⎭，由3222262k x k πππππ+≤+≤+，k Z ∈，得263k x k ππππ+≤≤+，k Z ∈，所以()f x 的单调递减区间为2,63k k ππππ⎡⎤++⎢⎥⎣⎦，k Z ∈.可知①正确；由2sin 1336f πππ⎛⎫⎛⎫-=-+=- ⎪ ⎪⎝⎭⎝⎭，可知()f x 的图象关于直线3x π=-对称，所以②正确；当,4x ππ⎡⎤∈⎢⎥⎣⎦时，2132,636x πππ⎡⎤+∈⎢⎥⎣⎦，所以()sin 26f x x π⎡⎛⎫=+∈-⎢ ⎪⎝⎭⎣⎦，故③正确. 故选：D.【点睛】本题考查正弦型函数的性质，考查了转化思想，计算能力，属于基础题.9.已知F 是抛物线24y x =的焦点，点()00,P x y 在抛物线上，且2PF =，则0y =（）A. 2B. -2C. 2或-2D.3116【答案】D 【解析】【分析】抛物线的标准方程为214x y =，然后得出其准线方程，然后利用抛物线的定义求解即可. 【详解】抛物线的标准方程为214x y =，则其准线方程为116y =-，由2PF =得()00,P x y 到准线的距离为2，所以01216y ⎛⎫--= ⎪⎝⎭，所以03116y =．故选：D【点睛】本题考查的是抛物线定义的应用，较简单.10.已知()4,0A 、()0,2B ，若点(),C a b 在线段AB (不含端点)上，则11a b +-的最小值为（） A. 522-B. 322-C.322- D.522- 【答案】A 【解析】【分析】由条件得到()240,0a b a b +=>>，然后可推出11152211a a a b +++-=+-，然后利用基本不等式求解即可.【详解】由()4,0A 、()0,2B 可得直线AB 的方程为142x y+=，即24x y += 因为点(),C a b 在线段AB (不含端点)上，所以()240,0a b a b +=>> 所以1141411511511552222222222111111a a a a a a a a a a a b --+-++-=-=+=+=+-≥⋅-+++=+-++ 当且仅当1121a a +=+，即21a =-时等号成立故选：A【点睛】本题主要考查的是利用基本不等式求最值，考查了学生的转化能力，属于中档题.11.函数f （x ）＝sin x ·11x x e e +-的部分图象大致为（）A. B. C. D.【答案】C【解析】【分析】根据函数的奇偶性以及当x 取接近于0的正数时函数的正负判断即可.【详解】因为sin y x =和e 1e 1x x y +=-都是奇函数,所以()e 1sin e 1x x f x x +=⋅-是偶函数,排除B 和D .当x 取接近于0的正数时,应有()0f x >,所以排除A . 故选：C.【点睛】本题主要考查了根据函数解析式判断函数图像的方法,需要根据奇偶性与函数的正负判断.属于基础题.12.如图，圆形纸片的圆心为O ，半径为5cm ，该纸片上的正六边形ABCDEF 的中心为O ，G 、H 、M 、N 、P 、Q 为圆O 上的点，△GAB ，△HBC ，△MCD ，△NDE ，△PEF ，△QAF 分别是以AB ，BC ，CD ，DE ，EF ，FA 为底边的等腰三角形，沿虚线剪开后，分别以AB ，BC ，CD ，DE ，EF ，FA 为折痕折起△GAB ，△HBC ，△MCD ，△NDE ，△PEF ，△QAF ，使得G 、H 、M 、N 、P 、Q 重合，得到六棱锥．当正六边形ABCDEF 的边长变化时，所得六棱锥体积(单位：cm 3)的最大值为（）A. 815B.8153C. 15D.4153【答案】B 【解析】【分析】连接OM ，交CD 与点K ，由题意，OM CD ⊥，设OK x =，则23CD x =，5KM x =-，求出棱锥的高，和底面面积，由体积公式求得体积的表达式，引入函数()452510f x x x =-，5(0,)2x ∈，利用导数可求得其最大值．【详解】如图，连接OM ，交CD 与点K ，由题意，OM CD ⊥，设OK x =，则23CD x =，5KM x =-，六棱锥的高222225102510h KM OK x x x x =-=-+-=-，22346233ABCDEF S x x =⋅⋅=正六边形，则212325103ABCDEF V S h x x =⋅=⋅-正六边形4523=2510x x ⋅-，令()452510f x x x =-，5(0,)2x ∈，()3410050f x x x '=-，令()0f x '>，即4320x x -<，2x <，即(0,2)x ∈时，()f x 递增，当5(2,)2x ∈时，()0f x '<，()f x 递减， ∴(2)f 是()f x 在5(0,)2上的唯一极大值，也是最大值．(2)80f =，max 2381580V =⨯=，所以体积最大值为3815cm ．故选：B ．【点睛】本题考查求棱锥的体积的最大值．解题关键是引入变量（题中的x ），然后把棱锥体积表示为这个变量的函数，利用导数的知识求得最大值．第Ⅱ卷(非选择题共90分)二、填空题(本大题共4小题，每小题5分，共20分．把答案填在答题卡的相应位置．) 13.已知函数()30ln 0x x f x x x +≤⎧=⎨>⎩，，，若f （m ）≥2，则实数m 的取值范围为________．【答案】10m -≤≤或2m e ≥ 【解析】分析】利用分类讨论表示不等式，进而写出其并集结果. 【详解】由题可知，()30 ln 0x x f x x x +≤⎧=⎨>⎩，，，则()2f m ≥⇔032m m ≤⎧⎨+≥⎩或ln 2m m >⎧⎨≥⎩⇔10m -≤≤或2e m ≥．故答案为：10m -≤≤或2m e ≥【点睛】本题考查在分段函数中由函数值的范围求参数的取值范围，属于基础题.14.已知长轴长为2a ，短轴长为2b 的椭圆的面积为ab π．现用随机模拟的方法来估计π的近似值，先用计算机产生n 个数对(),i i x y ，1,2,3,i n =，其中i x ，i y 均为[0,2]内的随机数，再由计算机统计发现其中满足条件i y <的数对有m 个，由此可估计π的近似值为______________．【答案】8mn．【解析】【分析】由i x ，i y []0,2∈，根据i y <表示的数对对应的点(),i i x y 在椭圆2214x y +=的内部，且在第一象限，求出i y <满足条件的点(),i i x y 的概率，再转化为几何概型的面积类型求解．【详解】i x ，i y []0,2∈，∴i y <表示的数对对应的点(),i i x y 在椭圆2214x y +=的内部，且在第一象限，其面积为2142ππ⨯⨯=，故222m n π≈⨯，得8m nπ≈．故答案为：8mn.【点睛】本题主要考查了几何型概率应用，解题关键是掌握几何型概率求法，考查了分析能力和计算能力，属于基础题.15.以双曲线C：22221(0,0)x ya ba b-=>>的右焦点F为圆心，半焦距为半径作圆，与双曲线的渐近线交于O，A，B三点．若△AOB的周长为7a，则双曲线C的离心率为________．【解析】【分析】根据直线和圆相交时的弦长公式，三角形的周长，结合双曲线离心率的公式进行转化求解即可．【详解】∵双曲线的一个焦点为F（c，0），双曲线的一条渐近线为yba=x，即bx﹣ay＝0，∴焦点到渐近线的距离bcd bc===，所以圆心到渐近线的距离为b，因为圆的半径为c，所以2OA a==，同理2OB a=．因为tanbAOxa∠=，所以sinbAOxc∠=，所以AB2sinOA AOx=∠422b abac c=⨯⨯=，所以4227aba a ac++=，得43b c=，所以()222169c a c-=，解得cea==．故答案为：7.【点睛】本题主要考查双曲线离心率的计算，根据直线和圆相交的弦长公式建立方程关系是解决本题的关键，属于基础题.16.已知对一切x>0，不等式1xex->a恒成立，则a的取值范围为______________．【答案】(],1-∞【解析】【分析】由题意得，e 1x a x ->⇔e 10x ax -->，令()e 1xf x ax =--，()e x f x a '=-，对a 分1a ≤和1a >两种情况导函数的正负，得出原函数的单调性和最值，可得a 的范围.【详解】0x >时，e 1x a x->⇔e 10x ax -->，令()e 1xf x ax =--，则()e x f x a '=-，当1a ≤时，()0f x '>，所以()()00f x f >=，符合题意；当1a >时，由()0f x '=得ln x a =（ln 0a >），所以()0,ln x a ∈时，()0f x '<，所以()()00f x f <=，这与e 10x ax -->矛盾．所以a 的取值范围为(],1-∞．故答案为：(],1-∞.【点睛】本题考查不等式的恒成立问题，关键在于构造函数，讨论其导函数的正负，得出所构造的函数的单调性，再运用恒成立的思想，得以求参数的范围，属于难度题.三、解答题(本大题共6小题，共70分．解答应写出必要的文字说明、证明过程或演算步骤．) 17.已知正项数列{a n }的前n 项和为S n ，满足a 1＝1，a n a n ＋1＝4S n -1．（1）求数列{a n }的通项公式；（2）b n ＝121n n a a ++，求数列{b n }的前n 项和T n ．【答案】（1）21n a n =-；（2）()323n nT n =+.【解析】【分析】（1）由141n n n a a S +=-，得12141n n n a a S +++=-，两式相减得()1214n n n n a a a a +++-=，再由{}n a 为正项数列，得10n a +≠，可得24n n a a +-=，从而数列{}n a 的奇数项和偶数项分别成等差数列，再由等差数列的通项的求法，可得答案．（2）由于21n a n =-，可得11122123n b n n ⎛⎫=- ⎪++⎝⎭．运用裂项相消法可求和.【详解】（1）．∵141n n n a a S +=-，∴12141n n n a a S +++=-，两式相减得()1214n n n n a a a a +++-=， ∵{}n a 为正项数列，∴10n a +≠，∴24n na a +-=，∴数列{}n a 的奇数项和偶数项分别成等差数列．在141n n n a a S +=-中令1n =得，12141a a a =-，∵11a =，∴解得23a =，故数列{}n a 为等差数列，且公差为2，∴()12121n a a n n =+-=-，即数列{}n a 的通项公式为21n a n =-．（2）．由（1）知()()1211111212322123n n n b a a n n n n ++⎛⎫===- ⎪++++⎝⎭，则1211111111123525722123n n T b b b n n ⎛⎫⎛⎫⎛⎫=+++=-+-++- ⎪ ⎪ ⎪++⎝⎭⎝⎭⎝⎭1112323n ⎛⎫=- ⎪+⎝⎭()323nn =+．所以()323n nT n =+.【点睛】本题考查数列的前n 项与通项的关系，以及运用裂项相消法求数列的和的方法，属于中档题．18.已知△ABC 中，A 、B 、C 的对边分别为a 、b、c ，sin sin tan cos cos B CA B C+=+．（1）求角A ；（2）若a ，求b 2+bc 的取值范围．【答案】（1）3A π=；（2）(0,3+．【解析】【分析】（1）由切化弦思想结合两角差的正弦公式得出()()sin sin A B C A -=-，求出A B -和C A -的取值范围，可得出A B C A -=-或()()A B C A π-+-=±（不成立），结合三角形的内角和定理可得出角A 的值；（2）由正弦定理结合三角恒等变换思想得出2b bc +233B π⎛⎫=-+ ⎪⎝⎭，由角B 的取值范围，结合正弦函数的基本性质可求得2b bc +的取值范围. 【详解】（1）由sin sin tan cos cos B C A B C +=+得sin sin sin cos cos cos A B CA B C+=+，即sin cos sin cos A B A C +cos sin A B = cos sin A C +，也即sin cos A B cos sin A B -=cos sin A C sin cos A C -，所以()sin A B - ()sin C A =-，所以A B C A -=-或()()+A B C A π--=±（不成立），所以2B C A +=，则3A π=．（2）由正弦定理得2sin sin sin b c aB C A===，所以2sin b B =，2sin c C =．因为3A π=，所以23C B π=-，所以2b bc +224sin sin sin 3B B B π⎛⎫⎛⎫=+- ⎪ ⎪⎝⎭⎝⎭2334sin cos sin 2B B B ⎛⎫=+ ⎪ ⎪⎝⎭()3sin 231cos 2B B =+-23sin 233B π⎛⎫=-+ ⎪⎝⎭．因为203B π<<，所以233B πππ-<-<，所以3sin 213B π⎛⎫- ⎝-⎪⎭<≤，所以023sin 2+33233B ⎛⎫<-≤+ ⎪⎝⎭π，故2b bc +的取值范围为(0,323⎤+⎦．【点睛】本题考查三角形中角的计算，同时也考查了三角形中与边长相关的代数式的取值范围的计算，涉及正弦定理的应用，考查计算能力，属于中等题.19.如图，在四棱锥P -ABCD 中，底面ABCD 为菱形，∠APC ＝90°，∠BPD ＝120°，PB ＝PD ．（1）求证：平面APC ⊥平面BPD ；（2）若AB ＝2AP ＝2，求三棱锥C -PBD 的体积．【答案】（1）详见解析；（2）12．【解析】【分析】（1）记AC 与BD 交点为O ，利用BD OP ⊥，BD AC ⊥证得线面垂直，从而可证得面面垂直；（2）设PO m =，利用Rt BOC 求得m ，从而得,,AC BD PC 的长度，过P 作PH AC ⊥，垂足为H ，由（1）可证PH 就是四棱锥的高，求出这个高及底面面积, 用换底法可得体积．【详解】（1）证明：记AC 与BD 交点为O ，∵PB PD =，O 为BD 的中点，∴BD OP ⊥，又∵ABCD 为菱形，∴BD AC ⊥．∵AC 和OP 是平面APC 内两条相交直线，∴BD ⊥平面APC ．又BD ⊂平面BPD ，∴平面APC ⊥平面BPD ．（2）设PO m =，∵90APC ∠=︒，∴2AC m =，又120BPD ∠=︒，所以60BPO ∠=︒，所以3BO m =，因为2BC AB ==，所以在Rt BOC 中，由勾股定理得222(3)2m m +=，0m >，∴1m =，∴3CP =．过P 作PH AC ⊥，垂足为H ，由（1）知，BD ⊥平面APC ，∴平面APC ⊥平面ABCD ．又平面APC平面ABCD AC =，所以PH ⊥平面ABCD ．在Rt PAC △中，得3PA PC PH AC ⋅==，所以三棱锥C PBD -的体积C PBD V -P BCD V -=13BCD S PH =⋅△111311233262OC BD PH =⨯⋅⋅=⨯⨯⨯=．【点睛】本题考查证明面面垂直，考查求棱锥的体积，解题方法是换底法．换底后直接利用棱锥体积公式求得体积．20.Fibonacci 数列又称黄金分割数列，因为当n 趋向于无穷大时，其相邻两项中的前项与后150618+≈-.．已知Fibonacci 数列的递推关系式为121213nn n a a a a a n --==⎧⎨=+≥⎩，．（1）证明：Fibonacci 数列中任意相邻三项不可能成等比数列；（2）Fibonacci 数列{a n }的偶数项依次构成一个新数列，记为{b n }，证明：{b n ＋1-H 2·b n }为等比数列．【答案】（1）详见解析；（2）详见解析．【解析】【分析】（1）利用反证法，假设存在n a ，1n a +，2n a +三项成等比数列，则21+2n n n a a a +=，进而由已知关系证得1n n a a +=是无理数，这与其递推公式中反应的为有理数矛盾，得证；（2）由题表示2n n b a =，进而由已知n a 的递推关系表示出n b 的递推公式，再构造等比数列{}1n n b mb +-，进而由一一对应关系计算出对应参量，最后由等比数列定义得证.【详解】（1）证明：（反证法）假设存在n a ，1n a +，2n a +三项成等比数列，则21+2n n n a a a +=，所以()21+1n n n n aa a a +=+，所以21110n n n n a aa a ++⎛⎫+-= ⎪⎝⎭，解得1n n a a +=，由条件可知Fibonacci 数列的所有项均大于0，所以1n n a a +，又Fibonacci 数列的所有项均为整数（由递推公式），所以1nn a a +应该为有理数，这与1n n a a +（无理数）矛盾（其相邻两项中的前项与后项的比值越来越接近黄金分割数，而不是恰好相等），所以假设不成立，故原命题成立．（2）证明：由条件得2n n b a =，21222n n n a a a ++=-，所以()224232222212222222212233n n n n n n n n n n n n n b a a a a a a a a a a b b ++++++++++==+=+=+-=-=-，即213n n n b b b ++=-，设()()21121n n n n n n n b mb n b mb b m n b mnb +++++-=-⇒=+-，则31m m n mn n ⎧=⎪+=⎧⎪⇒⎨⎨=⎩⎪=⎪⎩或m n ⎧=⎪⎪⎨⎪=⎪⎩所以211n n n n b b +++⎫=-⎪⎪⎝⎭或211n n n n b b +++⎫-=-⎪⎪⎝⎭所以)22211n n n n b H b b H b +++-⋅-⋅，所以21{}n n b H b +-⋅．【点睛】本题考查数列中的新定义问题的证明，涉及反证法的考查，还考查了构造等比数列，属于难题.21.已知椭圆C ：22221(0)x y a b a b +=>>的离心率为2，且经过点M (1，2)．（1）求椭圆C 的标准方程；（2）已知直线l 不过点P (0，1)，与椭圆C 交于A 、B 两点，记直线PA 、PB 的斜率分别为k 1、k 2，且满足k 1＋k 2＝1，求证：直线l 过定点，并求出该定点坐标．【答案】（1）2214x y +=；（2）证明详见解析；该定点坐标为()2,1--．【解析】【分析】（1c a =222c a b =-，得2a b =，再由椭圆经过点M (1，可求出椭圆C 的标准方程.（2）设()11,A x y ，()22,B x y ．设直线PA方程为11y k x =+,由直线PA 的方程与椭圆方程联立解得A 点坐标，同理解得B 点坐标,从而求出直线l 的斜率，得出l 方程，求出直线l 所过的定点.【详解】解：（1）．设椭圆焦距为2c，则2c a =，又222c a b =-，得2a b =，所以C 的方程化为222214x y b b +=，将1,2M ⎛ ⎝⎭代入有2213144b b +=解得1b =，所以椭圆C 的标准方程为2214x y +=．（2）．设()11,A x y ，()22,B x y ．设直线PA 的方程为11y k x =+由11y k x =+与椭圆方程2214x y +=联立，得()221114x k x ++=化简得：()22111480k xk x ++=解得1121814k x k -=+，211211414k y k -=+，同理，解得2222814k x k -=+，222221414k y k -=+．所以直线l 的斜率为()()2221222121122212112111222114141414118814141211414k k y y k k k k k k k x x k k k k k k k ----+++=====--------++，所以直线l 的方程为()()1121121y y x x k -=--，即 ()2112221118141141421k k y x k k k ⎛⎫-=++ ⎪++-⎝⎭（*）．取0k =，得直线1y x =+，取1k =-，得直线1799y x =-，联立两直线解得交点()2,1--，经检验，()2,1--符合方程（*），所以直线l 过定点()2,1--．【点睛】本题考查根据离心率和椭圆上的点求椭圆方程，由直线方程与椭圆方程联立求出交点坐标，进而求出直线斜率，求出直线所过定点，属于中档题. 22.已知函数()xf x e ax =-．（1）讨论函数()f x 的单调性；（2）证明：当a ＝3时，函数g()()ln x f x x x =-有且只有两个零点．【答案】（1）分类讨论，详见解析；（2）详见解析．【解析】【分析】（1）由()xf x e a '=-，分0a ≤和0a >两种情况进行讨论得出函数的单调性.（2）函数g()()ln x f x x x =-有且只有两个零点,即方程()0g x =有且只有两个实数根，即ln 30x e x x --=有且只有两个实数根，设()ln 3xe x x xϕ=--，求出导数，求出函数()x ϕ的单调区间，结合零点存在原理得出结论,使得问题得证.【详解】解：（1）()f x 的定义域为R ，()x f x e a '=-．①0a ≤时，()0f x '>，则()f x 在R 是单调递增；②0a >时，由()0f x '=得ln x a =，当ln x a <时，()0f x '<，()f x 单调递减；当ln x a >时，()0f x '>，()f x 单调递增．综上，0a ≤时()f x 在R 是单调递增；0a >时，()f x 在(),ln a -∞单调递减，在()ln ,a +∞单调递增．（2）．()0g x =⇔ln 30x e x x --=，令()ln 3xe x x xϕ=--，则()21()x e x x x x ϕ--'=，令()()1xp x e x x =--，显然01x <≤时，()0p x <，1x >时，()10x p x xe '=->，所以()p x ()1+∞，上单调递增. (1)10p =-<,2(2)20p e =->易知存在唯一121x >>，使1()0p x =，且()10,x x ∈时，()0p x <，即()0x ϕ'<，()x ϕ单调递减；()1,x x ∈+∞时，()0p x >，即()0x ϕ'>，()x ϕ单调递增，所以()x ϕ至多有两个零点．又1()2ϕln 230=->，(1)30e ϕ=-<，33(3)ln335033e e ϕ=-->->，故()x ϕ在区间1,12⎛⎫⎪⎝⎭和()1,3各有一个零点．所以函数()g x 有且只有两个零点．【点睛】本题考查导数中含参数的单调性的分类讨论，利用导数证明函数的零点个数，利用导数证明函数的零点个数时要讨论出函数的单调性结合零点存在原理来证明，属于中档题.。

安徽省芜湖市2019-2020学年七年级(下)期末考试数学试卷解析版

2019-2020学年安徽省芜湖市七年级（下）期末数学试卷一、选择题：（本大题10个小题，每小题4分，共30分）在每个小题的下面，都给出了代号为A、B、C、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中．1．（4分）下列计算正确的是（）A．﹣22＝4B．＝±4C．＝D．＝22．（4分）下列调查工作适合采用普查方式的是（）A．学校在给学生订做校服前进行的尺寸大小的调查B．质检部门对各厂家生产的电池使用寿命的调查C．电视台对正在播出的某电视节目收视率的调查D．环保部门对某段水域的水污染情况的调查3．（4分）已知点A（a，b）在第四象限，那么点B（b，﹣a﹣1）在（）A．第一象限B．第二象限C．第三象限D．第四象限4．（4分）如图，直线a∥b，将一块含30°角（∠BAC＝30°）的直角三角尺按图中方式放置，其中A和C 两点分别落在直线a和b上．若∠1＝20°，则∠2的度数为（）A．20°B．30°C．40°D．50°5．（4分）在下列实数，3.14159265，，﹣8，，，中无理数有（）A．3个B．4个C．5个D．6个6．（4分）如图，在△ABC中，BC＝5，∠A＝70°，∠B＝75°，把△ABC沿直线BC的方向平移到△DEF的位置，若CF＝3，则下列结论中错误的是（）A．BE＝3B．∠F＝35°C．DF＝5D．AB∥DE7．（4分）《九章算术》中的方程问题：“五只雀、六只燕，共重1斤（等于16两），雀重燕轻．互换其中一只，恰好一样重，问：每只雀、燕的重量各为多少？”设每只雀、燕的重量各为x两，y两，列方程组为（）A．B．C．D．8．（4分）下列说法正确的是（）A．x＝3.14是不等式2x﹣5＞0的一个解B．+5＜2x是一元一次不等式C．不等式组有一个正整数解D．不等式：﹣2x+3＞0的解集是：x＞9．（4分）在平面直角坐标系中，点A（﹣3，2），B（3，5），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（）A．6，（﹣3，5）B．10，（3，﹣5）C．1，（3，4）D．3，（3，2）10．（4分）如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②CA平分∠BCG；③∠ADC＝∠GCD；④∠DFB＝∠CGE．其中正确的结论有（）个A．1B．2C．3D．4二、填空题：（本大题5个小题，每小题4分，共20分）11．（4分）求实数的整数部分数字是．12．（4分）如图，直线a和b被直线c所截，∠1＝110°，当∠2＝时，直线a∥b成立．13．（4分）关于x的不等式（3﹣2a）x＜1的解集是x＞，则a的取值范围是．14．（4分）在矩形ABCD中，放入六个形状、大小相同的长方形，所标尺寸如图所示，则图中阴影部分的面积是cm2．15．（4分）已知点A（﹣4，0），B（2，0），点C在y轴上，且△ABC的面积等于12，则点C的坐标为．三、简答题：（本大题6个小题、共50分，解答时每小题必须给出必要的演算过程或推理步骤．）16．（1）解方程组；（2）解不等式组并将解集在数轴上表示．17．（7分）如图，BC∥AD，∠1＝∠E，求证：∠A＝∠C．18．（8分）如图，在平面直角坐标系中，每个小正方形的边长为一个单位长度．已知△ABC的顶点A（﹣2，5）、B（﹣4，1）、C（2，3），将△ABC平移得到A'B'C'，点A（a，b）对应点A'（a+3，b﹣4）（1）画出△A'B'C'并写出点B'、C'的坐标．（2）试求△A'B'C'的面积．（3）在x轴上存在一点P，使得S△ABP＝7，则点P的坐标是．19．（6分）某中学有学生2400名，为了响应市“科学应对、群防群控、增强体质、战胜疫情”的号召，学校决定利用课外活动时间举行体育锻炼，为了让学生在篮球、足球、排球和乒乓球这四项球类运动中选择一项球类进行锻炼，对学生开展了随机调查，并将结果绘制成如图所示不完整的统计图．请根据以上信息，完成下列问题：（1）本次调查共抽取了多少名学生？（2）求在被调查的学生中，最喜爱乒乓球的人数，并补全条形统计图；（3）请你估计该阳光中学的学生中最喜爱篮球运动的学生人数约有多少名？20．（9分）某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，如表是近两周的销售情况：销售时段销售数量销售收入A种型号B种型号第一周3台4台1200元第二周5台6台1900元（进价、售价均保持不变，利润＝销售收入﹣进货成本）（1）求A、B两种型号的电风扇的销售单价；（2）若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？（3）在（2）的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．21．（10分）如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F．（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为．请说明理由．（2）当△PMN所放位置如图②所示时，∠PFD与∠AEM的数量关系为．（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．2019-2020学年安徽省芜湖市七年级（下）期末数学试卷参考答案与试题解析一、选择题：（本大题10个小题，每小题4分，共30分）在每个小题的下面，都给出了代号为A、B、C、D 的四个答案，其中只有一个是正确的，请将正确答案的代号填在题后的括号中．1．（4分）下列计算正确的是（）A．﹣22＝4B．＝±4C．＝D．＝2【分析】直接利用二次根式、立方根的性质分别化简得出答案．【解答】解：A、﹣22＝﹣4，故此选项错误；B、＝4，故此选项错误；C、＝2，故此选项错误；D、＝2，正确．故选：D．【点评】此题主要考查了立方根以及算术平方根，正确化简各数是解题关键．2．（4分）下列调查工作适合采用普查方式的是（）A．学校在给学生订做校服前进行的尺寸大小的调查B．质检部门对各厂家生产的电池使用寿命的调查C．电视台对正在播出的某电视节目收视率的调查D．环保部门对某段水域的水污染情况的调查【分析】由普查得到的调查结果比较准确，但所费人力、物力和时间较多，而抽样调查得到的调查结果比较近似．【解答】解：A、学校在给学生订做校服前进行的尺寸大小的调查，人数较少，应采用全面调查，故此选项符合题意；B、质检部门对各厂家生产的电池使用寿命的调查，调查具有破坏性，应采用抽样调查，故此选项不合题意；C、电视台对正在播出的某电视节目收视率的调查，范围较广，意义不大，应采用抽样调查，故此选项不合题意；D、环保部门对某段水域的水污染情况的调查，不可能全面调查，应采用抽样调查，故此选项不符合题意；故选：A．【点评】本题考查了抽样调查和全面调查的区别，选择普查还是抽样调查要根据所要考查的对象的特征灵活选用，一般来说，对于具有破坏性的调查、无法进行普查、普查的意义或价值不大，应选择抽样调查，对于精确度要求高的调查，事关重大的调查往往选用普查．3．（4分）已知点A（a，b）在第四象限，那么点B（b，﹣a﹣1）在（）A．第一象限B．第二象限C．第三象限D．第四象限【分析】直接利用各象限内点的坐标特点得出答案．【解答】解：∵点A（a，b）在第四象限，∴a＞0，b＜0，∴﹣a﹣1＜0，∴点B（b，﹣a﹣1）在第三象限．故选：C．【点评】此题主要考查了点的坐标，正确记忆各象限内点的坐标特点是解题关键．4．（4分）如图，直线a∥b，将一块含30°角（∠BAC＝30°）的直角三角尺按图中方式放置，其中A和C 两点分别落在直线a和b上．若∠1＝20°，则∠2的度数为（）A．20°B．30°C．40°D．50°【分析】直接利用平行线的性质结合三角形内角和定理得出答案．【解答】解：∵直线a∥b，∴∠1+∠BCA+∠2+∠BAC＝180°，∵∠BAC＝30°，∠BCA＝90°，∠1＝20°，∴∠2＝40°．故选：C．【点评】此题主要考查了平行线的性质，正确掌握平行线的性质是解题关键．5．（4分）在下列实数，3.14159265，，﹣8，，，中无理数有（）A．3个B．4个C．5个D．6个【分析】无理数常见的三种类型：①开方开不尽的数，②无限不循环小数，③含有π的数．【解答】解：，，∴，3.14159265，﹣8，是有理数，无理数有：，，共3个．故选：A．【点评】本题主要考查的是无理数的概念，熟练掌握无理数的概念是解题的关键．6．（4分）如图，在△ABC中，BC＝5，∠A＝70°，∠B＝75°，把△ABC沿直线BC的方向平移到△DEF的位置，若CF＝3，则下列结论中错误的是（）A．BE＝3B．∠F＝35°C．DF＝5D．AB∥DE【分析】根据平移的性质，平移只改变图形的位置，不改变图形的大小与形状，平移后对应点的连线互相平行，对各选项分析判断后利用排除法．【解答】解：∵把△ABC沿BC的方向平移到△DEF的位置，BC＝5，∠A＝70°，∠B＝75°，∴CF＝BE＝3，∠F＝∠ACB＝180°﹣∠A﹣∠B＝180°﹣70°﹣75°＝35°，AB∥DE，∴A、B、D正确，不符合题意；C错误，符合题意，故选：C．【点评】本题考查了平移的性质，熟练掌握平移性质是解题的关键．7．（4分）《九章算术》中的方程问题：“五只雀、六只燕，共重1斤（等于16两），雀重燕轻．互换其中一只，恰好一样重，问：每只雀、燕的重量各为多少？”设每只雀、燕的重量各为x两，y两，列方程组为（）A．B．C．D．【分析】根据题意可以列出相应的二元一次方程组，从而可以解答本题．【解答】解：由题意可得，，故选：C．【点评】本题考查由实际问题抽象出二元一次方程组，解答本题的关键是明确题意，列出相应的方程．8．（4分）下列说法正确的是（）A．x＝3.14是不等式2x﹣5＞0的一个解B．+5＜2x是一元一次不等式C．不等式组有一个正整数解D．不等式：﹣2x+3＞0的解集是：x＞【分析】解出不等式（组）的解集，根据不等式的解的定义，就是能使不等式成立的未知数的值，就可以作出判断．【解答】解：A、由于不等式2x﹣5＞0的解集为x＞2.5，所以x＝3.14是不等式2x﹣5＞0的一个解，正确，符合题意；B、+5＜2x表示是一元一次不等式，故错误，不符合题意．C、解不等式x+3＜5得x＜2，解不等式3x﹣1＞8得x＞3，所以不等式组无解，错误，不符合题意；D、不等式x﹣3＞2的解集是x＜，故错误，不符合题意；故选：A．【点评】本题考查了不等式（组）的解集，解答此题关键是掌握解不等式的方法．9．（4分）在平面直角坐标系中，点A（﹣3，2），B（3，5），C（x，y），若AC∥x轴，则线段BC的最小值及此时点C的坐标分别为（）A．6，（﹣3，5）B．10，（3，﹣5）C．1，（3，4）D．3，（3，2）【分析】根据坐标的定义可求得y值，根据线段BC最小，确定BC⊥AC，垂足为点C，进一步求得BC的最小值和点C的坐标．【解答】解：依题意可得：∵AC∥x轴，A（﹣3，2）∴y＝2，根据垂线段最短，当BC⊥AC于点C时，点B到AC的距离最短，即BC的最小值＝5﹣2＝3，此时点C的坐标为（3，2），故选：D．【点评】本题考查已知点求坐标及如何根据坐标描点，正确画图即可求解．10．（4分）如图，△ABC的角平分线CD、BE相交于F，∠A＝90°，EG∥BC，且CG⊥EG于G，下列结论：①∠CEG＝2∠DCB；②CA平分∠BCG；③∠ADC＝∠GCD；④∠DFB＝∠CGE．其中正确的结论有（）个A．1B．2C．3D．4【分析】根据平行线的性质、角平分线的定义、垂直的性质及三角形内角和定理依次判断即可得出答案．【解答】解：①∵EG∥BC，∴∠CEG＝∠ACB，又∵CD是△ABC的角平分线，∴∠CEG＝∠ACB＝2∠DCB，故①正确；②∵∠CEG＝∠ACB，而∠GEC与∠GCE不一定相等，∴CA不一定平分∠BCG，故②错误；③∵∠A＝90°，∴∠ADC+∠ACD＝90°，∵CD平分∠ACB，∴∠ACD＝∠BCD，∴∠ADC+∠BCD＝90°．∵EG∥BC，且CG⊥EG，∴∠GCB＝90°，即∠GCD+∠BCD＝90°，∴∠ADC＝∠GCD，故③正确；④∵∠ABC+∠ACB＝90°，∵CD平分∠ACB，BE平分∠ABC，∴∠EBC＝∠ABC，∠DCB＝∠ACB，∴∠DFB＝∠EBC+∠DCB＝（∠ABC+∠ACB）＝45°，∵∠CGE＝90°，∴∠DFB＝∠CGE，故④正确．故选：C．【点评】本题主要考查的是三角形内角和定理、平行线的性质，熟知直角三角形的两锐角互余是解答此题的关键．二、填空题：（本大题5个小题，每小题4分，共20分）11．（4分）求实数的整数部分数字是35．【分析】直接估算无理数的大小进而得出整数部分．【解答】解：∵352＝1225，∴35＜＜36，∴实数的整数部分数字是：35．故答案为：35．【点评】此题主要考查了估算无理数的大小，正确估算无理数的范围是解题关键．12．（4分）如图，直线a和b被直线c所截，∠1＝110°，当∠2＝70°时，直线a∥b成立．【分析】根据平行线的判定定理即可得到结论．【解答】解：当∠2＝70°时，直线a∥b，∵∠1＝110°，∴∠3＝70°，∵∠2＝70°，∴∠3＝∠2，∴直线a∥b．故答案为：70°．【点评】本题考查了平行线的判定定理，熟练掌握平行线的判定定理是解题的关键．13．（4分）关于x的不等式（3﹣2a）x＜1的解集是x＞，则a的取值范围是a＞．【分析】根据解一元一次不等式的依据可得关于a的不等式，解之可得．【解答】解：∵（3﹣2a）x＜1的解集是x＞，∴3﹣2a＜0，解得a＞，故答案为：a＞．【点评】本题主要考查解一元一次不等式的基本能力，严格遵循解不等式的基本步骤是关键，尤其需要注意不等式两边都乘以或除以同一个负数不等号方向要改变．14．（4分）在矩形ABCD中，放入六个形状、大小相同的长方形，所标尺寸如图所示，则图中阴影部分的面积是44cm2．【分析】设小长方形的长、宽分别为xcm，ycm，根据图示可以列出方程组，然后解这个方程组即可求出小长方形的面积，接着就可以求出图中阴影部分的面积．【解答】解：设小长方形的长、宽分别为xcm，ycm，依题意得，解之得，∴小长方形的长、宽分别为8cm，2cm，∴S阴影部分＝S四边形ABCD﹣6×S小长方形＝14×10﹣6×2×8＝44cm2．【点评】此题是一个信息题目，要求学生会根据图示找出数量关系，然后利用数量关系列出方程组解决问题．15．（4分）已知点A（﹣4，0），B（2，0），点C在y轴上，且△ABC的面积等于12，则点C的坐标为（0，4）或（0，﹣4）．【分析】先设C点的坐标是（0，x），根据图可知×AB×OC＝×6•|x|＝12，解即可求x，进而可求C 点坐标．【解答】解：如右图所示，设C点的坐标是（0，x），∵S△ABC＝12，∴×AB×OC＝×6•|x|＝12，∴|x|＝4，故点C的坐标是（0，4）或（0，﹣4）．故答案为（0，4）或（0，﹣4）．【点评】本题考查了三角形的面积，坐标与图形的性质等知识，解题的关键是不要漏解．三、简答题：（本大题6个小题、共50分，解答时每小题必须给出必要的演算过程或推理步骤．）16．（1）解方程组；（2）解不等式组并将解集在数轴上表示．【分析】（1）方程组利用加减消元法求出解即可；（2）先求出两个不等式的解集，再求其公共解．【解答】解：（1），①×2﹣②得：﹣11y＝﹣22，解得：y＝2，把y＝2代入①得：x＝1，∴方程组的解为；（2）解①得x≥﹣4，解②得x＜1，所以不等式组的解集为﹣4≤x＜1，用数轴表示为．【点评】此题考查了解二元一次方程组，以及解一元一次不等式组，熟练掌握运算法则是解本题的关键．17．（7分）如图，BC∥AD，∠1＝∠E，求证：∠A＝∠C．【分析】由∠1＝∠E，可判定AB∥EC，根据平行线的性质，可得∠ADE＝∠A，又由BC∥AD，可得∠C ＝∠ADE，即可求解．【解答】证明：∵∠1＝∠E，∴AB∥EC，∴∠ADE＝∠A，∵BC∥AD，∴∠C＝∠ADE，∴∠A＝∠C．【点评】此题考查了平行线的判定与性质．此题难度不大，注意掌握数形结合思想的应用．18．（8分）如图，在平面直角坐标系中，每个小正方形的边长为一个单位长度．已知△ABC的顶点A（﹣2，5）、B（﹣4，1）、C（2，3），将△ABC平移得到A'B'C'，点A（a，b）对应点A'（a+3，b﹣4）（1）画出△A'B'C'并写出点B'、C'的坐标B′（﹣1，﹣3），C′（5，﹣1）．（2）试求△A'B'C'的面积10．（3）在x轴上存在一点P，使得S△ABP＝7，则点P的坐标是（﹣8，0）或（﹣1，0）．【分析】（1）分别作出A，B，C的对应点A′，B′，C′即可解决问题．（2）利用分割法求三角形的面积即可．（3）分两种情形，分别构建方程解决问题即可．【解答】解：（1）如图，△A'B'C'即为所求，B′（﹣1，﹣3），C′（5，﹣1）．故答案为B′（﹣1，﹣3），C′（5，﹣1）．（2）S△A′B′C′＝4×6﹣×2×4﹣×2×4﹣×2×6＝10．故答案为10．（3）设P（m，0），当点P在直线AB的右侧时，×2×1+×（m+4）×5﹣×1×（m+4）＝7，解得m＝﹣1，当点P在直线AB的左侧时，×5×（﹣4﹣m）+×（﹣2﹣m）×4﹣×5×（﹣2﹣m）＝7，解得m＝﹣8，∴满足条件的点P的坐标为（﹣8，0）或（﹣1，0）．故答案为（﹣8，0）或（﹣1，0）．【点评】本题考查作图﹣平移变换，三角形的面积等知识，解题的关键是熟练掌握平移变换的性质，学会利用参数构建方程解决问题．19．（6分）某中学有学生2400名，为了响应市“科学应对、群防群控、增强体质、战胜疫情”的号召，学校决定利用课外活动时间举行体育锻炼，为了让学生在篮球、足球、排球和乒乓球这四项球类运动中选择一项球类进行锻炼，对学生开展了随机调查，并将结果绘制成如图所示不完整的统计图．请根据以上信息，完成下列问题：（1）本次调查共抽取了多少名学生？（2）求在被调查的学生中，最喜爱乒乓球的人数，并补全条形统计图；（3）请你估计该阳光中学的学生中最喜爱篮球运动的学生人数约有多少名？【分析】（1）用篮球的人数除以篮球的人数所占的百分比，即可解答；（2）用总人数乘以最喜爱乒乓球的人数所占的百分比，即可补全统计图；（3）用阳光中学的总人数乘以最喜爱篮球运动的学生人数所占的百分比即可．【解答】解：（1）本次调查共抽取的学生数是：160÷40%＝400（人）；（2）喜爱乒乓球的人数有：400×30%＝120（人），补全统计图如下：（3）根据题意得：2400×40%＝960（名），答：阳光中学的学生中最喜爱篮球运动的学生人数约有960名．【点评】本题主要考查了条形统计图和扇形统计图的识别，观察条形统计图、扇形统计图获得有效信息是解题关键．20．（9分）某电器超市销售每台进价分别为160元、120元的A、B两种型号的电风扇，如表是近两周的销售情况：销售时段销售数量销售收入A种型号B种型号第一周3台4台1200元第二周5台6台1900元（进价、售价均保持不变，利润＝销售收入﹣进货成本）（1）求A、B两种型号的电风扇的销售单价；（2）若超市准备用不多于7500元的金额再采购这两种型号的电风扇共50台，求A种型号的电风扇最多能采购多少台？（3）在（2）的条件下，超市销售完这50台电风扇能否实现利润超过1850元的目标？若能，请给出相应的采购方案；若不能，请说明理由．【分析】（1）设A、B两种型号电风扇的销售单价分别为x元、y元，根据3台A型号4台B型号的电扇收入1200元，5台A型号6台B型号的电扇收入1900元，列方程组求解；（2）设采购A种型号电风扇a台，则采购B种型号电风扇（50﹣a）台，根据金额不多余7500元，列不等式求解；（3）根据A种型号电风扇的进价和售价、B种型号电风扇的进价和售价以及总利润＝一台的利润×总台数，列出不等式，求出a的值，再根据a为整数，即可得出答案．【解答】解：（1）设A、B两种型号电风扇的销售单价分别为x元、y元，依题意得：，解得：，答：A、B两种型号电风扇的销售单价分别为200元、150元．（2）设采购A种型号电风扇a台，则采购B种型号电风扇（50﹣a）台．依题意得：160a+120（50﹣a）≤7500，解得：a≤37．答：超市最多采购A种型号电风扇37台时，采购金额不多于7500元．（3）根据题意得：（200﹣160）a+（150﹣120）（50﹣a）＞1850，解得：a＞35，∵a≤37，且a应为整数，∴在（2）的条件下超市能实现利润超过1850元的目标．相应方案有两种：当a＝36时，采购A种型号的电风扇36台，B种型号的电风扇14台；当a＝37时，采购A种型号的电风扇37台，B种型号的电风扇13台．【点评】此题考查了二元一次方程组和一元一次不等式的应用，解答本题的关键是读懂题意，设出未知数，找出合适的等量关系和不等关系，列方程组和不等式求解．21．（10分）如图，已知AB∥CD，现将一直角三角形PMN放入图中，其中∠P＝90°，PM交AB于点E，PN交CD于点F．（1）当△PMN所放位置如图①所示时，则∠PFD与∠AEM的数量关系为∠PFD+∠AEM＝90°．请说明理由作PG∥AB，如图①所示则PG∥CD，∴∠PFD＝∠1，∠2＝∠AEM，∵∠1+∠2＝∠P＝90°，∴∠PFD+∠AEM＝∠1+∠2＝90°，．（2）当△PMN所放位置如图②所示时，∠PFD与∠AEM的数量关系为∠PFD﹣∠AEM＝90°．（3）在（2）的条件下，若MN与CD交于点O，且∠DON＝30°，∠PEB＝15°，求∠N的度数．【分析】（1）由平行线的性质得出∠PFD＝∠1，∠2＝∠AEM，即可得出结果；（2）由平行线的性质得出∠PFD+∠1＝180°，再由角的互余关系即可得出结果；（3）由角的互余关系求出∠PHE，再由平行线的性质得出∠PFC的度数，然后由三角形的外角性质即可得出结论．【解答】解：（1）作PG∥AB，如图①所示：则PG∥CD，∴∠PFD＝∠1，∠2＝∠AEM，∵∠1+∠2＝∠P＝90°，∴∠PFD+∠AEM＝∠1+∠2＝90°，故答案为：∠PFD+∠AEM＝90°；（2）证明：如图②所示：∵AB∥CD，∴∠PFD+∠BHF＝180°，∵∠P＝90°，∴∠BHF+∠2＝90°，∵∠2＝∠AEM，∴∠BHF＝∠PHE＝90°﹣∠AEM，∴∠PFD+90°﹣∠AEM＝180°，∴∠PFD﹣∠AEM＝90°，故答案为∠PFD﹣∠AEM＝90°；（3）如图③所示：∵∠P＝90°，∴∠PHE＝90°﹣∠FEB＝90°﹣15°＝75°，∵AB∥CD，∴∠PFC＝∠PHE＝75°，∵∠PFC＝∠N+∠DON，∴∠N＝75°﹣30°＝45°．【点评】本题考查了平行线的性质、角的互余关系；熟练掌握平行线的性质，弄清角之间的数量关系是解决问题的关键．。