第四章-数字图像处理中的基本运算
《数字图像处理》教学大纲

《数字图像处理》教学大纲
一、课程简介
数字图像处理是机器视觉、模式识别、医学图像处理等的基础,本课程为工程专业的学生提供数字图像处理的基本知识,是理论性和实践性都很强的综合性课程。
课程内容广泛涵盖了数字图像处理的基本原理,包括图像采样和量化、图像算术运算和逻辑运算、直方图、图像色彩空间、图像分割、图像形态学、图像频域处理、图像分割、图像降噪与图像复原、特征提取与识别等。
二、课程目标
通过本课程学习,学生可以掌握数字图像处理的基本方法,具备一定的解决图像处理应用问题的能力,培养解决复杂工程问题的能力。
具体目标如下:
1.掌握数字图像处理的基本原理、计算方法,能够利用专业知识并通过查阅资
料掌握理解相关新技术,对检测系统及处理流程进行创新性设计;
2.能够知晓工程领域中涉及到的数字图像处理技术,理解其适用场合、检测对
象及条件的限制,能根据给定的目标要求,针对工业检测中的工程问题选择和使用合适的技术和编程,进行仿真和分析;
3.能够知晓工程领域中所涉及的现代工具适用原理及方法,根据原理分析和仿
真结果,进行方案比选,确定设计方案,具有检测算法的设计能力;
4.通过校内外资源和现代信息技术,了解数字图像处理发展趋势,提高解决复
杂工程问题的能力。
三、课程目标对毕业要求的支撑关系
四、理论教学内容及要求
四、实验教学内容及要求
五、课程考核与成绩评定
六、教材及参考书。
数字图像处理-图像基本运算
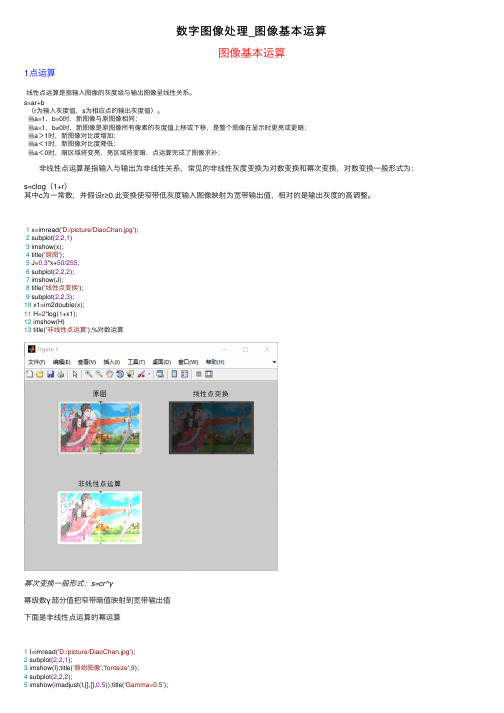
数字图像处理_图像基本运算图像基本运算1点运算线性点运算是指输⼊图像的灰度级与输出图像呈线性关系。
s=ar+b(r为输⼊灰度值,s为相应点的输出灰度值)。
当a=1,b=0时,新图像与原图像相同;当a=1,b≠0时,新图像是原图像所有像素的灰度值上移或下移,是整个图像在显⽰时更亮或更暗;当a>1时,新图像对⽐度增加;当a<1时,新图像对⽐度降低;当a<0时,暗区域将变亮,亮区域将变暗,点运算完成了图像求补; ⾮线性点运算是指输⼊与输出为⾮线性关系,常见的⾮线性灰度变换为对数变换和幂次变换,对数变换⼀般形式为:s=clog(1+r)其中c为⼀常数,并假设r≥0.此变换使窄带低灰度输⼊图像映射为宽带输出值,相对的是输出灰度的⾼调整。
1 x=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1)3 imshow(x);4 title('原图');5 J=0.3*x+50/255;6 subplot(2,2,2);7 imshow(J);8 title('线性点变换');9 subplot(2,2,3);10 x1=im2double(x);11 H=2*log(1+x1);12 imshow(H)13 title('⾮线性点运算');%对数运算幂次变换⼀般形式:s=cr^γ幂级数γ部分值把窄带暗值映射到宽带输出值下⾯是⾮线性点运算的幂运算1 I=imread('D:/picture/DiaoChan.jpg');2 subplot(2,2,1);3 imshow(I);title('原始图像','fontsize',9);4 subplot(2,2,2);5 imshow(imadjust(I,[],[],0.5));title('Gamma=0.5');7 imshow(imadjust(I,[],[],1));title('Gamma=1');8 subplot(2,2,4);9 imshow(imadjust(I,[],[],1.5));title('Gamma=1.5');2代数运算和逻辑运算加法运算去噪处理1 clear all2 i=imread('lenagray.jpg');3 imshow(i)4 j=imnoise(i,'gaussian',0,0.05);5 [m,n]=size(i);6 k=zeros(m,n);7for l=1:1008 j=imnoise(i,'gaussian',0,0.05);9 j1=im2double(j);10 k=k+j1;11 End12 k=k/100;13 subplot(1,3,1),imshow(i),title('原始图像')14 subplot(1,3,2),imshow(j),title('加噪图像')15 subplot(1,3,3),imshow(k),title(‘求平均后的减法运算提取噪声1 I=imread(‘lena.jpg’);2 J=imnoise (I,‘lena.jpg’,0,0.02);3 K=imsubtract(J,I);4 K1=255-K;5 figure;imshow(I);7 figure;imshow(K1);乘法运算改变图像灰度级1 I=imread('D:/picture/SunShangXiang.jpg')2 I=im2double(I);3 J=immultiply(I,1.2);4 K=immultiply(I,2);5 subplot(1,3,1),imshow(I);subplot(1,3,2),imshow(J);6 subplot(1,3,3);imshow(K);逻辑运算1 A=zeros(128);2 A(40:67,60:100)=1;3 figure(1)4 imshow(A);5 B=zeros(128);6 B(50:80,40:70)=1;7 figure(2)8 imshow(2);9 C=and(A,B);%与10 figure(3);11 imshow(3);12 D=or(A,B);%或13 figure(4);14 imshow(4);15 E=not(A);%⾮16 figure(5);17 imshow(E);3⼏何运算平移运算实现图像的平移1 I=imread('lenagray.jpg');2 subplot(1,2,1);3 imshow(I);4 [M,N]=size(I);g=zeros(M,N);5 a=20;b=20;6for i=1:M7for j=1:N8if((i-a>0)&(i-a<M)&(j-b>0)&(j-b<N)) 9 g(i,j)=I(i-a,j-b);10else11 g(i,j)=0;12 end13 end14 end15 subplot(1,2,2);imshow(uint8(g));⽔平镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(i,N-j+1);7 end8 end9 subplot(122);imshow(uint8(g));垂直镜像变换1 I=imread('lena.jpg');2 subplot(121);imshow(I);3 [M,N]=size(I);g=zeros(M,N);4for i=1:M5for j=1:N6 g(i,j)=I(M-i+1,j);7 end8 end9 subplot(122);imshow(uint8(g));图像的旋转1 x=imread('D:/picture/DiaoChan.jpg');2 imshow(x);3 j=imrotate(x,45,'bilinear');4 k=imrotate(x,45,'bilinear','crop');5 subplot(1,3,1),imshow(x);6 title(‘原图')7 subplot(1,3,2),imshow(j);8 title(‘旋转图(显⽰全部)')9 subplot(1,3,3),imshow(k);10 title(‘旋转图(截取局部)')⼏种插值法⽐较1 i=imread('lena.jpg');2 j1=imresize(i,10,'nearest');3 j2=imresize(i,10,'bilinear');4 j3=imresize(i,10,'bicubic');5 subplot(1,4,1),imshow(i);title(‘原始图像')6 subplot(1,4,2),imshow(j1);title(‘最近邻法')7 subplot(1,4,3),imshow(j2);title(‘双线性插值法')8 subplot(1,4,4),imshow(j3);title(‘三次内插法')放缩变换1 x=imread('D:/picture/ZiXia.jpg')2 subplot(2,3,1)3 imshow(x);4 title('原图');5 Large=imresize(x,1.5);6 subplot(2,3,2)7 imshow(Large);8 title('扩⼤为1.5');9 Small=imresize(x,0.1);10 subplot(2,3,3)11 imshow(Small);12 title('缩⼩为0.3');13 subplot(2,3,4)14 df=imresize(x,[600700],'nearest');15 imshow(df)16 title('600*700');17 df1=imresize(x,[300400],'nearest');18 subplot(2,3,5)19 imshow(df1)20 title('300*400');后记:(1)MATLAB基础知识回顾1:crtl+R是对选中的区域注释,ctrl+T是取消注释2:有的代码中点运算如O=a.*I+b/255 ,其中b除以255原因是:灰度数据有两种表式⽅法:⼀种是⽤unit8类型,取值0~255;另⼀种是double类型,取值0~1。
数字图像处理基本知识

数字图像处理基本知识数字图像处理基木知识图像处理最早出现于20世纪50年代,当时的电子计算机己经发展到一定水平,人们开始利用计算机来处理图形和图像信息。
数字图像处理作为一门学科大约形成于20世纪60年代初期。
早期的图像处理的目的是改善图像的质量,它以人为对象,以改善人的视觉效果为目的。
图像处理中,输入的是质量低的图像,输出的是改善质量后的图像,常用的图像处理方法有图像增强、复原、编码、压缩等。
数字图像处理常用方法:1)图像变换:由于图像阵列很大,直接在空间域中进行处理,涉及计算量很大。
因此,往往采用各种图像变换的方法,如傅立叶变换、沃尔什变换、离散余弦变换等间接处理技术,将空间域的处理转换为变换域处理,不仅可减少计算量,而且可获得更有效的处理(如傅立叶变换可在频域中进行数字滤波处理)。
目前新兴研究的小波变换在时域和频域中都具有良好的局部化特性,它在图像处理中也有着广泛而有效的应用。
2)图像编码压缩:图像编码压缩技术可减少描述图像的数据量(即比特数),以便节省图像传输、处理时间和减少所占用的存储器容量。
压缩可以在不失真的前提下获得,也可以在允许的失真条件下进行。
编码是压缩技术中最重要的方法,它在图像处理技术中是发展最早且比较成熟的技术。
3)图像增强和复原:图像增强和复原的目的是为了提高图像的质量,如去除噪声,提高图像的清晰度等。
图像增强不考虑图像降质的原因,突出图像中所感兴趣的部分。
如强化图像高频分量,可使图像中物体轮廓清晰,细节明显;如强化低频分量可减少图像中噪声影响。
图像复原要求对图像降质的原因有一定的了解,一般讲应根据降质过程建立“降质模型”,再采用某种滤波方法,恢复或重建原来的图像。
4)图像分割:图像分割是数字图像处理中的关键技术之一。
图像分割是将图像中有意义的特征部分提取出来,其有意义的特征有图像中的边缘、区域等,这是进一步进行图像识别、分析和理解的基础。
虽然目前己研究出不少边缘提取、区域分割的方法,但还没有一种普遍适用于各种图像的有效方法。
第四章-数字图像处理中的基本运算

非线性拉伸实例3
第4章 图像处理中的基本运算
第4章 图像处理中的基本运算
非线性拉伸实例4
第4章 图像处理中的基本运算 非线性拉伸实例5
第4章 图像处理中的基本运算
非线性拉伸实例6
第4章 图像处理中的基本运算
非线性拉伸实例7
第4章 图像处理中的基本运算
4.2.2 点运算与直方图
点运算是一种确定的函数关系下所进行的像素变换 运算,因此,点运算之后输出图像和输入图像之间 的直方图也具有与变换函数相关联的对应关系。 从图4-3中可以找到它们之间的关系,即灰度级小区 间内输入像素的个数,等于输出像素的个数,而且 输入、输出图像的阴影部分面积可以用小矩形的面 积近似替代(替代积分式)。 HB(DB)ΔDB=HA(DA)ΔDA 最后输出的直方图的值为(详细推导见P73-74)
H A (DA ) H B ( DB ) df ( D A ) dDA
第4章 图像处理中的基本运算
4.2.3. 点运算的应用
(1) 对比度增强 在一些数字图像中,技术人员所关注的特征 可能仅占据整个灰度级非常小的一个范围。点 运算可以扩展所关注部分的灰度信息的对比度, 使之占据可显示灰度级的更大部分。又称为对 比度拉伸。
第4章 图像处理中的基本运算
4.3 代数运算
1、概念 2、运算类型及应用
第4章 图像处理中的基本运算
1. 代数运算概念
代数运算是指两幅输入图像之间进行点 对点的加、减、乘、除运算得到输出图像的 过程。如果记输入图像为A(x,y)和B(x,y), 输出图像为C(x,y),则有如下四种形式:
(1) (2) (3) (4) C(x,y) C(x,y) C(x,y) C(x,y) = = = = A(x,y)+ B(x,y) A(x,y)- B(x,y) A(x,y)×B(x,y) A(x,y)/B(x,y)
数字图像处理各章要求必做题及参考答案
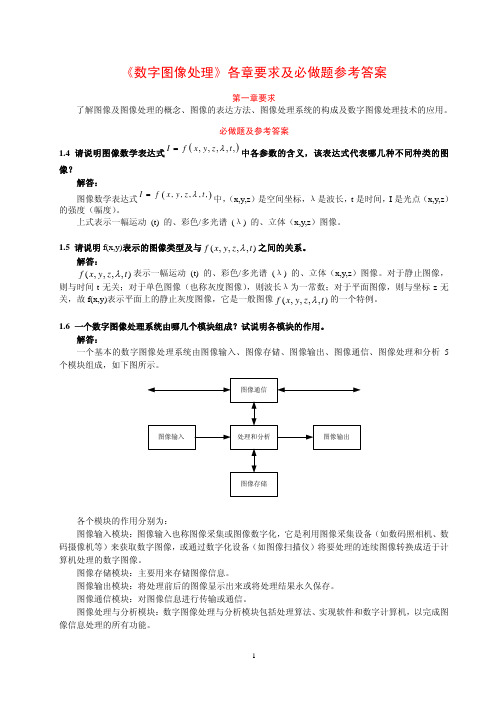
图像通信
图像输入
处理和分析
图像输出
图像存储
各个模块的作用分别为: 图像输入模块:图像输入也称图像采集或图像数字化,它是利用图像采集设备(如数码照相机、数 码摄像机等)来获取数字图像,或通过数字化设备(如图像扫描仪)将要处理的连续图像转换成适于计 算机处理的数字图像。 图像存储模块:主要用来存储图像信息。 图像输出模块:将处理前后的图像显示出来或将处理结果永久保存。 图像通信模块:对图像信息进行传输或通信。 图像处理与分析模块:数字图像处理与分析模块包括处理算法、实现软件和数字计算机,以完成图 像信息处理的所有功能。
2.10(1) 存储一幅 1024×768,256 个灰度级的图像需要多少 bit? (2) 一幅 512×512 的 32 bit 真彩图像的容量为多少 bit? 解答:
(1)一幅 1024×768,256 个灰度级的图像的容量为: b=1024× 768×8 = 6291456 bit (2)一幅 512×512 的 32 位真彩图像的容量为: b=512 × 512 × 32=8388608 bit
的图像具有如题表 4.4.2 所示的灰度级分布。
题表 4.4.1
灰度级
0
1
2
3
4
5
6
7
各灰度级概率分布
0.14 0.22 0.25 0.17 0.10 0.06 0.03 0.03
题表 4.4.2
灰度级
0
1
2
3
4
5
6
7
各灰度级概率分布
0
0
0
0.19 0.25 0.21 0.24 0.11
解答: (1)直方图均衡化结果如下表所示
数字图像处理各章要求必做题及参考答案

−a
v
−a
v
∫ ( ) =
2E v
⎡ ⎢⎣
0 −a
e− jux − e jux
sin v(x + a)dx⎤⎥⎦
∫ =
−4 jE v
⎡ ⎢⎣
0 −a
sin
ux
sin
v(
x
+
a)dx
⎤ ⎥⎦
( ) = 4 jE (u sin va − v sin ua) v u2 − v2
3
第三章要求 1. 了解图像的几何变换; 2. 了解图像的离散傅立叶变换,掌握其重要性质; 3. 了解变换的一般表示形式; 4. 了解图像的离散余弦变换的原理 ; 5. 掌握图像的离散沃尔什-哈达玛变换; 6. 了解 K-L 变换的原理。
4 4
4 4
4⎥⎥ 4⎥
⎢⎣1 4 4 1⎥⎦
⎢⎣4 4 1 1⎥⎦
⎢⎣4 4 4 4⎥⎦
解答:
由H2 =
1 ⎡1 2 ⎢⎣1
1⎤ -1⎥⎦
和H
2
N
=
1 ⎡HN 2 ⎢⎣HN
HN -H N
⎤ ⎥⎦
得
⎡1 1 1 1 ⎤
H4
=
1 2
⎢⎢1 ⎢1
-1 1
1 -1
-1⎥⎥ -1⎥
⎢⎣1
-1
-1
1
⎥ ⎦
⎡10 0 0 −6⎤
X = ⎡⎣x1
x 2
x3 ⎤⎦T 的协方差矩阵 CX 。
解答:
⎧⎡1⎤ ⎡1⎤ ⎡1⎤⎫ ⎡3⎤
∑ 根据式 mx
=
1 M
M
xk
k =1
得 mX
=
1 3
MATLAB数字图像处理实验--图像基本运算

MATLAB数字图像处理实验--图像基本运算一、实验目的1.理解图像点运算、代数运算、几何运算的基本定义和常见方法;2.掌握在MTLAB中对图像进行点运算、代数运算、几何运算的方法;3.掌握在MATLAB中进行插值的方法4.运用MATLAB语言进行图像的插值缩放和插值旋转5.进一步熟悉了解MATLAB语言的应用。
二、实验设备与软件1.PC计算机系统2.MATLAB软件,包括图像处理工具箱(Image Processing Toolbox)3.实验图片三、实验内容及结果分析3.1图像的点运算选择pout.tif作为实验图像,实验原理及内容参照《MATLAB图像处理编程及应用》程序代码:I=imread('pout.tif');figure;subplot(1,3,1);imshow(I);title('原图');J=imadjust(I,[0.3;0.6],[0.1;0.9]);subplot(1,3,2);imshow(J);title('线性扩展');I1=double(I);I2=I1/255;C=2;K=C*log(1+I2);subplot(1,3,3);imshow(K);title('非线性扩展');M=255-I;figure;subplot(1,3,1);imshow(M);title('灰度倒置');N1=im2bw(I,0.4);N2=im2bw(I,0.7);subplot(1,3,2);imshow(N1);title('二值化阈值0.4');subplot(1,3,3);imshow(N2);title('二值化阈值0.7');执行结果:原图线性扩展非线性扩展灰度倒置二值化阈值0.4二值化阈值0.7实验1结果图3.2图像的代数运算选择两幅图像,一幅是原图像,一幅为背景图像,采用正确的图像代数运算方法,分别实现图像叠加、混合图像的分离和图像的局部显示效果。
数字图像处理04章04

第4章 图像处理中的基本运算
双线性插值的特点
➢ 计算量大,但缩放后图像质量高,不会出 现图像不连续的情况。 ➢ 具有低通滤波器的性质,使高频分量减弱, 所以使图像的轮廓在一定程度上受损。
第4章 图像处理中的基本运算
双线性插值
根据点P(x0,y0)的四个相邻点的灰度值, 通过两次插值计算出灰度值f(x0,y0)
✓双线性插值(一阶插值):采用在(x ,y)
周围四个网格点的灰度值进行内插
第4章 图像处理中的基本运算
双线性插值公式
f (x0 , y0 )
f (x, y) [ f (x 1, y) f (x, y)] [ f (x, y 1) f (x, y)] [ f (x 1, y 1) f (x, y)
第4章 图像处理中的基本运算
四. 灰度插值
图像的比例缩放、 旋转变换时等,变换过程需要两 个独立的算法:
一个算法完成几何变换; 一个算法用于灰度级插值.
第4章 图像处理中的基本运算
灰度插值的概念
数字图像处理只能对坐标网格点(离散点) 的值进行变换。而坐标变换后产生的新坐标 值同网格点值往往不重合,因此需要通过内 插的方法将非网格点的灰度值变换成网格点 的灰度值,这种算法称为灰度内插。
✓最邻近插值法 ✓双线性插值(一阶插值)
第4章 图像处理中的基本运算
最邻近插值法
计算与点P(x0,y0)临近的四个点; 将与点P(x0,y0)最近的整数坐标点(x,y)
的灰度值取为P(x0,y0) 点灰度近似值。
最邻近插值法实质 就是最临近点重复
第4章 图像处理中的基本运算
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
d c
g(x, y)
[ f (x, y) a] c a f (x, y) b ba
c
f (x, y) a
宽 窄
第4章 图像处理中的基本运算
(2)分段线性点运算 将感兴趣的灰度范围线性扩展,抑制不感兴趣
的灰度区域,就要使用分段线性点运算。
设f(x,y)灰度范围为[0,Mf],g(x,y)灰度范围 为[0,Mg],分段线性点运算如下图所示:
像设备的非线性和图像记录设备动态范围太窄 等因素,都会产生对比度不足的弊病,使图像中 的细节分辨不清.
这时可通过点运算将灰度范围线性扩展. 设f(x,y)灰度范围为[a,b],g(x,y)灰度范 围为[c,d]. 则线性点运算公式为:
第4章 图像处理中的基本运算
线性点运算公式
d
f (x, y) b
度: 暗(不变):中(增加):亮(不变) 暗(降低):中(增加):亮(降低) 暗(加强):中(压低):亮(加强) 公式见下页。
第4章 图像处理中的基本运算
(1) DB=f(DA)=DA+CDA(DM-DA)
(2)
f
(DA )
Dm 2
1
1 απ sin( )
s
in[απ(
DA DB
1 2
第4章 图像处理中的基本运算
差值法的应用举例
(a)差影法可以用于混合图像的分离
-
=
第4章 图像处理中的基本运算
(b) 检测同一场景两幅图像之间的变化
设:
时刻1的图像为T1(x,y), 时刻2的图像为T2(x,y) g(x,y) = T2 (x,y) - T1(x,y)
=
-
g(x,y)
T1(x,y)
)]
2
(3)
f
(DA )
Dm 2
1
1 απ tan( )
tan[απ( DA DB
12 )]
2
第4章 图像处理中的基本运算
255
255
218
输出DB
输出DB
128 255
输入DA
加亮-减暗图像
32
128 255
输入DA
加暗-减亮图像
亮度调整
第4章 图像处理中的基本运算
非线性拉伸实例1 对比度拉伸
拉伸效果:图像加亮、减暗
第4章 图像处理中的基本运算
非线性拉伸实例2
第4章 图像处理中的基本运算 非线性拉伸实例3
第4章 图像处理中的基本运算
第4章 图像பைடு நூலகம்理中的基本运算
非线性拉伸实例4
第4章 图像处理中的基本运算
非线性拉伸实例5
第4章 图像处理中的基本运算
非线性拉伸实例6
第4章 图像处理中的基本运算
255 142
DB
0
255
DA
降低对比度
第4章 图像处理中的基本运算
降低对比度举例
255
DB
0
255
DA
第4章 图像处理中的基本运算
③ 如果a=1,b≠0,操作仅使所有像素的 灰度值上移或下移,其效果是使整个图像 更暗或更亮
255
255
DB
DB
0
整个图像DA 更亮
0
DA
255
整个图像更暗
255
(2) 光度学标定 点运算可消除图像传感器的非线性的影响。
第4章 图像处理中的基本运算
(3) 显示标定 一些显示设备不能保持数字图像上像素的灰
度值和显示屏幕上相应点的亮度之间的线性关系。 这一缺点可以通过点运算予以克服,即在图像显 示之前,先设计合理的点运算关系,可将点运算 和显示非线性组合起来互相抵消,以保持在显示 图像时的线性关系。 (4) 轮廓线
(1) C(x,y) = A(x,y)+ B(x,y) (2) C(x,y) = A(x,y)- B(x,y) (3) C(x,y) = A(x,y)×B(x,y) (4) C(x,y) = A(x,y)/B(x,y)
第4章 图像处理中的基本运算
2. 运算类型及应用
(1)加运算 (2)减运算 (3)乘运算 (4)除运算
点运算。即:
DB f (DA) aDA b
255
输出DB b
f(DA)=aDA+b
0
输入DA
255
第4章 图像处理中的基本运算
① 如果a>1,输出图像的对比度增大
255
DB
0 48
218 255
DA
提高对比度
第4章 图像处理中的基本运算
提高对比度举例
第4章 图像处理中的基本运算
② 如果a<1,输出图像的对比度减小
第4章 图像处理中的基本运算
4.2 点运算
在图像处理中,点运算是一类简单却非常 具有代表性的重要算法之一,也是其他图 像处理运算的基础。运用点运算可以改变 图像像素占据的灰度值范围,但不会改变 图像内的空间位置关系。
点运算包括以下内容: 1.定义 2:分类
3:应用
第4章 图像处理中的基本运算
HB(DB)ΔDB=HA(DA)ΔDA 最后输出的直方图的值为(详细推导见P73-74)
H B (DB )
H A (DA ) df (DA )
dDA
第4章 图像处理中的基本运算
4.2.3. 点运算的应用
(1) 对比度增强 在一些数字图像中,技术人员所关注的特征
可能仅占据整个灰度级非常小的一个范围。点 运算可以扩展所关注部分的灰度信息的对比度, 使之占据可显示灰度级的更大部分。又称为对 比度拉伸。
点运算可为图像加上轮廓线。 (5) 剪裁
对于8bit图像,通过点运算,在每个像素值 被存储之前,输出灰度级一定要剪裁到0~255 的范围内。
第4章 图像处理中的基本运算
4.3 代数运算
1、概念 2、运算类型及应用
第4章 图像处理中的基本运算
1. 代数运算概念
代数运算是指两幅输入图像之间进行点 对点的加、减、乘、除运算得到输出图像的 过程。如果记输入图像为A(x,y)和B(x,y), 输出图像为C(x,y),则有如下四种形式:
在银行金库内,摄像头每隔一固定时间拍摄一 幅图像,并与上一幅图像做差影,如果图像差 别超过了预先设置的阈值,则表明可能有异常 情况发生,应自动或以某种方式报警;
用于遥感图像的动态监测,差值图像可以发现 森林火灾、洪水泛滥,监测灾情变化等;
也可用于监测河口、海岸的泥沙淤积及监视江 河、湖泊、海岸等的污染;
第4章 图像处理中的基本运算
④如果a=1,b=0时,输出、输入图像相同
255
DB
0
DA
255
第4章 图像处理中的基本运算
⑤ 如果a为负值,暗区域将变亮,亮区域将变暗
255
DB
0
DA
255
第4章 图像处理中的基本运算
255
DB
0
DA
255
第4章 图像处理中的基本运算
线性点运算公式 当图象成像时曝光不足或过度, 或由于成
第4章 图像处理中的基本运算
第4章 图像处理中的基本运算
分段线性点运算公式
宽
g(x, y)
Mg d [ f (x, y) b] d
Mf b
d c b a [ f (x, y) a] c
c f (x, y)
a
窄
b f (x, y) M f
a f (x, y) b
0 f (x, y) a
第4章 图像处理中的基本运算
第四章:数字图像处理中的基本运算
第4章 图像处理中的基本运算
图像处理基本运算概述
图像处理中,经常要采用各种各样的算法。根 据数字图像处理运算中输入信息与输出信息的 类型,图像处理典型算法从功能上具有以下几 种:
(1)单幅图像 (2)多幅图像 (3)单幅或多幅图像
单幅图像 单幅图像
1. 定义
所谓点运算是指像素值(像素点的灰度值)通 过运算之后,可以改善图像的显示效果。这是一 种像素的逐点运算。
点运算与相邻的像素之间没有运算关系,是原 始图像与目标图像之间的影射关系。是一种简单 但却十分有效的图像处理方法。
点运算又称为“对比度增强”、“对比度拉 伸”、“灰度变换”
第4章 图像处理中的基本运算
K=2
K=4
K=16
第4章 图像处理中的基本运算
生成图象叠加效 果:可以得到各种 图像合成的效果, 也可以用于两张图 片的衔接
第4章 图像处理中的基本运算
(2)减法运算
C(x,y) = A(x,y) - B(x,y)
主要应用
消除背景影响
差影法(检测同一场景两幅图像之间的 变化)
第4章 图像处理中的基本运算
第4章 图像处理中的基本运算
(3)非线性点运算:输出灰度级与输入灰度级呈 非线性关系的点运算。
255 输出
0
输入
255
非线性点运算灰度变换函数的斜率处处为正, 这类函数保留了图像的基本外貌。
第4章 图像处理中的基本运算
非线性点运算的函数形式可以表示为: DB = f (DA)
同灰样度,值D。A为f表输示入非点线的性灰函度数值。,DB为相应输出点的 有三种典型的非线性点运算函数,可以改变对比
g(x,y) = 1/M (g0(x,y)+g1(x,y)+…+ g M (x ,y))
前提:噪音h(x,y)i为互不相关,且均值为0时, 上述图象均值将降低噪音的影响。
第4章 图像处理中的基本运算
相加
图例:求平均消除加性随
机噪声,k=1,2,3,4,16,
K=1
表示1幅图像平均、2幅
图像相加后求平均…
