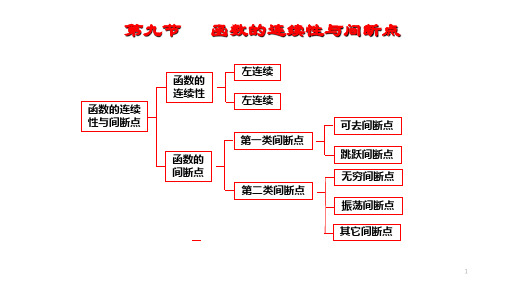
连续函数图象的分解与一类剪切集

合集下载

微积分课件2.7连续函数

解由于
lim f ( x) lim(x2 1) 1
x0
x0
且
lim f (x) lim(2x b) b
x0
x0
又因为f(x)在点 x = 0处连续，故
lim f (x) lim f (x)
x0
x0
即 b 1
若函数 ƒ(x)在开区间 (a , b) 内的每一点都连续, 则称函
数ƒ(x)在开区间 (a , b) 内连续; 若函数ƒ(x)在开区间 (a , b) 内连续, 且在左端点 a 右连
lim
x x0
f ( x) 不存在;
(3)
ƒ(x)在 x0 处虽有定义,
且
lim f ( x) 存在, 但
x x0
lim
x x0
f (x)
f ( x0 )
依据函数在间断点处的左、右极限是否都存在，通常
把函数的间断点划分为两类. 设点 x0是函数 ƒ(x)的间断点.
第一类间断点：左右极限都存在的间断点；
f (1)
1 e1 arctan 1
4 (1 e)
例10
xn 1
lim
x 1
xm
;(m, n 1
N)
解因为 an bn (a b)(an1 an2b
abn2 bn1 )
故
xn 1
lim
x1
xm
1
n个
( x 1) ( xn1 xn2 1)
lim
x 1
(x
1) ( xm1
y f (x0 x) f (x0 )
为函数对应的增量(或改变量).
定义2.7.2 设函数 ƒ(x) 在 x0 的某邻域内有定义, 如果
lim y

专升本数学连续ppt课件

无穷级数具有可交换性、可结合性和可分配性等性质，这些性质使得无穷级数的运算更加方便。
无穷级数的收敛性是一个重要的性质，它决定了无穷级数的和是否有限。收敛级数的和可以通过求和公式或极限方法来求解。
无穷级数的应用
无穷级数在数学分析中有着广泛的应用，它可以用来表示函数、解决一些数学问题以及描述自然现象等。
相加或相乘。
无穷级数可以分为两类：收敛级数和发散级数。收敛级数的和是有限的，而发散级
数的和是无穷的。
无穷级数在数学分析中有着广泛的应用，它可以用来表示函数、解决一些数学问题以及描
述自然现象等。
无穷级数的性质
无穷级数具有可加性和可乘性，即对于任意两个无穷级数，它们的和或积仍然是一个无穷级数。
在物理学中，无穷级数被广泛应用于描述物理现象和规律，例如在量子力学、电磁学和流体动力学等领域。
在计算机科学中，无穷级数可以用来进行快速计算和近似计算，例如在计算机图形学、数值分析和密码学等领域。
05
空间解析几何
向量代数
向量数乘
数乘是向量代数中的一种运算，通过一个实数和一个向量相乘得到一个新的向量。
间断的类型
总结词
间断是连续的反义词，表示函数在某点或某区间内不连续。
详细描述
间断可以分为多种类型，包括第一类间断和第二类间断。第一类间断包括可去间断点和跳跃间断点，而第二类间断则包括无穷间断和震荡间断。
连续与间断的性质
总结词
连续和间断的性质是数学中研究的重要内容，它们在函数的极限、导数和积分等领域有着广泛的应用。
向量的方向角
方向余弦是描述向量方向的三个数值，可以通过三角函数计算得到。
向量的方向余弦
向量的方向角是描述向量方向的角度，可以通过反三角函数计算得到。

图像分解原理

图像分解原理
图像分解是一种将复杂的图像分解为多个简单结构组成的技术。

它不仅可以帮助我们理解图像的构成，还能提供分析和处理图像的基础。

图像分解的基本原理是将图像分解为一系列较小且相互独立的部分，这些部分被称为图像的基本元素。

这些基本元素可以是线条、点、形状或纹理等。

通过分解图像，我们可以观察和分析每个基本元素的特征和关系。

图像分解的过程通常包括以下几个步骤：
1. 图像预处理：对图像进行预处理，例如去噪、增强对比度等操作，以减少干扰和提高图像质量。

2. 图像分割：将图像分割为不同的区域或对象。

这可以通过不同的方法实现，如边缘检测、阈值分割等。

3. 特征提取：从每个分割区域中提取出具有代表性的特征。

这些特征可以是形状、颜色、纹理等。

4. 基本元素提取：通过对分割区域进行细分和简化，将其进一步分解为更小的基本元素。

这可以通过拟合曲线、提取边缘等方法实现。

5. 分析和重建：分析每个基本元素的特征和关系，并将它们重新组合以重建原始图像。

这可以通过线性和非线性重建技术实
现。

图像分解的主要应用包括图像压缩、图像识别、目标跟踪等领域。

通过分解图像，我们可以更好地理解图像的结构和内容，从而实现更有效的图像处理和分析任务。

§2.2——F集合截集和分解定理

ˆ B (u )∆ A(u ) + B (u ) − A(u ) • B (u ) A(u ) +
A(u ) • B (u ) 为普通实数乘法。
4) 其余模糊算子 Einstein:
(ε , ε )
+ • + •
Hamacher: (r , r ) (Y , λ ) Yager:
a a
2、范数
T范数：范数：设映射 T:[0,1]2→[0,1]，如果 ∀a,b,c∈[0,1],满足如下条件：满足如下条件： 1) 交换律 T(a,b)=T(b,a); 2) 结合律 T(T(a,b),c)=T(a,T(b,c)); 3) 单调性若a1≤a2,b1≤b2,则(a1,b1)≤T(a2,b2); 4) 边界条件：边界条件：T(1,a)=a; 则称为T三角模，三角模，也称为T范数；范数；常见T范数算子如：范数算子如：(∧,
支集：支集： SuppA = {u u ∈U , A(u ) > 0} 核： KerA = {u u ∈U , A(u ) = 1} 若：KerA≠φ，则称A为正规F集。
例3、设
A=
0.5 0.7 0 0.9 1 + + + + u1 u 2 u 3 u 4 u 5
，则：
当λ＝1时： A1 = {u 5 }
1
U{( x, y) x = 1且0 ≤ y ≤ 1} U{( x, y) y = 1且0 ≤ x ≤ 1}
1
0
四、F集的截集
1、F集的λ-截集：截集：定义：定义：设A∈ℑ(U),λ∈[0,1],则： 1） Aλ ={u|u∈U,A(u)≥λ}，称 Aλ 为A的 λ-截集，截集，λ称为置信水平(或阈值)；

连续函数图象的分解

９ｌ４
应用数
学
定理１［。设厂∈ ｃ（Ｅｏ，１］），Ｓ∈ Ｅ１，２］，则存在连续函数ｈ，ｇ∈ ｃ（Ｅｏ，１］）使得
ｆ— ｈ＋ｇ，并且ｄｉｍＨＧ（Ｅｏ，１］）一ｄｉｍＨＧ（Ｅｏ，１］）一ｓ。
可以证明
在｛（，，ｇ，＾）∈ Ｃ（Ｅｏ，１］）。：ｆ— ｇ＋ｈ）中是稠密的．如果１≤ ａ，口≤ ’ ， ≤２，我们将在本文证明下面更强结果：
定理２假设１ ≤ａ，卢 ≤ｙ ≤２，那么对任意连续函数厂∈ Ｃ（Ｅｏ，１］），如果ｄｉｍＧｒ（Ｅｏ，１］）一ｙ，则存在函数ｇ，ｈ∈ Ｃ（Ｅｏ，１］）使得
ｄｉｍ（Ｇｒ（Ｋ））＝又因为Ｋ是紧集，令［Ｏ，ＶＩ＼Ｋ —Ｕ（ｎ，ｂ），
其中｛（ “ ，ｂ））为一列互不相交的开区间．
对每个固定的ｉ，我们先考虑函数厂在闭区间［ａ，］上限制的图象．利用定理ｌ，把函数ｌ［ａｌ，ｂ１］分解如下
湖北武汉４３００７４）
摘要：本文证明：给定１ ≤ｓ ≤ ≤ ２，对于区间［Ｏ，１］上的任意连续函数－厂，如果ｆ的
图象的Ｈａｕｓｄｏｒｆｆ维数不小于ｔ，那么存在连续函数ｇ，ｈ使得
ｆ＝＝＝ｇ＋ｈ，并且ｄｉｍＨＧ（［ｏ，１］）：＝：５，ｄｉｍＧ（［ｏ，１］）一ｔ，

连续性函数

连续性函数
连续性函数是数学中一个重要的概念，它是一个函数，在域上定义了它的解。

在概念上，一个连续函数是指一类函数，它们在域上具有不间断的变化，如果给定一个点，那么在包含这个点的邻近点会有一个细微的变化，并且这种变化会持续下去，直到函数的最终值被达到，而不会出现不可理解的突然变化。

连续性函数的定义起源于17世纪初的牛顿，当时牛顿发现了连续性的概念，并将这一概念用于分析定义连续函数的数学形式。

它的定义是指当X从a向b变化时，函数f（x）在这段距离内没有停止变化，而是渐进变化。

因此，可以说，连续函数就是没有断点的函数。

将连续性函数应用于数学理论中，主要可以划分为两种形式：一类是一元连续函数，一类是多元连续函数。

它们在数学上的表示形式不一样，但都具有同样的定义，即当X从a向b变化时，函数f（x）在这段距离内没有停止变化，而是渐进变化。

一元连续函数的表示形式很简单，它只需要一个变量X，它的公式可以表示为：f(x)=x^2-1，其中X为函数的自变量，x2-1为函数的因变量。

可以看出，当X沿着定义域变化时，函数f（x）的因变量也会随着X的变化而不间断地增加或减少。

而多元连续函数的表示形式要复杂一些，它需要多个变量X1、X2、X3……，它的公式可以表示为：
f(X1,X2,X3,...)=X1^2+X2^2+X3^2+...，其中X1、X2、X3等为函数的自变量，X1^2+X2^2+X3^2等为函数的因变量。

高等数学第1章第九节函数的连续性与间断点

有定义，但 lim f ( x)不存在；
0
x x0
x （3）虽在
0 有定义，且
lim f ( x)存在，但
x x0
x x 则函数 f ( x)在点 0不连续，而点 0 称为函数
或间断点。
若函数 f ( x)
lim
x x0
f (x)
f ( x0 );
f ( x) 的不连续点
5
函数间断点的几种常见类型：
0,
1,
x 1 x 1, x 1
x,
f
(
x
)
0,
x,
x,
x x
1 1
0, x,
x 1
0,
x,
x 1 x 1 1 x 1 x 1 x 1
14
f 1 0 lim x 1 f 1 x10
f 1 0 lim x 1 f 1 x10
函数在 x 1处既不左连续，也不右连续。 x 1是跳跃间断点。
x
3
证明：函数
y sin x 是连续函数。
证：设 x (,),
x x 当有增量
时，则
y sin( x x) sin x 2sin x cos(x x )
cos x x 1
2
2
2
y sin( x x) sin x 2 sin x .
2
又因为当 0 时， sin
f 1 0 lim 3 x 2 x10
则
x 1是跳跃间断点，属于第一类间断点。
所以 x 0
13
例7 讨论函数判断其类型。
1 x2n
f ( x) lim
x 的连续性，若有间断点
n 1 x 2n
0,

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

连续函数图象的分解与一类剪切集
本文主要研究连续函数图象的分解与分形维数(豪斯多夫维数,填充维数)的关系以及一类剪切集的分形测度.在第一章介绍本文的背景,第二章给出预备知识的基础上,用了三章的篇幅分别对上述三方面的问题展开了详细的论述.在第三章,我们考虑区间[0,1]上的连续函数的图象的分解与豪斯多夫维数之间的关系,我们回答了Bayart和Heurtaeux提出的一个问题.具体的,证明了：任意f∈C([0,1]),β∈[1,2],存在连续函数h,g∈C([0,1])使得.f=h+g并且
dimHG9([0,1])=dimH Gh([0,1])=β,其中Gg([0,1]),Gh([0,1])表示函数g,h的图像：Gg([0,1])={(x,g(x))：x∈[0,1]},Gh([0,1])=.{(x,h(x))：x∈[0,1]}.在第四章,我们分两部分内容：第一部分,我们利用填充维数与上盒维数的关系,把Humke和Petruska的结果推广到高维空间中,即如果X是Rn中的不可数紧子集,那么是C(X)中的拓扑普适集；第二部分讨论连续函数图象的分解与填充维数的关系.首先,我们得到：对任意f,g∈C(X),如果dimp(Gg)≠dimp(Gf),那么把该结果应用到函数分解上,我们有：假设β∈[1,2],f∈C([0,1]),那么存在连续函数g,h∈C([0,1])满足当且仅当dimp(Gf([0,1]))≤β.最后,还证明了是1-普适集(1-prevalent).在第五章,我们给出一类剪切集的h-填充测度与h-豪斯多夫测度的上下界估计,其中h是加倍的维数函数.最后,我们在第六章总结了本文的主要结果,并提出了一些可以进一步研究的问题.。