(完整)投资学计算题精选
投资学试题计算题答案(仅供参考)

二.计算题(30分,每题10分)
1.某股票去年每股股息为5元,预期股息年增长率为6%,该股票贝塔值为1.8,市场收益为10%,长期国债收益率为5%。
问:
(1)该股票投资者的必要收益率?
5%+1.8*(10%-5%)=14%
(2)该股票的内在价值?
5*(1+6%)/(14%-6%)=A
(3)若目前股价为50元,该股票实际收益率为多少?
(A-50)/50
2.假定你花1100元购买面值为1000元、票面利率为9%、6年到期的债券。
问:
(1)该债券的期望收益率是多少?
(1000*9%*6-1100)/1100=A
(2)若通货膨胀率为3%,实际收益率为多少?
A-3%
3.某公司在8月15日确定11月初购买50万磅铜,8月15日铜现货价格为77.60美元,3个月铜期货价格为79.50美元,每张期货合约为2.5万磅。
问:
(1)公司为做对冲,需要购买多少张铜期货合约?
50/2.5
(2)若11月1日,铜现货价格为87.20美元,期货价格为88.95美元,如果做对冲,铜的购买成本是多少?
87.20-(88.95-79.50)
(3)如果不做对冲,铜的购买成本是多少?
87.20。
(完整版),投资学练习题及答案汇总,推荐文档

二、单选
1、根据 CAPM,一个充分分散化的资产组合的收益率和哪个因素相关( A )。 A.市场风险 B.非系统风险 C.个别风险 D.再投资风险
2、在资本资产定价模型中,风险的测度是通过( B )进行的。
A.个别风险 B.贝塔系数
C.收益的标准差
D.收益的方差
3、市场组合的贝塔系数为( B )。
A、0
6、下列属于非系统性风险范畴的是:( ABC ) A.经营风险 B.违约风险 C.财务风险 D.通货膨胀风险 E.流动性风险
四、判断题
1、贝塔值为零的股票的预期收益率为零。FT 2、CAPM 模型表明,如果要投资者持有高风险的证券,相应地也要更高的回报率。T 3、通过将 0.75 的投资预算投入到国库券,其余投向市场资产组合,可以构建贝塔值为 0.75 的资产组合。F 4、CAPM 模型认为资产组合收益可以由系统风险得到最好的解释。T 5、如果所有的证券都被公平定价,那么所有的股票将提供相等的期望收益率。F 6、投资组合中成分证券相关系数越大,投资组合的相关度高,投资组合的风险就越小。 F 7、对于不同的投资者而言,其投资组合的效率边界也是不同的。F 8、偏好无差异曲线位置高低的不同能够反映不同投资者在风险偏好个性上的差异。T 9、在市场模型中,β 大于 1 的证券被称为防御型证券。F 10、同一投资者的偏好无差异曲线不可能相交。T
14、反映证券组合期望收益水平和单个因素风险水平之间均衡关系的模型是( A )
A.单因素模型
B.特征线模型 C.资本市场线模型 D.套利定价模型
三、多项选择题
1、关于资本市场线,下列说法正确的是( ABD )。 A、资本市场线是所有有效资产组合的预期收益率和风险关系的组合轨迹 B、资本市场线是从无风险资产出发经过市场组合的一条射线 C、风险厌恶程度高的投资者会选择市场组合 M 点右上方的资产组合 D、风险厌恶程度低的投资者会选择市场组合 M 点右上方的资产组合
《证券投资学》期末复习资料计算题与论述题汇总

证券投资学复习一、计算题1.债券收益率计算P170-176 参考P171-172例:某债券在第一年年初的价格为1000元, 在这一年年末, 该债券以950元的价格出售。
这种债券在这一年年末支付了20元的利息。
这一年的持有期利率为多少?解: 持有期利率=(950-1+20)/1000= -3%P171题4-1:某债券面值为1000元, 5年期, 票面利率为10%, 现以950元的发行价向全社会公开发行, 则投资者在认购债券后到持至期满时可获得的直接收益率为:Yd=×100%=10.53%P172题4-2:在例4-1中的债券若投资者认购后持至第三年末以995元市价出售, 则持有期收益率为:Yh=×100%=12.11%P172题4-3:某债券面值为1000元, 还有5年到期, 票面利率为5%, 当前的市场价格为1019.82元, 投资者购买该债券的预期到期收益率为:1019.82=++++Y=4.55%P173题4-4:某附息债券, 面值为1000元, 每年付一次利息, 年利率为12%, 期限为10年。
某投资者在二级市场上以960元的价格买入, 4年后该债券到期, 投资者在这4年中利用所得利息进行再投资的收益率为10%。
投资者持有该债券的复利到期收益率为:Yco={-1 }×100%=12.85%2.债券发行价格计算P233-P236页例如:零息债券, 为1000元, 3年期, 发行时市场利率为6%, 请问该债券的发行价格应为多少?解: 发行价格=1000/(1+6%3=839.6P236例6-2:某息票债券, 面值1000元, 3年期, 每年付一次利息, 票面利息为10%, 当市场利率也为10%时, 发行价为:P=1000×10% /(1+10%)+1000×10% /(1+10%)2+1000×10% /(1+10%)3+1000 /(1+10%)3=1000(元)在例6-2中, 若债券发行时市场利率为12%, 则债券发行价为:P=1000×10% /(1+12%)+1000×10% /(1+12%)2+1000×10% /(1+12%)3+1000 /(1+12%)3=951.98(元)在例6-2中, 如果债券实际发行时市场利率为8%, 则债券发行价格为:P=1000×10% /(1+8%)+1000×10% /(1+8%)2+1000×10% /(1+8%)3+1000 /(1+8%)3=1051.54(元)3.股利贴现模型计算P252页1)、某公司2006年每股收益为4元, 其中50%收益用于派发股息, 近3年公司的股息保持10%的增长率, 且将保持此速度增长。
投资学计算题

投资学计算题投资学练习题1、菲利普·莫⾥斯发⾏⼀种半年付息的债券,具有如下特征:利率为8%,收益率为8%,期限为15年,麦考利久期为10年。
⑴利⽤上述信息,计算调整后的久期。
⑵解释为什么调整后的久期是计算债券利率敏感性的较好⽅法.⑶确定调整后的久期变动的⽅向,如果:①息票率为4%,⽽不是8%;②到期期限为7年⽽不是15年.2、你管理着⼀价值100万元的资产组合,你的⽬标久期为10年。
可以从两种债券中选择:五年期零息债券和永久债券,当期收益率均为5%⑴你愿意持有两种债券的份额各为多少?⑵如果现在的⽬标久期为9年,则明年的持有⽐例会如何变化?3、某公司在2000年1⽉1⽇以950元价格购买⼀张⾯值为1000元的新发⾏债券,其票⾯利率8%,5年后到期,每年12⽉31⽇付息⼀次,到期归还本⾦要求(1)2000 年1⽉1⽇该债券投资收益率是多少(2)假定2004年1⽉1⽇的市场利率下降到6%,那么此时债券的价值是多少(3)假定2004 年1⽉1⽇该债券的市价为982元,此时购买该债券的投资收益率是多少(4)假定2002年1⽉1⽇的市场利率为12%,债券市价为900元,你是否购买该债券?4、已知⼀张3 年期的1000 元⾯值的零息票债券的到期收益率为7.4%,第⼀年利率为6.1%,第⼆年的远期利率为6.9%,那么第三年的远期利率是多少?由此看出来市场对未来宏观经济特征有什么看法?如果现在该债券的售价为802 元,这说明什么?5、现有三年期国债两种,分别按⼀年和半年付息⽅式发⾏,其⾯值为1000元,票⾯利率为6%,市场利率为8%,其发⾏价格分别是多少?6、假设⽬前市场上的利率期限结构是平坦的,市场年利率均为10%(⼀年计⼀次复利),⼀个债券基⾦经理⾯临着市场上的两种债券:债券A⾯值1000元,息票率为8%,⼀年付⼀次利息;债券B⾯值1000元,息票率为10%,⼀年付⼀次利息。
这两个债券都是三年后到期,到期时⼀次性偿还本⾦,但是该经理只打算进⾏⼀年期的投资,并且该经理预期⼀年后市场利率期限结构将近乎平⾏地下降,⽽市场普遍认为⼀年后市场利率基本不变。
投资学计算题

1.已知以下资料,计算并回答问题:可能的经济状况与 A 、B 、C 和M 的预期收益率分布表如下⑴ A 、B 、C 与M 的期望收益率、方差和标准差分别是多少?(2)由 A 、B 构建一个组合,该组合的协方差和相关系数各为多少?A 、B 之间的协方差计算结果为0.000192,大于零,两者在收益率上负相关,不可以进行资产组合,不具备套期保值效用。
(3)由A 、B 构建的最小方差组合的期望收益率和方差分别为多少?最小方差组合的资金组合权数A 为-100%、B 为200%。
最小方差组合的期望收益率与方差为:0146969.0000216.00244948.00006.00097979.0000096.00195959.0000384.0000216.06.0)032.002.0(4.0)032.005.0(0006.06.0)03.001.0(4.0)03.006.0(000096.06.0)028.002.0(4.0)028.004.0(000384.06.0)046.003.0(4.0)046.007.0(032.06.002.04.005.003.06.001.04.006.0028.06.002.04.004.0046.06.003.04.007.0222222222222=========⨯-+⨯-==⨯-+⨯-==⨯-+⨯-==⨯-+⨯-==⨯+⨯==⨯+⨯==⨯+⨯==⨯+⨯=m c b a m c b a m c b a E E E E σσσσσσσσ000192.06.0)028.002.0)(046.003.0(4.0)028.004.0)(046.007.0(),(0=⨯--+⨯--=b a r r v C %200%1002)1(111000192.02000096.0000384.0000192.0000096.0),(2),(222=-==--=-=-=⨯-+-=-+-=b a a b b a b a b a b a x x x x r r Cov r r Cov x σσσ最小方差组合的期望收益率为1%、方差为零,该组合位于坐标系的纵轴上。
投资学计算题

投资学计算题投资学计算题部分CAPM模型1、某股票的市场价格为50元,期望收益率为14%,⽆风险收益率为6%,市场风险溢价为8%。
如果这个股票与市场组合的协⽅差加倍(其他变量保持不变),该股票的市场价格是多少?假定该股票预期会永远⽀付⼀固定红利。
现在的风险溢价=14%-6%=8%;β=1新的β=2,新的风险溢价=8%×2=16%新的预期收益=6%+16%=22%根据零增长模型:50=7V31.822、假设⽆风险债券的收益率为5%,某贝塔值为1的资产组合的期望收益率是12%,根据CAPM模型:①市场资产组合的预期收益率是多少?②贝塔值为零的股票的预期收益率是多少?③假定投资者正考虑买⼊⼀股股票,价格是40元。
该股票预计来年派发红利3美元,投资者预期可以以41美元的价格卖出。
若该股票的贝塔值是-0.5,投资者是否买⼊?①12%,②5%,③利⽤CAPM模型计算股票的预期收益:E(r)=5%+(-0.5) ×(12%-5%)=1.5%利⽤第⼆年的预期价格和红利计算:E(r)1=10%投资者的预期收益超过了理论收益,故可以买⼊。
3、已知:现⾏国库券的利率为5%,证券市场组合平均收益率为15%,市场上A、B、C、D 四种股票的β系数分别为0.91、1.17、1.8和0.52;B、C、D股票的必要收益率分别为16.7%、23%和10.2%。
要求:①采⽤资本资产定价模型计算A股票的必要收益率。
②计算B股票价值,为拟投资该股票的投资者做出是否投资的决策,并说明理由。
假定B 股票当前每股市价为15元,最近⼀期发放的每股股利为2.2元,预计年股利增长率为4%。
③计算A、B、C投资组合的β系数和必要收益率。
假定投资者购买A、B、C三种股票的⽐例为1:3:6。
④已知按3:5:2的⽐例购买A、B、D三种股票,所形成的A、B、D投资组合的β系数为0.96,该组合的必要收益率为14.6%;如果不考虑风险⼤⼩,请在A、B、C和A、B、D两种投资组合中做出投资决策,并说明理由。
投资学计算题

投资学计算题(总16页) --本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--第三章证券投资概述•假设:–公司A:边际所得税率为40%,资金成本为10%,股利收入的80%享受免税待遇。
–公司B:发行优先股,股利为8%,边际所得税率为12%。
•投资策略:–公司A以10%的年利率向公司B借款,然后把筹集的资金投资于公司B的优先股。
证明1:公司A的这种投资是有意义的–由于利息支出计入税前成本,因此公司A实际税后成本为10%×(1-40%)=6%。
–公司A投资于优先股的股息税后收入为:8%-8%×(1-80%)×40%=% 。
•证明2:这笔交易对公司B来说亦是盈利的。
–公司B通过借出资金获得利息收入,税后收益为10%×(1-12%)=%,而公司B向公司A支付的优先股股息为8%。
第五章无风险证券的投资价值【例1】求每年收入为 2000 元,期限为5 5 年,利息率为 10% 的这一系列金额的终值。
FVA=2000×(1+10%)0+2000×(1+10%)1+2000×(1+10%)2+2000×(1+10%)3+2000×(1+10%)4=2000+2000×+2000×+2000×+2000×=12210【例2】拟在5年后还清100000元债务,从现在起每年等额存入银行一笔款项。
若银行存款利率为10%,每年需存多少元解:由于有利息因素,不必每年存入20000元,只要存入较少的金额,5年后本利和即可达到100000元。
A=100000×i/[(1+i)n-1]=100000×1/(F/A,10%,5)=100000×1/=100000×=16380元【例3】假设某人出租房屋,每年末收取1000 元,租期5年,问在利率为 10% 时,这些现金相当于现在的多少金额期限为5年,利率为10%,金额为1000元的年金的现值计算。
(完整版)证券投资学计算题练习
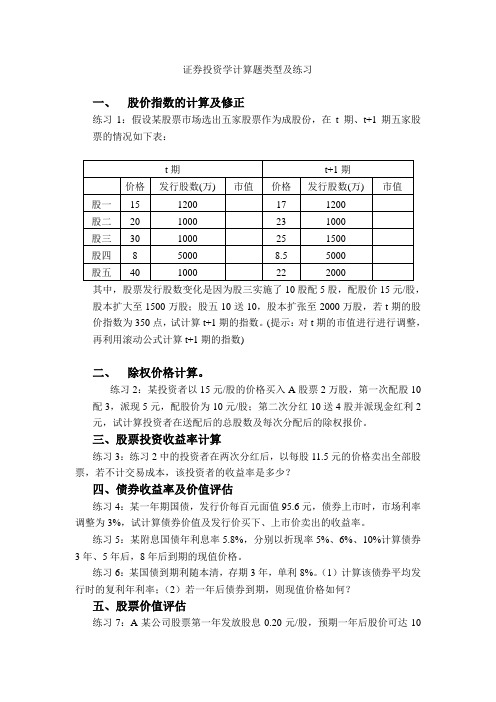
证券投资学计算题类型及练习一、股价指数的计算及修正练习1:假设某股票市场选出五家股票作为成股份,在t 期、t+1期五家股票的情况如下表:其中,股票发行股数变化是因为股三实施了10股配5股,配股价15元/股,股本扩大至1500万股;股五10送10,股本扩张至2000万股,若t期的股价指数为350点,试计算t+1期的指数。
(提示:对t期的市值进行进行调整,再利用滚动公式计算t+1期的指数)二、除权价格计算。
练习2:某投资者以15元/股的价格买入A股票2万股,第一次配股10配3,派现5元,配股价为10元/股;第二次分红10送4股并派现金红利2元,试计算投资者在送配后的总股数及每次分配后的除权报价。
三、股票投资收益率计算练习3:练习2中的投资者在两次分红后,以每股11.5元的价格卖出全部股票,若不计交易成本,该投资者的收益率是多少?四、债券收益率及价值评估练习4:某一年期国债,发行价每百元面值95.6元,债券上市时,市场利率调整为3%,试计算债券价值及发行价买下、上市价卖出的收益率。
练习5:某附息国债年利息率5.8%,分别以折现率5%、6%、10%计算债券3年、5年后,8年后到期的现值价格。
练习6:某国债到期利随本清,存期3年,单利8%。
(1)计算该债券平均发行时的复利年利率;(2)若一年后债券到期,则现值价格如何?五、股票价值评估练习7:A某公司股票第一年发放股息0.20元/股,预期一年后股价可达10元,计算股票在折现率为8%时的现值价格。
若股息成长率为5%,或股息成长值为0.01元,现值价格为多少?练习8:A 某公司股票第一年发放股息0.20元/股,前5年的股息成长率为12%,以后恢复到正常的5%,计算折现率为8%时的现值价格。
练习9:练习8中若股息占收益的比例为50%,试计算现值的市盈率,及五年后趋于正常时的市盈率。
六、证券组合投资练习10:若两股票Z 与Y 的收益率均值分别为03.0,05.0==y z E E ,方差为8.0%,16.0%,36.022===zy y z ρσσ若,试计算风险最小组合的投资比例。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
投资学计算题部分CAPM模型1、某股票的市场价格为50元,期望收益率为14%,无风险收益率为6%,市场风险溢价为8%。
如果这个股票与市场组合的协方差加倍(其他变量保持不变),该股票的市场价格是多少?假定.=14%-6%=8%;β=18%×2=16%6%+16%=22%50=7V25%,某贝塔值为1的资产组合的期望收益率是12%,根据CAPM40元。
该股票预计来年派发红利3美元,投资者预期可以以41美元的价格卖出。
若该股票的贝塔值是-0.5,投资者是否买入?①12%,②5%,③利用CAPM模型计算股票的预期收益:E(r)=5%+(-0.5) ×(12%-5%)=1。
5%利用第二年的预期价格和红利计算:E(r)1=10%3、已知5%,证券市场组合平均收益率为15%,市场上A、B、C、D四种0。
91、1.17、1.8和0.52;B、C、D股票的必要收益率分别为16。
7%、23%和A股票的必要收益率。
②计算B股票价值,为拟投资该股票的投资者做出是否投资的决策,并说明理由。
假定B股票当前每股市价为15元,最近一期发放的每股股利为2。
2元,预计年股利增长率为4%。
③计算A、B、C投资组合的β系数和必要收益率。
假定投资者购买A、B、C三种股票的比例为1:3:6.④已知按3:5:2的比例购买A、B、D三种股票,所形成的A、B、D投资组合的β系数为0。
96,该组合的必要收益率为14.6%;如果不考虑风险大小,请在A、B、C和A、B、D两种投资组合中做出投资决策,并说明理由。
①A股票必要收益率=5%+0.91×(15%-5%)=14。
1%②B股票价值=2。
2×(1+4%)/(16。
7%-4%)=18。
02(元)因为股票的价值18。
02高于股票的市价15,所以可以投资B股票。
③投资组合中A股票的投资比例=1/(1+3+6)=10%投资组合中B股票的投资比例=3/(1+3+6)=30%投资组合中C股票的投资比例=6/(1+3+6)=60%投资组合的β系数= 0.91×10%+1。
17×30%+1.8×60%=1。
52投资组合的必要收益率=5%+1.52×(15%-5%)=20.2%④本题中资本资产定价模型成立,所以预期收益率等于按照资本资产定价模型计算的必要收益率,即A、B、C投资组合的预期收益率大于A、B、D投资组合的预期收益率,所以如果不考虑风险大小,应选择A 、B 、C 投资组合.4、某公司2000年按面值购进国库券50万元,票面年利率为8%,三年期。
购进后一年,市场利率上升到9%,则该公司购进该债券一年后的损失是多少? 国库券到期值=50×(1+3×8%)=62(万元)52.18(万元)一年后的本利和=50×(1+8%)=54(万元) 损失=54-52。
18=1.82(万元)5。
假设某投资者选择了A 、B 两个公司的股票构造其证券投资组合,两者各占投资总额的一半。
已知A 股票的期望收益率为24%,方差为16%,B 股票的期望收益为12%,方差为9%。
请计算当A 、B 两只股票的相关系数各为:(1)1=AB ρ;(2)0=AB ρ;(3)1-=AB ρ时,该投资者的证券组合资产的期望收益和方差各为多少?%%.%.r P 1812502450=⨯+⨯=AB B A B A B B A A P x x x x ρσσσσσ222222++=(1)当1=AB ρ时,%.........P 25121090160505020905016050222=⨯⨯⨯⨯⨯+⨯+⨯=σ(2)当0=AB ρ,%.....P2560905016050222=⨯+⨯=σ (3)当1-=AB ρ,%.........P 2501090160505020905016050222=⨯⨯⨯⨯⨯-⨯+⨯=σ6、某投资组合等比率地含有短期国债、长期国债和普遍股票,它们的收益率分别是5.5%、7。
5%和11。
6%,试计算该投资组合的收益率。
解: ()%2.8%6.11%5.7%5.531=++=P r 7、有三种共同基金:股票基金A ,债券基金B 和回报率为8%的以短期国库券为主的货币市场基金。
其中股票基金A 的期望收益率20%,标准差0。
3;债券基金B 期望收益率12%,标准差0。
15。
基金回报率之间的相关系数为0.10。
求两种风险基金的最小标准差资产组合的投资比例是多少?这种资产组合收益率的期望值和标准差各是多少? 解:2P=w A2A2+w B2B 2+2w A w BA BρAB=w A 2A 2+(1-w A )2B2+2w A (1-w A )ABρABE (R P )=17.4%×0。
2+82。
6%×0。
12=13。
4% σ=13.9%8、股票A 和股票B 的有关概率分布如下:状态概率股票A 的收益率(%)股票B 的收益率(%) 1 0。
10 10 8 2 0。
20 13 7 3 0。
20 12 6 4 0。
30 14 9 5 0.2015 8 期望收益 13.2 7。
7 标准差1.471。
10212122222=--+--=∂∂AB B A A AB B A A B A A A AP w )w ()w (w w ρσσρσσσσσ%.W %.............W B ABB A B A AB B A B A 68241710150302150150303010150301501502222==⨯⨯⨯-⨯+⨯⨯⨯-⨯=-+-=ρσσσσρσσσ(1)股票A 和股票B 的期望收益率和标准差分别为多少? (2)股票A 和股票B 的协方差和相关系数为多少?(3)若用投资的40%购买股票A ,用投资的60%购买股票B ,求投资组合的期望收益率(9。
9%)和标准差(1。
07%)。
(4)假设有最小标准差资产组合G ,股票A 和股票B 在G 中的权重分别是多少? 解:(4)9、建立资产组合时有以下两个机会:(1)无风险资产收益率为12%;(2)风险资产收益率为30%,标准差0.4.如果投资者资产组合的标准差为0。
30,则这一资产组合的收益率为多少? 解:运用CML 方程式10、在年初,投资者甲拥有如下数量的4种证券,当前和预期年末价格为:%7.75%3.242222==-+-=B ABB A B A ABB A B A W W ρσσσσρσσσ这一年里甲的投资组合的期望收益率是多少?11、下面给出了每种经济状况的概率和各个股票的收益:(1)请分别计算这两只股票的期望收益率、方差和标准差;E(R)=7。
3%σA=4.9%A)=2。
5%σB=21。
36%E(RB(2)请计算这两只股票的协方差和相关系数;σAB =0。
009275 ρAB =0.88(3)请用变异系数评估这两只股票的风险;CV (A )=4.9%/7.3%=0.671 CV(B )=21。
36%/2.5%=8。
544 结论:与A 股票相比,投资B 股票获得的每单位收益要承担更大的投资风险(4)制作表格,确定在这两只股票不同投资比重(A 股票比重从0%开始,每次增加10%)时,投资组合的收益、方差和标准差。
AB 组合收益与风险13、假定无风险利率为6%,市场收益率为16%,股票A 当日售价为25元,在年末将支付每股0。
5元的红利,其贝塔值为1.2,请预期股票A 在年末的售价是多少? 解%.)P (E 182550251=+- E(P 1)=29注:此为股票估值与CAPM 模型应用的综合题型。
12、假定无风险收益率为5%,贝塔值为1的资产组合市场要求的期望收益率是12%。
则根据资本资产定价模型:(1)市场资产组合的期望收益率是多少?(12%)(2)贝塔值为0的股票的期望收益率是多少?(5%)(3)假定投资者正考虑买入一股票,价格为15元,该股预计来年派发红利0.5元,投资者预期可以以16.5元卖出,股票贝塔值β为0.5,该股票是否应该买入?(该股票是高估还是低估了)解:%.%..8581315515516>=+-结论:买进注:此为股票估值与CAPM模型应用的综合题型。
14、假设你可以投资于市场资产组合和短期国库券,已知:市场资产组合的期望收益率是23%,标准差是32%,短期国库券的收益率是7%。
如果你希望达到的期望收益率是15%,那么你应该承担多大的风险?如果你持有10000元,为了达到这个期望收益率,你应该如何分配你的资金?解:15%=7%+(23%-7%)×σP/32%得到:σP=16%W1×7%+(1-W1)×23%=15%得到:W1=0。
5如果投入资本为10000元,则5000元买市场资产组合,5000元买短期国库券。
15、假设市场上有两种风险证券A、B及无风险证券F。
在均衡状态下,证券A、B的期望收益率和β系数分别为:2.15.0%15)(%10)(====BABArErEββ,,,,求无风险利率f r。
解:根据已知条件,可以得到如下方程式:f r +0.5×(E (R M )-f r )=10%f r +1。
2×(E (R M )-f r )=15% 解得:f r =6。
43%15、DG 公司当前发放每股2美元的红利,预计公司红利每年增长5%。
DG 公司股票的β系数是1。
5,市场平均收益率是8%,无风险收益率是3%。
(1)该股票的内在价值为多少?E (R i )=3%+1。
5×(8%-3%)=10。
5% 2×(1+5%)/(10。
5%-5%)=38.18(2)如果投资一年后出售,预计一年后它的价格为多少?2×(1+5%)2/(10.5%-5%)=40。
091.已知以下资料,计算并回答问题:可能的经济状况与 A 、B 、C 和M 的预期收益率分布表如下⑴ A 、B 、C 与M 的期望收益率、方差和标准差分别是多少?0006.06.0)03.001.0(4.0)03.006.0(000096.06.0)028.002.0(4.0)028.004.0(000384.06.0)046.003.0(4.0)046.007.0(032.06.002.04.005.003.06.001.04.006.0028.06.002.04.004.0046.06.003.04.007.022*******=⨯-+⨯-==⨯-+⨯-==⨯-+⨯-==⨯+⨯==⨯+⨯==⨯+⨯==⨯+⨯=c b a m c b a E E E E σσσ(2)由 A 、B 构建一个组合,该组合的协方差和相关系数各为多少?A 、B 之间的协方差计算结果为0.000192,大于零,两者在收益率上负相关,不可以进行资产组合,不具备套期保值效用.(3)由A 、B 构建的最小方差组合的期望收益率和方差分别为多少?最小方差组合的资金组合权数A 为-100%、B 为200%. 最小方差组合的期望收益率与方差为:最小方差组合的期望收益率为1%、方差为零,该组合位于坐标系的纵轴上。
