总统证法勾股定理
勾股定理常见证法

勾股定理有多种证明方法,以下是其中一些常见证法:1. 欧几里德证明:通过勾股圆方图证明勾股定理,大正方形的面积等于4个直角三角形加上一个小正方形面积之和。
2. 加菲尔德证明:在梯形中构造三个直角三角形,利用梯形面积等于三个直角三角形的面积之和,证明勾股定理。
3. 小K证明:通过相似三角形,边长之比相等,证明勾股定理。
4. 辅助圆证明:以点B为圆心,BA为半径作圆,延长BC交圆于点E,D,则三角形DCA相似ACE,从而证明勾股定理。
5. 切割定理证明:直角三角形ABC,以点B为圆心BC为半径作圆,交AB及AB延长线于D,E,则BE=BC=BD=a,从而证明勾股定理。
6. 面积合成证明:利用图形拼接证明勾股定理。
7. 行列式证明:n阶行列式等于以n个向量为边在n维空间中张成的n维体的体积,从而证明勾股定理。
8. 赵爽弦图证法:利用弦图构造直角三角形,利用面积法证明勾股定理。
9. 毕达哥拉斯证法:利用正方形分割法证明勾股定理。
10. 书本证明方法:利用八个全等的直角三角形和三个边长分别为a、b、c的正方形构造两个正方形,从而证明勾股定理。
11. 三角形相似推导:利用三角形相似的性质推导勾股定理。
12. 切割线定理证明:利用切割线定理和相似三角形证明勾股定理。
13. 托勒密定理证明:利用托勒密定理和相似三角形证明勾股定理。
14. 利用切线长定理:利用切线长定理和相似三角形证明勾股定理。
15. 总统证法:美国第20任总统加菲尔德在五年前证明了勾股定理,其方法被称为“总统证法”,具体为梯形面积等于三个直角三角形的面积之和。
16. 射影定理证明:利用射影定理和相似三角形证明勾股定理。
17. 余弦定理证明:当90度角时,利用余弦定理证明勾股定理。
18. 达芬奇的证明:利用几何图形和比例关系证明勾股定理。
19. 高斯公式证明:利用高斯公式(也叫鞋带公式)证明多边形面积,从而证明勾股定理。
以上是常见的勾股定理的证法,其中最常用的是面积法,同时还会结合其他几何知识如相似三角形、切割线定理、射影定理等进行证明。
勾股定理的六种证明

证明一
b a c ∴ (a + b)2 = c2 + 4(½ab) a2 + 2ab + b2 = c2 + 2ab a2 + b2 = c2
证明二
c c2 = (a − b)2 + 4(½ab) = a2 − 2ab + b2 + 2ab ∴ c2 = a2 + b2
【证法2】(1876年美国总统Garfield证明) 证法2 1876年美国总统Garfield证明) 年美国总统Garfield证明 以a、b 为直角边,以c为斜边作两个全等的直角三角形,则 每个直角三角形的面积等于 1 ab 把这两个直角三角形拼成如图所示形状,使A、E、B三点在一条 直线上. . ∵ RtΔEAD ≌ RtΔCBE, ∴ ∠ADE = ∠BEC. . ∵ ∠AED + ∠ADE = 90º,∴ ∠AED + ∠BEC = 90º. . ∴ ∠DEC = 180º―90º= 90º.∴ ΔDEC是一个等腰直角三角形, . 1 2 它的面积等于 c
• 1881 年成为美国第 20 任总統 • 1876 年提出有关证明
证明二及证明三的比较 明二及证明三的比较
• 两个证明基本上完全 相同!
证明四
a2
b2
证明四
证明四
证明四
证明四
∴ a2 + b2 = c2 c2
青朱出入图
• 刘徽(生於公元三世紀) • 三国魏晋时代人。 • 魏景元四年(即 263 年)为 古籍《九章算术》作注释。 • 在注作中,提出以「出入相 补」的原理來证明「勾股定 理」。后人称该图为「青朱 入出图」。
勾股定理的6种最常用证明方法
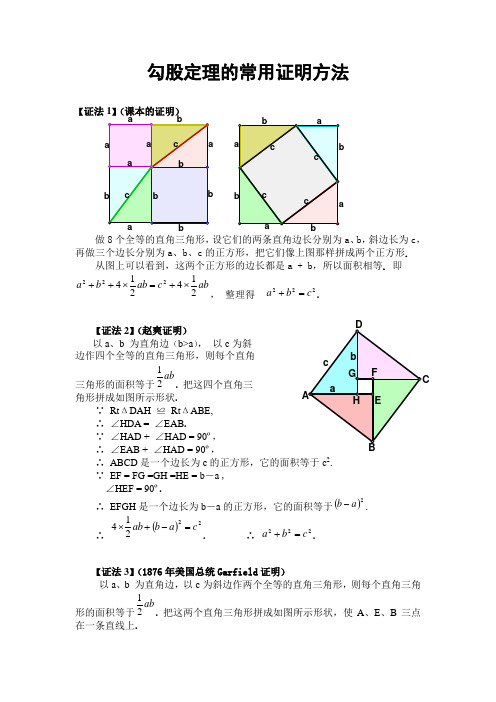
勾股定理的常用证明方法【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.【证法2】(赵爽证明) 以a 、b 为直角边(b>a ), 以c 为斜边作四个全等的直角三角形,则每个直角三角形的面积等于ab21. 把这四个直角三 角形拼成如图所示形状. ∵ Rt ΔDAH ≌ Rt ΔABE, ∴ ∠HDA = ∠EAB .∵ ∠HAD + ∠HAD = 90º,∴ ∠EAB + ∠HAD = 90º,∴ ABCD 是一个边长为c 的正方形,它的面积等于c 2. ∵ EF = FG =GH =HE = b ―a , ∠HEF = 90º.∴ EFGH 是一个边长为b ―a 的正方形,它的面积等于()2a b -.∴ ()22214c a b ab =-+⨯. ∴ 222c b a =+.【证法3】(1876年美国总统Garfield 证明)以a 、b 为直角边,以c 为斜边作两个全等的直角三角形,则每个直角三角形的面积等于ab 21. 把这两个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上.∵RtΔEAD ≌RtΔCBE, ∴∠ADE = ∠BEC.∵∠AED + ∠ADE = 90º,∴∠AED + ∠BEC = 90º.∴∠D EC = 180º―90º= 90º.∴ΔDEC是一个等腰直角三角形,它的面积等于2 21c.又∵∠DAE = 90º, ∠EBC = 90º, ∴AD∥BC.∴ABCD是一个直角梯形,它的面积等于()2 21b a+.∴()222121221cabba+⨯=+. ∴222cba=+.【证法4】(邹元治证明)以a、b为直角边,以c为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab21.把这四个直角三角形拼成如图所示形状,使A、E、B三点在一条直线上,B、F、C三点在一条直线上,C、G、D三点在一条直线上.∵RtΔHAE ≌RtΔEBF,∴∠AHE = ∠BEF.∵∠AEH + ∠AHE = 90º,∴∠AEH + ∠BEF = 90º.∴∠HEF = 180º―90º= 90º.∴四边形EFGH是一个边长为c的正方形. 它的面积等于c2.∵RtΔGDH ≌RtΔHAE,∴∠HGD = ∠EHA.∵∠HGD + ∠GHD = 90º,∴∠EHA + ∠GHD = 90º.又∵∠GHE = 90º,∴∠DHA = 90º+ 90º= 180º.∴ABCD是一个边长为a + b的正方形,它的面积等于()2b a+.∴()22214cabba+⨯=+. ∴222cba=+.【证法5】(欧几里得证明)做三个边长分别为a 、b 、c 的正方形,把它们拼成如图所示形状,使H 、C 、B 三点在一条直线上,连结 BF 、CD . 过C 作CL ⊥DE ,交AB 于点M ,交DE 于点L .∵ AF = AC ,AB = AD , ∠FAB = ∠GAD , ∴ ΔFAB ≌ ΔGAD ,∵ ΔFAB 的面积等于221a , ΔGAD 的面积等于矩形ADLM 的面积的一半,∴ 矩形ADLM 的面积 =2a . 同理可证,矩形MLEB 的面积 =2b .∵ 正方形ADEB 的面积= 矩形ADLM 的面积 + 矩形MLEB 的面积 ∴ 222b a c += ,即 222c b a =+.【证法6】(辛卜松证明)设直角三角形两直角边的长分别为a 、b ,斜边的长为c . 作边长是a+b 的正方形ABCD . 把正方形ABCD 划分成上方左图所示的几个部分,则正方形ABCD的面积为()ab b a b a 2222++=+;把正方形ABCD 划分成上方右图所示的几个部分,则正方形ABCD 的面积为 ()22214c ab b a +⨯=+ =22c ab +.∴ 22222c ab ab b a +=++,∴ 222c b a =+.D。
关于“勾股定理”的60种证法
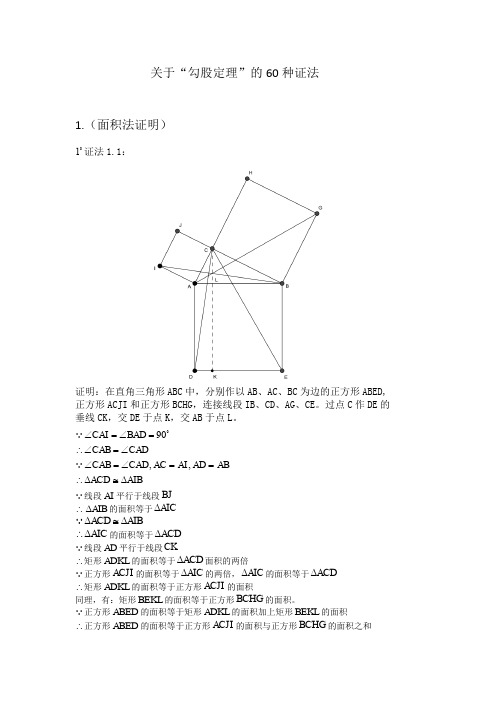
关于“勾股定理”的60种证法1.(面积法证明)1 证法1.1:证明:在直角三角形ABC 中,分别作以AB 、AC 、BC 为边的正方形ABED,正方形ACJI 和正方形BCHG ,连接线段IB 、CD 、AG 、CE 。
过点C 作DE 的垂线CK ,交DE 于点K ,交AB 于点L 。
90,,CAI BAD CAB CADCAB CAD AC AI AD AB ACD AIB∠=∠=∴∠=∠∠=∠==∴∆≅∆线段AI 平行于线段BJ ∴AIB ∆的面积等于AIC ∆ACD AIB ∆≅∆AIC ∴∆的面积等于ACD ∆ 线段AD 平行于线段CK∴矩形ADKL 的面积等于ACD ∆面积的两倍正方形ACJI 的面积等于AIC ∆的两倍,AIC ∆的面积等于ACD ∆ ∴矩形ADKL 的面积等于正方形ACJI 的面积同理,有:矩形BEKL 的面积等于正方形BCHG 的面积。
正方形ABED 的面积等于矩形ADKL 的面积加上矩形BEKL 的面积∴正方形ABED 的面积等于正方形ACJI 的面积与正方形BCHG 的面积之和即222AC BC AB +=.Remark :此为欧几里得(Euclid,约公元前330年-公元前275年)在几何原本中的证明方法。
2 证法1.2:证明:在上图中,整个正方形的面积为2()a b +,又等于四个直角三角形的面积加上里面的小正方形的面积,等于22ab c +。
因此,22()2a b ab c +=+,此即:222a b c +=。
Remark :此证法据Bretschneider 和Hankel 的推测,为毕达哥拉斯(Pythagoras ,约公元前580~约前500)的证法。
3 证法1.3(总统证明法)如图,三角形ABC 与三角形BDE 完全相等,易证三角形ABE 为等腰直角三角形。
整个直角梯形ACDE 的面积为21()2a b +,又等于两个直角三角形的面积加上等腰直角三角形ABE 的面积,等于212ab c +,故2211()22a b ab c +=+。
勾股定理总统证法

勾股定理总统证法在数学界,勾股定理一直是最有名的定理之一。
它的证明方式也有多种,其中最为著名的就是总统证法。
总统证法又称为李氏定理,距今已有2000多年的历史。
它的原作者不可考,但它的精神活跃在我们的数学世界中,给大家带来很多视角。
勾股定理指:任意一个直角三角形,它的斜边的平方等于它的两条直边的平方和。
具体地说,即:a^2 + b^2 = c^2总统证法是古代古希腊数学家著名的定理,他们用它来证明勾股定理。
他们使用一个四边形的概念,把它划分成四个直角三角形,并令其斜边的平方等于这些三角形的两条直边的平方和。
以下是证明勾股定理的总统证法的具体步骤:(1)把四边形划分成四个直角三角形,四边形中心两边的内角均为90°,其余各内角均为45°。
(2)给四边形赋予正方形形式,此时四边形被划为四个直角三角形,即:A-B-C-DA-C-B-DA-D-C-BA-B-D-C(3)把四边形的边赋予任意数值,如a, b, c, d,则每三角形的斜边长度分别为a, b, c, d。
(4)因为(AC)+(CB)=(AD);(BC)+(AD)=(CB);(AB)+(CD)=(BD);(BD)+(CD)=(AB);所以有:(a^2+b^2) = (c^2+d^2) = (a^2+d^2) = (b^2+c^2)。
因此,证明了勾股定理:任意一个直角三角形,它的斜边的平方等于它的两条直边的平方和。
总统证法是一种非常有效的勾股定理证明方式,它也证明了数学的美妙之处,源自古希腊数学家的智慧。
总统证法的理论支持,使得勾股定理的证明更加准确,令数学变得更加完美。
它也激发了人类对数学的持续探索,使得数学日益进步。
最后,总统证法也使我们更加深刻地理解勾股定理,并知晓学习数学之美。
勾股定理是一个奥秘又伟大的定理,它丰富而深刻,只有经过不懈努力才可以得以理解。
学习这个定理,不仅可以提高我们数学的能力,还可以激发我们对数学的热爱,提高我们的求知欲望。
勾股定理的证明比较全的证明方法

A
B
这棵树漂亮吗?如果在树上挂上 几串彩色灯泡,再挂上些小铃铛、小 彩球、小礼盒、小的圣诞老人,是不 是更像一棵圣诞树.
也许有人会问:“它与勾股定理 有什么关系吗?”
仔细看看,你会发现,奥妙在树 干和树枝上,整棵树都是由下方的这 个基本图形组成的:一个直角三角形 以及分别以它的每边为一边向外所作 的正方形.
来进行的.
G
已知:如图,以在Rt△ABC中,
H
F
∠ACB=90°,分别以a、b、c 为边向外作正方形.
C
K
ba
c
A
B
求证:a2 3
传说中毕达哥拉斯的证法
证明:从Rt△ABC的三边向外各作一个正方形(如图),作CN⊥DE 交AB于M,那么正方形ABED被分成两个矩形.连结CD和KB.
总统为什么会想到去证明勾股定理呢?难道他是数学家或数学爱好者?答案是 否定的.事情的经过是这样的:
1876年一个周末的傍晚,在美国首都华盛顿的郊外,有一位中年人正在散步, 欣赏黄昏的美景,他就是当时美国俄亥俄州共和党议员伽菲尔德.他走着走着,突 然发现附近的一个小石凳上,有两个小孩正在聚精会神地谈论着什么,时而大声争 论,时而小声探讨.由于好奇心驱使伽菲尔德循声向两个小孩走去,想搞清楚两个 小孩到底在干什么.只见一个小男孩正俯着身子用树枝在地上画着一个直角三角 形.于是伽菲尔德便问他们在干什么?只见那个小男孩头也不抬地说:“请问先生, 如果直角三角形的两条直角边分别为3和4,那么斜边长为多少呢?”伽菲尔德答到: “是5呀.”小男孩又问道:“如果两条直角边分别为5和7,那么这个直角三角形的 斜边长又是多少?”伽菲尔德不加思索地回答到:“那斜边的平方一定等于5的平方 加上7的平方.”小男孩又说道:“先生,你能说出其中的道理吗?”伽菲尔德一时 语塞,无法解释了,心理很不是滋味.
勾股定理证法

勾股定理:直角三角形中,两条直角边的平方和等于斜边的平方,即在以a、b为直角边,c为斜边的三角形中有a^2+b^2=c^2。
方法•1/16证法一(邹元治证明):以a、b为直角边,以c为斜边做四个全等的三角形,按下图所示相拼,使A、E、B三点共线,B、F、C 三点共线,C、G、D三点共线。
∵Rt△HAE≌Rt△EB F∴∠AHE=∠BEF∵∠AHE+∠AEH=90°∴∠BEF+∠AEH=90°∵A、E、B共线∴∠HEF=90°,四边形EFGH为正方形由于上图中的四个直角三角形全等,易得四边形ABCD为正方形∴正方形ABCD的面积=四个直角三角形的面积+正方形EFGH的面积∴(a+b)^2=4•(1/2)•ab+c^2,整理得a^2+b^2=c^2•2/16证法二(课本的证明):如上图所示两个边长为a+b的正方形面积相等,所以a^2+b^2+4•(1/2)•ab=c^2+4•(1/2)•ab,故a^2+b^2=c^2。
•3/16证法三(赵爽弦图证明):以a、b为直角边,以c为斜边做四个全等的三角形,按下图所示相拼。
易得四边形ABCD和四边形EFGH都是正方形∴正方形ABCD的面积=四个直角三角形的面积+正方形EFGH的面积∴c^2=4•(1/2)•ab+(b-a)^2 ,整理得a^2+b^2=c^2•4/16证法四(总统证明):如下图所示。
易得△CDE为等腰直角三角形∴梯形ABCD的面积=两个直角三角形的面积+一个等腰三角形的面积∴1/2•(a+b)•(a+b)=2•(1/2)•ab+(1/2)•c^2,整理得a^2+b^2=c^2•5/16证法五(梅文鼎证明):以a、b为直角边,以c为斜边做四个全等的三角形,按下图所示相拼,使DEF在同一直线上,过C点作CI垂直于DF,交DF于I点。
易得四边形ABEG、四边形CBDI、四边形FGHI都为正方形。
∴多边形EGHCB的面积=正方形ABEG的面积-两个直角三角形的面积且多边形EGHCB的面积=正方形CBDI的面积+正方形FGHI的面积-两个直角三角形的面积∴正方形ABEG的面积=正方形CBDI的面积+正方形FGHI的面积∴c²=a²+b²•6/16证法六(项明达证明):以a、b为直角边,以c为斜边做两个全等的三角形,做一个边长为c的正方形,按下图所示相拼,使E、A、C在同一条直线上。
勾股定理的十六种证明方法

勾股定理的几种证明方法我们刚刚学了勾股定理这重要的知识,老师告诉我们,勾股定理的证明方法非常得多,其数量之大足可以撰写出一部书来,我对知识的探求欲望被激发了出来,随即到网络上查找了勾股定理的证明方法,现在我收集到了几种。
【证法1】(课本的证明)做8个全等的直角三角形,设它们的两条直角边长分别为a 、b ,斜边长为c ,再做三个边长分别为a 、b 、c 的正方形,把它们像上图那样拼成两个正方形.从图上可以看到,这两个正方形的边长都是a + b ,所以面积相等. 即abc ab b a 214214222⨯+=⨯++, 整理得 222c b a =+.这是课本上面为我们提供的毕达哥拉斯的证明方法,我在网络上查阅资料发现:毕达哥拉斯是西方公认的发现勾股定理的数学家,因此,我们可以在外国的一些资料上发现,勾股定理在西方被称为毕达格拉斯定理。
【证法2】(邹元治证明)以a 、b 为直角边,以c 为斜边做四个全等的直角三角形,则每个直角三角形的面积等于ab 21.把这四个直角三角形拼成如图所示形状,使A 、E 、B 三点在一条直线上,B 、F 、C 三点在一条直线上,C 、G 、D 三点在一条直线上.∵ Rt ΔHAE ≌ Rt ΔEBF,∴ ∠AHE = ∠BEF .∵ ∠AEH + ∠AHE = 90º,∴ ∠AEH + ∠BEF = 90º. ∴ ∠HEF = 180º―90º= 90º.∴ 四边形EFGH 是一个边长为c 的正方形. 它的面积等于c2.∵ Rt ΔGDH ≌ Rt ΔHAE, ∴ ∠HGD = ∠EHA .∵ ∠HGD + ∠GHD = 90º,∴ ∠EHA + ∠GHD = 90º.又∵ ∠GHE = 90º,∴ ∠DHA = 90º+ 90º= 180º.∴ ABCD 是一个边长为a + b 的正方形,它的面积等于()2b a +.∴ ()22214c ab b a +⨯=+. ∴ 222c b a =+.这个证明对我来讲也很好理解,它利用了全等三角形的性质和因式分解的知识,这对于我们初二的学生来说,是能够领会的。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
总统证法勾股定理
1.于任意正三角形,其有三条边,分别被称为直角边、长边和短边,分别表示为a、b、c;
2.于直角边的平方等于长边和短边的平方之和,故有:a^2 + b^2 = c^2;
3.此,当a、b、c都大于0时,总统证法勾股定理成立。
总统证法勾股定理是古希腊数学家勾股(Pythagoras)第一个提出的有关三角形的几何定理,被称为勾股定理。
它的定义是:在直角三角形中,直角的边的平方的和等于斜边的平方,即a^2 + b^2 = c^2。
总统证法勾股定理是相当重要的几何定理。
它可以被用于计算三角形的某个边的长度,当另外两边的长度已知时。
在工程、建筑和设计领域中,也经常采用勾股定理来计算几何形状的大小和角度。
此外,总统证法勾股定理也经常被用来求解向量,以及描述物体运动的物理关系。
总统证法勾股定理可以说是数学史上最重要的几何定理之一,它在古希腊科学家希及克罗(Hicetas)的定义之前就已存在。
勾股(Pythagoras)本人没有提出总统证法勾股定理,而是由其学生依西修斯(Euryphaeus)利用它来证明一个问题。
此外,勾股定理也曾被希腊哲学家苏格拉底(Socrates)提出,但是他并没有证明此定理。
历史上,总统证法勾股定理的证明也有很多种。
林肯(Franklin)在1840年提出了一个基于抽象几何定理的证明。
他指出,如果一个三角形的底边是平移而不是旋转的,那么这个三角形依然满足总统证
法勾股定理。
因为他的抽象几何证明简单明了,林肯的总统证法勾股定理也就成为了今天最流行的证明版本。
另外,总统证法勾股定理在一个不同的角度来看也有很多奇妙的应用。
它可以用来计算曲线的面积,计算二维图形的形状,甚至可以用来求解三维图形或立体几何图形。
此外,还有用总统证法勾股定理计算椭圆的周长、圆的面积以及三角型面积的应用,也不可忽视。
总而言之,总统证法勾股定理是数学史上一项重要的几何定理,它至今仍然是一个学术界及工程界最重要的几何工具之一。
它曾多次被用于数学的研究和科学的实践,成为数学发展的重要组成部分。
