地图投影 第二章地图投影方法变形分类
地图投影第二章地图投影方法变形分类

1
2
a b=r2
3
4
CHENLI
a> r,b=r 5
a≠b≠r 6
23
CHENLI
24
三、投影变形的性质和大小
长度比和长度变形:
投影面上一微小线段(变形椭圆半径)和球 面上相应微小线段(球面上微小圆半径,已按规 定的比例缩小)之比。
m表示长度比, Vm表示长度变形
m ds' ds
Vm m 1
Q(0,0),球面上的各点便以新极点Q为原点,以方
位角和天顶距 Z 表示其位置,从而构成球面极坐标系。
CHENLI
32
球面极坐标系
第二节 地理坐标
在地图测制中是把地球表面作为旋转椭球面处理。 地球椭球面上各点的位置,是以地理坐标即经度 和纬度来确定。经纬度是一种绝对的坐标系统。
P,P1—北、南极
CHENLI
2
地图投影,简单的说就是将参考椭球面上的元素 (大地坐标、角度和边长)按一定的数学法则化 算到平面上的过程。
x y
ff12((LL,,BB))
CHENLI
3
二、投影方式: 1.平行投影
CHENLI
4
2.透视投影
CHENLI
5
3. 广义投影
CHENLI
6
三、地图投影实质: 建立平面上的点(用平面直角坐标或极坐标
CHENLI
16
2. 投影变形的概念 地图投影不能保持平面与球面之间在
长度(距离)、角度(形状)、面积等方 面完全不变。
地球仪上经纬线网格和地图上比较:
CHENLI
17
球面经纬网经过投影之后,其几何特征 受到扭曲——地图投影变形:长度(距离)、 角度(形状)、面积。
地图学第二章之二
高斯-克吕格投影
——假设一个椭圆柱横套在地球椭球面上,使其与某 一条经线相切,将椭球面上的经纬线投影到椭圆柱面 上,然后将椭圆柱展成平面;
P
椭圆柱
A C
X P B D 赤道 Y
A C
B D
投影
P
P
投影特点:
投影特点
(1)中央经线和赤道被投影为互相垂直的直线,而 且是投影的对称轴; (2)投影后没有角度变形;
中国政区图,为能完整连续地表示,应选用斜轴方位。
教学用图,选择变形不大的任意投影,如等距投影。
出版方式影响
单幅图的投影选择比较简单; 系列图或图集中的一个图组,应选择同一变形性 质的投影,便于比较; 整个地图集,是由不同主题的图组所构成,在投 影选择上要有变化,应采用同一系统的投影,根 据情况,在变形性质上变化。
(3)中央经线上没有长度变形,离开中经越远变形 越大,最大变形在赤道上。
3.常用的圆锥投影
(1)等角圆锥投影 (2)高斯-克吕格投影
等角圆锥投影
投影条件:地图上没有角度变形,w=0;每一点上经线长度比 与纬线长度比相等,m = n。
a.等角切圆锥投影
1)相切的纬线没有变形,长度比为1。
2)纬线投影后为同心圆弧并且离开标准纬线越远,变形程度
总
结
方位投影的特点是:在投影平面上,由投影点
(平面与球面的切点)向各方向的方位角与实 地相等,其等变形线是以投影中心为圆心的同 心圆。
(2)圆柱投影
以圆柱面作为投影面,使圆柱面与球展为
平面而成。
正轴圆柱投影—圆柱的轴和地轴一致(最常用) ;
方法:假设将地球按比例缩小成一个透明的地球仪
般的球体,在球心、球面、或球外安置一个光源,
5地图投影分类

2 按投影方式分类
第 14 页
几何投影
2.1 几何投影
第 15 页
2.1.1 按辅助投影面的类型划分
圆锥投影
(1)圆柱投影
第 16 页
圆柱投影
Executive branch
以圆柱面作为投影面,使圆柱 面与球面相切或相割,将球面 上的经纬线投影到圆柱面上, 然后将圆柱面展为平面而成
(1)圆柱投影
面积 变形
投影后面积 相等 即p=ab=1
长轴越长 短轴越短
角度变形很大
无变形 P=1
(3)任意投影
第9 页
①
含义
投影图上,长度、面
积和角度都有变形, 它既不等角又不等积
投影前 投影后
适用于对各种变形精
度要求不高的一般参
考图和教学图等
(4)等距投影
第 10 页
④
含义 在正轴投影中,通常
在特定方向上没有长
2.1 几何投影
第 19 页
2.1.2 按辅助投影面与地球椭球体的位置关系划分
斜轴投影
2.1 几何投影
第 20 页
辅助投影面与地轴垂直 或者圆锥、圆柱面的轴 与地轴重合的投影。
1正轴投影 2横轴投影
辅助投影面的中 心法线或圆锥、 圆柱面的轴与地 轴斜交。
3斜轴投影 辅助投影面与地轴平行,或者圆锥、 圆柱面的轴与地轴垂直的投影。
第1 页
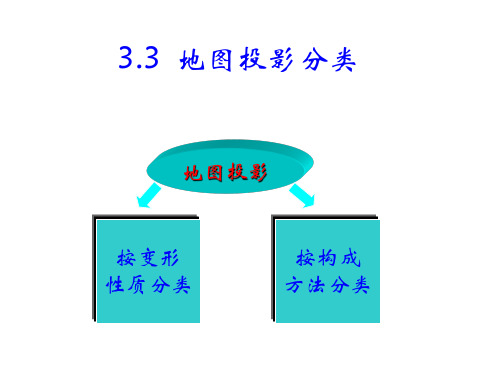
1 按变形性质分类
第2 页
①
②
③
④
等角 投影
等积 投影
任意 投影
等距 投影
(1)等角投影
第3 页
①含义Biblioteka 投影面上某点的任意两 方向线夹角与椭球面上 相应两线段夹角相等, 即角度变形为零
空中导航-地图投影及其分类

19世纪20年代经高斯拟定
约束条件
❖中央经线与投影面相切,投影 后保持长度不变
❖投影后等角
❖ 等角横圆柱投影特点
赤道为直线,与切经线相差90°的经线是直线,其 他经线凹向切经线;
地图等角; 切经线上无失真(切经线左右各3 ° 范围长度失真
图
❖ 高斯投影坐标网
经纬网(地理坐标网)
114°00 14
16
30° 40´
202
α
3396
94 -δ TH/TC
92
18 20 A( 20218 , 3394 )
90
TH/TC= α+(± δ)
δ= ΔλSINΦ 中央经线以东取正,以西取负
❖ 4.兰伯特投影
❖ 也叫等角切(割)正 圆锥投影,德国数学 家Lambert首创,百 万航图和世界地形图 的数学基础
大圆航线为直线,等角航线为凹向极点的螺 旋曲线
❖ 用途
极地领航用图 标画大圆航线的辅助用图
zk1
N
S N
S N
S
N
N
S
S
N
N
S
S
N N
S S 返回
…………
3°E 9°E 01 02
3°W 60
返回
最小比例尺
返回
谢谢
地图等角;标准纬线上无失真。 大圆航线凸向大比例尺一方;等角航线凹向极
点 。
❖ 用途:
世界百万普通地图和百万航图的主要投影方法
❖ 5.极地方位投影
投影原理:将地球视为一透明球体,球心置一点 光源,投影面为平面,投影面通过极点与地球相 切,地球表面的经纬网格投射在平面上。
❖ 极地方位投影特点
(完整)2.2地图投影的变形

比较
二、主方向和变形椭圆
1、主方向
主方向:两个在椭球面上正交的方向投影到平面上后仍
然正交,则这两个方向为主方向。
性质:主方向投影后具有最大和最小尺度比。
b
b’
a o
c a’ Io\′
c’dBiblioteka d’2、变形椭圆取地面上一个微分圆(小到可忽略地球曲面的影响, 把它当作平面看待),它投影到平面上通常会变为椭圆, 通过对这个椭圆的研究,分析地图投影的变形状况。这 种图解方法就叫变形椭圆。
= 0 不变 > 0 变大 < 0 变小
四、面积比和面积变形 1、面积比
投影平面上一微小面积dF′与椭球体面上相应 的微小面积dF之比。
据阿波隆尼定理,有 m2 + n2 = a2 + b2
m·n·sinq = a·b
面积比是变量,随位置的不同而变化。
2、面积变形
投影平面上一微小面积dF′与椭球体面上相 应的微小面积dF之差值同这微分面积dF之比 。
地图投影变形的分布规律
任何地图都有投影变形; 不同区域大小的投影其投影变形不同; 地图上存在没有变形的点(或线); 距没有变形的点(或线)愈远,投影变形愈大,反之亦然; 地图投影反映的实地面积越大,投影变形越大,反之越小。
X ' m 为经线长度比; Y ' n
X
Y
X'm
X
Y'n Y
为纬线长度比
VP=( dF′- dF )/ dF= dF′/ dF –1=P-1
= 0 不变 > 0 变大 < 0 变小
五、角度变形
投影面上任意两方向线的夹角与椭球体面上相 应的两方向线的夹角之差,称为角度变形。
地图学第二章复习题及答案

地图学第二章复习题及答案第二章复习题一、选择题1.将地球椭球面上的点投影到平面上,必然会产生变形,长度变形是长度比与1的(B)。
A.积B.差C.和D.商2.为了阐明作为投影变形结果各点上产生的角度和面积变形的概念,法国数学家底索采用了一种图解方法,即通过(D)来论述和显示投影在各方向上的变形。
A.透视光线B.参考椭圆C.数学方法D.变形椭圆3.按投影变形性质分类,可将地图投影分为等角投影、等积投影和(A)。
A.任意投影B.方位投影C.圆柱投影D.圆锥投影4.圆锥投影中纬线投影后为(D),经线投影后为相交于一点的直线束,且夹角与经差成正比。
A.直线B.相交于圆心的直线束C.相交于某一点的弧线D.同心圆圆弧5.我国自1978年以后采用(C)作为百万分一地形图的数学基础。
A.等面积圆锥投影B.等距离圆锥投影C.等角圆锥投影D.等角方位投影6.正轴等距圆锥投影沿(A)保持等距离,即m=1。
A.经线B.纬线。
C.旋转轴D.标准纬线。
7.正轴圆锥投影的变形只与(B)发生关系,而与经差无关,因此同一条纬线上的变形是相等的,也就是说,圆锥投影的等变形线与纬线一致。
A.经线B.纬线C.距离D.方向8.圆锥投影最适宜用于(D)处沿纬线伸展的制图区域的投影。
A.高纬度B.低纬度C.赤道D.中纬度9.就制图区域形状而言,方位投影适宜于具有圆形轮廓的地区,就制图区域地理位置而言,在两极地区,适宜用(A)投影。
A.正轴B.斜轴C.横轴D.纵轴10.横轴等积方位投影在广大地区的小比例尺制图中,特别是(B)中应用得很多。
A.全球地图B.东西半球图C.各大洲地图D.两极地图11.在正常位置的圆柱投影中,纬线表象为(A),经线表象为平行直线。
A.平行直线B.相交于圆心的直线束C.相交于某一点的弧线D.同心圆圆弧12.等角航线是地面上两点之间的一条特殊的定位线,它是两点间同(C)构成相同方位角的一条曲线。
A.所有纬线B.投影轴C.所有经线D.大圆航线13.1949年中华人民共和国成立以后,就确定(D)为我国地形图系列中1:50万,1:20万,1:10万,1:5万,1:2.5万,1:1万及更大比例尺地形图的数学基础。
第二章上 地球体与地图投影

地球椭球体 地球椭球面
大地水准面
二、地理坐标
以地球的北极、南极、赤道以及本初子午线作为 基本要素,即可构成地球球面的地理坐标系统 。
用经纬度表示地面点位的球面坐标。地理 坐标又按坐标所依据的基准线和基准面的不同 以及求坐标方法的不同,可分为:
天文经纬度 大地经纬度 地心经纬度
大地经纬度:表示地面点在参考椭球面上的位置, 大地经纬度 用大地经度L 、大地纬度 B 和大地高H表示。
正轴切圆柱投影的经纬网:
那么m、n与a、b有何关系: z 当投影后,经纬线正交,那么m、n与a、b一致:
z
当投影后,经纬线不正交,经纬线的交角为θ,那 么m、n与a、b不一致,根据下列公式计算:
m2 + n2 = a2 + b2 m·n·sinθ = a·b
③长度变形(Vμ):长度比与1的差。 Vμ =μ−1
> 0 变大 = 0 不变 < 0 变小
ω
思考题:
1、在某一幅地图上某一点沿经线方向长度比为 1.072,纬线方向长度比为0.931,经纬线交角 为60度,求a,b,P 。 2、已知地图上某点长短轴方向长度比分别为 a=3,b=1,则最大角度变形为多少?
(四)标准线与等变形线
在各种投影地图上,不同点的变形值常常是不一样的,为 了便于观察和了解绘制区域变形的分布,因此,常用标准线和 等变形线来表示制图区域的变形分布特征。
3、在1:100万等积圆锥投影的地图上,某点的经 线长度比为0.95,自该点向东量得图上距离为 2.10cm,求实地长度为多少?(已知经纬线正交)
(二)按构成方式分类
z方位投影 z圆柱投影 z圆锥投影 z伪圆锥投影 z伪圆柱投影 z多圆锥投影 z其他投影
地图投影分类与变换.

地图投影分类与变换1.地图投影的分类投影的种类很多,分类方法不尽相同,通常采用的分类方法有两种:一是按变形的性质进行分类:二是按承影面不同(或正轴投影的经纬网形状)进行分类。
(1)按变形性质分类按地图投影的变形性质地图投影一般分为:等角投影、等(面)积投影和任意投影三种。
等角投影:没有角度变形的投影叫等角投影。
等角投影地图上两微分线段的夹角与地面上的相应两线段的夹角相等,能保持无限小图形的相似,但面积变化很大。
要求角度正确的投影常采用此类投影。
这类投影又叫正形投影。
等积投影:是一种保持面积大小不变的投影,这种投影使梯形的经纬线网变成正方形、矩形、四边形等形状,虽然角度和形状变形较大,但都保持投影面积与实地相等,在该类型投影上便于进行面积的比较和量算。
因此自然地图和经济地图常用此类投影。
任意投影:是指长度、面积和角度都存在变形的投影,但角度变形小于等积投影,面积变形小于等角投影。
要求面积、角度变形都较小的地图,常采用任意投影。
(2)按承影面不同分类按承影面不同,地图投影分为圆柱投影、圆锥投影和方位投影等(图1)。
图1 方位投影、圆锥投影和圆柱投影示意图①圆柱投影它是以圆柱作为投影面,将经纬线投影到圆柱面上,然后将圆柱面切开展成平面。
根据圆柱轴与地轴的位置关系,可分为正轴、横轴和斜轴三种不同的圆柱投影,圆柱面与地球椭球体面可以相切,也可以相割(图2a)。
其中,广泛使用的是正轴、横轴切或割圆柱投影。
正轴圆柱投影中,经线表现为等间隔的平行直线(与经差相应),纬线为垂直于经线的另一组平行直线(图2b)。
图2 圆柱投影的类型及其投影图形②圆锥投影它以圆锥面作为投影面,将圆锥面与地球相切或相割,将其经纬线投影到圆锥面上,然后把圆锥面展开成平面而成。
这时圆锥面又有正位、横位及斜位几种不同位置的区别,制图中广泛采用正轴圆锥投影(图3)。
在正轴圆锥投影中,纬线为同心圆圆弧,经线为相交于一点的直线束,经线间的夹角与经差成正比。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
m ds '
ds
Vm m 1
= 0 不变 > 0 变大 < 0 变小
长度比是变量,随位置和方向的变化 而变化。
25
角度变形: 投影面上任意两方向线所夹之角与球面上
相应的两方向线夹角之差,称为角度变形。
以ω表示角度最大变形。
26
最大角度变形可用极值长度比a,b表示
B
c
a
A bC o
37
球面三角形的基本公式(基本定理)是:
(1)正弦公式:
sin a sin b sin c
sin A sin B sin C
B
(2)边的余弦公式:
cos a cos b cos c sin b sin c cos A cos b cos a cos c sin a sin c cos B cos c cos a cos b sin a sin b cos C
第2章 地图投影方法、变形和分类
2.1 地图投影的基本方法 2.2 地图投影的变形 2.3 球面极坐标及其换算 2.4 地图投影的分类
1
2.1 地图投影的基本方法
投影面:将地球表面的点、线、面投影于其上的承 受面
地图投影的原理是在原面与投影面之间建立点、线、 面的一一对应关系
地图投影的方法: 几何透视法 数学分析法
垂直于垂直圈的各圆,叫做等高圈, 其中通过球心的为大圆,其余为小圆。
✓方位角
过A点的垂直圈与过新极点的经线圈的交角, 为方位角。从意义上来看,方位角相当于。
球面极坐标系
✓天顶距
A点至新极点Q的垂直圈弧长,即天顶距。从形式上来看,
天顶距相当于。
34
于是,地球面上任一点A,它既可以 用地理坐标, 确定,也可以用球面 极坐标, Z来确定,而且两种坐标系 可以进行换算。
10
11
沿经线直接展开?
12
沿纬线直接展开?
13
沿经线直接展开?
14
沿经线直接展开?
15
§2.2 地图投影的变形
一、投影变形的概念 1. 投影变形产生原因——地球的形状
16
2. 投影变形的概念 地图投影不能保持平面与球面之间在
长度(距离)、角度(形状)、面积等方 面完全不变。
地球仪上经纬线网格和地图上比较:
特殊方向
长轴方向(极大值)a 主方向
短轴方向(极小值)b 经线方向 m ;纬线方向 n
据阿波隆尼定理,有 m2 + n2 = a2 + b2
m·n·sinq = a·b 22
结论:微分圆长、短半轴的大小,等于该点
主方向的长度比。也就是说,如果一 点上主方向的长度比(极值长度比)已经确 定,则微分圆的大小和形状即可确定。
sin a b
2 ab
实用上常以下公式求得:
tan(45 ) b
2
a
长度变形是各种变形的基础!
27
面积比和面积变形:
投影平面上微小面积(变形椭圆面积) dF′与球面上相应的微小面积(微小圆面积) dF之比。
P 表示面积比 Vp 表示面积变形
P dF ' πar *br a b
dF
B
c
a
A
bC
o
39
(6)余切公式
ctga sin b cosb cosC sin CctgA ctga sin c cos c cos B sin BctgA ctgbsin c cos c cos A sin ActgB ctgbsin a cos a cos C sin CctgB ctgc sin a cos a cos B sin BctgC ctgc sin b cosb cos A sin ActgC
cos a ctgBctgC, cos B sin C cosb, cosC sin B cos c,
πr 2
Vp p 1
= 0 不变 > 0 变大 < 0 变小
P = a·b = m ·n (q = 90)(主方向和经向纬向一致) P = m ·n ·sin q (q≠ 90)(阿波隆尼定理)
面积比是变量,随位置的不同而变化。 28
2.3 球面坐标及其换算
球面坐标的意义和换算公式 地理坐标换算球面极坐标
为了简化投影公式的推导和计算工作,可以通过地理 坐标与球面极坐标的换算,仍然利用正轴投影公式, 就可以实现斜轴或横轴投影的计算以及经纬网的构成。
31
球面极坐标系的建立
通常根据制图区域的形状和地理位置,选择一个新极点
Q(0,0),球面上的各点便以新极点Q为原点,以方
位角和天顶距 Z 表示其位置,从而构成球面极坐标系。
B
c
a
A
bC
o
40
如果球面三角形中有一个角假设A是直角的话,它称为 直角球面三角形。用sinA=1,cosA=0和ctgA=0分别代入正 弦公式边的余弦公式,角的余弦公式和余切公式,则可以 依次得到:
sin b sin asin B, sin c sin asin C, cos a cos bcos C,
35
(2)由边正弦与邻角余弦之积的定理,有:
sin Z cos cos(90 ) sin(90 0 ) sin(90 ) cos(90 0 ) cos( 0 )
sin cos0 cos sin0 cos( 0 )
(3)由正弦定理,有:
化简得,
sin Z sin(90 )
sin( 0 )
(5)第二五元素公式:
sin Acos b cos B sin C sin B cos C cos a sin Acos c cos C sin B sin C cos B cos a sin B cos c cos C sin A sin C cos Acos b sin B cos a cos Asin C sin Acos C cos b sin C cos a cos Asin B sin Acos B cos c sin C cos b cos B sin A sin B cos Acos c
X
Y
代入: X2 + Y2 = R2,令R=1,得
X '2 m2
Y '2 n2
1
微小圆→变形椭圆
该方程证明: 地球面上的微小 圆,投影后通常会变为椭圆,即
以O'为原点,以相交成q角的两共
轭直径的坐标轴的椭圆方程式。 21
主方向(底索定律):无论采用何种转换方法,球面
上每一点至少有一对正交方向线,在投影平面上仍 然保持其正交关系”。在投影后仍保持正交的一对 线的方向成为主方向。取主方向为作为微分椭圆的 坐标轴
(3)角的余弦公式:
cos A cos B cos C sin B sin C cos a cos B cos Acos C sin Asin C cos b cos C cos Acos B sin Asin B cos c
c
a
A
bC
o
38
(4)第一五元素公式:
sin a cos B cos b sin c sin b cos c cos A sin a cos C cos c sin b sin c cos b cos A sin b cos C cos c sin a sin c cos a cos B sin b cos A cos a sin c sin a cos c cos B sin c cos A cos a sin b sin a cos b cos C sin c cos B cos b sin a sin b cos a cos C
x f1 (, )
y f 2 (, )
就是将参考椭球面上的元素(大地坐标、角度和 边长)按一定的数学法则化算到平面上的过程。
7
2.2 地图投影的变形
椭球面上的各点的大地坐标,按照一定的数学法 则,变换为平面上相应点的平面直角坐标,通常 称为地图投影。 ✓地理坐标为球面坐标,不方便进行距离、方位、 面积等参数的量算 ✓地球椭球体为不可展曲面 ✓地图为平面,符合视觉心理,并易于进行距离、 方位、面积等量算和各种空间分析
长度变 形
角度变 形
面积变形和 长度变形
19
二、变形椭圆
取地面上一个微分圆(小到可忽略地球曲面 的影响,把它当作平面看待),它投影到平面上通 常会变为椭圆,通过对这个椭圆的研究,分析地图 投影的变形状况。这种图解方法就叫变形椭圆。
X ' m 为经线长度比 Y ' n 为纬线长度比
X
Y
20
X'm Y'n
地球曲面转换成地图平面,不仅仅存在着比例尺变换,而且还存在着投影转换的问题
8
地图投影,简单的说就是将参考椭球面上的元素 (大地坐标、角度和边长)按一定的数学法则化 算到平面上的过程。
x y
ff12((LL,,BB))
9
地图投影的基本思想是,先将参考椭球面上的点 化算到投影面上(可展曲面),再将投影面沿母 线切开展为平面。 从本质上讲,地图投影就是按一定的条件确定大 地坐标和直角坐标之间的一一对应关系。
17
球面经纬网经过投影之后,其几何特征 受到扭曲——地图投影变形:长度(距离)、 角度(形状)、面积。
18
地图投影的变形
地图投影中不可避免地存在着变形,建立一个投影时 不仅要建立(x,y)与( ,)之间的关系,而且要研究投 影变形的分布与大小。地图投影的变形主要体现在:
长度变形 面积变形 角度变形
29
球面坐标系的意义
正轴投影以地理坐标,为参数,投影经纬网形状比较 简单,计算方便。但在使用上受到地理位置的限制。例 如,正轴方位投影只适用于两极地区,正轴圆柱投影适 用于赤道附近地区,正轴圆锥投影适用于沿纬线延伸的 中纬度地区。
