整式的乘除整章练习题(完整)
浙教版七年级(下)数学第3章整式的乘除章节练习
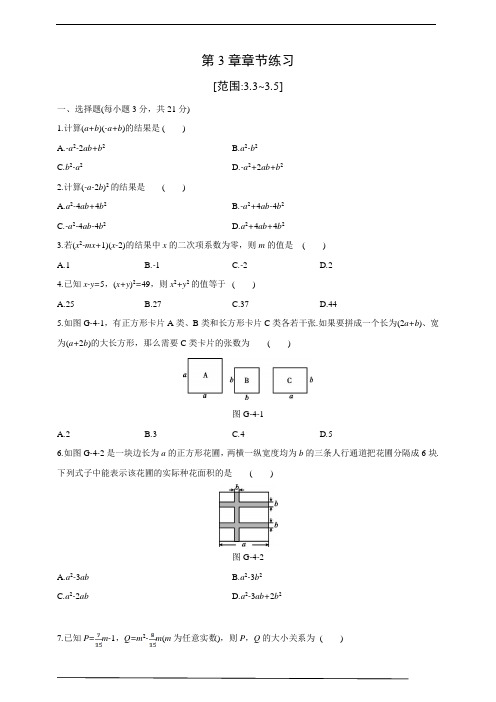
第3章章节练习[范围:3.3~3.5]一、选择题(每小题3分,共21分)1.计算(a+b)(-a+b)的结果是 ()A.-a2-2ab+b2B.a2-b2C.b2-a2D.-a2+2ab+b22.计算(-a-2b)2的结果是()A.a2-4ab+4b2B.-a2+4ab-4b2C.-a2-4ab-4b2D.a2+4ab+4b23.若(x2-mx+1)(x-2)的结果中x的二次项系数为零,则m的值是()A.1B.-1C.-2D.24.已知x-y=5,(x+y)2=49,则x2+y2的值等于()A.25B.27C.37D.445.如图G-4-1,有正方形卡片A类、B类和长方形卡片C类各若干张.如果要拼成一个长为(2a+b)、宽为(a+2b)的大长方形,那么需要C类卡片的张数为()图G-4-1A.2B.3C.4D.56.如图G-4-2是一块边长为a的正方形花圃,两横一纵宽度均为b的三条人行通道把花圃分隔成6块.下列式子中能表示该花圃的实际种花面积的是()图G-4-2A.a2-3abB.a2-3b2C.a2-2abD.a2-3ab+2b27.已知P=m-1,Q=m2-m(m为任意实数),则P,Q的大小关系为()A.P<QB.P=QC.P>QD.由m的值确定二、填空题(每小题3分,共21分)8.整式A与m2-2mn+n2的和是(m+n)2,则A=.9.已知ab=5,(a-b)2=5,则(a+b)2=.10.若(x+2)(x-a)=x2+bx-10,则ab的值为.11.若(a+b-3)2+|a-b+5|=0,则a2-b2=.12.已知a+b=,ab=1,则(a-2)(b-2)的值为.13.已知ab=a+b+1,则(a-1)(b-1)=.14.一组数:2,1,3,x,7,y,23,…满足“从第三个数起,若前面两个数依次为a,b,则紧随其后的数就是2a-b”,例如:这组数中的第三个数“3”是由“2×2-1”得到的,那么这组数中的y表示的数为.三、解答题(共58分)15.(8分)计算:(1)(a+b)2-b(2a+b);(2)(x+1)(x-1)+x(3-x).16.(8分)解方程:(1)(2a-3)(a+1)=2a2-2;(2)3(2x+1)2-12(x+1)(x-1)=0.17.(10分)先化简,再求值:(a+b)(a-b)+(a+b)2-2a2,其中ab=-1.18.(10分)王老师家买了一套新房,其结构如图G-4-3所示(单位:m).他打算将卧室铺上木地板,其余部分铺上地砖.(1)木地板和地砖分别需要多少平方米?(2)如果地砖的价格为每平方米x元,木地板的价格为每平方米3x元,那么王老师需要花多少钱?图G-4-319.(10分)观察下列等式:32-4×12=5,①52-4×22=9,②72-4×32=13,③…根据上述规律解决下列问题:(1)完成第四个等式:92-4×()2=;(2)写出你猜想的第n(n为正整数)个等式(用含n的式子表示),并验证.20.(12分)把几个图形拼成一个新的图形,再通过图形面积的计算,常常可以得到一些有用的式子,或可以求出一些不规则图形的面积.(1)图G-4-4①是将几个面积不完全相等的小正方形与小长方形拼成一个边长为a+b+c的正方形,试用不同的方法计算这个图形的面积,你能发现什么结论?请写出来;(2)图②是将两个边长分别为a和b的正方形拼在一起,B,C,G三点在同一直线上,连结BD和BF.若两个正方形的边长满足a+b=10,ab=20,请你求出阴影部分的面积.图G-4-4详解详析1.C2.D3.C4.C[解析] x2+y2=[(x+y)2+(x-y)2]=×(49+25)=37.5.D[解析] 大长方形的面积=(2a+b)·(a+2b)=2a2+5ab+2b2,所以大长方形是由2张A类正方形卡片、5张C类长方形卡片、2张B类正方形卡片组成的.故选D.6.D[解析] ∵正方形花圃的边长为a,人行通道的宽为b,∴经过平移后,实际种花部分是一个长为(a-b),宽为(a-2b)的长方形,其面积=(a-2b)(a-b)=a2-3ab+2b2.故选D.7.A8.4mn9.25[解析] ∵ab=5,(a-b)2=5,∴(a+b)2=(a-b)2+4ab=5+20=25.10.-15[解析] (x+2)(x-a)=x2+(2-a)x-2a=x2+bx-10,可得2-a=b,-2a=-10,解得a=5,b=-3,则ab=-15.故答案为-15.11.-15[解析] 由题意,得a+b-3=0且a-b+5=0,∴a=-1,b=4,∴a2-b2=(-1)2-42=1-16=-15.12.2[解析] (a-2)(b-2)=ab-2(a+b)+4=2.13.2[解析] (a-1)(b-1)=ab-a-b+1.当ab=a+b+1时,原式=a+b+1-a-b+1=2.故答案为2.14.-915.解:(1)原式=a2+2ab+b2-2ab-b2=a2.(2)原式=x2-1+3x-x2=3x-1.16.解:(1)(2a-3)(a+1)=2a2-2,2a2-a-3=2a2-2,-a=1,a=-1.(2)3(2x+1)2-12(x+1)(x-1)=0,3(4x2+4x+1)-12(x2-1)=0,12x2+12x+3-12x2+12=0,12x+15=0,x=-.17.解:原式=a2-b2+a2+2ab+b2-2a2=2ab.当ab=-1时,原式=-2.18.解:(1)卧室的面积是2b(4a-2a)=4ab(m2),厨房、卫生间、客厅的面积和是b·(4a-2a-a)+a·(4b-2b)+2a·4b=ab+2ab+8ab=11ab(m2),即木地板需要4ab m2,地砖需要11ab m2.(2)11ab·x+4ab·3x=11abx+12abx=23abx(元),即王老师需要花23abx元.19.解:(1)417(2)(2n+1)2-4n2=4n+1.验证:∵左边=(2n+1)2-4n2=4n2+4n+1-4n2=4n+1=右边,∴等式成立.20.[解析] (1)此题根据面积的不同求解方法,可得到不同的表示方法.一种是3个正方形的面积和6个长方形的面积和,一种是大正方形的面积,可得等式(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.(2)利用S阴影=正方形ABCD的面积+正方形ECGF的面积-三角形BGF的面积-三角形ABD的面积求解.解:(1)S=(a+b+c)2或S=a2+b2+c2+2ab+2bc+2ac.结论:(a+b+c)2=a2+b2+c2+2ab+2bc+2ac.(2)∵a+b=10,ab=20,∴S阴影=a2+b2-(a+b)•b-a2=a2+b2-ab=(a+b)2-ab=×102-×20=50-30=20.。
整式乘除单元测试题及答案

整式乘除单元测试题及答案一、选择题:1. 已知 \( a^2 - 4 \) 可以分解为 \( (a+2)(a-2) \),那么下列哪个表达式不能被 \( a^2 - 4 \) 整除?A. \( a^3 - 4a \)B. \( a^3 - 8 \)C. \( a^3 - 4a + 4 \)D. 提供的选项都是错误的2. 如果 \( x - 1 \) 是多项式 \( x^3 - 2x^2 + x - 2 \) 的一个因子,那么 \( x \) 的值是多少?A. 1B. 2C. 0D. 3二、填空题:1. 计算 \( (3x^2 - 2x + 1) \div (x - 1) \) 的结果为__________。
2. 将多项式 \( 2x^3 - 5x^2 + 3x - 6 \) 除以 \( x - 2 \) 的商是 __________。
三、简答题:1. 证明 \( (x - 1)^3 = x^3 - 3x^2 + 3x - 1 \)。
2. 给定多项式 \( P(x) = x^4 - 2x^3 + x^2 - 2x + 1 \),求\( P(1) \) 的值。
四、解答题:1. 已知 \( (x + y)^2 = 9 \) 和 \( (x - y)^2 = 1 \),求 \( x^2 + y^2 \) 的值。
2. 计算 \( \frac{2x^3 - 8x^2 + 6x}{2x - 4} \) 的简化形式。
五、应用题:1. 一个长方形的长是宽的两倍,如果长和宽的乘积是 24,求长方形的长和宽。
2. 某工厂生产一种零件,每个零件的成本是 \( c \) 元,售价是\( 2c \) 元。
如果工厂卖出了 \( n \) 个零件,求工厂的总利润。
答案:一、选择题:1. 答案:D. 提供的选项都是错误的。
2. 答案:A. 1二、填空题:1. 答案:\( 3x - 1 \)2. 答案:\( 2x^2 - 7x + 3 \)三、简答题:1. 证明:\( (x - 1)^3 = x^3 - 3x^2 + 3x - 1 \) 可以通过展开\( (x - 1) \) 的三次幂来验证。
整式的乘除测试题练习8套(含答案)

整式的乘除练习题(8套)含答案整式的乘除测试题练习一一、精心选一选(每小题3分,共30分) 1、下面的计算正确的是( )A 、1234a a a =⋅B 、222b a )b a (+=+C 、22y 4x )y 2x )(y 2x (-=--+-D 、2573a a a a =÷⋅ 2、在n m 1n x )(x +-=⋅中,括号内应填的代数式是( )A 、1n m x ++B 、2m x +C 、1m x +D 、2n m x ++ 3、下列算式中,不正确的是( )A 、xy 21y x y x 21)xy 21)(1x2x (n 1n 1n n -+-=-+-+-B 、1n 21n n x )x (--= C 、y x x 2x31)y x 2x 31(x n 1n n 2nn --=--+D 、当n 为正整数时,n 4n 22a )a (=- 4、下列运算中,正确的是( )A 、222ac 6c b 10)c 3b 5(ac 2+=+B 、232)a b ()b a ()1b a ()b a (---=+--C 、c b a )c b a (y )a c b (x )1y x )(a c b (-+-----+=++-+D 、2)a b 2(5)b a 3)(b 2a ()a 2b 11)(b 2a (--+-=-- 5、下列各式中,运算结果为422y x xy 21+-的是( )A 、22)xy 1(+-B 、22)xy 1(--C 、222)y x 1(+-D 、222)y x 1(-- 6、已知5x 3x 2++的值为3,则代数式1x 9x 32-+的值为( ) A 、0 B 、-7 C 、-9 D 、3 7、当m=( )时,25x )3m (2x 2+-+是完全平方式 A 、5± B 、8 C 、-2 D 、8或-28、某城市一年漏掉的水,相当于建一个自来水厂,据不完全统计,全市至少有5106⨯个水龙头,5102⨯个抽水马桶漏水。
八年级数学上册整式的乘除(习题及答案)

例题示范
例 1:计算 (2 x3y)2 ( 2y) ( 8x8 y3 4x2 ) ( 2x2 ) . 【操作步骤】 ( 1)观察结构划部分: (2 x3 y)2 ( 2 y) ( 8x8y3 4x2) ( 2x2)
①
②
( 2)有序操作依法则:辨识运算类型,依据对应的法则运算.
第一部分:先算积的乘方,然后是单项式相乘;
③(
23
2x )
(
3
3x
y)
2
;
④ 3b3 ( 2ac) ( 2ab) 2 .
2. ① 3xy2 (2 xz2 3x2 y) _____________________;
② 4xy 1 y3 2 ____________bc
___________________;
③ ( 4m2n4 8m4n2 ) (2 mn) 2 _______________;
第2页 共5页
④ ___________________ m2
mn2
3n
1 .
2
8. 计算:
① ( 4a3c2 )2 (4a3c2 ) ( a2c) ( 2ac );
② 4(a2 a 2) (2 a 1)2 ;
③ (a
2b )(2 a
b)
3
(a b
3
2ab )
( ab) .
思考小结
1. 老师出了一道题,让学生计算 (a b)( p q) 的值. 小聪发现这是一道“多 ×多”的问题,直接利用握手原则展开即可. (a b)( p q) =
第3页 共5页
3
4
④ (2 ab 2 )2 (2 a 2 b ) ________________________;
(完整版)最新北师大版数学七年级下册第一章_整式的乘除知识点总结及练习题

☆☆☆ 北师大版数学七年级【下册】第一章 整式的乘除一、 同底数幂的乘法同底数幂的乘法法则: n m n ma a a +=⋅(m,n 都是正数)是幂的运算中最基本的法则,在应用法则运算时,要注意以下几点:①法则使用的前提条件是:幂的底数相同而且是相乘时,底数a 可以是一个具体的数字式字母,也可以是 一个单项或多项式;②指数是1时,不要误以为没有指数;③不要将同底数幂的乘法与整式的加法相混淆,对乘法,只要底数相同指数就可以相加;而对于加法,不仅底数相同,还要求指数相同才能相加;④当三个或三个以上同底数幂相乘时,法则可推广为p n m p n ma a a a ++=⋅⋅(其中m 、n 、p 均为正数);⑤公式还可以逆用:n m nm a a a⋅=+(m 、n 均为正整数)二.幂的乘方与积的乘方1。
幂的乘方法则:mnnm a a =)((m ,n 都是正数)是幂的乘法法则为基础推导出来的,但两者不能混淆.2. ),()()(都为正数n m a a a mn mn nm ==.3。
底数有负号时,运算时要注意,底数是a 与(-a )时不是同底,但可以利用乘方法则化成同底,如将(-a )3化成—a 3⎩⎨⎧-=-).(),()(,为奇数时当为偶数时当一般地n a n a a n n n4.底数有时形式不同,但可以化成相同。
5.要注意区别(ab )n与(a+b)n意义是不同的,不要误以为(a+b )n=a n+b n(a 、b 均不为零).6.积的乘方法则:积的乘方,等于把积每一个因式分别乘方,再把所得的幂相乘,即nnnb a ab =)((n 为正整数)。
7.幂的乘方与积乘方法则均可逆向运用。
三. 同底数幂的除法1。
同底数幂的除法法则:同底数幂相除,底数不变,指数相减,即n m n ma a a -=÷ (a ≠0,m 、n 都是正数,且m 〉n ).2。
在应用时需要注意以下几点:①法则使用的前提条件是“同底数幂相除"而且0不能做除数,所以法则中a ≠0。
华师大版八年级数学上册《整式的乘除》单元试卷检测练习及答案解析

华师大版八年级数学上册《整式的乘除》单元试卷检测练习及答案解析一、选择题1、下列运算正确的是()A.(a3)2=a6B.2a+3a=5a2C.a8÷a4=a2D.a2·a3=a62、若、、是正整数,则=()A.B.C.D.3、若,,则等于()A.B.C.2 D.4、计算的结果是()A.B.C.D.5、若,,则代数式的值等于()A.B.C.D.26、若(x2+px+q)(x2+7)的计算结果中,不含x2项,则q的值是()A.0 B.7 C.-7 D.±77、已知x+y=-5,x-y=2,则x2-y2=()A.. B.C.D.8、如果是一个完全平方式,那么的值是().A.B.C.D.9、计算(36x6-16x2)÷4x2的结果为()A.9x3﹣4x2B.9x4+4 C.9x3+4x D.9x4﹣4 10、某同学粗心大意,因式分解时,把等式x4-■=(x2+4)(x+2)(x-▲)中的两个数字弄污了,则式子中的■,▲对应的一组数字可以是( )A.8,1 B.16,2C.24,3 D.64,8二、填空题11、分解因式:3a3-3a=______.12、已知x a=3,x b=4,则x3a﹣2b的值是_____.13、计算:=_______.14、若的结果中不含x的一次项,则=________.15、已知x﹣y=4,则代数式x2﹣2xy+y2﹣25的值为_____.16、已知一个三角形的面积为8x3y2-4x2y3,一条边长为8x2y2,则这条边上的高为___________.17、计算:(﹣a)2÷(﹣a)= ,0.252007×(﹣4)2008= .18、已知,则=______.19、计算的结果是_______.20、若=7,则___________.三、计算题21、计算:(1)(2)(3)(4)22、因式分解:⑴⑵⑶⑷四、解答题23、一个三角形的底边长为,高为,该三角形面积为S,试用含的代数式表示S,并求当时,S的值.24、先化简,再求值:,其中x =-1,y =.25、计算:(1)已知a+b=-3,ab=5,求多项式4a2b+4ab2-4a-4b的值;(2)已知x2-3x-1=0,求代数式3-3 x2+9x的值?26、已知(x2+px+8)与(x2﹣3x+q)的乘积中不含x3和x2项,求p、q的值.27、阅读:将代数式转化为的形式,(期中为常数),则其中.(1)仿照此法将代数式化为的形式,并指出的值.(2)若代数式可化为的形式,求的值.参考答案1、A2、C3、A4、B5、B6、C7、D8、D9、D10、B11、3a(a+1)(a-1)12、13、214、-815、-916、2x-y17、﹣a,﹣4.18、-219、.20、±321、(1)1;(2);(3);(4)2.22、⑴==⑵==⑶===4⑷=== 23、.24、原式==025、(1)-48;(2)026、p=3,q=1.27、①;②答案详细解析【解析】1、分析:结合选项分别进行幂的乘方、合并同类项、同底数幂的乘除法等运算,然后选择计算正确选项即可.详解:A、(a3)2=a6,原式计算正确,故本选项正确;B、2a+3a=5a,原式计算错误,故本选项错误;C、a8÷a4=a4,原式计算错误,故本选项错误;D、a2·a3=a5,原式计算错误,故本选项错误.故选A.点睛:本题考查了幂的乘方乘方,合并同类项,同底数幂的乘除法. 熟练掌握它们的计算法则是计算正确的关键.2、分析:首先根据同底数幂的乘法将括号里面的进行计算,然后根据积的乘方计算法则得出答案.详解:原式=,故选C.点睛:本题主要考查的是同底数幂的乘法以及幂的乘方计算,属于基础题型.解决这个问题的关键就是明确幂的计算法则.3、分析:先把23m﹣2n化为(2m)3÷(2n)2,再求解.详解:∵2m=3,2n=5,∴23m﹣2n=(2m)3÷(2n)2=27÷25=.故选A.点睛:本题主要考查了同底数幂的除法及幂的乘方与积的乘方,解题的关键是把23m﹣2n化为(2m)3÷(2n)2.4、试题解析:故选B.5、∵,,∴(x-1)(y+1)=xy+x-y-1=.故选B.6、(x2+px+q)(x2+7)=x4+7x2+px3+7px+qx2+7q=x4+px3+(7+q)x2+7px+7q,因为计算结果中不含x2项,所以7+q=0,所以q=-7;故选C.7、本题考查平方差公式进行因式分解,因为x2-y2=(x+y)(x-y),将x+y=-5,x-y=2,代入得: -5×2=-10,因此,正确选项是D.8、∵形如的式子叫完全平方式,而,∴若是完全平方式,则,∴,故选D.9、多项式除以单项式,先把这个多项式的每一项分别除以单项式,再把所得的商相加.所以(36x6-16x2)÷4x2= 9x4﹣4考点:整式的除法.10、由(x2+4)(x+2)(x-▲)得出▲=2,则(x2+4)(x+2)(x-2)=(x2+4)(x2-4)=x4-16,则■=16.故选B.【点睛】此题考查了学生用平方差公式分解因式的掌握情况,灵活性比较强.11、分析:提取公因式法和公式法相结合进行因式分解即可.详解:原式故答案为:点睛:考查因数分解,提取公因式法和公式法相结合进行因式分解.注意分解一定要彻底.12、分析:直接利用同底数幂的除法运算法则计算得出答案.详解:∵x a=3,x b=4,∴x3a﹣2b=(x a)3÷(x b)2=33÷42=.故答案为:.点睛:本题主要考查了同底数幂的乘除运算,正确将原式变形是解题的关键.13、分析:先把改写成2100=,然后逆用积的乘方公式(ab)m=a m·b m,即a m·b m=(ab)m解答.详解:====2.点睛:本题考查了偶次幂的性质和积的乘方运算,解答本题的关键是逆用乘方运算公式.14、试题解析:结果中不含的一次项.故答案为:15、解: x2﹣2xy+y2﹣25=(x﹣y)2﹣25 =42﹣25=﹣9,故答案为:﹣9.16、∵三角形的面积为8x3y2-4x2y3,一条边长为8x2y2,∴这条边上的高为2(8x3y2-4x2y3) ÷8x2y2=16x3y2÷8x2y2-8x2y3÷8x2y2=2x-y,故答案为:2x-y.17、试题分析:根据同底数幂的除法底数不变指数相减,可得答案;根据同底数幂的乘法底数不变指数相加,可得积的乘方,根据积的乘方,可得答案.解:(﹣a)2÷(﹣a)=﹣a,0.252007×(﹣4)2008=[0.25×(﹣4)]2007×(﹣4)=﹣4,故答案为:﹣a,﹣4.18、本题利用拆常数项凑完全平方的方法进行求解,,可变形为:,即,根据非负数的非负性可得:解得: :,所以19、原式===12017=-.故答案为-.点睛:积的乘方公式:(ab)n=a n b n(n为正整数)的逆运算:a n b n = (ab)n(n为正整数)也成立.20、(x+)2=x2+2+=7+2=9,x+=±3.故答案为±3.点睛:(1)(x+)2=x2+2+;(x-)2=x2-2+.21、试题分析:(1)原式=;(2)原式=;(3)原式=;(4)原式=.考点:整式的混合运算.22、试题解析:点睛:因式分解:把一个多项式分解成几个整式的积的形式.因式分解的主要方法:提公因式法,公式法,十字相乘法,分组分解法.23、分析:利用三角形的面积公式得到三角形的面积S=(4a+2)(2a-1),然后利用平方差公式计算可得用含a的代数式表示S;再将a=2代入计算即可求解.详解:,当时,.点睛:本题考查了多项式乘多项式,平方差公式的知识,解决此类问题的关键是牢记平方差公式.24、分析:首先根据乘法公式将括号去掉,然后进行合并同类项,最后根据多项式除以单项式的法则得出答案,将x和y的值代入化简后的式子进行计算得出答案.详解:原式===,将x =,y =代入上式,原式=0.点睛:本题主要考查的是多项式的乘法和除法的计算法则,属于基础题型.在解决这个问题的时候,公式的应用是非常关键的.25、分析:(1)、首先进行分组分解,然后提取公因式,最后利用整体代入的思想进行求解;(2)、首先提取公因式-3,然后整体代入进行求解.详解:(1)、解:原式 ="4" ab(a+b)-4(a+b)="(4" ab-4)(a+b)=4(ab-1)(a +b)当a+b=-3,ab=5时,原式=4×(5-1)×(-3)=4×4×(-3)=-48(2)、原式=-3(x2-3x-1),当x2-3x-1="0," 原式=-3×0=0.点睛:本题主要考查的是利用因式分解进行简便计算,属于基础题型.解决这个问题的关键就是将所求的代数式进行因式分解.26、试题分析:根据整式的乘法,化简完成后,根据不含项的系数为0求解即可.试题解析:∵(x2+px+8)(x2﹣3x+q)=x4﹣3x3+qx2+px3﹣3px2+pqx+8x2﹣24x+8q=x4+(p﹣3)x3+(q﹣3p+8)x2+(pq﹣24)x+8q.∵乘积中不含x2与x3项,∴p﹣3=0,q﹣3p+8=0,∴p=3,q=1.27、试题分析:根据完全平方公式的结构,按照要求即可得出答案.试题解析:①则②则.。
整式的乘除(含答案)

第4课 整式的乘除 目的:复习幂的运算法则,整式的乘除运算.中考基础知识1. 幂的运算法则:a m ·a n=______(m ,n 都是正整数),(a m )n =_______(m ,n 都是正整数).a m ÷a n =_______(m ,n 都是正整数,且m>n ,a ≠0),(ab )n =______(n 为正整数).2.整式的乘除(1)单项式×单项式:4a 2x 5·(-3a 3bx )=_________,(2)单项式×多项式:m (a+b+c )=__________,(3)多项式×多项式:(a+b )(m+n-d )=_______.(4)单项式÷单项式:-12a 5b 3x 2÷4a 3x 2=________.3.乘法公式(1)平方差公式:(a+b )(a-b )=________.(2)完全平方公式:(a+b )2=_______,(a-b )2=_________.(3)立方和、立方差公式:(a+b )(a 2-ab+b 2)=________,__________=a 3-b3 4.在做整式乘除时,严格按照运算法则进行,做每一步都应有计算依据,•充分利用乘法公式简化计算. 备考例题指导例1.下列计算正确的是( )(A )x 5+x 5=x 10 (B )(3ab 2)3=9a 3b6 (C )a 2·a 3=a 6 (D )(-c )6÷(-c )5=-c (c ≠0)选(D )例2.(2005,金华市)如图,沿正方形的对角线对折,•把对折后重合的两个小正方形内的单项式相乘,乘积是___________(只要写出一个结论)a2a b-2b 答案:2a 2或-2b 2任写一个.例3.化简(a-b )3·(b-a )2÷(b-a )3.分析:底数不同,不能直接乘除,但注意到a-b 与b-a 是互为相反数,而且(a-b )3=-(b-a )3 解:原式=-(b-a )3·(b-a )2÷(b-a )3 =-(b-a )3+2-3 (注意乘除在一起要依次运算)=-(b-a )2 例4.计算(1)(-2b-5)(2b-5);(2)(a+b-1)(a-b+1).分析:在(a+b )(a-b )=a 2-b 2中,其左边的两个多项式有两项(a 与a )相同,有两项b 与-b 是互为相反数.这里平方差公式的使用条件.解:(1)原式=(-5)2-(2b)2=25-4b2.(2)原式=[a+(b-1)][a-(b-1)]=a2-(b-1)2=a2-(b2-2b+1)=a2-b2+2b-1备考巩固练习1.填空题(1)-x3·(-x)5=________;[(-x)3]2·(-x)3=________;(-2x2y3)2·(-12xy)3=________.(2)-6x(x-2y)=_______;(x-6)(x+7)=________;(x-2)(x-y)=________.(3)(2x-3y)2=________;(3a+b)2=________.(4)(x+1)(x2-x+1)=_______;(_______-2b)(_______)=a3-(________).(5)若4m·8m-1÷2m=32,则m=________.2.选择题(1)下列各式中,计算正确的是()(A)a2·a3=a6(B)a3÷a2=a2 (C)(a2)3=a6(D)(3a2)4=9a8(2)(2005,黄冈)下列计算中正确的是()(A)x5+x5=2x10(B)-(-x)3·(-x)5=-x8(C)(-2x2y)3·4x-3=-24x3y3(D)(12x-3y)(-12x+3y)=14x2-9y23.(2004,太原市)某公园一块草坪的形状如图所示(阴影部分),用代数式表示它的面积为__________.4.化简求值:(a+2b)(a2+4b2)(a-2b),其中a=2,b=-12.5.解答下列各题:(1)若a-1a=3,求a2+21a的值.(2)若3x2-mxy+6y2是一个完全平方式,求m的值.(3)已知x+y=2,xy=12,求x3+y3的值.(4)计算(8x2m-3-6x m+2-4x m)÷(-2x m-3).6.(2003,四川)观察下面的式子:31=3,32=9,33=27,34=81,35=243,36=729,37=2187,38=6561,39=19683,……它们的个位数字的变化有一定规律,用你发现的规律直接写出910的个位数字是几?7.(2005,苗城)先化简后求值:[(x-y)2+(x+y)(x-y)]÷2x,其中x=3,y=1.5 答案:1.(1)x8;-x9;-12x7y9(2)-6x2+12xy;x2+x-42;x2-xy-2x+2y(3)4x2-12xy+9y2,9a2+6ab+b2(4)x3+1;(a-2b)(a2+2ab+b2)=a3-8b3(5)22m·23m-3÷2m=25,m=22.(1)D (2)C 3.22a24.原式=(a2-4b2)(a2+4b2)=a4-16b4,当a=2,b=-1 2原式=24-16×(-12)4=16-1=155.(1)由a-1a=3得(a-1a)2=9∴a 2-2+21a =9 ∴a 2+21=11(2)∵3x 2-mxy+6y 2=x )2-mxy+y )2∴m=±=± 或用△=0,求m .(3)x 3+y 3=(x+y )(x 2-xy+y 2)=(x+y )[(x+y )2-3xy] =2(22-3×12)=2×52=5 (4)原式=-4x m +3x 5+2x 36.17.原式=1.5。
最新北师大版数学七年级下册第一章-整式的乘除知识点总结及练习题

(B)(5x-1)(1-5x)=25x2-1 (D)(x-3)(x-9)=x2-27 18.如
果 x2-kx-ab=(x-a)(x+b),则 k 应为…………………………………(
)
(A)a+b (B)a-b (C)b-a
(三)计算(每题 4 分,共 24 分)
19.(1)(-3xy2)3·( 1x3y)2; 6
.
6.(1 )-2+0=
;4101×0.2599=
.
3
7.20 2×19 =1 (
)·( )=
.
33
8.用科学记数法表示-0.0000308=
.
9.(x-2y+1)(x-2y-1)2=( )2-( )2=
.
10.若(x+5)(x-7)=x2+mx+n,则 m=
,n=
.
(二)选择题(每小题 2 分,共计 16 分)
☆☆☆ 北师大版数学七年级【下册】 一、 同底数幂的乘法
第一章 整式的乘除
同底数幂的乘法法则: am an amn (m,n 都是正数)是幂的运算中最基本的法则,在应用法则运算时,要
注意以下几点: ①法则使用的前提条件是:幂的底数相同而且是相乘时,底数 a 可以是一个具体的数字式字母,也可以是
一个单项或多项式; ②指数是 1 时,不要误以为没有指数; ③不要将同底数幂的乘法与整式的加法相混淆,对乘法,只要底数相同指数就可以相加;而对于加法,不仅底数相同,还要求指数相 同才能相加;
第4页
20.用简便方法计算:(每小题 3 分,共 9 分)
(1)982;
(2)899×901+1;
(3)(10 )2002·(0.49)1000. 7
(四)解答题(每题 6 分,共 24 分) 21.已知 a2+6a+b2-10b+34=0,求代数式(2a+b)(3a-2b)+4ab 的值.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第13章 整式的乘除第1课时 幂的运算(一)1.计算:(1)791010⨯=_________; (2)34111222⎛⎫⎛⎫⎛⎫= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭_____________.2.计算:(1) 23x x = ___________; (2)74m m =______________.3.计算:(1)()43aa -=________; (2)()()42x x x ---= ____________.4.计算:()()()234m n n m n m ---=____________.5.计算:(1)322d d d d +=__________; (2)5462m m m m m -=__________.6.(1)若710maa a =,则m=_________; (2)若8m m a a a =,则m=_________.7.一长方体的长、宽、高分别是710cm 、610cm 、310cm ,则它的体积是_________3cm . 8.下列运算正确的是 ( )A . 339xx x = B . 336x x x = C . 3332x x x = D .3262x x x =9.下列计算正确的是 ( )A .()()235a a a --=- B .()()()264a a a --=-C .()()374aa a --=- D .4312a a a -=-10.下列各式计算结果为7x 的是 ( )A . ()()25x x -- B . ()25x x --C .()()43x x -- D . 34x x +11.已知2,5abx x ==,则a bx+等于 ( )A .7B .10C .20D .50 12.已知311aa a χχ+=,则χ的值为 ( )A .2B .3C .4D .513.计算.(1) ()()2322x y y x --; (2) 131n n yy y y -++;(3);()()334433x x x x x x x ++-- (4)52342n n x x x x x x --14.一台电子计算机每秒可作1010次计算,它工作3510⨯秒可作多少次运算15.已知12km 的土地上,一年内从太阳得到的能量相当于燃烧810⨯kg 煤所产生的能量,那么我国6210km ⨯的土地上,一年内从太阳得到的能量相当于燃烧多少千克煤16.我们约定1010ab a b ⊗=⨯,如25231010⊗==.(1)试求123⊗和48⊗的值; (2)想一想:()a b c ⊗⊗是否与()a b c ⊗⊗的值相等验证你的结论.第13章 整式的乘除第2课时 幂的运算(二)1.计算:(1)()320.3⎡⎤-=⎣⎦_________; (2) ()7102=_________.2.计算:(1)()43a =__________; (2) ()2x m =________.3.计算:(1)()43χ-=___________; (2)()35a -=__________.4.计算:(1)()54a b ⎡⎤-=⎣⎦___________; (2)()32m n --=⎡⎤⎣⎦________________. 5.计算:(1)()()2334m m --=________; (2)()()3221m m bb +=____________.6.下列计算正确的是 ( ) A .()257a a = B .()3327a a = C .()236a a = D .()2121n n a a ++=7.下列各式中错误的是 ( )A . ()()2510nnx y x y ⎡⎤-=-⎣⎦B .()()nm mn a b a b ⎡⎤+=+⎣⎦C .()()236a b a b ⎡⎤-=-⎣⎦ D .()()3131m m x y x y --⎡⎤-=-⎣⎦8.计算()()8424x x 的结果为 ( )A .18x B .24x C .28x D .32x 9.计算1001000mn 的结果为 ( )A .100000m n+ B .2310m n+ C .100m D .1000mn10.若5544332,3,4a b c ===,则a 、b 、c 的大小关系是 ( )A .b >c >aB .a >b >cC .c >a >bD .a <b <c 11.计算. (1)()532y y y ; (2)()()3122n n n x x x -;(3)()()3511m m b b +-; (4)()()235a b b a ⎡⎤--⎣⎦;(5)()()()332x y x y x y ⎡⎤---⎣⎦; (6)()()2122nn x x x +-.12.已知正方体的棱长为()23a b cm +,试分别求出这个正方体的表面积和体积.13.(1)已知182482mm m =,求m 的值;(2)已知22ma =,求()32m a 的值.14.求1007和2003的末位数字.15.求满足()()23320nnn n ----=的正整数n 的值.第13章 整式的乘除第3课时 幂的运算(三)1.计算:(1)()32x =_________; (2)()23mx y =____________.2.计算:(1)212ab ⎛⎫-= ⎪⎝⎭__________; (2)()322xy -=__________.3.计算:(1)()32310-⨯=__________; (2)()34410-⨯=______________.4.计算:(1)()()223222a a a +=____________;(2)()()()428236x y x y +-=_______.5.已知2,3nnx y ==,则()nxy =____________.6.计算:(1)200820083553⎛⎫⎛⎫-= ⎪⎪⎝⎭⎝⎭______________. (2)741497⎛⎫-⨯= ⎪⎝⎭____________.7.下列计算正确的是 ( ) A .()326ab ab = B .()22236xy x y =C .()22424a a -=- D .()2323mm m a b a b = 8.下列计算正确的个数为 ( ) (1)()224ab ab = (2)()333412ab a b = (3)()428216x x -=- (4)()2234524m n m n =A .0个B .1个C .2个D .3个 9.若()3915m n x y x y =,则m 、n 的值为 ( )A .m=9,n=5B .m=3,n=5C .m=5,n=3D .m=6,n=1210.计算: 6640.753⎛⎫⨯- ⎪⎝⎭的结果为 ( )A .0B .1C .-5D .16411.计算: (1)()4233xy z -; (2)()()25332a b ⎡⎤-⎢⎥⎣⎦;(3)()()4225243a a a aa +--; (4)()()()2323337235x x xx x -+12.先化简再求值.()3233212a bab ⎛⎫-+- ⎪⎝⎭,其中1,44a b ==.13.若25nx =,求()()223234nn x x -的值.14.太阳可以近似地看作是球体,如果用V 、r 分别代表球的体积和半径,那么343V r π=. 太阳的半径约为6×610千米,它的体积大约是多少立方千米15.你能确定510256625⨯的位数吗请大胆试一试.第13章 整式的乘除第5课时 整式的乘法(一)1.计算:(1)232xy x y -=___________;(2)24342535x y x y z ⎛⎫⎛⎫-=⎪ ⎪⎝⎭⎝⎭__________.2.计算:(1)221323ab abcabc =_____________; (2)2352231343a bc c abc ⎛⎫⎛⎫--= ⎪ ⎪⎝⎭⎝⎭_____________. 3.计算. (1)()()()35210310510⨯⨯⨯=________________,(2)()()()345310410510⨯⨯⨯=________________.4.计算.(1)()2122xyz xy ⎛⎫-= ⎪⎝⎭__________;(2)()221322m mn mn ⎛⎫--= ⎪⎝⎭__________.5.卫星脱离地球进入太阳系的速度是1.12⨯410米/秒,则3.6310⨯秒卫星行走________米.6.计算()24334x y x y ⎛⎫-⎪⎝⎭的结果为 ( ) A .6253x y B .84x y - C .624x y - D .62x y 7.下列计算正确的是 ( )A .23639x xy x y = B .()()22323ab ab a b-=-C .()()2233mn m n m n-=- D .()232339xy xy x y --=8.若()()()6571051021010na ⨯⨯⨯=⨯,则a 、n 的值分别为 ( )A .7,11a n ==B .a = 5,n = 12C .a =7,n =13D .a =2,n =13 9.计算()()()232341.210510210-⨯⨯⨯⨯⨯的结果为 ( )A .205.7610⨯ B .195.7610⨯C .202.8810⨯D .192.8810⨯ 10.计算. (1)()2332310.534x y x y z xyz ⎛⎫⎛⎫-- ⎪ ⎪⎝⎭⎝⎭; (2)()()()2330.30.27ay bx a by11.计算.(1)()()22233ab a b a b ab +-;(2) ()()()23222222x y xy xy xy --+.12.先化简再求值. ()()()()222335364a b b ab ab ab a -+----,其中a =12,b=.13.光的速度大约是3510⨯千米/秒,从太阳系以外距离地球最近的一颗恒星(比邻星)发出的光,需要4年时间才能到达地球,一年以3710⨯秒计算,求这颗恒星与地球的距离.14.已知1292nm n a b a b +-的积与435a b 是同类项,求m 、n 的值.15.已知435,477m n ==. 求代数式()()()()321322m n m n m n m n ⎡⎤-+--+-⎡⎤⎣⎦⎢⎥⎣⎦的值.第6课时 整式的乘法(二)1.计算:(1) a (2a 2一3a +1)=________;(2)(42x 一3x+6)12x =____________. 2.计算:(1)3a b(2a 2b--a b+1) =_____________;(2)(34a b 2+3a b 一23b )(12a b)=_____________.3.计算:(1)(一22x )(2x -12x 一1) =____________; (2) 322213342x y x y x ⎛⎫+-⎪⎝⎭(一12xy) =______________.4.计算:(1)3x(5x -2)一5x(1+3x)=____________; (2)32x (1--2x)+2x(32x -x+1)=___________.5.若A 表示一个单项式,B 表示一个三项式,则AB 是__________项式.6.下列各式中,计算正确的是 ( )A .(a -3b+1)(一6a )=一6a2+18a b+6aB .()232191313x y xy x y ⎛⎫--+=+ ⎪⎝⎭C .6mn(2m+3n -1) =12m 2n+18mn 2-6mn D .一a b(a2一a -b) =-a 3b -a2b--a b 27.计算(62x -4xy+3y 2)·213x y ⎛⎫-⎪⎝⎭的结果为 ( ) A .一2x4y+43x 2y 2+x 2y 3 B .一2x 4y -43x 2y 2-x 2y 3C .一2x 4y+43x 3y 2一x 2y 3D .一2x 4y 一43x 3y 2+x 2y 38.计算a2(a +1) -a (a2-2a -1)的结果为 ( )A .一a 2一a B .2a 2+a +1 C .3a2+a D .3a2-a9.一个长方体的长、宽、高分别是2x 一3、3x 和x ,则它的体积等于 ( ) A .22x —32x B .6x -3 C .62x -9x D .62x -92x 10.计算.(1)(2x 3一32x +4x -1)(一3x);(2)()22213632xy y x xy ⎛⎫-+-- ⎪⎝⎭.11.计算. (1)2a 2-a (2a -5b)-b(5a -b);(2)22249312324ab a b ab b ⎛⎫⎛⎫--+ ⎪ ⎪⎝⎭⎝⎭.12.先化简,再求值.(1)m 2(m+3)+2m(m 2—3)一3m(m 2+m -1),其中m 52=;(2)4a b(a 2b -a b 2+a 6)一2a b 2(2a2—3a b+2a ),其中a =3,b=2.13.(1)解方程:x(x 2+3)+ 2x (2x -3)--3x(2x -x -1)=12;(2)解不等式:2x(x一1)一3(2x+5x一6)>l+4x(1一14 x).14.若n为自然数,则n(2n+1) -2n(n-3)的值是7的倍数吗试说明理由.15.若(3x+2y) 2+2x+3y+5=0.化简(一122x y)(xy2+42x y-6x3)+2xy(x3y-2x4)+xy2,并求它的值.第7课时整式的乘法(三)1.计算:(1)(y—12)(y+13)=___________;(2)(x+20)(x+10) =__________.2.计算:(1)(2x一5)(x+4)=___________; (2)(2y—1)(2y+3) =__________.3.计算:(1)(x+3y)(3x-4y)=__________; (2)(2a一b)(3a+b) =___________.4.计算:(1)(22x+3y2)(22x-5y2)=__________;(2)52x一(2x-1)(3x+ 1) =__________.5.计算:(1)(3m+2n)(3m-2n-1) =____________;(2)(2x+3)( 2x一5x-1) =___________.6.下列计算中,错误的是 ( )A.(x+1)(x+4) =2x+5x+4 B.(m一2)(m+3) =m2+m一6C.(y+4)(y一5) =y2+9y一20 D.(x一3)(x一6) =2x一9x+18 7.计算结果为2m2-7mn+6n2的是 ( )A.(2m—n)(m 6n) B.(2m-3n)(m-2n)C.(2m一3n)(m+2n) D.(2m+3n)(m+2n)8.计算t2一(t+1)(t-5)的结果为 ( ) A.4t-5 B.一4t一5 C.一4t+5 D.4t+59.若(x-2)(x+3) =2x+px+q,贝p、q的值是 ( ) A.p=5,q=6 B.p=l,q=-6 C.p=1,q=6 D.p=5,q=一610.计算.(1)(12x+3)(22x一4x+1); (2)(3x3一2x+1))2-x)(3)3(x一2)(x+1)一2(x一5)(x-3); (4)x(2x一4)一(x+3)( 2x一3x+2) .11.先化简,再求值.(1)3(x+5)(x一3) -5(x一2)(x+3),其中32x :(2)(3x-2)(x-3)一2(x+6)(x-5)+3(2x-7x+13),其中132x .12.计算下图中阴影部分的面积.13.把一个长方形的长增加2 cm,宽减少l cm,它的面积不变;把它的长减少3 cm,宽增加4 cm,面积也不变,求这个长方形原来的面积.14.已知:如图,现有a×a、b×b的正方形纸片和a×b的矩形纸片各若干块,试选用这些纸片(每种纸片至少用一次)在下面的虚线方框中拼成一个矩形(每两个纸片之间既不重叠,也无空隙,拼出的图中必须保留拼图的痕迹),使拼出的矩形面积为2a2+5a b+2b2,并标出此矩形的长和宽.15.你能求(x 一1)(99x +98x +97x +…+x+1)的值吗遇到这样的问题,我们可以先思考一下,从简单的情形人手,分别计算下列各式的值. (1)(x -1)(x+1) =_____________; (2)(x —1)( 2x +x+1) =_____________; (3)(x -1)(3x + 2x +x+1) =____________; …由此我们可以得到:(x 一1)( 99x +98x +97x +…+x+1) =___________, 请你利用上面的结论,完成下列两题的计算: (4)992+982+972+…+2+1; (5)()()()504948222-+-+-+…+(一2)+1.第8课时 乘法公式(一)1.计算:(1)(1--2y)(1+2y)=___________; (2)(2x+3)(3—2x)=____________. 2.计算:(1)(一2y 一3x)(3x 一2y)=__________; (2)(一2y 2-3x)(3x 一2y 2)=_________.3.计算:(1)( a2b —c 3)(a2b+c 3)=_________; (2)(-3a b+c)(3a b+c)=___________.4.计算:(1)(2x+1)(2x 一1)(4x 2+1)=__________;(2)2111242x x x ⎛⎫⎛⎫⎛⎫-++ ⎪⎪⎪⎝⎭⎝⎭⎝⎭=_______________. 5.计算:(1)(x+5) 2一(x 一5) 2=_____________;(2)(m+t)(m 一t)一(3m+2t)(3m--2t)=____________. 6.利用平方差公式计算.(1)1.02 ×0.98=___________; (2)12151433⨯=______________. 7.下列运算中,正确的是 ( ) A .(a 一2b)( a -2b)= a2-4b 2B .(-a +2b)( a 一2b)= -a2一2b 2C .(a +2b)( a 一2b)= -a 2-2b 2 D .(一a 一2b)(一a +2b)= a2-4b 28.在下列各式中,运算结果为36y 2+49x 2的是 ( ) A .(一6y+7x)(一6y 一7x) B .(一6y+7x)(6y 一7x) C .(7x 一4y)(7x+9y) D .(一6y 一7x)(6y 一7x)9.在①(一3x -y)(3x+y);②(一3x —y)(3x -y);③(一3x+y)(3x 一y);④(一3x+y) (3x+y)这四个式子中,能利用平方差公式计算的是 ( ) A .①② B .②③ C .③④ D .②④10.利用平方差公式计算(x 一1)(x+1)(x 2+1),正确的结果是 ( ) A .x 4-1 B .x 4+1 C .(x 一1) 4D .(x+1) 411.利用平方差公式计算.(1)59.8×60.2; (2)99×101×10 001. 12.计算.(1)x 2(x -2y)(x+2y)一(x 2+y)(x 2-y); (2)( a +1)( a 一1)( a 2+1)( a4+1)(8a +1).13.先化简,再求值.(1)2(3a +1)(1--3a )+(a -2)(2+a ),其中a =2;(2)(2x -y)(y+2x)一(2y+x)(2y -),其中x=1,y=2.14.利用平方差公式计算.(1)1002一992+982-972+962-952+…+22一12;(2)222111111234⎛⎫⎛⎫⎛⎫--- ⎪⎪⎪⎝⎭⎝⎭⎝⎭…22111199100⎛⎫⎛⎫--⎪⎪⎝⎭⎝⎭.15.计算图中阴影部分的面积,其中R=7.22 cm ,r=1.39 cm .(π取3.14,结果保留整塑)16.已知962-1可以被在60至70之间的两个整数整除,求这两个整数.乘法公式(1)一、基础训练1.下列运算中,正确的是( )A.(a+3)(a-3)=a2-3 B.(3b+2)(3b-2)=3b2-4 C.(3m-2n)(-2n-3m)=4n2-9m2 D.(x+2)(x-3)=x2-6 2.在下列多项式的乘法中,可以用平方差公式计算的是()A.(x+1)(1+x) B.(12a+b)(b-12a)C.(-a+b)(a-b) D.(x2-y)(x+y2)3.对于任意的正整数n,能整除代数式(3n+1)(3n-1)-(3-n)(3+n)的整数是() A.3 B.6 C.10 D.94.若(x-5)2=x2+kx+25,则k=()A.5 B.-5 C.10 D.-105.×=________; 6.a2+b2=(a+b)2+______=(a-b)2+________.7.(x-y+z)(x+y+z)=________; 8.(a+b+c)2=_______.9.(12x+3)2-(12x-3)2=________.10.(1)(2a-3b)(2a+3b);(2)(-p2+q)(-p2-q);(3)(x-2y)2;(4)(-2x-12y)2.11.(1)(2a-b)(2a+b)(4a2+b2);(2)(x+y-z)(x-y+z)-(x+y+z)(x-y-z).12.有一块边长为m的正方形空地,想在中间位置修一条“十”字型小路,•小路的宽为n,试求剩余的空地面积;用两种方法表示出来,比较这两种表示方法,•验证了什么公式二、能力训练13.如果x2+4x+k2恰好是另一个整式的平方,那么常数k的值为()A.4 B.2 C.-2 D.±214.已知a+1a=3,则a2+21a,则a+的值是()A.1 B.7 C.9 D.1115.若a-b=2,a-c=1,则(2a-b-c)2+(c-a)2的值为()A.10 B.9 C.2 D.116.│5x-2y│·│2y-5x│的结果是()A.25x2-4y2 B.25x2-20xy+4y2 C.25x2+20xy+4y2 D.-25x2+20xy-4y217.若a2+2a=1,则(a+1)2=_________.三、综合训练18.(1)已知a+b=3,ab=2,求a2+b2;(2)若已知a+b=10,a2+b2=4,ab的值呢19.解不等式(3x-4)2>(-4+3x)(3x+4).20.观察下列各式的规律.12+(1×2)2+22=(1×2+1)2;22+(2×3)2+32=(2×3+1)2;32+(3×4)2+42=(3×4+1)2;…(1)写出第2007行的式子;(2)写出第n行的式子,并说明你的结论是正确的.乘法公式(2)1.计算:(1)(2x2+13)(2x2-13);(2)(3a+b)(b-3a);(3)(-2x-3y)(2x-3y).2.判断下列各式能否用平方差公式计算,若能,请把结果计算出来.(1)(2x-13y)(-13x-2y);(2)(-2m+3n)(2n+3m);(3)(-3m+2)(3m-2);(4)(13a-b)(-b-13a).3.判断:(1)(b-4a)2=b2-16a2.()(2)(12a+b)2=14a2+ab+b2.()(3)(4m-n)2=16m2-4mn+n2.()(4)(-a-b)2=a2-2ab+b2.()4.计算:(1)(2a-3)2;(2)(-2a-13)2.5.运用乘法公式计算:(1)1997×2003;(2);(3)(9923)2;(4)1523×1613.6.如图,老张家有一块L形菜地,要把L形菜地按图那样分成面积相等的梯形,种上不同的蔬菜,这两个梯形的上底都是a米,下底都是b米,高都是(b-a)米,请你算一下,这块菜地面积共有多少当a=10,b=30时,面积是多少7.计算(a+b-c)2. 8.计算(a+4b-3c)2.9.计算(3x+y-2)2. 10.计算(x+y+z)(x-y-z).11.计算(a+4b-3c)(a-4b-3c). 12.计算(3x+y-2)(3x-y+2).13.已知:a+b=9,a2+b2=21,求ab. 14.已知a+1a=10,求a2+21a的值.15.若已知a-1a=3,且a>1a,求a2+21a的值.因式分解(1)一、基础训练1.若多项式-6ab+18abx+24aby的一个因式是-6ab,那么其余的因式是() A.-1-3x+4y B.1+3x-4y C.-1-3x-4y D.1-3x-4y2.多项式-6ab 2+18a 2b 2-12a 3b 2c 的公因式是( ) A .-6ab 2c B .-ab 2C .-6ab 2D .-6a 3b 2c 3.下列用提公因式法分解因式正确的是( )A .12abc-9a 2b 2=3abc (4-3ab ) B .3x 2y-3xy+6y=3y (x 2-x+2y ) C .-a 2+ab-ac=-a (a-b+c ) D .x 2y+5xy-y=y (x 2+5x ) 4.下列等式从左到右的变形是因式分解的是( )A .-6a 3b 2=2a 2b ·(-3ab 2) B .9a 2-4b 2=(3a+2b )(3a-2b ) C .ma-mb+c=m (a-b )+c D .(a+b )2=a 2+2ab+b 25.下列各式从左到右的变形错误的是( ) A .(y-x )2=(x-y )2B .-a-b=-(a+b )C .(m-n )3=-(n-m )3D .-m+n=-(m+n )6.若多项式x 2-5x+m 可分解为(x-3)(x-2),则m 的值为( ) A .-14 B .-6 C .6 D .47.(1)分解因式:x 3-4x=_______;(2)因式分解:ax 2y+axy 2=________. 8.因式分解:(1)3x 2-6xy+x ; (2)-25x+x 3;(3)9x 2(a-b )+4y 2(b-a ); (4)(x-2)(x-4)+1. 二、能力训练9.计算54×99+45×99+99=________.10.若a 与b 都是有理数,且满足a 2+b 2+5=4a-2b ,则(a+b )2006=_______.11.若x 2-x+k 是一个多项式的平方,则k 的值为( )A .14B .-14C .12D .-1212.若m 2+2mn+2n 2-6n+9=0,求2m n的值.13.利用整式的乘法容易知道(m+n )(a+b )=ma+mb+na+nb ,现在的问题是: 如何将多项式ma+mb+na+nb 因式分解呢用你发现的规律将m 3-m 2n+mn 2-n 3因式分解.14.由一个边长为a的小正方形和两个长为a,宽为b的小矩形拼成如图的矩形ABCD,则整个图形可表达出一些有关多项式分解因式的等式,请你写出其中任意三个等式.15.说明817-299-913能被15整除.因式分解(2)1.3a4b2与-12a3b5的公因式是_________.2.把下列多项式进行因式分解(1)9x2-6xy+3x;(2)-10x2y-5xy2+15xy;(3)a(m-n)-b(n-m).3.因式分解:(1)16-125m2;(2)(a+b)2-1;(3)a2-6a+9;(4)12x2+2xy+2y2.4.下列由左边到右边的变形,属于因式分解的是()A.(x+2)(x-2)=x2-4 B.x2-2x+1=x(x-2)+1C.a2-b2=(a+b)(a-b) D.ma+mb+na+nb=m(a+b)+n(a+b)5.因式分解:(1)3mx2+6mxy+3my2;(2)x4-18x2y2+81y4;(3)a4-16;(4)4m2-3n(4m-3n).6.因式分解:(1)(x+y)2-14(x+y)+49;(2)x(x-y)-y(y-x);(3)4m2-3n(4m-3n).7.用另一种方法解案例1中第(2)题.(1)4a2-b2+6a-3b;(2)x2-y2-z2-2yz.9.已知:a-b=3,b+c=-5,求代数式ac-bc+a2-ab的值.第12课时因式分解1.(1)多项式8x3y2一18xy2z的公因式是_____________;(2)多项式2x2y+6xy-10y的公因式是_____________.2.(1)多项式4x3-12x2-18x的公因式是2x,则另一个因式是______________;(2)多项式-7a b-14a bx+49a by的公因式是-7a b,则另一个因式是_____________.(1) a(2x-y)一b(y一2x)=_____________:(2)3((a一b)2一4(b一a)=_____________.4.分解因式.(1)5x(a+b一c) -l0y(a+b一c)=_____________;(2)5m2 (a一b)一l0m(a-b)2=_____________.5.分解因式.(1)x4-x2=____________________:(2)b2 (a一4)+(4一a)=_________________.6.分解因式.(1)一12x2+xy一12y2=_________________;(2)2m3一28m2n2+98mn4=__________________.7.下列等式从左到右的变形属于因式分解的是 ( )A.(x+1)(x-1)=x2一1 B.(2x)2一y2=(2x+y)(2x—y)C.a x+a y—a=a (x+y)一a D.5a2y-10a y+20y=5y(a2—2a)+20y 8.把多项式9a2b2-18a b2+45a2b分解因式时,公因式是 ( )A.9a2b B.45a2b2 C .9a b D.18a b29.下列各式中,分解因式正确的是 ( )A.6(x一2)+x(2一x)=(x一2)(6+x) B.x3+2x2+x=x(x2+2x) C.a (a一b) 2+a b(a一b)= a2 (a-b) D.3x2+6x=3x(x+6) 10.下列各式中,分解结果为2a (x-3) 2的是 ( ) A.2a x2-6x+9 B.2a x2-18aC.2a x2+12a x+18a D.2a x2—12a x+18a11.下列多项式①10a m一15a;②4xm2一9x;③4a m2一12a m+9a;④一4m2—9中,含有因式2m-3的有 ( )A.1个 B.2个 C.3个 D.4个(1)16a 2b -25bc 2; (2)( a -b) 4一(b -a )2:(3)()()2293xy x y --+; (4)()()()322x y x y x y -+--13.分解因式(1)-a 2-4a b -4b 2; (2)4a2x 2-8a2x ;(3)3a (b 2+9)2-108a b 2; (4)9a b 2(x -y)+6a 2b(x -y) -a 3(y -x) .14.(1)已知m+n=3,mn=23,求m 3n 一m 2n 2+mn 3的值;(2)已知a (a 一1)一(a 2-b)=3,求a b 一12(a 2+b 2)的值.15.试说明四个连续自然数的积加上1是一个完全平方数.16.有两个孩子的年龄分别为x 、y ,且满足x 2+xy=99,你能求出这两个孩子的年龄吗因式分解 姓名1.下列因式分解中,正确的是( )(A) 1- 14 x 2= 14 (x + 2) (x- 2) (B)4x –2 x 2 – 2 = - 2(x- 1)2(C) ( x- y )3–(y- x) = (x – y) (x – y + 1) ( x –y – 1) (D) x 2–y 2– x + y = ( x + y) (x – y – 1)(3 ) 1x2–y2 =1( x + y) (x – y ),(4 )x2 +1x2=-( x -1x)2从左到是因式分解的个数为()(A) 1 个 (B) 2 个 (C) 3 个 (D) 4个3.若x2+mx+25 是一个完全平方式,则m的值是()(A)20 (B) 10 (C) ± 20 (D) ±104.若x2+mx+n能分解成( x+2 ) (x – 5),则m= ,n= ; 5.若二次三项式2x2+x+5m在实数范围内能因式分解,则m= ; 6.若x2+kx-6有一个因式是(x-2),则k的值是 ;7.把下列因式因式分解:(1)a3-a2-2a (2)4m2-9n2-4m+1(3)3a2+bc-3ac-ab (4)9-x2+2xy-y28.在实数范围内因式分解:(1)2x2-3x-1 (2)-2x2+5xy+2y29.分解下列因式:(1).10a(x-y)2-5b(y-x) (2).a n+1-4a n+4a n-1 (3).x3(2x-y)-2x+y (4).x(6x-1)-1(5).2ax-10ay+5by+6x (6).1-a2-ab-14b2*(7) 3X2-7X+2 (8).(x2+x)(x2+x-3)+2 (9).x5y-9xy5 (10).-4x2+3xy+2y2 (11).4a-a5 (12).2x2-4x+1(13).4y 2+4y -510.多项式x 2-y 2, x 2-2xy +y 2, x 3-y 3的公因式是 。
